هيكل بيانات B- شجرة

مرحبا بالجميع! لقد أطلقنا مجموعة جديدة للدورة التدريبية "خوارزميات للمطورين" ، واليوم نريد أن نشارك ترجمة مثيرة للاهتمام أعدت لطلاب هذه الدورة.



في أشجار البحث ، مثل شجرة البحث الثنائية ، وشجرة AVL ، والشجرة الحمراء السوداء ، إلخ. تحتوي كل عقدة على قيمة واحدة فقط (مفتاح) وحد أقصى من نسلين. ومع ذلك ، هناك نوع خاص من شجرة البحث تسمى شجرة B (وضوحا شجرة ثنائية). فيه ، تحتوي العقدة على أكثر من قيمة (مفتاح) وأكثر من اثنين من نسل. تم تطوير B-tree في عام 1972 بواسطة Bayer و McCrate وكان يطلق عليها شجرة البحث Height Balanced m-way Search Tree . تلقى اسمها الحديث B- شجرة في وقت لاحق.

يمكن تعريف شجرة B على النحو التالي:
شجرة B هي شجرة بحث متوازنة تحتوي فيها كل عقدة على العديد من المفاتيح ولديها أكثر من طفلين.

هنا ، يعتمد عدد المفاتيح في العقدة وعدد أحفادها على ترتيب شجرة B. كل شجرة ب لديها أمر.

تحتوي B-tree of order m على الخصائص التالية:

الخاصية 1: عمق جميع الأوراق هو نفسه.
الخاصية 2: يجب أن تحتوي جميع العقد باستثناء الجذر على الأقل (m / 2) - مفاتيح واحدة وحد أقصى من مفاتيح m-1 .
الخاصية 3: يجب أن يكون لكل العقد بدون أوراق ، باستثناء الجذر (أي جميع العقد الداخلية) ، أحفاد m / 2 على الأقل.
الخاصية 4: إذا كان الجذر عبارة عن عقدة خالية من الأوراق ، فيجب أن يكون له على الأقل ذرين.
الخاصية 5: يجب أن تحتوي عقدة بدون أوراق مع مفاتيح n-1 على n أطفال.
الخاصية 6: يجب ترتيب كافة المفاتيح في العقدة بترتيب تصاعدي لقيمها.

على سبيل المثال ، تحتوي B-tree ذات الترتيب 4 على 3 قيم رئيسية بحد أقصى و 4 أطفال بحد أقصى لكل عقدة.


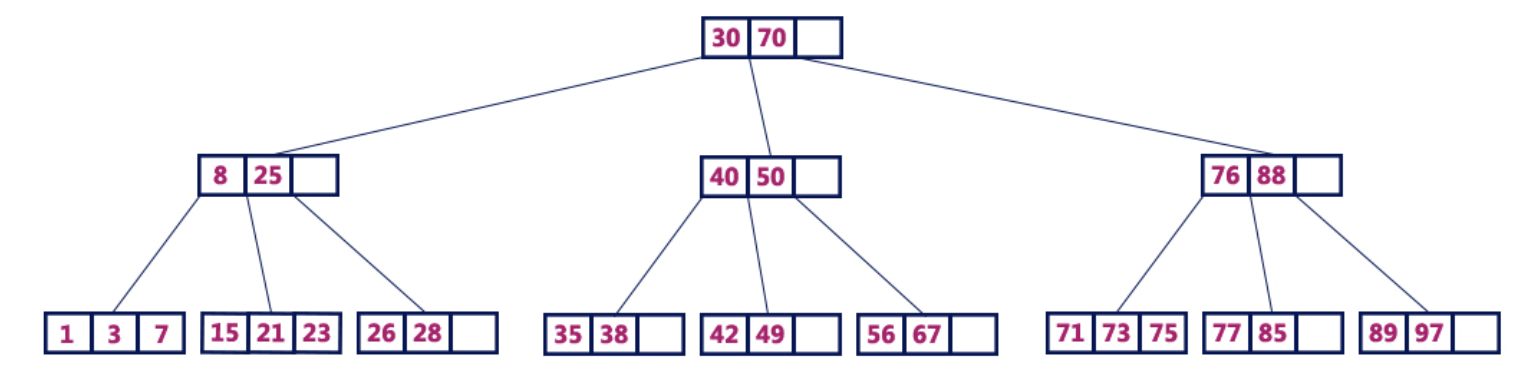B- شجرة 4 أوامر

عمليات B- شجرة

يمكن إجراء العمليات التالية على شجرة B:

1. بحث
2. إدراج
3. إزالة

البحث ب شجرة

تتشابه عمليات البحث B-tree مع عمليات البحث ثنائية الشجرة. في شجرة البحث الثنائية ، يبدأ البحث من الجذر وفي كل مرة يتم فيها اتخاذ قرار ثنائي الاتجاه (تابع الشجرة الفرعية اليسرى أو اليمنى). في شجرة B ، يبدأ البحث أيضًا من عقدة الجذر ، ولكن في كل خطوة يتم اتخاذ قرار من جانب n ، حيث n هو العدد الإجمالي لأحفاد العقدة المعنية. في شجرة B ، تعقيد البحث هو O (log n) . البحث كالتالي:

الخطوة 1: قراءة العنصر للبحث.
الخطوة 2: قارن العنصر الذي تم البحث عنه بقيمة المفتاح الأولى في عقدة الجذر الخاصة بالشجرة.
الخطوة 3: إذا كانت مطابقة ، طباعة: "العقدة وجدت!" واستكمال البحث.
الخطوة 4: إذا كانت غير متطابقة ، تحقق من أن قيمة العنصر أكثر أو أقل من قيمة المفتاح الحالي.
الخطوة 5: إذا كان العنصر الذي تبحث عنه أصغر ، فاستمر في البحث عن الشجرة الفرعية اليسرى.
الخطوة 6: إذا كان العنصر المطلوب أكبر ، فقم بمقارنة العنصر بالقيمة الرئيسية التالية في العقدة وكرر الخطوات 3 و 4 و 5 و 6 حتى يتم العثور على التطابق أو حتى تتم مقارنة العنصر الذي تم البحث عنه بآخر قيمة مفتاح في عقدة الورقة.
الخطوة 7: إذا لم تتطابق قيمة المفتاح الأخير في عقدة القائمة مع البحث ، فطبع "العنصر غير موجود!" واستكمال البحث.

عملية إدراج B- شجرة

في شجرة B ، لا يمكن إضافة عنصر جديد إلا إلى عقدة ورقة. هذا يعني أنه يتم دائمًا إضافة زوج جديد من مفاتيح القيمة فقط إلى عقدة الورقة. إدراج كالتالي:

الخطوة 1: تحقق مما إذا كانت الشجرة فارغة.
الخطوة 2: إذا كانت الشجرة فارغة ، فقم بإنشاء عقدة جديدة بقيمة مفتاح جديدة واعتبرها العقدة الجذرية.
الخطوة 3: إذا لم تكن الشجرة فارغة ، ابحث عن عقدة ورقة مناسبة تضاف إليها قيمة جديدة باستخدام منطق شجرة البحث الثنائية.
الخطوة 4: في حالة وجود خلية فارغة في عقدة الورقة الحالية ، أضف قيمة مفتاح جديدة إلى عقدة الورقة الحالية ، بعد الترتيب المتزايد لقيم المفاتيح داخل العقدة.
الخطوة 5: إذا كانت العقدة الحالية ممتلئة ولا تحتوي على خلايا حرة ، فقم بتقسيم عقدة الورقة عن طريق إرسال القيمة المتوسطة إلى العقدة الأصل. كرر الخطوة حتى تلتزم القيمة المراد إرسالها إلى العقدة.
الخطوة 6: إذا حدث الفصل مع جذر الشجرة ، يصبح المتوسط ​​جذر الشجرة الجديد ويزيد ارتفاع الشجرة بواحد.

مثال:

لنقم بإنشاء شجرة B من الترتيب 3 بإضافة أرقام من 1 إلى 10.

إدراج (1):
نظرًا لأن "1" هو العنصر الأول للشجرة ، يتم إدراجه في عقدة جديدة وتصبح هذه العقدة هي جذر الشجرة.



إدراج (2):
تتم إضافة العنصر 2 إلى عقدة أوراق موجودة. الآن لدينا عقدة واحدة فقط ، وبالتالي فهي كل من الجذر والورقة في نفس الوقت. تحتوي هذه الورقة على خلية فارغة. ثم يحصل "2" في هذه الخلية الفارغة.



إدراج (3):
تتم إضافة العنصر 3 إلى عقدة أوراق موجودة. الآن لدينا عقدة واحدة فقط ، وهي الجذر والورقة. لا تحتوي هذه الورقة على خلية فارغة. لذلك ، نفصل هذه العقدة عن طريق إرسال متوسط ​​القيمة (2) إلى العقدة الأصل. ومع ذلك ، لا تحتوي العقدة الحالية على عقدة أصل. لذلك ، تصبح القيمة المتوسطة العقدة الجذرية للشجرة.



إدراج (4):
العنصر "4" أكبر من عقدة الجذر مع القيمة "2" ، في حين أن عقدة الجذر ليست ورقة. لذلك ، نحن نتحرك على طول الشجرة اليمنى من "2". نأتي إلى عقدة الورقة ذات القيمة "3" ، التي تحتوي على خلية فارغة. وبالتالي ، يمكننا إدراج العنصر "4" في هذه الخلية الفارغة.



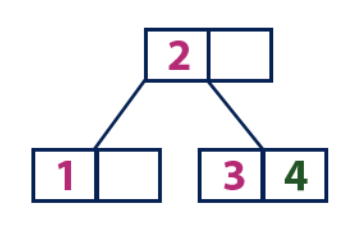إدراج (5):
العنصر "5" أكبر من عقدة الجذر مع القيمة "2" ، في حين أن عقدة الجذر ليست ورقة. لذلك ، نحن نتحرك على طول الشجرة اليمنى من "2". نأتي إلى عقدة الورقة ونجد أنه ممتلئ بالفعل وليس به خلايا فارغة. ثم نقسم هذه العقدة عن طريق إرسال القيمة المتوسطة (4) إلى العقدة الأصلية (2). تحتوي العقدة الأصل على خلية فارغة لها ، لذلك تتم إضافة القيمة "4" إلى العقدة التي توجد فيها بالفعل قيمة "2" ، ويتم إضافة عنصر جديد "5" كصفحة جديدة.



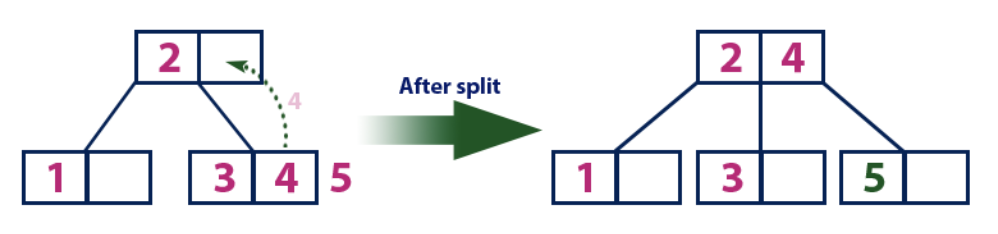إدراج (6):
العنصر "6" أكبر من عناصر الجذر "2" و "4" ، وهي ليست ورقة. نتحرك على طول الشجرة الصحيحة للعنصر "4". نصل إلى ورقة بقيمة "5" ، والتي تحتوي على خلية فارغة ، لذلك يتم وضع العنصر "6" فقط فيه.



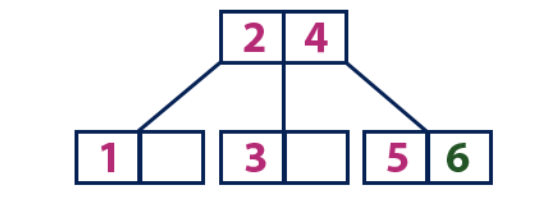إدراج (7):
العنصر "7" أكبر من عناصر الجذر "2" و "4" ، وهي ليست ورقة. نتحرك على طول الشجرة الصحيحة للعنصر "4". نصل إلى عقدة ورقة ونرى أنه ممتلئ. نقسم هذه العقدة عن طريق إرسال متوسط ​​قيمة "6" إلى العقدة الأصل مع العنصرين "2" و "4". ومع ذلك ، فإن العقدة الأصلية ممتلئة أيضًا ، لذلك نقسم العقدة بالعناصر "2" و "4" ، ونرسل القيمة "4" إلى العقدة الأصل. فقط هذه العقدة ليست هناك بعد. في هذه الحالة ، تصبح العقدة ذات العنصر "4" هي الجذر الجديد للشجرة.



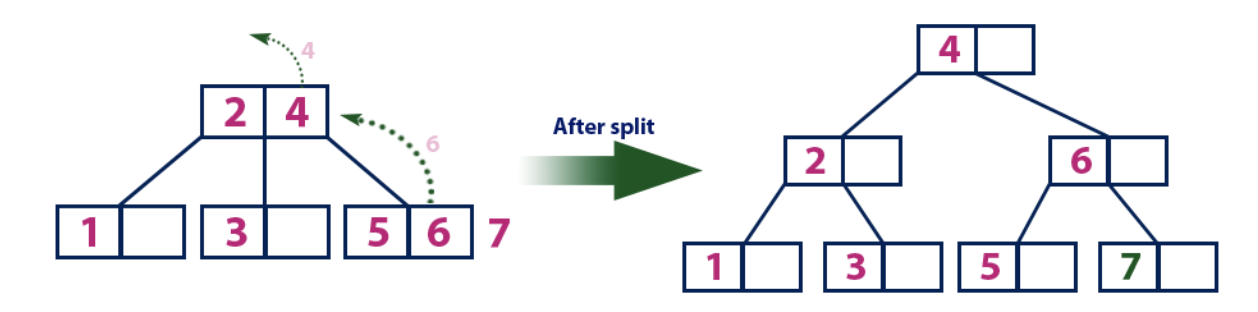إدراج (8):
العنصر 8 أكبر من عقدة الجذر بقيمة 4 ، وليست عقدة الجذر ورقة. نتحرك على طول الشجرة الفرعية الصحيحة من العنصر "4" ونأتي إلى العقدة بقيمة "6". "8" أكبر من "6" والعقدة مع العنصر "6" ليست ورقة ، لذلك نحن نتحرك على طول الشجرة الفرعية الصحيحة من "6". نصل إلى عقدة الورقة مع "7" ، التي تحتوي على خلية فارغة ، لذلك نضع "8" فيها.



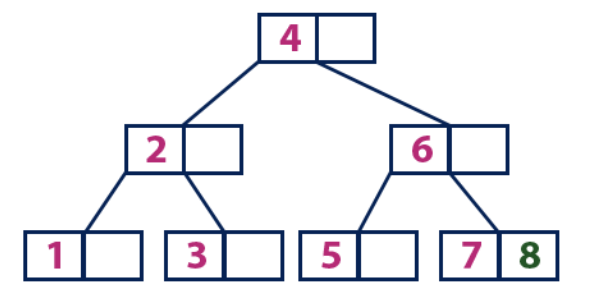إدراج (9):
العنصر 9 أكبر من عقدة الجذر بقيمة 4 ، والعقدة الجذر ليست ورقة. نتحرك على طول الشجرة الفرعية الصحيحة من العنصر "4" ونأتي إلى العقدة بقيمة "6". "9" أكبر من "6" والعقدة مع العنصر "6" ليست ورقة ، لذلك نحن نتحرك على طول الشجرة الفرعية الصحيحة من "6". نصل إلى عقدة ورقة مع القيم "7" و "8". إنه ممتلئ. نقسم هذه العقدة عن طريق إرسال متوسط ​​القيمة (8) إلى العقدة الأصل. تحتوي العقدة الأصل "6" على خلية فارغة ، لذلك نضع "8" فيها. في هذه الحالة ، يتم إضافة عنصر جديد "9" إلى قائمة العقدة.



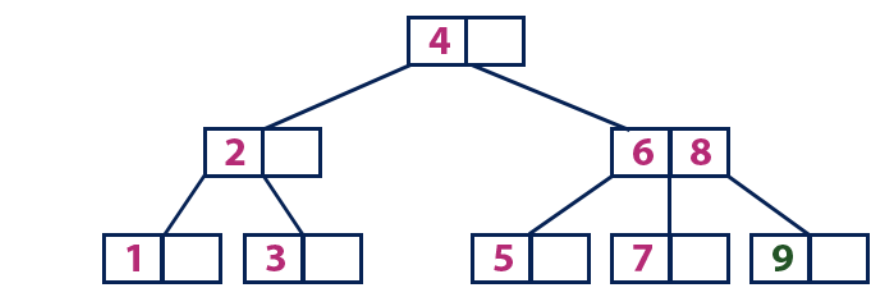
إدراج (10):
العنصر "10" أكبر من عقدة الجذر مع القيمة "4" ، في حين أن عقدة الجذر ليست ورقة. نتحرك على طول الشجرة الفرعية الصحيحة من العنصر "4" ونأتي إلى العقدة مع القيم "6" و "8". "10" أكبر من "6" و "8" والعقدة مع هذه العناصر ليست ورقة ، لذلك نحن نتحرك على طول الشجرة الفرعية الصحيحة من "8". نصل إلى العقدة الورقية بقيمة "9". لديه خلية فارغة ، لذلك نضع "10" هناك.



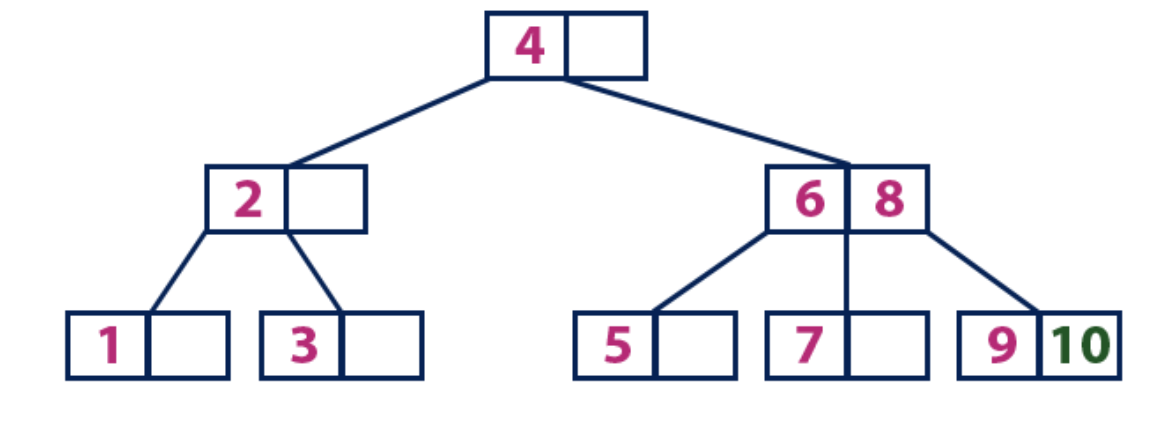
نقترح أن تفهم بشكل مستقل في الممارسة العملية كيف يتم ترتيب B-tree باستخدام هذا التصور .

نحن في انتظار الجميع في درس مجاني مفتوح ، والذي سيعقد في 12 يوليو. اراك قريبا!