من وظيفة رياضية سحرية - حل واحد للحكم عليهم جميعًا

قبل ثلاث سنوات ، أدهشت مارينا فيازوفسكايا من المعهد الفيدرالي السويسري للتكنولوجيا في لوزان علماء الرياضيات من خلال اكتشاف الطريقة الأكثر كثافة لتعبئة المجالات من نفس الحجم في فضاءات ثنائية و 24 (في الحالة الثانية ، بمساعدة أربعة مؤلفين مشاركين). والآن ، أثبتوا هم والمؤلفون المشاركون شيئًا أكثر إثارة للدهشة: فالتكوينات التي تحل مشكلة تعبئة المجالات الكثيفة بالأبعاد المذكورة أيضًا تحل أيضًا عددًا لا حصر له من المشكلات الأخرى المتعلقة بأفضل ترتيب للنقاط التي تحاول تجنب بعضها البعض.

يمكن للنقاط ، على سبيل المثال ، أن تدل على مجموعة لا حصر لها من الإلكترونات التي تتصدى وتحاول أن تستقر في التكوين بأقل طاقة. أو ، قد تشير هذه النقاط إلى مراكز البوليمرات الطويلة الملتوية الموجودة في المحلول ، في محاولة لترتيب نفسها حتى لا تتصادم مع الجيران. هناك العديد من الخيارات لمثل هذه المشاكل ، وليس من الواضح أن كل واحد سيكون لديه نفس الحل. يعتقد علماء الرياضيات أن هذا هو الحال في معظم الأبعاد.

لكن المساحات ، التي تتكون من 8 و 24 بُعدًا ، تحتوي على تكوين خاص ومتناسق جدًا للنقاط ، كما نعلم الآن ، يحل جميع هذه المشكلات المختلفة في وقت واحد. في لغة الرياضيات ، تسمى هاتان التوصيتان "الأمثل عالمياً".

يلخص هذا الاكتشاف الجديد على نطاق واسع العمل السابق لفيازوفسكايا وزملائها. قال توماس هالس ، عالم الرياضيات بجامعة بيتسبيرج ، الذي أثبت في عام 1998 أن الترتيب الهرمي المعروف للبرتقال هو الطريقة الأكثر كثافة لتعبئة الكرات في الفضاء ثلاثي الأبعاد.

ينضم ثمانية و 24 بعدًا واحدًا في قائمة صغيرة من الأبعاد التي تحتوي على التكوينات المثلى عالميًا. على المستوى الثنائي الأبعاد ، هناك مرشح لتحقيق الكمال العالمي - شبكة من المثلثات متساوية الأضلاع - ولكن لا يوجد دليل. في العالم ثلاثي الأبعاد ، تسود حديقة حيوانات كاملة: تكوينات مختلفة من النقاط تظهر نتائج مختلفة في ظروف مختلفة ، وبالنسبة لبعض المشاكل لا يوجد لدى علماء الرياضيات حتى تخمينات مقبولة حول أفضل التكوين.

وقال ريتشارد شوارتز ، عالم الرياضيات في جامعة براون في بروفيدنس: "غيّر القياس ، أو غيّر المهمة قليلاً ، وأصبح الوضع غير مفهوم". "لا أعرف لماذا يتم ترتيب الكون الرياضي بهذا الشكل".

إن إثبات أن الأمثلية العالمية أصعب بكثير من حل مشكلة تعبئة الكرات. على وجه الخصوص ، لأن الأمثلية العالمية تتضمن عددًا لا حصر له من المهام المختلفة في آن واحد ، ولكن أيضًا لأن هذه المهام أكثر تعقيدًا في حد ذاتها. في تعبئة الكرات ، لا يهتم كل كرة إلا بأقرب جيرانه ، ولكن في مشكلة مثل توزيع الإلكترونات ، يتفاعل كل من الإلكترونات مع كل الآخرين ، بغض النظر عن المسافة بينهم. "حتى في ضوء عملي المبكر ، لم أكن أتوقع أن يكون هذا الدليل الأمثل عالمياً" ، قال هالس.

قالت سيلفيا سيرفاتي ، عالمة رياضيات بجامعة نيويورك: "إنه أمر مثير للإعجاب للغاية". "هذا الشيء على قدم المساواة مع اختراقات رياضية كبرى في القرن التاسع عشر."

شهادة السحر

قد يبدو من الغريب أن الأبعاد 8 و 24 يجب أن تتصرف بشكل مختلف عن ، على سبيل المثال ، الأبعاد 7 أو 18 أو 25. لكن علماء الرياضيات عرفوا منذ زمن طويل أن التعبئة الكثيفة للكائنات في الفضاء تعمل بشكل مختلف في أبعاد مختلفة. على سبيل المثال ، ضع في اعتبارك كرة متعددة الأبعاد ، تم تعريفها ببساطة على أنها مجموعة من النقاط تقع على مسافة ثابتة من المركز. إذا قارنا حجم الكرة مع حجم أصغر مكعب يصفه ، فكلما زاد البعد ، كان المكعب أصغر حجمًا في الكرة. إذا كنت تريد إرسال كرة قدم ثلاثية الأبعاد في أصغر صندوق ممكن ، فستشغل الكرة أقل من 2٪ من حجم الصندوق - وكل شيء آخر سيكون مساحة فارغة.

في كل بُعد أكبر من ثلاثة أبعاد ، من الممكن إنشاء تكوين مشابه لهرم البرتقال ، ومع الأبعاد المتزايدة ، تنمو الفجوات بين المجالات. بعد أن وصلنا إلى البعد الثامن ، واجهنا فجأة حقيقة أنه في هذه المساحات توجد مساحة كافية للضغط على المجالات هناك. والنتيجة هي تكوين متماثل للغاية يسمى شبكة E ₈ . في البعد الرابع والعشرين ، تنشأ شبكة Lich بطريقة مماثلة ، عندما يمكن حشر كرات إضافية في الفجوات ، مما يخلق بناءًا مشهورًا آخر للتعبئة في المجالات.

لأسباب لا يفهمها علماء الرياضيات تمامًا ، تظهر هاتان المشابعتان فجأة إما في أحد مجالات الرياضيات أو في مجال آخر ، من نظرية الأعداد والتحليل الرياضي إلى الفيزياء الرياضية. قال هنري كوهن من معهد مايكروسوفت لبحوث نيو إنغلاند في كامبريدج ، ماساتشوستس ، أحد مؤلفي العمل الخمسة: "لا أعرف أحد الأسباب وراء كل هذا".

على مدار أكثر من عشر سنوات ، كان لدى علماء الرياضيات أدلة رقمية مقنعة على أن الشبكة E ₈ وشبكة Lich هما الأمثل عالمياً في أبعادهما - لكن حتى وقت قريب لم يكن لديهم أي فكرة عن كيفية إثبات ذلك. ثم في عام 2016 ، اتخذ Vyazovskaya الخطوة الأولى نحو ذلك ، حيث أثبت أن هاتين المشابكتين هما أفضل الطرق لتعبئة الكرات.

وإذا كان دليل Hales للحالة ثلاثية الأبعاد يمتد على مئات الصفحات ويتطلب حسابات باهظة الثمن على الكمبيوتر ، فإن الدليل من Vyazovskaya لحالة E ₈ يناسب 23 صفحة. يرتبط جوهر حججها بتعريف الوظيفة "السحرية" (كما يسميها علماء الرياضيات الآن) ، والتي تعطي ما يطلق عليه هال "شهادة" لـ E ₈ للحصول على أفضل تعبئة للكرات - من الصعب الحصول على هذا الدليل ، ولكن بعد ظهوره ، يكون لديه إقناع فوري. على سبيل المثال ، إذا طلب منك شخص ما إذا كان هناك عدد حقيقي x بحيث يصبح كثير الحدود x ² - 6x + 9 سالبًا ، فيمكنك التفكير في الإجابة. ومع ذلك ، فإن إدراك أن كثير الحدود هذا يعادل (x - 3) ² ، ستفهم على الفور أن الإجابة "لا" ، لأن مربع العدد الحقيقي لا يمكن أن يكون سالبًا.

أثبتت طريقة البحث عن الوظيفة السحرية لـ Vyazovskaya أنها قوية - وتقريباً قوية للغاية. مهمة تعبئة الكرات لا تتعلق إلا بتفاعل النقاط القريبة ، ولكن يبدو أن نهج فيازوفسكايا يعمل لتفاعلات بعيدة المدى ، كما هو الحال مع الإلكترونات عن بعد.

عدم اليقين في أبعاد أعلى

لإظهار أن تكوين النقاط في الفضاء هو الأمثل عالمياً ، من الضروري أولاً تحديد هذه العالمية. لا يوجد أي تكوين نقطي مثالي لأي غرض: على سبيل المثال ، عندما تعمل قوة الجذب على النقاط ، فإن التكوين ذي الطاقة الأقل لا يمثل بعض الشبكات ، ولكنه كومة هائلة توجد فيها جميع النقاط في مكان واحد.

حصر فيازوفسكايا وكوهن وزملاؤهم نطاق دراستهم على عالمية القوى البغيضة. وبصورة أكثر تحديداً ، اعتبروا قوى رتابة ، أي تلك التي يصبح فيها التنافر أقوى عندما تقترب النقاط من بعضها البعض. تضم هذه العائلة الواسعة العديد من القوى المشتركة للعالم المادي. يتضمن ذلك قوانين القوة الخاصة بالكون - بما في ذلك قانون Coulomb للجزيئات المشحونة كهربائيًا ، و Gaussians ، وظائف على شكل جرس تصف سلوك الكيانات ذات الأجزاء التنافرية المستقلة ، مثل البوليمرات الطويلة. تقع مهمة تعبئة الكرات على الحافة الخارجية لهذا الكون: الشرط المتمثل في عدم تقاطع الكرات يتحول إلى تنافر قوي بشكل لا نهائي عندما تكون المسافة بين مركزها أقل من قطرها.

بالنسبة لأي من هذه القوى الرتيبة ، فإن السؤال الذي يطرح نفسه - ما سيكون التكوين مع أقل طاقة - "الحالة الأرضية" - لمجموعة لا حصر لها من الجزيئات؟ في عام 2006 ، طور " كون" و "كومار " طريقة للعثور على حدود طاقة أصغر للحالة الأرضية من خلال مقارنة وظيفة تصف الطاقة مع وظائف "مساعدة" أصغر بخصائص ملائمة للغاية. لقد وجدوا كمية لا حصر لها من الوظائف المساعدة لكل بعد ، لكنهم لم يعرفوا كيفية العثور على أفضل وظيفة مساعدة.


خمسة مؤلفين للعمل الجديد: هنري كوهن ، أبخيناف كومار ، مارينا فيازوفسكايا ، ستيفن ميلر ودانيلو رادتشينكو

في معظم القياسات ، لا تشبه القيود العددية التي اكتشفها Kohn و Kumar طاقة أفضل تكوين ممكن. ولكن في البعدين 8 و 24 ، اقتربت الحدود بشكل مذهل من الطاقة E ₈ وشبكة Lich لكل قوة طاردة قام عليها Kon و Kumar باختبار طريقتهما. كان من الطبيعي التفكير فيما إذا كانت هناك أي وظيفة مساعدة مثالية من شأنها أن تعطي حدودًا تتزامن تمامًا مع الطاقة E ₈ أو شعرية Lich ، لأي قوة طاردة. بالنسبة لمهمة تعبئة الكرات ، كان هذا بالضبط ما فعلته فيازوفسكايا قبل ثلاث سنوات: لقد اكتشفت وظيفة مساعدة "سحرية" مثالية ، تدرس فئة من الوظائف تسمى الوظائف المعيارية ، التي جعلتها خصائص التماثل الخاصة بها منذ قرون موضوعًا للدراسة.

عندما يتعلق الأمر بمشكلات أخرى تتعلق بالنقاط المثيرة للاشمئزاز ، على سبيل المثال ، مشكلة الإلكترونات ، فقد عرف الباحثون الخصائص التي ينبغي أن ترضيها أي وظيفة سحرية: في بعض النقاط ، يجب أن تأخذ قيمًا خاصة ، وينبغي أن يأخذ تحويل فورييه الذي يقيس الترددات الطبيعية للوظيفة ، القيم الخاصة في نقاط أخرى. ما لم يعرفوه هو ما إذا كانت هذه الوظيفة موجودة.

عادة ما يكون من السهل جدًا إنشاء وظيفة تقوم بما تحتاجه في نقاطك المفضلة ، لكن من الصعب جدًا التحكم في الوظيفة وصورة فورييه في نفس الوقت. قال كوهن: "عندما تبدأ في عمل شيء ما ، فإن الآخر يفعل شيئًا مختلفًا تمامًا عن رغباتك".

في الواقع ، هذا الصعب ليس أكثر من مبدأ متنكر من عدم اليقين في الفيزياء. مبدأ عدم اليقين في Heisenberg هو أنه يشير إلى أنه كلما زادت معرفتك بموقع الجسيمات ، كلما قلت معرفتك بزخمه ، والعكس بالعكس ، هي حالة خاصة لهذا المبدأ العام ، لأن موجة زخم الجسيم هي تحويل فورييه لموجة موقعه.

في حالة القوة البغيضة في البعدين 8 أو 24 ، طرح فيازوفسكايا فرضية جريئة: القيود التي أراد الفريق فرضها على وظيفته السحرية وصورة فورييه هي بالضبط على الحدود بين الممكن والمستحيل. لقد اشتبهت في أنه إذا أضفت أي قيود أخرى ، فلن يكون هناك مثل هذه الوظيفة ؛ إذا قمت بتقليل القيود ، فقد يكون هناك العديد من هذه الوظائف. اقترحت أنه في الحالة التي تهتم بالفريق ، يجب أن تكون هناك وظيفة مناسبة واحدة بالضبط.

وقال كوهن: "أعتقد أن هذه واحدة من ميزات مارينا الرائعة". "إنها ثاقبة للغاية ، وأيضا شجاع جدا."

في ذلك الوقت ، كان "كون" متشككًا - بدا أن حدقة فيازوفسكايا جيدة جدًا لدرجة يصعب تصديقها - لكن الفريق أثبت ذلك في النهاية. لم يظهروا فقط أنه لكل قوة تنافر هناك وظيفة سحرية واحدة بالضبط ، ولكنهم قدموا أيضًا وصفة لتصنيعها. كما هو الحال بالنسبة لمناطق التغليف ، فقد أعطى هذا التصميم فورًا شهادات تحسين لشبكتي E ₈ و Lich. قال شوارتز: "إنها نتيجة هائلة."

شبكة الثلاثي

بالإضافة إلى حل مشكلة التفاؤل العالمي ، يجيب دليل جديد على السؤال الملح الذي واجهه علماء الرياضيات منذ أن حل Vyazovskaya مشكلة التعبئة في المجالات قبل ثلاث سنوات: من أين جاءت وظيفتها السحرية؟ قال فيازوفسكايا: "أعتقد أن الكثيرين كانوا في حيرة". "لقد سألوا: ما الهدف من هذا؟"

في عمل جديد ، أوضحت فيازوفسكايا وزملاؤها أن الوظيفة السحرية لتعبئة الكرات هي الأولى في سلسلة من لبنات الأشكال المركبة التي يمكن استخدامها لإنشاء وظائف سحرية لكل قوة طاردة. قالت فيازوفسكايا: "لديها الآن العديد من الإخوة والأخوات".

لا يزال يبدو رائعا لكون أن الصورة عملت بشكل جيد. وقال "في الرياضيات ، يجب تحقيق بعض الأشياء من خلال المثابرة والقوة الغاشمة". "وهناك أوقات ، كما هي الآن ، كما لو أن الرياضيات تريد حدوث شيء ما".

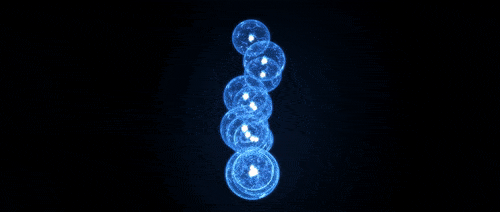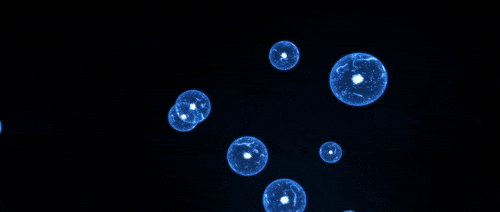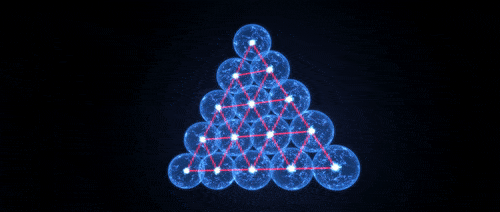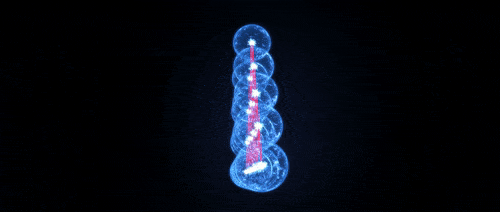
والسؤال الطبيعي التالي هو ما إذا كان يمكن تكييف هذه الأساليب لإثبات الأمثلية العالمية للمرشح الوحيد المتبقي: المشابك من مثلثات متساوية الأضلاع على متن طائرة ثنائية الأبعاد. يقول إدوارد ساف ، عالم الرياضيات في جامعة فاندربيلت في ناشفيل ، إنه بالنسبة إلى علماء الرياضيات ، فإن حقيقة عدم تمكن أي شخص من تقديم أدلة في مثل هذه الظروف البسيطة تعتبر "عارًا رهيبًا للمجتمع بأسره".

على عكس E ₈ وشبكة Leach ، تظهر شبكة ثلاثية الأبعاد ثلاثية الأبعاد في أماكن مختلفة في الطبيعة ، من هياكل الخلية إلى موقع مسارات التحويل في الموصلات الفائقة. يعني الفيزيائيون بالفعل أمثلية هذه الشبكة في مجموعة واسعة من السياقات القائمة على سلسلة من التجارب والمحاكاة. لكن ، يقول كوهن ، لا أحد لديه تفسير مفاهيمي لسبب أن الشبكة الثلاثية يجب أن تكون مثالية عالمياً - وهو ما نأمل أن يوفر دليلاً رياضياً.

Dimension 2 هو الوحيد ، باستثناء 8 و 24 ، حيث يعمل الحد الأدنى العددي لـ Kohn و Kumar بشكل جيد. هذا يشير بوضوح إلى أن وظيفة سحرية يجب أن توجد في بعدين. ومع ذلك ، بالكاد يمكن نقل طريقة الأمر لإنشاء وظائف سحرية إلى هذه المنطقة الجديدة: إنها تعتمد بشدة على حقيقة أن الأرقام التي تشير إلى المسافات بين النقاط في E ₈ وشبكة Lich تتصرف بشكل جيد ، ولا يحدث ذلك في بعدين. وقال كوهن: "يبدو أن هذا البعد يتجاوز القدرات البشرية حتى الآن".

حتى الآن ، يحتفل علماء الرياضيات برؤيتهم الجديدة المرتبطة بعوالم غريبة من الفراغات 8- و 24 الأبعاد. هذا ، كما قال شوارتز ، هو "واحد من أفضل الأشياء التي سأراها على الأرجح في حياتي."