👩🏿‍💼 💇🏻 😷 التوقف عن استخدام RSA 🎶 👎🏼 🔂

مرحبا ٪ اسم المستخدم ٪!

RSA هي أول خوارزمية تشفير غير متماثلة تستخدم على نطاق واسع والتي لا تزال شائعة في هذه الصناعة. انها بسيطة نسبيا للوهلة الأولى. يمكن حساب تشفير RSA وتوقيعه على قطعة من الورق ، والتي غالباً ما يقوم بها الطلاب في العمل المختبري.
ولكن هناك ببساطة عدد كبير من الفروق الدقيقة التي بدونها يمكن للطفل كسر تنفيذ RSA الخاص بك.

لسبب ما ، لا يزال الناس يعتقدون أن RSA خوارزمية جيدة. ولكن في الواقع ، فإن نطاق اللقطة في الساق عند تطبيق RSA ضخم للغاية. من الصعب التحقق من المعلمات الضعيفة ، إن لم تكن مستحيلة. ويشجع الأداء الضعيف للخوارزمية المطورين على استخدام طرق محفوفة بالمخاطر لتحسينها.

والأسوأ من ذلك ، أن هجمات الحشو أوراكل التي تم اختراعها منذ أكثر من 20 عامًا لا تزال صالحة حتى اليوم.
حتى لو كان من الممكن نظريًا تطبيق RSA بشكل صحيح ، فمن الناحية العملية يكاد يكون من المستحيل تحقيق مثل هذا "العمل الفذ". وقد أكدت هذه الثغرات الأمنية التي ظهرت باستمرار منذ عقود.

بضع كلمات عن خوارزمية RSA

إذا كنت تعرف كيفية عمل RSA ، فيمكنك تخطي هذا الجزء.

RSA هو نظام تشفير بالمفتاح العام له استخدامان.

الأول هو التشفير ، عندما تنشر أليس المفتاح العمومي الخاص بها ، وبوب ، مع العلم أنه ، يمكنه تشفير رسالة تستطيع أليس قراءتها فقط ، فك تشفيرها باستخدام مفتاحها الخاص.

والثاني هو توقيع رقمي ، مما يسمح لـ Alice بتوقيع الرسالة بمفتاحها الخاص حتى يتمكن الجميع من التحقق من هذا التوقيع باستخدام مفتاحها العام.

تختلف كلتا الخوارزميات في التفاصيل غير المهمة ، لذلك سوف نسميها ببساطة RSA.

لبدء العمل مع RSA ، تحتاج Alice إلى اختيار إعدادين أساسيين p و q ، اللذين يشكلان معاً مجموعة من الأرقام modulo N = pq . إذن ، أليس بحاجة إلى اختيار الأس المفتوح و الأس الأسري

e d = 1 m o d (p - 1) (q - 1)

$ed = 1 \ mod (p-1) (q-1)$ . في جوهرها ، يجب أن يكون e و d بسيطين.

بمجرد تحديد هذه الخيارات ، يمكن أن يرسل بوب رسالة إلى أليس ، الحوسبة

C = M^{e} (m o d N)

$C = M ^ e (mod \ N)$ . يمكن أليس فك تشفير الرسالة عن طريق الحوسبة

M = C^{d} (m o d N)

$M = C ^ d (mod \ N)$ .
التوقيع الرقمي هو عكس ذلك تماما. إذا أرادت Alice توقيع الرسالة ، فإنها تحسب التوقيع

S = M^{d} (m o d N)

$S = M ^ d (mod \ N)$ يمكن أن بوب التحقق من خلال التأكد من الرسالة

M = S^{e} (m o d N)

$M = S ^ e (mod \ N)$

هذا كل شيء ، هذه هي الفكرة الرئيسية. سنعود إلى أوراغ Padding لاحقًا ، ولكن الآن لنرى ما الذي يمكن عمله إذا تم تحديد معلمات RSA بشكل غير صحيح.

بداية النهاية

لكي تعمل RSA ، تحتاج إلى تحديد عدد غير قليل من المعلمات. لسوء الحظ ، فإن الطرق التي يبدو أنها بريئة من اختيارهم يمكن أن تضر بالأمن. دعنا نذهب من خلال كل منهم ونرى ما مفاجآت غير سارة تنتظرك.

رئيس الجيل

يستند أمان RSA إلى حقيقة أن وجود عدد كبير N ، وهو ناتج عن فترتين أساسيتين p و q ، يتحلل N إلى عوامل أولية دون معرفة p و q يصعب القيام به. المطورون مسؤولون عن اختيار الأعداد الأولية التي تشكل وحدة RSA. هذه العملية بطيئة للغاية مقارنةً بإنشاء المفاتيح لبروتوكولات التشفير الأخرى ، حيث يكفي فقط اختيار عدد قليل من وحدات البايت العشوائية. لذلك ، بدلاً من إنشاء رقم أولي عشوائي حقًا ، يحاول المطورون غالبًا إنشاء أرقام ذات شكل معين. انها دائما تقريبا ينتهي بشكل سيء. هناك العديد من الطرق لاختيار الأعداد الأولية بحيث يكون العوملة N بسيطًا. على سبيل المثال ، يجب أن تكون p و q فريدة على مستوى العالم. إذا تم إعادة استخدام p أو q في وحدات RSA الأخرى ، فيمكن حساب كلا العاملين بسهولة باستخدام خوارزمية GCD. تجعل مولدات الأرقام العشوائية السيئة هذا السيناريو أمرًا محتملًا ، وقد أظهرت الدراسات أن حوالي 1٪ من حركة مرور TLS في عام 2012 تعرضت لمثل هذا الهجوم.

علاوة على ذلك ، يجب اختيار p و q بشكل مستقل عن بعضهما البعض. إذا كانت p و q تشترك في حوالي نصف البتات الأكثر أهمية ، فيمكن حساب N باستخدام طريقة Fermat. في الواقع ، حتى اختيار خوارزمية اختبار البساطة يمكن أن يكون له آثار أمنية. ولعل أكثر الهجمات انتشارًا هي مشكلة ROCA في RSALib ، والتي أثرت على العديد من البطاقات الذكية ووحدات النظام الأساسي الموثوق بها وحتى مفاتيح Yubikey. هنا ، عند إنشاء المفاتيح ، يتم استخدام الأرقام الأولية فقط من نموذج معين لتسريع العمليات الحسابية. الأعداد الأولية المتولدة بهذه الطريقة تافهة لاكتشافها باستخدام أساليب صعبة في نظرية الأعداد. بمجرد التعرف على نظام ضعيف ، تسمح الخصائص الجبرية الخاصة بالأعداد الأولية للمهاجم باستخدام طريقة Coppersmith لتحليل N.

يجب أن يؤخذ في الاعتبار أنه في أي من هذه الحالات ، فإن توليد الأعداد الأولية بهذه الطريقة هو حقيقة واضحة تؤدي إلى فشل كامل للنظام. وذلك لأن الخواص النظرية للأعداد الأولية الضئيلة لها تأثير كبير على أمان RSA. إن توقع قيام مطور عادي بالانتقال إلى حقل الألغام الرياضي هذا يقوض بشكل خطير الأمن.

العارض السري د

نظرًا لأن استخدام مفتاح خاص كبير يؤثر سلبًا على فك التشفير ووقت التوقيع ، فإن للمطورين حافزًا لاختيار d صغير ، لا سيما في حالة الأجهزة ذات استهلاك الطاقة المنخفض ، مثل البطاقات الذكية. ومع ذلك ، يمكن للمهاجم استرداد المفتاح الخاص عندما يكون d أقل من الجذر من الدرجة الرابعة في N. بدلاً من ذلك ، يجب على المطورين اختيار قيمة كبيرة من d ، بحيث يمكن استخدام نظرية البقية الصينية لتسريع فك التشفير. ومع ذلك ، يزيد تعقيد هذا النهج من احتمال حدوث أخطاء بسيطة في التنفيذ يمكن أن تؤدي إلى استرداد المفتاح.

أنت تقول إنك عادةً أثناء تهيئة RSA ، تقوم أولاً بإنشاء وحدة نمطية ، وتستخدم حلاً ثابتًا ثابتًا ، ثم اختر سراً؟
نعم ، هذا يمنع الهجمات ذات الأس السري الصغير إذا كنت تستخدم دائمًا أحد الأسس المفتوحة الموصى بها e .
لسوء الحظ ، يفترض هذا أيضًا أن المطورين سيفعلون ذلك حقًا. في العالم الواقعي ، غالبًا ما يقوم مطورو البرامج بأشياء غريبة ، على سبيل المثال ، اختر أولاً d ثم فكر في الأمر

افتح العارضين e

كما هو الحال مع العارض السري ، يريد المطورون استخدام العارضين الصغار المفتوحين للحفظ عند التحقق من التوقيع والتوقيع. عادةً ما يتم استخدام أعداد فيرما الأولية في هذا السياق ، خاصةً e = 3 و 17 و 65537.

على الرغم من حقيقة أن cryptographers يوصون باستخدام 65537 ، فغالبًا ما يختار المطورون e = 3 ، مما يؤدي إلى العديد من نقاط الضعف في نظام تشفير RSA.

(هنا ، استخدم المطوروون e = 1 ، والذي لا يشفر فعلًا نصًا خاطئًا على الإطلاق.)

عندما يكون e = 3 أو بحجم مشابه ، يمكن أن يحدث خطأ كبير. غالبًا ما يتم دمج الأسس الصغيرة المفتوحة مع الأخطاء الشائعة الأخرى التي تسمح للمهاجم بفك تشفير نصوص معينة أو عامل N.

على سبيل المثال ، يتيح هجوم Franklin-Reuters للمهاجمين فك تشفير رسالتين متصلتين بمسافة ثابتة معروفة. بمعنى آخر ، لنفترض أن Alice ترسل Bob فقط "buy" أو "sell". سيتم ربط هذه الرسائل بقيمة معروفة وستسمح للمهاجم بتحديد أي منها يعني "شراء" وأي "بيع" دون فك تشفير الرسالة. قد تؤدي بعض الهجمات الصغيرة e إلى استعادة المفتاح.

إذا كان الأس المفتوح صغيراً (وليس فقط 3) ، يمكن للمهاجم الذي يعرف عدة أجزاء من المفتاح السري استرداد البتات المتبقية وكسر نظام التشفير. على الرغم من أنه يمكن إصلاح العديد من هجمات e = 3 RSA هذه بواسطة الحشو ، إلا أن المطورين الذين يقومون بتنفيذ RSA بأنفسهم غالبًا ما ينسون استخدامها.

توقيعات RSA عرضة أيضًا للعارضين العموميين الصغار. في عام 2006 ، اكتشف Bleichenbacher هجومًا يسمح للمهاجمين بتزوير توقيعات تعسفية في العديد من تطبيقات RSA ، بما في ذلك تلك المستخدمة في Firefox و Chrome. هذا يعني أنه يمكن التلاعب بأي شهادة TLS من تطبيق عرضة للإصابة بهجمات الفيروسات. يستغل هذا الهجوم حقيقة أن العديد من المكتبات تستخدم أس عامًا صغيرًا ولا تقوم بعملية تدقيق محاذاة بسيطة عند معالجة تواقيع RSA. هجوم Bleichenbacher على التوقيع بسيط جدًا بحيث يتم تضمينه في العديد من التمارين في دورات التشفير.

اختيار الخيارات مهمة صعبة

من العوامل الشائعة لجميع هذه الهجمات على المعلمات أن العدد الإجمالي للمتغيرات المحتملة للمعلمات أكبر بكثير من عدد المتغيرات الآمنة.

من المفترض أن المطورين أنفسهم سيديرون عملية الاختيار المعقدة هذه ، حيث يجب إنشاء كل شيء ما عدا الأس المفتوح أثناء التهيئة.
لا توجد طرق سهلة للتحقق من موثوقية المعلمات . بدلاً من ذلك ، يحتاج المطورون إلى قاعدة رياضية جدية ، لا ينبغي توقع وجودها من الموظفين العاديين. على الرغم من أن استخدام RSA مع المحاذاة يمكن أن يوفر لك إذا كان لديك معلمات خاطئة ، إلا أن الكثير منهم يفضلون عدم القيام بذلك.

حشوة أوراكل الهجمات

كما أوضحنا أعلاه ، ببساطة استخدام RSA من خارج منطقة الجزاء لا يعمل تمامًا. على سبيل المثال ، فإن مخطط RSA المبين في المقدمة سيخلق نصوص مشفرة متطابقة إذا تم تشفير نفس النص الشائع أكثر من مرة. هذه مشكلة لأنها ستتيح للمهاجم معرفة محتوى الرسالة من السياق ، دون أن يتمكن من فك تشفيرها. هذا هو السبب في أننا بحاجة إلى محاذاة الرسائل مع عدد قليل من وحدات البايت العشوائية. لسوء الحظ ، فإن مخطط المحاذاة الأكثر استخدامًا على نطاق واسع ، PKCS # 1 v1.5 ، غالبًا ما يكون عرضة للهجوم المزعوم أوراكل الحشو.

تم اكتشاف الهجوم الأولي على PKCS # 1 v1.5 في عام 1998 بواسطة Daniel Bleikhanbacher. على الرغم من أنها تجاوزت العشرين من العمر ، إلا أنها لا تزال اليوم ذات صلة بالعديد من الأنظمة. غالبًا ما تتضمن الإصدارات الحديثة من هذا الهجوم أوراكل إضافيًا ، وهو أكثر تعقيدًا بقليل من الذي وصفه في الأصل Bleikhanbacher ، على سبيل المثال ، وقت استجابة الخادم أو تنفيذ أي تخفيض لبروتوكول في TLS. أحد الأمثلة المروعة بشكل خاص هو هجوم ROBOT ، الذي كان فظيعًا للغاية حيث تمكن فريق من الباحثين من توقيع الرسائل باستخدام مفاتيح سرية على Facebook و PayPal. قد يجادل البعض بأن هذا ليس خطأ RSA حقًا - فالرياضيات الأساسية على ما يرام ؛ فقد أفسد الناس معيارًا مهمًا منذ عقود. والحقيقة هي أن لدينا بالفعل ، منذ عام 1998 ، خطة محاذاة قياسية مع أدلة السلامة الصارمة ، OAEP. ولكن تقريبا لا أحد يستخدمه. حتى عندما يحدث هذا ، فمن المعروف أن OAEP يصعب تنفيذه ، وغالبًا ما يكون عرضة لهجوم Manger ، وهو هجوم أوراكل آخر يمكن استخدامه لاستعادة النص الشائع.

المشكلة الأساسية هنا هي أن المحاذاة ضرورية عند استخدام RSA ، وهذا التعقيد الإضافي يفتح مجالًا كبيرًا للهجمات على نظام التشفير. يمكن أن يكون لشيء واحد من المعلومات ، "ما إذا كانت الرسالة محاذاة بشكل صحيح" ، مثل هذا التأثير الكبير على الأمن الذي يجعل تطوير المكتبات الآمنة أمرًا مستحيلًا من الناحية العملية. TLS 1.3 لم يعد يدعم RSA ، لذلك يمكننا توقع عدد أقل من هذه الهجمات في المستقبل.

ولكن بينما يواصل المطورون استخدام RSA في تطبيقاتهم الخاصة ، ستستمر هجمات Padding Oracle.

ما يجب القيام به

غالبًا ما يفضل الناس استخدام RSA لأنهم يجدون أنه أبسط من الناحية النظرية من بروتوكول DSA المعقد أو تشفير المنحنى الإهليلجي (ECC). ولكن على الرغم من أن RSA أكثر سهولة ، إلا أنها تفتقر حقًا إلى الحماية من الخداع.

بادئ ذي بدء ، هناك اعتقاد خاطئ شائع بأن الإهليلجيه خطير للغاية ، لأن اختيار منحنى سيء يمكن أن يبطل كل شيء. صحيح أن اختيار المنحنى له تأثير كبير على الأمن ، ولكن أحد فوائد استخدام ECC هو أنه يمكن إجراء اختيار المعلمة للجمهور. يقوم مصممو التشفير باختيار المعلمات لك ، لذلك يحتاج المطورون فقط إلى إنشاء بايتات عشوائية من البيانات لاستخدامها كمفاتيح. يمكن للمطورين بناء نظريا تطبيق ECC مع المعلمات الرهيبة ولن تكون قادرة على التحقق من أشياء مثل نقاط منحنى غير صحيحة ، لكنها عادة لا تفعل ذلك. التفسير المحتمل هو أن الرياضيات وراء ECC معقدة للغاية بحيث يشعر عدد قليل جدًا من الناس بالثقة الكافية لتنفيذها. بمعنى آخر ، هذا الخوف يجبر الناس على استخدام المكتبات التي أنشأها مشفرون يعرفون أشياءهم. RSA ، من ناحية أخرى ، بسيط للغاية بحيث يمكن تنفيذه (بشكل سيء) في غضون ساعة.

ثانياً ، لا تتطلب أي مطابقة رئيسية تستند إلى خوارزمية Diffie-Hellman أو مخطط التوقيع (بما في ذلك خيارات منحنى إهليلجي) المحاذاة ، وبالتالي فهي مقاومة تمامًا لهجمات Padding Oracle. هذا انتصار كبير ، بالنظر إلى أن RSA لديها سجل طويل للغاية من المحاولات لتجنب هذه الفئة من نقاط الضعف.

نوصي باستخدام Curve25519 لتبادل المفاتيح و ed25519 للتوقيعات الرقمية. يجب إجراء التشفير باستخدام بروتوكول ECIES ، الذي يجمع بين تبادل مفتاح ECC وخوارزمية تشفير متماثل. تم تصميم Curve25519 لمنع فئات الهجوم تمامًا التي قد تحدث لمنحنيات أخرى ، كما أنه سريع جدًا. علاوة على ذلك ، يتم تطبيقه في العديد من المكتبات ، على سبيل المثال libsodium ، المجهز بوثائق سهلة القراءة ومتوفر بمعظم اللغات.

التوقف عن استخدام RSA. على محمل الجد.

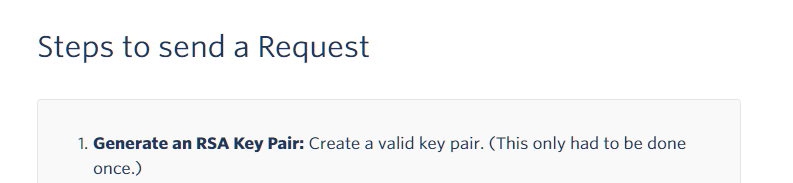
( لا يزال Twilio يستخدم مفاتيح RSA)

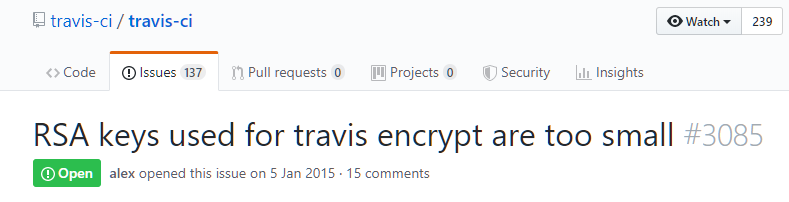
( لا يزال Travis CI يستخدم مفاتيح 1024 بت ولا يسمح باستبدالها)

كان RSA علامة فارقة مهمة في تطوير الاتصالات الآمنة ، لكن العقدين الماضيين من أبحاث التشفير جعلتهما قديمين. تم توحيد الخوارزميات على المنحنيات الإهليلجية لكل من التبادلات الرئيسية والتوقيعات الرقمية في عام 2005 وتم دمجها منذ ذلك الحين في المكتبات البديهية ومقاومة إساءة الاستخدام ، مثل libsodium. تشير حقيقة أنه لا يزال يتم استخدام RSA على نطاق واسع اليوم على حد سواء خطأ من جانب cryptographers بسبب وصف غير مناسب للمخاطر الكامنة في RSA والمطورين الذين يبالغون في تقدير قدرتهم على نشرها بنجاح. يجب أن يبدأ مجتمع الأمان في التفكير في الأمر كمشكلة قطيع - على الرغم من أن البعض منا قد يكون قادراً على التنقل في عملية بالغة الخطورة لإعداد أو تطبيق RSA ، توضح الاستثناءات للمطورين أن RSA لا تزال ذات صلة من بعض النواحي. على الرغم من العديد من التحذيرات والتحذيرات على StackExchange و GitHub README ، فإن قلة قليلة من الناس يعتقدون أنهم هم الذين سيدمرون RSA ، وبالتالي يواصلون العمل بتهور. في النهاية ، سوف يدفع المستخدمون مقابل ذلك. لهذا السبب يجب أن نتفق جميعًا على أن استخدام RSA في عام 2019 أمر غير مقبول تمامًا. لا استثناءات.

المقالة الأصلية باللغة الإنجليزية.

VirgilSecurity، Inc. تطوير SDK سهل الاستخدام ومطور لخدمات حماية البيانات. نحن نسمح للمطورين باستخدام الخوارزميات الحالية مع الحد الأدنى من المخاطر الأمنية.

سكرتير خاص أوصي بأن تقرأ أيضًا عن تضمين مستتر في المفتاح العام RSA.

التوقف عن استخدام RSA