تخيل أنك تحتاج إلى إنشاء رقم عشوائي موزع بشكل موحد من 1 إلى 10. وهذا هو ، عدد صحيح من 1 إلى 10 ضمناً ، مع احتمال متساو (10٪) لكل حدوث. ولكن ، على سبيل المثال ، بدون الوصول إلى العملات المعدنية أو أجهزة الكمبيوتر أو المواد المشعة أو غيرها من المصادر المماثلة للأرقام العشوائية (الزائفة). لديك فقط غرفة مع الناس.

لنفترض أن هناك ما يزيد قليلاً عن 8500 طالب في هذه الغرفة.

أبسط شيء هو سؤال شخص ما: "مهلاً ، اختر رقمًا عشوائيًا من واحد إلى عشرة!". الرجل يرد: "سبعة!". ! ممتاز الآن لديك رقم. ومع ذلك ، تبدأ في التساؤل عما إذا كان يتم توزيعها بالتساوي.

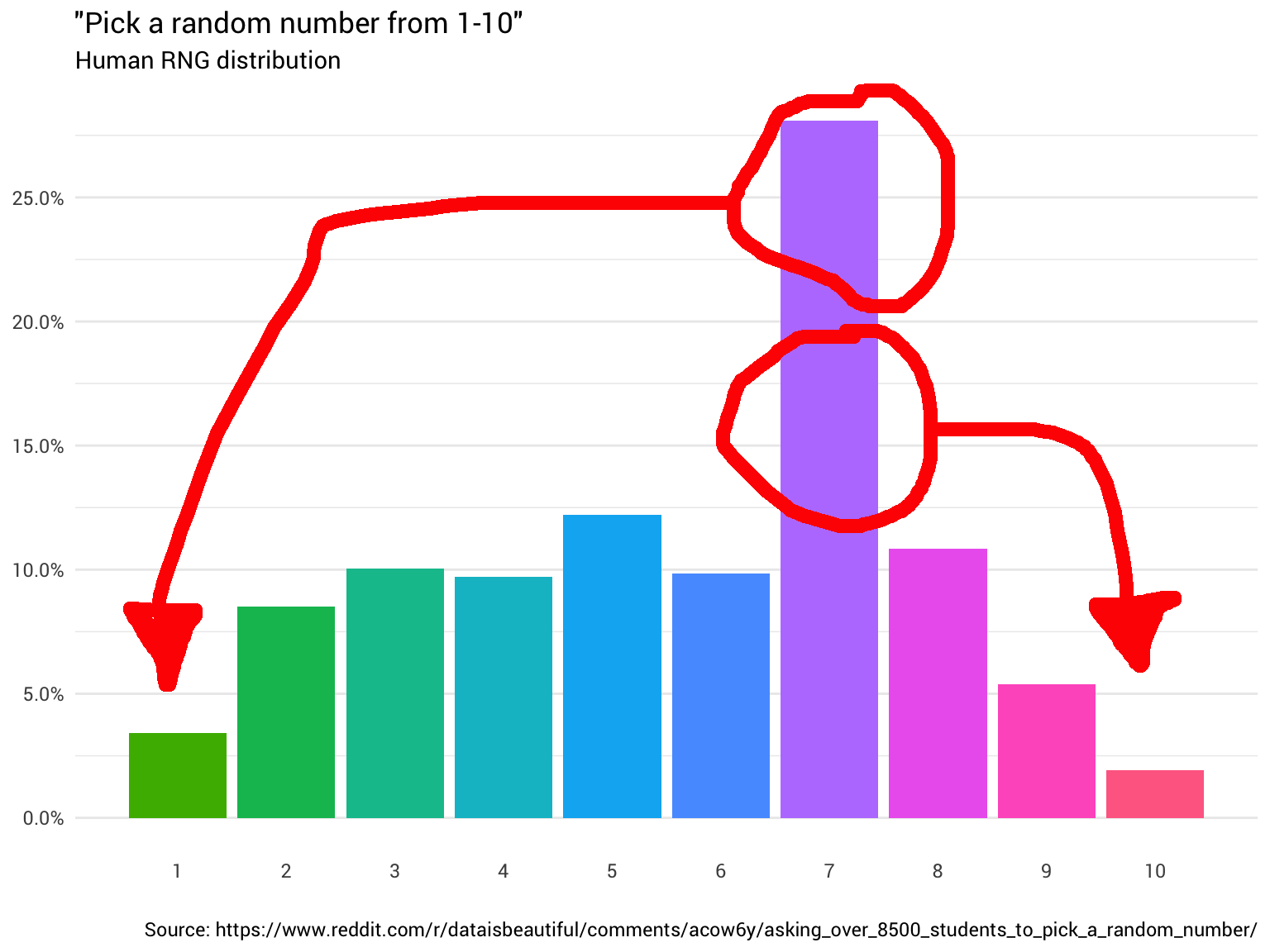
لذلك قررت أن تسأل عدد قليل من الناس. تستمر في سؤالهم وحساب إجاباتهم وتقريب الأرقام الكسرية وتجاهل أولئك الذين يعتقدون أن النطاق من 1 إلى 10 يتضمن 0. في النهاية ، تبدأ في رؤية أن التوزيع ليس حتى على الإطلاق:

library(tidyverse) probabilities <- read_csv("https://git.io/fjoZ2") %>% count(outcome = round(pick_a_random_number_from_1_10)) %>% filter(!is.na(outcome), outcome != 0) %>% mutate(p = n / sum(n)) probabilities %>% ggplot(aes(x = outcome, y = p)) + geom_col(aes(fill = as.factor(outcome))) + scale_x_continuous(breaks = 1:10) + scale_y_continuous(labels = scales::percent_format(), breaks = seq(0, 1, 0.05)) + scale_fill_discrete(h = c(120, 360)) + theme_minimal(base_family = "Roboto") + theme(legend.position = "none", panel.grid.major.x = element_blank(), panel.grid.minor.x = element_blank()) + labs(title = '"Pick a random number from 1-10"', subtitle = "Human RNG distribution", x = "", y = NULL, caption = "Source: https://www.reddit.com/r/dataisbeautiful/comments/acow6y/asking_over_8500_students_to_pick_a_random_number/") 

بيانات من رديت

أنت صفعة جبينك. حسنًا ، بالطبع ، لن يكون عشوائيًا. بعد كل شيء ، لا يمكن أن تثق في الناس .

ماذا تفعل؟

أتمنى أن أجد بعض الوظائف التي تحول توزيع "RNG البشري" إلى توزيع موحد ...

الحدس هنا بسيط نسبيا. تحتاج فقط إلى أخذ كتلة التوزيع من حيث تزيد عن 10٪ ، ونقلها إلى حيث تقل عن 10٪. بحيث تكون جميع الأعمدة على الرسم البياني في نفس المستوى:



من الناحية النظرية ، يجب أن توجد مثل هذه الوظيفة. في الواقع ، يجب أن يكون هناك العديد من الوظائف المختلفة (من أجل التقليب). في الحالة القصوى ، يمكنك "قص" كل عمود إلى كتل صغيرة بلا حدود وإنشاء توزيع بأي شكل (مثل طوب Lego).

بالطبع ، مثل هذا المثال المتطرف هو مرهق بعض الشيء. من الناحية المثالية ، نريد الاحتفاظ بأكبر قدر ممكن من التوزيع الأولي (على سبيل المثال ، جعل أقل عدد ممكن من القطع والحركات).

كيف تجد مثل هذه الوظيفة؟

حسنًا ، شرحنا أعلاه يبدو كثيرًا مثل البرمجة الخطية . من ويكيبيديا:

البرمجة الخطية (LP ، وتسمى أيضًا التحسين الخطي) هي طريقة لتحقيق أفضل نتيجة ... في نموذج رياضي تمثل متطلباته بالعلاقات الخطية ... النموذج القياسي هو الشكل المعتاد والأكثر حدسي لوصف مشكلة البرمجة الخطية. يتكون من ثلاثة أجزاء:

• وظيفة الخطية إلى الحد الأقصى
  
• قيود مشكلة في النموذج التالي
  
• متغيرات غير سلبية

وبالمثل ، يمكن صياغة مشكلة إعادة التوزيع.

عرض المشكلة

لدينا مجموعة من المتغيرات $$$(x_ {i، j}$ ، يشفر كل منها جزءًا صغيرًا من الاحتمال المعاد توزيعه من عدد صحيح $$$i$ (1 إلى 10) إلى عدد صحيح $$$j$ (من 1 إلى 10). لذلك ، إذا $$$(x_ {7،1} = 0.2 دولا$ ، نحن بحاجة إلى نقل 20 ٪ من الإجابات من سبعة إلى واحد.

 variables <- crossing(from = probabilities$outcome, to = probabilities$outcome) %>% mutate(name = glue::glue("x({from},{to})"), ix = row_number()) variables 

  ## # قلاب: 100 × 4
 ## من الاسم التاسع
 ## <dbl> <dbl> <glue> <int>
 ## 1 1 1 × (1،1) 1
 ## 2 1 2 × (1،2) 2
 ## 3 1 3 × (1،3) 3
 ## 4 1 4 × (1،4) 4
 ## 5 1 5 × (1،5) 5
 ## 6 1 6 × (1،6) 6
 ## 7 1 7 × (1،7) 7
 ## 8 1 8 × (1،8) 8
 ## 9 1 9 × (1.9) 9
 ## 10 1 10 × (1،10) 10
 ## # ... مع 90 المزيد من الصفوف 

نريد تحديد هذه المتغيرات بحيث تزيد كل الاحتمالات المعاد توزيعها عن 10٪. وبعبارة أخرى ، لكل منهما $$$j$ من 1 إلى 10:

$$

$$x_ {1، j} + x_ {2، j} + \ ldots \ x_ {10، j} = 0.1$$

يمكننا تمثيل هذه القيود كقائمة بالصفائف في R. فيما بعد ، نربطها بمصفوفة.

 fill_array <- function(indices, weights, dimensions = c(1, max(variables$ix))) { init <- array(0, dim = dimensions) if (length(weights) == 1) { weights <- rep_len(1, length(indices)) } reduce2(indices, weights, function(a, i, v) { a[1, i] <- v a }, .init = init) } constrain_uniform_output <- probabilities %>% pmap(function(outcome, p, ...) { x <- variables %>% filter(to == outcome) %>% left_join(probabilities, by = c("from" = "outcome")) fill_array(x$ix, x$p) }) 

يجب علينا أيضًا التأكد من الحفاظ على الكتلة الكاملة من الاحتمالات من التوزيع الأولي. لذلك للجميع $$$j$ في النطاق من 1 إلى 10:

$$

$$x_ {1، j} + x_ {2، j} + \ ldots \ x_ {10، j} = 0.1$$

 one_hot <- partial(fill_array, weights = 1) constrain_original_conserved <- probabilities %>% pmap(function(outcome, p, ...) { variables %>% filter(from == outcome) %>% pull(ix) %>% one_hot() }) 

كما ذكرنا سابقًا ، نريد تعظيم المحافظة على التوزيع الأصلي. هذا هو هدفنا:

$$

 maximise_original_distribution_reuse <- probabilities %>% pmap(function(outcome, p, ...) { variables %>% filter(from == outcome, to == outcome) %>% pull(ix) %>% one_hot() }) objective <- do.call(rbind, maximise_original_distribution_reuse) %>% colSums() 

بعد ذلك نقوم بتمرير المشكلة إلى ملف حلال ، على سبيل المثال ، حزمة lpSolve في R ، مع دمج القيود التي تم إنشاؤها في مصفوفة واحدة:

 # Make results reproducible... set.seed(23756434) solved <- lpSolve::lp( direction = "max", objective.in = objective, const.mat = do.call(rbind, c(constrain_original_conserved, constrain_uniform_output)), const.dir = c(rep_len("==", length(constrain_original_conserved)), rep_len("==", length(constrain_uniform_output))), const.rhs = c(rep_len(1, length(constrain_original_conserved)), rep_len(1 / nrow(probabilities), length(constrain_uniform_output))) ) balanced_probabilities <- variables %>% mutate(p = solved$solution) %>% left_join(probabilities, by = c("from" = "outcome"), suffix = c("_redistributed", "_original")) 

يتم إعادة التوزيع التالي:

 library(gganimate) redistribute_anim <- bind_rows(balanced_probabilities %>% mutate(key = from, state = "Before"), balanced_probabilities %>% mutate(key = to, state = "After")) %>% ggplot(aes(x = key, y = p_redistributed * p_original)) + geom_col(aes(fill = as.factor(from)), position = position_stack()) + scale_x_continuous(breaks = 1:10) + scale_y_continuous(labels = scales::percent_format(), breaks = seq(0, 1, 0.05)) + scale_fill_discrete(h = c(120, 360)) + theme_minimal(base_family = "Roboto") + theme(legend.position = "none", panel.grid.major.x = element_blank(), panel.grid.minor.x = element_blank()) + labs(title = 'Balancing the "Human RNG distribution"', subtitle = "{closest_state}", x = "", y = NULL) + transition_states( state, transition_length = 4, state_length = 3 ) + ease_aes('cubic-in-out') animate( redistribute_anim, start_pause = 8, end_pause = 8 ) 

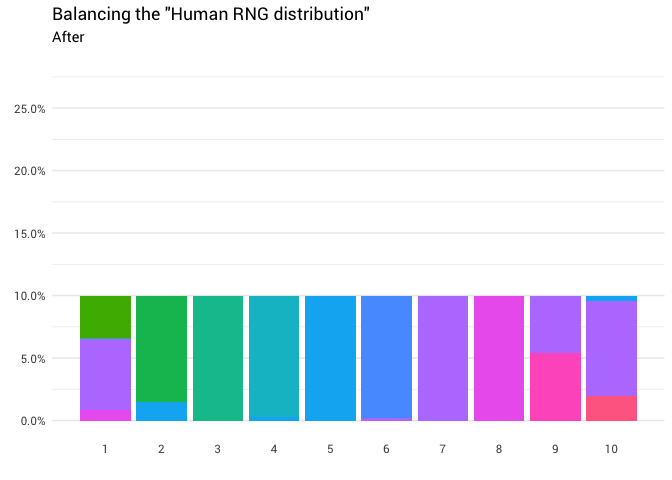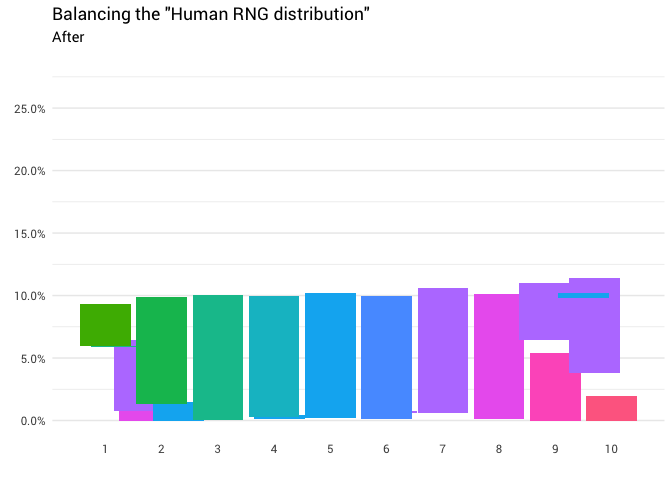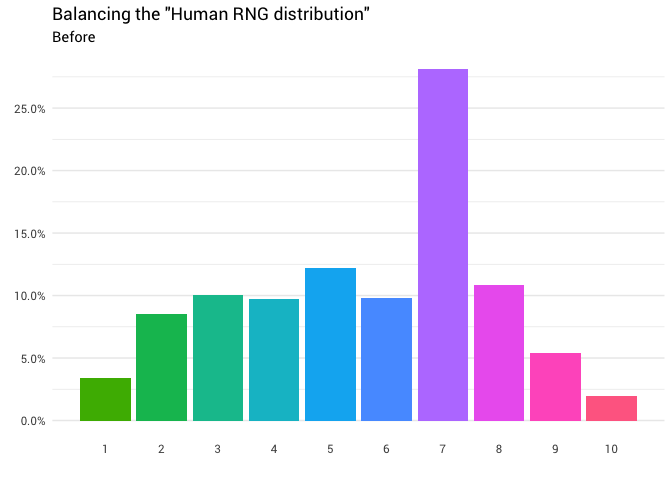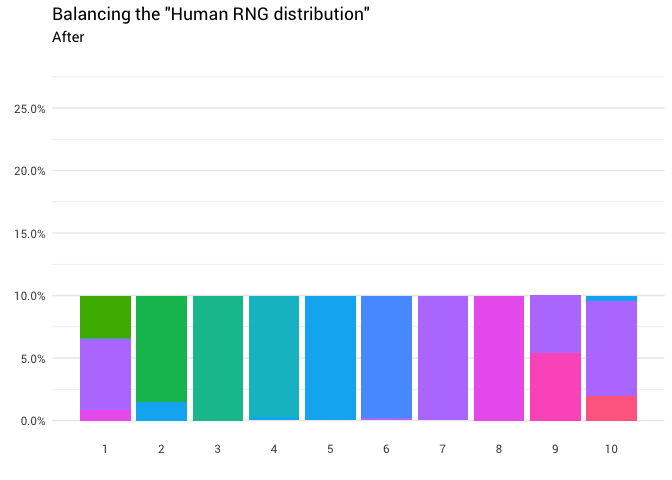
! ممتاز الآن لدينا وظيفة إعادة التوزيع. دعونا نلقي نظرة فاحصة على كيفية تحرك الكتلة بالضبط:

 balanced_probabilities %>% ggplot(aes(x = from, y = to)) + geom_tile(aes(alpha = p_redistributed, fill = as.factor(from))) + geom_text(aes(label = ifelse(p_redistributed == 0, "", scales::percent(p_redistributed, 2)))) + scale_alpha_continuous(limits = c(0, 1), range = c(0, 1)) + scale_fill_discrete(h = c(120, 360)) + scale_x_continuous(breaks = 1:10) + scale_y_continuous(breaks = 1:10) + theme_minimal(base_family = "Roboto") + theme(panel.grid.minor = element_blank(), panel.grid.major = element_line(linetype = "dotted"), legend.position = "none") + labs(title = "Probability mass redistribution", x = "Original number", y = "Redistributed number") 

يوضح هذا المخطط أنه في حوالي 8٪ من الحالات عندما يتصل شخص ما بثمانية كرقم عشوائي ، يجب أن تأخذ الإجابة كوحدة واحدة. في 92 ٪ المتبقية من الحالات ، وقال انه لا يزال الثمانية.

سيكون من السهل للغاية حل المشكلة إذا تمكنا من الوصول إلى مولد الأرقام العشوائية الموزعة بالتساوي (من 0 إلى 1). ولكن ليس لدينا سوى غرفة كاملة من الناس. لحسن الحظ ، إذا كنت مستعدًا للتصالح مع بعض الأخطاء الطفيفة ، فيمكنك إعداد RNG جيد من الناس دون أن تطلب أكثر من مرتين.

بالعودة إلى التوزيع الأصلي ، لدينا الاحتمالات التالية لكل رقم ، والتي يمكن استخدامها لإعادة تعيين أي احتمال ، إذا لزم الأمر.

 probabilities %>% transmute(number = outcome, probability = scales::percent(p)) 

  ## # نقش: 10 × 2
 ## رقم الاحتمال
 ## <dbl> <chr>
 ## 1 1 3.4 ٪
 ## 2 2 8.5 ٪
 ## 3 3 10.0 ٪
 ## 4 4 9.7 ٪
 ## 5 5 12.2 ٪
 ## 6 6 9.8 ٪
 ## 7 7 28.1 ٪
 ## 8 8 10.9 ٪
 ## 9 9 5.4 ٪
 ## 10 10 1.9 ٪ 

على سبيل المثال ، عندما يعطينا شخص ما ثمانية كرقم عشوائي ، نحتاج إلى تحديد ما إذا كان يجب أن يصبح هؤلاء الثمانية وحدة أم لا (الاحتمال 8٪). إذا سألنا شخصًا آخر عن رقم عشوائي ، فعندئذٍ باحتمال قدره 8.5٪ ، سيرد على "اثنين". إذا كان هذا الرقم الثاني هو 2 ، فنحن نعلم أنه يجب علينا إرجاع الرقم 1 كرقم عشوائي موزع بشكل موحد .

بتوسيع هذا المنطق ليشمل جميع الأرقام ، نحصل على الخوارزمية التالية:

• اسأل شخص عن رقم عشوائي ، $$$n_1$ .
• $$$n_1 = 1 ، 2 ، 3 ، 4 ، 6 ، 9 ،$ أو $$ :
  
  • رقم عشوائي الخاص بك $$$n_1$
• إذا $$$n_1 = 5$ :
  
  • اسأل شخصًا آخر عن رقم عشوائي ( $$$n_2 دولا$ )
  • إذا $$$n_2 = 5$ (12.2٪):
    
    • رقمك العشوائي 2
  • إذا $$$n_2 = 10 دولا$ (1.9٪):
    
    • رقمك العشوائي 4
  • خلاف ذلك ، رقمك العشوائي هو 5
• إذا $$$n_1 = 7 دولا$ :
  
  • اسأل شخصًا آخر عن رقم عشوائي ( $$$n_2 دولا$ )
  • إذا $$$n_2 = 2 دولا$ أو $$ (20.7٪):
    
    • رقمك العشوائي 1
  • إذا $$$n_2 = 8 دولا$ أو $$ (16.2٪):
    
    • رقمك العشوائي هو 9
  • إذا $$$n_2 = 7 دولا$ (28.1٪):
    
    • رقمك العشوائي هو 10
  • خلاف ذلك ، رقمك العشوائي هو 7
• إذا $$$n_1 = 8 دولا$ :
  
  • اسأل شخصًا آخر عن رقم عشوائي ( $$$n_2 دولا$ )
  • إذا $$$n_2 = 2 دولا$ (8.5٪):
    
    • رقمك العشوائي 1
  • خلاف ذلك ، رقمك العشوائي هو 8

باستخدام هذه الخوارزمية ، يمكنك استخدام مجموعة من الأشخاص للحصول على شيء قريب من مولد الأرقام العشوائية الموزعة بالتساوي من 1 إلى 10!