اليوم سوف ننظر في حزمة رسومية للغة جوليا تسمى الأقصر . هذه واحدة من تلك الأدوات التي تحول عملية إنشاء صور متجهة إلى حل المشاكل المنطقية مع عاصفة من العواطف المصاحبة.
الحذر! ضمن المقطع 8.5 ميغابايت من الصور وخفيفة الوزن وصور متحركة البيض المخدر والأشياء الأربعة الأبعاد ، والتي قد تتسبب في رؤية ملطخة طفيفة للعقل!
تركيب
https://julialang.org - قم بتنزيل التوزيع Julia من الموقع الرسمي. بعد ذلك ، ببدء المترجم الفوري ، نوجه الأوامر إلى وحدة التحكم الخاصة به:
using Pkg Pkg.add("Colors") Pkg.add("ColorSchemes") Pkg.add("Luxor")
التي من شأنها تثبيت حزم للعمل المتقدم مع الألوان والأقصر نفسها.
المشاكل المحتملة
المشكلة الرئيسية لكل من البرمجة الحديثة بشكل عام والمفتوح المصدر بشكل خاص هو أن بعض المشاريع مبنية على مشاريع أخرى ، أو توارث جميع الأخطاء ، أو حتى إنشاء مشاريع جديدة بسبب عدم التوافق. مثل العديد من الحزم الأخرى ، تستخدم الأقصر حزم julia الأخرى لعملها ، والتي بدورها تمثل أصداء الحلول الحالية.
لذلك ، لم ترغب ImageMagick.jl في تنزيل الملفات وحفظها. تم العثور على الحل على الصفحة الأصلية - اتضح أنه لا يحب الأبجدية السيريلية بطرق.
نشأت المشكلة الثانية مع حزمة الرسومات ذات المستوى المنخفض في القاهرة على Windows 7. سأخفي الحل هنا:
الرقص مع الدف- نكتب في المترجم
]add Gtk - حزمة العمل مع واجهة المستخدم الرسومية ستبدأ في التثبيت والأرجح أنها ستسقط أثناء الإنشاء - بعد ذلك ، قم بتنزيل gtk + -bundle_3.6.4-20130513_win64
- أثناء التثبيت ، كان كل شيء ضروريًا في المجلد الذي يحتوي على حزم Julia ، ولكن لم يتم الانتهاء من gtk أثناء تنفيذ العنصر ، لذلك قمنا بتنزيل الإصدار النهائي لجهازنا - نرمي محتويات الأرشيف الذي تم تنزيله في الدليل C: \ Users \ User.julia \ الحزم \ WinRPM \ Y9QdZ \ deps \ usr \ x86_64-w64-mingw32 \ sys-root \ mingw (قد يختلف المسار الخاص بك)
- شغِّل جوليا
]build Gtk وبعد البناء using Gtk ، ومن أجل الإخلاص ، أعد بناء الأقصر: ]build Luxor - نعيد تشغيل julia ، ويمكننا استخدام كل ما نحتاج إليه بأمان:
using Luxor
في حالة حدوث مشاكل أخرى ، حاول العثور على قضيتك
إذا كنت ترغب في محاولة الرسوم المتحركة
تقوم حزمة الأقصر بإنشاء رسوم متحركة باستخدام ffmpeg ، بشرط أن تكون موجودة على جهاز الكمبيوتر الخاص بك. ffmpeg عبارة عن مكتبة مفتوحة المصدر متعددة المنصات لمعالجة ملفات الفيديو والصوت ، وهذا شيء مفيد للغاية (هناك رحلة جيدة على المحور ). تثبيته:
- تحميل ffmpeg خارج الموقع. في حالتي ، هذا تنزيل للنوافذ
- فك حزم وكتابة المسار إلى ffmpeg.exe في متغير المسار .
المزيد عن الانسداد في المسار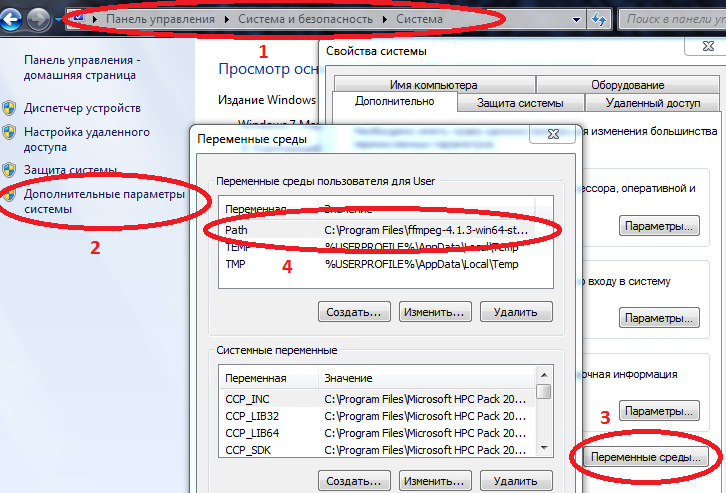
الكمبيوتر / خصائص النظام / معلمات النظام المتقدمة / متغيرات البيئة / المسار (إنشاء إن لم يكن) وإضافة المسار إلى ffmpeg.exe الخاص بك هناك
مثال C: \ Program Files \ ffmpeg-4.1.3-win64-static \ bin
إذا كان Path يحتوي بالفعل على قيم ، فافصل بينها بفاصلة منقوطة.
الآن إذا كنت تقود ffmpeg مع المعلمات اللازمة في وحدة التحكم بالأوامر ( cmd ) ، فستبدأ وستعمل ، وسوف تتواصل جوليا معها فقط.
مرحبا العالم
لنبدأ بمخزون صغير - عند إنشاء صورة ، يتم إنشاء ملف رسومي وحفظه في دليل العمل. بمعنى أنه عند العمل في REPL ، سيتم انسداد المجلد الجذر julia بالصور ، وإذا قمت بالرسم في Jupyter ، فسوف تتراكم الصور بجوار دفتر المشروع ، وبالتالي ، فمن المعتاد تعيين دليل العمل في مكان منفصل قبل بدء العمل:
using Luxor cd("C:\\Users\\User\\Desktop\\mycop")
إنشاء الرسم الأول
Drawing(220, 220, "hw.png") origin() background("white") sethue("black") text("Hello world") circle(Point(0, 0), 100, :stroke) finish() preview()

ينشئ Drawing() رسمًا ، افتراضيًا بتنسيق PNG ، يكون اسم الملف الافتراضي هو "luxor-drawing.png" ، والحجم الافتراضي هو 800 × 800 ، ولكل التنسيقات باستثناء png يمكنك تحديد أحجام غير عدد صحيح ، ويمكنك أيضًا استخدام أحجام ورق ("A0" "،" A1 "،" A2 "،" A3 "،" A4 "...)
finish() - ينتهي الرسم ويغلق الملف. يمكنك فتحه في تطبيق عرض خارجي باستخدام preview() ، والتي عند العمل في Jupyter (IJulia) ستعرض ملف PNG أو SVG في المفكرة. عند العمل في Juno ، سيعرض ملف PNG أو SVG في لوحة Graph. في Repl ، تسمى أداة التعامل مع الصور التي قمت بتعيينها لهذا التنسيق في نظام التشغيل الخاص بك.
يمكن كتابة الشيء نفسه في شكل قصير باستخدام وحدات الماكرو
@png begin text("Hello world") circle(Point(0, 0), 100, :stroke) end
بالنسبة إلى تنسيقات المتجهات EPS و SVG و PDF ، يعمل كل شيء بالطريقة نفسها.
بيضة اقليدية

هذه طريقة مثيرة للاهتمام إلى حد ما لرسم بيضة ، وإذا قمت بتوصيل النقاط الرئيسية وقطعت على طول الخطوط الواردة ، سوف يخرج tangram ممتاز
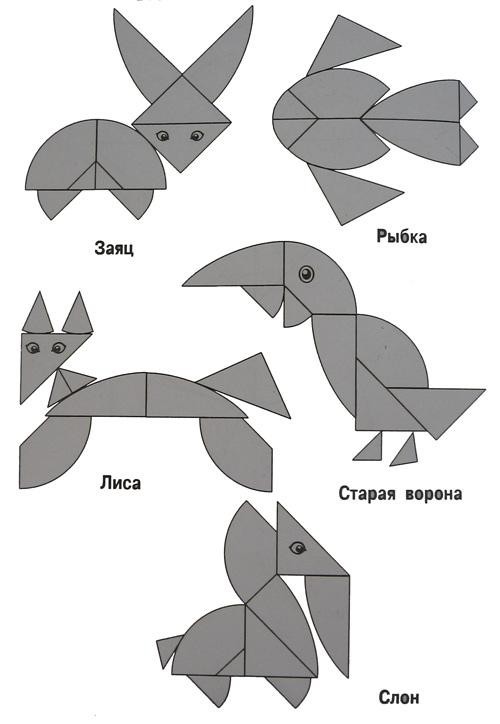
لنبدأ بالدائرة:
@png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) end 200 200 "egg0"

كل شيء بسيط للغاية: setdash("dot") - ارسم بالنقاط ، sethue("gray30") - لون الخط: أصغر ، أغمق ، أقرب إلى 100 بياضاً. يتم تعريف فئة النقطة بدوننا ، ويمكن تحديد مركز الإحداثيات (0،0) بالحرف O إضافة دائرتين وتوقيع النقاط:
@png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke) end 600 400 "egg2"
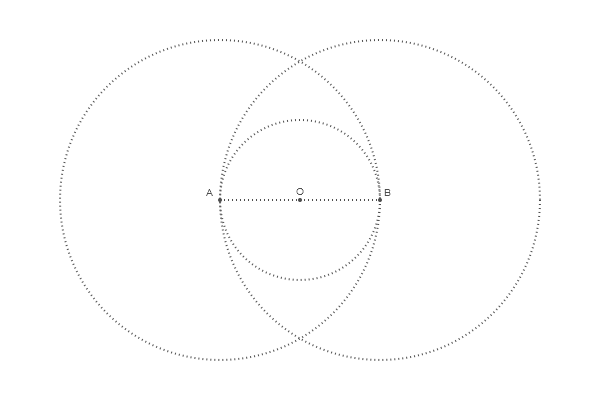
للبحث عن نقاط التقاطع ، توجد وظيفة تسمى intersectionlinecircle() تجد النقطة أو النقاط التي يتقاطع فيها الخط مع الدائرة. وبالتالي ، يمكننا أن نجد نقطتين حيث تتقاطع إحدى الدوائر مع خط عمودي وهمي مرسوم عبر O. نظرًا للتماثل ، يمكننا معالجة الدائرة A.
@png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke)
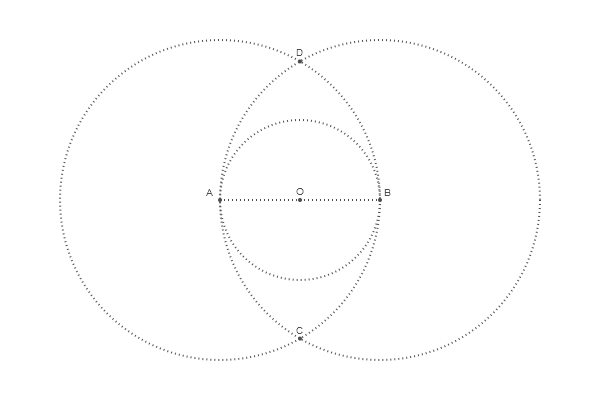
لتحديد مركز الدائرة العليا نجد التقاطع OD
قانون @png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke)

يتحدد نصف قطر الدائرة الثانوية بالقيود على دائرتين كبيرتين:
قانون @png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke)

البيضة جاهزة! يبقى تجميعه من أربعة أقواس محددة بواسطة وظيفة arc2r() وملء المساحة:
قانون @png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke)
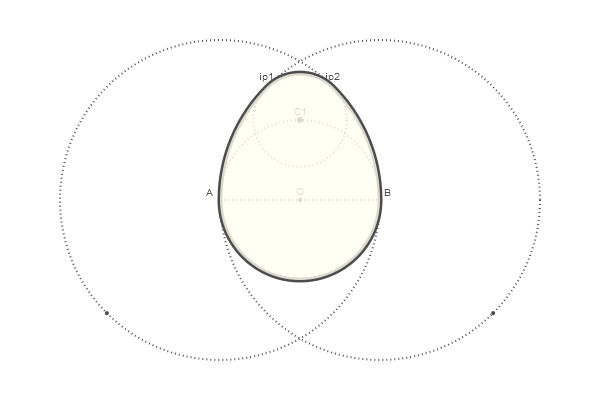
والآن ، من أجل الانغماس بشكل صحيح ، سنحقق إنجازاتنا
الوظيفة function egg(radius, action=:none) A, B = [Point(x, 0) for x in [-radius, radius]] nints, C, D = intersectionlinecircle(Point(0, -2radius), Point(0, 2radius), A, 2radius) flag, C1 = intersectionlinecircle(C, D, O, radius) nints, I3, I4 = intersectionlinecircle(A, C1, A, 2radius) nints, I1, I2 = intersectionlinecircle(B, C1, B, 2radius) if distance(C1, I1) < distance(C1, I2) ip1 = I1 else ip1 = I2 end if distance(C1, I3) < distance(C1, I4) ip2 = I3 else ip2 = I4 end newpath() arc2r(B, A, ip1, :path) arc2r(C1, ip1, ip2, :path) arc2r(A, ip2, B, :path) arc2r(O, B, A, :path) closepath() do_action(action) end
نحن نستخدم ألوان عشوائية ، وطلاء الطبقات والشروط الأولية المختلفة:
@png begin setopacity(0.7) for θ in range(0, step=π/6, length=12) @layer begin rotate(θ) translate(100, 50)


بالإضافة إلى الحد والتعبئة ، يمكنك استخدام المخطط التفصيلي كمنطقة لقطة (قص صورة أخرى في شكل بيضة) أو كأساس لمختلف المصممين. تقوم وظيفة egg () بإنشاء مخطط تفصيلي وتسمح لك بتطبيق إجراء ما عليها. من الممكن أيضًا تحويل إنشاءنا إلى مضلع (مجموعة من النقاط). تقوم التعليمة البرمجية التالية بتحويل مخطط البويضة إلى مضلع ، ثم تحريك كل نقطة أخرى من المضلع إلى منتصف المسافة النقطية.
@png begin egg(160, :path) pgon = first(pathtopoly()) pc = polycentroid(pgon) circle(pc, 5, :fill) for pt in 1:2:length(pgon) pgon[pt] = between(pc, pgon[pt], 0.5) end poly(pgon, :stroke) end 350 500 "polyegg"

يظهر المظهر غير المتساوي للنقاط الداخلية هنا نتيجة لإعدادات اتصال الخط الافتراضي. تجربة مع setlinejoin("round") لمعرفة ما إذا كان هذا يغير الهندسة أم لا. حسنًا ، offsetpoly() الآن offsetpoly() إنشاء محيط مضلع خارج أو داخل مضلع موجود ..
@png begin egg(80, :path) pgon = first(pathtopoly()) pc = polycentroid(pgon) for pt in 1:2:length(pgon) pgon[pt] = between(pc, pgon[pt], 0.9) end for i in 30:-3:-8 randomhue() op = offsetpoly(pgon, i) poly(op, :stroke, close=true) end end 350 500 "polyeggs"

التغييرات الصغيرة في انتظام النقاط التي تم إنشاؤها عن طريق تحويل المسار إلى مضلع ، وعدد مختلف من العينات التي قام بها ، يتم تضخيمها باستمرار في معالم متعاقبة.
حيوية
أولاً ، دعنا نحدد الوظائف التي تنفذ خلفية البيضة وعرضها ، اعتمادًا على رقم الإطار:
قانون using Colors demo = Movie(400, 400, "test") function backdrop(scene, framenumber) background("black") end function frame(scene, framenumber) setopacity(0.7) θ = framenumber * π/6 @layer begin rotate(θ) translate(100, 50) egg(50, :path) setline(10) randomhue() fillpreserve() randomhue() strokepath() end end
يتم تنفيذ الرسوم المتحركة بواسطة مجموعة بسيطة من الأوامر:
animate(demo, [ Scene(demo, backdrop, 0:12), Scene(demo, frame, 0:12, easingfunction=easeinoutcubic, optarg="made with Julia") ], framerate=10, tempdirectory="C:\\Users\\User\\Desktop\\mycop", creategif=true)
ما الذي يسبب في الواقع لدينا ffmpeg
run(`ffmpeg -f image2 -i $(tempdirectory)/%10d.png -vf palettegen -y $(seq.stitle)-palette.png`) run(`ffmpeg -framerate 30 -f image2 -i $(tempdirectory)/%10d.png -i $(seq.stitle)-palette.png -lavfi paletteuse -y /tmp/$(seq.stitle).gif`)
أي ، يتم إنشاء سلسلة من الصور ، ثم يتم تجميع GIF من هذه الإطارات:

Pentahor
هو خمسة - جوهر - البسيط الصحيح ثلاثي الأبعاد. لرسم ومعالجة الكائنات ثنائية الأبعاد على صور ثنائية الأبعاد ، نحددها أولاً
الطبقة 4-الأبعاد نقطة struct Point4D <: AbstractArray{Float64, 1} x::Float64 y::Float64 z::Float64 w::Float64 end Point4D(a::Array{Float64, 1}) = Point4D(a...) Base.size(pt::Point4D) = (4, ) Base.getindex(pt::Point4D, i) = [pt.x, pt.y, pt.z, pt.w][i] struct Point3D <: AbstractArray{Float64, 1} x::Float64 y::Float64 z::Float64 end Base.size(pt::Point3D) = (3, )
بدلاً من تحديد العديد من العمليات يدويًا ، يمكننا تعريف هيكلنا كنوع فرعي من AbstractArray ( المزيد حول الفئات كواجهات )
المهمة الرئيسية التي يجب حلها هي كيفية تحويل نقطة 4D إلى نقطة ثنائية الأبعاد. لنبدأ بمهمة أبسط: كيفية تحويل نقطة ثلاثية الأبعاد إلى نقطة ثنائية الأبعاد ، أي كيف يمكننا رسم شخصية ثلاثية الأبعاد على سطح مستو؟ النظر في مكعب بسيط. يمكن أن يكون للأسطح الأمامية والخلفية نفس إحداثيات X و Y وتختلف فقط في قيمها Z.
قانون @png begin fontface("Menlo") fontsize(8) setblend(blend( boxtopcenter(BoundingBox()), boxmiddlecenter(BoundingBox()), "skyblue", "white")) box(boxtopleft(BoundingBox()), boxmiddleright(BoundingBox()), :fill) setblend(blend( boxmiddlecenter(BoundingBox()), boxbottomcenter(BoundingBox()), "grey95", "grey45" )) box(boxmiddleleft(BoundingBox()), boxbottomright(BoundingBox()), :fill) sethue("black") setline(2) bx1 = box(O, 250, 250, vertices=true) poly(bx1, :stroke, close=true) label.(["-1 1 1", "-1 -1 1", "1 -1 1", "1 1 1"], slope.(O, bx1), bx1) setline(1) bx2 = box(O, 150, 150, vertices=true) poly(bx2, :stroke, close=true) label.(["-1 1 0", "-1 -1 0", "1 -1 0", "1 1 0"], slope.(O, bx2), bx2, offset=-45) map((x, y) -> line(x, y, :stroke), bx1, bx2) end 400 400 "cube.png"

لذلك ، تتمثل الفكرة في إسقاط مكعب من ثلاثي الأبعاد إلى ثنائي الأبعاد ، مع توفير القيمتين الأوليين وضربهما أو تغييرهما بالقيمة الثالثة. سوف تحقق
كيف يعمل؟ const K = 4.0 function convert(Point, pt3::Point3D) k = 1/(K - pt3.z) return Point(pt3.x * k, pt3.y * k) end @png begin cube = Point3D[ Point3D(-1, -1, 1), Point3D(-1, 1, 1), Point3D( 1, -1, 1), Point3D( 1, 1, 1), Point3D(-1, -1, -1), Point3D(-1, 1, -1), Point3D( 1, -1, -1), Point3D( 1, 1, -1), ] circle.(convert.(Point, cube) * 300, 5, :fill) end 220 220 "points"

باستخدام نفس المبدأ ، لنقم بإنشاء طريقة لتحويل نقاط 4D ووظيفة تأخذ قائمة من النقاط ذات الأبعاد الأربعة وتعيينها مرتين على قائمة بالنقاط ثنائية الأبعاد المناسبة للرسم.
function convert(Point3D, pt4::Point4D) k = 1/(K - pt4.w) return Point3D(pt4.x * k, pt4.y * k, pt4.z * k) end function flatten(shape4) return map(pt3 -> convert(Point, pt3), map(pt4 -> convert(Point3D, pt4), shape4)) end
بعد ذلك ، قم بتعيين الرؤوس والوجوه وتحقق من كيفية عملها بالألوان
TYK! const n = -1/√5 const pentachoron = [Point4D(vertex...) for vertex in [ [ 1.0, 1.0, 1.0, n], [ 1.0, -1.0, -1.0, n], [-1.0, 1.0, -1.0, n], [-1.0, -1.0, 1.0, n], [ 0.0, 0.0, 0.0, n + √5]]]; const pentachoronfaces = [ [1, 2, 3], [1, 2, 4], [1, 2, 5], [1, 3, 4], [1, 3, 5], [1, 4, 5], [2, 3, 4], [2, 3, 5], [2, 4, 5], [3, 4, 5]]; @png begin setopacity(0.2) pentachoron2D = flatten(pentachoron) for (n, face) in enumerate(pentachoronfaces) randomhue() poly(1500 * pentachoron2D[face], :fillpreserve, close=true) sethue("black") strokepath() end end 300 250 "5ceil"

يجب أن يعرف كل مطور لعبة يحترم نفسه الأسس الرياضية لرسومات الماكينات . إذا لم تحاول أبدًا ضغط أو تدوير أو عكس أقداح الشاي في برنامج OpenGL - فلا تشعر بالقلق ، كل شيء بسيط للغاية. لعكس نقطة نسبيًا إلى خط مستقيم ، أو لتدوير مستوى حول محور معين ، تحتاج إلى ضرب الإحداثيات بمصفوفة خاصة. في الواقع ، سوف نحدد مصفوفات التحويل التي نحتاجها:
التقط أكثر function XY(θ) [cos(θ) -sin(θ) 0 0; sin(θ) cos(θ) 0 0; 0 0 1 0; 0 0 0 1] end function XW(θ) [cos(θ) 0 0 -sin(θ); 0 1 0 0; 0 0 1 0; sin(θ) 0 0 cos(θ)] end function XZ(θ) [cos(θ) 0 -sin(θ) 0; 0 1 0 0; sin(θ) 0 cos(θ) 0; 0 0 0 1] end function YZ(θ) [1 0 0 0; 0 cos(θ) -sin(θ) 0; 0 sin(θ) cos(θ) 0; 0 0 0 1] end function YW(θ) [1 0 0 0; 0 cos(θ) 0 -sin(θ); 0 0 1 0; 0 sin(θ) 0 cos(θ)] end function ZW(θ) [1 0 0 0; 0 1 0 0; 0 0 cos(θ) -sin(θ); 0 0 sin(θ) cos(θ)]; end function rotate4(A, matrixfunction) return map(A) do pt4 Point4D(matrixfunction * pt4) end end
عادةً ما تقوم بتدوير النقاط على مستوى ذي صلة بكائن أحادي البعد. تقع النقاط الثلاثية حول خط ثنائي الأبعاد (غالبًا ما يكون هذا أحد محاور XYZ). وبالتالي ، فمن المنطقي أن تدور نقاط 4D بالنسبة للطائرة ثلاثية الأبعاد. لقد حددنا المصفوفات التي تقوم بالدوران رباعي الأبعاد حول مستوى مُحدد بواسطة محورين X و Y و Z و W. الطائرة عادةً ما تكون الطائرة XY هي سطح سطح الرسم. إذا كنت ترى الطائرة XY كشاشة كمبيوتر ، فستكون الطائرة XZ متوازية مع طاولتك أو الأرضية ، وتكون الطائرة YZ هي الجدار الموجود بجانب طاولتك على اليمين أو اليسار. ولكن ماذا عن XW ، YW و ZW؟ هذا هو لغز الأشكال ثلاثية الأبعاد: لا يمكننا رؤية هذه الطائرات ، يمكننا فقط أن نتخيل وجودها من خلال ملاحظة كيف تتحرك الأشكال من خلالها وحولها.
الآن نقوم بتعيين وظائف الإطارات وخياطة الرسوم المتحركة:
المفسد using ColorSchemes function frame(scene, framenumber, scalefactor=1000) background("white")

حسنا ، وزاوية أخرى:
قانون function frame(scene, framenumber, scalefactor=1000) background("antiquewhite") setlinejoin("bevel") setline(1.0) setopacity(0.2) eased_n = scene.easingfunction(framenumber, 0, 1, scene.framerange.stop) pentachoron2D = flatten( rotate4( pentachoron, XZ(eased_n * 2π) * YW(eased_n * 2π))) for (n, face) in enumerate(pentachoronfaces) sethue(get(ColorSchemes.diverging_rainbow_bgymr_45_85_c67_n256, n/length(pentachoronfaces))) poly(scalefactor * pentachoron2D[face], :fillpreserve, close=true) sethue("black") strokepath() end end makemovie(500, 500, "pentachoron-xz-yw.gif", scalefactor=2000)
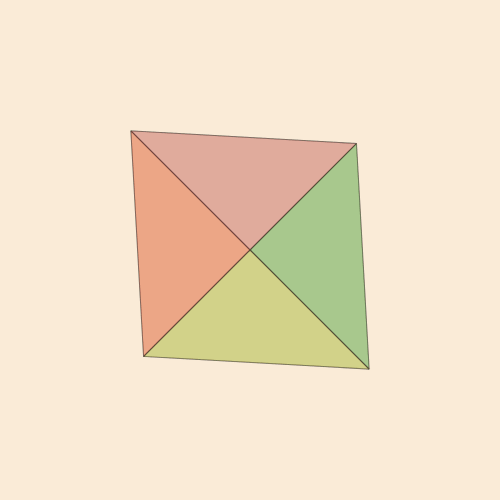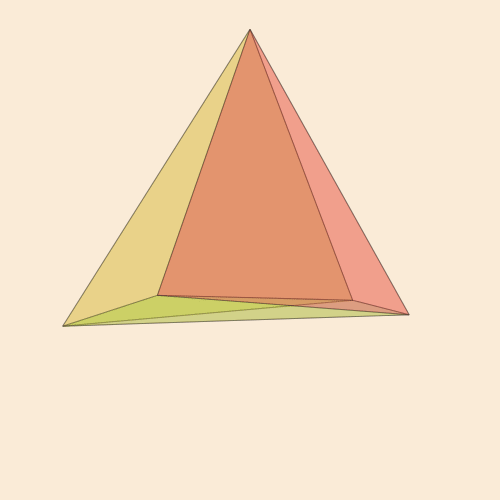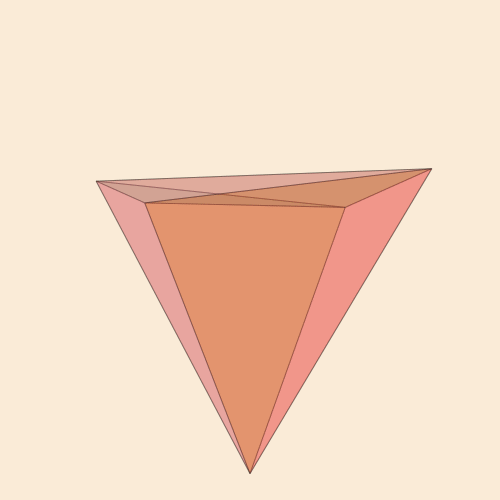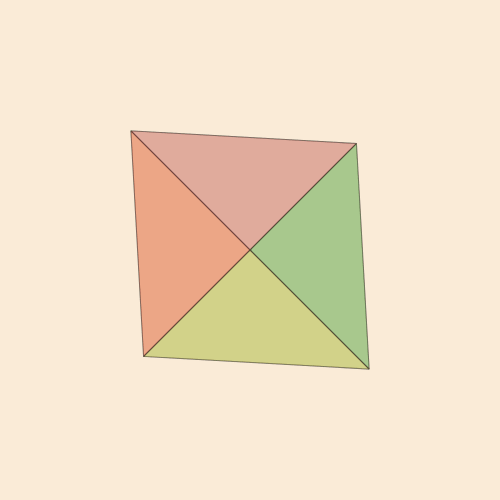
الرغبة في إدراك كائن ثلاثي الأبعاد الأكثر شعبية ، Tesseract ، أمر طبيعي تمامًا.
قمم وجوه const tesseract = [Point4D(vertex...) for vertex in [ [-1, -1, -1, 1], [ 1, -1, -1, 1], [ 1, 1, -1, 1], [-1, 1, -1, 1], [-1, -1, 1, 1], [ 1, -1, 1, 1], [ 1, 1, 1, 1], [-1, 1, 1, 1], [-1, -1, -1, -1], [ 1, -1, -1, -1], [ 1, 1, -1, -1], [-1, 1, -1, -1], [-1, -1, 1, -1], [ 1, -1, 1, -1], [ 1, 1, 1, -1], [-1, 1, 1, -1]]] const tesseractfaces = [ [1, 2, 3, 4], [1, 2, 10, 9], [1, 4, 8, 5], [1, 5, 6, 2], [1, 9, 12, 4], [2, 3, 11, 10], [2, 3, 7, 6], [3, 4, 8, 7], [5, 6, 14, 13], [5, 6, 7, 8], [5, 8, 16, 13], [6, 7, 15, 14], [7, 8, 16, 15], [9, 10, 11, 12], [9, 10, 14, 13], [9, 13, 16, 12], [10, 11, 15, 14], [13, 14, 15, 16]];
إنشاء الرسوم المتحركة function frame(scene, framenumber, scalefactor=1000) background("black") setlinejoin("bevel") setline(10.0) setopacity(0.7) eased_n = scene.easingfunction(framenumber, 0, 1, scene.framerange.stop) tesseract2D = flatten( rotate4( tesseract, XZ(eased_n * 2π) * YW(eased_n * 2π))) for (n, face) in enumerate(tesseractfaces) sethue([Luxor.lighter_blue, Luxor.lighter_green, Luxor.lighter_purple, Luxor.lighter_red][mod1(n, 4)]...) poly(scalefactor * tesseract2D[face], :fillpreserve, close=true) sethue([Luxor.darker_blue, Luxor.darker_green, Luxor.darker_purple, Luxor.darker_red][mod1(n, 4)]...) strokepath() end end makemovie(500, 500, "tesseract-xz-yw.gif", scalefactor=1000)

الواجبات المنزلية: أتمتة إنشاء صفيف من الإحداثيات وأرقام قمة الرأس ( التباديل مع التكرار وبدون التكرار ، على التوالي ). أيضًا ، لم نستخدم جميع مصفوفات الترجمة ؛ كل منظور جديد يطرح "Wow!" جديد ، لكنني قررت عدم زيادة تحميل الصفحة. حسنًا ، يمكنك تجربة الكثير من الوجوه والأبعاد.
مراجع