الصورة مأخوذة من المنشورمقدمة
واحدة من أكثر المهام إلحاحا في معالجة الإشارات الرقمية هي مهمة تنظيف الإشارة من الضوضاء. لا تحتوي أي إشارة عملية على معلومات مفيدة فحسب ، بل تحتوي أيضًا على آثار لبعض الآثار الخارجية للتداخل أو الضوضاء. بالإضافة إلى ذلك ، أثناء تشخيص الاهتزازات ، للإشارات من أجهزة استشعار الاهتزاز طيف تردد غير ثابت ، مما يعقد مهمة التصفية.
هناك العديد من الطرق المختلفة لإزالة الضوضاء عالية التردد من الإشارة. على سبيل المثال ، تحتوي مكتبة Scipy على عوامل تصفية تستند إلى طرق تصفية مختلفة: Kalman؛ تجانس الإشارة من خلال متوسطها على طول المحور الزمني ، وغيرها.
ومع ذلك ، فإن ميزة طريقة تحويل المويجات المنفصلة (DWT) هي مجموعة متنوعة من أشكال المويجات. يمكنك تحديد المويجات ، والتي سيكون لها شكل مميز للظواهر المتوقعة. على سبيل المثال ، يمكنك تحديد إشارة في نطاق تردد معين ، يكون شكله مسؤولًا عن ظهور عيب.
الغرض من هذا المنشور هو تحليل طرق تصفية إشارات مجسات الاهتزاز باستخدام تحويل إشارة DWT ، ومرشح Kalman وطريقة المتوسط المتحرك.
مصدر البيانات للتحليل
في المنشور ، سيتم تحليل تشغيل المرشحات على أساس أساليب تصفية مختلفة باستخدام
مجموعة بيانات ناسا . البيانات التي تم الحصول عليها على منصة التجريبية PRONOSTIA:

تحتوي المجموعة على بيانات حول إشارات استشعار الاهتزاز لارتداء أنواع مختلفة من المحامل. تم توضيح الغرض من المجلدات التي تحتوي على ملفات الإشارة في
الجدول :
يتم توفير مراقبة حالة المحامل بواسطة إشارات مجسات الاهتزاز (مقاييس التسارع الأفقية والعمودية) والقوة ودرجة الحرارة.

الإشارات المستلمة لمدة ثلاثة أحمال مختلفة:
- ظروف العمل الأولى: 1800 دورة في الدقيقة و 4000 ن ؛
- ظروف العمل الثانية: 1650 دورة في الدقيقة و 4200 N ؛
- ظروف التشغيل الثالثة: 1500 دورة في الدقيقة و 5000 نيوتن
بالنسبة لهذه الشروط ، باستخدام التحويل المستمر لإشارة المويجات ، نقوم ببناء
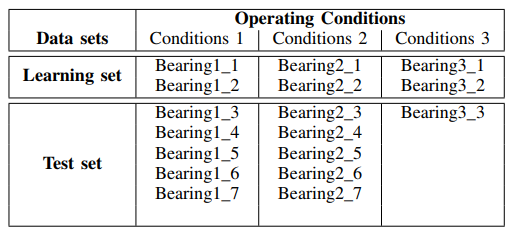
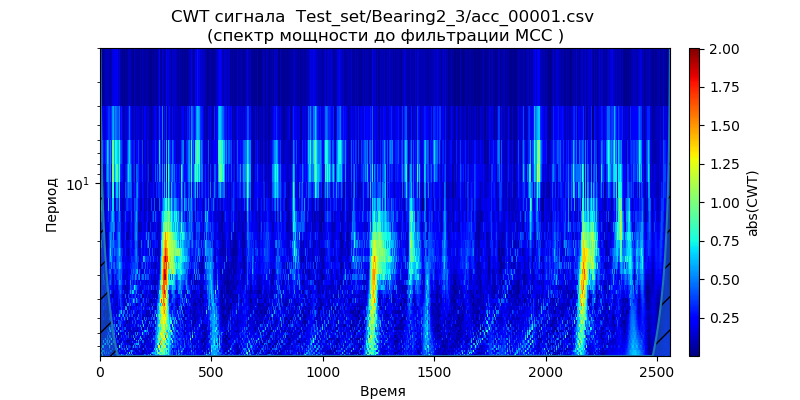
سكالوجراف القدرة الطيفية للبيانات من مجموعة الاختبار - ملف واحد (لنوع واحد من المحامل) من المجلدات: ['Test_set / Bearing1_3 / acc_00001.csv' ، 'Test_set / Bearing2_3 / acc_00001. CSV '،' Test_set / Bearing3_3 / acc_00001.csv '] (انظر الجدول 1).
قائمة المقاييسimport scaleogram as scg import pandas as pd from pylab import * import pywt filename_n = ['Test_set/Bearing1_3/acc_00001.csv', 'Test_set/Bearing2_3/acc_00001.csv', 'Test_set/Bearing3_3/acc_00001.csv'] for filename in filename_n: df = pd.read_csv(filename, header=None) signal = df[4].values wavelet = 'cmor1-0.5' ax = scg.cws(signal, scales=arange(1, 40), wavelet=wavelet, figsize=(8, 4), cmap="jet", cbar=None, ylabel=' ', xlabel=" ", yscale="log", title='- %s \n( )'%filename) show()


ويترتب على المقاييس المعطاة أن لحظات زيادة قوة الطيف تظهر في وقت مبكر وتُظهر التردد لظروف التشغيل: 1650 دورة في الدقيقة و 4200 N ، مما يشير إلى تدهور سريع للمحامل في نطاق التردد هذا للقوة المخفضة. سنستخدم هذه الإشارة ('Test_set / Bearing2_3 / acc_00001.csv') لتحليل طرق إزالة الضوضاء.
تفكيك الإشارة باستخدام DWT
في
المنشور ، رأينا كيف يتم تطبيق بنك التصفية على DWT الذي يمكنه فك إشارة في نطاقات التردد الفرعية الخاصة به. تمثل معاملات التقريب (cA) جزء التردد المنخفض للإشارة (مرشح المتوسط). تمثل معاملات التفاصيل (cD) جزء التردد العالي للإشارة. بعد ذلك ، سنبحث كيف يمكن استخدام DWT لفك إشارة في نطاقات التردد الفرعية واستعادة الإشارة الأصلية.
هناك طريقتان لحل مشكلة تفكيك الإشارة باستخدام أدوات PyWavelets:
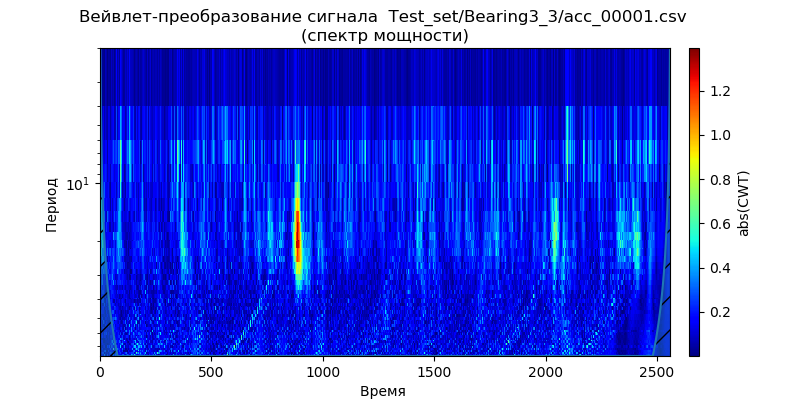
تتمثل الطريقة الأولى في تطبيق pywt.dwt () على الإشارة لاستخراج معاملات التقريب والتفاصيل (cA1 ، cD1). ثم ، لاستعادة الإشارة ، سنستخدم pywt.idwt ():
إدراج import pywt from scipy import * import pandas as pd from pylab import * filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) signal = df[4].values (cA1, cD1) = pywt .dwt (signal, 'db2', 'smooth') r_signal = pywt.idwt (cA1, cD1, 'db2', 'smooth') fig, ax =subplots(figsize=(8,4)) ax.plot(signal, 'b',label=' ') ax.plot(r_signal, 'r', label=' ', linestyle='--') ax.legend(loc='upper left') ax.set_ylabel(' ', fontsize=12) ax.set_xlabel('', fontsize=12) ax.set_title(' ( pywt.dwt()) \n ( pywt.idwt()) ') show()
الطريقة الثانية لتطبيق وظيفة pywt.wavedec () على الإشارة هي استعادة كل معاملات التقريب والتفاصيل إلى مستوى معين. تأخذ هذه الوظيفة الإشارة والمستوى الأولي كمدخل وتُرجع مجموعة واحدة من معاملات التقريب (المستوى n) ومجموعة n من معاملات التفاصيل (من المستوى 1 إلى المستوى n). للتفكيك ، قم بتطبيق pywt.waverec ():
إدراج import pywt import pandas as pd from pylab import * filename = 'Test_set/Bearing3_3/acc_00026.csv' df = pd.read_csv(filename, header=None) signal = df[4].values coeffs = pywt.wavedec(signal, 'db2', level=8) r_signal = pywt.waverec(coeffs, 'db2') fig, ax = plt.subplots(figsize=(8,4)) ax.plot(signal, 'b',label=' ') ax.plot(r_signal, 'r ',label= ' ', linestyle='--') ax.legend(loc='upper left') ax.set_ylabel(' ', fontsize=12) ax.set_xlabel('', fontsize=12) ax.set_title(' - level.\n ( pywt.wavedec()) ') show()

الطريقة الثانية لتفكيك واستعادة الإشارة هي أكثر ملاءمة ، فهي تتيح لك ضبط المستوى المطلوب على الفور من التفكيك.
إزالة الضوضاء عالية التردد عن طريق القضاء على بعض معاملات التفاصيل أثناء تفكيك الإشارة
سنقوم باستعادة الإشارة من خلال حذف بعض معاملات التفاصيل. نظرًا لأن معاملات التفاصيل تمثل الجزء عالي التردد من الإشارة ، فإننا ببساطة نقوم بتصفية هذا الجزء من طيف التردد. إذا كان هناك ضوضاء عالية التردد في الإشارة ، فهذه طريقة لتصفية ذلك.
في مكتبة PyWavelets ، يمكن القيام بذلك باستخدام وظيفة معالجة العتبة pywt.threshol ():
pywt.threshold (بيانات ، قيمة ، وضع = "ناعم" ، بديل = 0) ¶
البيانات: array_like
البيانات الرقمية.القيمة: العددية
قيمة العتبة.الوضع: {'soft' ، 'hard' ، 'garrote' ، 'أكبر' ، 'أقل'}
يحدد نوع العتبة التي سيتم تطبيقها على المدخلات. الافتراضي هو "لينة".بديل: تعويم ، اختياري
قيمة الاستبدال (الافتراضي: 0).الإخراج: مجموعة
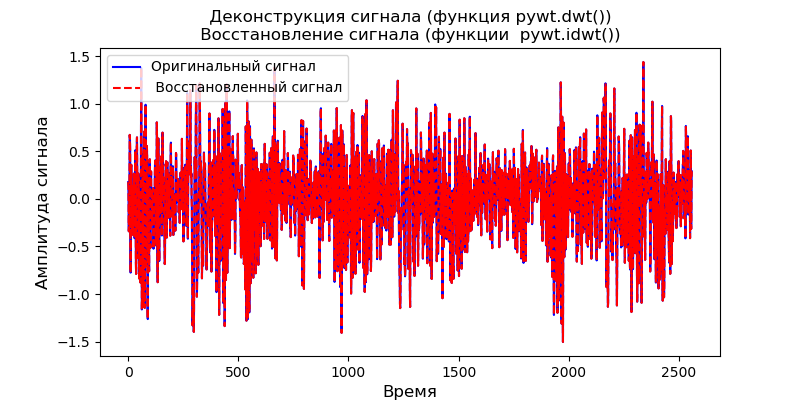
مجموعة عتبة.من الأفضل مراعاة تطبيق وظيفة معالجة العتبة لقيمة عتبة معينة باستخدام المثال التالي:
>>>> from scipy import* >>> import pywt >>> data =linspace(1, 4, 7) >>> data array([1. , 1.5, 2. , 2.5, 3. , 3.5, 4. ]) >>> pywt.threshold(data, 2, 'soft') array([0. , 0. , 0. , 0.5, 1. , 1.5, 2. ]) >>> pywt.threshold(data, 2, 'hard') array([0. , 0. , 2. , 2.5, 3. , 3.5, 4. ]) >>> pywt.threshold(data, 2, 'garrote') array([0. , 0. , 0., 0.9,1.66666667, 2.35714286, 3.])
نرسم الرسم البياني لوظيفة العتبة باستخدام القائمة التالية:
إدراج from scipy import* from pylab import* import pywt s = linspace(-4, 4, 1000) s_soft = pywt.threshold(s, value=0.5, mode='soft') s_hard = pywt.threshold(s, value=0.5, mode='hard') s_garrote = pywt.threshold(s, value=0.5, mode='garrote') figsize=(10, 4) plot(s, s_soft) plot(s, s_hard) plot(s, s_garrote) legend(['soft (0.5)', 'hard (0.5)', 'non-neg. garrote (0.5)']) xlabel(' ') ylabel(' ') show()
يوضح الرسم البياني أن عتبة Garott غير السالبة متوسطة بين العتبة الناعمة والصلبة. مطلوب زوج من العتبات التي تحدد عرض منطقة الانتقال.
تأثير وظيفة العتبة على خصائص المرشح
على النحو التالي من الرسم البياني أعلاه ، وظيفتان عتبيتان فقط "ناعمة" و "garrote" مناسبة لنا ، لدراسة تأثيرهما على خصائص المرشح ، نكتب القائمة:
إدراج import pandas as pd from pylab import * import pywt filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) signal = df[4].values v='bior4.4' thres=['soft' ,'garrote'] for w in thres: def lowpassfilter(signal, thresh, wavelet=v): thresh = thresh*nanmax(signal) coeff = pywt.wavedec(signal, wavelet, level=8,mode="per" ) coeff[1:] = (pywt.threshold(i, value=thresh, mode=w ) for i in coeff[1:]) reconstructed_signal = pywt.waverec(coeff, wavelet, mode="per" ) return reconstructed_signal fig, ax = subplots(figsize=(8,4)) ax.plot(signal, color="b", alpha=0.5, label=' ') rec = lowpassfilter(signal, 0.4) ax.plot(rec, 'r', label='DWT ', linewidth=2) ax.legend() ax.set_title(' :%s\n :%s'%(v,w), fontsize=12) ax.set_ylabel(' ', fontsize=12) ax.set_xlabel('', fontsize=12) show()

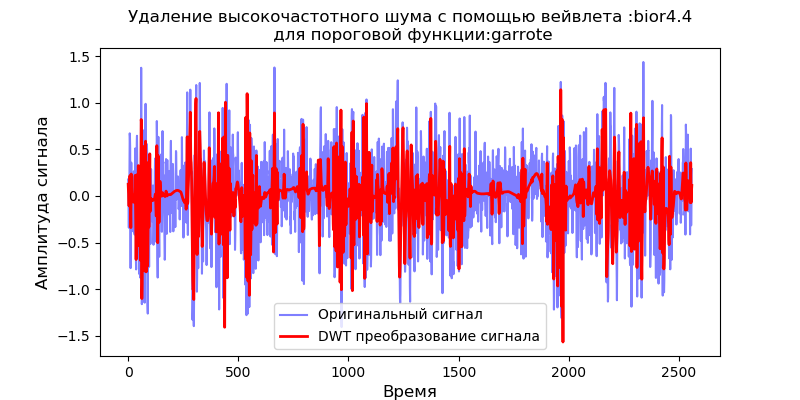
على النحو التالي من الرسوم البيانية ، توفر الوظيفة اللينة تجانسًا أفضل من وظيفة 'garrote' ، لذلك سوف نستخدم الوظيفة اللينة في المستقبل.
تأثير عتبة التفاصيل على خصائص المرشح
بالنسبة لنوع المرشح قيد النظر ، فإن عتبة تغيير معاملات التفاصيل هي خاصية مهمة ، وبالتالي ، فإننا ندرس تأثيرها باستخدام القائمة التالية:
إدراج import pandas as pd from pylab import * import pywt filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) signal = df[4].values v='bior4.4' thres=[0.1,0.4,0.6] for w in thres: def lowpassfilter(signal, thresh, wavelet=v): thresh = thresh*nanmax(signal) coeff = pywt.wavedec(signal, wavelet, level=8,mode="per" ) coeff[1:] = (pywt.threshold(i, value=thresh, mode='soft' ) for i in coeff[1:]) reconstructed_signal = pywt.waverec(coeff, wavelet, mode="per" ) return reconstructed_signal fig, ax = subplots(figsize=(8,4)) ax.plot(signal, color="b", alpha=0.5, label=' ') rec = lowpassfilter(signal,w) ax.plot(rec, 'r', label='DWT ', linewidth=2) ax.legend() ax.set_title(' :%s\n %s'%(v,w), fontsize=12) ax.set_ylabel(' ', fontsize=12) ax.set_xlabel('', fontsize=12) show()



على النحو التالي من الرسوم البيانية التي تم الحصول عليها ، يؤثر مستوى عتبة التفاصيل على مقياس الأجزاء التي تم فحصها. مع زيادة العتبة ، تطرح المويجة ضوضاء من مستوى متزايد باستمرار حتى يحدث زيادة مفرطة في مقياس التفاصيل ويبدأ التحول في تشويه شكل الإشارة الأصلية ، وبالنسبة لإشاراتنا ، يجب ألا تكون العتبة أعلى من 0.63.
تأثير المويجات على خصائص المرشح
تحتوي مكتبة PyWavelets على عدد كاف من الموجات لتحويل DWT ، والتي يمكن الحصول عليها مثل هذا:
>>> import pywt >>> print(pywt.wavelist(kind= 'discrete')) ['bior1.1', 'bior1.3', 'bior1.5', 'bior2.2', 'bior2.4', 'bior2.6', 'bior2.8', 'bior3.1', 'bior3.3', 'bior3.5', 'bior3.7', 'bior3.9', 'bior4.4', 'bior5.5', 'bior6.8', 'coif1', 'coif2', 'coif3', 'coif4', 'coif5', 'coif6', 'coif7', 'coif8', 'coif9', 'coif10', 'coif11', 'coif12', 'coif13', 'coif14', 'coif15', 'coif16', 'coif17', 'db1', 'db2', 'db3', 'db4', 'db5', 'db6', 'db7', 'db8', 'db9', 'db10', 'db11', 'db12', 'db13', 'db14', 'db15', 'db16', 'db17', 'db18', 'db19', 'db20', 'db21', 'db22', 'db23', 'db24', 'db25', 'db26', 'db27', 'db28', 'db29', 'db30', 'db31', 'db32', 'db33', 'db34', 'db35', 'db36', 'db37', 'db38', 'dmey', 'haar', 'rbio1.1', 'rbio1.3', 'rbio1.5', 'rbio2.2', 'rbio2.4', 'rbio2.6', 'rbio2.8', 'rbio3.1', 'rbio3.3', 'rbio3.5', 'rbio3.7', 'rbio3.9', 'rbio4.4', 'rbio5.5', 'rbio6.8', 'sym2', 'sym3', 'sym4', 'sym5', 'sym6', 'sym7', 'sym8', 'sym9', 'sym10', 'sym11', 'sym12', 'sym13', 'sym14', 'sym15', 'sym16', 'sym17', 'sym18', 'sym19', 'sym20']
يعتمد تأثير المويجات على خاصية المرشح على وظيفتها البدائية. لإثبات هذا الاعتماد ، نختار ملفين من عائلة Dobeshi - db1 و db38 ، ونفكر في هذه العائلات:
إدراج import pywt from pylab import* db_wavelets = ['db1', 'db38'] fig, axarr = subplots(ncols=2, nrows=5, figsize=(14,8)) fig.suptitle(' : db1,db38', fontsize=14) for col_no, waveletname in enumerate(db_wavelets): wavelet = pywt.Wavelet(waveletname) no_moments = wavelet.vanishing_moments_psi family_name = wavelet.family_name for row_no, level in enumerate(range(1,6)): wavelet_function, scaling_function, x_values = wavelet.wavefun(level = level) axarr[row_no, col_no].set_title("{} : {}. : {}. :: {} ".format( waveletname, level, no_moments, len(x_values)), loc='left') axarr[row_no, col_no].plot(x_values, wavelet_function, 'b--') axarr[row_no, col_no].set_yticks([]) axarr[row_no, col_no].set_yticklabels([]) tight_layout() subplots_adjust(top=0.9) show()
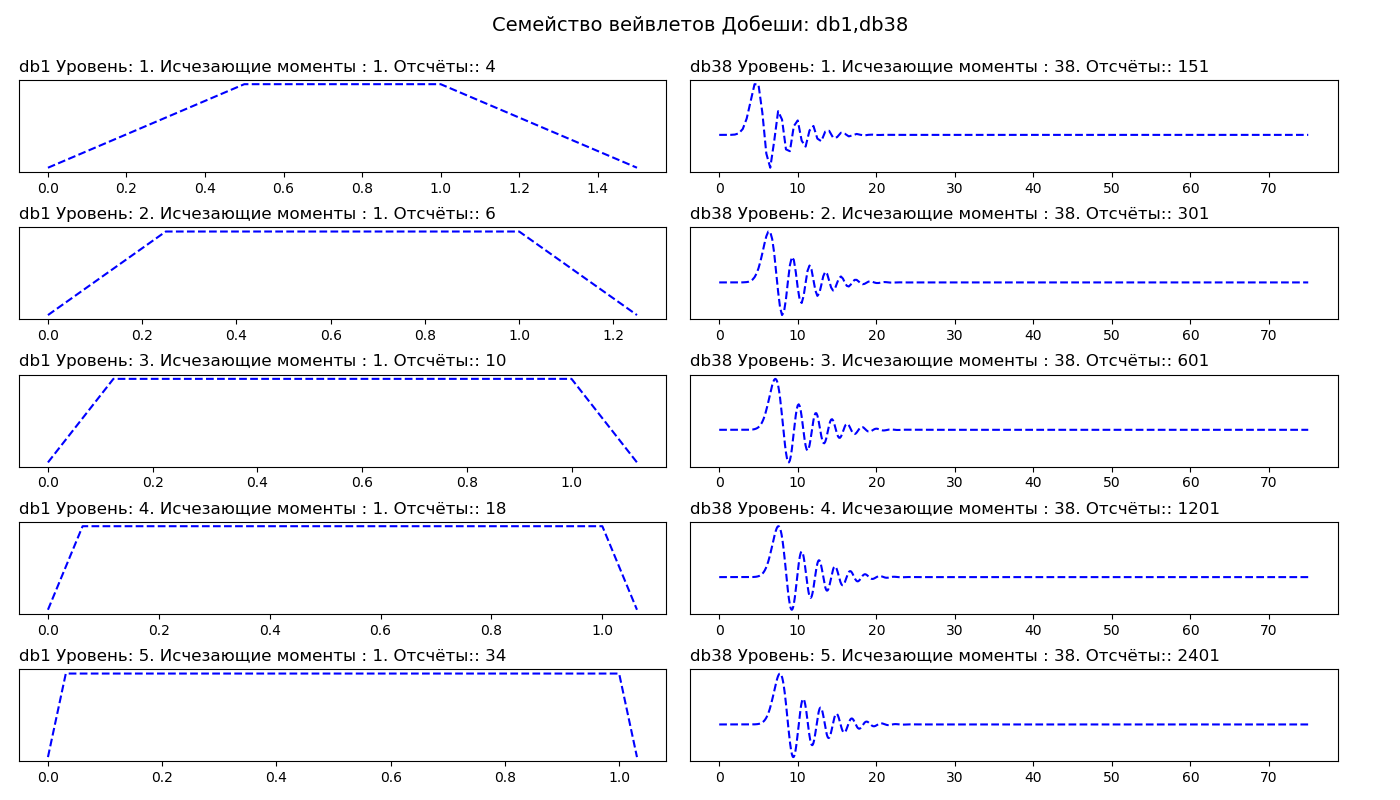
في العمود الأول ، نرى موجات Daubeshi من الترتيب الأول (db1) ، في العمود الثاني من الترتيب الثامن والثلاثين (db38). وبالتالي ، لدى db1 لحظة واحدة من الانقراض ، و db38 به 38 دقيقة من الانقراض. يرتبط عدد لحظات الاختفاء بترتيب التقريب وسلاسة المويجات. إذا كان للمويجات نقاط اختفاء P ، فيمكن أن تقريب كثير الحدود من الدرجة P - 1.
إنشاء موجات أكثر سلاسة تقريب إشارة أكثر سلاسة ، والعكس صحيح - تتبع موجات "قصيرة" بشكل أفضل ذروة الوظيفة التقريبية. عند اختيار المويجات ، يمكننا أيضًا الإشارة إلى مستوى التحلل. افتراضيًا ، تقوم PyWavelets بتحديد الحد الأقصى لمستوى التحلل المحتمل لإشارة الدخل. يعتمد الحد الأقصى لمستوى التحلل على طول إشارة الدخل والمويجات:
إدراج import pandas as pd import pywt filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) data = df[4].values w=['db1', 'db38'] for v in w: n_level=pywt.dwt_max_level(len(data),v) print(' %s : %s ' %(v,n_level))
ل db1 المويجات ، الحد الأقصى لمستوى التحلل: 11
بالنسبة إلى المويجات db38 ، الحد الأقصى لمستوى التحلل: 5
بالنسبة للقيم التي تم الحصول عليها من المستويات القصوى لتحلل المويجات ، فإننا نعتبر تشغيل المرشح لإزالة الضوضاء عالية التردد:
إدراج import pandas as pd import scaleogram as scg from pylab import * import pywt filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) signal = df[4].values discrete_wavelets =[('db38', 5),('db1',11)] for v in discrete_wavelets: def lowpassfilter(signal, thresh = 0.63, wavelet=v[0]): thresh = thresh*nanmax(signal) coeff = pywt.wavedec(signal, wavelet, mode="per" ) coeff[1:] = (pywt.threshold(i, value=thresh, mode='soft' ) for i in coeff[1:]) reconstructed_signal = pywt.waverec(coeff, wavelet, mode="per" ) return reconstructed_signal wavelet = pywt.DiscreteContinuousWavelet(v[0]) phi, psi, x = wavelet.wavefun(level=v[1]) fig, ax = subplots(figsize=(8,4)) ax.set_title(" : %s,level=%s"%(v[0],v[1]), fontsize=12) ax.plot(x,phi,linewidth=2) fig, ax = subplots(figsize=(8,4)) ax.plot(signal, color="b", alpha=0.5, label=' ') rec = lowpassfilter(signal, 0.4) ax.plot(rec, 'r', label='DWT ', linewidth=2) ax.legend() ax.set_title(' \n :%s,level=%s'%(v[0],v[1]),fontsize=12) ax.set_ylabel(' ', fontsize=12) ax.set_xlabel('', fontsize=12) wavelet = 'cmor1-0.5' ax = ax = scg.cws(rec, scales=arange(1,128), wavelet=wavelet,figsize=(8, 4), cmap="jet", ylabel=' ', xlabel=" ", yscale="log", title='CWT \n( DWT )') show()

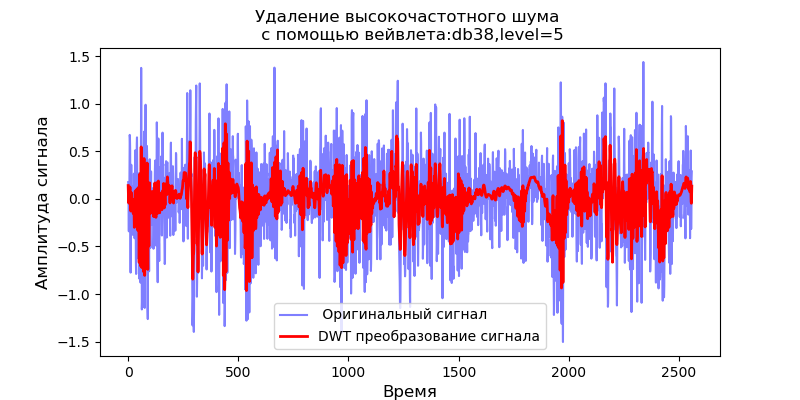
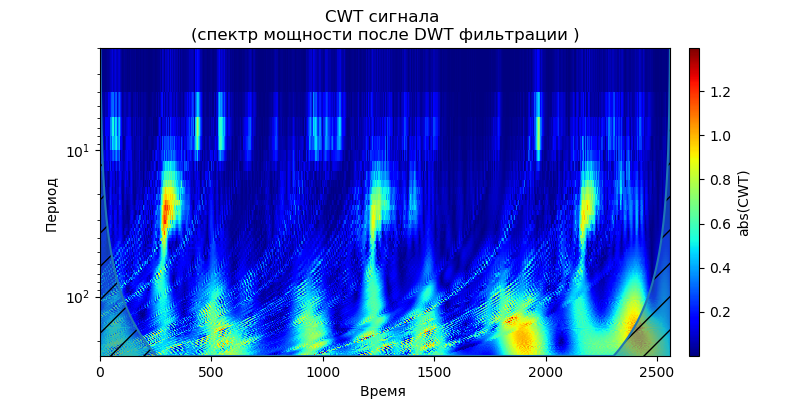

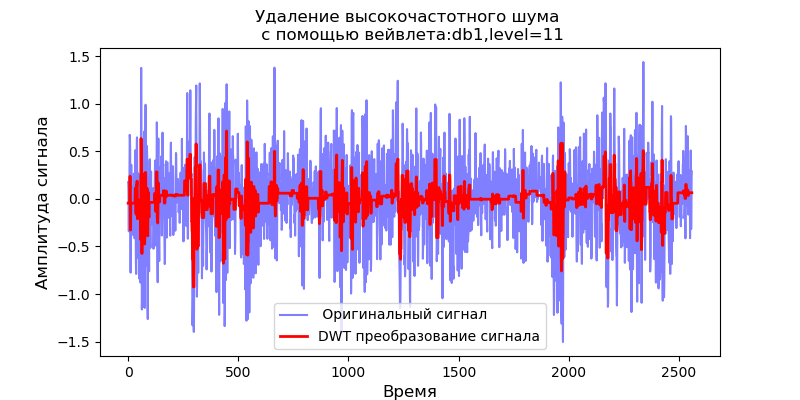

ويترتب على ذلك من الطول الموجي المذكور للإشارات عند خرج المرشح ، والتي تتبع ، بالنسبة إلى المويجات db38 ، ذروة قدرة الطيف بمناطق موضعية ، وتختفي هذه المناطق من خلال المويجات db1. تجدر الإشارة إلى أنه ، على سبيل المثال ، يمكن أن تقارب المويجات db38 تقريبًا إشارة درجة 37 متعددة الحدود. هذا يمتد تصنيف الإشارات ، على سبيل المثال ، لتحديد أعطال المعدات وفقا لإشارات أجهزة استشعار الاهتزاز.
نظرًا لأن الإشارة بعد التصفية باستخدام wavelet Daubechies تشكل سلسلة زمنية باستخدام معاملات التقريب والتحلل كخصائص السلسلة ، يمكن للمرء تحديد درجة قرب هذه السلسلة ، مما يسهل بشكل كبير عملية البحث والتصنيفمرشح كالمان لإزالة الضوضاء عالية التردد
يستخدم مرشح Kalman على نطاق واسع لتصفية الضوضاء في الأنظمة الديناميكية المختلفة. النظر في نظام ديناميكي مع متجه الدولة س.
حيث F هي المصفوفة الانتقالية
w (Q) هي عملية عشوائية (ضوضاء) مع صفر توقع رياضي ومصفوفة التباين Q.
سنلاحظ تحولات الحالة للنظام مع وجود خطأ قياس معروف في كل لحظة من الزمن. تتكون إزالة الضوضاء باستخدام طريقة كالمان من خطوتين - الاستقراء والتصحيح ، يبدو الأمر كذلك.
ضبط معلمات النظام:
Q- مصفوفة من التغاير الضوضاء (عملية الضوضاء المتغايرة).
H هي مصفوفة المراقبة (القياس).
R - تباين ضوضاء الملاحظة (قياس ضجيج التشابك).
P = Q هي القيمة الأولية لمصفوفة التغاير لمتجه الحالة.
z (t) هي الحالة المرصودة للنظام.
x = z (0) هي القيمة الأولية لتقييم حالة النظام.
لكل ملاحظة z ، سنقوم بحساب الحالة المصفاة x
ولهذا نقوم بتنفيذ الخطوات التالية.
• الخطوة 1: الاستقراء
1. الاستقراء (التنبؤ) لحالة النظام
2. حساب مصفوفة التغاير لمتجه الحالة استقراء
• الخطوة 2: تصحيح
1. حساب ناقلات الخطأ ، انحراف الملاحظة من الحالة المتوقعة
2. حساب مصفوفة التغاير لمتجه الانحراف (خطأ متجه)
3. حساب المكاسب كالمان
4. تصحيح تقدير ناقلات الحالة
5. نقوم بتصحيح مصفوفة التغاير لتقدير متجه حالة النظام
قائمة لتنفيذ الخوارزمية from scipy import* from pylab import* import pandas as pd def kalman_filter( z, F = eye(2), # (transitionMatrix) Q = eye(2)*3e-3, # (processNoiseCov) H = eye(2), # (measurement) R = eye(2)*3e-1 # (measurementNoiseCov) ): n = z.shape[0]
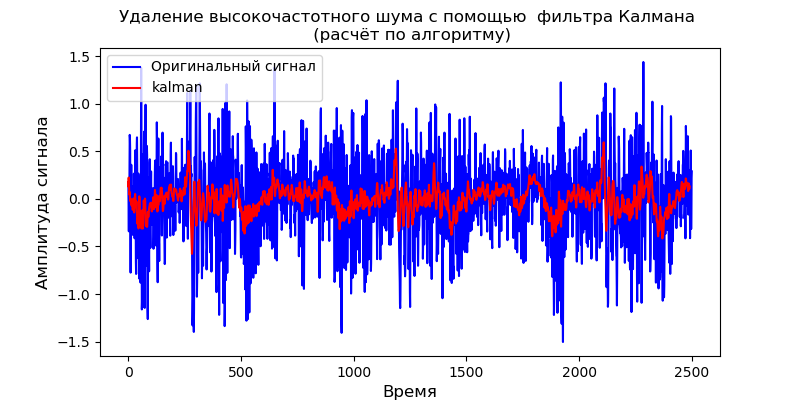
بالنسبة للنموذج الديناميكي المحدد ، يمكنك استخدام مكتبة pyKalman:
إدراج from pykalman import KalmanFilter import pandas as pd from pylab import * import scaleogram as scg filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) signal = df[4].values measurements =signal kf = KalmanFilter(transition_matrices=[1] ,



يزيل مرشح Kalman ضوضاء عالية التردد ، لكنه لا يسمح بتغيير شكل إشارة الخرج.
تتحرك طريقة المتوسط
عند تحديد الاتجاه الرئيسي للتغييرات في تسلسل متذبذب بقوة ، تنشأ مشكلة تجنّبها باستخدام طريقة المتوسط المتحرك. قد يكون هذا قراءات جهاز استشعار مستوى الوقود في السيارة أو ، كما في حالتنا ، بيانات أجهزة استشعار عالية التردد فيما يتعلق بتدهور المحامل بسرعة. يمكن اعتبار المشكلة استعادة بعض التسلسل r الذي تم فرض الضوضاء عليه.
المتوسط المتحرك البسيط لـ SMA القصير (المتوسط المتحرك البسيط). لحساب قيمة التصفية الحالية
نحن فقط نعدل العناصر السابقة في التسلسل ، لذلك يبدأ المرشح في العمل مع عنصر التسلسل n.
إدراج <source lang="python">from scipy import * import pandas as pd from pylab import * import pywt import scaleogram as scg def get_ave_values(xvalues, yvalues, n = 6): signal_length = len(xvalues) if signal_length % n == 0: padding_length = 0 else: padding_length = n - signal_length//n % n xarr = array(xvalues) yarr = array(yvalues) xarr.resize(signal_length//n, n) yarr.resize(signal_length//n, n) xarr_reshaped = xarr.reshape((-1,n)) yarr_reshaped = yarr.reshape((-1,n)) x_ave = xarr_reshaped[:,0] y_ave = nanmean(yarr_reshaped, axis=1) return x_ave, y_ave def plot_signal_plus_average(time, signal, average_over = 5): fig, ax = subplots(figsize=(8, 4)) time_ave, signal_ave = get_ave_values(time, signal, average_over) ax.plot(time_ave, signal_ave,"b", label = ' (n={})'.format(5)) ax.set_xlim([time[0], time[-1]]) ax.set_ylabel(' ', fontsize=12) ax.set_title(' SMA', fontsize=14) ax.set_xlabel('', fontsize=12) ax.legend() return signal_ave filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) df_nino = df[4].values N = df_nino.shape[0] time = arange(0, N) signal = df_nino signal_ave=plot_signal_plus_average(time, signal) wavelet = 'cmor1-0.5' ax = ax = scg.cws(signal, scales=arange(1,40), wavelet=wavelet, figsize=(8, 4),cmap="jet", ylabel=' ', xlabel=" ", yscale="log", title='CWT %s \n( )'%filename) ax = ax = scg.cws(signal_ave, scales=arange(1,40), wavelet=wavelet, figsize=(8, 4), cmap="jet", ylabel=' ', xlabel=" ", yscale="log", title='CWT %s \n( )'%filename) show()


كما يلي من scalogram ، فإن طريقة SMA تنظف بشكل سيء الإشارة من الضوضاء عالية التردد ، و
كما ذكر أعلاه يستخدم للتجانس.
الاستنتاجات:
- باستخدام وحدة المقياس ، تم الحصول على CWT scalograms من ثلاث إشارات لمستشعر اهتزاز الاختبار لظروف اختبار مختلفة للمحامل من نفس النوع. وفقا لبيانات scalogram ، تم اختيار إشارة مع علامات واضحة على التدهور المتأخر. تم استخدام هذه الإشارة لإظهار تشغيل المرشحات في جميع الأمثلة المقدمة.
- يتم النظر في أساليب مكتبة PyWavelets لتفكيك واستعادة إشارة استشعار الاهتزاز باستخدام الوحدات النمطية pywt.dwt () و pywt.idwt () والوحدة النمطية pywt.wavedec () لمستوى المويجات المعطى.
- تُظهر الأمثلة ميزات التطبيق لوحدة pywt.threshol () لتصفية معاملات تحسين DWT ، المسؤولة عن الجزء عالي التردد من الطيف باستخدام وظائف العتبة لقيمة عتبة معينة.
- يتم النظر في تأثيرات المويجات DWT المضادة للخصوبة على شكل إشارة تطهيرها من الضوضاء.
- يتم الحصول على نموذج مرشح Kalman للوسط الديناميكي ، ويتم اختبار النموذج على إشارة اختبار مستشعر الاهتزاز. مؤامرة إزالة الضوضاء هي نفسها التي تم الحصول عليها باستخدام وحدة pyKalman. طبيعة الرسم البياني يتزامن مع scalogram.
- .