
تم إعداد ترجمة المقال خاصة لطلاب الدورة التدريبية "الخوارزميات للمطورين" .
يعد الفرز الهرمي (أو فرز الكومة ، HeapSort) طريقة فرز مقارنة تستند إلى بنية بيانات مثل كومة الذاكرة المؤقتة الثنائية. إنه مشابه للفرز حسب الاختيار ، حيث نبحث أولاً عن الحد الأقصى للعنصر ونضعه في النهاية. بعد ذلك ، نكرر نفس العملية للعناصر المتبقية.
دعونا أولا تحديد شجرة ثنائية كاملة. الشجرة الثنائية المكتملة هي شجرة ثنائية تحتوي كل مستوى ، مع استثناء محتمل من الأخير ، على مجموعة كاملة من العقد ، وتقع جميع الأوراق على اليسار (Source Wikipedia ).
الكومة الثنائية عبارة عن شجرة ثنائية كاملة يتم فيها تخزين العناصر بترتيب خاص: القيمة في العقدة الأصلية أكبر من (أو أقل من) القيم الموجودة في العقدتين الفرعيتين. الخيار الأول يسمى max-heap ، والثاني min-heap. يمكن تمثيل كومة بواسطة شجرة ثنائية أو صفيف.
لماذا يتم استخدام تمثيل الصفيف المستند إلى كومة الذاكرة المؤقتة الثنائية؟
نظرًا لأن كومة الذاكرة المؤقتة الثنائية عبارة عن شجرة ثنائية كاملة ، يمكن تمثيلها بسهولة كصفيف ، ويكون التمثيل المستند إلى الصفيف فعالًا من حيث استهلاك الذاكرة. إذا تم تخزين العقدة الأصل في الفهرس I ، فيمكن حساب الطفل الأيسر على أنه 2 I + 1 ، ويمكن حساب الطفل الأيمن على أنه 2 I + 2 (بشرط أن يبدأ الفهرسة عند 0).
خوارزمية الفرز الهرمي بالترتيب التصاعدي:
- بناء أقصى كومة من المدخلات.
- في هذه المرحلة ، يتم تخزين أكبر عنصر في جذر الكومة. استبدلها بالعنصر الأخير من الكومة ، ثم قم بتقليل حجمها بمقدار 1. أخيرًا ، قم بتحويل الشجرة الناتجة إلى كومة كومة ذات جذر جديد.
- كرر الخطوات أعلاه حتى يصبح حجم الكومة أكبر من 1.
كيفية بناء حفنة؟
يمكن تطبيق إجراء تحويل الكومة (المشار إليها فيما يلي باسم إجراء كومة الذاكرة المؤقتة) على عقدة فقط إذا تم بالفعل تحويل العقد التابعة لها. وبالتالي ، يجب إجراء التحويل من الأسفل إلى الأعلى. دعونا معرفة ذلك مع مثال:
: 4, 10, 3, 5, 1 4(0) / \ 10(1) 3(2) / \ 5(3) 1(4) . heapify 1: 4(0) / \ 10(1) 3(2) / \ 5(3) 1(4) heapify 0: 10(0) / \ 5(1) 3(2) / \ 4(3) 1(4) heapify .
التوصية: يرجى حل المشكلة على "الممارسة" أولاً قبل متابعة الحل .
C ++
// C++ #include <iostream> using namespace std; // i, // arr[]. n - void heapify(int arr[], int n, int i) { int largest = i; // int l = 2*i + 1; // = 2*i + 1 int r = 2*i + 2; // = 2*i + 2 // if (l < n && arr[l] > arr[largest]) largest = l; // , if (r < n && arr[r] > arr[largest]) largest = r; // if (largest != i) { swap(arr[i], arr[largest]); // heapify(arr, n, largest); } } // , void heapSort(int arr[], int n) { // ( ) for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // for (int i=n-1; i>=0; i--) { // swap(arr[0], arr[i]); // heapify heapify(arr, i, 0); } } /* n*/ void printArray(int arr[], int n) { for (int i=0; i<n; ++i) cout << arr[i] << " "; cout << "\n"; } // int main() { int arr[] = {12, 11, 13, 5, 6, 7}; int n = sizeof(arr)/sizeof(arr[0]); heapSort(arr, n); cout << "Sorted array is \n"; printArray(arr, n); }
جافا
// Java public class HeapSort { public void sort(int arr[]) { int n = arr.length; // ( ) for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // for (int i=n-1; i>=0; i--) { // int temp = arr[0]; arr[0] = arr[i]; arr[i] = temp; // heapify heapify(arr, i, 0); } } // i, // arr[]. n - void heapify(int arr[], int n, int i) { int largest = i; // int l = 2*i + 1; // = 2*i + 1 int r = 2*i + 2; // = 2*i + 2 // if (l < n && arr[l] > arr[largest]) largest = l; // , if (r < n && arr[r] > arr[largest]) largest = r; // if (largest != i) { int swap = arr[i]; arr[i] = arr[largest]; arr[largest] = swap; // heapify(arr, n, largest); } } /* n */ static void printArray(int arr[]) { int n = arr.length; for (int i=0; i<n; ++i) System.out.print(arr[i]+" "); System.out.println(); } // public static void main(String args[]) { int arr[] = {12, 11, 13, 5, 6, 7}; int n = arr.length; HeapSort ob = new HeapSort(); ob.sort(arr); System.out.println("Sorted array is"); printArray(arr); } }
الثعبان
# Python # i, arr[]. n - def heapify(arr, n, i): largest = i # Initialize largest as root l = 2 * i + 1 # left = 2*i + 1 r = 2 * i + 2 # right = 2*i + 2 # , if l < n and arr[i] < arr[l]: largest = l # , if r < n and arr[largest] < arr[r]: largest = r # , if largest != i: arr[i],arr[largest] = arr[largest],arr[i] # # heapify . heapify(arr, n, largest) # def heapSort(arr): n = len(arr) # max-heap. for i in range(n, -1, -1): heapify(arr, n, i) # for i in range(n-1, 0, -1): arr[i], arr[0] = arr[0], arr[i] # heapify(arr, i, 0) # arr = [ 12, 11, 13, 5, 6, 7] heapSort(arr) n = len(arr) print ("Sorted array is") for i in range(n): print ("%d" %arr[i]), # Mohit Kumra
C حاد
// C# using System; public class HeapSort { public void sort(int[] arr) { int n = arr.Length; // ( ) for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // for (int i=n-1; i>=0; i--) { // int temp = arr[0]; arr[0] = arr[i]; arr[i] = temp; // heapify heapify(arr, i, 0); } } // i, // arr[]. n - void heapify(int[] arr, int n, int i) { int largest = i; // int l = 2*i + 1; // left = 2*i + 1 int r = 2*i + 2; // right = 2*i + 2 // if (l < n && arr[l] > arr[largest]) largest = l; // , if (r < n && arr[r] > arr[largest]) largest = r; // if (largest != i) { int swap = arr[i]; arr[i] = arr[largest]; arr[largest] = swap; // heapify(arr, n, largest); } } /* n */ static void printArray(int[] arr) { int n = arr.Length; for (int i=0; i<n; ++i) Console.Write(arr[i]+" "); Console.Read(); } // public static void Main() { int[] arr = {12, 11, 13, 5, 6, 7}; int n = arr.Length; HeapSort ob = new HeapSort(); ob.sort(arr); Console.WriteLine("Sorted array is"); printArray(arr); } } // // Akanksha Ra (Abby_akku)
PHP
<?php // Php // i, // arr[]. n - function heapify(&$arr, $n, $i) { $largest = $i; // $l = 2*$i + 1; // = 2*i + 1 $r = 2*$i + 2; // = 2*i + 2 // if ($l < $n && $arr[$l] > $arr[$largest]) $largest = $l; // , if ($r < $n && $arr[$r] > $arr[$largest]) $largest = $r; // if ($largest != $i) { $swap = $arr[$i]; $arr[$i] = $arr[$largest]; $arr[$largest] = $swap; // heapify($arr, $n, $largest); } } // , function heapSort(&$arr, $n) { // ( ) for ($i = $n / 2 - 1; $i >= 0; $i--) heapify($arr, $n, $i); // for ($i = $n-1; $i >= 0; $i--) { // $temp = $arr[0]; $arr[0] = $arr[$i]; $arr[$i] = $temp; // heapify heapify($arr, $i, 0); } } /* n */ function printArray(&$arr, $n) { for ($i = 0; $i < $n; ++$i) echo ($arr[$i]." ") ; } // $arr = array(12, 11, 13, 5, 6, 7); $n = sizeof($arr)/sizeof($arr[0]); heapSort($arr, $n); echo 'Sorted array is ' . "\n"; printArray($arr , $n); // Shivi_Aggarwal ?>
الاستنتاج:
: 5 6 7 11 12 13
هنا هو رمز C السابق للرجوع اليها.
ملاحظات:
الفرز الهرمي هو خوارزمية مناسبة تماما. تنفيذه النموذجي غير مستقر ، ولكن يمكن القيام به على هذا النحو (انظر هنا ).
تعقيد الوقت: تعقيد الوقت من heapify هو O (Logn). التعقيد الزمني لـ createAndBuildHeap () هو O (n) ، وإجمالي وقت تشغيل الفرز الهرمي هو O (nLogn).
تطبيقات هرمية الترتيب:
- فرز مجموعة مرتبة (أو مرتبة حسب المواضع K) تقريبًا ؛
- k أكبر (أو أصغر) العناصر في الصفيف .
خوارزمية الفرز الهرمية لها استخدام محدود ، لأن Quicksort و Mergesort أفضل في الممارسة العملية. ومع ذلك ، يتم استخدام بنية البيانات كومة الذاكرة المؤقتة نفسه في كثير من الأحيان. راجع تطبيقات بنية بيانات الكومة
لقطات:
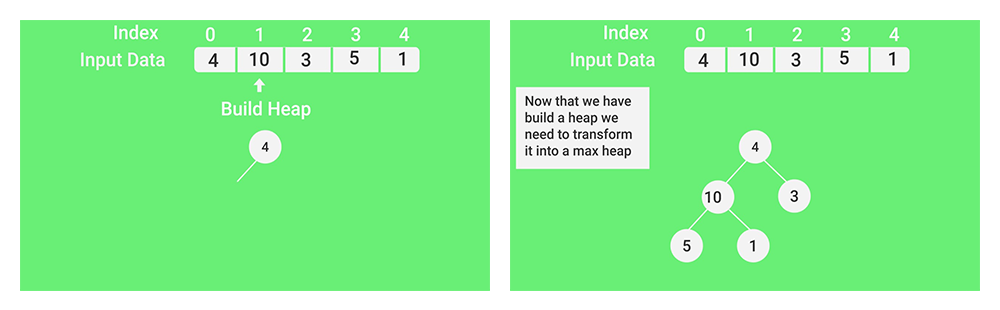
- (الآن وبعد أن أنشأنا الكومة ، نحتاج إلى تحويلها إلى max-heap)

- (في أقصى كومة الذاكرة المؤقتة ، تكون العقدة الأصل أكبر دائمًا من العقد الفرعية أو مساوية لها
10 أكثر من 4. لذلك ، نحن مبادلة 4 و 10)
- (في أقصى كومة الذاكرة المؤقتة ، تكون العقدة الأصل أكبر دائمًا من العقد الفرعية أو مساوية لها
5 more 4. لذلك ، نحن مبادلة الأماكن 5 و 4)

- (قم بتبديل العقدتين الأولى والأخيرة وحذف الأخير من الكومة)
اختبار الهرم
خوارزميات الفرز الأخرى على GeeksforGeeks / GeeksQuiz:
فرز سريع ، فرز حسب الاختيار ، فرز الفقاعات ، إدراج فرز ، ترتيب الفرز ، ترتيب هرمي ، ترتيب الفرز ، فرز الفرز ، فرز الفرز ، حظر الفرز ، ترتيب الفرز ، ترتيب الفرز مع قائمة .
ورشة الفرز
يرجى ترك تعليقات إذا وجدت شيئًا خاطئًا أو إذا كنت ترغب في مشاركة معلومات إضافية حول الموضوع الذي تمت مناقشته أعلاه.