كتاب "التعلم الآلي للأعمال والتسويق"

أصبحت علوم البيانات جزءًا لا يتجزأ من أي نشاط تسويقي ، وهذا الكتاب هو صورة حية للتحول الرقمي في التسويق. تحليل البيانات والخوارزميات الذكية أتمتة المهام التسويقية تستغرق وقتا طويلا. أصبحت عملية صنع القرار أكثر كمالًا فحسب ، بل أصبحت أيضًا أسرع ، وهي ذات أهمية كبيرة في بيئة تنافسية متسارعة باستمرار.

"هذا الكتاب هو صورة حية للتحول الرقمي في التسويق. إنه يوضح كيف أصبحت علوم البيانات جزءًا لا يتجزأ من أي نشاط تسويقي. يصف بالتفصيل كيف تساهم النهج المعتمدة على تحليل البيانات والخوارزميات الذكية في التشغيل الآلي للمهام التسويقية الكثيفة العمالة التقليدية. أصبحت عملية صنع القرار أكثر تقدمًا فحسب ، بل أصبحت أيضًا أسرع ، وهو أمر مهم في بيئتنا التنافسية المتسارعة باستمرار. يجب قراءة هذا الكتاب من قِبل متخصصي معالجة البيانات ومتخصصي التسويق ، ومن الأفضل أن يقرأوه معًا. " أندريه سبرانت ، مدير التسويق الاستراتيجي ، ياندكس.

مقتطفات. 5.8.3. نماذج عامل مخفي

في خوارزميات التصفية المشتركة التي تمت مناقشتها حتى الآن ، تستند معظم الحسابات إلى العناصر الفردية لمصفوفة التصنيف. تقوم الأساليب المستندة إلى القرب بتقييم التصنيفات المفقودة مباشرةً من القيم المعروفة في مصفوفة التصنيف. تضيف الطرق المستندة إلى النماذج طبقة تجريدية أعلى مصفوفة التقييم ، مما يخلق نموذجًا تنبؤيًا يلتقط أنماطًا معينة من العلاقات بين المستخدمين والعناصر ، لكن التدريب النموذجي لا يزال يعتمد بشكل كبير على خصائص مصفوفة التصنيف. نتيجة لذلك ، تواجه تقنيات التصفية التعاونية هذه المشكلات التالية:

يمكن أن تحتوي مصفوفة التصنيف على ملايين المستخدمين ، وملايين العناصر والمليارات من التصنيفات المعروفة ، مما يخلق مشاكل خطيرة من التعقيد الحسابي وإمكانية التوسع.

مصفوفة التصنيف عادة ما تكون قليلة جدًا (في الممارسة العملية ، قد يكون حوالي 99٪ من التصنيفات مفقودة). يؤثر هذا على الاستقرار الحسابي لخوارزميات التوصية ويؤدي إلى تقديرات غير موثوق بها عندما لا يكون لدى المستخدم أو العنصر جيران متشابهان بالفعل. غالبًا ما تتفاقم هذه المشكلة من خلال حقيقة أن معظم الخوارزميات الأساسية إما موجهة من قبل المستخدم أو العنصر ، مما يحد من قدرتها على تسجيل جميع أنواع التشابه والعلاقات المتاحة في مصفوفة التصنيف.

عادة ما تكون البيانات في مصفوفة التصنيف مرتبطة بقوة بسبب أوجه التشابه بين المستخدمين والعناصر. هذا يعني أن الإشارات المتاحة في مصفوفة التصنيف ليست متفرقة فحسب ، بل هي زائدة عن الحاجة ، مما يساهم في تفاقم مشكلة قابلية التوسع.

تشير الاعتبارات المذكورة أعلاه إلى أن مصفوفة التصنيف الأصلية قد لا تمثل أفضل تمثيل للإشارات ، وينبغي النظر في تمثيلات بديلة أخرى أكثر ملاءمة لتصفية المفاصل. لاستكشاف هذه الفكرة ، دعنا نعود إلى نقطة البداية ونفكر قليلاً في طبيعة خدمات التوصية. في الواقع ، يمكن اعتبار خدمة التوصية كخوارزمية تتنبأ بالتصنيفات بناءً على قدر من التشابه بين المستخدم والعنصر:


تتمثل إحدى طرق تحديد مقياس التشابه في استخدام نهج العامل المخفي ومستخدمي الخريطة والعناصر للنقاط في بعض الفضاء ذي الأبعاد k بحيث يتم تمثيل كل مستخدم وكل عنصر بواسطة ناقل k:


يجب بناء المتجهات بحيث تكون الأبعاد المقابلة p و q قابلة للمقارنة مع بعضها البعض. بمعنى آخر ، يمكن اعتبار كل بُعد علامة أو مفهومًا ، أي أن puj هو مقياس لقرب المستخدم u والمفهوم j ، و qij ، على التوالي ، مقياس للعنصر i والمفهوم j. في الممارسة العملية ، غالبًا ما يتم تفسير هذه الأبعاد على أنها أنواع وأنماط وسمات أخرى تنطبق في نفس الوقت على المستخدمين والعناصر. التشابه بين المستخدم والعنصر ، وبالتالي ، يمكن تعريف التصنيف على أنه منتج المتجهات المقابلة:


نظرًا لأنه يمكن تقسيم كل تصنيف إلى منتج من متجهين ينتميان إلى مساحة مفهوم لا يتم ملاحظتها مباشرةً في مصفوفة التقييم الأصلية ، تسمى p و q العوامل المخفية. بطبيعة الحال ، يعتمد نجاح هذا النهج التجريدي كليًا على كيفية تحديد العوامل الخفية وبناءها. للإجابة على هذا السؤال ، نلاحظ أنه يمكن إعادة كتابة التعبير 5.92 في شكل مصفوفة على النحو التالي:


حيث P هي مصفوفة n × k مجمعة من المتجهات p ، و Q هي مصفوفة m × k مجمعة من المتجهات q ، كما هو مبين في الشكل. 5.13. يتمثل الهدف الرئيسي لنظام تصفية مشترك عادةً في تقليل أخطاء التنبؤ في التصنيف إلى الحد الأدنى ، مما يسمح لك بتحديد مشكلة التحسين بشكل مباشر بالنسبة إلى مصفوفة العوامل المخفية:



بافتراض أن عدد الأبعاد المخفية k ثابت و k ≤ n و k ≤m ، فإن مشكلة التحسين 5.94 تنخفض إلى مشكلة التقريب ذات الترتيب المنخفض ، والتي بحثناها في الفصل 2. لشرح النهج المتبع في الحل ، دعنا نفترض للحظة أن مصفوفة التصنيف مكتملة. في هذه الحالة ، تشتمل مشكلة التحسين على حل تحليلي من حيث تحليل القيمة الفردية (SVD) لمصفوفة التصنيف. على وجه الخصوص ، باستخدام خوارزمية SVD القياسية ، يمكن تحلل المصفوفة في نتاج ثلاث مصفوفات:


حيث U هي المصفوفة n × n الموروثة حسب الأعمدة ، Σ هي المصفوفة المائلة n × m ، و V هي المصفوفة m × m المصفوفة بالأعمدة. يمكن الحصول على الحل الأمثل للمشكلة 5.94 من حيث هذه العوامل ، المقطوعة إلى أبعاد k الأكثر أهمية:


وبالتالي ، يمكن الحصول على العوامل الخفية التي هي الأمثل من حيث دقة التنبؤ عن طريق التحلل المفرد ، كما هو مبين أدناه:


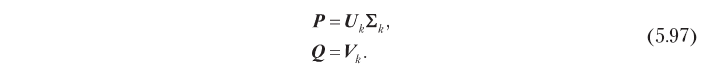
يساعد نموذج العوامل المخفية المستند إلى SVD في حل مشكلات التصفية المشتركة الموضحة في بداية هذا القسم. أولاً ، يستبدل مصفوفة تصنيف n × m كبيرة بمصفوفات n × k و m × k ، والتي عادةً ما تكون أصغر بكثير ، لأنه في الممارسة العملية يكون العدد الأمثل للأبعاد المخفية k صغيرًا في الغالب. على سبيل المثال ، هناك حالة تمكنت فيها مصفوفة التصنيف التي تضم 500000 مستخدم و 17000 عنصر من التقريب جيدًا باستخدام 40 قياسات [Funk، 2016]. علاوة على ذلك ، يحل SVD الارتباط في مصفوفة التصنيف: مصفوفات العوامل الكامنة المحددة في 5.97 هي غير طبيعية في الأعمدة ، أي الأبعاد المخفية ليست مرتبطة. إذا كان هذا صحيحًا في الممارسة العملية ، فإن SVD يحل أيضًا مشكلة التباين ، لأن الإشارة الموجودة في مصفوفة التقييم الأولية تتركز بفعالية (تذكر أننا نختار أبعاد k بأعلى طاقة إشارة) ، وأن مصفوفات العوامل الكامنة ليست متناثرة. يوضح الشكل 5.14 هذه الخاصية. تعمل خوارزمية القرب المستندة إلى المستخدم (5.14 ، أ) على طي متجهات التقييم المتناثر لعنصر معين ومستخدم معين للحصول على درجة تقييم. على النقيض من ذلك ، فإن نموذج العامل الخفي (5.14 ، ب) ، يُقدِّر التصنيف عن طريق الإلتواء بين متجهين ذي أبعاد منخفضة وكثافة طاقة أعلى.


يبدو النهج الموصوف للتو وكأنه حل متماسك لمشكلة العوامل الخفية ، ولكن في الواقع له عيب خطير بسبب افتراض أن مصفوفة التصنيف كاملة. إذا كانت مصفوفة التقييم متناثرة ، وهو ما يحدث دائمًا تقريبًا ، فلن يمكن تطبيق خوارزمية SVD القياسية مباشرةً ، نظرًا لعدم قدرتها على معالجة العناصر المفقودة (غير المحددة). الحل الأبسط في هذه الحالة هو ملء التصنيفات المفقودة ببعض القيمة الافتراضية ، ولكن هذا قد يؤدي إلى تحيز خطير في التنبؤ. بالإضافة إلى ذلك ، فإنه غير فعال من الناحية الحسابية لأن التعقيد الحسابي لمثل هذا الحل يساوي تعقيد SVD للمصفوفة الكاملة x ، في حين أنه من المستحسن أن يكون هناك طريقة ذات تعقيد تتناسب مع عدد التصنيفات المعروفة. يمكن حل هذه المشكلات باستخدام طرق التحلل البديلة الموضحة في الأقسام التالية.

5.8.3.1. التحلل غير محدود

تعد خوارزمية SVD القياسية حلاً تحليليًا لمشكلة التقريب منخفضة المستوى. ومع ذلك ، يمكن اعتبار هذه المشكلة مشكلة تحسين ، ويمكن أيضًا تطبيق أساليب التحسين العامة عليها. أحد أبسط الطرق هو استخدام طريقة النسب التدرج لصقل قيم العوامل المخفية بشكل متكرر. نقطة البداية هي تعريف دالة التكلفة J كخطأ التنبؤ المتبقي:


يرجى ملاحظة أننا هذه المرة لا نفرض أي قيود ، مثل التعامد ، على مصفوفة العوامل المخفية. عند حساب تدرج دالة التكلفة فيما يتعلق بالعوامل المخفية ، نحصل على النتيجة التالية:


حيث E هي مصفوفة الخطأ المتبقية:


تعمل خوارزمية النسب التدرج على تقليل دالة التكلفة عن طريق التحرك في كل خطوة في الاتجاه السلبي للتدرج. لذلك ، يمكنك العثور على العوامل المخفية التي تقلل من الخطأ التربيعي للتنبؤ بالتصنيف عن طريق تغيير المصفوفات P و Q لتتلاقى ، وفقًا التعبيرات التالية:


حيث α هي سرعة التعلم. عيب طريقة النسب التدرج هو الحاجة إلى حساب المصفوفة بأكملها من الأخطاء المتبقية وتغيير جميع القيم في وقت واحد من العوامل الخفية في كل التكرار. نهج بديل ، والذي قد يكون أكثر ملاءمة لمصفوفات كبيرة ، هو النسب التدرج العشوائي [فونك ، 2016]. تستخدم خوارزمية نزول التدرجات العشوائية العشوائية حقيقة أن الخطأ الإجمالي للتنبؤ J هو مجموع الأخطاء للعناصر الفردية في مصفوفة التصنيف ؛ لذلك ، يمكن تقريب التدرج العام J بتدرج في نقطة بيانات واحدة ، ويمكن تغيير العوامل المخفية إلى حد ما. يظهر التنفيذ الكامل لهذه الفكرة في الخوارزمية 5.1.


المرحلة الأولى من الخوارزمية هي تهيئة مصفوفة العوامل الخفية. اختيار هذه القيم الأولية ليس مهمًا للغاية ، ولكن في هذه الحالة ، يتم اختيار توزيع موحد للطاقة من التصنيفات المعروفة بين العوامل الخفية التي تم إنشاؤها عشوائيًا. ثم تقوم الخوارزمية بتحسين أبعاد المفهوم بالتتابع. لكل قياس ، فإنه يتكرر بشكل متكرر حول جميع التصنيفات الموجودة في مجموعة التدريب ، ويتوقع كل تصنيف باستخدام القيم الحالية للعوامل المخفية ، ويقدر الخطأ ويصحح قيم العوامل وفقًا التعبيرات 5.101. يتم إكمال تحسين القياس عند استيفاء شرط التقارب ، وبعد ذلك تنتقل الخوارزمية إلى القياس التالي.

تساعد الخوارزمية 5.1 في التغلب على قيود طريقة SVD القياسية. يعمل على تحسين العوامل المخفية من خلال تنفيذ نقاط بيانات فردية ، وبالتالي تجنب المشكلات المتعلقة بالتصنيفات المفقودة والعمليات الجبرية ذات المصفوفات العملاقة. كما أن النهج التكراري يجعل نزول التدرج العشوائي أكثر ملاءمة للتطبيقات العملية من نزول التدرج ، الذي يعدل المصفوفات بأكملها باستخدام التعبيرات 5.101.

مثال 5.6

في الواقع ، فإن النهج القائم على العوامل المخفية هو مجموعة كاملة من أساليب تمثيل التدريس التي يمكن أن تحدد الأنماط الضمنية في مصفوفة التقييم وتمثلها بوضوح في شكل مفاهيم. في بعض الأحيان يكون للمفاهيم تفسير ذو معنى تمامًا ، خاصة تلك ذات الطاقة العالية ، على الرغم من أن هذا لا يعني أن جميع المفاهيم لها دائمًا معنى ذي معنى. على سبيل المثال ، يمكن لتطبيق خوارزمية تحلل المصفوفة على قاعدة بيانات لتصنيفات الأفلام أن ينشئ عوامل تتوافق تقريبًا مع الأبعاد النفسية ، مثل الميلودراما والكوميديا ​​والرعب وما إلى ذلك. دعونا نوضح هذه الظاهرة بمثال رقمي صغير يستخدم مصفوفة التصنيف من الجدول. 5.3:


أولاً ، قم بطرح المتوسط ​​العام 2.8 = 2.82 من جميع العناصر لتوسيط المصفوفة ، ثم قم بتنفيذ الخوارزمية 5.1 باستخدام k = 3 القياسات المخفية ومعدل التعلم α = 0.01 للحصول على مصفوفة العوامل التاليتين:


يتوافق كل صف في هذه المصفوفات مع مستخدم أو فيلم ، ويتم عرض كل ناقلات الصف 12 في الشكل. 5.15. يرجى ملاحظة أن العناصر الموجودة في العمود الأول (أول متجه للمفاهيم) لها أكبر القيم ، وأن القيم في الأعمدة اللاحقة تتناقص تدريجياً. يتم تفسير ذلك من خلال حقيقة أن ناقلات المفهوم الأول تلتقط أكبر قدر من طاقة الإشارة من الممكن التقاطها بقياس واحد ، بينما يلتقط ناقل المفهوم الثاني جزءًا فقط من الطاقة المتبقية ، وما إلى ذلك ، لاحظ أيضًا أن المفهوم الأول يمكن تفسيره دلالة على أنه محور الدراما - فيلم الحركة ، حيث يتوافق الاتجاه الإيجابي مع نوع فيلم الحركة ، والسالب - لنوع الدراما. ترتبط التصنيفات الموجودة في هذا المثال ارتباطًا وثيقًا ، لذلك يمكن أن نرى بوضوح أن أول ثلاثة مستخدمين والأفلام الثلاثة الأولى لها قيم سلبية كبيرة في متجه المفهوم الأول (أفلام الدراما والمستخدمون الذين يحبون هذه الأفلام) ، في حين أن آخر ثلاثة مستخدمين والآخر ثلاثة للأفلام معاني إيجابية كبيرة في نفس العمود (أفلام الحركة والمستخدمون الذين يفضلون هذا النوع). البعد الثاني في هذه الحالة بالذات يتوافق بشكل أساسي مع تحيز المستخدم أو العنصر ، والذي يمكن تفسيره كسمة نفسية (مدى أهمية أحكام المستخدم؟ شعبية الفيلم؟). مفاهيم أخرى يمكن اعتبارها ضوضاء.


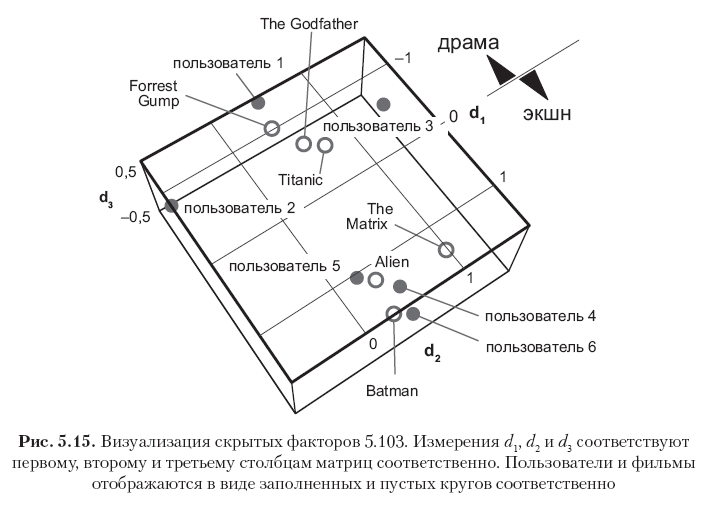
مصفوفة العوامل الناتجة ليست متعامدة تمامًا في الأعمدة ، ولكنها تميل إلى أن تكون متعامدة ، لأن هذا ينجم عن تحسين حل SVD. يمكن ملاحظة ذلك من خلال النظر إلى منتجات PTP و QTQ ، والتي هي قريبة من المصفوفات القطرية:


المصفوفات 5.103 هي في الأساس نموذج تنبؤي يمكن استخدامه لتقييم التصنيفات المعروفة والمفقودة. يمكن الحصول على التقديرات بضرب عاملين وإضافة المتوسط ​​العالمي:


النتائج بدقة إنتاج المعروفة والتنبؤ في عداد المفقودين في التصنيف وفقا لتوقعات بديهية. يمكن زيادة دقة التقديرات أو إنقاصها عن طريق تغيير عدد القياسات ، ويمكن تحديد العدد الأمثل من القياسات في الممارسة العملية عن طريق التدقيق المتبادل واختيار تسوية معقولة بين التعقيد الحسابي والدقة.

»يمكن الاطلاع على مزيد من المعلومات حول الكتاب على موقع الناشر
» المحتويات
» مقتطفات

خصم 25 ٪ على كوبون الباعة المتجولين - التعلم الآلي

عند دفع النسخة الورقية من الكتاب ، يتم إرسال كتاب إلكتروني عبر البريد الإلكتروني.