مرحبا بالجميع!
في كثير من الأحيان يلجأ الناس إلي مع أسئلة حول المهام من مجال معالجة الإشارات الرقمية (DSP). أقول بالتفصيل الفروق الدقيقة ، أقترح المصادر الضرورية للمعلومات. لكن جميع المستمعين ، كما أظهر الوقت ، يفتقرون إلى المهام العملية والأمثلة في عملية تعلم هذا المجال. في هذا الصدد ، قررت كتابة دورة تفاعلية قصيرة حول معالجة الإشارات الرقمية ووضعها في
المجال العام .
يتم تنفيذ معظم المواد التدريبية الخاصة بالعروض التقديمية المرئية والتفاعلية باستخدام
دفتر ملاحظات Jupyter . من المفترض أن يكون للقارئ معرفة أساسية بمجال الرياضيات العليا ، بالإضافة إلى معرفة لغة لغة بيثون قليلاً.

قائمة المحاضرات
تحتوي هذه الدورة على مواد في شكل محاضرات منتهية حول مواضيع مختلفة من مجال معالجة الإشارات الرقمية. يتم تقديم المواد باستخدام مكتبات Python (حزم numpy ، scipy ، matplotlib ، إلخ). المعلومات الأساسية لهذه الدورة مأخوذة من محاضراتي التي أعطيتها ، كطالب دراسات عليا ، لطلاب معهد موسكو للطاقة (NRU MEI). تم استخدام جزء من المعلومات المستقاة من هذه المحاضرات في الندوات التدريبية في
مركز الإلكترونيات المعاصرة ، حيث عملت كمحاضر. بالإضافة إلى ذلك ، تتضمن هذه المادة ترجمة مقالات علمية متنوعة ، وتجميع المعلومات من مصادر موثوقة ومن المؤلفات حول معالجة الإشارات الرقمية ، بالإضافة إلى الوثائق الرسمية حول حزم التطبيقات والوظائف المدمجة لمكتبات بايث وسكريبتيد بيثون.
بالنسبة لمستخدمي MATLAB (GNU Octave) ، فإن إتقان المادة من وجهة نظر كود البرنامج ليس بالأمر الصعب ، لأن الوظائف الرئيسية وسماتها متطابقة إلى حد كبير وتشبه الأساليب الموجودة في مكتبات Python.
يتم تجميع جميع المواد حسب الموضوعات الرئيسية لمعالجة الإشارات الرقمية:
- إشارات: التناظرية ، منفصلة ، الرقمية. Z التحويل
- تحويل فورييه: السعة وإشارة الطور ، DFT و FFT ،
- الإلتواء والارتباط. الإلتفاف الخطي والدوري. الإلتواء السريع
- عمليات عشوائية. الضوضاء البيضاء. دالة الكثافة الاحتمالية
- إشارات حتمية. التحوير: AM ، FM ، FM ، LFM. تلاعب
- تصفية الإشارات: آي آي آر ، فلاتر التنوب
- وظائف النافذة في تصفية المهام. الكشف عن إشارات ضعيفة.
- إعادة أخذ العينات: الهلاك والاستيفاء. مرشحات CIC ، تتحرك مرشحات المتوسط
قائمة المحاضرات كافية
ولكن ، بطبيعة الحال ، غير مكتملة للتعرف على تمهيدية بمجال DSP. مع وقت الفراغ ، أخطط لدعم وتطوير هذا المشروع.
أين تجد؟
جميع المواد
مجانية تمامًا ومتاحة كمستودع مفتوح على
جيثب كمشروع مفتوح المصدر . يتم تقديم المواد بتنسيقين - في شكل Jupyter Notebooks للعمل التفاعلي والدراسة والتحرير ، وفي شكل ملفات HTML تم تجميعها من هذه الأجهزة المحمولة (بعد تنزيلها من github ، يكون لديهم تنسيق مناسب تمامًا للقراءة والطباعة).
فيما يلي وصف
موجز جدًا لأقسام الدورة مع توضيحات ومصطلحات وتعريفات قصيرة. المعلومات الأساسية متوفرة في المحاضرات الأولية ، وهنا فقط لمحة موجزة!
الإشارات. Z التحويل
القسم التمهيدي ، والذي يحتوي على معلومات أساسية عن أنواع الإشارات. تم تقديم مفهوم التسلسل المنفصل ووظيفة دلتا ووظيفة Heaviside (قفزة الوحدة).
يمكن تقسيم جميع الإشارات وفقًا لطريقة العرض على المجموعة إلى أربع مجموعات:
- التناظرية - يتم وصفها بواسطة وظائف مستمرة في الوقت المناسب ،
- منفصلة - يتم مقاطعة في الوقت المناسب مع خطوة محددة عن طريق أخذ العينات ،
- كميا - لديها مجموعة من المستويات المحددة (عادة في السعة) ،
- الرقمية - مزيج من خصائص الإشارات المنفصلة والكميات.
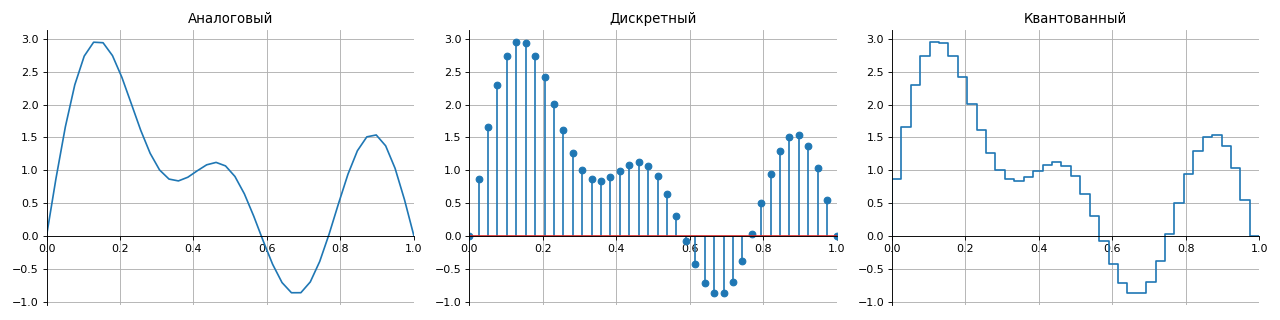
لإعادة الإعمار الصحيح لإشارة تناظرية من إشارة رقمية دون تشويه وفقدان ، يتم استخدام نظرية أخذ العينات المعروفة باسم نظرية
Kotelnikov (Nyquist-Shannon) .
يمكن استعادة أي إشارة مستمرة ذات طيف محدود بشكل فريد وبدون خسارة من خلال العينات المنفصلة التي يتم التقاطها بتردد يزيد بدقة عن ضعف التردد العلوي للطيف لإشارة مستمرة.
مثل هذا التفسير صحيح بشرط أن الوظيفة المستمرة للوقت تشغل نطاق تردد من 0 إلى قيمة التردد العلوي. إذا تم اختيار خطوات التقدير والتحجيم بشكل غير صحيح ، سيتم تحويل الإشارة من شكل تمثيلي إلى شكل منفصل مع تشوهات.
في هذا القسم أيضًا ، يتم وصف
التحول Z وخصائصه ، ويتم عرض تمثيل التسلسلات المنفصلة في النموذج Z.
مثال على تسلسل منفصل محدد:
x(nT) = {2, 1, -2, 0, 2, 3, 1, 0}
.
مثال على نفس التسلسل في شكل Z:
X (z) = 2 + z
-1 - 2z
-2 + 2z
-4 + 3z
-5 + 1z
-6تحويل فورييه. خصائص. DFT و FFT
يصف هذا القسم مفهوم الوقت ومجال التردد للإشارة. يتم تقديم تعريف تحويل فورييه المنفصل (DFT). تعتبر DFTs المباشرة والعكسية وخصائصها الرئيسية. يظهر الانتقال من DFT إلى خوارزمية تحويل فورييه السريع (FFT) في القاعدة 2 (خوارزميات التدمير في التردد والوقت). تعكس فعالية FFT بالمقارنة مع DFT.
على وجه الخصوص ، يصف هذا القسم حزمة Python scipy.ffpack لحساب مختلف تحويلات فورييه (الجيب ، جيب التمام ، المباشر ، معكوس ، متعدد الأبعاد ، حقيقي).
يتيح لك تحويل فورييه تمثيل أي وظيفة كمجموعة من الإشارات التوافقية! تحويل فورييه هو أساس أساليب الالتواء وتصميم الروابط الرقمية ، ويستخدم بنشاط في التحليل الطيفي ، ويستخدم عند العمل بأعداد طويلة.
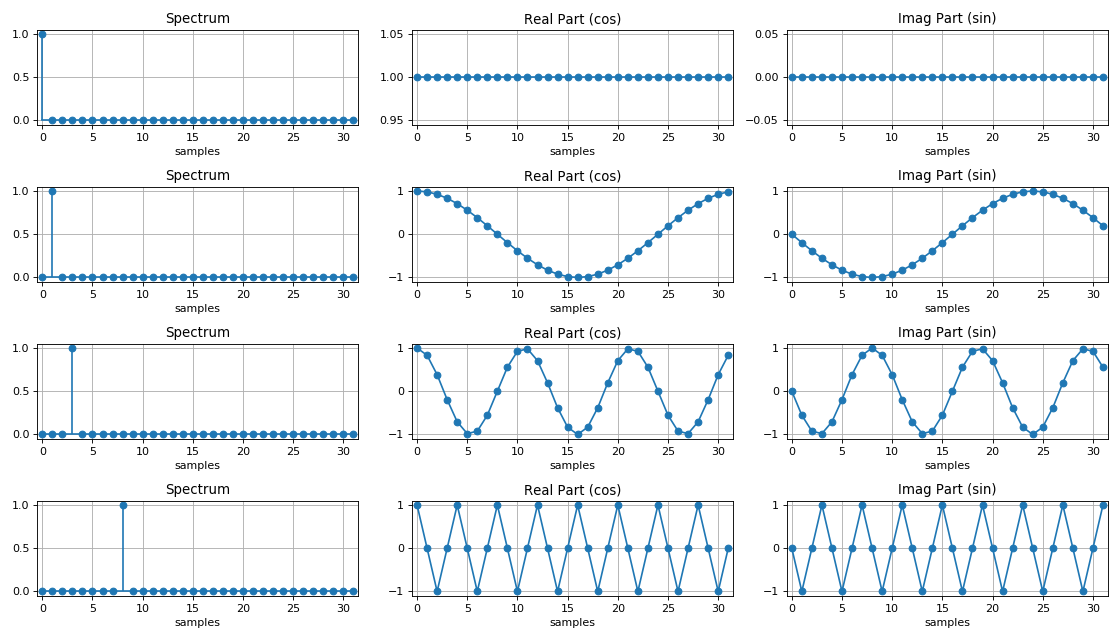
ميزات أطياف الإشارات المنفصلة:
1. الكثافة الطيفية للإشارة المنفصلة هي وظيفة دورية لها فترة تساوي تردد أخذ العينات.
2. إذا كان التسلسل المنفصل
حقيقيًا ، فإن معامل الكثافة الطيفية لمثل هذا التسلسل هو وظيفة
متساوية ، والحجة هي وظيفة تردد
فردي .
طيف الإشارة التوافقي:
مقارنة بين فعالية DFT و FFT
تعتمد كفاءة خوارزمية FFT وعدد العمليات المنفذة خطيًا على طول التسلسل N:
كما ترون ، كلما زاد طول التحويل ، زادت المدخرات في موارد الحوسبة (من حيث سرعة المعالجة أو عدد وحدات الأجهزة)!
يمكن تمثيل أي شكل موجي تعسفي كمجموعة من الإشارات التوافقية بترددات مختلفة. بمعنى آخر ، فإن إشارة الشكل المعقد في المجال الزمني بها مجموعة من العينات المعقدة في مجال التردد ، والتي تسمى * التوافقيات *. هذه العينات تعبر عن سعة ومرحلة التأثير التوافقي بتردد معين. كلما كانت مجموعة التوافقيات في مجال التردد أكبر ، كلما كان الشكل الموجي المعقد أكثر دقة.

الإلتواء والارتباط
يقدم هذا القسم مفهوم الارتباط والالتواء لتسلسلات عشوائية وحتمية منفصلة. تظهر العلاقة بين الارتباط الذاتي ووظائف الارتباط المتبادل مع الالتواء. يتم وصف خصائص الالتواء ، على وجه الخصوص ، يتم النظر في طرق الالتواء الخطي والدوري لإشارة منفصلة مع تحليل مفصل على مثال التسلسل المنفصل. بالإضافة إلى ذلك ، يتم عرض طريقة لحساب الإلتواء "السريع" باستخدام خوارزميات FFT.
في المشاكل الحقيقية ، غالبًا ما يتم طرح السؤال حول درجة تشابه عملية ما مع عملية أخرى أو حول استقلال عملية ما عن عملية أخرى. بمعنى آخر ، يجب تحديد العلاقة بين الإشارات ، أي لإيجاد
ارتباط . يتم استخدام طرق الارتباط في مجموعة واسعة من المهام: البحث عن إشارة ، رؤية الكمبيوتر ومعالجة الصور ، في مشاكل الرادار لتحديد خصائص الأهداف وتحديد المسافة إلى كائن. بالإضافة إلى ذلك ، يتم استخدام الارتباط للبحث عن إشارات ضعيفة في الضوضاء.
يصف
الالتواء تفاعل الإشارات مع بعضها البعض. إذا كانت إحدى الإشارات هي الاستجابة النبضية للمرشح ، فإن الالتواء في تسلسل الإدخال مع استجابة النبضة ليس سوى تفاعل الدائرة مع فعل الإدخال. بمعنى آخر ، فإن الإشارة الناتجة تعكس مرور الإشارة عبر المرشح.
يتم استخدام وظيفة الارتباط التلقائي (ACF) في معلومات الترميز. يرجع اختيار تسلسل التشفير وفقًا لمعايير الطول والتردد والشكل إلى حد كبير إلى خصائص الارتباط لهذا التسلسل. يحتوي أفضل تسلسل للشفرة على أقل احتمال للكشف أو التشغيل الخاطئ (للكشف عن الإشارات للأجهزة العتبة) أو التزامن الخاطئ (لإرسال واستقبال تسلسل الكود).
يقدم هذا القسم جدولًا يقارن فعالية الالتواء السريع والالتفاف المحسوب بالصيغة المباشرة (بعدد المضاعفات الحقيقية).
كما ترون ، لأطوال FFT حتى 64 ،
يفقد الالتواء السريع على الطريقة المباشرة. ومع ذلك ، مع زيادة في طول FFT ، تتغير النتائج في الاتجاه المعاكس - يبدأ الالتواء السريع في التفوق على الطريقة المباشرة. من الواضح ، كلما طالت فترة تحويل فورييه ، كان المكسب في طريقة التردد أفضل.
إشارات عشوائية والضوضاء
في هذا القسم ، يتم تقديم مفهوم الإشارات العشوائية ، وكثافة الاحتمالات ، وقانون التوزيع العشوائي. تعتبر اللحظات الرياضية - المتوسط (التوقع الرياضي) والتباين (أو جذر هذه الكمية هو الانحراف المعياري). في هذا القسم أيضًا ، يعتبر التوزيع الطبيعي والمفهوم المتعلق
بالضوضاء البيضاء المصدر الرئيسي للضوضاء (التداخل) أثناء معالجة الإشارة.
الإشارة العشوائية هي دالة زمنية غير معروفة مسبقًا قيمها ولا يمكن التنبؤ بها إلا ببعض
الاحتمالات . تشمل الخصائص الرئيسية للإشارات العشوائية ما يلي:
- قانون التوزيع (وقت الإقامة النسبي لقيمة الإشارة في فترة زمنية معينة) ،
- التوزيع الطيفي لقوة الإشارة.
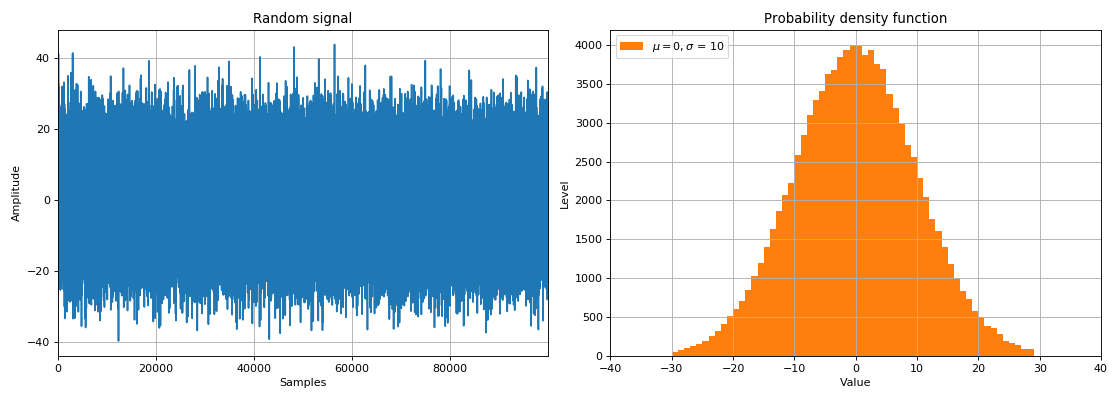
في مهام DSP ، تنقسم الإشارات العشوائية إلى فئتين:
- تقلبات عشوائية - ضوضاء تتكون من مجموعة من الترددات والسعات المختلفة ،
- إشارات تحمل معلومات ، من أجل معالجتها ، من الضروري اللجوء إلى الأساليب الاحتمالية.
باستخدام متغيرات عشوائية ، يمكننا محاكاة تأثير وسيط حقيقي على مرور إشارة من مصدر إلى مستقبل البيانات. عندما تمر إشارة عبر رابط صاخب ، تتم إضافة ما يسمى الضوضاء البيضاء إلى الإشارة. وكقاعدة عامة ، يتم توزيع الكثافة الطيفية لهذه الضوضاء بشكل متساوٍ (متساوٍ) على جميع الترددات ، ويتم توزيع قيم الضوضاء في المجال الزمني عادةً (قانون التوزيع الغوسي). نظرًا لأن الضوضاء البيضاء تُضاف فعليًا إلى اتساع الإشارة في عينات الوقت المحددة ، يُطلق عليها الضوضاء البيضاء الغوسية (AWGN).
إشارات ، التحوير والتلاعب
يوضح هذا القسم الطرق الأساسية لتغيير معلمة أو أكثر من الإشارة التوافقية. يتم تقديم مفاهيم السعة والتردد والطور. على وجه الخصوص ، يتم تسليط الضوء على تعديل التردد الخطي المستخدم في مشاكل الرادار. وتظهر الخصائص الرئيسية للإشارات ، أطياف الإشارات المشكَّلة حسب معلمات التشكيل.

للراحة ، تم إنشاء مجموعة من الوظائف في بيثون تنفذ أنواع التعديل أعلاه. مثال لتنفيذ إشارة غرد:
def signal_chirp(amp=1.0, freq=0.0, beta=0.25, period=100, **kwargs): """ Create Chirp signal Parameters ---------- amp : float Signal magnitude beta : float Modulation bandwidth: beta < N for complex, beta < 0.5N for real freq : float or int Linear frequency of signal period : integer Number of points for signal (same as period) kwargs : bool Complex signal if is_complex = True Modulated by half-sine wave if is_modsine = True """ is_complex = kwargs.get('is_complex', False) is_modsine = kwargs.get('is_modsine', False) t = np.linspace(0, 1, period) tt = np.pi * (freq * t + beta * t ** 2) if is_complex is True: res = amp * (np.cos(tt) + 1j * np.sin(tt)) else: res = amp * np.cos(tt) if is_modsine is True: return res * np.sin(np.pi * t) return res
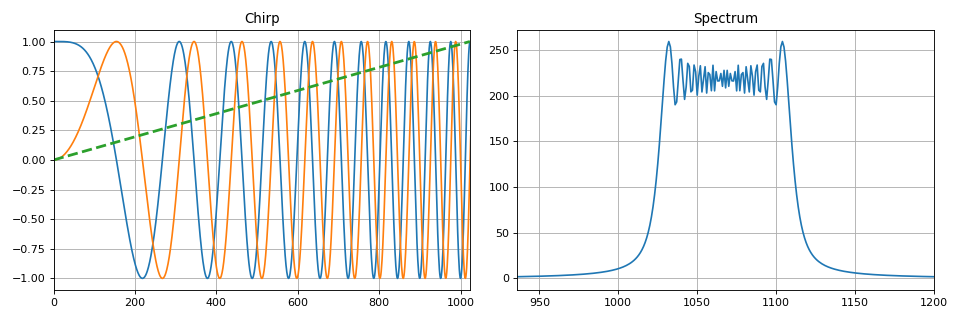
أيضا في هذا القسم من نظرية نقل أنواع الرسائل المنفصلة من التشكيل الرقمي - يتم وصف التلاعب. كما هو الحال في الإشارات التناظرية ، يمكن التلاعب بالتسلسلات التوافقية الرقمية من حيث السعة والمرحلة والتردد (أو عدة معلمات في آن واحد).

المرشحات الرقمية - IIR و FIR
قسم كبير بما فيه الكفاية مخصص للتصفية الرقمية للتسلسلات المنفصلة. في مهام معالجة الإشارات الرقمية ، تتدفق البيانات عبر دوائر تسمى
المرشحات . تتميز المرشحات الرقمية ، مثل المرشحات التناظرية ، بخصائص مختلفة - التردد: استجابة التردد ، استجابة الطور ، الوقت: استجابة الاندفاع ، بالإضافة إلى خصائص النقل للمرشح. تُستخدم المرشحات الرقمية بشكل أساسي لتحسين جودة الإشارة - لعزل الإشارة من تسلسل البيانات ، أو لتقليل الإشارات غير المرغوب فيها - لقمع إشارات معينة في تسلسل العينة الوارد.

يسرد القسم المزايا والعيوب الرئيسية للمرشحات الرقمية (مقارنة بالتناظرية). يتم تقديم مفهوم الدافع وخصائص النقل للمرشح. يتم النظر في فئتين من المرشحات - مع استجابة الاندفاع اللانهائي (IIR) واستجابة الاندفاع المحدود (FIR). يتم عرض طريقة لتصميم المرشحات في شكل
قانوني ومباشر . بالنسبة لمرشحات FIR ، يتم النظر في مسألة كيفية التبديل إلى نموذج تكراري.
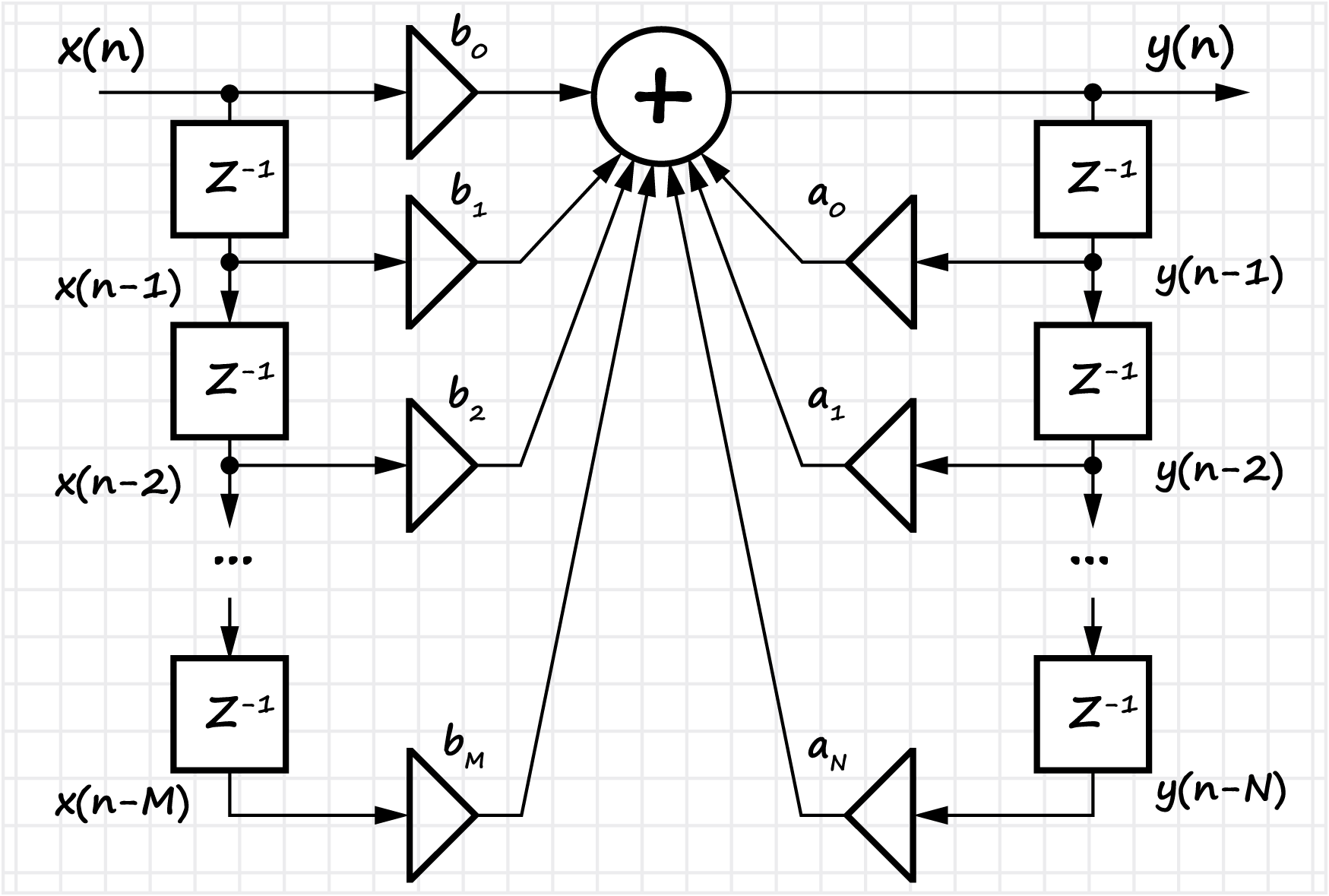
بالنسبة لمرشحات FIR ، تظهر عملية تصميم المرشح من مرحلة تطوير المواصفات الفنية (مع الإشارة إلى المعلمات الرئيسية) ، إلى تنفيذ البرامج والأجهزة - البحث عن معاملات المرشح (مع مراعاة شكل تمثيل العدد وعمق البتات ، إلخ). يتم تقديم تعريفات مرشحات FIR المتماثلة واستجابة المرحلة الخطية وعلاقتها بمفهوم تأخير المجموعة.

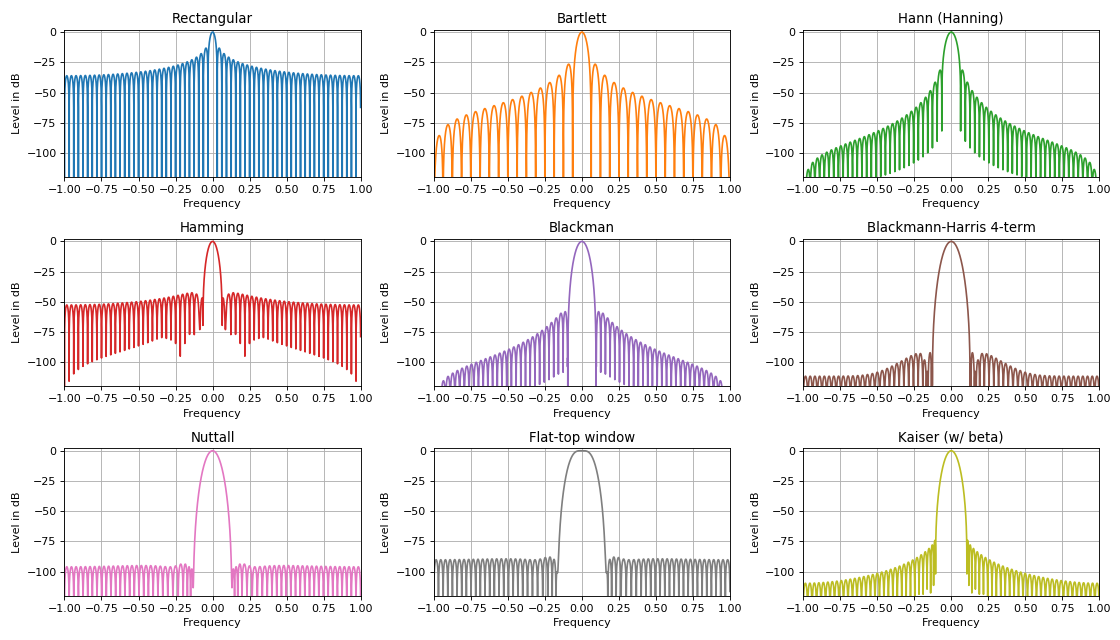
وظائف النافذة في تصفية المهام
في مهام معالجة الإشارات الرقمية ، يتم استخدام وظائف النوافذ بأشكال مختلفة ، والتي عند تثبيتها على إشارة في المجال الزمني ، يمكنها تحسين خصائصها الطيفية نوعيًا. يرجع عدد كبير من النوافذ المتنوعة في المقام الأول إلى واحدة من السمات الرئيسية لأي نافذة تراكب. يتم التعبير عن هذه الميزة في العلاقة بين مستوى الفصوص الجانبية وعرض الفص المركزي. حكم:
كلما زاد قمع الفصوص الجانبية للطيف ، زاد الفص الرئيسي للطيف والعكس.

أحد تطبيقات وظائف النافذة: اكتشاف إشارات ضعيفة على خلفية إشارات أقوى عن طريق قمع مستوى الفصوص الجانبية. وظائف النافذة الرئيسية في مهام DSP هي: مثلثات ** ، ثلاثية جيبية ، Lanczos ، Hann ، Hamming ، Blackman ، Harris ، نافذة Blackman-Harris ، نافذة مسطحة أعلى ، نافذة Natall ، Gauss ، Kaiser ** وغيرها. يتم التعبير عن معظمهم من خلال سلسلة محدودة عن طريق جمع إشارات التوافقية مع أوزان محددة. يتم تطبيق هذه الإشارات بشكل مثالي في الممارسة على أي أجهزة (دوائر منطق قابلة للبرمجة أو معالجات إشارة).
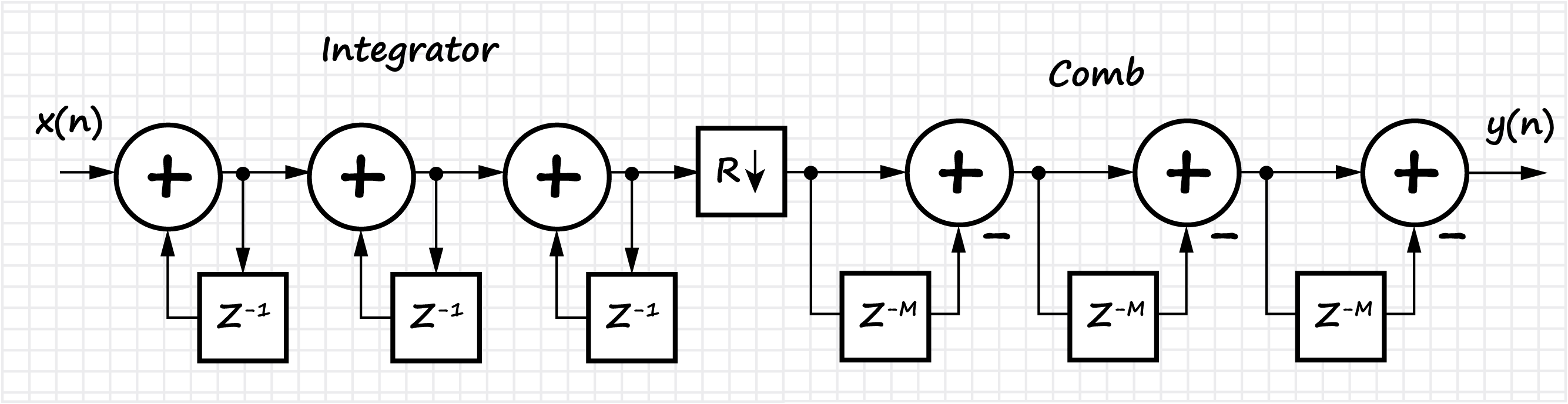
اختزال. الهلاك والاستيفاء
يناقش هذا القسم مشكلات معالجة الإشارات متعددة السرعات - التغيرات في تردد أخذ العينات. تشير المعالجة متعددة السرعات للإشارات (المعالجة متعددة الطبقات) إلى أنه في عملية التحويل الخطي للإشارات الرقمية ، من الممكن تغيير تردد أخذ العينات في اتجاه التناقص أو الزيادة ، أو في عدد كسري من المرات. يؤدي ذلك إلى معالجة أكثر كفاءة للإشارات ، حيث يفتح إمكانية استخدام الحد الأدنى من ترددات أخذ العينات المسموح بها ، ونتيجة لذلك ، انخفاض كبير في أداء الحوسبة المطلوب للنظام الرقمي المصمم.
الهلاك (
الهلاك ) - الاختزال.
الاستيفاء - زيادة معدل أخذ العينات.
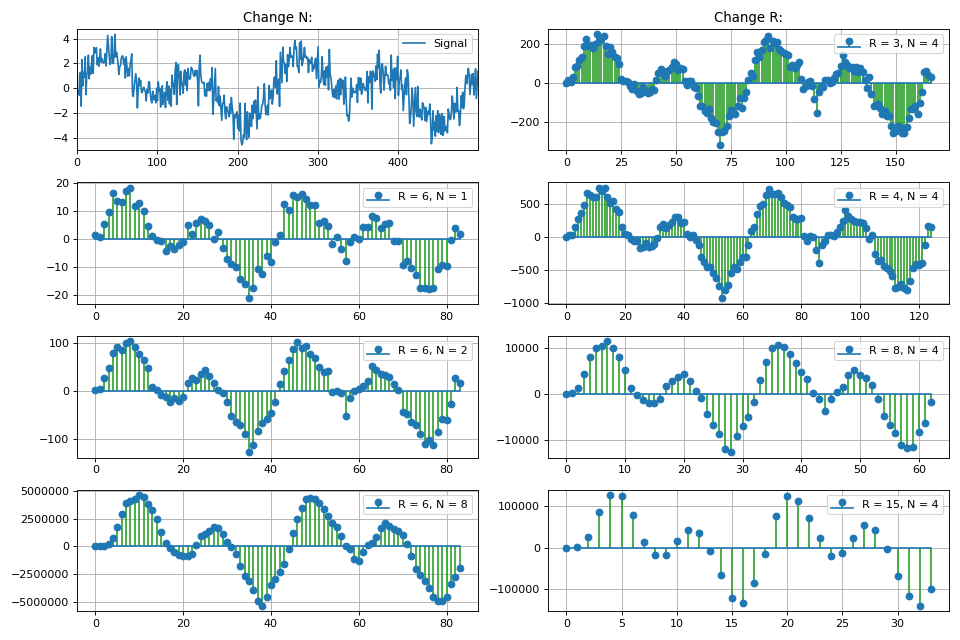
ينظر القسم أيضًا في فئة مرشحات FIR المتجانسة ، والتي تسمى عوامل التصفية المتكاملة - المشط (CIC ، Cascaded integrator - comb). يتم عرض الخصائص والخصائص الأساسية لمرشحات CIC. بسبب الخطية للعمليات الرياضية التي تحدث في مرشح CIC ، من الممكن أن تتسلسل عدة مرشحات على التوالي ، مما يعطي انخفاضًا نسبيًا في مستوى الفصوص الجانبية ، ولكنه يزيد أيضًا من "انسداد" الفص الرئيسي لخاصية تردد السعة.
الرسم البياني لاستجابة التردد للمرشح اعتمادا على معامل الهلاك:
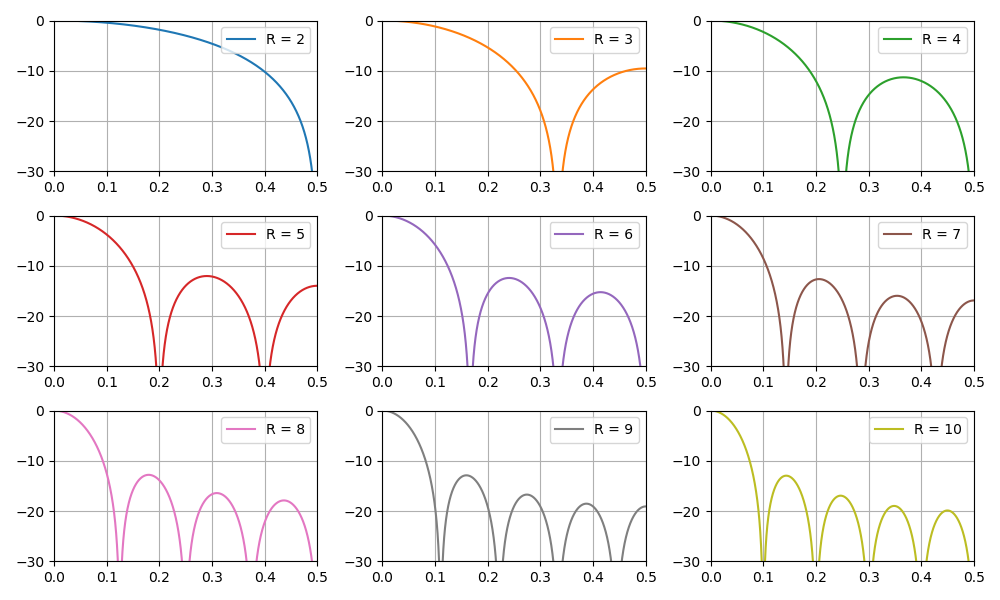
في هذا القسم أيضًا ، نناقش مسألة زيادة عمق البت للبيانات عند إخراج مرشح CIC ، وفقًا لمعاييرها. هذا مهم بشكل خاص في مهام تنفيذ البرامج ، خاصة على FPGAs.
من أجل التنفيذ العملي لمرشحات CIC في بيثون ،
تم تطوير CicFilter لفصل منفصل
يقوم بتنفيذ طرق الإبادة والاستيفاء. يظهر أيضًا تغييرات في معدل العينة باستخدام الأساليب المضمنة من حزمة Python scipy.
بيثون فئة CicFilter لمعالجة الإشارات الرقمية class CicFilter: """ Cascaded Integrator-Comb (CIC) filter is an optimized class of finite impulse response (FIR) filter. CIC filter combines an interpolator or decimator, so it has some parameters: R - decimation or interpolation ratio, N - number of stages in filter (or filter order) M - number of samples per stage (1 or 2)* * for this realisation of CIC filter just leave M = 1. CIC filter is used in multi-rate processing. In hardware applications CIC filter doesn't need multipliers, just only adders / subtractors and delay lines. Equation for 1st order CIC filter: y[n] = x[n] - x[n-RM] + y[n-1]. Parameters ---------- x : np.array input signal """ def __init__(self, x): self.x = x def decimator(self, r, n): """ CIC decimator: Integrator + Decimator + Comb Parameters ---------- r : int decimation rate n : int filter order """
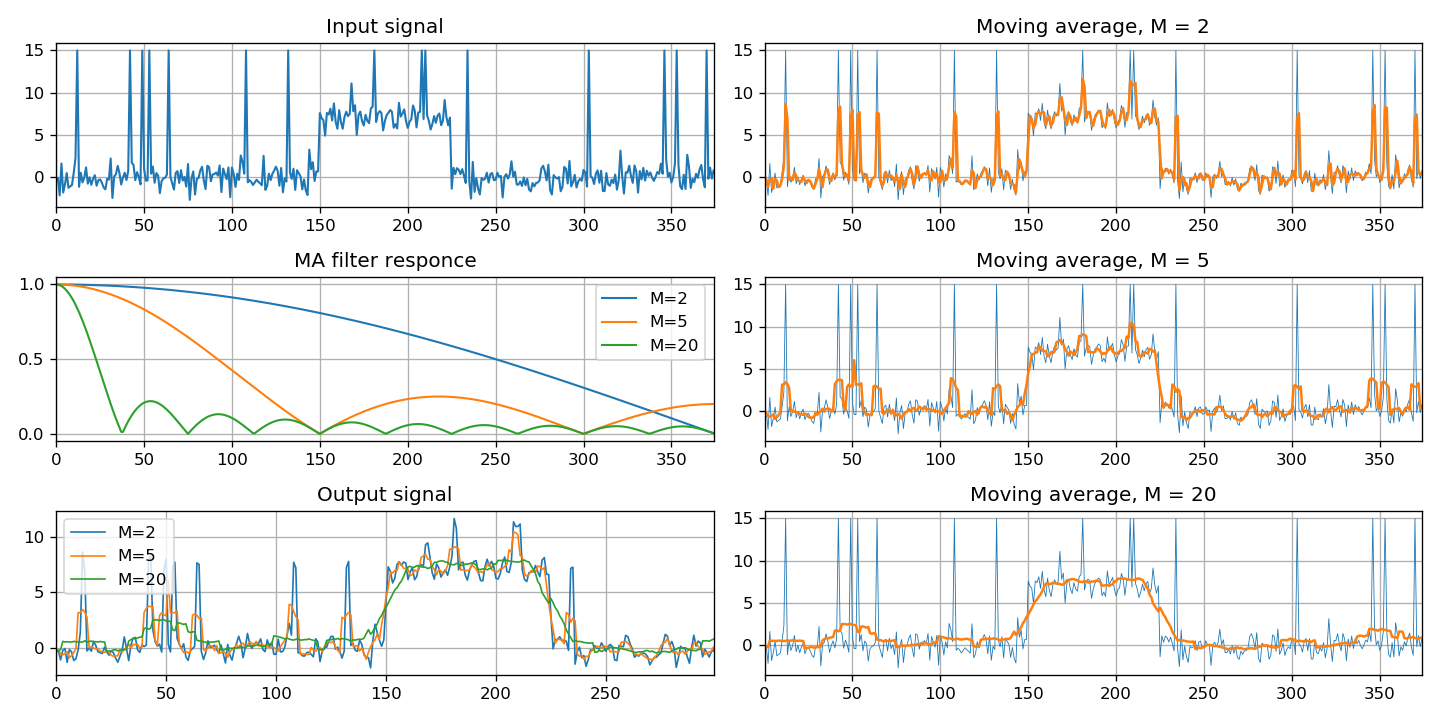
أخيرًا ، يوفر هذا القسم فئة خاصة من المرشحات - المتوسط المتحرك. يتم عرض ثلاث طرق تنفيذ: من خلال تجميع الإشارات ، باستخدام مرشح FIR ومرشح IIR.
استنتاج
آمل أن تجلب دورة المحاضرة هذه بالتزامن مع مقالاتي السابقة حول معالجة إشارات FPGA الرقمية فوائد عملية وتساعد القارئ على فهم أساسيات معالجة الإشارات الرقمية بشكل أفضل. سيتم تحسين هذا المشروع واستكماله بمواد جديدة مفيدة لا تقل إثارة للاهتمام. متابعة التطور!
بالإضافة إلى هذه المادة ، أؤيد
مشروعي وأطوره على وحدات DSP الرئيسية (في بيثون). أنه يحتوي على حزمة لتوليد إشارات مختلفة ، فئة من مرشحات CIC لحل مشاكل الإزالة والاستيفاء ، خوارزمية لحساب معاملات مرشح FIR الصحيح ، مرشح متوسط متحرك ، خوارزمية لحساب FFT طويل للغاية من خلال طرق تحويل ثنائية الأبعاد (الأخيرة كانت مفيدة للغاية عند العمل مع تنفيذ الأجهزة على FPGAs) .
شكرا لاهتمامكم!