كتابة شبكة عصبية بسيطة باستخدام الرياضيات و numpy

لماذا المقالة التالية حول كيفية كتابة الشبكات العصبية من نقطة الصفر؟ للأسف ، لم أتمكن من العثور على مقالات وصفت فيها النظرية والكود من البداية إلى نموذج العمل الكامل. لقد حذرت على الفور من أنه سيكون هناك الكثير من الرياضيات. أفترض أن القارئ معتاد على أساسيات الجبر الخطي ، والمشتقات الجزئية ، وعلى الأقل جزئيًا ، مع نظرية الاحتمالات ، وكذلك بيثون و Numpy. سنتعامل مع شبكة عصبية متصلة بالكامل و MNIST.

الرياضيات. الجزء 1 (بسيط)

ما هي طبقة متصلة بالكامل (طبقة FC)؟ عادةً ما يقولون شيئًا مثل "طبقة متصلة بالكامل عبارة عن طبقة ، كل خلية منها متصلة بجميع الخلايا العصبية في الطبقة السابقة". ليس من الواضح ما هي الخلايا العصبية ، وكيف ترتبط ، ولا سيما في الشفرة. الآن سأحاول تحليل هذا بمثال. فليكن هناك طبقة من 100 خلية عصبية. أعلم أنني لم أوضح بعد ما هو عليه ، لكن دعنا نتخيل فقط أن هناك 100 خلية عصبية ولديهم مدخلات من حيث يتم إرسال البيانات ، ومخرجات من أين يقدمون البيانات. ويتم تغذية صورة بالأبيض والأسود بحجم 28 × 28 بكسل للإدخال - قيم 784 فقط ، إذا قمت بتمديدها في ناقل. يمكن استدعاء صورة طبقة الإدخال. ثم ، ولكل من الخلايا العصبية 100 للاتصال مع كل "الخلايا العصبية" أو ، إذا أردت ، قيمة الطبقة السابقة (أي ، الصورة) ، فمن الضروري أن كل من الخلايا العصبية 100 تقبل 784 قيم الصورة الأصلية. على سبيل المثال ، سيكون كل عدد من الخلايا العصبية المائة كافياً لمضاعفة 784 قيم للصورة بحوالي 784 رقم وإضافتها معًا ، ونتيجة لذلك ، يخرج رقم واحد. وهذا هو ، الخلايا العصبية:

$$عرض $$ $$ \ النص {إخراج النورون} = \ النص {بعض الأرقام} _ {1} \ cdot \ text {قيمة الصورة} _1 ~ + \\ + ~ ... ~ + ~ \ text {some- هذا الرقم} _ {784} \ cdot \ text {قيمة الصورة} _ {784} $$ عرض $$

ثم اتضح أن لكل خلية عصبية 784 رقمًا ، وجميع هذه الأرقام: (عدد الخلايا العصبية في هذه الطبقة) × (عدد الخلايا العصبية في الطبقة السابقة) =$$ $ مضمنة $ 100 \ times784 $ مضمنة = 78400 رقم. تسمى هذه الأرقام عادةً أوزان الطبقة. ستعطي كل خلية عصبية عددها ، ونتيجة لذلك نحصل على ناقل 100 الأبعاد ، وفي الواقع يمكننا أن نكتب أن هذا ناقل 100-الأبعاد تم الحصول عليها عن طريق ضرب ناقلات الأبعاد 784 (صورتنا الأصلية) بمصفوفة الوزن$$ $ مضمنة $ 100 \ times784 $ مضمنة :

$$عرض $$ $$ \ boldsymbol {x} ^ {100} = W_ {100 \ times784} \ cdot \ boldsymbol {x} ^ {784} $$ عرض $$

علاوة على ذلك ، يتم تمرير 100 رقم الناتجة إلى وظيفة التنشيط - بعض الوظائف غير الخطية - والتي تؤثر على كل رقم على حدة. على سبيل المثال ، السيني ، الظل الزائدي ، ReLU وغيرها. وظيفة التنشيط غير خطية بالضرورة ، وإلا فإن الشبكة العصبية ستتعلم فقط التحولات البسيطة.



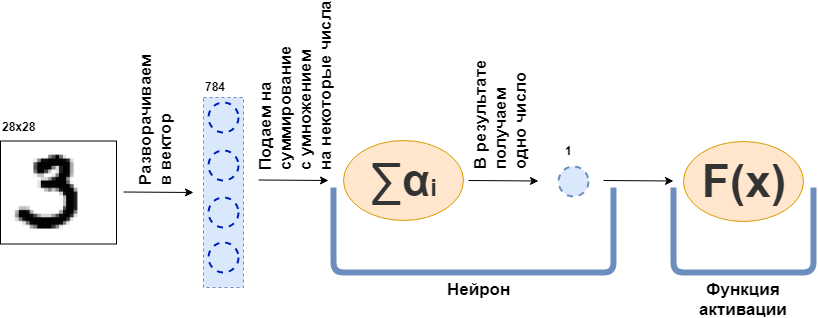
بعد ذلك ، يتم تغذية البيانات الناتجة مرة أخرى إلى طبقة متصلة بالكامل ، ولكن مع عدد مختلف من الخلايا العصبية ، ومرة ​​أخرى إلى وظيفة التنشيط. هذا يحدث عدة مرات. الطبقة الأخيرة من الشبكة هي الطبقة التي تنتج الجواب. في هذه الحالة ، تكون الإجابة هي معلومات حول الرقم الموجود في الصورة.



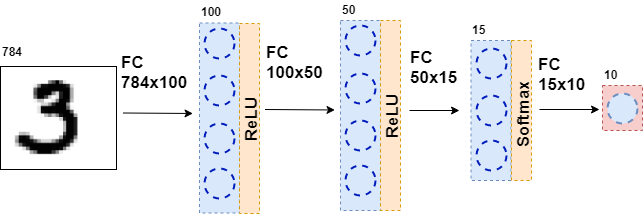
أثناء تدريب الشبكة ، من الضروري أن نعرف الشكل الظاهر في الصورة. وهذا هو ، أن يتم تعيين مجموعة البيانات. ثم يمكنك استخدام عنصر آخر - وظيفة الخطأ. إنها تنظر إلى استجابة الشبكة العصبية وتقارنها بالإجابة الحقيقية. بفضل هذا ، فإن الشبكة العصبية تتعلم.

بيان عام للمشكلة

مجموعة البيانات بأكملها عبارة عن موتر كبير (سوف نسمي صفيف بيانات متعدد الأبعاد بتينسور)$$ $ inline $ \ boldsymbol {X} = \ left [\ boldsymbol {x} _1 ، \ boldsymbol {x} _2 ، \ ldots ، \ boldsymbol {x} _n \ right] $ inline $ حيث$$ $ inline $ \ boldsymbol {x} _i $ inline $ - كائن i ، على سبيل المثال ، صورة ، والتي هي أيضا موتر. لكل كائن هناك$$ $ inline $ y_i $ inline $ - الإجابة الصحيحة على الكائن الأول. في هذه الحالة ، يمكن تمثيل الشبكة العصبية كدالة تأخذ كائنًا كمدخل وتعطي إجابة عليه:

$$عرض $$ $$ F (\ boldsymbol {x} _i) = \ hat {y} _i $$ عرض $$

الآن دعونا نلقي نظرة فاحصة على الوظيفة$$ $ inline $ F (\ boldsymbol {x} _i) $ inline $ . بما أن الشبكة العصبية تتكون من طبقات ، فإن كل طبقة على حدة هي وظيفة. وهذا يعني

$$عرض $$ $ F (\ boldsymbol {x} _i) = f_k (f_ {k-1} (\ ldots (f_1 (\ boldsymbol {x} _i))))) = \ hat {y} _i $$ عرض $ $

هذا هو ، في أول وظيفة - الطبقة الأولى - يتم تقديم صورة في شكل بعض الموتر. وظيفة$$ $ inline $ f_1 $ inline $ يعطي بعض الإجابة - أيضا موتر ، ولكن من بعد مختلف. وسوف يطلق هذا الموتر التمثيل الداخلي. الآن يتم تغذية هذا التمثيل الداخلي لإدخال الوظيفة$$ $ inline $ f_2 $ inline $ ، والذي يعطي تمثيلها الداخلي. وهلم جرا ، حتى وظيفة$$ $ inline $ f_k $ inline $ - الطبقة الأخيرة - لن تعطي إجابة$$ $ inline $ \ hat {y} _i $ inline $ .

المهمة الآن هي تدريب الشبكة - لجعل إجابة الشبكة تتطابق مع الإجابة الصحيحة. تحتاج أولاً إلى قياس مدى خطأ الشبكة العصبية. قياس هذا هو وظيفة خطأ.$$ $ inline $ L (\ hat {y} _i، y_i) $ inline $ . ونفرض قيودًا:

1.$$ $ inline $ \ hat {y} _i \ xrightarrow {} y_i \ Rightarrow L (\ hat {y} _i، y_i) \ xrightarrow {} 0 $ inline $
2.$$ $ inline $ \ موجود ~ dL (\ hat {y} _i، y_i) $ inline $
3.$$ $ inline $ L (\ hat {y} _i، y_i) \ geq 0 $ inline $

يتم فرض التقييد 2 على جميع وظائف الطبقات$$ $ inline $ f_j $ inline $ - دعهم جميعًا يكونون مختلفين.

علاوة على ذلك ، في الواقع (لم أذكر هذا) تعتمد بعض هذه الوظائف على المعلمات - أوزان الشبكة العصبية -$$ $ inline $ f_j (\ boldsymbol {x} _i | \ boldsymbol {\ omega} _j) $ inline $ . والفكرة كلها هي لالتقاط هذه الأوزان بحيث$$ $ inline $ \ hat {y} _i $ inline $ تزامن مع$$ $ inline $ y_i $ inline $ على جميع كائنات مجموعة البيانات. ألاحظ أن ليس كل الوظائف لها أوزان.

إذن ، أين توقفنا؟ جميع وظائف الشبكة العصبية مختلفة ، وظيفة الخطأ هي أيضا قابلة للتمييز. تذكر إحدى خصائص التدرج اللوني - أوضح اتجاه نمو الوظيفة. نستخدم هذا ، القيود 1 و 3 ، حقيقة أن

$$عرض $$ $ L (F (\ boldsymbol {x} _i)) = L (f_k (f_ {k-1} (\ ldots (f_1 (\ boldsymbol {x} _i)))))) = L (\ hat {y} _i) $$ عرض $$

وحقيقة أنني أستطيع النظر في المشتقات الجزئية والمشتقات من وظيفة معقدة. الآن هناك كل ما تحتاجه من أجل حساب

$$عرض $$ $$ \ frac {\ الجزئي L (F (\ boldsymbol {x} _i))} {\ جزئي \ boldsymbol {\ omega_j}} $$ عرض $$

لأي أنا و ي. يوضح هذا المشتق الجزئي الاتجاه الذي يجب تغييره$$ $ inline $ \ boldsymbol {\ omega_j} $ inline $ للتكبير$$ $ مضمنة $ L $ مضمنة . لتقليل كنت بحاجة لاتخاذ خطوة إلى الجانب$$ $ inline $ - \ frac {\ جزئية L (F (\ boldsymbol {x} _i))} {\ جزئي \ boldsymbol {\ omega_j}} $ $ مضمّن لا شيء معقد.

لذلك تم بناء عملية التدريب على الشبكة على النحو التالي: مرارا وتكرارا في دورة نمر بها مجموعة البيانات بأكملها (وهذا ما يسمى عصر) ، لكل كائن مجموعة البيانات التي نعتبرها$$ $ inline $ L (\ hat {y} _i، y_i) $ inline $ (وهذا ما يسمى تمرير إلى الأمام) والنظر في مشتق جزئي$$ $ مضمنة $ \ جزئي L $ مضمنة لجميع الأوزان$$ $ inline $ \ boldsymbol {\ omega_j} $ inline $ ، ثم قم بتحديث الأوزان (وهذا ما يسمى بالمرور الخلفي).

ألاحظ أنني لم أدخل بعد أي وظائف وطبقات محددة. إذا لم يكن من الواضح في هذه المرحلة ما يجب القيام به مع كل هذا ، أقترح مواصلة القراءة - سيكون هناك المزيد من الرياضيات ، ولكن الآن سوف يتم طرحها مع أمثلة.

الرياضيات. الجزء 2 (صعب)

وظيفة خطأ

سأبدأ من النهاية واستخلاص وظيفة الخطأ لمشكلة التصنيف. بالنسبة لمشكلة الانحدار ، فإن الاشتقاق لوظيفة الخطأ موصوف جيدًا في كتاب "التعلم العميق. الانغماس في عالم الشبكات العصبية ".

للبساطة ، هناك شبكة عصبية (NN) تفصل بين صور القط وصور الكلاب ، وهناك مجموعة من صور القطط والكلاب التي توجد إجابة صحيحة عليها$$ $ inline $ y_ {true} $ inline $ .

$$عرض $$ $ NN (صورة | \ أوميغا) = y_ {pred} $$ عرض $

كل ما سأفعله بعد ذلك يشبه إلى حد كبير طريقة الاحتمالية القصوى. ولذلك ، فإن المهمة الرئيسية هي العثور على وظيفة الاحتمال. إذا تجاهلنا التفاصيل ، فإن هذه الوظيفة التي تقارن التنبؤ بالشبكة العصبية والإجابة الصحيحة ، وإذا تزامنتا ، فإنها تعطي قيمة كبيرة ، إن لم تكن ، العكس. إن احتمال وجود إجابة صحيحة يتبادر إلى الذهن مع المعلمات المعطاة:

$$عرض $$ $$ ع (y_ {pred} = y_ {true} | \ Omega) $$ عرض $$

والآن سنحقق بعض الخدعة ، والتي ، على ما يبدو ، لا تتبع من أي مكان. اسمح للشبكة العصبية بإعطاء إجابة على شكل متجه ثنائي الأبعاد ، ومجموع قيمه هو 1. يمكن تسمية العنصر الأول من هذا المتجه على أنه مقياس ثقة بأن القطة موجودة في الصورة ، والعنصر الثاني هو مقياس الثقة الذي وضعه الكلب في الصورة. نعم ، إنه الاحتمال تقريبًا!

$$عرض $$ $ NN (صورة | \ Omega) = \ left [\ start {matrix} p_0 \\ p_1 \\\ end {matrix} \ right] $$ عرض $$

الآن يمكن إعادة كتابة وظيفة الاحتمال كـ:

$$عرض $$ $$ p (y_ {pred} = y_ {true} | \ Omega) = p_ \ Omega (y_ {pred}) ^ t_ {0} * (1 - p_ \ Omega (y_ {pred}))) ^ t_ {1} = \\ p_0 ^ {t_0} * p_1 ^ {t_1} $$ عرض $$

حيث$$ $ inline $ t_0 ، t_1 $ inline $ تسميات الفئة الصحيحة ، على سبيل المثال ، إذا$$ $ inline $ y_ {true} = cat $ inline $ ثم$$ $ inline $ t_0 == 1 ، t_1 == 0 $ $ مضمّن إذا$$ $ inline $ y_ {true} = dog $ inline $ ثم$$ $ inline $ t_0 == 0 ، t_1 == 1 $ $ $ مضمنة . وبالتالي ، يتم دائمًا النظر في احتمالية الفصل الذي كان ينبغي التنبؤ به بواسطة شبكة عصبية (ولكن ليس بالضرورة التنبؤ به). الآن يمكن تعميم هذا على أي عدد من الفصول (على سبيل المثال ، فصول م):

$$عرض $$ $$ p (y_ {pred} = y_ {true} | \ Omega) = \ prod_0 ^ m p_i ^ {t_i} $$ عرض $$

ومع ذلك ، في أي مجموعة بيانات هناك العديد من الكائنات (على سبيل المثال ، كائنات N). أريد أن تعطي الشبكة العصبية الإجابة الصحيحة على كل أو أكثر من الكائنات. ولهذا تحتاج إلى مضاعفة نتائج الصيغة أعلاه لكل كائن من مجموعة البيانات.

$$عرض $$ $ الحد الأقصى Likelyhood = \ prod_ {j = 0} ^ N \ prod_ {i = 0} ^ m p_ {i، j} ^ {t_ {i، j}} $$ عرض $$

للحصول على نتائج جيدة ، تحتاج هذه الوظيفة إلى تعظيمها. ولكن ، أولاً ، من الأصعب تقليله ، لأن لدينا تدرج في مؤشر ستوكاستيك وكل الكعك من أجله - فقط قم بتعيين سالب ، وثانياً ، من الصعب العمل مع عمل ضخم - إنه لوغاريتم.

$$عرض $$ $ CrossEntropyLoss = - \ sum \ limit_ {j = 0} ^ {N} \ sum \ limit_ {i = 0} ^ {m} t_ {i، j} \ cdot \ log (p_ {i، j }) $$ عرض $$

! رائع وكانت النتيجة الانتروبيا أو ، في الحالة الثنائية ، logloss. هذه الوظيفة سهلة العد ويمكن تمييزها بشكل أسهل:

$$عرض $$ $$ \ frac {\ جزئي CrossEntropyLoss} {\ جزئية p_j} = - \ frac {\ boldsymbol {t_j}} {\ boldsymbol {p_ {j}}} $$ عرض $$

تحتاج إلى التمييز بين خوارزمية backpropagation. ألاحظ أن وظيفة الخطأ لا تغير البعد الموجه. إذا كان الناتج ، كما في حالة MNIST ، متجهًا للإجابات بعشرة أبعاد ، فعند حساب المشتق ، نحصل على متجه بعشر الأبعاد للمشتقات. شيء آخر مثير للاهتمام هو أن عنصر واحد فقط من المشتق لن يكون صفرا ، وعندها$$ $ inline $ t_ {i، j} \ neq 0 $ inline $ ، وهذا هو ، مع الإجابة الصحيحة. وكلما قل احتمال وجود إجابة صحيحة تنبأت بها شبكة عصبية في كائن ما ، كلما زادت وظيفة الخطأ.

ميزات التنشيط

عند إخراج كل طبقة متصلة بالكامل من الشبكة العصبية ، يجب أن تكون وظيفة التنشيط غير الخطية موجودة. بدونها ، من المستحيل تدريب شبكة عصبية ذات معنى. إذا نظرنا إلى المستقبل ، فإن طبقة متصلة بالكامل من الشبكة العصبية هي مجرد مضاعفة لبيانات الإدخال بواسطة مصفوفة الوزن. في الجبر الخطي ، وهذا ما يسمى خريطة خطية - وظيفة خطية. مزيج من وظائف الخطية هي أيضا وظيفة خطية. ولكن هذا يعني أن مثل هذه الوظيفة يمكنها فقط تقريب الوظائف الخطية. للأسف ، هذا ليس سبب الحاجة إلى الشبكات العصبية.

Softmax

عادةً ما يتم استخدام هذه الوظيفة على الطبقة الأخيرة من الشبكة ، حيث إنها تحول المتجه من الطبقة الأخيرة إلى متجه لـ "الاحتمالات": كل عنصر من عناصر المتجه يقع من 0 إلى 1 ومجموعه هو 1. إنه لا يغير بُعد المتجه.

$$عرض $$ $ Softmax_i = \ frac {e ^ {x_i}} {\ sum \ limit_ {j} e ^ {x_j}} $$ عرض $$

الآن دعنا ننتقل إلى البحث عن المشتقات. ل$$ $ inline $ \ boldsymbol {x} $ inline $ هو ناقل ، وجميع عناصره موجودة دائمًا في المقام ، ثم عند أخذ المشتق نحصل على اليعاقبة:

$$عرض $$ $ J_ {Softmax} = \ تبدأ {الحالات} x_i - x_i \ cdot x_j ، i = j \\ - x_i \ cdot x_j ، i \ neq j \ end {cases} $$ عرض $$

الآن عن backpropagation. يأتي ناقل المشتقات من الطبقة السابقة (عادة ما تكون هذه دالة خطأ)$$ $ inline $ \ boldsymbol {dz} $ inline $ . في حالة$$ $ inline $ \ boldsymbol {dz} $ inline $ جاء من وظيفة خطأ على mnist ،$$ $ inline $ \ boldsymbol {dz} $ inline $ - ناقل 10 الأبعاد. ثم يعقوبي لديه البعد 10x10. للحصول على$$ $ inline $ \ boldsymbol {dz_ {new}} $ inline $ ، والذي ينتقل إلى الطبقة السابقة (لا تنس أننا ننتقل من النهاية إلى بداية الشبكة عندما ينتشر الخطأ مرة أخرى) ، نحتاج إلى مضاعفة$$ $ inline $ \ boldsymbol {dz} $ inline $ في$$ $ inline $ J_ {Softmax} $ inline $ (صف لكل عمود):

$$عرض $$ $ dz_ {new} = \ boldsymbol {dz} \ الأوقات J_ {Softmax} $$ عرض $$

في الخرج ، نحصل على ناقل 10-الأبعاد للمشتقات$$ $ inline $ \ boldsymbol {dz_ {new}} $ inline $ .

ReLU

$$عرض $$ $ ReLU (x) = \ start {cases} x، x> 0 \\ 0، x <0 \ end {cases} $$ عرض $$

بدأت ReLU تستخدم على نطاق واسع بعد عام 2011 ، عندما تم نشر مقال "الشبكات العصبية ذات المعدل المتناثر العميق". ومع ذلك ، كانت هذه الوظيفة معروفة سابقا. ينطبق مفهوم "قوة التنشيط" على ReLU (لمزيد من التفاصيل ، راجع كتاب "التعلم العميق. الانغماس في عالم الشبكات العصبية"). لكن الميزة الرئيسية التي تجعل ReLU أكثر جاذبية من وظائف التنشيط الأخرى هي حسابها المشتق البسيط:

$$عرض $$ $$ d (ReLU (x)) = \ start {cases} 1، x> 0 \\ 0، x <0 \ end {cases} $$ عرض $$

وبالتالي ، فإن ReLU أكثر كفاءة من الناحية الحسابية من وظائف التنشيط الأخرى (السيني ، الظل المائل ، إلخ).

طبقة متصلة بالكامل

الآن هو الوقت المناسب لمناقشة طبقة متصلة بالكامل. الأهم من ذلك كله ، لأنه في هذه الطبقة توجد جميع الأوزان ، والتي يجب ضبطها حتى تعمل الشبكة العصبية بشكل جيد. طبقة متصلة بالكامل هي ببساطة مصفوفة وزن:

$$عرض $$ $ W = | w_ {i، j} | $$ عرض $$

يتم الحصول على تمثيل داخلي جديد عند ضرب مصفوفة الوزن في عمود الإدخال:

$$عرض $$ $$ \ boldsymbol {x} _ {new} = W \ cdot \ boldsymbol {x} $$ عرض $$

حيث$$ $ inline $ \ boldsymbol {x} $ inline $ له حجم$$ $ $ $ $ inline \ _shape $ $ $ $ inline $ و$$ $ inline $ x_ {new} $ inline $ -$$ $ $ مضمنة الإخراج \ _shape $ $ مضمنة . على سبيل المثال$$ $ inline $ \ boldsymbol {x} $ inline $ - 784 ناقلات الأبعاد ، و$$ $ inline $ \ boldsymbol {x} _ {new} $ inline $ هو ناقل 100-الأبعاد ، ثم المصفوفة W بحجم 100x784. اتضح أن على هذه الطبقة 100x784 = 78،400 الأوزان.

مع الانتشار الخلفي للخطأ ، يحتاج المرء إلى أخذ المشتق فيما يتعلق بكل وزن من هذه المصفوفة. تبسيط المشكلة واتخاذ فقط مشتق فيما يتعلق$$ $ inline $ w_ {1،1} $ inline $ . عند ضرب المصفوفة والناقل ، يكون العنصر الأول للناقل الجديد$$ $ inline $ \ boldsymbol {x} _ {new} $ inline $ يساوي$$ $ inline $ x_ {new ~ 1} = w_ {1،1} \ cdot x_1 + ... + w_ {1،784} \ cdot x_ {784} $ inline $ ، والمشتق$$ $ inline $ x_ {new ~ 1} $ inline $ في$$ $ inline $ w_ {1،1} $ inline $ سوف تكون بسيطة$$ $ inline $ x_1 $ inline $ ، تحتاج فقط إلى اتخاذ مشتق من المبلغ أعلاه. يحدث بالمثل لجميع الأوزان الأخرى. ولكن هذا ليس خطأ خوارزمية الانتشار الخلفي ، طالما أنها مجرد مصفوفة من المشتقات. عليك أن تتذكر أنه من الطبقة التالية إلى هذا (الخطأ ينتقل من النهاية إلى البداية) يأتي متجه تدرج 100 - الأبعاد$$ $ inline $ d \ boldsymbol {z} $ inline $ . العنصر الأول من هذا المتجه$$ $ inline $ dz_1 $ inline $ سوف تتضاعف جميع عناصر مصفوفة المشتقات التي "شاركت" في الخلق$$ $ inline $ x_ {new ~ 1} $ inline $ ، على سبيل المثال ،$$ $ inline $ x_1، x_2، ...، x_ {784} $ inline $ . وبالمثل ، فإن بقية العناصر. إذا قمت بترجمة هذا إلى لغة الجبر الخطي ، فسيتم كتابتها هكذا:

$$عرض $$ $$ \ frac {\ الجزئي L} {\ الجزئي W} = (d \ boldsymbol {z} ، ~ dW) = \ left (\ start {matrix} dz_ {1} \ cdot \ boldsymbol {x} \ \ ... \\ dz_ {100} \ cdot \ boldsymbol {x} \ end {matrix} \ right) _ {100} $$ عرض $$

الإخراج هو مصفوفة 100x784.


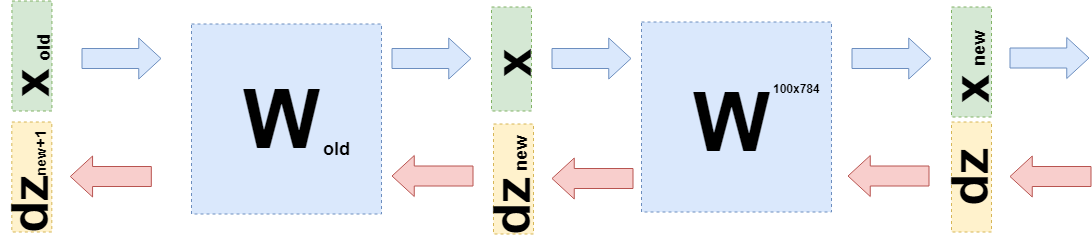
أنت الآن بحاجة إلى فهم ما يجب نقله إلى الطبقة السابقة. لهذا وللفهم الأفضل لما حدث الآن ، أريد أن أكتب ما حدث عند أخذ المشتقات على هذه الطبقة بلغة مختلفة قليلاً ، للابتعاد عن تفاصيل "ما هو مضروب" إلى الدوال (مرة أخرى).

عندما أردت ضبط الأوزان ، أردت أخذ مشتق من وظيفة الخطأ لهذه الأوزان:$$ $ inline $ \ frac {\ جزئية L} {\ جزئية W} $ مضمنة $ . تم توضيح أعلاه كيفية أخذ مشتقات وظائف الخطأ ووظائف التنشيط. لذلك ، يمكننا النظر في مثل هذه الحالة (في$$ $ inline $ d \ boldsymbol {z} $ inline $ جميع مشتقات وظيفة الخطأ ووظائف التنشيط موجودة بالفعل):

$$عرض $$ $$ \ frac {\ الجزئي L} {\ الجزئي W} = d \ boldsymbol {z} \ cdot \ frac {\ الجزئي \ boldsymbol {x} _ {new} (W)} {\ الجزئي W} $ عرض $ $

يمكن القيام بذلك ، لأنه يمكنك التفكير فيه$$ $ inline $ \ boldsymbol {x} _ {new} $ inline $ كدالة W:$$ $ inline $ \ boldsymbol {x} _ {new} = W \ cdot \ boldsymbol {x} $ inline $ .
يمكنك استبدال هذا في الصيغة أعلاه:

$$عرض $$ $$ \ frac {\ الجزئي L} {\ الجزئي W} = d \ boldsymbol {z} \ cdot \ frac {\ الجزئي W \ cdot \ boldsymbol {x}} {\ الجزئي W} = d \ boldsymbol { z} \ cdot E \ cdot \ boldsymbol {x} $$ عرض $$

حيث E عبارة عن مصفوفة تتكون من وحدات (ليست مصفوفة وحدة).

الآن عندما تحتاج إلى أخذ مشتق من الطبقة السابقة (حتى لو كانت لبساطة العمليات الحسابية ، فإنها ستكون أيضًا طبقة متصلة تمامًا ، ولكن في الحالة العامة لا تغير أي شيء) ، فأنت بحاجة إلى التفكير$$ $ inline $ \ boldsymbol {x} $ inline $ كدالة في الطبقة السابقة$$ $ inline $ \ boldsymbol {x} (W_ {old}) $ inline $ :

$$عرض $$ $$ \ بدء {المجمعة} \ frac {\ الجزئي L} {\ الجزئي W_ {old}} = d \ boldsymbol {z} \ cdot \ frac {\ جزئي \ boldsymbol {x} _ {new} (W )} {\ الجزئي W_ {old}} = d \ boldsymbol {z} \ cdot \ frac {\ الجزئي W \ cdot \ boldsymbol {x} (W_ {old})} {\ الجزئي W_ {old}} = \\ = d \ boldsymbol {z} \ cdot \ frac {\ الجزئي W \ cdot W_ {old} \ cdot \ boldsymbol {x} _ {old}} {\ الجزئي W_ {old}} = d \ boldsymbol {z} \ cdot W \ cdot E \ cdot \ boldsymbol {x} _ {old} = \\ = d \ boldsymbol {z} _ {new} \ cdot E \ cdot \ boldsymbol {x} _ {old} \ end {gathered} $$ عرض $$

أي$$ $ inline $ d \ boldsymbol {z} _ {new} = d \ boldsymbol {z} \ cdot W $ inline $ وتحتاج إلى إرسال إلى الطبقة السابقة.

قانون

يهدف هذا المقال أساسًا إلى شرح رياضيات الشبكات العصبية. سأكرس القليل جدا من الوقت للرمز.

هذا مثال على تنفيذ دالة الخطأ:

class CrossEntropy: def forward(self, y_true, y_hat): self.y_hat = y_hat self.y_true = y_true self.loss = -np.sum(self.y_true * np.log(y_hat)) return self.loss def backward(self): dz = -self.y_true / self.y_hat return dz 

الطبقة لديها طرق لتمرير مباشرة وعكسية. في وقت التمرير المباشر ، يخزن مثيل الفصل البيانات داخل الطبقة ، وفي وقت مرور الإرجاع ، يستخدمها لحساب التدرج اللوني. يتم بناء الطبقات المتبقية بنفس الطريقة. بفضل هذا ، يصبح من الممكن كتابة عصبية متصلة بالكامل بهذا النمط:

 class MnistNet: def __init__(self): self.d1_layer = Dense(784, 100) self.a1_layer = ReLu() self.drop1_layer = Dropout(0.5) self.d2_layer = Dense(100, 50) self.a2_layer = ReLu() self.drop2_layer = Dropout(0.25) self.d3_layer = Dense(50, 10) self.a3_layer = Softmax() def forward(self, x, train=True): ... def backward(self, dz, learning_rate=0.01, mini_batch=True, update=False, len_mini_batch=None): ... 

يمكن العثور على الرمز الكامل هنا .
كما أنصح بدراسة هذا المقال عن حبري .

استنتاج

آمل أن أتمكن من شرح وإظهار أن الرياضيات البسيطة جدًا تقف وراء الشبكات العصبية وأن هذا ليس مخيفًا على الإطلاق. ومع ذلك ، من أجل فهم أعمق ، يجدر محاولة كتابة "الدراجة" الخاصة بك. يسعد التصحيحات والاقتراحات بقراءة التعليقات.