استخدم كل مطور لنظام Android RecyclerView لعرض القوائم ، وواجه كل منهم مشكلة تحديث البيانات في القائمة حتى ظهرت فئة DiffUtil السحرية في عام 2016. سأشرح على الأصابع كيف يعمل بالفعل ، وأحاول تبديد سحره.
قليلا من التاريخ
واحدة من العناصر الأكثر شيوعا في تطبيقات الهاتف المحمول هي القائمة ، في حالتنا RecyclerView . يمكن أن تكون هذه قوائم لأي شيء: عناوين المكاتب ، وقوائم الأصدقاء في الشبكات الاجتماعية. الشبكات ، سجل الطلبات في تطبيقات سيارات الأجرة ، إلخ. يتم توحيد كل هذه الحالات بضرورة تغيير البيانات في القائمة باستمرار إلى أخرى جديدة ، على سبيل المثال ، عندما قام المستخدم بتمرير سريع لتحديث القائمة أو تصفيتها أو بأي طريقة أخرى تلقي حزمة من البيانات الجديدة من الخلف.
لتنفيذ هذا السلوك ، اختار سلف مطور Android الحديث ما هي البيانات وكيف تغيرت ، ودعا الأساليب المناسبة من RecyclerView . ومع ذلك ، تغير كل شيء عندما أصدرت Google إصدار مكتبة الدعم 25.1.0 ، مضيفة DiffUtil هناك ، مما سمح لك بتحويل القائمة القديمة بطريقة سحرية إلى قائمة جديدة دون إعادة إنشاء RecyclerView بالكامل. في هذه المقالة ، سوف DiffUtil سحر DiffUtil وأشرح كيف يعمل.
كيفية العمل مع DiffUtil؟
للعمل مع DiffUtil يجب تطبيق DiffUtil.Callback ، استدعاء الأسلوب calculateDiff(@NonNull Callback cb) وتطبيق DiffResult المستلمة على RecyclerView باستخدام أسلوب dispatchUpdatesTo() . ماذا يحدث عندما calucalteDiff(@NonNull Callback cd) طريقة calucalteDiff(@NonNull Callback cd) ؟ تُرجع هذه الطريقة DiffResult ، والتي تحتوي على مجموعة من العمليات لتحويل القائمة الأصلية إلى قائمة جديدة. يتم تطبيق التحديثات عن طريق المكالمات إلى notifyItemRangeInserted notifyItemRangeRemoved ، و notifyItemMoved و notifyItemRangeChanged notifyItemMoved و notifyItemRangeChanged . الأساليب الثلاثة الأولى تغيير بنية القائمة ، وهي مواضع العناصر ، دون تغيير العناصر نفسها وعدم استدعاء onBindViewHolder() عليها (باستثناء العنصر الذي تتم إضافته). الأخير يغير العنصر نفسه ويستدعي onBindViewHolder() لتغيير طريقة عرض العنصر.
يتحقق DiffUtil من قائمتين بحثًا عن الاختلافات باستخدام خوارزمية مايرز ، والتي تحدد فقط وجود / عدم وجود تغييرات ، ولكنها لا تعرف كيفية العثور على حركة العناصر. للقيام بذلك ، DiffUtil عبر DiffUtil التي تم إنشاؤها بواسطة خوارزمية مايرز (المزيد حول هذا لاحقًا) ، ثم يبحث عن الحركات. يتم تشكيل DiffResult ل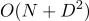 
إذا كانت الخوارزمية لا تتحقق من حركة العناصر و 
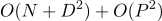، حيث P هو عدد العناصر المضافة والمحذوفة.
مايرز خوارزمية
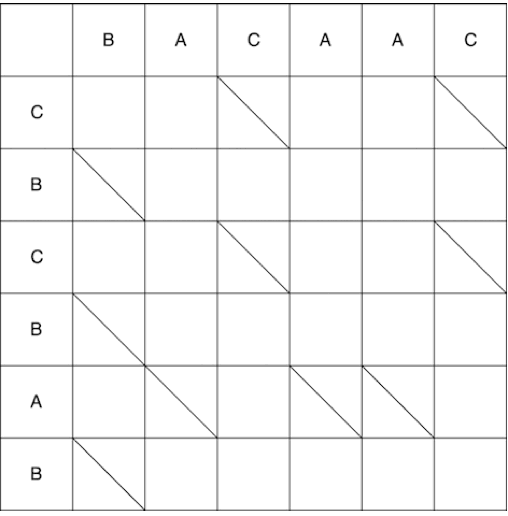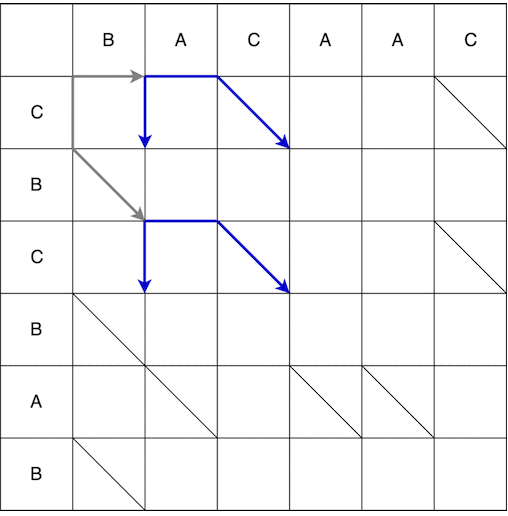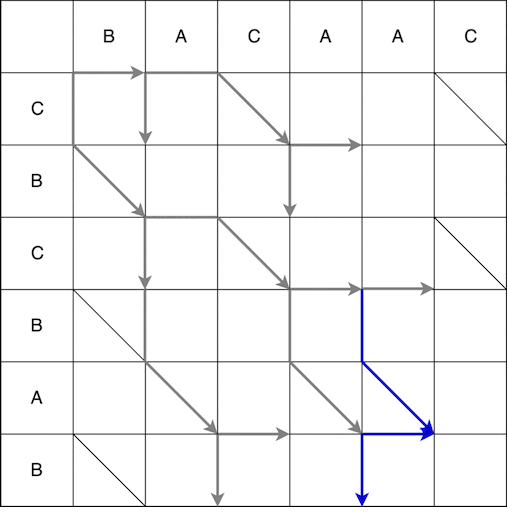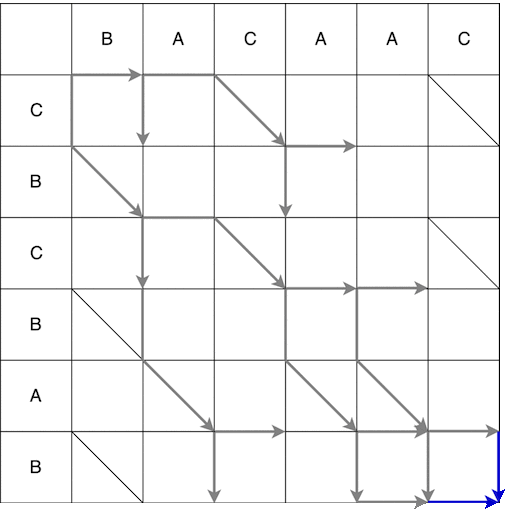
بعد ذلك ، سيتم النظر في شرح لخوارزمية مايرز على الأصابع ، وستكون روابط إلى تفسيرات رياضية للخوارزمية (بالإضافة إلى مقالات رائعة أخرى حول الموضوع) في نهاية المقالة. النظر في تسلسلين: BACAAC و CBCBAB. من الضروري كتابة سلسلة من التحولات على التسلسل الأول ، وبعدها نحصل على الثانية. نكتب التسلسلات في الجدول كما يلي: ستشير القائمة القديمة إلى العناصر الأولى للأعمدة ، وستكون القائمة الجديدة هي العناصر الأولى في الصفوف.
شطب الخلايا التي تتقاطع فيها عناصر متطابقة من كلا التسلسلين:
تتمثل المهمة الأخرى في الانتقال من الركن الأيسر العلوي من المصفوفة إلى الزاوية اليمنى السفلى بأقل عدد من الخطوات. يمكنك التحرك على طول الوجوه الأفقية والرأسية. إذا وصلت إلى النقطة التي يبدأ فيها الخط المائل ، فيجب عليك التحرك على طوله ، لكن تكلفة مثل هذه الخطوة هي 0. وبناءً على ذلك ، تكون تكلفة الخطوة على الحواف هي 1.
من النقطة (0 ؛ 0) يمكننا الانتقال إلى اليمين وإلى الأسفل. عند الانتقال لأسفل ، يجب أن تذهب قطريًا بشكل إضافي. تسمى الحركة التي تم إجراؤها في خطوة واحدة الأفعى ، وفي هذه الحالة تلقى 2 ثعبان: (0؛ 0) -> (0؛ 1) و (0؛ 0) -> (1؛ 2). يشير السهم إلى نهاية الثعبان ، أي إذا كانت هناك خطوة إلزامية على طول المائل بعد الخطوة العمودي / الأفقي ، فسيكون السهم في الخطوة على طول القطر. يظهر البناء الكامل للثعابين من نقطة البداية إلى النهاية أدناه. تم حذف بعض المسارات على الفيديو بسبب من الواضح أنها ليست الأقصر.
نتيجة لذلك ، نحصل على العديد من المسارات الأقصر الممكنة ، وبعضها معروض أدناه.
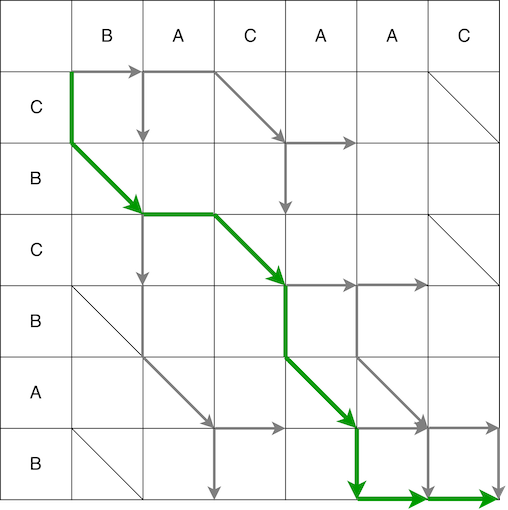
كيف يمكن أن يساعد تمرير مصفوفة من أقصى اليسار إلى أقصى اليمين في تحديد تسلسل الإجراءات (البرنامج النصي) لتحويل تسلسل واحد إلى آخر؟ ماذا تعني الخطوات الأفقية والرأسية والقطرية؟ الخطوة على طول المصفوفة في أحد الاتجاهات المحتملة هي الإجراءات على السطر القديم:
- الخطوة الأفقية - حذف من الخط القديم
- الخطوة العمودية - إضافة إلى الخط القديم
- خطوة قطرية - لا تغيير
باستخدام المسار الثاني كمثال ، نقارن المسار والنص الناتج. الخطوة الأولى عمودية ، مما يعني أننا نضيف الحرف "C" إلى الموضع 0 في السطر القديم.
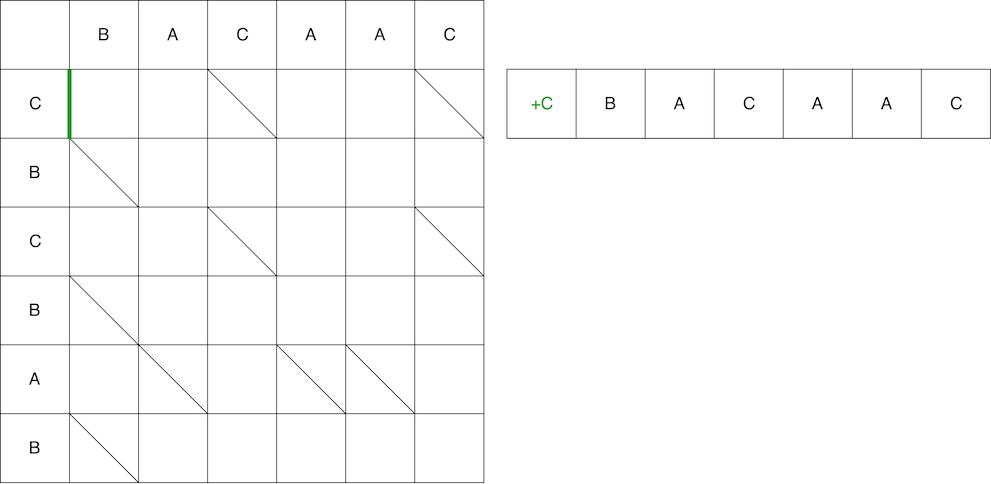
ومع ذلك ، ليس هذا هو الثعبان كله. بعد ذلك ، يجب أن نتحرك قطريا. عند التحرك قطريًا ، يظل العنصر B بدون تغيير. نتيجة لذلك ، يتكون الثعبان من حركة رأسية + حركة قطرية.
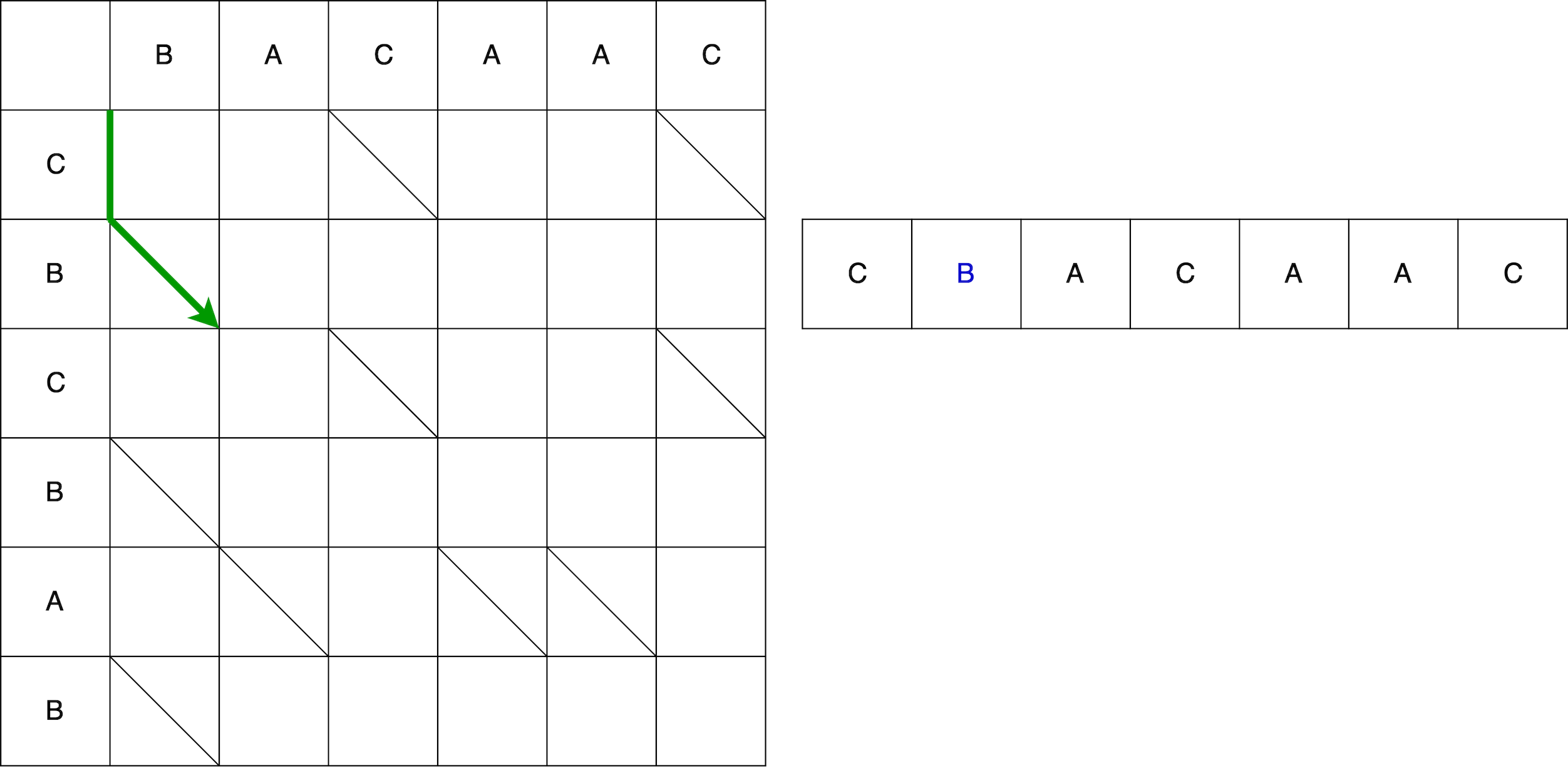
بعد ذلك ، ثعبان أفقيا - إزالة العنصر A. من السطر القديم
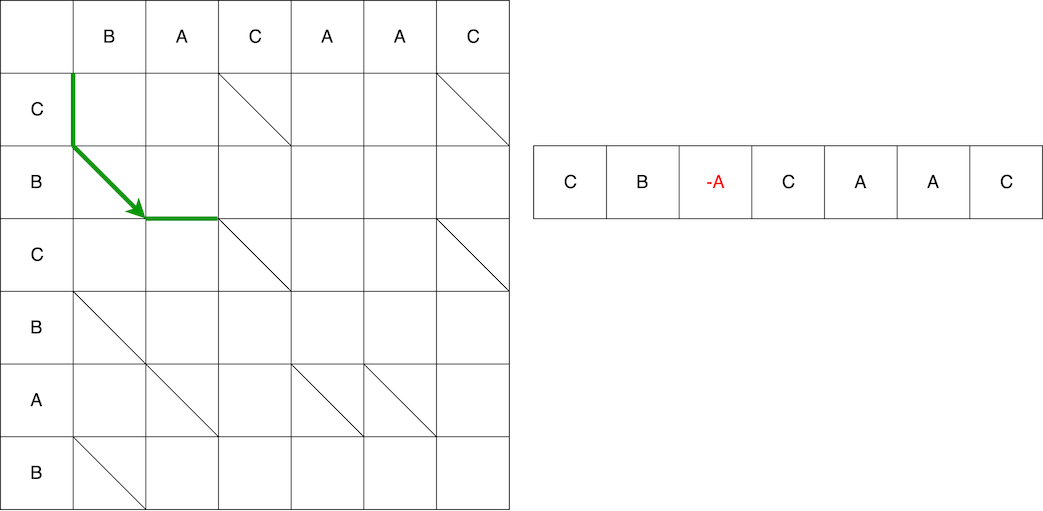
يُظهر الفيديو المسار بالكامل من البداية إلى النهاية مع تغيير في السلسلة المصدر حتى يتم تحويله إلى الأخير.
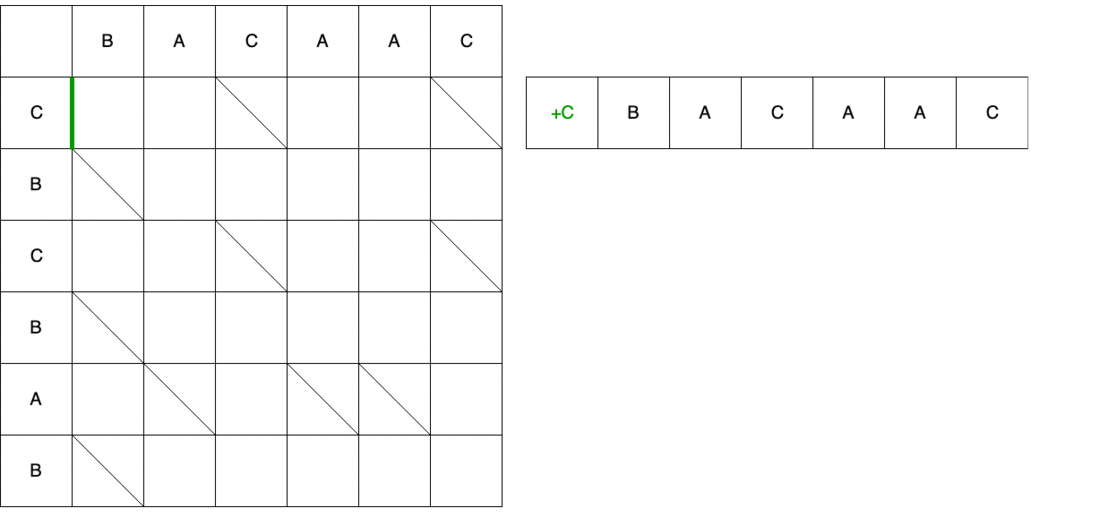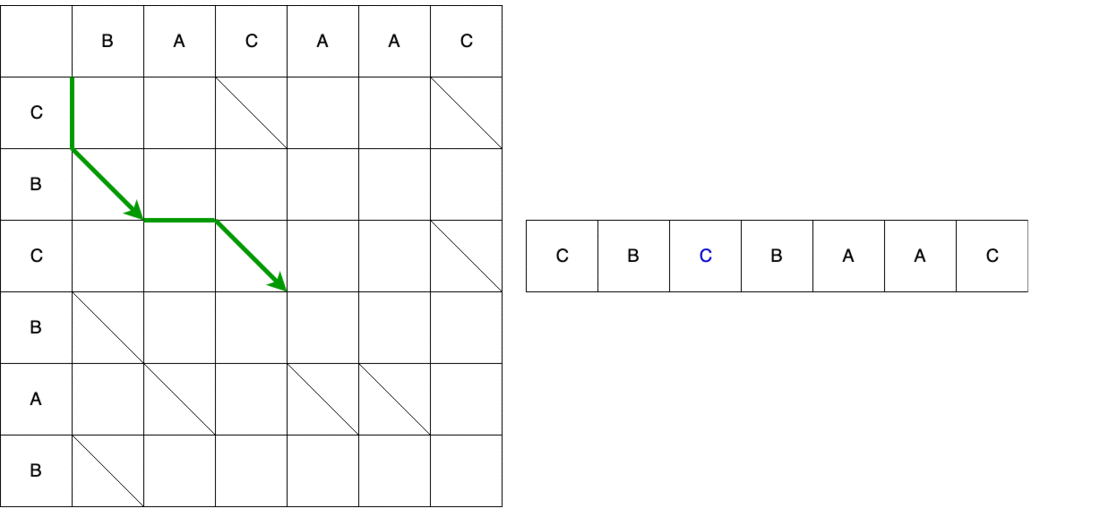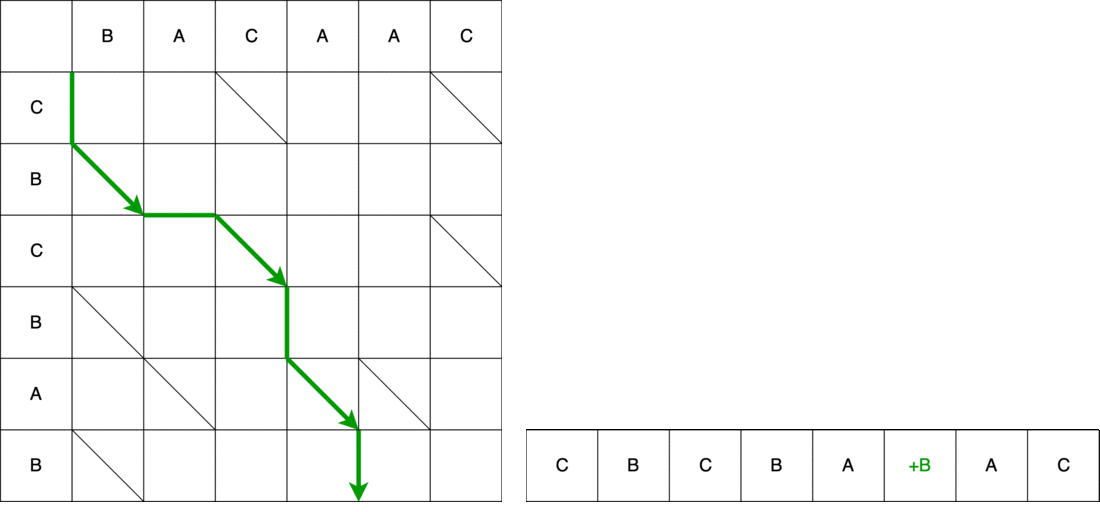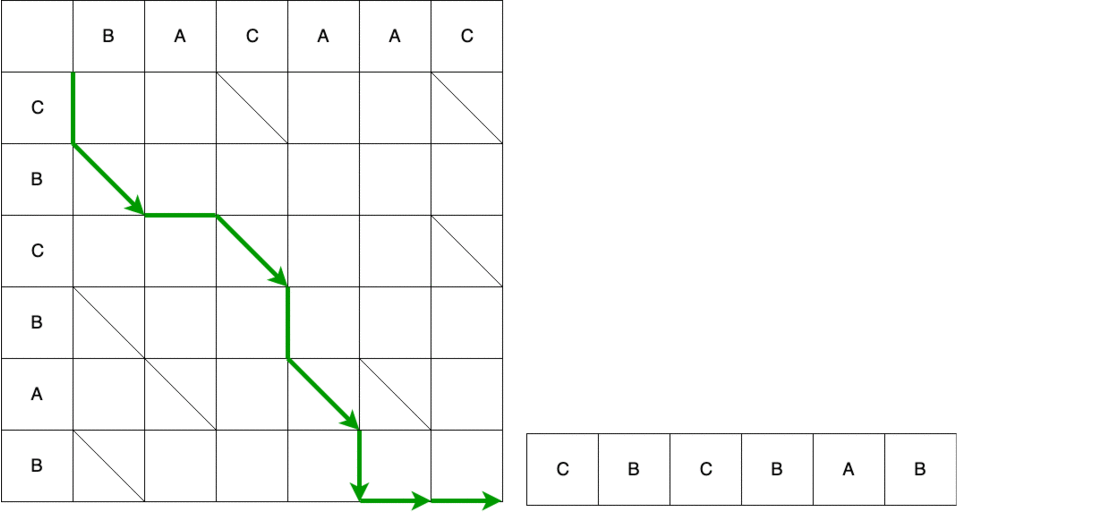
نتيجة خوارزمية مايرز هي برنامج نصي مع مجموعة من الحد الأدنى لعدد الإجراءات التي يجب القيام بها لتحويل تسلسل واحد إلى آخر. في DiffUtil يتم استخدام خوارزمية مايرز للبحث عن العناصر المختلفة التي تحددها طريقة areItemsTheSame() . بالإضافة إلى تكوين قائمة من الثعابين ، عند المرور عبر القوائم ، تقوم خوارزمية مايرز بإنشاء قوائم لحالات عناصر عناصر القوائم القديمة والجديدة. يتم تمرير كل هذه البيانات ، بالإضافة إلى detectMoves و رد الاتصال الذي تم تنفيذه بواسطة المستخدم ، إلى مُنشئ DiffResult(Callback callback, List<Snake> snakes, int[] oldItemStatuses, int[] newItemStatuses, boolean detectMoves) .
أثناء كتابة هذا المقال ، تمكنت من اكتشاف ما يحدث بالضبط في DiffResult : الخوارزمية تمر عبر الثعابين وتعيين العلامات على العناصر (في قوائم الحالة) ، والتي تحدد ما حدث بالضبط للعنصر. باستخدام هذه العلامات ، عند تطبيق التغييرات على RecyclerView يتم تحديد الطريقة التي يتم بها تطبيق التحديثات على: notifyItemRangeInserted, notifyItemRangeRemoved, notifyItemMoved notifyItemRangeChanged . بمزيد من التفصيل سأتحدث عن هذا في المرة القادمة.
مراجع