الشبكات العصبية والتعلم العميق ، الفصل 3 ، الجزء 3: كيفية اختيار معلمات الشبكة العصبية؟

حتى الآن ، لم أشرح كيف أختار قيم المعلمات الفائقة - سرعة التعلم η ومعلمة التنظيم λ وما إلى ذلك. أنا فقط أعطيت قيم العمل لطيفة. في الممارسة العملية ، عند استخدام شبكة عصبية لمهاجمة مشكلة ، قد يكون من الصعب العثور على معلمات تشعبية جيدة. تخيل ، على سبيل المثال ، أننا أخبرنا للتو بمشكلة MNIST ، وبدأنا العمل عليها ، ولا نعرف أي شيء عن قيم المقاييس الفائقة المناسبة. لنفترض أننا كنا محظوظين بالصدفة ، وفي التجارب الأولى اخترنا العديد من المعلمات الفائقة كما فعلنا بالفعل في هذا الفصل: 30 خلية عصبية مخفية ، حجم رزمة صغيرة 10 ، تدريب لمدة 30 عصور ، واستخدام إنتروبيا. ومع ذلك ، اخترنا معدل التعلم 10.0 = 10.0 ، ومعلمة التنظيم 1000 = 1000.0. وهنا ما رأيته في هذه الجولة:

>>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10]) >>> net.SGD(training_data, 30, 10, 10.0, lmbda = 1000.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 1030 / 10000 Epoch 1 training complete Accuracy on evaluation data: 990 / 10000 Epoch 2 training complete Accuracy on evaluation data: 1009 / 10000 ... Epoch 27 training complete Accuracy on evaluation data: 1009 / 10000 Epoch 28 training complete Accuracy on evaluation data: 983 / 10000 Epoch 29 training complete Accuracy on evaluation data: 967 / 10000 

تصنيفنا لا يعمل بشكل أفضل من أخذ العينات العشوائية! شبكتنا تعمل كمولد ضوضاء عشوائي!

"حسنًا ، هذا سهل الإصلاح" ، يمكنك القول ، "فقط قلل من المعلمات الفائقة مثل سرعة التعلم والتنظيم". لسوء الحظ ، هناك سلفًا أنه ليس لديك معلومات حول ماهية هذه المعلمات الفائقة التي تحتاج إلى ضبطها بالضبط. ربما تكون المشكلة الرئيسية هي أن الخلايا العصبية المخفية الثلاثين لدينا لن تعمل أبدًا ، بغض النظر عن كيفية اختيار المعلمات الفوقية الأخرى؟ ربما نحتاج إلى 100 خلية عصبية على الأقل؟ أو 300؟ أو الكثير من الطبقات المخفية؟ أو نهج مختلف لإخراج الترميز؟ ربما تتعلم شبكتنا ، لكننا بحاجة إلى تدريبها أكثر من عصور؟ ربما حجم الحزم الصغيرة صغير جدا؟ ربما كنا لنعمل بشكل أفضل إذا عدنا إلى الوظيفة التربيعية للقيمة؟ ربما نحتاج إلى تجربة طريقة مختلفة لتهيئة الأوزان؟ وهلم جرا وهكذا دواليك. في فضاء المعلمات الفائقة ، من السهل أن تضيع. وقد يؤدي هذا بالفعل إلى الكثير من الإزعاج إذا كانت شبكتك كبيرة جدًا ، أو تستخدم كميات هائلة من بيانات التدريب ، ويمكنك تدريبها لساعات أو أيام أو أسابيع دون تلقي نتائج. في مثل هذه الحالة ، تبدأ ثقتك بنفسك. ربما كانت الشبكات العصبية هي النهج الخاطئ لحل مشكلتك؟ ربما كنت استقال وتفعل تربية النحل؟

في هذا القسم ، سأشرح بعض الطرق التي يمكنك استخدامها لتكوين المعلمات الفائقة في شبكة عصبية. الهدف من ذلك هو مساعدتك على الخروج بسير عمل يتيح لك تكوين معلمات تشعبية بشكل جيد. بالطبع ، لا يمكنني تغطية الموضوع الكامل للتحسين الفائق. هذه منطقة ضخمة ، وهذه ليست مشكلة يمكن حلها بالكامل ، أو وفقًا للاستراتيجيات الصحيحة للحل التي يوجد بها اتفاق عالمي. هناك دائمًا فرصة لتجربة بعض الحيل الأخرى للضغط على نتائج إضافية من شبكتك العصبية. لكن الاستدلال في هذا القسم يجب أن يمنحك نقطة انطلاق.

الاستراتيجية العامة

عند استخدام شبكة عصبية لمهاجمة مشكلة جديدة ، تتمثل الصعوبة الأولى في الحصول على نتائج غير تافهة من الشبكة ، أي تجاوز الاحتمال العشوائي. قد يكون ذلك صعباً بشكل مدهش ، خاصةً عندما تواجه فئة جديدة من المهام. دعونا نلقي نظرة على بعض الاستراتيجيات التي يمكن استخدامها لهذا النوع من الصعوبة.

لنفترض ، على سبيل المثال ، أنك أول من يهاجم مهمة MNIST. أنت تبدأ بحماس كبير ، ولكن الفشل التام لشبكتك الأولى أمر محبط بعض الشيء ، كما هو موضح في المثال أعلاه. ثم تحتاج إلى تفكيك المشكلة في أجزاء. تحتاج إلى التخلص من كل التدريب والصور الداعمة ، باستثناء صور الأصفار والصور. ثم حاول تدريب الشبكة على التمييز بين 0 و 1. هذه المهمة ليست أسهل من تمييز جميع الأرقام العشرة فحسب ، بل إنها تقلل أيضًا مقدار بيانات التدريب بنسبة 80٪ ، وتسريع عملية التعلم بمقدار 5 مرات. يتيح لك ذلك إجراء تجارب أسرع بكثير ، ويمنحك الفرصة لفهم كيفية إنشاء شبكة جيدة بسرعة.

يمكن زيادة تسريع التجارب عن طريق تقليل الشبكة إلى الحد الأدنى للحجم الذي من المحتمل أن يتم تدريبه بشكل مفيد. إذا كنت تعتقد أن الشبكة [784 ، 10] من المحتمل جدًا أن تكون قادرًا على تصنيف أرقام MNIST بشكل أفضل من عينة عشوائية ، ثم ابدأ في التجربة. سيكون أسرع بكثير من التدريب [784 ، 30 ، 10] ، ويمكنك بالفعل تطويره لاحقًا.

يمكن الحصول على تسريع آخر للتجارب من خلال زيادة وتيرة التتبع. في برنامج network2.py ، نراقب جودة العمل في نهاية كل عصر. معالجة 50000 صورة لكل فترة ، يجب أن ننتظر وقتًا طويلًا - حوالي 10 ثوانٍ لكل فترة على الكمبيوتر المحمول أثناء التدريب على الشبكة [784 ، 30 ، 10] - قبل الحصول على تعليقات حول جودة التدريب على الشبكة. بالطبع ، لا تستغرق عشر ثوانٍ وقتًا طويلاً ، ولكن إذا كنت ترغب في تجربة بضع عشرات من البارامترات المختلفة ، فإنها تبدأ في الإزعاج ، وإذا كنت ترغب في تجربة مئات أو الآلاف من الخيارات ، فهي مدمرة فقط. يمكن تلقي التعليقات بشكل أسرع بكثير من خلال تتبع دقة التأكيد في كثير من الأحيان ، على سبيل المثال ، كل 1000 صورة تدريب. بالإضافة إلى ذلك ، بدلاً من استخدام المجموعة الكاملة المكونة من 10000 صورة تأكيد ، يمكننا الحصول على تقدير أسرع بكثير باستخدام 100 صورة تأكيد فقط. الشيء الرئيسي هو أن الشبكة ترى صورًا كافية للتعلم حقًا ، وللحصول على تقدير جيد بما فيه الكفاية للفعالية. بالطبع ، شبكتنا 2.py لم تقدم بعد مثل هذا التتبع. لكن كعكازات لتحقيق هذا التأثير لأغراض توضيحية ، نقوم بقص بيانات التدريب الخاصة بنا إلى أول 1000 صورة من صور MNIST. دعنا نحاول أن نرى ما يحدث (على بساطة الكود ، لم أستخدم فكرة ترك الصور فقط 0 و 1 - يمكن تحقيق ذلك أيضًا بجهد أكبر).

 >>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 10.0, lmbda = 1000.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 10 / 100 Epoch 1 training complete Accuracy on evaluation data: 10 / 100 Epoch 2 training complete Accuracy on evaluation data: 10 / 100 ... 

ما زلنا نحصل على ضوضاء نقية ، ولكن لدينا ميزة كبيرة: يتم تحديث الملاحظات في كسور من الثانية ، وليس كل عشر ثوان. هذا يعني أنه يمكنك تجربة أسرع بكثير من خلال اختيار المعلمات الفائقة ، أو حتى تجربة العديد من البارامترات المختلفة في وقت واحد تقريبًا.

في المثال أعلاه ، تركت قيمة λ تساوي 1000.0 ، كما كان من قبل. ولكن نظرًا لأننا قمنا بتغيير عدد أمثلة التدريب ، فإننا بحاجة إلى التغيير λ بحيث يكون ضعف الأوزان هو نفسه. هذا يعني أننا نغير λ بحلول 20.0. في هذه الحالة ، سيظهر ما يلي:

 >>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 10.0, lmbda = 20.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 12 / 100 Epoch 1 training complete Accuracy on evaluation data: 14 / 100 Epoch 2 training complete Accuracy on evaluation data: 25 / 100 Epoch 3 training complete Accuracy on evaluation data: 18 / 100 ... 

آها! لدينا إشارة. ليست جيدة بشكل خاص ، ولكن هناك. يمكن أن يؤخذ هذا بالفعل كنقطة بداية ، وتغيير المعلمات الفائقة لمحاولة الحصول على مزيد من التحسينات. لنفترض أننا قررنا أننا بحاجة إلى زيادة سرعة التعلم (كما قد تفهمها ، فقد قررنا بشكل غير صحيح ، لسبب أننا سنناقش لاحقًا ، ولكن دعونا نحاول القيام بذلك في الوقت الحالي). لاختبار تخميننا ، نلتفت إلى 100.0:

 >>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 100.0, lmbda = 20.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 10 / 100 Epoch 1 training complete Accuracy on evaluation data: 10 / 100 Epoch 2 training complete Accuracy on evaluation data: 10 / 100 Epoch 3 training complete Accuracy on evaluation data: 10 / 100 ... 

كل شيء سيء! على ما يبدو ، كان تخميننا غير صحيح ، ولم تكن المشكلة في القيمة المنخفضة جدًا لسرعة التعلم. نحاول تشديد η على قيمة صغيرة من 1.0:

 >>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 1.0, lmbda = 20.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 62 / 100 Epoch 1 training complete Accuracy on evaluation data: 42 / 100 Epoch 2 training complete Accuracy on evaluation data: 43 / 100 Epoch 3 training complete Accuracy on evaluation data: 61 / 100 ... 

هذا أفضل! وبالتالي يمكننا الاستمرار أكثر ، والتواء كل معلمة ، وتحسين الكفاءة تدريجيا. بعد دراسة الموقف والبحث عن قيمة محسّنة لـ η ، ننتقل إلى البحث عن قيمة جيدة لـ λ. ثم سنقوم بإجراء تجربة ذات بنية أكثر تعقيدًا ، على سبيل المثال ، مع شبكة من 10 خلايا عصبية مخفية. بعد ذلك ، نقوم مرة أخرى بضبط المعلمات η و λ. ثم سنزيد الشبكة إلى 20 الخلايا العصبية المخفية. قرص قليلا في hyperparameters. وهكذا ، قم بتقييم الفعالية في كل خطوة باستخدام جزء من البيانات الداعمة الخاصة بنا ، واستخدام هذه التقديرات لتحديد أفضل المعايير الفوقية. في عملية التحسينات ، يستغرق الأمر المزيد والمزيد من الوقت لمعرفة تأثير ضبط المعلمات الفائقة ، حتى نتمكن من تقليل وتيرة التتبع تدريجياً.

كاستراتيجية شاملة ، يبدو هذا النهج واعداً. ومع ذلك ، أريد العودة إلى تلك الخطوة الأولى في البحث عن معلمات تشعبية تسمح للشبكة بالتعلم بطريقة ما على الأقل. في الواقع ، حتى في المثال أعلاه ، كان الوضع متفائلاً للغاية. العمل مع شبكة لا تتعلم أي شيء يمكن أن يكون مزعج للغاية. يمكنك ضبط المعلمات الفائقة لعدة أيام ، وعدم تلقي إجابات ذات معنى. لذلك ، أود التأكيد مرة أخرى على أنه في المراحل المبكرة تحتاج إلى التأكد من أنه يمكنك الحصول على تعليقات سريعة من التجارب. بشكل حدسي ، قد يبدو أن تبسيط المشكلة والبنية سوف يبطئك فقط. في الواقع ، هذا يسرع العملية ، لأنه يمكنك العثور على شبكة ذات إشارة ذات معنى أسرع بكثير. بعد تلقي هذه الإشارة ، ستتمكن غالبًا من الحصول على تحسينات سريعة عند ضبط المعلمات الفوقية. كما هو الحال في العديد من مواقف الحياة ، والأكثر صعوبة هو بدء العملية.

حسنًا ، هذه إستراتيجية عامة. الآن دعونا نلقي نظرة على التوصيات المحددة لوصف hyperparameters. سأركز على سرعة التعلم η ، ومعلمة التنظيم L2 λ ، وحجم الحزمة المصغرة. ومع ذلك ، ستكون العديد من التعليقات قابلة للتطبيق على معلمات تشعبية أخرى ، بما في ذلك تلك المتعلقة بهندسة الشبكات ، وأشكال أخرى من التنظيم ، وبعض المعلمات التي سوف نتعلمها في الكتاب لاحقًا ، على سبيل المثال ، معامل الزخم.

سرعة التعلم

لنفترض أننا أطلقنا ثلاث شبكات MNIST بثلاث سرعات تعلم مختلفة ، η = 0.025 ، η = 0.25 ، و η = 2.5 ، على التوالي. سنترك بقية المقاييس الفوقية كما كانت في الأقسام السابقة - 30 عصور ، وحجم الحزمة المصغرة هو 10 ، λ = 5.0. سنعود أيضًا إلى استخدام جميع الصور التدريبية البالغ عددها 50000 صورة. في ما يلي رسم بياني يوضح سلوك تكلفة التدريب (تم إنشاؤه بواسطة multiple_eta.py):



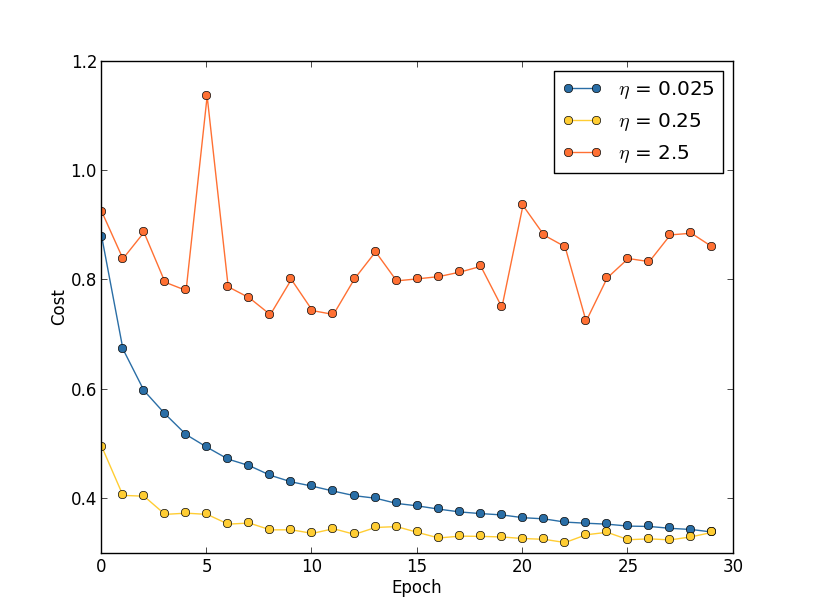
عند 0.0 = 0.025 ، تنخفض التكلفة بسلاسة إلى الحقبة الأخيرة. مع η = 0.25 ، تنخفض التكلفة مبدئيًا ، لكن بعد 20 حقبة ، تكون مشبعة ، وبالتالي فإن معظم التغييرات تكون صغيرة ، ومن الواضح أنها تقلبات عشوائية. مع η = 2.5 ، تختلف التكلفة إلى حد كبير منذ البداية. لفهم سبب هذه التقلبات ، نذكر أن نزول الانحدار العشوائي يجب أن ينزلنا تدريجياً إلى وادي دالة التكلفة:



تساعد هذه الصورة على تخيل ما يحدث بشكل حدسي ، ولكنها ليست تفسيرًا كاملًا وشاملاً. بتعبير أدق ، ولكن لفترة وجيزة ، يستخدم أصل التدرج التقريبي من الدرجة الأولى لوظيفة التكلفة لفهم كيفية تقليل التكلفة. بالنسبة للأكبر become ، يصبح أعضاء دالة تكلفة الترتيب الأعلى أكثر أهمية ، ويمكنهم السيطرة على السلوك عن طريق كسر نزول التدرج. من المحتمل أن يحدث هذا بشكل خاص عند الاقتراب من الحد الأدنى والحد الأدنى المحلي لدالة التكلفة ، حيث أنه بجانب هذه النقاط يصبح التدرج صغيرًا ، مما يسهل على الأعضاء ذوي الرتب العليا السيطرة.

ومع ذلك ، إذا كانت η كبيرة جدًا ، فستكون الخطوات كبيرة جدًا بحيث يمكنها القفز إلى الحد الأدنى ، بسبب تصاعد الخوارزمية من الوادي. ربما هذا هو ما يجعل السعر يتذبذب عند η = 2.5. يؤدي اختيار η = 0.25 إلى حقيقة أن الخطوات الأولية تقودنا حقًا نحو الحد الأدنى من دالة التكلفة ، وفقط عندما نصل إليها ، نبدأ في مواجهة صعوبات في القفز. وعندما نختار η = 0.025 ، لن نواجه مثل هذه الصعوبات خلال أول 30 حقبة. بالطبع ، فإن اختيار مثل هذه القيمة الصغيرة لـ η يخلق صعوبة أخرى - أي أنه يبطئ منحدر الانحدار العشوائي. أفضل طريقة هي البدء بـ η = 0.25 ، وتعلم 20 فترة ، ثم الانتقال إلى 0.0 = 0.025. سنناقش لاحقًا معدل التعلم المتغير هذا. في غضون ذلك ، دعونا نتناول مسألة إيجاد قيمة مناسبة لسرعة التعلم η.

مع وضع ذلك في الاعتبار ، يمكننا اختيار η على النحو التالي. أولاً ، نقوم بتقييم القيمة الحدية η التي تبدأ بها تكلفة بيانات التدريب في الانخفاض فورًا ، لكنها لا تتقلب ولا تزيد. هذا التقدير لا يجب أن يكون دقيقًا. يمكن تقدير الطلب من خلال البدء بـ η = 0.01. إذا انخفضت التكلفة في العصور القليلة الأولى ، فإن الأمر يستحق المحاولة η = 0.1 ، ثم 1.0 ، وهكذا ، حتى تجد قيمة تتقلب فيها القيمة أو تزيد في العصور الأولى. والعكس بالعكس ، إذا كانت القيمة تتقلب أو تزيد في العهود الأولى بـ η = 0.01 ، فحاول η = 0.001 ، 0.00 = 0.0001 ، حتى تجد القيمة التي تنخفض بها التكلفة في العهود القليلة الأولى. يمنحك هذا الإجراء ترتيب قيمة العتبة η. إذا كنت ترغب في ذلك ، فيمكنك تحسين تقييمك باختيار أعلى قيمة لـ η ، حيث تنخفض التكلفة في الفترات الأولى ، على سبيل المثال ، η = 0.5 أو η = 0.2 (لا يلزم الدقة الفائقة هنا). هذا يعطينا تقدير لقيمة العتبة η.

من الواضح أن القيمة الحقيقية لـ η ، يجب ألا تتجاوز العتبة المحددة. في الواقع ، لكي تظل القيمة useful مفيدة للعديد من العصور ، من الأفضل استخدام قيمة أصغر مرتين من العتبة. عادةً ما يسمح لك هذا الاختيار بتعلم العديد من العصور دون إبطاء تعلمك بشكل كبير.

في حالة بيانات MNIST ، سيؤدي اتباع هذه الاستراتيجية إلى تقدير لترتيب العتبة η عند 0.1. بعد بعض التنقيح ، نحصل على القيمة 0.5 = 0.5. باتباع الوصفة أعلاه ، يجب أن نستخدم η = 0.25 لسرعة التعلم لدينا. لكن في الواقع ، وجدت أن η = 0.5 عملت جيدًا لمدة 30 عصرًا ، لذلك لم أكن قلقًا بشأن تقليلها.

كل هذا يبدو واضحا جدا. ومع ذلك ، يبدو أن استخدام تكلفة التدريب لتحديد to يتناقض مع ما قلته سابقًا - أننا نختار معلمات تشعبية ، ونقيم فعالية الشبكة باستخدام بيانات تأكيدية محددة. في الواقع ، سوف نستخدم دقة التأكيد لتحديد بارامترات التنظيم ، وحجم الحزمة المصغرة ومعلمات الشبكة مثل عدد الطبقات والخلايا العصبية المخفية ، وما إلى ذلك. لماذا نفعل الأشياء بشكل مختلف مع سرعة التعلم؟ بصراحة ، يرجع هذا الاختيار إلى تفضيلاتي الجمالية الشخصية ، وربما يكون متحيزًا. الحجة هي أنه يجب على معلمات تشعبية أخرى تحسين دقة التصنيف النهائي في مجموعة الاختبار ، لذلك فمن المنطقي اختيارها بناءً على دقة التأكيد. ومع ذلك ، فإن معدل التعلم يؤثر بشكل غير مباشر فقط على دقة التصنيف النهائي. هدفه الرئيسي هو التحكم في حجم الخطوة من النسب التدرج ، وتتبع تكلفة التدريب بأفضل طريقة من أجل التعرف على حجم الخطوة كبير للغاية. ولكن لا يزال هذا هو تفضيل الجمالية الشخصية. في المراحل المبكرة من التدريب ، تنخفض تكلفة التدريب عادة فقط في حالة زيادة دقة التأكيد ، لذلك في الممارسة يجب ألا يهم معايير الاستخدام.

باستخدام توقف مبكر لتحديد عدد عصور التدريب

كما ذكرنا في هذا الفصل ، فإن التوقف المبكر يعني أنه في نهاية كل عصر ، نحتاج إلى حساب دقة التصنيف على البيانات الداعمة. عندما يتوقف عن التحسن ، نتوقف عن العمل. نتيجة لذلك ، يصبح تعيين عدد العصور أمرًا بسيطًا. على وجه الخصوص ، هذا يعني أننا لسنا بحاجة لمعرفة كيفية تحديد عدد مرات الوصول إلى معلمات تشعبية أخرى. هذا يحدث تلقائيا. علاوة على ذلك ، فإن التوقف المبكر يمنعنا تلقائيًا من إعادة التدريب. يعد هذا أمرًا جيدًا بالطبع ، على الرغم من أنه قد يكون من المفيد إيقاف التوقف المبكر في المراحل المبكرة من التجارب حتى تتمكن من رؤية علامات إعادة التدريب واستخدامها لضبط نهج التنظيم.

لتنفيذ RO ، نحتاج إلى وصف أكثر تحديدًا لما يعنيه "إيقاف تحسين دقة التصنيف". كما رأينا ، يمكن أن تقفز الدقة بعيدًا جدًا حتى عندما يتحسن الاتجاه العام. إذا توقفنا للمرة الأولى ، عندما تنخفض الدقة ، فمن المؤكد أننا لن نصل إلى مزيد من التحسينات الممكنة. أفضل طريقة هي التوقف عن التعلم إذا لم تتحسن دقة التصنيف لفترة طويلة. لنفترض ، على سبيل المثال ، أننا نشارك في MNIST. بعد ذلك يمكننا أن نقرر إيقاف العملية إذا لم تتحسن دقة التصنيف على مدار العشر سنوات الماضية. هذا يضمن عدم توقفنا مبكرًا بسبب الفشل في التدريب ، لكننا لن ننتظر إلى الأبد لأية تحسينات لن تحدث.

هذه القاعدة "لا تحسن على عشرة عصور" مناسبة تمامًا لدراسة MNIST الأولية. ومع ذلك ، يمكن أن تصل الشبكات في بعض الأحيان إلى هضبة بالقرب من دقة تصنيف معينة ، وتبقى هناك لبعض الوقت ، ثم تبدأ بالتحسن مرة أخرى. إذا كنت بحاجة إلى تحقيق أداء جيد للغاية ، فقد تكون قاعدة "عدم التحسن خلال العشر عصور" عدوانية جدًا لذلك. لذلك ، أوصي باستخدام قاعدة "لا تحسين لعشر عصور" للتجارب الأولية ، واعتماد قواعد أكثر ليونة تدريجيًا عندما تبدأ في فهم سلوك شبكتك بشكل أفضل: "بدون تحسينات في عشرين عصرًا" ، "بدون تحسينات في خمسين عصرًا" ، وهكذا على. بالطبع ، هذا يعطينا hyperparameter أخرى لتحسين! ولكن في الممارسة العملية ، عادة ما يكون من السهل ضبط هذا hyperparameter لتحقيق نتائج جيدة. وبالنسبة للمهام الأخرى بخلاف MNIST ، قد تكون قاعدة "عدم التحسن خلال عشرة عصور" عدوانية للغاية ، أو غير عدوانية بالقدر الكافي ، اعتمادًا على تفاصيل مهمة معينة.ومع ذلك ، بعد أن جربت قليلًا ، من السهل جدًا العثور على استراتيجية مناسبة للتوقف المبكر.

لم نستخدم بعد توقفًا مبكرًا في تجاربنا مع MNIST. هذا يرجع إلى حقيقة أننا أجرينا العديد من المقارنات للطرق المختلفة للتعلم. لمثل هذه المقارنات ، من المفيد استخدام نفس عدد العصور في جميع الحالات. ومع ذلك ، فإن الأمر يستحق تغيير network2.py عن طريق إدخال RO في البرنامج.

المهام

• قم بتعديل network2.py بحيث يظهر أمر الشراء (PO) هناك وفقًا لقاعدة "لا تغيير لـ n epochs" ، حيث تمثل n معلمة قابلة للتكوين.
• فكر في قاعدة التوقف المبكرة بخلاف "لم يتغير في n eras." من الناحية المثالية ، ينبغي أن تسعى القاعدة إلى حل وسط بين الحصول على الدقة مع التأكيد العالي ووقت التدريب القصير إلى حد ما. أضف قاعدة إلى network2.py ، وقم بإجراء ثلاث تجارب تقارن دقة التحقق من الصحة وعدد مرات التدريب مع قاعدة "لا تغيير على 10 عصور".

خطة تغيير سرعة التعلم

بينما حافظنا على سرعة التعلم η ثابتة. ومع ذلك ، من المفيد في كثير من الأحيان تعديله. في المراحل المبكرة من عملية التدريب ، من المرجح أن يتم تعيين أوزان خاطئة تمامًا. لذلك ، سيكون من الأفضل استخدام معدل تدريب مرتفع ، مما يتسبب في تغيير الأوزان بشكل أسرع. ثم يمكنك تقليل سرعة التدريب لإجراء ضبط أدق على المقاييس.

كيف نضع خطة لتغيير سرعة التعلم؟ هنا يمكنك تطبيق العديد من النهج. خيار طبيعي واحد هو استخدام نفس الفكرة الأساسية كما هو الحال في ريال عماني. نحافظ على سرعة التعلم ثابتة حتى تبدأ دقة التأكيد في التدهور. ثم نخفض ثاني أكسيد الكربون بمقدار معين ، على سبيل المثال ، مرتين أو عشر مرات. نكرر هذا عدة مرات حتى يكون ثاني أكسيد الكربون 1024 (أو 1000) مرات أقل من الأولي. والانتهاء من التدريب.

يمكن أن تؤدي خطة تغيير سرعة التعلم إلى تحسين الكفاءة وتفتح أيضًا فرصًا هائلة لاختيار الخطة. وهذا يمكن أن يكون صداع - يمكنك أن تنفق إلى الأبد تحسين الخطة. بالنسبة للتجارب الأولى ، أقترح استخدام قيمة واحدة ثابتة لثاني أكسيد الكربون. هذا سوف يعطيك تقريب أول جيد. في وقت لاحق ، إذا كنت ترغب في الضغط على أفضل كفاءة خارج الشبكة ، فإن الأمر يستحق التجربة مع الخطة لتغيير سرعة التعلم كما وصفتها. يوضح العمل العلمي سهل القراءة إلى حد ما لعام 2010 مزايا سرعات التعلم المتغيرة عند مهاجمة MNIST.

ممارسة

• قم بتعديل network2.py بحيث تنفذ الخطة التالية لتغيير سرعة التعلم: قلل السجل إلى النصف في كل مرة تفي دقة التأكيد بقاعدة "لا تغيير في 10 حقبات" ، وتوقف عن التعلم عندما تنخفض سرعة التعلم إلى 1/128 من السرعة الأولية.

المعلمة التنظيم λ

أوصي ببدء عدم التنظيم على الإطلاق (λ = 0،0) ، وتحديد قيمة η ، كما هو موضح أعلاه. باستخدام القيمة المحددة ، يمكننا حينئذ استخدام البيانات الداعمة لتحديد قيمة جيدة. ابدأ بـ λ = 1.0 (ليس لدي حجة جيدة لصالح مثل هذا الاختيار) ، ثم قم بزيادة أو تقليله بمقدار 10 مرات لزيادة الكفاءة في العمل مع تأكيد البيانات. بعد العثور على الترتيب الصحيح للحجم ، يمكننا ضبط القيمة بدقة أكثر. بعد ذلك ، من الضروري العودة إلى التحسين η مرة أخرى.

ممارسة

• , , λ η. , λ? , η?

إذا استخدمت التوصيات الواردة في هذا القسم ، فسترى أن القيم المحددة لـ η و λ لا تتوافق دائمًا مع القيم التي استخدمتها سابقًا. إنه يحتوي فقط على قيود في النص ، مما يجعل من غير العملي في بعض الأحيان تحسين المعلمات الفائقة. فكر في كل مقارنات مناهج التدريب المختلفة التي نعمل عليها - مقارنة دالة التكلفة التربيعية وعبر الانتروبيا ، والطرق القديمة والجديدة لتهيئة الأوزان ، والتشغيل مع وبدون تنظيم ، وهكذا. لجعل هذه المقارنات ذات مغزى ، حاولت عدم تغيير المعلمات الفوقية بين المقارنات المقارنة (أو قياسها بشكل صحيح). بالطبع ، لا يوجد أي سبب لأن تكون نفس المعلمات الفائقة مثالية لجميع المناهج المختلفة للتعلم ، لذلك كانت المعلمات الفائقة التي أستخدمها نتيجة حل وسط.

كبديل ، يمكنني محاولة تحسين جميع المعلمات المفرطة لكل نهج للتعلم إلى أقصى حد. سيكون منهجًا أفضل وأكثر صدقًا ، نظرًا لأننا سنأخذ الأفضل من كل نهج إلى التعلم. ومع ذلك ، أجرينا العشرات من المقارنات ، وفي الممارسة العملية سيكون هذا مكلفًا للغاية من حيث الحساب. لذلك ، قررت التسوية ، لاستخدام خيارات مقياس تشفير جيدة بما فيه الكفاية (ولكن ليس بالضرورة الأمثل).

حزمة صغيرة الحجم

كيفية اختيار حجم حزمة مصغرة؟ للإجابة على هذا السؤال ، لنفترض أولاً أننا نشارك في التدريب عبر الإنترنت ، أي أننا نستخدم مجموعة صغيرة من الحجم 1.

المشكلة الواضحة في التعلم عبر الإنترنت هي أن استخدام الحزم المصغرة التي تتكون من مثال تدريبي واحد سيؤدي إلى أخطاء خطيرة في تقدير التدرج. لكن في الواقع ، لن تمثل هذه الأخطاء مشكلة خطيرة. السبب هو أن تقديرات التدرجات الفردية لا يجب أن تكون دقيقة للغاية. نحتاج فقط إلى الحصول على تقدير دقيق بما فيه الكفاية بحيث تنخفض وظيفة التكلفة لدينا. يبدو الأمر كما لو كنت تحاول الوصول إلى القطب المغناطيسي الشمالي ، ولكن سيكون لديك بوصلة غير موثوقة ، مع خطأ في كل قياس بمقدار 10-20 درجة. إذا قمت بفحص البوصلة بشكل متكرر ، وسوف تشير في المتوسط ​​إلى الاتجاه الصحيح ، فستتمكن في النهاية من الوصول إلى القطب المغناطيسي الشمالي.

بالنظر إلى هذه الحجة ، يبدو أننا يجب أن نستخدم التعلم عبر الإنترنت. ولكن في الواقع الوضع أكثر تعقيدًا إلى حد ما. في المهمة إلى الفصل الأخير ، أشرت إلى أنه لحساب تحديث التدرج اللوني لجميع الأمثلة في الحزمة المصغرة ، يمكنك استخدام تقنيات المصفوفة في نفس الوقت ، بدلاً من حلقة. اعتمادًا على تفاصيل الجهاز الخاص بك ومكتبة الجبر الخطي ، قد يكون من الأسرع بكثير حساب تقدير لحزمة صغيرة ، على سبيل المثال ، 100 بدلاً من حساب تقدير تدرج لحزمة صغيرة في دورة تضم 100 مثال تدريبي. قد يكون هذا ، على سبيل المثال ، أبطأ 50 مرة فقط وليس 100.

في البداية يبدو أن هذا لا يساعدنا كثيرًا. مع حجم الحزمة المصغرة 100 ، تبدو قاعدة تدريب الأوزان كما يلي:

$$

$$w \rightarrow w' = w-\eta \frac{1}{100} \sum_x \nabla C_x \tag{100}$$

حيث يذهب الجمع على أمثلة التدريب في الحزمة المصغرة. قارن مع

$$

$$w \rightarrow w' = w-\eta \nabla C_x \tag{101}$$

للتعلم عبر الإنترنت. حتى لو استغرق تحديث الحزمة المصغرة 50 مرة ، إلا أن التدريب عبر الإنترنت لا يزال هو الخيار الأفضل ، حيث سيتم تحديثنا أكثر من مرة. لكن لنفترض أنه في حالة الحزمة المصغرة ، قمنا بزيادة سرعة التعلم بمقدار 100 مرة ، ثم تتحول قاعدة التحديث إلى:

$$

$$w \rightarrow w' = w-\eta \sum_x \nabla C_x \tag{102}$$

هذا يشبه 100 مرحلة منفصلة من التعلم عبر الإنترنت مع سرعة التعلم من η. ومع ذلك ، فإن خطوة واحدة في التعلم عبر الإنترنت تستغرق 50 مرة فقط من الوقت. بالطبع ، هذا في الواقع ليس 100 مستوى من التعلم عبر الإنترنت بالضبط ، لأنه في الحزمة المصغرة يتم تقييم جميع ∇C _x لنفس مجموعة الأوزان ، على عكس التعلم التراكمي الذي يحدث في الحالة عبر الإنترنت. ومع ذلك ، يبدو أن استخدام حزم مصغرة أكبر سيعجل العملية.

بالنظر إلى كل هذه العوامل ، يعد اختيار أفضل حجم لحزمة صغيرة هو حل وسط. اختر صغيرة جدًا ولا تحصل على الفائدة الكاملة من مكتبات المصفوفات الجيدة المحسنة للأجهزة السريعة. اختر حجمًا كبيرًا جدًا ، ولن يتم تحديث الوزن كثيرًا. تحتاج إلى اختيار قيمة حل وسط تزيد من سرعة التعلم. لحسن الحظ ، فإن اختيار حجم الحزمة المصغرة التي يتم فيها زيادة السرعة يكون مستقلاً نسبيًا عن غيرها من البارامترات الفائقة (باستثناء الهيكل العام) ، وبالتالي ، لايجاد حجم الحزمة المصغرة جيدًا ، وليس من الضروري تحسينها. لذلك ، سيكون كافياً استخدام القيم المقبولة (وليس بالضرورة المثالية) لمقاييس التشعب الأخرى ، ثم تجربة عدة أحجام مختلفة من الرزم الصغيرة ، التدرج as ، كما هو موضح أعلاه.صمم رسمًا بيانيًا لدقة التأكيد مقابل الوقت (الوقت المنقضي الحقيقي ، وليس العصور!) ، واختر حجمًا صغيرًا للحزمة يمنح أسرع تحسين للأداء. باستخدام حجم الحزمة المصغرة المحدد ، يمكنك المتابعة لتحسين المعلمات الفائقة الأخرى.

بالطبع ، كما فهمت بالفعل بلا شك ، في عملنا لم أقم بتنفيذ هذا التحسين. في تنفيذنا للجمعية الوطنية ، لا يتم استخدام نهج سريع لتحديث الحزم الصغيرة على الإطلاق. لقد استخدمت ببساطة حجم الحزمة المصغرة 10 دون التعليق عليها أو شرحها ، في جميع الأمثلة تقريبًا. بشكل عام ، يمكننا تسريع عملية التعلم عن طريق تقليل حجم الحزمة المصغرة. لم أفعل ذلك ، على وجه الخصوص ، لأن تجاربي الأولية أشارت إلى أن التسارع سيكون متواضعًا إلى حد ما. ولكن في التطبيقات العملية ، نود بالتأكيد تنفيذ أسرع طريقة لتحديث الحزم الصغيرة ، ومحاولة تحسين حجمها من أجل زيادة السرعة الكلية.

التقنيات الآلية

وصفت هذه الأساليب التجريبية بأنها شيء يحتاج إلى التغيير والتبديل باليد. يعتبر التحسين اليدوي طريقة جيدة للتعرف على كيفية عمل NS. ومع ذلك ، وبالمناسبة ، ليس من المستغرب أن يكون قد تم القيام بالكثير من العمل بالفعل في أتمتة هذا المشروع. التقنية الشائعة هي البحث في الشبكة التي تنقل الشبكة بشكل منتظم في مساحة المعلمات الفائقة. يمكن الاطلاع على لمحة عامة عن إنجازات وقيود هذه التقنية (بالإضافة إلى توصيات بشأن البدائل المنفذة بسهولة) في عام 2012 . وقد تم اقتراح العديد من التقنيات المتطورة. لن أراجعهم جميعًا ، لكنني أود الإشارة إلى العمل الواعد لعام 2012 ، باستخدام التحسين البايزي للمعلمات الفوقية. كود العمل مفتوح للجميع ، ومع بعض النجاح تم استخدامه من قبل باحثين آخرين.

لخص

باستخدام قواعد الممارسة التي وصفتها ، لن تحصل على أفضل النتائج من PS الخاص بك من كل ما هو ممكن. لكن من المحتمل أن توفر لك نقطة انطلاق وأساسًا جيدًا لمزيد من التحسينات. على وجه الخصوص ، وصفت أساسا hyperparameters بشكل مستقل. في الممارسة العملية ، هناك علاقة بينهما. يمكنك تجربة η ، وتقرر أنك قد وجدت القيمة الصحيحة ، ثم ابدأ في تحسينها ، واكتشف أنها تنتهك تحسينك. في الممارسة العملية ، من المفيد التحرك في اتجاهات مختلفة ، حيث تقترب تدريجياً من القيم الجيدة. قبل كل شيء ، ضع في اعتبارك أن النهج الاستكشافية التي وصفتها هي قواعد ممارسة بسيطة ، ولكنها ليست شيئًا منقوشًا. تحتاج إلى البحث عن علامات على أن شيئًا ما لا يعمل ولديك الرغبة في التجربة. على وجه الخصوصراقب بعناية سلوك شبكتك العصبية ، خاصة دقة التأكيد.

ومما يزيد من تعقيد اختيار المقاييس الفائقة حقيقة أن المعرفة العملية التي يختارونها تنتشر على العديد من الأعمال والبرامج البحثية ، وغالبا ما تكون فقط في رؤساء الممارسين الفرديين. هناك قدر كبير من العمل مع وصف لما يجب القيام به (غالبًا ما يتعارض مع بعضها البعض). ومع ذلك ، هناك العديد من الأعمال المفيدة بشكل خاص التي توليف وتسليط الضوء على جزء كبير من هذه المعرفة. في ل بينجي جوشوا من عام 2012 يعطي نصائح عملية حول استخدام العودة انتشار أصل التدرج والتدريب للجمعية الوطنية، بما في ذلك الجمعية الوطنية وعميقة. يصف بنجيو العديد من التفاصيل بمزيد من التفصيل. مني ، بما في ذلك البحث المنهجي عن hyperparameters. وظيفة جيدة أخرى هي العمل.1998 Yanna Lekuna وغيرها. يظهر كلا العملين في كتاب مفيد للغاية لعام 2012 ، والذي يحتوي على العديد من الحيل التي تستخدم عادة في الجمعية الوطنية: " الشبكات العصبية: الحيل الحرفية ". الكتاب باهظ الثمن ، لكن العديد من مقالاته نشرت على الإنترنت من قبل مؤلفيها ، ويمكن العثور عليها في محركات البحث.

من هذه المقالات ، وخاصة من تجاربنا الخاصة ، هناك شيء واحد يصبح واضحًا: مشكلة تحسين المعلمات الفائقة لا يمكن حلها تمامًا. هناك دائمًا خدعة أخرى يمكنك تجربتها لتحسين الكفاءة. يقول الكتاب أنه لا يمكن الانتهاء من كتاب ، لكن يمكن إسقاطه فقط. وينطبق الشيء نفسه على تحسين NS: مساحة المعلمات الفائقة ضخمة جدًا بحيث لا يمكن إكمال التحسين ، ولكن يمكن إيقافها فقط ، مما يترك NS للأحفاد. لذلك سيكون هدفك هو تطوير سير عمل يتيح لك تنفيذ تحسين جيد بسرعة ، مع إتاحة الفرصة لك لتجربة المزيد من خيارات التحسين التفصيلية إذا لزم الأمر.

الصعوبات التي تواجه اختيار البارامترات تجعل بعض الناس يشكون من أن NSs تتطلب الكثير من الجهد مقارنة بتقنيات MO الأخرى. لقد سمعت العديد من المتغيرات من الشكاوى مثل: "نعم ، NS يمكن ضبطها بشكل جيد إعطاء أفضل كفاءة عند حل مشكلة. لكن من ناحية أخرى ، يمكنني تجربة مجموعة عشوائية (أو SVM ، أو أي تقنية أخرى مفضلة لديك) ، وهي تعمل فقط. ليس لدي وقت لمعرفة أي NA هو المناسب لي. " بالطبع ، من الناحية العملية ، من الجيد أن يكون لديك تقنيات سهلة الاستخدام تحت صديق. يعد هذا أمرًا جيدًا بشكل خاص عندما تبدأ العمل مع مهمة ، ولا يزال من غير الواضح ما إذا كان بإمكان وزارة المواصلات المساعدة في حلها على الإطلاق. من ناحية أخرى ، إذا كان من المهم بالنسبة لك تحقيق أفضل النتائج ، فقد تحتاج إلى تجربة عدة أساليب تتطلب معرفة أكثر تخصصًا. سيكون رائعاإذا كانت MO دائمًا سهلة ، لكن لا توجد أسباب تجعلها تافهة مسبقًا.

تقنيات أخرى

كل التقنيات المطورة في هذا الفصل لها قيمة في حد ذاتها ، لكن هذا ليس هو السبب الوحيد الذي وصفتها لهم. من المهم أن تتعرف على بعض المشكلات التي قد تنشأ في مجال NA ، وبأسلوب التحليل الذي يمكن أن يساعد في التغلب عليها. بطريقة ما ، نحن نتعلم كيفية التفكير في NS. في الجزء المتبقي من هذا الفصل ، سوف أصف بإيجاز مجموعة من التقنيات الأخرى. لن تكون أوصافهم عميقة كما في السابق ، ولكن ينبغي أن ينقلوا بعض الأحاسيس فيما يتعلق بمجموعة متنوعة من التقنيات التي واجهتها في مجال NA.

الاختلافات في النسب الانحدار العشوائي

خدمنا الانحدار العشوائي العشوائي من خلال backpropagation بشكل جيد أثناء الهجوم على مشكلة تصنيف الأرقام المكتوبة بخط اليد من MNIST. ومع ذلك ، هناك العديد من الطرق الأخرى لتحسين وظيفة التكلفة ، وأحيانًا تظهر كفاءة أعلى من نزول الانحدار العشوائي مع الحزم الصغيرة. في هذا القسم ، أصف باختصار اثنين من هذه النهج ، هسي والزخم.

الهسى أحد مواطن الهس

لتبدأ ، دعونا نضع جانبا الجمعية الوطنية. بدلاً من ذلك ، نحن ببساطة نعتبر المشكلة المجردة المتمثلة في تقليل دالة التكلفة C للعديد من المتغيرات ، w = w1 ، w2 ، ... ، أي C = C (w). بواسطة نظرية تايلور ، يمكن تقريب دالة التكلفة عند النقطة w:

$$

$$C(w+\Delta w) = C(w) + \sum_j \frac{\partial C}{\partial w_j} \Delta w_j \nonumber \\ + \frac{1}{2} \sum_{jk} \Delta w_j \frac{\partial^2 C}{\partial w_j \partial w_k} \Delta w_k + \ldots \tag{103}$$

يمكننا إعادة كتابتها بشكل أكثر إحكاما

$$

$$C(w+\Delta w) = C(w) + \nabla C \cdot \Delta w + \frac{1}{2} \Delta w^T H \Delta w + \ldots \tag{104}$$

حيث ∇C هي متجه التدرج العادي ، و H هي المصفوفة المعروفة باسم المصفوفة Hessian ، حيث يحتوي jk على C ² C / ∂w _j ∂w _k . لنفترض أننا نقترب من C بالتخلي عن المصطلحات العليا للاختباء خلف علامة القطع في الصيغة:

$$

$$C(w+\Delta w) \approx C(w) + \nabla C \cdot \Delta w + \frac{1}{2} \Delta w^T H \Delta w \tag{105}$$

باستخدام الجبر ، يمكن إظهار أنه يمكن تقليل التعبير على الجانب الأيمن عن طريق تحديد:

$$

$$\Delta w = -H^{-1} \nabla C \tag{106}$$

بالمعنى الدقيق للكلمة ، ولكي يكون هذا الحد الأدنى وليس الحد الأقصى ، يجب أن نفترض أن مصفوفة هسه إيجابية بشكل أكيد. بشكل حدسي ، هذا يعني أن الوظيفة C تشبه الوادي ، وليس الجبل أو السرج.

إذا كان (105) تقريبًا جيدًا لوظيفة التكلفة ، فمن المتوقع أن يؤدي الانتقال من النقطة w إلى النقطة w + Δw = w - H - 1 −C إلى تقليل دالة التكلفة إلى حد كبير. يوفر هذا خوارزمية تقليل تكلفة ممكنة:

• حدد نقطة البداية ث.
• قم بتحديث w إلى نقطة جديدة ، w ′ = w - H ⁻¹ ∇C ، حيث يتم حساب Hessian H و ∇C بالقيمة w.
• w' , w′′=w′−H′ ⁻¹ ∇′C, H ∇C w'.
• ...

في الممارسة العملية ، (105) هو مجرد تقريب ، ومن الأفضل أن تتخذ خطوات أصغر. سنفعل ذلك من خلال التحديث المستمر لـ w بواسطة Δw = −ηH - 1∇C ، حيث η هي سرعة التعلم.

يُعرف هذا النهج لتقليل دالة التكلفة باسم تحسين Hessian. هناك نتائج نظرية وتجريبية تُظهر أن الأساليب الهيسية تتقارب إلى حد أدنى في خطوات أقل من النسب المتدرجة القياسية. على وجه الخصوص ، من خلال تضمين معلومات عن التغييرات في الترتيب الثاني في دالة التكلفة ، من الممكن تجنب العديد من الأمراض التي تصادفها في التدرج النسبي في النهج الهسي. علاوة على ذلك ، هناك إصدارات من خوارزمية backpropagation التي يمكن استخدامها لحساب الهسه.

إذا كان تحسين Hessian رائعًا ، فلماذا لا نستخدمه في NS لدينا؟ لسوء الحظ ، على الرغم من أنه يحتوي على العديد من الخصائص المرغوبة ، إلا أن هناك خاصية غير مرغوب فيها للغاية: من الصعب للغاية تطبيقها. جزء من المشكلة هو الحجم الضخم لمصفوفة هسيان. افترض أن لدينا NS مع 10 ⁷ الأوزان والإزاحة. ثم في المصفوفة الهيسية المقابلة سيكون هناك 10 ⁷ × 10 ⁷ = 10 ¹⁴ عنصر. كثير جدا! نتيجة لذلك ، اتضح أنه من الصعب جدًا حساب H ⁻¹ ∇C في الممارسة. ولكن هذا لا يعني أنه من غير المجدي أن نعرف عنها. العديد من خيارات النسب المتدرجة مستوحاة من التحسين الهسي ، فهي ببساطة تتجنب مشكلة المصفوفات الكبيرة بشكل مفرط. دعونا نلقي نظرة على واحدة من هذه التقنيات ، دافع النسب التدرج.

الدافع على أساس النسب التدرج

حدسيًا ، تتمثل ميزة التحسين الهسي في أنه لا يتضمن فقط معلومات حول التدرج اللوني ، ولكن أيضًا معلومات حول تغييره. ويستند نزول التدرج القائم على الدافع على حدس مماثل ، ولكنه يتجنب المصفوفات الكبيرة من المشتقات الثانية. لفهم تقنية الاندفاع ، دعنا نتذكر أول صور نزول التدرج ، حيث فحصنا كرة تدحرجت في واد. ثم رأينا أن نزول التدرج ، على عكس اسمه ، يشبه قليلاً كرة تسقط إلى الأسفل. تعمل تقنية النبض على تغيير نزول التدرج في مكانين ، مما يجعله أشبه بالصورة المادية. أولاً ، تقدم مفهوم "السرعة" للمعلمات التي نحاول تحسينها. يحاول التدرج تغيير السرعة ، وليس "الموقع" مباشرةً ، على غرار كيفية تغيير القوى الفيزيائية للسرعة ،وتؤثر فقط بشكل غير مباشر على الموقع. ثانياً ، طريقة الاندفاع هي نوع من مصطلح الاحتكاك الذي يقلل السرعة تدريجياً.

دعنا نعطي تعريف أكثر دقة رياضيا. نقدم متغيرات السرعة v = v1 ، v2 ، ... ، واحد لكل متغير مناظر w _j (في الشبكة العصبية ، هذه المتغيرات تشمل بشكل طبيعي جميع الأوزان والتشريد). ثم نغير قاعدة تحديث نزول التدرج w → w ′ = w - toC إلى

$$

$$v \rightarrow v' = \mu v - \eta \nabla C \tag{107}$$

$$

$$w \rightarrow w' = w+v' \tag{108}$$

في المعادلات ، μ عبارة عن مقياس تشعبي يتحكم في مقدار الكبح أو الاحتكاك في النظام. لفهم معنى المعادلات ، من المفيد أولاً مراعاة الحالة التي تكون فيها μ = 1 ، أي عندما لا يكون هناك احتكاك. في هذه الحالة ، تظهر دراسة المعادلات أن الآن "القوة" ∇C تغير السرعة v وأن السرعة تتحكم في معدل التغيير w. بشكل حدسي ، يمكن اكتساب السرعة عن طريق إضافة أعضاء متدرجة باستمرار إليها. هذا يعني أنه إذا تحرك التدرج في اتجاه واحد تقريبًا خلال عدة مراحل من التدريب ، فيمكننا الحصول على سرعة حركة عالية بما فيه الكفاية في هذا الاتجاه. تخيل ، على سبيل المثال ، ما يحدث عند الانتقال إلى أسفل:



مع كل خطوة إلى أسفل المنحدر ، تزداد السرعة ، ونتحرك بشكل أسرع وأسرع إلى أسفل الوادي. هذا يسمح لتقنية السرعة أن تعمل بشكل أسرع بكثير من نزول التدرج القياسي. بطبيعة الحال ، المشكلة هي أنه بعد وصولنا إلى قاع الوادي ، سوف ننزلق عبره. أو إذا تغير التدرج اللوني بسرعة كبيرة ، فقد يتضح أننا نسير في الاتجاه المعاكس. هذا هو الهدف من إدخال hyperparameter μ في (107). قلت في وقت سابق أن μ يتحكم في مقدار الاحتكاك في النظام ؛ بتعبير أدق ، يجب تخيل مقدار الاحتكاك على أنه 1-μ. عندما μ = 1 ، كما رأينا ، لا يوجد احتكاك ، ويتم تحديد السرعة تمامًا بواسطة التدرج اللوني ∇C. والعكس بالعكس ، عندما يكون μ = 0 ، هناك الكثير من الاحتكاك ، لا يتم اكتساب السرعة ، ويتم تقليل المعادلتين (107) و (108) إلى معادلات النسب التدرجية المعتادة ، w → w η∇ = w - η∇C. في الممارسة العملية ،باستخدام قيمة μ في الفاصل الزمني بين 0 و 1 يمكن أن يعطينا ميزة القدرة على اكتساب السرعة دون خطر الانزلاق الحد الأدنى. يمكننا اختيار هذه القيمة μ باستخدام بيانات التأكيد المعلقة بنفس الطريقة التي نختار بها القيم η و λ.

حتى الآن لقد تجنبت تسمية hyperparameter μ. الحقيقة هي أن الاسم القياسي لـ μ تم اختياره بشكل سيء: يطلق عليه معامل الزخم. هذا يمكن أن يكون مربكا لأن μ ليس على الإطلاق مفهوم الزخم من الفيزياء. يرتبط بقوة أكبر مع الاحتكاك. ومع ذلك ، فإن مصطلح "معامل الزخم" يستخدم على نطاق واسع ، لذلك سوف نستمر في استخدامه أيضًا.

ميزة لطيفة لتقنية الدافع هي أنه لا يوجد شيء تقريبا يجب القيام به لتغيير تنفيذ النسب المتدرج لتضمين هذه التقنية فيه. لا يزال بإمكاننا استخدام التكاثر الخلفي لحساب التدرجات ، كما كان من قبل ، واستخدام أفكار مثل التحقق من الوجبات الصغيرة المختارة عشوائياً. في هذه الحالة ، يمكننا الحصول على بعض فوائد تحسين Hessian باستخدام معلومات حول تغييرات التدرج اللوني. ومع ذلك ، كل هذا يحدث دون عيوب ، ومع التغييرات الطفيفة فقط في الكود. في الممارسة العملية ، يتم استخدام تقنية الاندفاع على نطاق واسع وغالبًا ما تساعد في تسريع عملية التعلم.

تمارين

• ما الخطأ الذي يحدث إذا استخدمنا μ> 1 في تقنية النبض؟
• ما الخطأ الذي يحدث إذا استخدمنا μ <0 في تقنية النبض؟

مهمة

• إضافة نزول الانحدار العشوائي القائم على الزخم إلى network2.py.

طرق أخرى لتقليل وظيفة التكلفة

تم تطوير العديد من الأساليب الأخرى لتقليل وظيفة التكلفة ، ولم يتم التوصل إلى اتفاق حول أفضل طريقة. من خلال التعمق في موضوع الشبكات العصبية ، من المفيد الخوض في تقنيات أخرى ، لفهم كيفية عملها ، وما هي نقاط القوة والضعف فيها ، وكيفية وضعها موضع التنفيذ. في العمل الذي ذكرته سابقًا ، يتم تقديم ومقارنة العديد من هذه التقنيات ، بما في ذلك نزول التدرج المقترن وطريقة BFGS (وكذلك دراسة طريقة BFGS ذات الصلة عن كثب مع تقييد الذاكرة ، أو L-BFGS ). تقنية أخرى أظهرت مؤخرًا نتائج واعدة.، هذا هو التدرج المتسارع لـ Nesterov ، مما يحسن تقنية النبض. ومع ذلك ، فإن نزول التدرج البسيط يعمل بشكل جيد للعديد من المهام ، وخاصة عند استخدام الزخم ، لذلك سنلتزم نزول التدرج العشوائي حتى نهاية الكتاب.

نماذج أخرى من الخلايا العصبية الاصطناعية

حتى الآن ، أنشأنا NS باستخدام الخلايا العصبية السيني. من حيث المبدأ ، يمكن NS مبنية على الخلايا العصبية السيني حساب أي وظيفة. ولكن في الممارسة العملية ، فإن الشبكات المبنية على نماذج عصبية أخرى تكون أحيانًا متقدمة عن تلك الموجودة في السيني. اعتمادًا على التطبيق ، يمكن أن تتعلم الشبكات القائمة على مثل هذه النماذج البديلة بشكل أسرع أو التعميم بشكل أفضل على بيانات التحقق أو القيام بكليهما. اسمحوا لي أن أذكر بضعة نماذج بديلة من الخلايا العصبية لأعطيك فكرة عن بعض الخيارات الشائعة الاستخدام.

ربما يكون أبسط الاختلاف هو الخلايا العصبية تانغ استبدال وظيفة السيني مع الظل الزائدي. يتم تحديد ناتج الخلايا العصبية تانغ مع إدخال س ، ناقلات الأوزان ث ، والإزاحة ب كما

$$

$$\tanh(w \cdot x+b) \tag{109}$$

حيث تان هو الظل الزائدي بشكل طبيعي . اتضح أنه مرتبط بشكل وثيق مع الخلايا العصبية السيني. لرؤية هذا ، تذكر أن تان يعرف بأنه

$$

$$\tanh(z) \equiv \frac{e^z-e^{-z}}{e^z+e^{-z}} \tag{110}$$

باستخدام جبر صغير ، من السهل أن نرى ذلك

$$

$$\sigma(z) = \frac{1+\tanh(z/2)}{2} \tag{111}$$

وهذا هو ، تان هو مجرد توسيع السيني. بيانياً ، يمكنك أيضًا أن ترى أن وظيفة الدباغة لها نفس شكل السيني:



أحد الاختلافات بين الخلايا العصبية tang والخلايا العصبية السيني هو أن ناتج الأول يمتد من -1 إلى 1 ، وليس من 0 إلى 1. وهذا يعني أنه عند إنشاء شبكة تعتمد على الخلايا العصبية التانغية ، قد تحتاج إلى تطبيع مخرجاتك (ووفقًا لتفاصيل التطبيق ، وربما المدخلات) بشكل مختلف قليلاً عن شبكات السيني.

مثل الخلايا السينيّة ، يمكن لعصابات تانغ ، من حيث المبدأ ، حساب أي وظيفة (على الرغم من وجود بعض الحيل) ، ووضع علامات على المدخلات من -1 إلى 1. علاوة على ذلك ، فإن أفكار انتشار الظهر ونزول التدرج العشوائي يسهل تطبيقها على تانغ. - الخلايا العصبية ، وكذلك السيني.

ممارسة

• إثبات المعادلة (111).

ما نوع الخلايا العصبية التي يجب استخدامها في الشبكات ، تانغ أو السيني؟ الجواب ، بعبارة ملطفة ، ليس واضحًا! ومع ذلك ، هناك حجج نظرية وبعض الأدلة التجريبية على أن الخلايا العصبية تانغ تعمل في بعض الأحيان بشكل أفضل. دعنا نذهب لفترة وجيزة من خلال واحدة من الحجج النظرية لصالح الخلايا العصبية تانغ. لنفترض أننا نستخدم الخلايا العصبية السيني ، وأن جميع التنشيطات على الشبكة ستكون إيجابية. النظر في الأوزان w ^{l + 1} _jk المدرجة _للخلية العصبية رقم j في الطبقة رقم l + 1. قواعد الخلفي نشر (BP4) تقول لنا ان التدرج يرتبط بها من هو ^ل _ك دلتا ^{ل + 1،} _ي . نظرًا لأن عمليات التنشيط إيجابية ، ستكون علامة هذا التدرج هي نفسها علامة δ ^{l + 1} _j. هذا يعني أنه إذا كانت δ ^{l + 1} _j موجبة ، فسوف تنخفض جميع الأوزان w ^{l + 1} _jk أثناء الهبوط المتدرج ، وإذا كانت δ ^{l + 1} _j سالبة ، فإن جميع الأوزان w ^{l + 1} _jkسوف تزيد خلال النسب التدرج. بمعنى آخر ، كل الأوزان المرتبطة بنفس الخلية العصبية إما أن تزيد أو تنقص معًا. وهذه مشكلة ، لأنك قد تحتاج إلى زيادة بعض الأوزان مع تقليل الأوزان الأخرى. لكن هذا يمكن أن يحدث فقط إذا كانت بعض عمليات تنشيط الإدخال لها علامات مختلفة. يشير هذا إلى الحاجة إلى استبدال السيني بوظيفة تنشيط أخرى ، على سبيل المثال ، الظل الزائدي ، الذي يسمح لأنشطة التنشيط أن تكون إيجابية وسلبية. في الواقع ، نظرًا لأن التانه متماثل بالنسبة للصفر ، tanh (−z) = −tanh (z) ، يمكن للمرء أن يتوقع أنه ، تقريبًا ، سيتم توزيع عمليات التنشيط في الطبقات المخفية بالتساوي بين الإيجابية والسلبية. سيساعد ذلك على ضمان عدم وجود تحيز منتظم في تحديثات المقاييس في اتجاه واحد أو آخر.

ما مدى خطورة النظر في هذه الحجة؟ بعد كل شيء ، فمن مجريات الأمور ، لا يقدم أدلة صارمة على أن الخلايا العصبية تانغ متفوقة على تلك السيني. ربما تحتوي الخلايا العصبية السينيّة على بعض الخواص التي تعوض هذه المشكلة؟ في الواقع ، في كثير من الحالات ، أظهرت وظيفة تانه من الحد الأدنى إلى أي مزايا مقارنة مع السيني. لسوء الحظ ، ليس لدينا طرق بسيطة يتم تنفيذها بسرعة للتحقق من نوع الخلايا العصبية التي ستتعلم بشكل أسرع أو ستثبت أنها أكثر فعالية في التعميم لحالة معينة.

متغير آخر من الخلايا العصبية السيني هو الخلايا العصبية الخطية تصحيح ، أو وحدة خطية تصحيح ، ReLU. يتم تحديد الإخراج ReLU مع إدخال x ، متجه الأوزان w والإزاحة b كما يلي:

$$

$$\max(0, w \cdot x+b) \tag{112}$$

تبدو وظيفة استقامة الحد الأقصى بيانياً (0 ، z) كما يلي: من



الواضح أن هذه الخلايا العصبية مختلفة تمامًا عن كل من الخلايا العصبية السيني والتانغية. ومع ذلك ، فهي متشابهة من حيث أنها يمكن أن تستخدم أيضًا لحساب أي وظيفة ، ويمكن تدريبهم باستخدام الانتشار الخلفي ونزول التدرج العشوائي.

متى يجب علي استخدام ReLU بدلاً من الخلايا العصبية السيني أو تانغ؟ في الأعمال الحديثة على التعرف على الصور ( 1 ، 2 ، 3 ، 4) تم العثور على مزايا خطيرة لاستخدام ReLU عبر الشبكة بالكامل تقريبًا. ومع ذلك ، كما هو الحال مع الخلايا العصبية التانغية ، ليس لدينا حتى الآن فهم عميق حقًا للوقت الذي ستفضل فيه بالضبط ما هي قوائم ReLU ، ولماذا. للحصول على فكرة عن بعض المشاكل ، تذكر أن الخلايا العصبية السينيّة تتوقف عن التعلم عندما تكون مشبعة ، أي عندما يكون الناتج قريباً من 0 أو 1. كما رأينا عدة مرات في هذا الفصل ، فإن المشكلة هي أن الأعضاء reduce 'يخفضون التدرج اللوني أن يبطئ التعلم. الخلايا العصبية تانغ تعاني من صعوبات مماثلة في التشبع. في الوقت نفسه ، لن تؤدي الزيادة في المدخلات الموزونة على ReLU إلى جعلها مشبعة ، وبالتالي لن يحدث تباطؤ مماثل في التدريب. من ناحية أخرى ، عندما تكون المدخلات الموزونة على ReLU سالبة ، يختفي التدرج وتوقف الخلايا العصبية عن التعلم على الإطلاق.هذه مجرد بضع مشاكل عديدة تجعل من غير التافه فهم متى وكيف تتصرف ReLUs بشكل أفضل من الخلايا العصبية السيني أو تانغ.

لقد رسمت صورة من عدم اليقين ، مؤكدة أنه ليس لدينا حتى الآن نظرية قوية لاختيار وظائف التنشيط. في الواقع ، هذه المشكلة أكثر تعقيدًا مما وصفته ، نظرًا لوجود العديد من وظائف التنشيط المحتملة بلا حدود. أي واحد سوف يعطينا أسرع شبكة التعلم؟ والتي سوف تعطي أعظم دقة في الاختبارات؟ أنا مندهش من قلة الدراسات العميقة والمنهجية لهذه القضايا. من الناحية المثالية ، ينبغي أن يكون لدينا نظرية تخبرنا بالتفصيل كيفية اختيار (وربما التغيير على الفور) وظائف التنشيط لدينا. من ناحية أخرى ، لا ينبغي أن نتوقف عن الافتقار إلى نظرية كاملة! لدينا بالفعل أدوات قوية ، وبمساعدتهم يمكننا تحقيق تقدم كبير. حتى نهاية الكتاب ، سأستخدم الخلايا العصبية السينيّة كالأخرى الرئيسية ،لأنها تعمل بشكل جيد وتعطي توضيحات ملموسة للأفكار الرئيسية المتعلقة بالجمعية الوطنية. لكن ضع في اعتبارك أنه يمكن تطبيق نفس الأفكار على الخلايا العصبية الأخرى ، وهذه الخيارات لها مزاياها.

: , , ? ?

: , . , . . : , , ?

—

ذات مرة في مؤتمر حول أساسيات ميكانيكا الكم ، لاحظت ما بدا وكأنه عادة كلام مضحكة: في نهاية التقرير ، غالبًا ما بدأت أسئلة الجمهور بعبارة: "أحب وجهة نظرك حقًا ، ولكن ..." أساسيات الكم ليست مجال عملي المعتاد تمامًا ، ولفتت الانتباه إلى هذا النمط من طرح الأسئلة لأنني في المؤتمرات العلمية الأخرى لم أقابلها عمليًا حتى يُظهر السائل تعاطفًا مع وجهة نظر المتحدث. في ذلك الوقت ، قررت أن انتشار مثل هذه الأسئلة يدل على أن التقدم في الأساسيات الكمومية قد تحقق بعض الشيء ، وأن الناس بدأوا للتو في اكتساب الزخم. فيما بعد أدركت أن هذا التقييم كان قاسيًا جدًا. ناضل المتحدثون مع بعض أصعب المشاكل التي واجهتها عقول البشر. بطبيعة الحال ، كان التقدم بطيئا!ومع ذلك ، كانت هناك قيمة في سماع أخبار تفكير الناس حول هذا المجال ، حتى لو لم يكن لديهم شيء يذكر.

ربما لاحظت في هذا الكتاب "علامة عصبية" تشبه عبارة "أنا معجب للغاية". لشرح ما لدينا ، كنت في كثير من الأحيان لجأت إلى كلمات مثل "ارشادي" أو "تحدث تقريبا" ، تليها شرح لظاهرة معينة. هذه القصص يمكن تصديقها ، لكن الأدلة التجريبية كانت غالبًا سطحية. إذا درست الأدب البحثي ، فسترى أن هذا النوع من القصص يظهر في العديد من الأوراق البحثية على الشبكات العصبية ، وغالبًا ما يكون بصحبة مجموعة صغيرة من الأدلة التي تدعمها. كيف نتعامل مع هذه القصص؟

في العديد من مجالات العلوم - خاصةً عند دراسة الظواهر البسيطة - يمكن للمرء أن يجد دليلًا صارمًا وموثوقًا به على فرضيات عامة جدًا. ولكن في الجمعية الوطنية هناك عدد كبير من المعلمات والمعايير الفوقية ، وهناك علاقات معقدة للغاية بينهما. في مثل هذه الأنظمة المعقدة بشكل لا يصدق ، من الصعب للغاية الإدلاء ببيانات عامة موثوقة. فهم NS في كل الامتلاء ، مثل الأسس الكمومية ، يختبر حدود العقل البشري. غالبًا ما يتعين علينا الاستغناء عن الأدلة لصالح أو ضد العديد من الحالات المعينة المحددة لبيان عام. ونتيجة لذلك ، يُطلب في بعض الأحيان تغيير هذه البيانات أو التخلي عنها ، مع ظهور أدلة جديدة.

أحد الأساليب المتبعة في هذا الموقف هو اعتبار أن أي قصة إرشادية حول NS تتضمن تحديًا معينًا. على سبيل المثال ، فكر في التفسير الذي أشرت إليه حول سبب وجود استثناء (التسرب) من العمل في عام 2012.: "هذه التقنية تقلل من تكيف العصبونات المفصلية المعقدة ، حيث لا يمكن للخلية العصبية الاعتماد على وجود بعض الجيران. في النهاية ، عليه أن يتعلم سمات أكثر موثوقية يمكن أن تكون مفيدة في العمل مع العديد من المجموعات الفرعية العشوائية المختلفة من الخلايا العصبية. " عبارة غنية واستفزازية ، يمكنك بناءً عليها بناء برنامج بحثي كامل ، ستحتاج فيه إلى معرفة ما هو صحيح ، وأين هو خاطئ ، وما يجب توضيحه وتغييره. والآن هناك حقًا صناعة بأكملها من الباحثين الذين يدرسون الاستثناء (والعديد من الاختلافات) ، يحاولون فهم كيفية عمله والقيود المفروضة عليه. لذلك مع العديد من المناهج الإرشادية الأخرى التي ناقشناها. كل واحد منهم ليس مجرد تفسير محتمل ،ولكن أيضا تحديا للبحث وفهم أكثر تفصيلا.

بالطبع ، لن يكون لدى شخص واحد ما يكفي من الوقت للتحقيق في كل هذه التفسيرات الإرشادية بعمق كافٍ. سيستغرق المجتمع بأكمله من الباحثين في NS عقودًا لتطوير نظرية قوية حقًا لتدريب NS استنادًا إلى الأدلة. هل هذا يعني أن الأمر يستحق رفض التفسيرات الإرشادية باعتبارها متساهلة وتفتقر إلى الأدلة؟ لا! نحن بحاجة إلى مجريات الأمور التي تلهم تفكيرنا. وهذا مشابه لعصر الاكتشافات الجغرافية العظيمة: غالبًا ما تصرف العلماء الأوائل (وجعلوا اكتشافات) استنادًا إلى المعتقدات التي أخطأت بطريقة خطيرة. في وقت لاحق ، قمنا بتصحيح هذه الأخطاء ، وتجديد معرفتنا الجغرافية. عندما تفهم شيئًا سيئًا - كما فهم الباحثون الجغرافيا ، وكما نفهم NS اليوم - من المهم أن تدرس المجهول بجرأة ،من أن تكون على حق بدقة في كل خطوة من التفكير الخاص بك. لذلك ، يجب أن تعتبر هذه القصص إرشادات مفيدة حول كيفية التفكير في NSs ، والحفاظ على وعي صحي بالقيود المفروضة عليها ، ومراقبة موثوقية الأدلة بعناية في كل حالة. بمعنى آخر ، نحتاج إلى قصص جيدة من أجل التحفيز والإلهام ، وإجراء تحقيقات شاملة دقيقة للكشف عن حقائق حقيقية.