👩🏼‍🍳 🍺 💢 الفيزياء والاقتصاد. الاختلاف الجينيولوجي ومظاهره في تقنية المعلومات 👰🏼 🎈 🕴🏼

جئت إلى عالم تكنولوجيا المعلومات من الفيزياء النظرية. كان يعمل بشكل رئيسي في المهام الاقتصادية. تشارك - هذا: التحليل ، المعارف التقليدية ، البيان ، التصميم ، البرمجة. وبطبيعة الحال ، قارنت في كل وقت بين النهج المادية والاقتصادية لفهم قوانين الطبيعة والاقتصاد ، على التوالي. وجهة نظر معينة قد نضجت حول هذا الموضوع. عنها وسيتم مناقشتها.

1. حول الإدراك بشكل عام

هناك طريقتان للإدراك:

نهج أرسطو . هذا هو نهج شامل ويعامل الكائن كمربع أسود. هذه الظاهرة ، يدرس الكائن في كل الواقع ككل. والحقيقة تقول ، على سبيل المثال ، أن الأجسام الثقيلة تسقط على الأرض بشكل أسرع من الأجسام الخفيفة ؛ التي تركت لنفسها جسم متحرك يتوقف تدريجيا. يتعامل نهج أرسطو مع هذه الظاهرة كواقع لا يتجزأ ، وبالتالي يمكن تسميته ظاهرة.

نهج غاليليو . هذا هو النهج التحليلي للأنظمة. هذا هو نهج فرق تسد. هذه الظاهرة ، تتحلل الكائن إلى الأجزاء المكونة له ويتم دراسة كل منها على حدة ، مستخرجة عن بقية (تحليل). ثم ، يمكن دمج الصور الناتجة في صورة واحدة ، مع مراعاة تفاعل المكونات (التوليف). على سبيل المثال ، يعتبر سقوط الأجسام سقوط الأجسام في الفراغ. وهناك يتحولون إلى السقوط بنفس السرعة. ولكن في الواقع ، الاحتكاك ضد الهواء يمنعهم من السقوط بالتساوي. بعد دراسة هذه القوة بشكل منفصل ، يمكننا شرح نتيجة أرسطو. وبالمثل ، إذا انفصلنا عن قوى الاحتكاك ، فإن الجسم المتحرك سيتحرك دون توقف. وإذا أخذنا في الاعتبار قوة الاحتكاك ، نحصل على نتيجة أرسطو. نهج غاليليو يؤدي على الفور إلى الحاجة إلى دراسة القوات. هذا ، في النهاية ، يترجم إلى نظام متماسك من الفيزياء الكلاسيكية.

مرة أخرى ، من أجل الوضوح.

نهج أرسطو . هناك ظاهرة قيد الدراسة ، "سقوط جسم في الهواء إلى الأرض" - ظاهرة F. ، فنحن نأخذ أجسادًا مختلفة ونجد أن الأجسام الأثقل تسقط على الأرض بشكل أسرع من الأجسام الخفيفة.

نهج غاليليو . عند دراسة ظاهرة F ، يجب على المرء أن يأخذ في الاعتبار ليس فقط الوزن. نحن ندرس السقوط في الهواء. ودعونا نغير ليس فقط الوزن ، ولكن أيضًا الهواء. دعونا نحاول تقليل كثافته ، بحيث لا يوجد هواء في النهاية. ثم نجد أن جميع الأجسام تسقط في الفراغ بنفس التسارع. نجد معايير التأثير على الظاهرة ونحاول خلق ظروف يكون فيها معيار واحد مهمًا. هذا ليس في الطبيعة. لذلك ، يحتاج الفيزيائي إلى مختبر حيث يمكنه تغيير المعلمات. بعد دراسة تأثير معلمة واحدة ، يمكننا المضي قدمًا في دراسة تأثير معلمة أخرى. نحن نحاول تقليل تعقيد النهج كله في تكوين نهج أكثر بساطة. من خلال تغيير شكل الجسم الساقط ، يمكننا دراسة اعتماد قوة الاحتكاك على الهواء اعتمادًا على شكل الجسم. عن طريق تغيير معدل السقوط ، يمكننا اكتشاف اعتماد قوة الاحتكاك على السرعة. عن طريق تغيير ارتفاع الخريف ، يمكننا اكتشاف اعتماد التسارع على الارتفاع. من خلال تغيير الموقع الجغرافي على الأرض ، نجد اعتماد تسارع السقوط على الجغرافيا.

يتحدثون تقريبًا ، في مقاربة أرسطو ، يدرسون الواقع ، وفي مقاربة جاليليو يدرسون التجريدات ، ومنهم ، من خلال التوليف ، يذهبون إلى الواقع.

2. نموذج المعرفة المادية

الفيزياء هي نظرية مثالية للعديد من العلوم ، بما في ذلك الاقتصاد. في التجارب الفيزيائية ، يتم الحصول على سلسلة منفصلة من القيم. لكنهم يعتبرون تقريبًا للوظائف المستمرة ، والتي هي في الواقع مؤشرات مادية. ويحاول الفيزيائيون تخمين هذه الوظائف. لذا خمن غاليليو القطع المكافئة لمسار حجر ألقيت بزاوية إلى الأفق. خمن كبلر مسارات الكواكب - الحذف ، الخ بعد تخمين المسار ، نحصل على جهاز تنبؤي - القدرة على حساب قيمة الإحداثيات غير المستكشفة للمسار. للاختبار ، وضعوا تجربة - قم بتهيئة الظروف اللازمة للحصول على تجربة تجريبية. بعد ذلك ، وبعد التحقق من القيمة المتوقعة والقيمة التجريبية ، نحصل على تأكيد أو دحض للنظرية. هنا في بعض الأحيان خطأ الخطأ التجريبي يلعب دورا هاما. تكمن المعرفة المادية في تحديد الحتمية - قانون الحصول على دولة من الحالة الأولية:

S (t) = D (Q ، S (0))

$S (t) = D (Q ، S (0))$

S(0) -   D –  – ,  S(t)  S(0) Q –       . ,  ,      .

لذلك ، لحجر رمى من نقطة (0،0) بسرعة $v_0$ في زاوية $α$ إلى الأفق لدينا

عرض $$ $$ x (t) = v_0 t cos⁡ (α) ، y (t) = v_0 t sin⁡ (α) - (gt ^ 2) / 2 عرض $$ $$يتم تعيين الحالة الأولية S (0) بواسطة ثلاثة معلمات: نقطة المغادرة (0،0) ، السرعة الأولية $v_0$ زاوية $α$ .
يتم إعطاء تأثير البيئة Q من خلال تسارع الجاذبية g. عند توسيع نطاق المشكلة (السرعة الأولية العالية) ، لم يعد g ثابتًا.
يتم إعطاء الحتمية D بواسطة الصيغة أعلاه.

لمهمة أكثر واقعية ، يجب أن يؤخذ الاحتكاك ضد الهواء في الاعتبار. هذا يعقد الرياضيات للمشكلة ، ولكن المبدأ لا يزال هو نفسه. بدلا من الحجر ، يمكنك النظر في الطائرة. ثم تأتي قوة الدفع للطائرة ، وينظمها الطيار. يظهر أيضًا عامل غير مادي - إرادة الطيار. لا يمكننا أخذها في الاعتبار. لكننا نعرف أنه ليس محدودًا: لا يمكن أن يكون الجر بلا حدود ، ولا يمكن أن يكون التسارع بلا حدود. هذا يقدم عنصرا من اليقين في الحركة. يستخدمونها ، على سبيل المثال ، لبناء مسار صاروخ الدفاع الجوي.

دعنا نعود إلى حجر الطيران. ويتميز عدد لا حصر له من المعلمات المادية. على سبيل المثال ، يمكن أن يكون شكله معقدًا بشكل تعسفي. لكننا على يقين من أنه في بعض المناطق المفيدة يمكننا أن نعتبر الحجر نقطة جوهرية. هذا هو التجريد الرئيسي للميكانيكا الكلاسيكية. يتم تمثيل جميع الأنظمة كمجموعات من نقاط المواد المتفاعلة. هذا يجعل الحد المعرفي الرئيسي - تقليل سلوك النظام المعقد إلى سلوك مكوناته الأولية.

فيما يتعلق بالحد المعرفي المذكور ، يمكن التمييز بين نهجين معرفيين: الاختزالية والشمولية.

3. الاختزال والشمولية

الاختزال هو مبدأ تقليل خصائص النظام من خصائص النظم الفرعية وخصائص تفاعل الأنظمة الفرعية. يعمل بنجاح في الفيزياء.
النظر ، على سبيل المثال ، الغاز. بدون تحللها إلى أنظمة فرعية ، يمكننا أن نتعامل مع المفاهيم التجريبية والظواهرية: الضغط P ، درجة الحرارة T ، الحجم الخامس. من الناحية التجريبية ، نجد العلاقة التي تربط هذه المعلمات - معادلة حالة الغاز:

$display$ هذا هو ما يسمى المستوى الظاهري - العمل مع الظواهر (الظواهر) دون الخوض في بنيتها. هذا هو نهج أرسطو.الآن تطبيق نهج غاليليو. نحن نتحلل نظام "الغاز": تخيله كمجموعة من جزيئات التصادم. ثم نحدد P و T من خلال المعلمات الميكانيكية للجزيء. ويتم ذلك في الفيزياء الجزيئية. وبالتالي ، نقوم بتقليل نظام الغاز إلى النظم الفرعية للجزيئات. سيوضح ذلك معادلة الحالة أو نستنتجها لأنظمة جديدة.وفقًا لذلك ، لدينا في العمل تشبيه: يتم تقسيم الاقتصاد الكلي إلى الشركات والأسر. ولكن هنا الحد ليس كاملا بعد. للأسف ، لا يوجد نيوتن الاقتصادية. المشكلة هي تعقيد وتوافر عامل غير موضوعي في الفيزياء (على الرغم من وجود جدل حول دور الموضوع في ميكانيكا الكم).والآن عن الشمولية.الشمولية هي مبدأ أنه يمكن أن يكون هناك خصائص غير قابلة للاختزال في النظام. لذلك في علم الأحياء ، تستند عقيدة الحيوية إلى مفهوم entelechy ، قوة الحياة المتأصلة في الجسم ككل وغير قابلة للاختزال.تستغني الفيزياء حتى الآن عن مفهوم الشمولية.

4. الفورمولا والخوارزمية النماذج

نموذج الصيغة هو نموذج معرف بواسطة صيغة. سيتم اعتبار مفهوم "الصيغة" معروفًا.أمثلة في الفيزياء: معادلات نيوتن ، معادلات لاجرانج ، معادلات ماكسويل ، معادلات نافير-ستوكس ، معادلات هايزنبرغ-شرودنجر ، معادلات آينشتاين.أمثلة من الاقتصاد: صيغة Black-Scholes لسعر الخيار ، صيغة عرض النقود ، نموذج البرمجة الخطية لتحسين الحافظة المالية ، صيغ حساب الفائدة ، صيغ حساب المخاطر.مع نموذج صيغة ، يمكن للشخص العمل بدون جهاز كمبيوتر. هذا هو تقريبا جميع الرياضيات البحتة. ولكن هنا ، تلعب الخوارزمية دورًا متزايد الأهمية. لذلك لم يتم اختزال حل مشكلة الألوان الأربعة إلى أي صيغة ، ولكن كان يتطلب حلاً قوياً للعديد من الحالات الخاصة. تم هذا التمثال بواسطة أجهزة الكمبيوتر.نموذج حسابي - نموذج معرف بواسطة خوارزمية ، وربما لا يمكن اختزاله إلى صيغة. بالطبع ، من الممكن تصنيف الخوارزمية على أنها صيغ ، لكن هذه ليست نفس الصيغ الكلاسيكية. نموذج الخوارزمية واقعية مبدئيًا فقط باستخدام الكمبيوتريمكن دائمًا اختزال النموذج الرسمي إلى نموذج حسابي.مثال على نموذج الخوارزمية الأول هو مشكلة Fermi-Pasta-Ulam. إليكم اقتباس من كتاب أولام ، مغامرات الرياضيات.

تنويه

_{بمجرد أن يتم الانتهاء من الآلات ، أدرك فيرمي ، بحدسه وحسه السليم الكبير ، على الفور كل أهميته في دراسة مشاكل الفيزياء النظرية والفيزياء الفلكية والفيزياء الكلاسيكية.} _{ناقشنا هذه المسألة بأكثر الطرق تفصيلًا وقررنا محاولة صياغة بعض المشكلات التي ستكون بسيطة في صياغتها ، ولكن سيكون لها حل يتطلب حسابات طويلة جدًا ، مستحيلًا بمساعدة قلم وورق أو أجهزة حوسبة ميكانيكية موجودة.} _{بعد أن ناقشنا عددًا من المشكلات المحتملة ، استقرنا على مشكلة نموذجية واحدة تتعلق بالسلوك طويل الأجل لنظام ديناميكي وتتطلب تنبؤًا طويل المدى.} _{تعتبر سلسلة مرنة ذات نهايتين ثابتتين ، لا تتأثر فقط بقوة التشوه المرنة المعتادة التي تتناسب مع التشوه ، ولكن أيضًا بالقوة المادية غير الخطية الصغيرة.} _{كان من الضروري معرفة كيف ، بعد عدد كبير جدًا من فترات التذبذبات ، سيؤثر هذا اللاخطية تدريجياً على السلوك الدوري المعروف للتذبذبات في أحد المفاتيح ، وكيف ستكتسب المفاتيح الأساسية الأخرى سعةها ، وكيف ، حسب اعتقادنا ، ستتم الحركة الحرارية ، وتقليد السلوك ، وربما السوائل ، التي ، بصفتها صفائحية في البداية ، تصبح مضطربة أكثر فأكثر ، حتى يتم في النهاية تحويل حركتها العيانية إلى حرارة.} ساعدنا John Pasta ، عالم الفيزياء الذي وصل مؤخرًا إلى Los Alamos ، في إنشاء مخططات انسيابية وبرمجة ومعالجة المهام في MANIAC. قرر فيرمي أن يتعلم كيف يبرمج آلة. في تلك الأيام ، كان من الصعب القيام به أكثر من الآن ، عندما توجد بالفعل برامج جاهزة وقواعد ثابتة ، وهذا الإجراء نفسه تلقائي. ثم كان من الضروري تعلم الحيل المختلفة. لقد أتقن فيرمي هذه بسرعة كبيرة ، وعلمني شيئًا ، على الرغم من أنني كنت أعرف بالفعل ما يكفي لتكون قادرًا على تقييم نوع المهام التي يمكن حلها بهذه الطريقة ، وتحديد مدتها في عدد خطوات الحساب وفهم مبادئ تنفيذها.كما اتضح ، لقد اخترنا المهمة بنجاح كبير. كانت النتائج التي تم الحصول عليها من الناحية النوعية مختلفة تمامًا عن تلك التي توقعها Fermi بمعرفته العميقة بحركات الأمواج. كان الهدف الأولي هو معرفة ما هي سرعة طاقة السلسلة ، المضمنة أصلاً في موجة جيبية بسيطة (أُخذت ملاحظة كنغمة واحدة) ، ستنشئ تدريجياً تناغمات أعلى ، وكيف سيصل النظام إلى حالة فوضوية نهائية ، ويصف كيف شكل السلسلة ، وبالتالي فإن طبيعة توزيع الطاقة بين المفاتيح العليا والعليا. لكن لم يحدث شيء من هذا القبيل. لدهشتنا ، بدأت السلسلة في العزف فقط على بضع ملاحظات صماء ، والتي ربما تكون أكثر إثارة للدهشة ، بعد عدة مئات من الاهتزازات الترددية العادية ، أخذت مرة أخرى نفس الشكل الجيبي كما كان في البداية.أعلم أن فيرمي اعتبر هذا "اكتشافًا بسيطًا" ، كما قال هو نفسه. لكنه كان سيخبره بعد ذلك بعام ، عندما تمت دعوته لإلقاء محاضرة من قبل جيبس (حدث مشرف للغاية في الاجتماع السنوي للجمعية الرياضية الأمريكية). لقد مرض قبل الاجتماع ، ولم تحدث هذه المحاضرة أبدًا. ومع ذلك ، تم نشر تقرير عن هذا العمل ، كتبه فيرمي وباستا وأنا ، مع ذلك - كتقرير عن العمل في لوس ألاموس.يجب أن أوضح أن حركة الوسيط المستمر ، مثل السلسلة ، على سبيل المثال ، يمكن دراستها باستخدام الكمبيوتر إذا تخيلنا أن السلسلة تتكون من عدد محدود من الجزيئات - في حالتنا ، أربعة وستون أو مائة وثمانية وعشرون. (يتم تمثيل عدد العناصر بشكل أفضل كقوة لاثنين ، حيث أن ذلك يسهل المعالجة على الكمبيوتر.) هذه الجزيئات مترابطة بقوى تحتوي ، بالإضافة إلى المصطلحات الخطية عن بعد ، أيضًا على مصطلحات صغيرة غير خطية من الدرجة الثانية. ثم يحسب الجهاز بسرعة حركة كل من هذه النقاط في خطوات زمنية قصيرة. بعد احتساب مركز واحد ، تنتقل إلى مرحلة زمنية أخرى وتحسب موضعًا جديدًا ، وبالتالي تتكرر عدة مرات. لا توجد أي طريقة للقيام بهذا الحساب يدويًا ، فقد يستغرق الأمر آلاف السنين. الحل في شكل تحليلي باستخدام الأساليب الرياضية للتحليل الكلاسيكي للقرنين التاسع عشر والعشرين غير مقبول تماما هنا.وكانت النتائج مذهلة حقا. بذلت محاولات عديدة لتوضيح أسباب هذا السلوك الدوري والمنتظم ، والذي أصبح مصدرًا للأدب الضخم حول التذبذبات غير الخطية الموجودة حاليًا. كتب العمل عليهم مارتن كروسكال ، عالم فيزياء من برينستون ، ونورمان زابوسكي ، عالم رياضيات كان يعمل في مختبر بيل فون. في وقت لاحق ، قدم بيتر ليك مساهمته الرائعة في هذه النظرية. أجرى كل منهم تحليلا مثيرا للاهتمام من هذا النوع من المشاكل. يعرف عالم الرياضيات أن ما يسمى بالنظام الديناميكي Poincare العائدين ، والذي يضم الكثير من الجزيئات ، له طول ضخم - في الواقع ، على نطاق فلكي - وأنه يعود بسرعة إلى موقعه الأصلي هو الأكثر إثارة للدهشة.قرر فيزيائي آخر في لوس ألاموس ، هو جيمس سو ، معرفة ما إذا كانت الفترة التي تلي عودة شديدة إلى الوضعية الأولية تبدأ من جديد من نفس الحالة ، وماذا سيحدث بعد هذه "الفترة" الثانية. جنبا إلى جنب مع المعكرونة ومتروبوليس ، كرر الإجراء بأكمله ، ومما يدعو للدهشة ، عودة حدثت مرة أخرى ، ولكن بدقة أقل من واحد في المئة. تكررت هذه الصورة أكثر من ذلك ، ولكن بعد ستة أو اثني عشر مثل هذه الفترات ، بدأت الدقة في الزيادة مرة أخرى ، مما يدل على ظهور "فترة فائقة" معينة. لذلك ، تبعت غرابة أخرى ، لا أقل.

وهنا مقال عن هابري ، يتحدث عن الحالة الراهنة لمشكلة فيرمي باستا-أولام:حل علماء الرياضيات مشكلة Fermi-Pasta-Ulam

5. التنسيق

عن طريق تنسيق النظام ، أعني تعريف المعلمات الأساسية التي تحدد ، من حيث المبدأ ، تطور النظام. على سبيل المثال ، في ميكانيكا نقطة المواد ، يتم تعريف التنسيق بواسطة:

القوة الخارجية F
- نقطة كتلة المواد م
- الإحداثيات المكانية (س ، ص ، ض) = ص من نقطة المواد
- الوقت ر

يتم إعطاء تطور النظام بواسطة معادلة نيوتن

(d^{2} r (t)) / (d t^{2}) = (F (t)) / m

$(d ^ 2 r (t)) / (dt ^ 2) = (F (t)) / m$

ما هو تنسيق الكيان الاقتصادي؟ عملت مرة واحدة في نظام ذكاء الأعمال. المصطلح الرئيسي هو المؤشر. أساس النظام هو بطاقة الأداء. مئات المؤشرات. لكنني بحثت دون جدوى على الإنترنت للحصول على وصف لأساس المؤشرات - مجموعة من المؤشرات التي لا يمكن اختزالها إلى مؤشرات أخرى ، والتي من حيث المبدأ ، تحدد تمامًا تطور الكيان الاقتصادي. هذا ، كما أفهمها ، لم يتم التنسيق في الاقتصاد. وبالتالي ، فإن الحديث عن بعض القوانين الأساسية الديناميكية ليس ممكنًا بعد. من الممكن فقط ، بناءً على اتصال المؤشرات ، إجراء تحليل للسيناريو - للإجابة على السؤال "ماذا سيحدث للمؤشرات المشتقة إذا كانت المؤشرات الأساسية ستتغير وفقًا للسيناريو المحدد؟"

6. مثال مجردة. سلسلة زمنية التنبؤ مثل الفيزياء

يمكنك طرح مشكلة التنبؤ بناءً على السلسلة الزمنية الفعلية: بعدد من القيم الحقيقية ، يجب أن تحصل على القيمة المتوقعة للمؤشر - القيمة في المستقبل. هذا ينطوي على نوع من الحتمية الخفية للسلسلة الزمنية. كان هناك العديد من التخمينات العلمية والكنيسة العلمية حول هذا الموضوع. تعاملت أنا شخصياً مع أطباء العلوم الذين ادعوا أن منهجيتهم ستسمح لهم بالحصول على توقعات لسعر الصرف وأظهروا الأطروحات المقابلة مع كل أنواع فترات الثقة وغيرها من سمات قوانين التوزيع. ولكن ، عندما واجهت الواقع ، تم تفجير التقنيات.

في بعض الأحيان للحصول على توقعات ، قم بذلك:

خذ سلسلة الوقت الحقيقي {V (ti)}. الجدول - خط كسر الخط.
قم بوظيفة مستمرة W (t) بحيث W (ti) = V (ti). الرسم البياني هو منحنى مستمر.
يتم تحديد متعدد الحدود P (t) يقارب W (t) بدرجة كافية من الدقة. كثير الحدود يمكن اعتبار للجميع ر.
ثم لدينا توقعات للوقت المستقبلي T: V (T) = P (T)
كل هذا يعطي انطباع العلم ، ولكن فقط للوهلة الأولى. نعم ، إن وجود كثير الحدود التقريبي لـ W (t) مضمون من قبل نظرية Weierstrass من التحليل الزوجي. يمكننا أن نعدد بشكل تعسفي بدقة W (t). ولكن لا يمكن استخدامها للتنبؤات.

القيمة التقريبية للسلسلة الحقيقية هي 100٪ ، والقيمة التنبؤية هي صفر. يمكن اختراع كثيرات الحدود بشكل تعسفي ، لكنها ستقدم توقعات مختلفة.

عندما يصل T اليوم ونكتشف V (T) الحقيقي ، ثم من أجل السلسلة {{V (ti)} و V (T)} يمكننا بناء كثير الحدود Q (t) تقريبًا هذه السلسلة تقريبًا بشكل تعسفي ، لكن الوقت T لم يعد في المستقبل و Q (T) لم يعد التنبؤ ، ولكن حقيقة واقعة. كثير من الحدود P (t) و Q (t) بالتأكيد ليس من الضروري أن يتزامنا ولوقت التنبؤ الجديد T '> T سوف تظهر نتائج مختلفة. وهذا هو ، ليس هناك توقعات. يبدو أن هناك العلم ، ولكن لا توجد توقعات. هو مثل نظرية الملائكة في العصور الوسطى. يمكنها شرح كل شيء ، لكنها لا تستطيع التنبؤ بأي شيء.

الفرق بين الاستيفاء المادي والاستقراء عن الاقتصادي:

دقة البيانات التجريبية : تقريبية في الفيزياء ، دقيقة في الاقتصاد
وظائف المجال : مستمر في الفيزياء ، متقطع ، تدريجي في الاقتصاد
البيانات التجريبية : في الفيزياء ، المنفصلة ، في الاقتصاد المستمر مع الانقطاعات المنفصلة
القوانين الأساسية : في الفيزياء هناك. F = ma ، على سبيل المثال ؛ في الاقتصاد حتى الآن

7. الاقتصاد والفيزياء

في الاقتصاد ، تعد المسارات الحقيقية - غير المستمرة أساسًا - وظائف ثابتة تدريجية. على سبيل المثال ، يمكن لمؤشر "سعر العملة" أن يقفز في أي وقت. الوظائف الاقتصادية المستمرة - تقريبات من أجل تحليل matanalysis (إذا كان لديك مطرقة في يديك ، فأنت تريد أن تنظر في أي شيء مثل مسمار ...). كل معاملة محاسبية تسبب قفزات في قيم مؤشرات المشتقات من الحسابات. وهم غالبية المؤشرات. علاوة على ذلك ، كل تغيير في عدد العمال منفصل ، إلخ. يتناقض استمرارية المسارات الاقتصادية مع استمرارية معظم المسارات المادية. لذلك ، فإن جهاز تحليل الأمهات لا ينطبق مباشرة على المسارات الاقتصادية.

صورة للإدراك الجسدي. مسار حجر ألقيت بزاوية إلى الأفق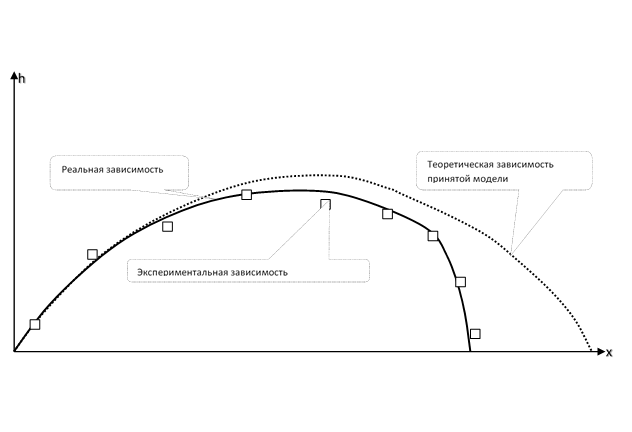

صورة للمعرفة الاقتصادية. سعر صرف العملة في البنك المركزي.

هذه هي وظيفة حقيقية التجريبية الحقيقية. إنه متقطع في نقاط زمنية عندما يتغير سعر الصرف.

في الفيزياء:

القيم الفيزيائية التجريبية تقريبية دائمًا تقريبًا
تشكل القيم الفيزيائية التجريبية سلسلة منفصلة.
تعتبر السلسلة المنفصلة التجريبية مضلعة لتقريب مستمر لأن الواقع مستمر. قد تتحول فكرة الاستمرارية إلى كذبة على المقاييس المكانية والزمانية الصغيرة. ثم الفيزياء سوف تغير وجهها.
مؤشرات أساسية محددة جيدا
تكون المسارات النظرية والحقيقية مستمرة دائمًا ويمكن تمييزها دائمًا تقريبًا (مسار النقطة المادية دائمًا ما يكون مختلفًا مرتين في الوقت المناسب)
نظرًا لاستمرار الديناميات الحقيقية والمسار الحقيقي ، فإن تقريبها المستمر الجيد له قوة تنبؤية: في حي صغير بما فيه الكفاية ، لن تكون الوظيفة بعيدة عن قيمتها الحقيقية الأخيرة.

في الاقتصاد:

يمكن اعتبار القيم الاقتصادية التجريبية دقيقة. فقط في الاقتصاد الكلي هناك مشكلة في الدقة بسبب العدد الهائل من الكيانات التجارية.
تتكون القيم الاقتصادية التجريبية من فواصل من الثبات ، تنقطع عند نقاط معينة في الوقت الذي تتغير فيه القيمة فجأة
لا يمكن اعتبار البيانات التجريبية بمثابة أرض اختبار لتقريب مستمر لأن الواقع متقطع.
غير محددة تماما مؤشرات الأساس. ليس من الواضح سبب الرقص.
نظرًا لتوقف المسار الحقيقي ، فإن أي تقريب مستمر جيد تعسفيًا لا يضمن التنبؤات في أي منطقة صغيرة تعسفية.
مسارات حقيقية تقريبا دائما متقطعة. وهذا يعني أن التصميم الاقتصادي يتطلب مقاربة مختلفة عن الميكانيكا الكلاسيكية.
في الاقتصاد ، هناك في البداية عامل الإرادة الحرة للكيان الاقتصادي. يتم تنظيم مداها من قبل الدولة. الحدود القصوى لهذه الحرية:
- الحرية الكاملة في سوق غير خاضع للوائح الدولة
- الحرية الجزئية في السوق الخاضعة للتنظيم الجزئي للدولة
- الافتقار التام للحرية في دولة مركزية تمامًا حيث لا يوجد سوق حر

المعرفة الاقتصادية لم تصل إلى مستوى مماثل للميكانيكا الكلاسيكية:

لم يتم تعريف المكونات الأولية لنوع نقطة المواد
غير محدد Q (المعايير البيئية) ، فإنه ليس من الواضح ما هو مهم ، ما هو غير مهم ،
لم يتم تنفيذ التقسيم الطبقي المفصل للأنظمة الاقتصادية ،
عملية الخفض غير واضحة وما إذا كان ذلك ممكنًا ؛ قانون الحتمية الاقتصادية غير واضح.

. – . – . ? , . . . . , – .

, . , , - .

8. IT

8.1.

. . . . , . . . . . . . , , . . … , . . , . . . , . . . . . . . . . . . – " . - "!? , . -1840( , ). . . , . , . , . , . . , , . (). . , , , : ", . ". ! . , , - .

8.2. -

. — . , , .. . . , . . – . , . , . – . . …

. . , . , , , . , . . . . . , - . . . . , : , . . . , , . . ? . . , .

. - , .

, , . , . . , .

. . . , . , . , : , . , . . .

, – Jump Processing. , . .

, . “ ”. , – . , , . – , . . , – .

8.3.

( ). . “”. . , . , . . – . . , . . . . , . . – . . , . … . ? , . , - . . . , . , , . . .

. , . , . , – . , . , – ( – ?).

8.4.

_{“ ”}

. () . . . , , . . , . . , , . . . – . , , . , . . , . جميل. . – . , . – . . , (, ). , . . , . . , , , . . . – . . . . . . . . . : , , , , , , , , … . 100 . ( , , ) . , ( , (SQL-) ). , . أي . . . , . . , : ”, . . . ”.

. , . , . : . , , .

. . . , , . . . . -.

() . , , ( ), . , . , – . , , , , , . . . , , . , “” “”. , “” “”. ? , .

: . . . , . . . . — . . : . : , …

. . , . . .

ملخص

, . . - . . — . لماذا هذا؟ .

: IT. .

الفيزياء والاقتصاد. الاختلاف الجينيولوجي ومظاهره في تقنية المعلومات