ننتقل إلى حساب الدوال المنطقية وفقًا للرسم البياني لفئة أوسع من السلوكيات. نحن نعتبر السلوكيات المستقلة الدورية التي لا تحتوي على إشارات متعددة (أو بطريقة أخرى: لا تحتوي على أحداث مفهرسة). قيود أخرى: للراحة ، لن نفكر في ربط الفروع المتوازية في OR. نحن نعتبر فقط اتصالًا بواسطة AND ، أي ، يتم تشغيل الحدث فقط عندما يتم تشغيل جميع الأحداث السابقة.
سنستخدم STG لوصف السلوك ، ولكن مع قيود إضافية. بالنسبة لكل مكان ، فإن عدد الأقواس التي تدخلها وتتركها يساوي تمامًا واحدًا لكل منهما. وفقًا لذلك ، يمكن اعتبار المكان الذي يحتوي على أقواس واردة وصادرة قوسًا واحدًا يربط بين حدثين (انتقالات). تبعا لذلك ، فإن التحركات تتحرك على طول الأقواس. نظرًا لأن السلوكيات التي تحتوي على إشارات متعددة لا يتم اعتبارها الآن ، فإن مؤشرات الأحداث محظورة ، فهي ليست ضرورية. أحداث فارغة محظورة. يُمنع الموقف أيضًا عند خروج قوسين مدرجين في حدث واحد من أحداث غير متوازية مع بعضها البعض (حالة خاصة من نفس الحدث). والغرض من ذلك هو التخلص من الأقواس التي لا تحمل حمولة دلالات. يعتبر الباقي صحيحًا (عاديًا ومباشرًا وآمنًا) من وجهة نظر سلوك STG ، مع مراعاة القيود المذكورة أعلاه. لا يحتوي السلوك على تعارضات CSC.
التعريف 1. الحدث الذي يدخل إليه القوس هو نتيجة للحدث الذي يخرج منه هذا القوس. وعلى العكس من ذلك ، فإن الحدث الذي يخرج منه القوس هو سبب الحدث الذي يدخل فيه هذا القوس.
التعريف 2. المسار - تسلسل لا نهاية له من الأحداث - نتيجة التغييرات في تسمية الرسم البياني ، بدءًا من مسار معين. كل حدث يدخل التسلسل عدد لا حصر له من المرات. كل هذا الدخول فريد من نوعه.
التعريف 3. تتبع الحدث A هو المسار الذي تكون فيه كل الأحداث إما كنتيجة مباشرة للحدث A ، أو نتيجة للإغلاق العابر لعلاقة نتيجة الأحداث فيما يتعلق بالحدث A. يتم تحديد العلامة الأولية لتتبع الحدث A على النحو التالي. إذا تم تغيير العلامة بشكل تعسفي ، بعد تشغيل الحدث A ، يتم إصلاح العلامات في أقواس الإخراج للحدث A. ثم تنتقل بقية العلامات إلى أن تصبح حركة العلامات مستحيلة دون تحرير العلامات في أقواس الإخراج الخاصة بالحدث A. وتكون العلامة الناتجة هي العلامة الأولية لتتبع الحدث A.
التعريف 4. نعرض علاقة الطلب لثلاث أحداث (أ ، ب ، ج). يتم ترتيب ثلاثة أحداث (مكتوبة A> B> C) إذا وفقط إذا حدث أي حدث للحدث B في التسلسل دائمًا قبل حدوث الحدث الأول ، لأي تتبع للحدث A.
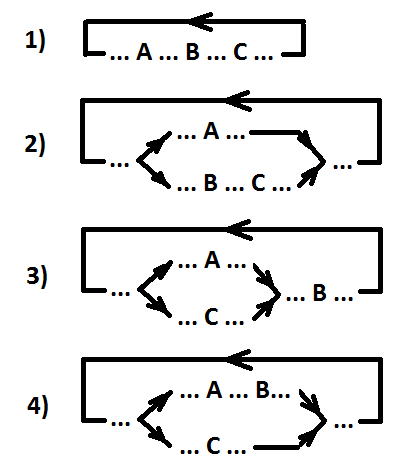
المذكرة. يمكن أن يكون الحدث A موازًا لكلا الحدثين B و C (أو C فقط) ، أو يمكن أن يكون كلا الحدثين A و B موازيًا للحدث C.
خيارات الموقع للأحداث المرتبة A و B و C (A> B> C).
التعريف 5. الإشارة b (التبديل B1 و B2) تلتقط الإشارة a (التبديل A1 و A2) فيما يتعلق بالأحداث X و Y (الأحداث X و Y متوازية أو متزامنة) إذا كانت الشروط التالية صحيحاً:
1) X> A1> A2 ؛
2) إذا كان الحدث A2 موازياً للحدث X وغير موازي للحدث Y ، فعندئذ X> A2> Y ؛
3) Y> B1> B2 ؛
4) إذا كان الحدث B2 موازياً للحدث Y وغير موازي للحدث X ، فعندئذ Y> B2> X ؛
5) Y> B1> A2 ؛
6) إذا كان الحدث A2 موازيا للحدث Y وغير موازي للحدث X ، فعندئذ Y> A2> X.
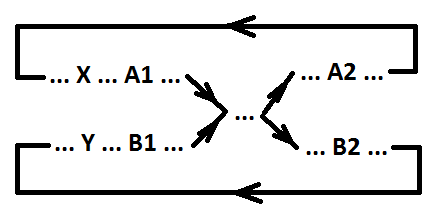
الملاحظة 1. تحدد الشروط 1 و 2 و 3 و 4 ترتيب تبديل الإشارات a و b على التوالي. تحدد الشروط 5 و 6 ترتيب حدث catch B1 وحدث catch A2.
ملاحظة 2. يمكن أن يكون الحدث X هو الحدث A1. في هذه الحالة ، تتدهور الشروط 1 و 2.
ملاحظة 3. يمكن أن يكون الحدث Y هو الحدث B1. في هذه الحالة ، تتدهور الشروط 3 و 4 و 5.
ملاحظة 4. يمكن أن يكون الحدث X هو الحدث A1 ، ويمكن أن يكون الحدث B1 هو الحدث Y. في هذه الحالة ، تتدهور الشروط 1 و 2 و 3 و 4 و 5.
الآن نبدأ في النظر في ما هو زرع. يتميز المتورط بالأحداث ، ونتيجة لذلك يغير المتورط معناها.
التعريف 6. حدث ، ونتيجة لذلك يقوم المتورط AND (OR) بتغيير قيمته من 1 (0) إلى 0 (1) ، سوف ندعو الحد الصحيح للمتورط. سيتم استدعاء الإشارة المقابلة لهذا الحدث في وضع التشغيل. يتحول المتورط.
التعريف 7. حدث ، ونتيجة لذلك يقوم المتورط AND (OR) بتغيير قيمته من 0 (1) إلى 1 (0) ، سوف ندعو الحد الأيسر للمتورط. سيتم إلغاء الإشارة المقابلة لهذا الحدث. المتورط ينطفئ.
التعريف 8. يُطلق على المتورط الذي لا تتوازى فيه أي حدود يمينية (أو أي اثنين من اليسار) مع بعضها البعض.
في الوقت الحالي ، لن نفكر في عمليات الزرع المتقطعة. سنعود إلى النظر أدناه.
لذلك ، لدينا: جميع الحدود الصحيحة للمتواطئين متوازية مع بعضها البعض ، وكذلك الحدود اليسرى للمتواطئين متوازية مع بعضها البعض.
خاصية مهمة. يتم تشغيل المتورط عند حدوث حدث واحد على الأقل ، وهو الحد الأيمن للمتورط. يتم إيقاف المتورط فقط عند حدوث جميع الأحداث التي تمثل الحدود اليسرى للمتورط.
الآن يبقى تحديد خصائص الإشارات التي تشكل الزرع.
التعريف 9. الإشارة التي يتم تضمينها في عملية الزرع ستسمى متغير.
الخاصية الأولى للمتغيرات. تشغيل وإيقاف إشارات متغير.
الخاصية الثانية للمتغيرات. بالنسبة إلى أي متغير تبديل (أحد مفاتيحه هو الحد الأيسر من المتورط L ، والآخر هو بعض الأحداث X) ، يجب أن يكون هناك حدث - بعض الحدود اليمنى R لنفس المتضمّن هي إما أن X و R هما نفس الحدث ، أو R > X> L.
الخاصية الثالثة للمتغيرات. بالنسبة إلى أي متغير شامل (أحد مفاتيحه هو الحد الأيمن من المتورط R ، والآخر هو بعض الأحداث X) ، يجب أن يكون هناك حدث - بعض الحدود اليسرى L لنفس المتضمن تكون إما أن X و L هما نفس الحدث ، أو R > X> L.
الخاصية الرابعة من المتغيرات. بالنسبة لأي متغير (التبديل بين X1 و X2) لا يتم تشغيله أو إيقاف تشغيله ، يجب أن يكون هناك حدثان: بعض الحدود اليسرى من L الضالعة وبعض الحدود اليمنى من R الضالعة مثل R> X1> L و R> X2> L . خلاف ذلك ، لا يمكن للمتورط الحفاظ على قيمة ثابتة في وضع إيقاف التشغيل.
الخاصية الخامسة للمتغيرات. بالنسبة لأي زوج: بعض متغيرات التبديل وبعض متغيرات التبديل ، يجب أن يكون هناك سلسلة من المتغيرات تلتقط بعضها البعض فيما يتعلق ببعض الحدود الصحيحة للمتضامن (في حالات الالتقاط المختلفة ، قد تختلف الحدود الصحيحة) ، بدءًا من متغير التبديل هذا وينتهي بمتغير التبديل هذا . خلاف ذلك ، لا يمكن للمتورط الحفاظ على قيمة ثابتة في وضع التشغيل.
الخاصية السادسة من المتغيرات. بالنسبة لأي متغير شامل a ، إذا كانت الحدود الصحيحة للمتورط هي الحدث + (a-) ، فسيتم تضمين هذا المتغير في سجل المتضمن AND (OR) مع الانقلاب ، وفي سجل المتورط OR (AND) دون انقلاب. بالنسبة إلى أي متغير تبديل a ، إذا كانت الحدود اليسرى للمتورط هي الحدث a- (a +) ، فسيتم تضمين هذا المتغير a في سجل المتضمن AND (OR) مع الانقلاب ، وفي سجل المتورط OR (AND) دون انقلاب.
الخاصية السابعة من المتغيرات. بحكم الخاصية الرابعة للمتغيرات ، بالنسبة لكل متغير لا يتم تشغيله أو إيقاف تشغيله ، يوجد حد يمين للمتسللين R وحدود يسرى للمتواطئين L بحيث يكون R> a +> L و R> a-> L. إذا كانت R> a +> a- ، فإن هذا المتغير يدخل المتورط في و مع الانقلاب ، و المتورط في OR بدون انقلاب. إذا كانت R> a-> a + ، فإن هذا المتغير يدخل المتورط AND بدون انقلاب ، والمتورط OR مع الانقلاب.
الخصائص السبعة المدرجة للمتغيرات هي خصائص ضرورية للمتورط. أيضا ، هذه الخصائص كافية لوصف يزرع.
المذكرة. لا يحظر الوصف أعلاه للزرع الموقف عندما تكون بعض الحدود اليسرى للزرع موازية لبعض الحدود اليمنى لنفس المتورط. معنى هذه الظاهرة هو أنه ، وفقًا لسرعة العمليات المتوازية ، قد لا يكون هذا الزرع في الوقت الفعلي ضروريًا لتنفيذ الإشارة المقابلة وفي الوقت الفعلي قد لا يتم إيقاف تشغيله (إذا كانت الحدود اليمنى تعمل في وقت أبكر من الحدود اليسرى).
الآن سننظر في كيفية بناء الشكل الطبيعي لوظيفة منطقية من المتورطين.
تعريف 10. إذا كان المتورط في وضع إيقاف التشغيل في بعض الحالات (قيمة الغرس AND (OR) هي 1 (0)) ، فإننا نقول أن المتورط يغطي هذه الحالة.
النظر في إشارة معينة س ، والتي نحتاج لحساب وظيفة منطقية. لإنشاء DNF (CNF) ، من الضروري أن يقوم المصممون AND (OR) بتغطية جميع الحالات التي تكون فيها الدالة x هي 1 (0). في هذه الحالة ، من الضروري ألا يقوم أي من هؤلاء - و (OR) - المقلدون بتغطية الحالات التي تكون فيها الوظيفة x هي 0 (1). أيضًا ، عند حساب الدوال المنطقية ، من الضروري مراعاة خصوصيات الدوائر: يجب على المتواطئين "التداخل". أي أنه إذا كان المتورط في حالة ما يمكن تشغيله (أي ، يمكن تشغيل حدث يمثل الحد الصحيح لهذا المتورط) ولا تتغير قيمة وظيفة الإشارة x أثناء التبديل ، فيجب أن يكون هناك متورط آخر يغطي هذه الحالة و لا يتم تشغيله عند تشغيل هذا الحدث.
الآن نحن بحاجة إلى توضيح ثلاثة أسئلة. ما هي الدولة من حيث الرسم البياني؟ كيفية تحديد الحالات التي تكون فيها وظيفة الإشارة x هي 1 (0)؟ كيفية تحديد الشروط التي تغطيها الزرع؟
لنبدأ بالولايات. أي وضع العلامات يمكن تحقيقه هو شرط. نظرًا لعدم وجود تعارضات في CSC ، فإن كل علامة قابلة للتحقيق تتوافق مع حالة فريدة (قابلة للتحقيق). في الحالات التي يتعذر الوصول إليها ، تكون قيمة الوظيفة تعسفية وليست هناك حاجة للنظر فيها. وبالتالي ، يتم وصف كل حالة نعتبرها بشكل فريد من خلال التصنيف المطابق. يتم تحديد موضع كل علامة بشكل فريد بواسطة القوس الذي تحدده. يرتبط كل قوس بشكل فريد بزوج من الأحداث (المرتبة): الحدث الذي يخرج منه القوس والحدث الذي يدخل فيه القوس. وبالتالي ، يتم وصف أي حالة يمكن الوصول إليها بشكل فريد من خلال مجموعة تتكون من أزواج من الأحداث المطلوبة.
التعريف 11. سيتم كتابة زوج من الأحداث التي تشير إلى قوس محدد {P، S} ، حيث P هو الحدث المسبب ، و S هو الحدث الناتج.
التعريف 12. سيتم استدعاء MM مجموعة الأزواج المطلوبة {P، S} ، التي تصف حالة يمكن بلوغها.
الآن ، دعونا نحدد لأي من الحالات قيمة الدالة x هي 1 ، والتي هي 0. ولندع الأحداث x + ناتجة عن n أحداث A1 و A2 و ... و An والأحداث x- الناجمة عن أحداث m B1 و B2 و ... ، BM.
قيمة الدالة x هي 1 إذا:
أو 1) لكل i من 1 إلى n ، ينتمي الزوج {Ai، x +} إلى MM المحدد ؛
أو 2) زوج {x + ، S} بحيث x +> S> x- ينتمي إلى MM المحدد ؛
أو 3) زوج {P، S} بحيث x +> P> x- و x +> S> x- ينتمي إلى MM المحدد ؛
أو 4) زوج {P ، x-} بحيث x +> P> x- ينتمي إلى MM المحدد وهناك يوجد i من 1 إلى m بحيث لا ينتمي الزوج {Bi، x-} إلى MM المحدد.
قيمة الدالة x هي 0 إذا:
أو 1) لكل i من 1 إلى m ، ينتمي الزوج {Bi، x-} إلى MM المحدد ؛
أو 2) زوج {x-، S} بحيث ينتمي x-> S> x + إلى MM المحدد ؛
أو 3) زوج {P، S} بحيث ينتمي x-> P> x + و x-> S> x + إلى MM المحدد ؛
أو 4) زوج {P ، x +} بحيث ينتمي x-> P> x + إلى MM المحدد وهناك i من 1 إلى n بحيث لا ينتمي الزوج {Ai، x +} إلى MM المحدد.
الآن نكتشف ما هي الشروط التي يغطيها الزرع. دع المتسابق له حدوده اليسرى L1 ، L2 ، ... ، Ln و m الحدود اليمنى R1 ، R2 ، ... ، Rm.
لا يغطي المتورط الحالة الموصوفة في MM المحدد إذا كان واحد على الأقل من الأزواج {P، S} المنتمي إلى MM المحدد يستوفي الشرط التالي: يوجد i من 1 إلى n و j من 1 إلى m بحيث
إما 1) Li و S هما نفس الحدث و Rj> P> Li ،
أو 2) Rj و P هما نفس الحدث و Rj> S> Li ،
أو 3) Rj> P> Li و Rj> S> Li.
هذا البيان صحيح بحكم الخاصية الخامسة للمتغيرات.
يغطي المتضمّن الحالة الموصوفة بواسطة MM المحدد إذا لم يكن الشرط التالي مستوفياً لأي من الأزواج {P، S} التي تنتمي إلى MM المحدد: يوجد i من 1 إلى n و j من 1 إلى m بحيث
إما 1) Li و S هما نفس الحدث و Rj> P> Li ،
أو 2) Rj و P هما نفس الحدث و Rj> S> Li ،
أو 3) Rj> P> Li و Rj> S> Li.
هذا البيان صحيح بحكم الخصائص الثانية والثالثة والرابعة للمتغيرات.
بالمعنى المجازي ، يغطي المتورط الحالة إذا كانت كل العلامات بين الحدود اليسرى واليمنى للمتضامن. إذا كانت هناك علامة واحدة على الأقل خارج هذه الحدود ، فإن عملية الزرع لا تغطي هذه الحالة.
الآن لدينا أداة لحساب الأشكال العادية (لا يزال غير واضح ، ومع ذلك ، لا يزال هناك سؤال مع يزرع متقطعة). لكننا مهتمون بالحد الأدنى من الأشكال العادية (مع مراعاة خصوصيات الدوائر الكهربائية). قبل المضي قدما ، دعونا نعود إلى النظر في المتورطين المتقطعين. النظر في I-implicant لإشارة DNF x (الحالة مع OR-implicant لـ CNF مشابه). لنفترض أن الحدين الأيسر لنفس المتسللين L1 و L2 غير متوازيين مع بعضهما البعض و L1> L2> x- (يتم اعتبار الحالة الخاصة بالحدود اليمنى بشكل مشابه). ثم يجب أن يكون هناك اثنين من الحدود الصحيحة للمتضامنين R1 و R2 بحيث يجب استيفاء الخواص الثانية والثالثة والرابعة والخامسة للمتغيرات من أزواج L1 و R2 و L2 و R1. إذا كان هناك حدود يسرى L3 متوازية مع L1 ، فيجب عندئذٍ الوفاء بالخصائص المذكورة أعلاه بالنسبة للزوج L3 و R2 (بالمثل ، في حالة وجود حدود مقابلة ، عمليات الزرع المتوازية مع الحدود L2 و R1 و R2). ولكن نظرًا لعدم استخدام إشارات متعددة ، يجب أن يكون هناك متورط غير متقطع بحدود L1 و R2 (وحدود مقابلة متوازية ، إذا كان لدى أي من المتورطين المتعرضين لها). في هذه الحالة ، يتكون المتضمن غير المتقطع من عدد أقل من المتغيرات ويغطي جميع الحالات التي يغطيها المتضمن المتقطع ، حيث تكون قيمة دالة الإشارة x هي 1. ومن هنا الاستنتاج: المتواطئين غير المتواصلين ليسوا متطرفين ولا يمكن استخدامها لحساب الحد الأدنى من الوظائف.
المزيد عن حساب الحد الأدنى من الوظائف في الجزء التالي.