مدينة بدون اختناقات مرورية

الفصل الثاني
( رابط إلى الفصل الأول )

فن تصميم شبكات الطرق

مشاكل النقل في المدينة من خلال عيون شخص من علوم الحاسب الآلي

إذا كنت قد أوصيت بمقال بعنوان "فن تصميم شبكات الطرق" ، فسأطلب على الفور معرفة عدد شبكات الطرق التي تم إنشاؤها بمشاركة مؤلفها. يجب أن أعترف ، أن نشاطي المهني كان بعيدًا عن بناء الطرق وكان مرتبطًا مؤخرًا بتصميم المعالجات الدقيقة ، حيث كنت من بين أمور أخرى ، منخرطة في استهلاك موارد تبديل البيانات. لقد حدث أن طاولتي وقفت أمام النافذة البانورامية ، التي فتحت منظرًا جميلًا للجزء الطويل من طريق فولغوغراد السريع وجزءًا من حلقة النقل الثالثة مع اختناقات مرورية لا نهاية لها من الصباح إلى المساء ، من الأفق إلى الأفق. وبعد ذلك ، في أحد الأيام ، بدا لي فجأة: "اللعنة ، لأن تعقيدات عملية تبديل البيانات التي أواجهها على شريحة يجب أن تكون مشابهة تمامًا للصعوبات التي يواجهها تدفق السيارات داخل شبكة الطرقات في الشوارع."
ربما ، كانت مجرد وجهة نظر من الخارج وتطبيق الأساليب التي لم تكن تقليدية في المنطقة التي شملتها الدراسة التي منحتني فرصة لفهم سبب الاختناقات المرورية وتقديم توصيات بشأن كيفية التغلب على مشكلتهم في الممارسة العملية.

فما هي حداثة النهج؟

تاريخياً ، يعتبر الغرض الرئيسي للطرق هو الفرصة التي تتيحها للسفر بسرعة لمسافات طويلة (بين روما والمقاطعات). مثل هذا الحكم له ما يبرره عندما يتعلق الأمر بشبكة الطرق السريعة بين المدن على المستوى الفيدرالي: تبدو المدن التي يتصلون بها بمثابة نقاط صغيرة نادرة على الأطلس ، وتمر معظم السيارات التي تسير بين هذه المدن دون أن تتحول إلى أي مكان.

ومع ذلك ، من الضروري فقط تسليم عدة صفحات وفتح خريطة تفصيلية لبعض المدن الكبيرة ، حيث تتغير الصورة فورًا: فالعناوين وحدها ، حيث يمكن بدء الرحلة أو إتمامها ، تبلغ حوالي عشرة آلاف بالفعل ، وكلها كثيفة نسبيًا صغير الحجم. في الوقت نفسه ، يمكن أن تعمل مئات الآلاف من السيارات في شوارع هذه المدينة في وقت واحد ، علاوة على ذلك ، فإن هدف كل منها ليس فقط ملء الطرق الفارغة بالفعل ، ولكن نقل شخص أو شحن من نقطة بعنوان معين " X " إلى نقطة بعنوان محدد " نعم ". معًا ، يعني هذا أنه يجب تكييف نظام النقل الحضري لحل مشكلة المعالجة المتوازية المتعددة بشكل فعال . وبالتالي ، فإن وظائف نظام النقل الحضري أصبحت مشابهة لشبكة الهاتف أو الكمبيوتر أكثر من شبكة الطرق بين المدن.

بالنظر إلى شبكة الطرق كدائرة تبديل لمطور الأجهزة أو مهندس في مجال تقنيات نقل المعلومات ، فهي طريقة طبيعية تمامًا للتحدث عن مشكلة ، ولكن بين الأشخاص المشاركين في الأبحاث حول مشاكل النقل ، فإن هذا الرأي جديد ، على حد علمي.

إن نظرية تبديل الإشارات هي علم هندسي ضيق ، وهي وحدها ، بطبيعة الحال ، لن تكون كافية للتخطيط لشارع منفصل ، أو تقاطع طريق ، أو التنبؤ بسلوك مسار حركة المرور على جزء مستقيم ومعزول من الطريق السريع. لحسن الحظ ، فإن القضايا المذكورة أعلاه يتم بحثها جيدًا اليوم ، وقد تم بالفعل استخدام الأساليب التي تم تطويرها لحلها. تسمح نظرية التبديل ، بدورها ، للمهندس المعماري بالتخلص من المخاطر عند تنفيذ جميع عناصر شبكة الطرق بشكل مثالي ، ولا تزال المدينة في حالة انهيار النقل. يوجد هذا الخطر لأن تنفيذ العنونة المتزامنة المتعددة يتطلب موارد كثيفة.
المهمة المستهلكة للوقت ، والمفتاح إلى حل فعال لا يتمثل في عرض الشوارع وراحة تبادل النقل بشكل مناسب ، بل هو الاختيار المناسب لأي مخطط تحويل معين ستنفذه شبكة الطرق المقترحة.

من هذا العمل ، على سبيل المثال ، سوف تكتشف لماذا يكون النوع "الشرياني" من شبكات النقل ، التي لا تزال تستخدم في المدن الحديثة ، "سيئًا" ومع نمو السكان سيؤدي بالضرورة إلى اختناقات مرورية. تفسر النتيجة الأخرى المثيرة للاهتمام ، والتي تتفق جيدًا مع الملاحظات ، سببًا في أنه من غير المحتمل أن يؤدي توسع الطرق لوحده ، قبل حدوث جميع الاختناقات المرورية بشكل حصري بالقرب من التقاطع ، إلى تحسين الموقف بطريقة ما حتى لو ظل عدد السيارات في المدينة كما هو.

عندما كتبت هذا المقال ، كان من المهم بالنسبة لي أن يكون مفهوما بالنسبة لمعظم المهندس المعماري العادي ، يمكن أن يكون مفيدا من خلال عمله. حاولت تعريف القارئ بتبديل القضايا بلغة بسيطة ، ووضع معايير لتقييم مدى تعامل شبكة طرق معينة مع مهمة المعالجة الموازية ، باستخدام أمثلة نموذجية أوضحت كيفية استخدام هذه المعرفة في الممارسة العملية.

هذه المقالة مخصصة لدائرة واسعة من القراء الذين لديهم دراية طفيفة بالدورة الجامعة في الرياضيات ، ونظرية الخوارزميات ، وهم على استعداد لتكريس 1 إلى 5 أيام لها.

فصل ودمج تدفقات السيارات

من الواضح بالنسبة للعديد من السائقين ، أن الصعوبات المرورية تنشأ أساسًا في أماكن الطرق التي تُجبر فيها السيارات لسبب ما على تغيير الممرات. ومن الأمثلة على ذلك الشوك والشقوق ومناطق الوصلات وطرق الوصول إلى الطرق السريعة ، وأجزاء من الطريق السريع حيث يتم حظر بعض الممرات بسبب حادث أو إصلاح طريق.
في هذا القسم ، سيتم إجراء محاولة لتقديم وصف كمي للعمليات التي تحدث في مثل هذه الحالات ، وسنبدأ بفهم كيفية إعادة بناء السيارات من مسار إلى آخر.

استراتيجيتان لإعادة بناء في صف مجاور

حركة المرور على طول الطريق السريع لها تباين طبيعي: شخص ما يفضل القيادة بشكل أسرع قليلاً ، شخص أبطأ قليلاً ، وبين بعض السيارات تنخفض المسافة وتصبح بالكاد مريحة للقيادة ، بينما تزيد بين الآخرين كثيرًا مما يسمح للسيارات بالتناسب هناك من الممرات المجاورة. قد يكون ظهور مثل هذه الفجوات في تدفق الممر المجاور مباشرة على جانب برنامج التشغيل العشوائي متكررًا أو غير كبير. إذا ، في الوقت الذي يحتاج فيه إلى إجراء مناورة ، لا توجد فجوة ، يمكن للسائق اللجوء إلى استراتيجيتين سلوكيتين على الأقل:

الاستراتيجية رقم 1
قد توجد عدة فجوات مناسبة بالقرب من موقعها. إذا كانت الحركة كثيفة بدرجة كافية ، فمن غير المحتمل أن يكون السائق قادرًا على إضافة السرعة وسد الفجوة اللازمة ، ولكن يبطئ الحركة قليلاً ويترك التيار المجاور يتغلب على نفسه لتساوي الفجوة التي كانت متأخرة في الأصل - لن تكون هناك مشكلة كبيرة. تكاليف هذه الإستراتيجية واضحة: السائق نفسه والسيارات التي تسير في حارة سيارته تفقد بعض الوقت بسبب الحاجة إلى تقليل السرعة.

الاستراتيجية رقم 2
للانتظار ، تحتاج إلى التحلي بالصبر والحصول على الوقت اللازم لذلك. قد يكون البديل محاولة لتنفيذ المناورة الضرورية "هنا" و "الآن". وفقًا لهذه الفكرة ، يعطي السائق إشارة إلى السيارات التي خلفه في الشريط الذي سيتحرك فيه. هؤلاء ، بدورهم ، استجابةً لإشارته ، ينبغي أن يتباطأوا قليلاً "وندعهم" إلى الأمام ، فإن السيارات التي تتحرك أمامها ، وبالتالي إعطاء الفجوة بالحجم اللازم ، سوف تتشكل في تدفقها. يتم توزيع تكاليف الوقت في هذه الحالة بين سيارات الممر حيث أعيد بناء السائق في النهاية.

في الحياة الواقعية ، يتم استخدام كلا الاستراتيجيتين في نفس الوقت: أولاً ، يتباطأ السائق وينتظر فجوة كبيرة نسبيًا في مجرى الممر المجاور ، وعندئذٍ فقط يعطي إشارة إلى السيارات التي تتحرك فيه حول نيتها إجراء مناورة إعادة البناء.

بطبيعة الحال ، ليست المداخل والمنحدرات والتضييقات هي السبب الوحيد لتغيير مسار الممر ، الأمر الذي يستحق التذكر عند تصميم الطرق. تعد قدرة السيارات ذات السرعات العالية على تجاوز حركة المرور غير المستعجلة أمرًا ضروريًا حتى لا يتدهور الموقف على الطريق السريع إلى قائمة انتظار كبيرة واحدة تزحف بسرعة أبطأ جرار. ومع ذلك ، فإن مشكلة التعايش بين المركبات التي تتحرك بسرعات مختلفة على الطريق لها طبيعة مختلفة قليلاً ويمكن فصلها عن المشكلات التي تم تناولها في هذه المقالة ، لأن عملية التجاوز والترتيبات المرتبطة بها ليست من أجل السائقين الذين يقومون بالإجراءات القسرية التي تتطلب منه التسرع . إذا كان هناك وقت للانتظار ، فوفقًا لنظرية الاحتمالات ، فإن هذه فرصة مناسبة لإجراء مناورة لتترك للسائق بمفرده ولهذا لا يحتاج على الإطلاق إلى التدخل في حركة سائقي السيارات الآخرين.

تكلفة خطوة واحدة
في الواقع ، قد يكون سلوك السائقين في غاية الصعوبة ، لكن من المهم بالنسبة لنا أولاً أن تظل النتيجة التي يتم الحصول عليها في ظل ظروف نموذجية معقولة: كل حركة قسرية لسيارة من مسار إلى آخر تفرض عقوبة مؤقتة على المشاركين في حركة المرور.

دعونا الآن تقييم كيف يعتمد مقدار الوقت الضائع على كثافة السيارات على الطريق.

سننظر في الحركة على طول كل حارة كتيار منفصل. في محاولة للبقاء على مسافة مريحة من السيارات الموجودة في نفس المسار ، يحجز السائقون جزءًا من طول مميز معين d في الجدول. دع السيارات تسقط في تيار لكل وحدة طول. نحن نوافق على وصف كثافة التدفق بأنها صغيرة ، أو ، نفس الشيء ، نقول أن "صغيرة إذا كان المنتج ρ × d أقل بكثير من الوحدة".

في الوقت الذي يدرك فيه السائق الحاجة إلى الانتقال إلى الصف التالي ، فإن احتمال وجود جزء من الكمية التي كان سيشغلها هناك لن يكون مجانيًا ، بصغر حجمه - سيكون متناسبًا تقريبًا مع نفسه. إذا حدث الحدث الموصوف بالفعل ، فستجد في المجموعتين سيارتين تتنافسان على مكان ما نتيجة للمناورات بعض التأخير في متوسط ​​القيمة الثابتة δ .

بافتراض small صغير ، فإن احتمال أن تصرفاتهم في هذه اللحظة ستؤثر على حركة السيارات الأخرى يمكن إهمالها. وبالتالي ، في الدرجة الأولى من الصغر فيما يتعلق بـ ρ ، سيكون الوقت الضائع من حركة واحدة هو α ⋅ ρ ، حيث يكون المعامل α كمية قابلة للقياس تجريبياً ، اعتمادًا على الثقافة والطقس وحدود السرعة (وما إلى ذلك) ، ولكن تظل ثابتة تقريبًا محليًا في الوقت المحدد ومن أجل هذه المدينة ككل.

شدة الخسائر على الموقع قبل الخروج
السيارات التي تغادر إلى المؤتمر ، قبل أن تصل إلى الطريق المنحدر (الشكل 2) ، يجب إعادة بناؤها ، في بعض الأحيان حتى عدة مرات ، في الصف المجاور على اليمين. كل مناورة من هذا القبيل تجعل من الصعب التحرك ، ونتيجة لذلك ، فإن متوسط ​​السرعة في القسم قبل الخروج أقل بشكل ملحوظ من أقسام "النقل" (المحرومة من المخارج ، "المداخل" والشوكة) من الطريق السريع.


التين. 2

لتمرير جزء من المسار بسرعة أقل - يستدير للسائقين (ولركابهم) فترة إضافية من الوقت في الرحلة. وبعبارة أخرى ، فإن منطقة الطريق السريع المتاخمة مباشرة للمنحدر هي مولد ثابت للخسائر المؤقتة.

افترض أن متوسط ​​سرعة الماكينة ν وكثافة التدفق ρ عند الحدود الأمامية لهذه المنطقة هي نفسها بالنسبة لجميع النطاقات.

افترض ، علاوة على ذلك ، أن الكثافة ρ ومعدل التدفق q الخارجين من المخرج (متوسط ​​عدد السيارات التي تصل إلى المنحدر لكل وحدة زمنية) صغير في وقت واحد ، s هو عدد الممرات على الطريق السريع. للوصول إلى المخرج ، سيقوم السائق بإجراء مناورات لإعادة البناء. إذا كانت كثافة التدفق على المنحدر أقل بكثير من ρ ، فلن تكلفه سوى المناورة الأخيرة من الناحية العملية "مجانًا" ، في حين أن الباقي سيتسبب في أي حال في خسائر α ⋅ ρ . في المتوسط ​​، سيكون عليك القيام (0 + 1 + 2 + ... + s - 1) / s = ( s - 1) / 2 مناورات "باهظة الثمن".

بالنظر إلى الصعوبات الناجمة عن مغادرة جميع السيارات لحضور المؤتمر ، يمكننا كتابة صيغة لشدة الخسائر المؤقتة:

I _out = q ⋅ α ρ ⋅ ( s - 1) / 2 = ( α / 2 ν ) ⋅ q ⋅ ( sρν ) ⋅ (1 - 1 / s )

القيمة p = ( sρν ) ليست أكثر من معدل التدفق لجميع السيارات التي تتحرك على طول الطريق السريع في الاتجاه المعني (متوسط ​​عدد السيارات التي تمر بالعمود لكل وحدة زمنية). تتيح لنا الملاحظة الأخيرة الفرصة لإعادة كتابة الصيغة الخاصة بي بشكل أكثر تناسقًا:

أنا _خارج = ( α / 2 ν ) ⋅ pq ⋅ (1 - 1 / s )

معدل الخسارة في القسم المجاور لطريق الوصول
إن الموقف الناشئ على الطريق السريع وراء المكان الذي يتصل به طريق الوصول يكرر إلى حد كبير الموقف على الموقع أمام المؤتمر ، على الرغم من وجود بعض الاختلافات.
اسمح لتيار صغير من السيارات ذات القوة q من خلال الطريق المنحدر الجانبي أن يصب في حركة المرور الرئيسية للطريق السريع (الشكل 3).


التين. 3

يبلغ طول المنحدر طولًا محدودًا ، لذا يجب أن تُبنى جميع السيارات القادمة حديثًا في الممر الأيمن الأقصى للطريق السريع. نتيجةً لذلك ، تكون كثافة حركة المرور في أقصى اليمين أعلى محليًا من المتوسط ​​على الطريق ، لذلك يقرر بعض السائقين فيها تغيير الممرات إلى صف مجاور أقل ازدحامًا على اليسار ، مما يؤدي بدوره إلى زيادة محلية في الكثافة بالفعل في الثانية الفرقة. ستستمر عملية الترحيل بين النطاقات حتى يتم تسوية كثافة التدفق عبر عرض الطريق السريع بأكمله. على افتراض أن متوسط ​​السرعة ν سيكون هو نفسه بالنسبة لجميع النطاقات n ، يمكننا أن نتوقع ، عند الانتهاء من عمليات الترحيل ، أن تزداد قدرة التدفق في كل منهما بمقدار (1 / s ) exactly بالضبط.

لمعرفة مقدار تكاليف "القلاع" هذه على السائقين ، نقوم أولاً بحساب قوة جميع تدفقات الترحيل. التدفق من الطريق المنحدر إلى المسار الأول للطريق السريع الذي نعرفه بالفعل: إنه يساوي q . للحصول على توازن في شكل زيادة قدرها (1 / s )، q ، يجب أن يكون التدفق في المسار الثاني من جانب الأول (1 - 1 / s ) ⋅ q ، من الثاني إلى الثالث - (1 - 2 / s ) ⋅ q ، من الجانب kth إلى ( k + 1) th - (1 - k / s ) ⋅ q . وفقًا للصيغة الأخيرة ، ستكون سعة تدفق الترحيل إلى أقصى اليسار (1 - ( s - 1) / s ) ⋅ q = (1 / s ) ⋅ q ، وفقًا للأمر السليم.

نظرًا لأننا نعرف المدة الزمنية لإعادة الإعمار الواحدة وقوة جميع تدفقات الهجرة ، يمكننا الآن حساب الكثافة الإجمالية للخسائر الناتجة عنها:

I _in = α ρ ⋅ q + α ρ ⋅ (1 - 1 / s ) + q + α ρ ⋅ (1 - 2 / s ) ⋅ q + ... + α ρ ⋅ (1 / s ) ⋅ q =

α ρ q (1 + 2 + ... + s ) / s =

α ρ q ( s + 1) / 2 =

( α / 2 ν ) ⋅ q ⋅ ( sρν ) ⋅ (1 + 1 / s ).

تذكر مرة أخرى أن sρν هو قوة تدفق جميع السيارات على طول الطريق السريع ، نحصل على صيغة التكلفة في شكلها النهائي:

أنا _في = ( α / 2 ν ) ⋅ pq ⋅ (1 + 1 / s ).

معدل فقدان شوكة متماثل
في الفقرات السابقة ، وجدنا خسائر من تفاعل التدفقات ، إحداهما كانت كبيرة بالضرورة ، والآخر صغير بالضرورة. لإظهار النهج المتبع في حل المشكلات عندما تكون قدرات كلا التدفقات قابلة للمقارنة من حيث الحجم ، دعونا نأخذ بعين الاعتبار تطرفًا آخر: مفترق تكون فيه اتجاهات "الابنة" شائعة على قدم المساواة للسائقين (الشكل 4).


التين. 4

للراحة ، سيتم تسمية السيارات التي تذهب إلى اليمين على مفترق الطرق "زرقاء" ، والسيارات التي تترك إلى اليسار - "حمراء". في البداية ، تتحرك السيارات من "الألوان" مختلطة ، ومشتتة بين جميع الممرات في الطريق السريع. عند اقترابها من التقاطع ، تبدأ السيارات الحمراء في الانحدار ببطء نحو الممرات اليسرى ، والسيارات الزرقاء باتجاه الممرات اليمنى ، حيث تتدفق الهجرة في كلا الاتجاهين بين الممرات المجاورة. على عكس مثال طريق الوصول ، لم تعد هذه التدفقات "صغيرة نسبيًا". بالمناسبة ، يوجد فقط بين الممرين المركزيين تبادل حركة مرور قسري ، تساوي شدته في أي من الاتجاهات (من اليسار إلى اليمين ، أو من اليمين إلى اليسار) ربع قوة التيار بأكمله تتحرك على طول الطريق السريع للسيارات. لحسن الحظ ، في هذه الحالة هناك طريقة جيدة بما يكفي لتقدير التكاليف الناتجة. أولاً ، نلاحظ أن عملية تقسيم السيارات إلى "أحمر" و "أزرق" على الأرجح تبدأ قبل فترة طويلة من الشوكة وتتقدم ببطء ، وبالتالي ، فمن ناحية ، يجب أن يكون لها تأثير ضئيل على كثافة حركة المرور في صف منفصل ، ومن ناحية أخرى ، تجعل الهجرة التدفقات الممتدة على مسافات طويلة ، وبالتالي إعطاء الفرصة لتمثيل كل منها على أنها مزيج من عدد كبير من تدفقات الطاقة المنخفضة (الشكل 5).


التين. 5

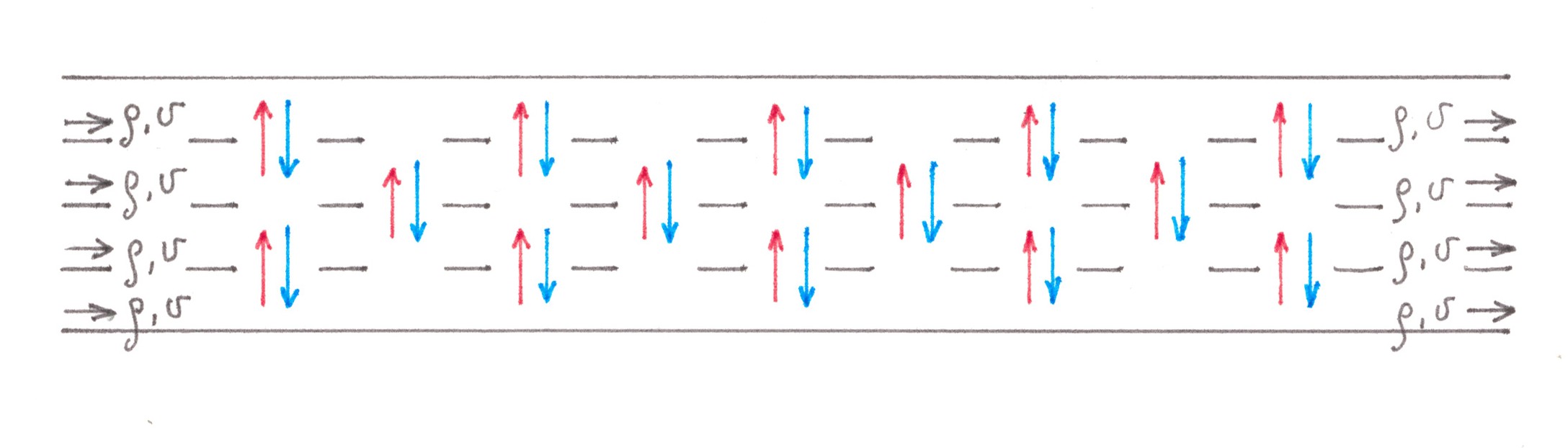
منذ الآن نحن نتحدث عن التدفقات الصغيرة ، وإن كان ذلك بأعداد أكبر ، فلا شيء يمنعنا من تقليل المشكلة قيد النظر إلى التدفقات التي تم حلها بالفعل. قسّم الطريق السريع عقلياً في الوسط إلى جزأين متساويين ، ثم قم بتوصيلهما مع عدد كبير من طرق الطائر أحادية المسار ، مما يسمح للسيارات الحمراء بالوصول إلى الجانب الأيسر والسيارات الزرقاء إلى اليمين (الشكل 6). نظرًا للتماثل الواضح ، عند حساب الخسائر الناتجة ، يمكننا التركيز على آلات من أي لون واحد ، على سبيل المثال ، الأزرق ، وفي النهاية مجرد مضاعفة النتيجة.


التين. 6

لذلك ، اجعل السرعة والكثافة متساوية في جميع الممرات وتبقى ثابتة في المنطقة بأكملها حيث يتم فصل السيارات بالألوان.في هذه الحالة ، سيكون معدل التدفق لجميع السيارات التي تتحرك على طول الطريق السريع:

p = 2 sρv .

دع q ₁ ، q ₂ ، ... q _m تدل على تدفقات السيارات الزرقاء التي تتحرك على طول لاعبي التخيل إلى النصف الأيمن من الطريق السريع. لنفترض أنه قبل وقت قصير من موقع الفصل في كل حارة من الطريق السريع ، يتم تمثيل كلا اللونين بنسب متساوية من 50 ٪ ، مما يعني أنه في المجموع
q ₁ + q ₂ + ... + q _m تساوي sρv / 2 ، أي p / 4.

الخسائر الناتجة عن الدفق q_i ، نظرًا لصغر حجمها ، يمكننا حساب المعادلة:

I _i =I _out +I _in = (α/ 2ν)⋅(p/ 2)⋅ q _i (1 - 1 /s) + (α/ 2ν)⋅(p/ 2)⋅ q _i (1 + 1 /s) = (α/ 2ν)p q _i

لخص التعبير الأخير على الكلi، والبحث عن الخسارة الناتجة السيارات فقط الزرقاء:

I _{الزرقاء} = ( α / 2 ν ) ⋅ ص ⋅ ( ف ₁ + س ₂ + ... + س _م ) = ( α / 2 ν ) ص ² /4.

خسارة كاملة، كما سبق ذكره، سيتم مضاعفة والمبلغ مرتين على النحو التالي:

I _شعبة = ( α / 2 ν ) ص ² /2.

تحليل الصيغ التي تم الحصول عليها
إذا فصلنا الشدة Iبمعنى ، مقدار الوقت الذي يفقده إجمالي المشاركين في الثانية بمقدار التدفق الجانبي q ، والذي بحكم التعريف يساوي عدد السيارات التي تربط أو تترك حركة المرور على الطريق السريع في ثانية واحدة ، نحصل على متوسط ​​الخسائر الناتجة عن إحدى هذه السيارات:

i _in = I _في / q = ( α / 2 ν ) ⋅ p ⋅ (1 + 1 / s )

i _out = I _out / q = ( α / 2 ν ) ⋅ p ⋅ (1 - 1 /s )

ولعل أهم شيء في هذه الصيغ هو التناسب المباشر بين تدفق الطاقة للسيارات على الطريق السريع p وتكلفة الوحدة i . يبدو كل شيء وكأن سيارة تسعى للانضمام ، أو العكس - لترك تدفق الحركة الرئيسية ، مما يتسبب في أضرار مستمرة لكل سائق قريب.

الملاحظة الثانية ، المثيرة للاهتمام وغير المتوقعة للغاية تتعلق بالتأثير الضعيف للغاية على شدة الخسائر الناتجة عن عدد الممرات بالقرب من الطريق السريع بجوار التقاطع مباشرة. كما ترون ، بالنظر إلى الصيغة الخاصة بـ " أنا _خارج" ، فإن المؤتمر عمومًا هو الأرخص بالنسبة للطريق ذو الممر الواحد ( s = 1 ، i _خارج = 0) ، والصعوبات الناجمة عن طريق الوصول المجاور لطريق سريع من ثلاثة حارات وستة حارات تختلف بنسبة

100 ٪فقط ⋅ [(1 + 1/3) - (1 + 1/6)] / (1 + 1/3) = 12.5٪.

عندما تفكر في أن كل سيارة من أي وقت مضى للانضمام إلى الحركة على الطريق السريع، وسوف يكون لتركها في نهاية المطاف، يبدو الشرعي عند حساب الخسارة في تقاطع بدلا من أنا _في و أنا _خارج لاستخدام قيمة موحدة

ط _مركبات = ( ط _في + أنا _في ) / 2 = ( α / 2 ν ) ⋅ p .

وعلى الرغم من عدم وجود في صيغة ط _AV من الاعتماد الصريح على عدد من العصابات، وعلينا أن نتذكر أن انتاجها (انظر اقتراحات ل I من _في و الأول من _خارج ) ويستند أساسا على افتراض وجود كثافة آلة صغيرة على الطريق، لذلك من غير المرجح أن تعطي نتائج مرضية، كائن تطبق على الطريق السريع الضيق مع الكثير من حركة المرور.

النتائج الأولية
في المناطق القريبة من التقاطعات ، تحدث حركة المرور حتما ، مع مرور الوقت بعيدا عن السائقين ، مما يقلل من متوسط ​​السرعة ، وهذا الأخير يؤدي إلى زيادة في كثافة السيارات ، ونتيجة لذلك ، احتمال حدوث اختناقات مرورية. سيتم استدعاء تكاليف الوقت المرتبطة بالفصل ودمج تدفقات السيارات بالتبديل.

توجد خسائر من نفس النوع بطريقة أو بأخرى في أي نظام تبديل: سواء أكان ذلك عبر الهاتف أو شبكة الكمبيوتر أو المعالج الدقيق متعدد النوى أو خدمة تسليم البريد.

عندما ينضم سائق ، أو ، على العكس ، يترك حركة المرور على الطريق السريع ، فإن تكاليف التبديل التي تتكبدها أفعاله تتناسب مع قوة تيار السيارات المرصودة في ذلك الوقت على الطريق السريع.

لتقليل خسائر التحويل في جميع أنحاء المدينة ، من الضروري التفكير بعناية في شبكة الطرق المنفذة فيها في مرحلة التصميم. بعد قليل سنحلل هذه المهمة بالتفصيل ، ولكن يمكن إدراج بعض التوصيات الواضحة الآن:

1. تتناسب خسائر التبديل مع سعة التدفق على الطريق السريع - ليس من الضروري توسيع الطرق دون الحاجة ، طريقتان صغيرتان صغيرتان يساوي ضعف واحد كبير ؛
2. تتناسب خسائر التحويل مع قوة التدفقات الجانبية - الأمر يستحق تصميم الشبكة بحيث كان على السائق أن ينحرف جانباً عدة مرات قدر الإمكان أثناء رحلته ؛
3. يجب أن يصبح التداخل المتبادل الناجم عن برامج تشغيل التدفقات الرئيسية والجانبية أصغر على نطاق المدينة إذا حاولت منع المسارات التي تتداخل فقط على مقطع قصير من المسار في مسار واحد.

الشروط الاقتصادية لوجود المدن.
موحد مدينة الوصول نموذج

ربما يكون أول شيء لبدء أي مشروع للتخطيط (أو إعادة التخطيط) لنظام النقل في المدينة هو محاولة تحديد نوع الهجرة التي تحتاجها المدينة الآن الآن وكيف ستتغير احتياجاتها في المستقبل.

يمكن إجراء مثل هذا التحليل إذا قمت أولاً بتقسيم المدينة إلى مناطق إقليمية ليست كبيرة جدًا ، ولكن ليس لكل منطقة إقليمية صغيرة ، وبعد ذلك يشير كل زوج من هذه المناطق إلى العدد التقريبي من الرحلات إلى جانب أو آخر والتي يحتاجها سكانها في وقت واحد أو آخر اليوم. من خلال وضع التنبؤات التي تم إجراؤها في طاولة مربعة ، ستتلقى بذلك مصفوفة لاحتياجات الهجرة لسكان المدينة.

بالنسبة لهذه المصفوفة ، يجدر البحث عن شبكة تسمح للسائقين والركاب بقضاء وقت أقل قدر ممكن في رحلة منفصلة وتتطلب من سلطات المدينة أقل قدر ممكن من الموارد لبناءهم.

عندما يتعلق الأمر بالمدن الحالية ، من المهم هنا عدم ارتكاب خطأ وعدم استبدال عدد الرحلات التي يحتاجها الناس فعليًا بعدد الرحلات التي تم إنشاؤها تاريخيًا تحت تأثير بعض العقبات أو الصعوبات في وقت عمل التصميم. ربما ، يمكن لشبكة النقل في برلين "قبل" و "بعد" سقوط الجدار الفاصل أن تكون المثال الأكثر وضوحًا لما قيل.

سيتعامل هذا القسم بشكل أساسي مع القضايا الإنسانية التي لست متخصصًا فيها ، لكنني أعتقد أن مناقشتها كهاوي هو أكثر صحة من مجرد تجنب المشكلة.

لتمثيل احتياجات السكان على نحو أفضل في مجال الهجرة ، فإن الأمر يستحق أن نبدأ بالسؤال الأساسي: "لماذا تحتاج المدن حقًا وما هي الوظيفة المفيدة التي تؤديها؟" .

دعونا نحاول الإجابة عليه ليس كمقيمين عاديين في المدن (والقرى) ، ولكن من منظور الشخص المسؤول عن عملية التحضر في بعض الدول الكبيرة والمتقدمة. من وجهة النظر هذه ، لم يعد من المهم ما هي الدوافع التاريخية التي كانت تتسبب في ازدحام الكثير من الناس في قطعة صغيرة من الأرض ، أو الأسباب التي تجعلهم يواصلون القيام بذلك الآن ، من المهم - ما هو التأثير الاقتصادي الذي يخلق مدن بحجم أو آخر ولأجل بسبب ما آليات يتحقق هذا التأثير.

في رأيي ، السبب الرئيسي لوجود المدن الكبيرة هو ، من ناحية ، الفرصة لشركات التكنولوجيا لإيجاد موظفين من المهن النادرة ، ومن ناحية أخرى ، الفرصة للأشخاص الذين أتقنوا المهن النادرة لبيع خدماتهم إلى الشركات المهتمة بهم بشروط تنافسية. في مدينة صغيرة (غير متخصصة) ، يكون إنتاج العديد من السلع والخدمات مستحيلًا بكل بساطة ، أو يضع شركات التكنولوجيا وموظفيها في موضع الرهائن المتبادلين ، دون إعطاء واحد أو آخر أي بدائل.

على سبيل المثال ، خذ مهنة غير نادرة لمدرسة الأدب بالمدرسة. وفقًا للإحصاءات ، فإن الحاجة إليها هي: مدرس واحد تقريبًا لكل 1000 نسمة. في المدرسة العادية ، يقوم 3-4 أشخاص بتدريس الأدب. يمكن أن يسمى اختيار وظيفة لمدرسة أدبية تنافسية إذا كان هناك ما لا يقل عن 4-5 مدارس ثانوية في مدينته ، والتي ، من حيث عدد السكان ، حوالي 15 ألف شخص.

على ما يبدو ، يشعر الأشخاص ذوو التخصص الهندسي بالراحة في سوق العمل في المدن التي يبلغ عدد سكانها 100 ألف على الأقل. بالطبع ، هناك أيضًا مثل هذه المهن ، التي لا يظهر الطلب عليها إلا في المدن التي يسكنها مليون شخص ، لكن المعنى الاقتصادي لملايين المدن لا يزال لغزا بالنسبة لي.

بعد كل ما سبق ، تبدو فرضيتان مفترضتان تمامًا (لا تؤثر صحة هذه المادة على حقيقة المحتوى الرئيسي للمقال):

1. أكثر الرحلات المتكررة التي يحتاجها الشخص العادي إلى السفر عبر مسافات تصل إلى 4-5 من أكثر الوظائف الواعدة بالنسبة له ؛
2. بالنسبة لجزء كبير من السكان الذين يمتلكون المهن النادرة والأكثر قيمة من الناحية الاقتصادية ، قد تكون المسافة بين أكثر الرحلات تكرارًا مقارنة بنصف قطر المدينة.

كتعبير محسّن عن الفرضيتين 1) و 2) ، في الأمثلة التي أستخدمها ، سأستخدم غالبًا نموذج مدينة ذات "وصول موحد" ، والذي يفترض أن قوة تدفقات الرحلات الشعبية هي نفسها بين أي فصولين ، أو بكلمات أخرى ، في جميع خلايا المصفوفة احتياجات الهجرة تستحق نفس العدد الإيجابي. إذا نظرت بشكل عشوائي إلى سجلات الرحلات التي تمت في مثل هذه المدينة خلال اليوم ، فبالنسبة للرحلة المميزة التالية ، ستحصل جميع الجهات على نفس الفرص في أن تكون بداية هذه الرحلة وأن تقدمها كنهاية ، ولا توجد علاقة بين موضع "الأولي" و "النهائي" »لا ينبغي مراعاة الأحياء.

شبكة طوبولوجيا الشبكات البسيطة

دعونا نحاول تطبيق الأفكار الموضحة في الفقرات السابقة على بعض أنواع خطط المدن المأخوذة من الحياة.

مدينة خطية
نشأت أول مستوطنات كبيرة في الغالب على طول الساحل ، في مناطق من قطاع رقيق من الأرض بين البحر والمنحدرات ، أو على طول طرق الطرق المزدحمة ، لذلك في عملية النمو اكتسبوا حدودًا ممدودة ضيقة. لقد نجا العديد من هذه المستوطنات حتى يومنا هذا ، مع الحفاظ على شكلها المطول وتحولها إلى مدن حديثة (الرسم التوضيحي أدناه).


(منطقة معزولة من ريو دي جانيرو ، المؤلف غير معروف)

غالبًا ما يوجد في مثل هذه المدينة طريق واحد واسع يتم بناؤه حوله. لنفترض أن كل ربع (منطقة التقسيم الإقليمي) يولد مجموعة من الرحلات بسعة واحدة ، من كل هذه الجهات - وأن المدينة نفسها تطيع نموذج الهجرة "الوصول الموحد".


التين. 7

دعونا نحاول أن نجد للشروط المذكورة أعلاه كيف يتغير متوسط ​​وقت السفر ومنطقة الطريق المطلوبة مع زيادة n .

لذلك ، اسمح لجميع الفصول بنفس الشكل والحجم ، ويزيد عددهم بمقدار λ (lambda). ومن الواضح أن

• يزداد طول الطريق الرئيسي بعامل λ .

بحكم النموذج المعتمد "للوصول الموحد" ، ستزيد أيضًا 50٪ من الرحلات التي بدأت في النصف الأيمن من المدينة في النصف الأيسر (عكس ذلك تمامًا) ، وبالتالي ، مع زيادة عدد الفصول بعامل λ ، ستزداد قوة التيار المار عبر وسط المدينة أيضًا بمقدار λ مرات سيكون التفكير المنطقي نفسه مع الاستنتاج نفسه صحيحًا ، بدلاً من الوسط ، نأخذ أي نقطة تقسم المدينة بنسبة معينة (1: 3 ، 2: 5) ، مما يعني أن

• يزداد تدفق الطاقة للسيارات على طول الطريق الرئيسي بعامل λ .
• يزداد عدد ممرات الطريق الرئيسية المطلوبة في كل قسم بعامل λ .

أكثر أو أقل وضوحا أن متوسط ​​طول الرحلة ، ومعها

• يزداد صافي وقت السفر الذي يقضيه في تغطية المسافة بعامل λ .

كل ما تبقى لنا هو حساب عدد مرات زيادة الوقت الضائع بسبب تكاليف التحويل في رحلة واحدة. في كل ربع عام ، يدخل تيار جانبي من وحدة الطاقة ويترك ، مما يولد معًا خسائر مؤقتة من الكثافة:

أنا = أنا _في + أنا _خارج = ( α / 2 ν ) p ⋅ 2 ،

حيث p هو معدل التدفق على الطريق الرئيسي. نحن نعلم بالفعل أن عدد الأرباع ومعدل التدفق على الطريق الرئيسي ينمو كما λ ، وبالتالي ، فإن إجمالي الوقت الضائع الناتجة عن الشبكة يزيد بعامل ² . من ناحية أخرى ، فإن عدد الرحلات التي تم إنشاؤها بواسطة الشبكة ، والتي يتم توزيع كل هذه الخسائر نتيجة لها ، يزداد بعامل λ ، حيث نحصل على ذلك

• يزداد صافي وقت السفر بسبب زيادة تكاليف التحويل بعامل λ .

دعنا نجمع كل النتائج في لوحة واحدة:

طوبولوجيا خطية
عدد نقاط العناوين (أرباع) سعة الوحدة .................................
المساحة الكلية للطرق ............................................... ........................................ ( ن ² )
وقت السفر النقي
أنفق على تغطية المسافة .............................................. ..... يا ( ن )
وقت السفر النقي
ضائع بسبب تكاليف التبديل ............................................ ......... يا ( ن )
عدد نقاط التبديل ............................................... .................................... ( ن )
عدد العقد التبديل ، مع الأخذ في الاعتبار قوة الجانب يتدفق ..................... O ( ن )

الترميز المستخدم: " y = O ( x )" ، يعني أن الكميات x و y تعتمد وظيفيًا ، وعندما ينمو x بلا حدود ، تميل النسبة x / y إلى رقم غير صفري محدد.

المدينة الخلوية
تتمثل الطريقة الثانية الشائعة للتخطيط في ترتيب الكتل في شكل مصفوفة مستطيلة ، على غرار طريقة وضع الأجزاء المجزأة في لوح شوكولاتة.

نحن نوافق على تسمية هذه المدن "الخلوية".


(لوس أنجلوس ، الصورة: ستيبانوف جلوري)

يوضح الشكل 8 مخططًا للمدينة الخلوية ، يتكون من n (مع الأخذ في الاعتبار "نصفي") الأرباع ، مكونًا مربعًا منتظمًا. يتم فصل الأحياء عن بعضها البعض من خلال ما مجموعه √ ن الطرق ، التي تعمل بشكل مشروط من الغرب إلى الشرق ، وطرق أخرى ، تمتد من الجنوب إلى الشمال. في الإجمال ، تشكل هذه الطرق تقاطعات √ n × √n ، يمكن جعل كل منها إما تقاطع إشارة ضوئية ، أو يتم تنفيذه من خلال جسر طريق وجسور.


التين. 8

بغض النظر عما إذا كانت حركة المرور في الشوارع في اتجاه واحد أو في اتجاهين ، يمكن القيام بأي رحلة من النقطة "أ" إلى النقطة "ب" في مدينة متقلب على طول طريق لا يتجاوز أكثر من شارعين ولا تتطلب أكثر من منعطف واحد عند التقاطع الطرق.

لنفترض أنه ، كما في المثال السابق ، يولد كل ربع سلسلة من رحلات سعة الوحدة ، وأن احتياجات الهجرة للسكان موصوفة في نموذج "الوصول الموحد". دعونا نحسب الآن ، بالنسبة لمدينة Cellular City ، تلك القوانين التي بموجبها يتغير متوسط ​​وقت السفر واستهلاك الموارد لبناء شبكة طرق مع زيادة عدد الفصول.

إذا زاد عدد الأرباع بعامل λ ، عندئذ:

• تزداد مساحة المدينة في λ مرات ، وأبعادها الخطية مع الحفاظ على النسب -
  في λ λ ،
• يزيد متوسط ​​طول السفر والوقت الصافي لتغطية المسافة ، بما يتناسب مع الأبعاد الخطية ، √ λ مرات ،
• يزداد عدد الشوارع وعدد الأحياء المجاورة لشارع واحد λ λ مرات ،
• قوة تدفق حركة المرور ، التي تتناسب مع عدد الفصول التي يكون فيها التدفق "على اتصال" (سيتم تقديم شرح لهذه الحقيقة لاحقًا) ، تزداد بمقدار √ λ مرة ،
• تنمو المساحة المطلوبة لجميع الطرق كـ (عدد الشوارع) × (طول شارع واحد) × (قوة تدفق الشارع) = √ λ ⋅ ⋅ λ λ ⋅ λ = λ √ λ

تنقسم التدفقات الجانبية إلى التدفقات التي تنطلق من أو باتجاه الأطراف وتتدفق حركة المرور من شارع إلى آخر عند تقاطعاتها. الأولى ، وفقًا للشروط ، تظل دائمًا مساوية للوحدة ، بعد الثانية ، إذا أخذنا في الاعتبار أن هناك أرباعًا في المدينة أكثر بكثير من الأحياء في شارع واحد ، فكل حركة المرور التي تتحرك على طولها تقريبًا تأتي أو تغادر الطريق السريع في الشارع. نتيجة لذلك ، يمكن تقدير التغير في حجم التدفقات الجانبية للثاني من خلال الصيغة (التغير في قوة تدفق الشارع) / ((الزيادة في عدد التقاطعات في شارع واحد) = √ λ / √ λ = 1. تشير المساواة في النسبة الأخيرة إلى الثابت إلى أن هذه التدفقات لا تتغير بشكل خاص مع زيادة في عدد الفصول ، وبالتالي ، فإن الزيادة في تكاليف التبديل الناتجة عن الشبكة ككل ستكون: (الزيادة في إجمالي عدد الفصول + التقاطعات) × (التغير في قيمة التدفق في شارع واحد) = λ √ λ . منذ قوة تدفق السفر الناتجة عن جميع الجهات زادت في then ، ثم

• صافي وقت السفر المفقود بسبب زيادة تكاليف التحويل بمقدار √ λ

تخيل النتيجة على شكل جهاز لوحي:

"طوبولوجيا الخلية"
عدد نقاط العناوين (أرباع) سعة الوحدة .................................
المساحة الكلية للطرق ............................................... .................................... O ( n √ n )
وقت السفر النقي
أنفق على تغطية المسافة .............................................. ... يا () ن )
وقت السفر النقي
ضائع بسبب تكاليف التبديل ............................................ ....... يا (√ ن )
عدد نقاط التبديل ............................................... .................................... ( ن )
عدد العقد التبديل ، مع الأخذ في الاعتبار قوة الجانب يتدفق ..................... O ( ن )

مقارنة الشبكات الخطية والخلوية مع بعضها البعض ، من الصعب ألا نلاحظ أن الزيادة في الموارد اللازمة للبناء والوقت الذي تقضيه في رحلة واحدة مع نمو المدينة للشبكة الأولى أسرع بكثير من الثانية. على سبيل المثال ، تتطلب المدينة الخلوية من أصل 100 ربع إسفلت أقل بعشرة أضعاف ، وتتطلب الرحلة عبرها وقتًا متوسطه 10 مرات أقل مما هو ضروري في مدينة خطية من نفس الحجم. وبالتالي ، فمن المنطقي استخدام شبكات الطرق ذات الطوبولوجيا الخطية فقط في المدن الصغيرة جدًا.

إذا نسيت لفترة من الوقت وجود تكاليف التحويل ، فيمكن اعتبار طوبولوجيا الخلوية وسيلة مثالية لتصميم شبكات الطرق ، حيث إنها تعطي تقدير O تقريبيًا مثاليًا لكل من متوسط ​​طول الرحلة ومنطقة الطريق المطلوبة. في الواقع ، بالنسبة لأي موقع "مضغوط" أكثر أو أقل من المدينة (مع وصول موحد) ، فإن طول الرحلة لن ينمو أبطأ من الجذر التربيعي لمنطقتها ، والتي عادة ما تكون متناسبة مباشرة مع السكان. نتيجة لذلك ، نحصل على كل نفس O () n ).

حقيقة أن طريقًا نموذجيًا في المدينة الخلوية يمتد عبر "زاوية" بدلاً من خط مستقيم ، من حيث المبدأ ، يمنح الحق في البحث عن طرق أفضل للتخطيط للمدن ، ولكن من غير المرجح توفير 20٪ (هذا المبلغ الذي يمكنك الفوز به في الحد الأقصى إذا تعلمت السيارات القيادة عبر الجدران) يوما ما سوف يجبرون المهندسين المعماريين على التخلي عن الترتيب المستطيل للشوارع والطرق.

يمكن الحصول على الحد الأدنى الممكن لتكلفة بناء الشبكة (وصيانتها) عن طريق تذكر أن كل سيارة تحتفظ بجزء من الممر لحركتها ، ونتيجة لذلك ، فإن إجمالي مساحة الطرق يتناسب مع ناتج متوسط ​​وقت السفر (متوسط ​​طول الرحلة) حسب عدد السيارات في المدينة : O () n ) × O ( n ) = O ( n √ n ) (مقارنة مع الجدول الخاص بـ Cell City).

إذا تحدثنا عن مقدار الوقت الضائع في السفر بسبب تكاليف التبديل ، فلا عجب إذن أن علاقتها مع مقدار الوقت الذي تستغرقه لتغطية المسافة لا تعتمد على عدد من الأحياء الفردية في المدينة الخلوية أو الخطية (O (( n )) / O (√ n ) = O (1) ، O ( n ) / O ( n ) = O (1)). بمعنى آخر ، فإن نسبة الوقت الضائع في السفر بسبب تبديل الأحداث في المدينة الكبيرة والمدينة الصغيرة ستكون هي نفسها. من هذا المنطلق يمكننا أن نستنتج أنه إذا لم تكن هناك مشاكل خطيرة في تبديل التكاليف في مدينة صغيرة (على سبيل المثال ، فقد بلغت 10-20 ٪) ، ثم في مدينة كبيرة لا يزال يتعين عدم ملاحظتها ، وإذا كانوا كذلك ، فإنهم أنفسهم لن يذهبوا إلى أي مكان ، بغض النظر عن نمو المدينة وتوسيعها.

نظرًا لأننا لا نعرف أيًا من البدائل صحيحًا (أو بالأحرى ، فإننا نعلم أن مشاكل حركة السيارات في المدن الكبيرة موجودة) ، فمن الجدير محاولة تحسين طوبولوجيا المدينة الخلوية حتى تنخفض تكاليف التحويل فيها على الأقل بمرور الوقت.

أمثلة مفيدة للشبكات غير الواقعية

دعونا نرى ما إذا كانت طوبولوجيا الخلوية تتبع التوصيات التي قمنا بتطويرها من خلال تحليل تبديل التدفقات على الطريق السريع.

1) لا تقم بتكبير الطرق دون الحاجة.
- نعم. يتم توزيع حركة المرور على العديد من الطرق (مقارنة مع Linear City).

2) تجنب خلق الظروف عندما تحتاج إلى إجراء عدد كبير من المنعطفات في رحلة واحدة.
- نعم. على الأرجح سيتم تنفيذ أي رحلة على طول طريق لا يتطلب سوى منعطف واحد في شوارع المدينة.

3) تجنب المواقف عند السفر على جزء واحد من الطريق ، والتي لا تحتوي طرقها سوى على جزء صغير من المسار المشترك.
- هنا ، ربما ، هناك شيء للعمل عليه. على الرغم من الحد الأدنى لعدد المنعطفات في الرحلة الواحدة ، فإن مسارها كجزء من تدفق الطرق السريعة الرئيسية يمر عبر عدد كبير من نقاط التبديل (O ( n )) ، حيث يضيع وقت ثمين.

تحفز الملاحظة الأخيرة على التحقق من السؤال التالي: "ما هي القيمة الدنيا لمتوسط ​​عدد نقاط التبديل التي يجب أن تمر الرحلة عبر شبكة طرق تربط الكتل n ؟"

بطبيعة الحال ، تكون مهمة البحث عن مثل هذه الشبكة منطقية فقط بشرط أن يكون عدد التدفقات المدمجة أو المشتركة بواسطة أي عقدة تبديل محددًا من البداية بقيمة محددة ثابتة. خلاف ذلك ، يمكنك دائمًا تقديم شبكة طرق تحتوي على نقاط عنوان n وتقاطع ضخم واحد.


(المؤلف غير معروف)

من الأسهل بكثير استكشاف المشكلة الحقيقية إذا كان من الممكن في السابق الكشف عن جزء على الأقل من الأنماط باستخدام بعض النماذج البسيطة ، حتى وإن لم تكن على الإطلاق ، نماذج واقعية. باتباع هذا المنطق ، سوف ننسى مؤقتًا القيود الهندسية لبناء طريق للمسافرين للسفر مسافات طويلة ، مع تركيز كل اهتمامهم على كيفية حل الشبكات المجردة لمشكلة المعالجة الموازية. فيما يتعلق بالعقد التبديل ، سنفترض الآن أن كل منهما إما يقسم الدفق إلى جزأين (عقدة القسمة) ، أو يجمع بين تدفقين في واحد.


التين. 9

عنوان شجرة
نفترض أن لدينا بدءا عنوان النقطة التي يبدأ كل شيء، من دون استثناء، والسفر، وحتى ن الانتهاء عنوان النقاط التي ينتهي (الشكل 9) على قدم المساواة مع احتمال.

يجب إنشاء شبكة نقل تتيح السفر عبر أقل عدد ممكن من نقاط التبديل.

يتمثل الحل الواضح (للمبرمجين) ، الذي يطرح نفسه هنا ، في استخدام شجرة ثنائية متوازنة ، وفي نفس الوقت تحتاج إلى وضع نقطة بداية واحدة في أعلى الشجرة ، ووضع نقاط النهاية n المتبقية واحدة في كل ورقة من أوراقها (الشكل 10). ستتم تسمية الشبكة التي تم إنشاؤها بالطريقة الموصوفة باسم شجرة العنوان المباشرة.


التين. 10

عند تغيير اتجاهات جميع التدفقات إلى الاتجاه المعاكس في شجرة العنوان المباشرة ، نحصل على شجرة العنوان العكسي ، والغرض منها هو ربط نقاط البداية n بإنهاء واحد.

في تلك الحالات حيث ن هو قوة اثنين، أي طريق داخل شجرة عنوان يمتد بالضبط تسجيل ₂ ن التحول العقد، والتي بلا شك (مقارب) هو أصغر من نفس المعلمة من الشبكة مع منقوشة (O (√ ن ))، أو الخطية ( يا ( ن )) طوبولوجيا.

أبسط نوعين من الشبكات اللوغاريتمية
باستخدام الشبكات "الشبيهة بالشجرة" كعناصر بناء ، ليس من الصعب تعميم الحل السابق للحالة عندما يكون هناك أكثر من نقطة بداية واحدة ، ولكن -ك . هناك طريقتان سهلتان للقيام بذلك.

تتمثل الطريقة الأولى في استخدام شجرة العنوان العكسي لجمع مسارات جميع الرحلات أولاً في دفق واحد مشترك ، ثم باستخدام شجرة العنوان المباشرة ، قسّم هذا الدفق إلى تدفقات فرعية ، تم توجيه كل منها إلى وجهتها (الشبكة في الأعلى في الشكل 11) ).


التين. 11

إذا كانت k و n هما قوتان ، في النهاية ، في أي مسار ، يمر أي مسار عبر سجل التبديل ₂ k + log ₂ n . الشبكات التي تم إنشاؤها وفقًا للخوارزمية الموصوفة للتو ، نوافق على استدعاء لوغاريتم (أحادي الاتجاه) مع دمج أولي .

يمكن الحصول على الطريقة الثانية لحل نفس المشكلة من خلال عكس ترتيب عمليات الدمج والفصل في الحل الأول. يتم تطبيقه على النحو التالي: لكل نقطة بداية ، قم بإنشاء مجموعة فريدة من التكرارات التخيلية لجميع نقاط عنوان النهاية ، ثم قم بتوصيلها بهذه التكرارات (وليس على الإطلاق وهمية) باستخدام شجرة عنوان مباشرة.

لاستكمال بناء الشبكة ، يبقى فقط الاتصال الآن بكل نقطة نهاية بشجرة العنوان العكسي مع التكرارات التخيلية k (الشبكة من الأسفل في الشكل 11).

عندما يكون كل من n و k قوة اثنين ، فإن عدد نقاط التبديل على مسار أي مسار داخل الشبكة المبنية حديثًا سوف يكون مساوياً مرة أخرى لتسجيل ₂ ك + سجل ₂ ن . نحن نوافق على استدعاء شبكات من هذا النوع (أحادي الاتجاه) لوغاريتمية مع فصل أولي .

تحويل الشبكات أحادية الاتجاه إلى متماثل
بشكل عام ، الشبكات أحادية الاتجاهسنتصل بأية شبكة إذا كانت نقاط العناوين المتصلة بها مقسمة إلى بداية ونهاية. بشكل افتراضي ، بالنسبة للشبكات أحادية الاتجاه ، سيتم افتراض أنه يوفر مسارًا واحدًا على الأقل للحركة المحتملة من أي نقطة بداية إلى أي نقطة انتهاء.

بالإضافة إلى رحلة تدوم مدى الحياة ، من الصعب ذكر أمثلة على الحالات التي تكون فيها بعض نقاط العناوين بمثابة طرق بداية فقط ، والبعض الآخر - يمكن أن يكون نهايتها فقط. سنجعل تفكيرنا أقرب إلى الواقع إذا قمنا أيضًا بتضمين شبكات ترتبط فيها أي من نقطتي العناوين بطرق في كلا الاتجاهين. نحن نوافق على استدعاء هذه الشبكات متماثل .

في الواقع ، لا توجد فجوة أيديولوجية بين الشبكات أحادية الاتجاه والشبكات المتماثلة: يمكن أيضًا استخدام كل شبكة متناظرة كشبكة أحادية الاتجاه ، ويمكن تحويل كل شبكة أحادية الاتجاه ، تربط في البداية عدد متساوٍ من نقاط البداية والنهاية ، بشبكة متماثلة (الشكل 12).


التين. 12

يوضح الشكلان 13 أ و 13 ب الأشكال "المتماثلة" للشبكة اللوغاريتمية مع الدمج الأولي والشبكة اللوغاريتمية مع الفصل الأولي. تُظهر الأمثلة الخاصة بهم الإمكانية الأساسية لربط الكتل n بهذا النوع من الشبكات ، والذي سيكون فيه عدد نقاط التبديل التي تمت زيارتها خلال أي رحلة متناسبة مع لوغاريتم عدد الكتل في المدينة.


التين. 13 أ


التين. 13 ب

تقدير أسفل دقيق
حتى الآن ، تم بالفعل تجميع مجموعة غنية من الشبكات بوظائف مختلفة بناءً على متوسط ​​عدد العقد التي تمت زيارتها أثناء الرحلة على عدد نقاط العناوين في المدينة. ومع ذلك ، ما زلنا لا نعرف مدى صغر هذا العدد من حيث المبدأ لعدد معين من الأوساط. يمكن الحصول على الحد الأدنى لقيمته باستخدام نهج المعلومات.

في الواقع ، حتى لو كانت شبكة طرق معينة تربط نقاط العنوان n ، واحتياجات الهجرة للسكان ، فإن أي رحلة ، بصرف النظر عن المكان الذي بدأت فيه ، لديها فرصة متساوية لإنهاء أي مكان في المدينة.

لحل المشكلة المقصودة ، سنقوم بإنشاء رسالة إعلامية إضافية ، باتباع هذه الوصفة: لفترة طويلة من الوقت ، سنجمع سجلات جميع الرحلات التي لها نقطة ثابتة في البداية ، وبترتيب عشوائي ، سنقوم بتدوين العناوين التي انتهت إليها هذه الرحلات. سوف تكون الرسالة الناتجة تسلسل عشوائي تتكون من اسم ن عنونة نقطة من المدينة.

تتمثل إحدى طرق إرسال هذه الرسالة إلى المريخ في تشفير جميع الأسماء أولاً بكلمات ثنائية بنفس الطول ، وبالتالي تحويل الرسالة الأصلية إلى تسلسل من الأصفار والأخرى ، ثم إرسال التسلسل الناتج عبر قناة اتصال رقمية. منذ لترميز تمييز مجموعة نإذا كانت الأسماء الثنائية لسجل الطول ₂ n مطلوبة ، فسيكون طول الرسالة الرقمية:

(عدد السجلات) × عدد الأحرف ₂ ن .

الشيء الأكثر إثارة للاهتمام هو أنه وفقًا لنظرية المعلومات ، بغض النظر عن خوارزمية الترميز المستخدمة ، من المستحيل ببساطة إرسال الرسالة نفسها في المتوسط ​​بعدد أقل من الأحرف الثنائية.

يمكن أن يكون البديل لنقل الأسماء المشفرة لنقاط النهاية مباشرة هو الطريقة التي يشار إليها في كل رحلة في أي من الاتجاهات المحتملة تحولت في طريقها عند مفترق الطرق التالي في الطريق. وفقًا لافتراضاتنا ، يمكن أن تكون جميع الشوكات الموجودة في الشبكة مزدوجة فقط ، لذلك ، للإشارة إلى الاتجاه في كل حالة ، يلزم 1 بت بالضبط. أي شخص لديه خريطة للمدينة ويعرف نقطة البداية ، فإن سلسلة البت المعتمدة ستكون كافية لتتبع كل مسار واستعادة التسلسل الأصلي لوجهاتهم. إذا كان متوسط عدد الشوك (وحدات التقسيم)، زار خلال الرحلة نفسها فضلا العاشر ، ثم طول طول الرسالة ثنائية في طريقة الترميز الجديد هو: (عدد الإدخالات) × س.

كما قيل سابقًا ، لا يمكن أن تكون طريقة الترميز الجديدة أكثر كفاءة من طريقة نقل العنوان الثنائي المباشر ، وبالتالي: (عدد السجلات) × × ≥ (عدد السجلات) × السجل ₂ ن ، ومن ثم:

× ≥ سجل ₂ ن .

على الرغم من أنه تم في البداية استنباط عدم المساواة الأخير لمجموعة من الرحلات التي كانت لها نقطة انطلاق ثابتة مشتركة ، فقد بدا أن مظهرها مستقل عن الاختيار المحدد لهذه النقطة ، لذلك لدينا الحق في تمديد النتيجة على الفور لجميع الرحلات في المدينة ، وبالتالي الحصول على الجزء الأول من التقدير المطلوب:

P1 ) شريطة أن يكون لكل رحلة جديدة فرصة متساوية في النهاية في أي من nنقاط عناوين المدينة ، لا يمكن أن يكون متوسط ​​عدد العقد المقسمة لكل مسار أقل من سجل ₂ n .

عند إعادة عقارب الساعة إلى الوراء ، ستجعل كل نقطة نهاية سفر هي نقطة البداية ، وكل عقدة من أقسام الشبكة الثنائية تعقد عقدة دمج ثنائية. تسمح لك هذه الخدعة الصغيرة بالحصول تلقائيًا على الجزء الثاني المفقود من التقدير من P1:

P2 ) بشرط أن يكون لكل رحلة مكتملة فرص متساوية للبدء في أي من نقاط العنوان n في المدينة ، لا يمكن أن يكون متوسط ​​عدد عقد الدمج لكل مسار أقل من log ₂ ن .

إذا استذكرنا وجود شبكة لوغاريتمية مع دمج أولي وشبكة لوغاريتمية مع فصل أولي ، فسنحصل على الفور على مثالين للشبكات المثلى من حيث عدد نقاط التبديل ، التي يتم زيارتها داخلها خلال المتوسط ​​خلال رحلة واحدة. دعونا نرى ما إذا كانت هذه الجودة تساعدهم على تقليل شدة خسائر التحويل التي تم إنشاؤها.

تبديل التكاليف في الشبكات اللوغاريتمية

إذا قارنا الشبكات مع الدمج الأولي والفصل الأولي ، فستبدو الشبكة الأولى أكثر جاذبية نظرًا لبساطتها. لسوء الحظ ، تحتوي هذه البساطة أيضًا على جانب انعكاس للعملة: الجمع بين جميع المسارات في تيار واحد يتعارض مع التوصية i1 ، وبالتالي يصبح سببًا محتملاً لفقدان وقت كبير. يبدو أن الشبكة ذات الفصل الأولي تتبع التوصيات i1 - i3 ، ومع ذلك ، وفقًا للشكل 13 ب ، فإنها تميل إلى زيادة سريعة في عدد حواف الطرق وعقد التبديل المستخدمة. الجودة الأخيرة يمكن أن تجعل الشبكات من هذا النوع مكلفة للغاية للاستخدام العملي.

سنقوم بتحليل هذه القضايا بمزيد من التفصيل. بادئ ذي بدء ، نحن نوافق على أن المدينة تخضع لنموذج الترحيل الخاص بالوصول الموحد ، كما أن تدفق السفر الناتج عن أي من نقاط عناوينها لديه سعة وحدة.

الفقد في شبكة مع دمج أولي
في الشكل 14 ، يمكنك رؤية رسم بياني للتدفقات الناشئة عن الترتيبات المشار إليها داخل الشبكة مع الدمج الأولي.


التين. 14

بدا لي من المريح تصوير الشبكة نفسها في شكلها أحادي الاتجاه ، مما يعني أن كل نقطة بداية ونهاية ، غير محددة بالرقم نفسه في الشكل ، تعني في الواقع نقطة العنوان نفسها في المدينة.

استنادًا إلى الرسم التخطيطي ، نحسب كثافة تكاليف التحويل الناتجة في الشبكة. لنبدأ بالنصف الأيسر ، حيث من خلال شجرة العنوان العكسي ، يتم جمع جميع المسارات في قطار واحد. تمثل كل عقدة تبديل في هذا الجزء من الشبكة المكان الذي تندمج فيه طريقتان سريعتان أحادي الاتجاه في واحدة (الشكل 15).


التين. 15

إذا تم تحميل كل من الطرق في البداية بكفاءة ، فبعد توحيدها ، لن تكون هناك حاجة لتقليل عدد الممرات ، ونتيجة لذلك ، يجب ألا يكون هناك أي انخفاض في تكاليف التبديل.

لنفترض أن تدفق طاقة الوحدة يكفي بالفعل لملء الطريق بفعالية في حارة على الأقل. في هذه الحالة ، وصلنا إلى نتيجة غير متوقعة إلى حد ما: اتحاد السيارات يتدفق داخل شبكة اللوغاريتمية مع الدمج الأولي يحدث تمامًا "مجانًا" ، دون التسبب في أي خسائر مؤقتة.

حساب التكاليف التي تنشأ في النصف الأيمن الصحيح ليس أكثر صعوبة. هذا الجزء من الشبكة عبارة عن شجرة عناوين مباشرة ، كل عقدة منها عبارة عن شوكة متناظرة في الطرق التي درسناها بالفعل. عند انقطاع التيار الكهربائي من تدفق الحادث ص كثافة الناشئة في فقدان شوكة يساوي ( α / 2 ν ) ⋅ ص ² /2. قوة التيار الذي يدخل شوكة الجذر هي: n ، وبالتالي ، فإن شدة الخسائر في عقدة الجذر هي: ( α / 2 ν ) ⋅ n ²/ 2. في كل جيل جديد من شجرة العنوان ، يتضاعف عدد الشوكات ، وتقل قوة التيار الذي يعمل عليها إلى النصف. نتيجة لذلك ، ستتخذ صيغة الخسارة داخل الشجرة بأكملها النموذج:

I _{t_div1} = ( α / 2 ν ) ⋅ (1/2) ⋅ [ n ² + 2 ( n / 2) ² + 4 ( n / 4) ² + ... + ( n / 2) ⋅ 2 ² ] =

( α / 2 ν ) ⋅ ( n / 2) ² [1 + 1/2 + 1/4 + ... + 2 /n ] ≈ ( α / 2 ν ) ⋅ n ²

نظرًا لأن قوة تدفق السفر الناتجة بشكل مشترك من قبل جميع نقاط العنوان هي n ، فإن متوسط ​​تكلفة الوقت للرحلة الواحدة ( α / 2 ν ) ⋅ n ، وبالتالي يُظهر خطيًا الاعتماد على حجم المدينة.

عندما يتعلق الأمر بالشبكات المجردة ، من الصعب إعطاء أي تقدير ذي معنى لمنطقة الطرق التي يستخدمونها. كمقياس بديل للتعقيد الهيكلي ، يمكن حساب إجمالي الطاقة لجميع التدفقات الجانبية. كما هو مخطط له ، يجب أن تعكس القيمة الناتجة تكلفة المورد لإقامة جميع التبادلات التي تتطلبها الشبكة. لا أستطيع أن أقول أنه من الناحية العملية ، سيكون لهذه الطريقة دائمًا تفسير جيد ، لكن ربما سأكون قادرًا على الحصول على فكرة تقريبية عن مقدار العمل في المستقبل.

داخل الشبكة اللوغاريتمية مع الدمج الأولي ، تكون التدفقات الجانبية موجودة فقط في شجرة العنوان المباشرة ، وتكون قوتها الإجمالية لكل جيل من العقد متماثلة: n / 2. مجموع شجرة سجل ₂ نأجيال من العقد ، لذلك طريقة جديدة لتقييم التعقيد يعطي تقدير التعقيد: O ( ن سجل ₂ ن ).

شبكة لوغاريتمية مع دمج أولي
عدد نقاط عناوين وحدة الطاقة ........................................ ............ n
متوسط ​​وقت السفر
المفقود بسبب تبديل التكاليف:
السلوك المقارب ........................ .................................................. ............................ يا ( ن )
القيمة الدقيقة ................ .................................................. ........................... ( α / 2 ν ) ⋅ n
عدد نقاط التبديل ............................................... .............................. O ( n )
عدد نقاط التبديل مع مراعاة قوة التدفقات الجانبية .... ............... O ( n log ₂ n )

الخسائر في الشبكة مع الفصل الأولي
دعنا ننتقل الآن إلى تحليل الشبكة اللوغاريتمية مع الفصل الأولي ، مرة أخرى على افتراض أن الشبكة تستخدم لتوصيل نقاط عناوين طاقة الوحدة في مدينة "الوصول الموحد".

يوضح الشكل 16 جزءًا منه ، يتكون من نقطة عنوان واحدة جنبًا إلى جنب مع أشجار العنوان المباشرة والعكسية المجاورة لهذه النقطة.


التين. 16

أولاً ، نقدر شدة خسائر التحويل الناتجة عن الجزء.
يمكن العثور على التكاليف المتكبدة في تقسيم التدفقات عن طريق استبدال الصيغة I _{t_div1} = ( α / 2 ν ) ⋅ n ² ، المشتقة من شجرة العنوان المباشرة في المثال السابق ، بدلاً من n - واحد. في الواقع ، فإن أشجار العنوان المباشر في الشكلين 16 و 14 لها نفس العمق وتتدفق في نفس سمكها ( _{تقريبًا).التشابه يعني القدرة على الحصول على مجموعة من القيم بضرب القيم من مجموعة أخرى برقم ثابت ، لتوضيح ، يمكن استخدام التشابه بين المثلثات على جوانبها} ). ونظرا للعلاقة من الدرجة الثانية بين حجم التحول التكاليف الناشئة في مفترق منفصل والطاقة المزودة بها تيار تخفيض وقت واحد من كل التيارات في ن مرات والحد من الخسائر في شجرة كاملة ل ن ² مرات، ولكن بدلا من الماضي ( α / 2 ν ) ⋅ ن ² نحن نحصل على قيمة تساوي:

I _{t_div2} = ( α / 2 ν ).

نحن الآن حساب قيمة التكاليف في النصف الأيسر من الجزء.
نظرًا لصغر التدفقات المدمجة للطريق داخل شجرة العنوان العكسي ، فلن يكون من المعقول هذه المرة بناء أوسع من مسارين. لم تعد عمليات الاندماج في ظل هذه الظروف خالية من التكلفة: على عكس المثال السابق ، توجد نقاط ضيقة على الطريق السريع (الشكل 17) ، حيث ستكون تكاليف التبديل ضرورية.


التين. 17

على افتراض أن السائق على دراية بالضيق القادم في وقت مبكر ، يمكننا أن نفترض أن عملية نقل السيارات من طريق مسدود بطيئة ، حيث تمتد مئات الأمتار على طول الطريق السريع. في هذه الحالة ، لدينا الحق في اللجوء إلى الخدعة التي استخدمناها سابقًا لحساب الخسائر في الشوكة المتناظرة - لتقسيم إجمالي تدفق الترحيل q إلى العديد من الأجزاء الصغيرة q _i ، ثم تفسير كل واحد منهم كتدفق جانبي من جانب الطريق المنحدر. يتم حساب الخسائر الناتجة عن كل من هذه العناصر الفرعية بواسطة المعادلة:
I _i = ( α / 2 ν ) ⋅ p q _i ⋅ (1 + 1 / s) ، ومع ذلك ، هناك نوعان من التفاصيل الدقيقة.

أولها أن السيارات لن تهاجر أبعد من الصف التالي.
وفي الواقع: يجب أن يكون للتدفقات في الممرين المركزيين ، بسبب التناظر الواضح ، دائمًا نفس الكثافة تقريبًا ، لذلك لن يكون لدى السائقين سبب وجيه لعبور الخط الأوسط. من الملاحظة التي تمت ، يترتب على ذلك في صيغة الخسائر الناجمة عن التدفق الجانبي الجزئي ، s تساوي 1.

بينما تغادر الآلات الممرات القصوى ، وتعيد ترتيبها في صفين مركزيين ، فإن طاقة التدفق داخل النطاقات المركزية تنمو تدريجياً ، وتتغير في كل حالة من P / 2 إلى P . وبالتالي ، فإن الدقة الثانية هي اعتماد كبير من صمن عدد substream i ، الذي يفرض علينا عدم الكتابة:

I _i = ( α / 2 ν ) ⋅ p q _i ⋅ (1 + 1 / s ) ،
لكن:
I _i = ( α / 2 ν ) p ( i ) ⋅ q _ط ⋅ (1 + 1 / ق ).
في الحالة التي يكون فيها العديد من الأجزاء الصغيرة التي تم تقسيم تدفق الترحيل فيها متساوية في الحجم ، يتم التعبير عن الاعتماد p ( i ) بواسطة رسم بياني خطي (الشكل 18)


التين. 18

لحساب شدة إجمالي الخسائر ، يجب على المرء إما اللجوء إلى التكامل ، أو (هذا يجعل من الممكن إجراء شكل بسيط بشكل خاص لوظيفة قابلة للتكامل) حيث أن p ( i ) تأخذ القيمة المتوسطة على الرسم البياني مساوية 3 P / 4. نظرًا لأن إجمالي تدفق الترحيل من جانب كل قطاع متطرف هو P / 2 ، فإن شدة الخسائر عند دمج منفصل ستكون:

I _دمج = 2 ⋅ ( α / 2 ν ) ⋅ (3 P / 4) ⋅ ( P / 2)

= ( α / 2 ν ) 3 ف ²/ 4.

العثور على فقدان المؤقتة التي تم إنشاؤها في المسار على عنوان شجرة عكس ينطبق على صيغة I _الدمج على كل عقدة لها:

أنا _{t_merge} = (3/4) ⋅ ( α / 2 ν ) [1 ⋅ (1/2) ² + 2 ⋅ (1/4) ² + 4 ⋅ (1/8) ² + ... + ( n / 2) ⋅ (1 / n ) ² ] ≈

≈ (3/4) ⋅ ( α / 2 ν ) [1/4 + 1/8 + 1/16 + ...] =

= (3/8)⋅ ( α / 2 ν ) [1/2 + 1/4 + 1/8 + ...] =

= (3/8) ⋅ ( α / 2 ν ).

ستكون التكاليف الإجمالية المتكبدة داخل الجزء الناتج عن دمج وفصل التدفقات هي:

I _{t_merge} + I _{t_div2} = ( α / 2 ν ) [1 + 3/8] = 11/8 ( α / 2 ν ).

شبكة لوغاريتمي مع الفصل التمهيدي يحتوي فقط ن تلك الشظايا، وبالضبط نيتم إنشاء تدفقات الوحدة من خلال نقاط العناوين الخاصة بها ، وبالتالي فإن القيمة التي وجدناها تواً تساوي خسائر التحويل التي تحدث في المتوسط ​​لكل رحلة.

في الواقع ، من المهم بالنسبة لنا ليس حتى عددًا معينًا ، وهو ما يساوي تكاليف التحويل المحددة ، ولكن تظل هذه التكاليف ثابتة مع زيادة n . يجعل الظرف الأخير شبكة اللوغاريتمية مع الفصل الأولي غير المقارب الأكثر اقتصادا فيما يتعلق بتبديل الخسائر ، بين جميع أنواع الشبكات التي درسناها في وقت سابق.

لسوء الحظ ، لا تكلف القيادة "مجانًا". على الرغم من الحجم الصغير التلاشي للعدد الهائل من التدفقات ، فإن كل شجرة عنوان مدرجة في الشبكة تحتوي على حوالي 2 نضلعين على الطريق مؤلف من حارات وعقد تبديل كاملة الحجم تقريبًا n . هناك 2 n شجرة في الشبكة ، مما يعني O ( n ² ) الحواف والعقد ، مما يجعلها ليست فقط الأكثر اقتصادا في الوقت المناسب ، ولكن أيضا أغلى شبكة لبناء ، من بين جميع الأمثلة التي تم النظر فيها.

بالنسبة لمجموع التدفقات الجانبية ، فإن قيمتها ، كما هو سهل الحساب ، تنمو بسرعة O ( n log2 n ) وفي هذه الحالة لا تحمل معنى كبير.

شبكة لوغاريتمية مع فصل أولي
عدد نقاط عناوين وحدة الطاقة ........................................ ............ ن
متوسط ​​وقت السفر ،
فقد بسبب تكاليف التبديل:
مقاربات .......................................... .................................................. .......... (1)
القيمة الدقيقة .................................. .................................................. ........... 11/8 ( α / 2 ν ).
عدد نقاط التبديل ............................................... .............................. O ( ن ² )
عدد نقاط التبديل مع مراعاة قوة التدفقات الجانبية ... ................ O ( n log ₂ n )

لوغاريتمي شبكة متوازنة

تتسبب خسائر التحويل الصغيرة بشكل استثنائي ، مع إمكانية استخدام شبكة اللوغاريتمية مع الفصل الأولي ، ولكن في نفس الوقت تستهلك الكثير من الموارد في بنائها ، في الرغبة في إيجاد طريقة لتغيير تصميمها بحيث يتم تقليل استهلاك الموارد بشكل كبير ، ولا تزيد تكاليف التبديل بشكل كبير.

من الواضح أن السبب الرئيسي وراء عدد كبير للغاية من الطرق في الشبكة هو الكفاءة المنخفضة للغاية لاستخدامها. ويعتبر هذا الأخير بشكل واضح في الشكل 19، مما يدل على الرسم البياني المفصل في شجرة عنوان مباشرة المجاورة لل ط نقطة عنوان -th.


التين. 19

في الرسم التخطيطي ، يشير الرقم الموجود أعلى حافة الشجرة إلى قوة تيار السفر الذي يمر عبر الحافة ، والفاصل الزمني أدناه هو مجموعة نقاط العناوين التي سيتم توزيع هذا الدفق عليها في النهاية. من المعتقد أن جميع الحواف الموجودة على الرسم البياني هي طرق سريعة مؤلفة من حاراتين ، ويشار إلى عدد الحواف في كل جيل من الشجرة في أسفل الشكل.

عند الفحص الدقيق ، قد تلاحظ أن القاعدة التي يتم بموجبها تقسيم تدفق السفر في عقدة معينة يتم تحديدها فقط من خلال موقع هذه العقدة داخل شجرة العنوان ولا تعتمد على عدد نقطة العنوان التي أدت إلى هذه الرحلات.

إذا كانت هناك عدة تدفقات موجهة إلى نفس المجموعة من النقاط ، وكل منها غير قوي بما يكفي لملء المسار المخصص له ، فلماذا لا تجمعها معًا على طريق سريع واحد. في الواقع ، هذه الفكرة البسيطة بشكل أساسي تجعل من الممكن بناء شبكة تجريدية جيدة ، وتوليد خسائر تحويل صغيرة نسبيا ، واقتصادية في عدد الطرق المستخدمة.

وبالعودة إلى شجرة عنوان ط إيث النقطة، ونحن نرى أن ينقسم القادمة في العقدة الجذرية للتيار في الشركات التابعة لها اثنين من تدفق قدرة 1/2 لكل منهما. يتكون قطار stepson الأول من رحلات موجهة إلى نقاط من الفاصل الزمني [1؛ n / 2] ، الثانية - رحلات موجهة إلى نقاط من الفاصل الزمني [( n / 2) + 1 ؛ن ].
باتباع الفكرة الموضحة أعلاه ، نجمع بين نفس النوع من تدفقات الربيب في كل نقطة فردية ونقطة العنوان التالية برقم زوجي يتبعها بالترتيب. تسمح مثل هذه التقنية لكل زوج من النقاط المختارة أن يكون له بدلاً من أربعة تدفقات بقوة 1/2 تدفق فقط من حجم الوحدة (الشكل 20). سنقدم الاختصار BN ₂ [i؛ أنا +1.


التين. 20

إذا لم يتم دمج تدفقات ربيب ، ولكن كان لا يزال داخل شجرة العنوان ، ثم في الجيل التالي من العقد التي تم الوصول إليها ، سيتم تقسيم كل منها مرة أخرى إلى قسمين ، متساوين في القوة وفي حجم مجموعات من تلك النقاط التي مكونات رحلاتهم.

لماذا كسر التقليد المعمول به ، لأنه بعد التوحيد لا يزال لدينا نفس مجموعة أنواع الدفق كما كان من قبل ، ولكن مع عدد أقل من ممثلي كل نوع فقط؟ - ينطبق على كل من تدفقات الخرج BN ₂ [i ؛ i +1] بالضبط نفس قاعدة الفصل التي تنطبق على دفق من نوعه داخل شجرة العنوان.

لا يوجد سبب لعدم تكرار البناء المنطقي الموصوف أعلاه للجمع بين التدفقات ذاتها بشكل حثيث. يوضح الشكل 21 مخططًا يجمع بين شظيتين من
BN ₂ في جزء واحد من BN ₄ ، ويبين الشكل 22 كيف تبدو الخوارزمية في الحالة العامة.


التين. 21


التين. 22

في النهاية ، سيتم الانتهاء من عملية توسيع التجزئة وتؤدي بنا إلى العنصر الوحيد BN _n [1 ؛ ن ] ، سوف نسميها الشبكة المتوازنة من النوع اللوغاريتمي (الشكل 23).


التين. 23

دعنا نتفحص هذه الشبكة لمعرفة مدى تعقيد وحجم خسائر التحويل الناتجة.
استنادًا إلى الطبيعة الاستقرائية لإجراء إنشاء الشبكة المتوازنة ، يمكن وصف عدد نقاط التبديل المضمنة في هيكلها بواسطة معادلة الإرجاع:

العقد (BN _k ) = العقدتان (BN _{k / 2} ) + 2 k ،

مع شرط الحدود:

العقد (BN ₁ ) = 0.

الحل لهذا النظام من المعادلات هو وظيفة:

العقد (BN _n ) = 2 n log ₂ n .

نظرًا لأن إنشاء BN _n يتطلب خطوات من السجل ₂ n من الاستقراء ، فكل رحلة سوف تمر عبر العقد الفاصلة log ₂ n ونفس عدد العقد المدمجة ، وتناوبها في مسيرها (الشكل 24).


التين. 24

الخسائر الناتجة داخل كل عقدة فصل:
( α / 2 ν ) ⋅ (1) 2/2 .

الخسائر الناتجة داخل كل عقدة دمج:
( α / 2 ν ) ⋅ 3 ⋅ (1/2) 2/4 = 3/16 ( α / 2 ν ).

بالنظر إلى أن كلاهما في الشبكة المتوازنة هما n log ₂ n ، نحصل على القيمة الدقيقة لخسائر التحويل الكلية:
11/16 ( α / 2 ν ) n log ₂ n ،

أن لكل رحلة واحدة:
11/16 ( α / 2 ν ) log ₂ n

لوغاريتمي شبكة متوازنة
عدد نقاط عناوين وحدة الطاقة ............................................. ....... ن
متوسط ​​وقت السفر
فقد بسبب تكاليف التبديل:
مقاربين ................................................. .................................................. ... O (سجل ₂ ن )
القيمة الدقيقة ............................................ ........................................... 11/16 ( α / 2 ν ) log ₂ n
عدد نقاط التبديل ............................................... .................................. (سجل n ₂ )
عدد نقاط التبديل ، مع مراعاة قوة الجانب يتدفق ................... O ( n log ₂ n )

تسمح الأرقام الموجودة أعلاه أن تُعتبر الشبكة المتوازنة حلاً وسطًا جيدًا بين مقدار الوقت الضائع المعروض والتعقيد الهيكلي العام. إن استخدامه كشبكة طرق لمدينة حقيقية أمر ممكن من حيث المبدأ ، لكنه بالكاد ممكن من الناحية الاقتصادية. يبدو لي أن المجال الذي يمكن أن يكون فيه استخدام الشبكة المتوازنة ذا فائدة كبيرة هو أنظمة المعلومات واسعة النطاق ذات المتطلبات الصارمة لمدى تأخر الإشارة ، مثل الاتصالات الخلوية والإنترنت والحوسبة الموزعة وأجهزة الكمبيوتر متعددة المعالجات. بالنسبة لنا ، القيمة الرئيسية للشبكة المتوازنة هي الطريقة التي بنيت بها. بعد ذلك بقليل ، باستخدام تعديل لهذه الطريقة ، سنكون قادرين على تحسين شبكات المراكز الخطية والخلوية التي تعتبر مهمة حقًا من الناحية العملية.

لماذا المدن التاريخية محكوم عليها بالاختناقات المرورية؟

قد يبدو بياني غير متوقع ، ولكن الإجابة عن السبب في أن المدن النامية بشكل طبيعي ، والتي تعاني عادة من الاختناقات المرورية ، قد وجدناها بالفعل في الفقرات السابقة. إذن ما الذي تتكون منه؟

والحقيقة هي أن العديد من المدن التاريخية التي نجت من عصر الحصون في العصور الوسطى (على سبيل المثال ، كل عواصم العالم القديم تقريبًا) ورثت منذ ذلك الوقت البنية الشعاعية للشوارع. لسوء الحظ (بالنسبة لسكانها المعاصرين) ، فإن شبكة الطرق ذات البنية المماثلة لا تتطور بشكل جيد: الموقع الكثيف للطرق الشعاعية بالقرب من المركز أصبح نادرًا جدًا على الأطراف. ونتيجة لذلك ، في عملية النمو السكاني ، أصبحت الشوارع التي كانت موجودة في البداية على هامش الطرق القليلة المؤدية إلى القلعة أكبر وأصبحت الشوارع التي ظهرت على الهامش قصيرة ولم تكتسب أهمية عبور كافية للنمو في العرض. نتيجة لذلك ، تشير شبكة الطرق التي نراها الآن في المدن التاريخية الكبيرة الآن في أغلب الأحيان إلى أنظمة النقل من النوع الشرياني ، وفي مصطلحاتنا - إلى نوع الشبكات اللوغاريتمية مع الدمج الأولي (غير المكتمل).


(طرق موسكو ، الصورة: ستيبانوف سلافا)

إذا تحدثنا عن طول المسار الذي يجب أن يقوده السائق على الطرق ، فإن تنفيذ هذا النوع من الشبكات ليس سيئًا: المسافة التي يتم قطعها غالبًا ما تختلف قليلاً عن مسافة الخط الثابت ، وقيمتها المتوسطة في المدينة ، كما يجب أن تكون لأنظمة النقل "اللائقة" ، ينمو بمعدل O (√ ن ). المشكلة برمتها هي أنه مع توسيع المدينة في الشبكة اللوغاريتمية مع دمج أولي ، تزداد تكاليف التبديل الناتجة عن ذلك بسرعة كبيرة: يعتمد مقدار الوقت الذي تم تمديد الرحلة فيه في المتوسط ​​بسببها على عدد الأشخاص الذين يعيشون في المدينة كـ O ( n) ). من الواضح أنه ابتداءً من n ، ستنتصر هذه المرة على الوقت الواضح للتغلب على المسافة ، بمعنى آخر ، ستظهر اختناقات مرورية في المدينة.

لا شك أن إعادة تنظيم نظام النقل في المدن التاريخية الكبيرة مهمة يمكن حلها. ومع ذلك ، من المهم أن نفهم هنا أن بناء شرايين نقل كبيرة أو اثنين أو خمسة ، وإن كان يحسن الوضع في المدينة بشكل طفيف ، إلا أن السبب الأساسي لاختناقات المرور لن يلغي. على ما يبدو ، فإن الطريقة الوحيدة للتغلب على أوجه القصور في الشبكة اللوغاريتمية مع الدمج الأولي هي استخدام شبكة أخرى. قد يكون المرشح الجيد هنا شبكة ذات طبولوجيا خلوية ، والتي يتزامن معها معدل نمو الوقت لتغطية المسافة ، على الأقل ، مع معدل نمو خسائر التحويل.


(ليلة برلين ، الصورة: فنسنت لافوريت)

ربما هذا هو السبب في أن برلين الحديثة ، على الرغم من أن لديها طرق سريعة شريانية كبيرة ، تتميز بالفعل بهيكل شبكي واضح للعيان.

هناك العديد من الحلول المثيرة للاهتمام في العالم حول كيفية جعل سكان المدن التاريخية أكثر قدرة على الحركة ، ولكن على الأرجح ينبغي منح الجائزة الرئيسية في الكفاح من أجل الوصول إلى وسائل النقل لمهندسي برشلونة.


(برشلونة شبكة الطرق المحدثة ، الصورة: فنسنت لافوريت)

نظرة تفصيلية على الشبكات الخطية والمدينة الخلوية

بعد العثور على أساليب التحليل وتحسينها على الشبكات المجردة ، فقد حان الوقت لتطبيقها على الحالات الأكثر واقعية للمدن ذات الهيكلية الخطية والخلية. سنحاول في هذا القسم تحليل تفاصيل روابط النقل الخاصة بهم بالتفصيل ، وتحديد القيمة العددية لشدة فقدان التبديل ، ومعرفة كيف تعتمد قيمتها على حجم الأرباع ، ومناقشة الاختلافات والتحسينات المحتملة.

مدينة خطية
هذه المرة ، ضع في اعتبارك مثالاً للمدينة التي يوجد بها شارعان في اتجاه واحد: الغرب بحركة من الشمال والشرق بحركة إلى الجنوب (الشكل 25).


التين. 25

دع كل ربع يولد تدفقًا من طاقة الوحدة. في هذه الحالة ، يوجد مسار سفر واحد من كتلة إلى حسابات أخرى لتدفق حركة المرور بمعدل 1 / n .

نحدد للمبتدئين قوة التدفقات الجانبية على الطرق السريعة في الشوارع. غرب
الشارع هو الطريقة الوحيدة للوصول إلى الربع برقم " أنا"
( ن - ط ) أرباع الكذب جنوبها ، والطريقة الوحيدة التي من الربع الأول هو الوصول إلى ( ط - 1) أرباع تقع شمالها. ويترتب على ذلك أن سعة حركة تبادل الحركة بين شارع زبادنيا والربع الأول تساوي:

q _{W_out} = ( n - i ) / n - للتيار الجانبي الذي يغادر West Street ،
q _{W_in} = ( i - 1) / n - للتيار الجانبي المجاور للحركة الموجودة عليه. من الواضح أن قوة الجانب المتدفق في شارع Vostochnaya تعتمد على i بطريقة متناظرة:
q _{E_out} = ( i - 1) / n هي قوة الشخص الذي يغادر ،
q _{E_in} = ( n - i ) / n هي قوة التيار الجانبي المجاور لحركة المرور في شارع الشرق.

بالطبع ، مجموع التدفقات الخارجة من الربع الرابع:

q _{E_in} + q _{W_in} = ( n - 1) / n ،
يطابق مجموع التدفقات التي تدخله:
q _{E_out} + q _{E_out} = ( n - 1) / n ،
وكلتا هاتين القيمتين لا تعتمدان على i بأي شكل من الأشكال (كل ربع له تدفق سفر بحجم 1 / ن ، يبدأ كل منهما وينتهي داخل نفسه).

للعثور على قوة التدفقات الرئيسية ، نرسم خطًا وهميًا عبر الطريق السريع الغربي على نفس المستوى مع الربع الرابع. في المجموع ، سوف يعبر هذا الخط:
(عدد الفصول من الأسفل) × (عدد الفصول من الأعلى) = ( n - i ) ( i - 1) من الطرق التي تنشئ معًا دفقًا مع القيمة:

P _W ( i ) = ( n - i ) ( i - 1) / n .

نفس الصيغة:
(عدد الفصول من الأسفل) × (عدد الفصول من أعلى) / ن ،
يجب التعبير عن تدفق الطاقة P _E في الشارع الشرقي ، بمعنى آخر:

P _E ( i ) = P _W ( i ) = P ( i ).

بمعرفة قوة جميع التدفقات الرئيسية والجانبية ، يمكننا حساب شدة الخسائر التي تحدث في الشبكة في المنطقة القريبة من الربع الرابع:

I ( i ) = ( α / 2 ν ) ⋅ P ( i ) ⋅ [( q _{E_in} + q _{W_in} ) ⋅ (1 + 1 / s ) + ( q _{E_out} + q _{E_out} ) ⋅ (1 - 1 / s )] =
= ( α / 2 ν ) ⋅ P ( i ) ⋅ [(1 - 1 / n ) ⋅ (1 + 1 / s ) + (1 - 1 / n ) ⋅ (1 - 1 / s )] =
= ( α / 2 ν ) ⋅ 2 P ( i ) ⋅ (1 - 1 / n ) =
= 2 ( α / 2 ν ) ⋅ (1 - 1 / n ) ⋅ ( n - i ) ( i - 1) / n =
= 2 ( α / 2 ν ) ⋅ (1 - 1 / n ) ⋅ ( n - i ) ⋅ ( i - 1) ⋅ (1 / n ).

إذا جمعنا التعبير الأخير على i ، فسنحصل على شدة الخسائر الناتجة عن الشبكة بالكامل ككل.

أنا = ∑ أنا ( أنا )
= ∑ _i 2 ( α / 2 ν ) ⋅ (1 - 1 / n ) ⋅ ( n - i ) ⋅ ( i - 1) ⋅ (1 / n ) =
= 2 ( α / 2 ν ) ⋅ (1 - 1 / n ) ⋅ n ² ⋅ ∑ _i (1 - i / n ) ⋅ ( i / n - 1 / n ) ⋅ (1 / n ) ≈
≈ 2 ( α / 2 ν ) ⋅ n ² ⋅ ∑ _i ( i / n ) ⋅ (1 - i / n ) ⋅ (1 / n ).

يمكن استبدال المجموع ∑ _i ( i / n ) ⋅ (1 - i / n ) ⋅ (1 / n ) بالتكامل مع دقة جيدة بواسطة تكامل:

∫ t (1 - t ) d t ( t ∈ [0؛ 1]) = 1/2 - 1/3 = 1/6.

من أين نتوصل إلى أن شدة تبديل الخسائر في مدينة خطية ذات كتل كتل سعة الوحدة هي:

أنا = ( α / 2 ν ) ن 2/3.

حتى هذه اللحظة ، درسنا فقط الأمثلة التي تولد فيها الجهات دائمًا تدفقات من طاقة الوحدة. دعونا نرى ما إذا كانت صيغة تبديل خسائر مدينة Linear City تتغير إذا لم يكن هناك مصدر واحد لوحدة الطاقة لكل ربع ، ولكن - λ (ستصبح الأرباع أكبر بمقدار λ مرات).

تأخذ مدينة مع كتل م . إذا كانت كتل توليد الطاقة تتدفق 1 ، فإن خسائر التبديل ستكون ( α / 2 ν ) م 2/3. تؤدي الزيادة في طاقة إنتاج السفر بعامل λ كل ثلاثة أشهر إلى زيادة λ في كل من التدفقات الرئيسية والجانبية في وقت واحد ، وبالتالي ، فإن التكاليف في كل تبادل ، وبالتالي داخل الشبكة ككل ، تزداد بعامل ² ، وتتخذ صيغة الخسارة الشكل:

I = ( α / 2 ν ) m ² ⋅ λ 2/3 .

بشكل عام ، لا يهم على الإطلاق كيف تعتمد خسائر التحويل على عدد الأحياء في المدينة ، الشيء الرئيسي بالنسبة لنا هو كيف تعتمد على تدفق الطاقة لجميع الرحلات التي يتم إنشاؤها داخلها ، أو بمعنى آخر ، على عدد مصادر طاقة الوحدة. في الحالة قيد النظر ، n تساوي m ⋅ λ ، لذلك:

I = ( α / 2 ν ) m ² ⋅ λ 2/3 =
= ( α / 2 ν ) ( m ⋅ λ ) 2/3 =
= ( α / 2 ν ) ن 2/3.

بمعنى آخر ، لا تعتمد خسائر التحويل في المدينة الخطية على صغر تقسيمها إلى أرباع.

المدينة الخلوية
تخيل مدينة خلوية تكون فيها طرق الشوارع العمودية متباعدة بارتفاع على مستويات مختلفة. هذا ممكن ، على سبيل المثال ، إذا تم رفع جميع طرق الشوارع المؤدية من الشمال إلى الجنوب على الجسور ، وتم بناء الطرق الممتدة من الغرب إلى الشرق على سطح الأرض. بالإضافة إلى ذلك ، إذا كانت جميع الشوارع بها حركة مرور في اتجاهين ، فسيتم إحالة خريطة الطريق في مثل هذه المدينة إلى الطوبولوجيا المعيارية (الشكل 26).

النقطة المهمة هنا ، بالطبع ، هي عدم تفعيل الشبكة الموصوفة أعلاه على محمل الجد: لن تبدو جذابة من الناحية الجمالية على خلفية منظر المدينة ، وعلاوة على ذلك ، بسبب الحاجة إلى تقاطعات متعددة المستويات ، فإنها ستأكل نصف مساحة الشارع جيدًا. ومع ذلك ، فإن هذه الشبكة الافتراضية البحتة هي طريقة جيدة للحصول على التقديرات اللازمة ، والتي يمكن في وقت لاحق توسيعها بسهولة لشبكات الطرق المثيرة للاهتمام حقًا من وجهة نظر قابليتها للتطبيق في المدن الحقيقية.

كالمعتاد ، سوف نفترض أن احتياجات الهجرة للمقيمين موصوفة بواسطة نموذج "الوصول الموحد" ، وسوف نبدأ نظرنا في الحالة عندما تكون سعة جميع تدفقات السفر الناتجة عن ربع منفصل 1.

في المثال مع "المدينة الخلوية القياسية" ، من المريح الابتعاد عن التقليد المعمول به والنظر في نقطة العنوان ليس كحقل منفصل ، ولكن كمنطقة إقليمية ذات شكل مربع ، والتي تجسد تقاطع الطرق السريعة في الشوارع وربع جميع الأحياء المجاورة لها. يوضح الشكل 27 الموضع النسبي للعديد من هذه المناطق ويظهر نمط حركة المرور داخل إحدى هذه المناطق. يوضح هذا الرسم البياني بوضوح أن أي سائق ، يغادر الربع ، لديه فرصة للوصول إلى الطريق السريع ، والتحرك في اتجاه أي جزء من أجزاء العالم الأربعة.


التين. 26

لإيجاد قيمة تكاليف التحويل الناتجة عن المدينة ، نقوم بحساب قوة جميع التدفقات الرئيسية والجانبية داخل كل منطقة من مناطقها الإقليمية. يسمح لنا شكل المناطق وترتيبها المتبادل باللجوء إلى تشبيه الشطرنج لحل المشكلة الأخيرة ، مع مراعاة المناطق كخلايا في الميدان ، وحركة السيارات بينها - حركات القارب (الشكل 27). من خلية إلى أخرى ، شريطة أن يكونوا في "وضع عام" لبعضهم البعض ، يمكن تحريك الرخ في حركتين ، وإذا كانت كلتا الخليتين تقعان على نفس الأفقي أو واحد الرأسي ، ثم في واحدة.


التين. 27

لتجنب العديد من التحفظات غير المريحة ، نفترض أن الخطوة التي لا تنتقل إليها الغراب في أي مكان مسموح بها أيضًا وفقًا لقواعدنا. يُطلق على مسار حركة الغراب ، الذي يتكون من حركتين ، إحداهما يتم تنفيذها بالضرورة رأسياً والأخرى أفقياً ، الأبسط. من المنطقي التفكير في التحرك "في مكانه" الرأسي والأفقي في نفس الوقت. في هذه الحالة ، يكون التصريح صحيحًا أن أي خليتين على اللوحة متصلتان ببعضهما البعض بواسطة طريقين أبسط مختلفين تمامًا.

بالنسبة للسائقين ، فإن الطريق "الأبسط" هو أسهل طريقة للحصول على الحد الأدنى من التداخل من منطقة إقليمية إلى أخرى ، لذلك فمن المعقول افتراض أن الرحلات الحقيقية ستتم على طول خطوط الطريق الأولية. وفقًا لنموذج "الوصول الموحد" الذي تم إنشاؤه بواسطة نقطة العنوان (المنطقة الإقليمية) ، يجب توزيع تدفق طاقة الوحدة بالتساوي بين جميع نقاط عنوان المدينة = ² d ، وبالتالي فإن سعة مسار السفر التي تنتقل عبر خط طريق واحد هي 1 / (2 n ).

نقوم بحساب تدفق الحجم الذي يمر عبر الخلية ( i ، j ) في الاتجاه من الجنوب إلى الشمال. أبسط طريق يعبر الخلية ( i ، j ) من الجنوب إلى الشمال في حالتين فقط. أولهم (الشكل 28 على اليسار):

1 أ) تقع الخلية الأولية للمسار في أحد آخر خطوط الكفاف (خطوط) ( د ) ؛
2 أ) نقطة نهاية المسار هي واحدة من أول خلايا ( 1 - 1) من العمود (عمودي) j ؛
3 أ) يبدأ المسار بقسم أفقي ، أو يقع بالكامل داخل العمود التاسع.


التين. 28

تبدو الشروط التي تصف الحالة الثانية متماثلة (الشكل 28 على اليمين):

1 ب) نقطة انطلاق المسار هي واحدة من آخر الخلايا ( d - i ) من jth العمودي ؛
2 ب) تكون الخلية الأخيرة من المسار في واحدة من الخطوط ( 1 - 1) الأولى
3 ب) يبدأ المسار بقسم عمودي أو يقع بالكامل داخل العمود j .

على رقعة الشطرنج لا يوجد سوى 2 × [ d ⋅ ( i - 1) + 1 ⋅ ( i - 1)] × ( d - i ) مناسبة لمتطلبات أبسط الطرق ، والتي تنشئ معًا دفق طاقة:

P _SN ( i ، j ) = ( d + 1) ⋅ ( i - 1) ⋅ ( d - i ) / n (= P _SN ( i )).

تحديد ي ، نحصل على الوظيفة

( P _SN ) _j ( i ) = P _SN ( i ، j = Const) ،

لوصف اعتماد قوة التيار الذي يتحرك شمالًا على طول الطريق السريع العمودي j ، على المسافة إلى الحد العلوي للمدينة ، المقاسة في الخلايا.
هناك العديد من الملاحظات الواضحة أو الأقل فيما يتعلق بالوظائف ( P _SN ) _j ( i ) ، دعنا نناقشها.

ربما نبدأ بظرف يصعب التغاضي عنه: P _SN ( i ، j ) مستقلة فعليًا عن الوسيطة الثانية. ونتيجة لذلك ، فإن الوظائف ( P _SN ) _j ( i ) = P _SN ( i ) لها نفس الشكل لجميع قيم j ، بمعنى آخر ، لا يؤثر الموضع المحدد للشارع داخل المدينة الخلوية على تحميله. بشكل رسمي ، تم إثبات العبارة الأخيرة فقط للطريق السريع المؤدي إلى الشمال ، ولكن نظرًا لتناظر المدينة ، فإنها تمتد تلقائيًا إلى الطريق السريع في الاتجاهات الأخرى أيضًا.

الآن دعونا نلقي نظرة على الصيغة نفسها لـ P _SN ( i ):

( d + 1) ⋅ ( i - 1) ⋅ ( d - i ) / (2 n ).

كما نرى ، فإن اعتماد P _SN بأكمله على i يكمن في التعبير ( i - 1) ⋅ ( d - i ). يمكن تفسير هذا التعبير على أنه نتاج أطوال الفواصل اليمنى واليسرى التي ينقسم إليها الجزء الصحيح من الطول d بعد أن يتم حذف العنصر i (الشكل 29 أ).


التين. 29A


التين. 29B

من الواضح أنك إذا غيرت "يمين" إلى "يسار" و "يسار" إلى "يمين" (الشكل 29 ب) ، فستظل نتيجة العمل كما هي. من هذه الملاحظة البسيطة ، في جوهرها ، هناك استنتاجان مفيدان للغاية بالنسبة لنا:

1. تكون الوظيفة P _SN ( i ) متماثلة فيما يتعلق بنقطة منتصف الشارع i = ( d + 1) / 2 ، بمعنى آخر ، تكون قدرة التدفق على مسافة Δ من الحدود الدنيا للمدينة هي نفسها تمامًا كما هي على مسافة Δ من الحد العلوي.
2. على العموم ، المدينة نفسها متناظرة لأعلى ولأسفل ، وبالتالي ، للحصول على الوظيفة ( P _NS ) _j ( i ) ، التي تصف تدفق الطاقة على الطريق السريع jth ، ولكن في اتجاه الجنوب ، يكفي أن تعكس ببساطة الرسم البياني للوظائف ( P _SN) ) _j ( i ) في السطر i = ( d + 1) / 2. بما أن ( P _SN ) _j ( i ) = P _SN ( i ) ، والرسم البياني لـ P _SN ( i ) فيما يتعلق بالسطر i = ( d + 1) / 2 متماثل ، ثم ( P _NS ) _j ( i ) = P _SN ( i ) = P _vert ( i ) ، بمعنى آخر ، يكون لتدفقات المرور المباشرة والقادمة قدرة متساوية في أي مكان في المدينة. يظهر الرسم البياني التقريبي لـ P _SN ( i ) في الشكل 30 (يُعتقد أن d >> 1 ، i >> 1 ، d - i >> 1).

التين. 30

من السهل العثور على قوى التدفقات الرئيسية على طول الطرق السريعة الأفقية باستخدام التماثلات الدورانية ؛ وبشكل رسمي ، تتلخص هذه العملية في الاستبدال البسيط لـ i بواسطة j في P _SN ( i ) ونسخة صغيرة من الفهرس السفلي.

الشيء التالي الذي يجب القيام به هو العثور على قوة التدفقات الجانبية. يمكن تقسيم الرحلات التي تدخل أو تترك حركة المرور على طريق سريع عمودي داخل الخلية ( i ، j ) إلى أربع فئات:

1. q _{in_transit} : — i - , — j - , ( i , j ) ( 31a);
2. q _{out_transit} : — j - , ( i , j ), — i - ( 31b);
3. q _in : — ( i , j ), — i - ( 31c);
4. q _out : — i - . — ( i , j ) ( 31d).

التين. 32: abcd بعد إعادة

حساب عدد خطوط المسار التي تنتمي إلى كل فئة منفصلة ، نستنتج أن قوى جميع التدفقات الأربعة متشابهة ومتساوية:

q ₀ = d ⋅ ( d - 1) / (2 n )

وجود قيم صلاحيات التدفقات الرئيسية والجانبية على الطريق السريع العمودي ، ليس من الصعب حساب مقدار التكاليف الناشئة عن التبديل. داخل خلية واحدة ( i ، j ) ، ستكون التكاليف مساوية لـ:

I _vert ( i ، j ) = ( α / 2 ν ) ⋅ P _vert( i ) ⋅ [( q _in + q _{in_transit} ) ⋅ (1 + 1 / s ) + ( q _out + q _{out_transit} ) ⋅ (1 - 1 / s )]
= 4 ( α / 2 ν ) ⋅ ( d + 1) ( i - 1) ( d - i ) ⋅ d ( d - 1) / 2 n ² ≈
≈ 2 ( α / 2 ν) ⋅ d ⁵ ⋅ ( i / d ) (1 - i / d ) ⋅ (1 / d ) ⁴ =
= 2 ( α / 2 ν ) ⋅ d ² ⋅ ( i / d ) (1 - i / d ) ⋅ (1 / د ).

للعثور على التكاليف المتكبدة في الشوارع الرأسية داخل المدينة بأكملها ، نحتاج إلى جمع I _vert ( i ، j) لكلا المؤشرين:

I _vert = ∑ _ij I _vert ( i ، j ) =
= 2 ( α / 2 ν ) ⋅ d ² ⋅ ∑ _ij ( i / d ) (1 - i / d ) ⋅ (1 / d ) .

بما أن حجم المصطلحات لا يعتمد على j بأي شكل من الأشكال ، فإن الجمع على المؤشر الثاني يعادل الضرب بـ d :

∑ _ij ( i / d) (1 - i / d ) ⋅ (1 / d ) = d ⋅ ∑ _i ( i / d ) (1 - i / d ) ⋅ (1 / d ).

يمكن تقريب المبلغ الأخير من خلال التكامل المألوف بالفعل لدينا:

∑ _i ( i / d ) (1 - i / d ) ⋅ (1 / d ) ≈ ∫ t (1 - t ) d t ( t∈ [0؛ 1]) = 1/2 - 1/3 = 1/6.

مما يعني أن

I _فير = ( α / 2 ν ) ⋅ د ³ /3 = ( α / 2 ν ) ⋅ ن √ ن / 3.

وعندما سئل ما هو مستوى تكاليف I _horiz ، والتي تحدث على الطريق السريع الأفقي، المدينة باستخدام التماثل يمكن أن يجيب:

أنا _horiz = I _فير = ( α / 2 ν ) ⋅ ن √ ن / 3.

وبالتالي ، فإن شدة تبديل الخسائر داخل الشبكة الكاملة للمدينة الخلوية القياسية هي:

I = I _vert + I _horiz = 2/3 ⋅ ( α / 2 ν ) ⋅ n √ n ،

ومتوسط ​​تكلفة الرحلة الواحدة

2/3 ⋅ ( α / 2 ν ) ⋅ √ n

تأثير حجم الخلية على قيمة تبديل الخسائر
تمثل الأحياء التي تولد تدفقات طاقة الوحدة حدًا اصطناعيًا لظروف المشكلة. نقوم بتوسيع النتائج التي تم الحصول عليها أعلاه إلى الحالات التي تكون فيها قوة تدفق السفر الناتجة عن خلية إقليمية واحدة مساوية لـ λ .
دع المدينة تتكون من م هذه الخلايا. إذا كان جميع خلايا سوى قوة واحدة، بلغت شدة الخسائر التحول الشاملة ل I ₁ = 2/3 ⋅ ( α / 2 ν ) ⋅ م √ م . زيادة عدد الرحلات المحرز في λ مرات λالساعة سوف تزيد من قدرات جميع الرئيسية والجانبية تيارات الطريق السريع الشارع، وهذا بدوره سيجعل في λ ² مرات تنمو ولدت كل ذلك ضمن تكاليف مدينة التبديل. سوف تأخذ الصيغة الجديدة لكثافة الخسائر بالشكل التالي:

I = 2/3 ⋅ ( α / 2 ν ) λ ² ⋅ m √ m

إذا افترضنا أن الخلية تتكون من λ نقاط عنوان طاقة الوحدة ، فسيكون العدد الإجمالي لهذه النقاط: n = λ م . دعنا نعبر عن أنني دالة n و λ :

I= 2/3 ⋅ ( α / 2 ν ) λ ² ⋅ m √ m =
2/3 ⋅ ( α / 2 ν ) ⋅ √ λ ⋅ ( λ √ λ ) ⋅ ( m √ m )
= 2/3 ⋅ √ λ ( α / 2 ν ) ⋅ ( λ m ) √ ( λ m )
= 2/3 ⋅√ λ ( α / 2 ν ) ⋅ n √ n .

سيكون متوسط ​​تكلفة الرحلة في ظل الظروف الجديدة 2/3 ⋅ √ λ ( α / 2 ν ) ⋅ √ n ، بما يزيد بمقدار λ λ مرات عن قيمتها في مدينة تتكون من أرباع سعة الوحدة.

تخبرنا الصيغة الأخيرة أنه بالنسبة لنفس السكان والكثافة السكانية والمساحة الكلية لجميع الطرق ، فإن تكلفة تبديل التكاليف أعلى ، وكلما زاد حجم المباني في وقت تصميم المدينة من قبل المهندس المعماري. في حالة توزيع سكان المدينة بشكل غير متساو على أراضيها ، بالطبع ، لا ينبغي إيلاء الاهتمام للأبعاد الهندسية ، ولكن في المقام الأول إلى متوسط ​​عدد الأشخاص داخل الحي ونشاط هجرتهم.


(صورة مركز مدينة نيويورك: فنسنت لافوريت)

الملاحظة أعلاه مهمة بشكل خاص عند تصميم مناطق بها مباني ناطحة سحاب. نظرًا للجمع بين الكثافة السكانية العالية وتنقلها العالي ، من المستحسن جعل الأرباع في المناطق المرتفعة الارتفاع أصغر بعدة مرات من الحجم المعتاد لبناء الطوابق القياسية. في الحضارات ، حيث بناء ناطحات السحاب لها تاريخ طويل ، فإن ممارسة عزل المباني الكبيرة المنفصلة ككتلة منتشرة على نطاق واسع.

اشارة المدينة الخلوية
في كل حالة ، عندما تتقاطع خطوط طريقين مشغولين على الخريطة ، يجب على المهندس المعماري الاختيار: إما أن يرفع أحد هذه الطرق إلى الجسر ، أو يسمح بتدفق الآخر بالمرور بحرية من الأسفل ، أو يدرك التقاطع في شكل تقاطع منتظم ، ويحل تعارض التدفق مما يؤدي إلى حركة المرور التنظيم. يجذب الخيار الثاني بساطته ، وعدم الحاجة إلى بناء هياكل هندسية واسعة النطاق ، إلى جانب أنه يوفر طريقة سهلة لعبور المشاة ، لهذه الأسباب في المدن التي يفضلونها في كثير من الأحيان.


(بعد ظهر وسط مدينة لوس أنجلوس ، الصورة: بوريس شين)

استخدام إشارات المرور في الشبكات ذات طوبولوجيا الخلية له خصائصه الخاصة. في الفصل الأول ، تبين أنه مع التزامن الصحيح لإشارات المرور ، لا يتعين على السيارات ، أثناء تحركها على طول الشارع نفسه ، التوقف عند التقاطعات: سوف يضيء ضوء أخضر دائمًا في اتجاهها. عادة ما يسمى هذا النوع من الظاهرة نظام الموجة الخضراء . لإنشاء ذلك ، يجب تقسيم تدفقات حركة المرور إلى منطقتين متناوبتين من نوعين: مليئة بالسيارات وخالية منها. بعد ذلك ، يتم اختيار طريقة تشغيل إشارات المرور هذه في الفترة الزمنية التي يمر فيها "الجزء" التالي بالتقاطع على طول أحد الشوارع ، والجزء السابق من السيارات التي تتحرك على طول الشارع المتعامد قد اجتازه بالفعل ، والجزء التالي لم يصل بعد (الشكل 33).


التين. 33 تحمل

القدرة على قيادة حركة المرور في الوضع الأخضر تكاليفها الخاصة وتفرض قيودًا معينة على تخطيط شوارع المدينة.

إذا نظرنا مرة أخرى إلى الشكل 33 ، فمن السهل أن نرى أنه في أي وقت من الأوقات لا يتم استخدام نصف مساحة كل الطرق بالفعل. للتعويض عن البساطة ، في النصف المستخدم من الطريق ، يجب أن تكون القوة المحلية لتدفقات السيارات وعدد الممرات اللازمة لها ضعف ما في المدينة ذات الجسور.

ثاني أهم الظروف المرتبطة باستخدام الأمواج الخضراء هو التنظيم الصارم لحجم الأرباع المسموح به: يجب أن يكون طولها (للشوارع ذات الاتجاهين) مضاعفًا لطول الموجة الخضراء المملوءة (قسم من المجرى الذي يمكن أن تتحرك فيه حركة دون عوائق) ، والتي تصل إلى حوالي 500 متر. كما هو مذكور في الفقرة السابقة ، تتطلب المناطق ذات الكثافة السكانية العالية زيادة في تواتر مواقع الطرق ، وبالتالي فإن التقييد من الأسفل على المسافة بين الطرق السريعة في الشوارع يمكن أن يسبب صعوبات مرورية.

من المثير للاهتمام أن نلاحظ أنه في وضع الموجات الخضراء ، تتغير القواعد قليلاً وفقًا لطرق السفر التي يتم تبديلها داخل الشبكة. على سبيل المثال ، يمكن إجراء اتصال سيارة أخرى بتدفق حركة المرور الرئيسي على طريق سريع بين المناطق المملوءة ، وبالتالي لا يسبب أي تكاليف تحويل خطيرة (النقطة "1" ، الشكل 34 أ).


التين. 34

بالطبع ، يجب أن تفقد هذه السيارة نفسها بعض الوقت في انتظار أقرب منطقة خالية قبل الدخول إلى الطريق السريع ، وبعد ذلك لا تزال تقف عند إشارة المرور حتى تصل إليها المنطقة الكاملة التالية (النقطة "2" الشكل 34 أ) ، ولكن حجم هذه الخسائر لا يعتمد إما على حجم المدينة أو على ازدحام حركة المرور في الشارع ، لذلك يمكن إهمالها على نطاق واسع.

يختلف الوضع تمامًا إذا حاولت سيارة ترك حركة المرور على طريق سريع في الشارع (الشكل 34 ب). هنا ، على الأرجح ، لا توجد طرق صعبة بالفعل لتقليل الخسائر الناجمة عن التحويل. علاوة على ذلك ، نظرًا لمضاعفة القوة المحلية للتدفق داخل المناطق المملوءة ، فإن إزالة سيارة منتقاة بطريقة تعسفية يكلفك وقتًا ضعف ما يكلفه ذلك في مدينة بها جسور. إجمالاً ، فإن "الدخول" الأقل تكلفة و "الخروج" الأكثر تكلفة من تيارات الشوارع يعوضان بعضهما البعض ، مما يجعل مدينة خلية إشارات المرور في هذا الصدد أفضل حالًا تقريبًا ، ولكن ليس أسوأ من Standard.

مدينة الخلوية في اتجاه واحد
بالإضافة إلى استخدام إشارات المرور ، هناك فرصة واحدة على الأقل للابتعاد عن التقاطع الوحشي في المدينة القياسية. يتكون من طرق تقسيم مكانيا (الشكل 35) مع الاتجاه المعاكس للحركة.


التين. 35

نتيجة لمثل هذه التغييرات ، سيتضاعف عدد الشوارع ، ستصبح جميعها أحادية الجانب ، ولكن الأهم من ذلك ، سيتم تبسيط التبادلات إلى حد كبير (الشكل 36).


التين. 36
نظرًا لأن عدد الطرق السريعة المؤدية إلى كل طرف من أطراف العالم ، وعدد الرحلات التي تمر بها ، ظلت كما هي ، فقد ظلت قدرات جميع التدفقات ، ومعها تكاليف التحويل في المدينة الخلوية ذات الاتجاه الواحد والمدينة القياسية التي تضم ربعين كبيرين (خطي) ، تطابق إذا قارنا المدن القياسية والمدينة أحادية الجانب بأحجام الربع نفسها ، فستكون للمدينة الثانية ضعف خسائر التحويل.

الشارع "الخطي".

كيف يمكن تقليل خسائر التحويل في الشبكة الخلوية؟ الإجابة على هذا السؤال سوف تسمح لنا باختيار القياس وقوة الذكاء.

النظر في تعديل غير عادي إلى حد ما للشبكة الخلوية ، مما يعني أن جميع الطرق السريعة الممتدة من الغرب إلى الشرق هي في اتجاهين ، في حين أن الطرق المتعامدة بالنسبة لهم مسموح بها في اتجاه واحد فقط: إما شمالًا أو جنوبًا ، وهذه الاتجاهات بديلة من شارع الى شارع

كما هو الحال دائمًا ، سوف نفترض أن المدينة تطيع نموذج الوصول الموحد ، وأن كل ربعها يولد تيارًا من طاقة الوحدة المشروطة.

في هذه الحالة ، يبدو من المعقول أن النواة داخل الربع ( أنا ، ي) يتم توزيع تدفق الرحلات ، مع تركها ، بين أقرب الشوارع على النحو التالي: 1/4 منه يصل إلى الطريق الأفقي من أعلى ، 1/4 أكثر إلى الطريق الأفقي من الأسفل ، 1/4 ⋅ i / d يتدفق إلى الشمال على طول الطريق السريع العمودي و
1/4 ⋅ (1 - i / d ) - على طول الطريق السريع العمودي الثاني إلى الجنوب (الشكل 37).

التين. 37

في الواقع ، وفقًا لخوارزميات بناء الطرق التي تمت مناقشتها مسبقًا ، وفقًا للإحصاءات ، ستبدأ نصف الرحلات من قسم أفقي ، وبالنسبة للسائقين الذين يفضلون هذا النصف ، يجب ألا يهم ما إذا كان مسارهم يقع شمال الربع ( i ، j ) أو الجنوب منه. سيبدأ النصف المتبقي من الرحلات بجزء عمودي من حركة المرور وسيتم تقسيمه بين الطريق السريع الجنوبي والشمالي فيما يتعلق بعدد الأرباع الواقعة ( i ، j ) جنوبًا إلى عدد الأرباع الواقعة شمالها.

بالنسبة لتدفق السفر الموجه إلى الداخل ( i ، j) ، فإن قاعدة الانقسام بالنسبة للطريق السريع المحيط بالربع ستكون متناظرة (الشكل 38).


التين. 38 من

بين التقاطعات الأربعة المتاخمة للربع ( i ، j ) ، نفكر بشكل منفصل في التدفقات الجانبية عند تقاطع الطريق السريع الأفقي السفلي والشارع الرأسي مع حركة المرور الشمالية (الشكل 38). تدفق السيارات التي تتحرك من شارع أفقي إلى عمودي هو:
1/2 ⋅ (عدد الفصول على أفقي) × (عدد الفصول على رأسية لا تقل عن ( i ، j )) ⋅ 1 / d ² =
= 1/2 ⋅ d ⋅ i / d ² =
= 1/2 ⋅ i / d .
حجم التدفق الجانبي في الاتجاه المعاكس هو:
1/2 ⋅ (عدد الكتل في قطاع أدناه بدقة ( ط ، ي )) × (عدد الكتل في رأسي) ⋅ 1 / د ² =
= 1/2 ⋅ ( د - ط ) ⋅ د / d ² =
= 1/2 ⋅ (1 - i / d ).

دعونا الآن نحول انتباهنا من Cellular City ككل إلى أي من شوارعها العمودية ، دعنا نسميها My_street. نظرًا للتناظر ، لن نحدد تفكيرنا على الإطلاق ، إذا افترضنا أن الحركة على طول My_street موجهة من الجنوب إلى الشمال (الشكل 39).


التين. 39

يوضح الشكل 40 الرسوم البيانية لقوة التدفقات الرئيسية والجانبية على الطريق السريع على طول My_street ، والتي ، كما قد يلاحظ القارئ ، تشبه بشكل لا يصدق الرسوم البيانية المماثلة للطريق السريع أحادي الاتجاه للمدينة الخطية (الشكل 26).



التين. 40

في هذه الأمثلة ، تتزامن أنماط التدفق تمامًا إذا تم تعيين التدفقات الجانبية المتعلقة بكل زوج من الأوساط المتعارضة والطريق السريع الأفقي الموجود تحتها داخل خلية My_street رسميًا في خلية إقليمية واحدة وهمية. كما يتضح من الجداول السابقة ، فإن شبكة الطرق في Linear City تولد بعضًا من أكبر خسائر التحويل بين شبكات الهندسة المعمارية التي درسناها بالفعل. من وجهة النظر هذه ، يبدو نمط حركة المرور داخل شارع مدينة ذات خلية واحدة غير فعال للغاية وهو عنصر يجب تجربته في المقام الأول.

الشبكة المتقدمة للمدينة الخطية
وهكذا ، فإننا نواجه مهمة تحسين الشبكة الخطية بحيث لا تتحول إلى "مربع". إن الظرف الذي يقدم أكبر قدر من عدم الكفاءة في تشغيل الشبكة الخطية هو توحيد جميع المسارات في اثنين فقط من التدفقات المرورية الكبيرة. في هذه الحالة ، تتمثل الخطوة المعقولة في تقسيم التدفقات على طول طريقي الشارع الرئيسيين إلى أجزاء Q متساوية. نظرًا لأن تكاليف الوقت الناتجة عن كل سيارة تنضم إلى حركة المرور أو تغادرها تتناسب مع كثافة حركة المرور عليها ، نتيجة لتقسيم خطوط الشوارع إلى أجزاء معزولة من Q (الشكل 41 أ) ، يجب أن يكون تحويل الخسائر داخل المدينة الخطية قد انخفض مرات Q.


التين. 41

مجرد بناء عشرة طرق قريبة على أمل أن يتم توزيع السائقين بأنفسهم بالتساوي - لسوء الحظ ، لا يبدو أن هناك أي شيء لديه فرصة للنجاح. يتمثل القرار الأكثر تفكيرًا في تصميم الشبكة بحيث لا يؤدي كل طريق إلى جميع الجهات ، ولكن فقط إلى "شريحة" صغيرة من المدينة ، حيث سيكون من الصعب الالتفاف عليها (الشكل 41 ب).

يمكنك أن ترى فكرة مماثلة في مخطط حركة المصاعد داخل المباني متعددة الطوابق. هناك ، يسمح لك كل مصعد بالدخول والخروج منه ليس في جميع الطوابق ، ولكن فقط ضمن مجموعة معينة من الارتفاعات. بأخذ هذا المفهوم ، دعنا نلقي نظرة فاحصة على الطريق r _k ، الذي يفتح الوصول إلى القطاع Δ _k = ( x _k ،x _{k +1} ] للرحلات التي بدأت (غير حصرية) إلى الجنوب من x _k (يُعتقد أن ترقيم الكتل يتم من أسفل إلى أعلى). على جانب كل ربع سنة، وعدد منها (بدقة) أقل من العاشر _{من ك} ، الطريق ص _ك يدخل تدفق ف _في السلطة | دلتا _للك | / ن (1 / ن إلى عنوان كل كتلة داخل دلتا _للك )، في نفس الوقت، فمن المفترض أن القدرة على إيقاف ص _كتجاه أي من الأحياء المذكورة مفقود إما بسبب قواعد المرور المعمول بها ، أو بسبب التصميم الخاص لشبكة الطرق.

تراكمت على الفترة [1، س _ك ] السيارات في نهاية المطاف تم توزيعها بالتساوي بين أرباع دلتا _للك ، لذلك إذا كنت لا السفر الى هناك، بداية ونهاية والتي تقع داخل دلتا _للك ، وتدفق الجانبي ف _بها في اتجاه كل الكتل في هذا المجال سيكون لديه قوة س _ك / ن (الشكل 42).


التين. 42

في الواقع ، مساهمة "الداخلية" تنتقل إلى قوة التدفقات الجانبية أيضا يحدث ، ومع ذلك ، فإن قيمة هذه المساهمة لا تتجاوز أبدا | | _k | / n ؛ لذلك ، في حالة x _k >> | | Δ _ك | ، يمكن إهمالها ببساطة. سيتم تمثيل القدرة p _k للتيار الرئيسي على طول r _k مع إجراء التبسيط برسم بياني يتكون من قسمين مستقيمين بحد أقصى P _k يساوي x _k ⋅ | | _ك | / ن . يمكن العثور على القيمة التقريبية لخسائر التبديل عند r _k بواسطة الصيغة:

I _k = ( α / 2 ν ) ⋅ ∑ _x [ q _in ( x ) ⋅ p _k ( x ) ⋅ (1 + 1 / s )] + ( α / 2 ν ) ⋅ ∑ _x [ q _out ( x ) ⋅ p _k ( x ) ⋅ (1 - 1 / s )] =

= ( α / 2 ν ) ⋅ (1 + 1 / s ) ∑ _x [| | _k | / n ⋅ p _k ( x )] + ( α / 2 ν ) ⋅ (1 - 1 / s ) ∑ _x [ x _k / n ⋅ p _k ( x )] =

= ( α / 2 ν ) ⋅ (1 + 1 / s ) ⋅ ( x _k ⋅ | Δ _k | / n ) ⋅ ( ∑ _x p _k ( x )) / x _k + ( α / 2 ν ) ⋅ (1 - 1 / s ) ⋅ ( x _k ⋅ | Δ _k | / n ) ⋅ ( ∑ _x p _k ( x )) / | | _ك | ،

حيث يتم أخذ المبلغ الأول على المنطقة x ∈ [1، x _k ] ، والثاني على x ∈ Δ _k . عبارات:

( ∑ _x p _k ( x )) / x _k و x ∈ [1، x _k ] و

( p _x p _k ( x )) / | | _k |، x ∈ Δ _k

لا يوجد أكثر من متوسط ​​قدرة التيار على طول r _k داخل الفواصل الزمنية المشار إليها. نظرًا لأن الرسم البياني للقدرة في هذه الفواصل الزمنية له شكل خط مستقيم ، فإن متوسط ​​القدرة في كلتا الحالتين هو P _k / 2. استبدال
س _ك ⋅ | Δ _ك | / ن على
ف _ك
أخيرًا نعطي صيغة شدة الخسارة إلى أبسط أشكالها:

I _k = 2 ( α / 2 ν ) ⋅ P _k ⋅ P _k / 2 = ( α / 2 ν ) ⋅ P _k ²

دعونا الآن نحاول حساب تسلسل x _{k من} أرقام تلك الأحياء التي يجب أن تقسم بها المدينة الخطية إلى شرائح. كمعيار لاختيار القطاعات ، نأخذ في الاعتبار أن أقصى قدرة لتدفق حركة المرور P _k على الطرق المناسبة لها نفس القيمة ، بمعزل عن k ، بمعنى آخر ، المساواة

س _ك ⋅ | Δ _ك | = كون.

تذكر ذلك | Δ _ك | = x _{k + 1} - x _k ، نصل إلى معادلة الفرق:

x _{k + 1} - x _k = Const / x _k .

على افتراض أن x و k متغيرات مستمرة ، واستبدال

x _{k + 1} - x _k = x ( k + 1) - x ( k )

في يوم x / d k ⋅ 1 ،

يمكننا تقريب معادلة الفرق من خلال الفرق:

d x / d k = Const / x <=> x d x = Const ⋅ d k .

من أين نحصل على حل x _k بالشكل العام:

س _ك = ج ₁ √ ( ك + ج ₂ ).

يبقى لنا أن نحدد قيمة الثوابت C ₁ و C ₂ من الشروط الحدودية ، ومع ذلك ، هناك دقة مهمة في هذه المسألة. على عكس الوضع في القطاعات المتبقية ، بدأت جميع السيارات التي تصل من الطريق السريع الغربي إلى أرباع الجزء في الرقم 1 ، داخل نفس الشريحة ، رحلتها. نتيجة لذلك ، سيكون شكل الرسم البياني لقوة التدفق على أول طريق سريع إلى الشمال على شكل قطع مكافئ منتظم مقلوب.

في الوقت نفسه ، فإن الشروط المسبقة التي تم الحصول عليها من الصيغة x _k تشير بشكل أساسي إلى أن الرسوم البيانية لقدرة التدفق على جميع الطرق السريعة يجب أن تكون قريبة من العرض الثلاثي ، ويجب أن تبدأ الرحلات نفسها خارج الجزء الذي يتم توجيهها فيه. يمكن تلبية هذه المتطلبات بدقة معقولة إذا قمنا بتقسيم الجزء الأول رسميًا إلى جزأين متساويين (يتم تناول القطع المكافئة بواسطة مثلث متساوي الساقين ومعظم الرحلات على طول الطريق السريع الأول موجهة بالفعل من النصف الجنوبي من الجزء رقم 1 إلى النصف الشمالي) ، دون زيادة عدد الطرق ( التين 43).


التين. 43

إنه منتصف الجزء الأول الذي يجب اعتباره النقطة × ₁ في صيغة x _k . من هنا نحصل على شرط الحدود الأول:

س ₂ = 2 × ₁ أو

√ (2 + C ₂ ) = 2 ⋅ √ (1 + C ₂ ) =>

ج ₂ = - 2/3.

يتم الحصول على شرط الحدود الثاني من شرط أن تكون الطرق والمقاطع Q بالضبط ، مما يعني أن x _{Q + 1} يجب أن تكون مساوية للربع التالي مع أكبر عدد في المدينة:

C ₁ √ ( Q + 1 - 2/3) = n + 1 ، من أين

C ₁ ≈ ( n + 1) / √ Q.

بهذه الطريقة:

x _k ≈ ( n + 1) ⋅ √ ( k - 2/3) / √ Q ،

| Δ _ك | ≈ d x / d k = ( n + 1) / 2√ ( k - 2/3) ⋅ √ Q

P _k = x _k ⋅ | | _ك | / ن =

= ( n + 1) 2/2 n ⋅ Q ≈ n / 2 Q

I _k = ( α / 2 ν ) ⋅ P _k ² =

= ( α / 2 ν ) ⋅ ( n / 2 Q ) ² .

نظرًا لأن جميع الطرق السريعة في الشوارع على مستوى الربع الثاني تسببت في خسائر بنفس الكثافة ، فإن قيمة تكاليف التحويل داخل الشبكة بالكامل ستكون:

I = 2 Q ⋅ ( α / 2 ν ) ⋅ ( n / 2 Q ) ² = ( α / 2 ν ) ⋅ n 2/2 Q.

كما ترون ، تم تحقيق الهدف المنشود: بعد تقسيم الطرق السريعة الرئيسية إلى أجزاء Q ، انخفضت الخسائر فعليًا بعامل Q (باستثناء معامل 1/3 إلى 1/2 الثابت الذي زاد مقارنةً بصيغة Linear City المعتادة). حسنًا ، تم إنجاز نصف المهمة ، ولكن يبقى تطبيق النتيجة لتحسين المدينة من خلال البنية الخلوية.

ناطحة سحاب مصعد في المدينة الخلوية
للبساطة ، سنكتفي بمثال لمدينة تكون فيها جميع الشوارع في اتجاه واحد. باستخدام القياس بين Linear City والشوارع الفردية للمدينة الخلوية ، نقسم الطريق السريع على طول الأخير إلى أجزاء Q. افتراضيًا ، يُعتقد أنه بمغادرة الربع ، يمكنك الوصول إلى أي طريق سريع يمر بالقرب منه. في الوقت نفسه ، من بين جميع الطرق السريعة الموضوعة على طول شارع واحد ، هناك اتجاه نحو ربع معين مع واحد منهم بالضبط. في عملية وضع القواعد ، يعتبر توحيدها وبساطتها في غاية الأهمية. ألقِ نظرة على الشكل 44:


التين. 44

جميع الشوارع لها نفس المظهر والقواعد نفسها ، أي من طرقها في ما كتل الحساب يفتح الوصول. يوضح الشكل 45 مخططًا للانعطافات المسموح بها بين الطرق السريعة. النظر إلى هذه الصورة يصعب عدم الخلط. كثيرا ما يقال نفس الشيء عن مخطط المترو في بعض المدن الكبيرة. ومع ذلك ، في كلتا الحالتين ، يصبح كل شيء واضحًا وبسيطًا إذا كنت تعرف منطق الفكرة. تبدو القاعدة المنطقية للدوران المسموح به بسيطة للغاية: إذا كنت تقود على طريق سريع تقطع الطرق بشكل عمودي على حركتك ويمكنك أن تتحول إلى ربع يقع خلفها مباشرةً ، يمكنك تشغيل أي من هذه الطرق.


التين. 45

طبولوجيا Skyscraper Lift متوافقة مع كل من إشارات المرور والجسور. إنه أمر صعب ، لكن يمكن تعميمه على شبكات ليست بالضرورة ذات بنية خلوية أو خطية. هذا الأخير مهم حقًا بالنسبة للمدن التاريخية ، حيث من غير المحتمل أن يكون من الصواب هدم نصف المعالم التاريخية من أجل وضع العديد من الشوارع الصغيرة المستقيمة ، ولكن يوجد بالفعل شوارع كبيرة جدًا يمكنها استيعاب عدة طرق سريعة أو ثلاثة مسارات.

حول مشاكل النقل وعمل الرياضيات

من الجيد إكمال العمل المضني نصف السنوي. العمل الذي كتبته ، بالطبع ، لا يحل جميع مشاكل وصعوبات تصميم الطرق - هذا العمل يتطلب عددًا كبيرًا من الأشخاص المتنوعين للغاية. ومع ذلك ، فإن نتائجها توفر فرصة لرؤية الأخطاء المهمة في المدن التي بنيت بالفعل وتوفر طرقًا لكيفية تجنب هذه الأخطاء في المستقبل. لم يكن الغرض من هذه المقالة بمثابة كتاب مرجعي يغطي جميع الحالات المحتملة التي يمكن للمهندس مواجهتها في الواقع العملي - لقد فكرت في مهمتي الرئيسية لإعطاء وجهة نظر جديدة ، لتطوير طريقة جديدة للسبب والتحدث عن المشكلة ، لتوفير الحد الأدنى الضروري من أمثلة النماذج البسيطة التي أعدها القارئ يمكن بالفعل توسيع نفسي.

يصبح الأمر محزنًا عندما تدرك مقدار الوقت الذي ضيعه سكان المدينة في الاختناقات المرورية لمجرد أنه في الوقت المناسب لم يكن هناك عالم رياضيات يمكنه قضاء المساء في مشكلة قابلة للحل تمامًا. كم من هذه المشاكل لا تزال تحيط حياتنا أو تختبئ في مهنتك؟ هل الشخص جالس بالقرب منك في العمل الذي لديه أدوات وقلم رصاص وورقة؟

آمل أن يتغير كل شيء للأفضل.

شكرا لاهتمامكم وحظا سعيدا!
سيرجي كوفالينكو.

2019 سنة
magnolia@bk.ru


(الصورة: فنسنت لافوريت)