نهج الجشع وفتحات الآلات. تحليل مهام ML المسار من بطولة البرمجة

نواصل نشر تحليلات المهام التي تم اقتراحها في البطولة الأخيرة. التالي في السطر هي المهام التي اتخذت من جولة التأهيل لأخصائيي التعلم الآلي. هذا هو المسار الثالث من أربعة (الخلفية ، الواجهة الأمامية ، ML ، التحليلات). يحتاج المشاركون إلى صنع نموذج لتصحيح الأخطاء المطبعية في النصوص ، واقتراح استراتيجية للعب على ماكينات القمار ، ووضع نظام توصيات للمحتوى ، وإنشاء عدة برامج أخرى.

أ. الأخطاء المطبعية

حالة

(الكتابة) (من منتدى واحد)
- من يتكون هذا الهراء؟
- علماء الفيزياء الفلكية. هم الناس أيضا.
- لقد ارتكبت 10 أخطاء في كلمة "الصحفيين".

يرتكب العديد من المستخدمين أخطاء في الكتابة ، بعضها بسبب ضرب المفاتيح ، والبعض الآخر بسبب أميتهم. نريد التحقق مما إذا كان المستخدم يمكن أن يعني في الواقع كلمة أخرى غير الكلمة التي كتبها.

بشكل أكثر رسمية ، افترض أن نموذج الخطأ التالي يحدث: يبدأ المستخدم بكلمة يريد كتابتها ، ثم يقوم بعد ذلك بعدد من الأخطاء فيها. كل خطأ هو استبدال لبعض سلسلة فرعية من الكلمة لسلسلة فرعية أخرى. خطأ واحد يتوافق مع استبدال فقط في موقف واحد (أي إذا كان المستخدم يريد أن يرتكب خطأ واحد من قبل القاعدة "abc" → "cba" ، ثم من سلسلة "abcabc" يمكنه الحصول على "cbaabc" أو "abccba"). بعد كل خطأ ، تتكرر العملية. يمكن استخدام نفس القاعدة عدة مرات في خطوات مختلفة (على سبيل المثال ، في المثال أعلاه ، يمكن الحصول على "cbacba" في خطوتين).

يجب تحديد الحد الأدنى لعدد الأخطاء التي يمكن أن يرتكبها المستخدم إذا كان يفكر في كلمة معينة وكتب كلمة أخرى.

قرار

دعنا نحاول إنشاء كل الكلمات الممكنة من الإملاء الصحيح دون أكثر من 4 أخطاء. في أسوأ الحالات ، قد يكون هناك O ((L﹒N) ⁴ ). في حدود المشكلة ، هذا عدد كبير إلى حد ما ، لذلك تحتاج إلى معرفة كيفية الحد من التعقيد. بدلاً من ذلك ، يمكنك استخدام خوارزمية الالتقاء في الوسط: إنشاء كلمات لا تزيد عن 2 أخطاء ، وكذلك الكلمات التي يمكنك من خلالها الحصول على كلمة مكتوبة بواسطة المستخدم مع عدم وجود أكثر من خطأين. لاحظ أن حجم كل مجموعة من هذه المجموعات لن يتجاوز 10 ⁶ . إذا لم يتجاوز عدد الأخطاء التي ارتكبها المستخدم 4 ، فسوف تتقاطع هذه المجموعات. وبالمثل ، يمكننا التحقق من أن عدد الأخطاء لا يتجاوز 3 و 2 و 1.

 struct FromTo { std::string from; std::string to; }; std::pair<size_t, std::string> applyRule(const std::string& word, const FromTo &fromTo, int pos) { while(true) { int from = word.find(fromTo.from, pos); if (from == std::string::npos) { return {std::string::npos, {}}; } int to = from + fromTo.from.size(); auto cpy = word; for (int i = from; i < to; i++) { cpy[i] = fromTo.to[i - from]; } return {from, std::move(cpy)}; } } void inverseRules(std::vector<FromTo> &rules) { for (auto& rule: rules) { std::swap(rule.from, rule.to); } } int solve(std::string& wordOrig, std::string& wordMissprinted, std::vector<FromTo>& replaces) { std::unordered_map<std::string, int> mapping; std::unordered_map<int, std::string> mappingInverse; mapping.emplace(wordOrig, 0); mappingInverse.emplace(0, wordOrig); mapping.emplace(wordMissprinted, 1); mappingInverse.emplace(1, wordMissprinted); std::unordered_map<int, std::unordered_set<int>> edges; auto buildGraph = [&edges, &mapping, &mappingInverse](int startId, const std::vector<FromTo>& replaces, bool dir) { std::unordered_set<int> mappingLayer0; mappingLayer0 = {startId}; for (int i = 0; i < 2; i++) { std::unordered_set<int> mappingLayer1; for (const auto& v: mappingLayer0) { auto& word = mappingInverse.at(v); for (auto& fromTo: replaces) { size_t from = 0; while (true) { auto [tmp, wordCpy] = applyRule(word, fromTo, from); if (tmp == std::string::npos) { break; } from = tmp + 1; { int w = mapping.size(); mapping.emplace(wordCpy, w); w = mapping.at(wordCpy); mappingInverse.emplace(w, std::move(wordCpy)); if (dir) { edges[v].emplace(w); } else { edges[w].emplace(v); } mappingLayer1.emplace(w); } } } } mappingLayer0 = std::move(mappingLayer1); } }; buildGraph(0, replaces, true); inverseRules(replaces); buildGraph(1, replaces, false); { std::queue<std::pair<int, int>> q; q.emplace(0, 0); std::vector<bool> mask(mapping.size(), false); int level{0}; while (q.size()) { auto [w, level] = q.front(); q.pop(); if (mask[w]) { continue; } mask[w] = true; if (mappingInverse.at(w) == wordMissprinted) { return level; } for (auto& v: edges[w]) { q.emplace(v, level + 1); } } } return -1; } 

B. العصابات المسلحة

حالة

هذه مهمة تفاعلية.

أنت نفسك لا تعرف كيف حدث ذلك ، ولكنك وجدت نفسك في قاعة بها آلات القمار مع حقيبة كاملة من الرموز. للأسف ، في شباك التذاكر ، يرفضون قبول الرموز المميزة ، وقررت تجربة حظك. هناك العديد من ماكينات القمار في القاعة التي يمكنك لعبها. لعبة واحدة مع فتحة آلة تستخدم رمز واحد. في حالة الفوز ، يمنحك الجهاز دولارًا واحدًا ، في حالة الخسارة - لا شيء. كل جهاز لديه احتمالية ثابتة للفوز (لا تعرفه) ، لكنه يختلف عن الأجهزة المختلفة. بعد دراسة موقع الشركة المصنعة لهذه الآلات ، اكتشفت أن احتمال الفوز لكل جهاز يتم اختياره عشوائيًا في مرحلة التصنيع من توزيع بيتا مع بعض المعلمات.

تريد زيادة أرباحك المتوقعة إلى الحد الأقصى.

قرار

هذه المشكلة معروفة جيدًا ، ويمكن حلها بطرق مختلفة. طبق القرار الرئيسي لهيئة المحلفين استراتيجية أخذ عينات Thompson ، ولكن نظرًا لأن عدد الخطوات كان معروفًا في بداية البرنامج ، فهناك استراتيجيات أكثر مثالية (على سبيل المثال ، UCB1). علاوة على ذلك ، يمكن للمرء حتى الحصول على مع استراتيجية الجشع epsilon: مع وجود احتمال معين ، تلعب آلة عشوائية ومع الاحتمال (1 - ε) تلعب آلة مع أفضل إحصائيات النصر.

 class SolverFromStdIn(object): def __init__(self): self.regrets = [0.] self.total_win = [0.] self.moves = [] class ThompsonSampling(SolverFromStdIn): def __init__(self, bandits_total, init_a=1, init_b=1): """ init_a (int): initial value of a in Beta(a, b). init_b (int): initial value of b in Beta(a, b). """ SolverFromStdIn.__init__(self) self.n = bandits_total self.alpha = init_a self.beta = init_b self._as = [init_a] * self.n # [random.betavariate(self.alpha, self.beta) for _ in range(self.n)] self._bs = [init_b] * self.n # [random.betavariate(self.alpha, self.beta) for _ in range(self.n)] self.last_move = -1 random.seed(int(time.time())) def move(self): samples = [random.betavariate(self._as[x], self._bs[x]) for x in range(self.n)] self.last_move = max(range(self.n), key=lambda x: samples[x]) self.moves.append(self.last_move) return self.last_move def set_reward(self, reward): i = self.last_move r = reward self._as[i] += r self._bs[i] += (1 - r) return i, r while True: n, m = map(int, sys.stdin.readline().split()) if n == 0 and m == 0: break alpha, beta = map(float, sys.stdin.readline().split()) solver = ThompsonSampling(m) for _ in range(n): print >> sys.stdout, solver.move() + 1 sys.stdout.flush() reward = int(sys.stdin.readline()) solver.set_reward(reward) 

C. محاذاة الجمل

حالة

واحدة من أهم المهام لتدريب نموذج الترجمة الآلية الجيدة هي حالة جيدة من الجمل المتوازية. عادةً ما يكون مصدر العروض المتوازية مستندات موازية. اتضح أنه في كثير من الأحيان لبناء مجموعة معينة من الجمل المتوازية ، لا تحتاج إلى معرفة أي شيء سوى أطوالها. على وجه الخصوص ، قد تلاحظ أنه كلما طالت مدة الجملة في لغة المصدر ، كلما تمت ترجمتها على الأرجح. تكمن بعض الصعوبات في حقيقة أنه أثناء الترجمة يمكن أن يتغير عدد الجمل في النص: في بعض الأحيان يمكن دمج جملتين متجاورتين في الترجمة في جملة واحدة ، أو العكس - يمكن تقسيم جملة واحدة إلى جملتين. في بعض الحالات النادرة ، قد يتم حذف الجمل بالكامل في الترجمة ، أو قد تظهر الترجمة في الترجمة التي لم تكن بالأصل.

بشكل أكثر رسمية ، افترض أن النموذج التوليفي التالي للمرفقات الموازية صحيح. في كل خطوة ، نقوم بأحد الإجراءات التالية:

1. توقف

مع الاحتمال p _{h ،} ينتهي توليد الأجسام.

2. [1-0] تخطي العروض

مع الاحتمال p _d نسند جملة واحدة إلى النص الأصلي. نحن لا ننسب أي شيء للترجمة. يتم تحديد طول الجملة باللغة الأصلية L ≥ 1 من التوزيع المنفصل:

.

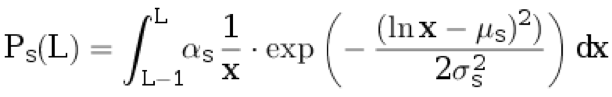
فيما يلي معلمات التوزيع ، و α _s هي معامل التطبيع المختار بحيث .

3. [0-1] أدخل الاقتراح

مع الاحتمال p _i نخصص جملة واحدة للترجمة. نحن لا ننسب أي شيء إلى الأصل. يتم تحديد طول الجملة في لغة الترجمة L ≥ 1 من توزيع منفصل:

.

هنا، _t ، σ _t هي معلمات التوزيع ، و α _t هي معامل التطبيع المختار بحيث .

4. الترجمة

مع الاحتمال (1 - p _d - p _i - p _h ) نأخذ طول الجملة باللغة الأصلية L _s ≥ 1 من التوزيع p _s (مع التقريب لأعلى). بعد ذلك ، نقوم بإنشاء طول الجملة في لغة الترجمة L _t ≥ 1 من التوزيع المنفصل الشرطي:

.

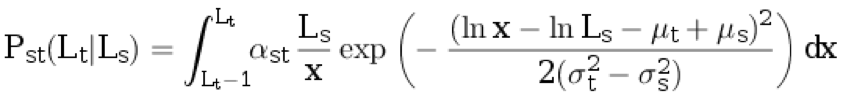
هنا α _st هو معامل التطبيع ، ويتم وصف المعلمات المتبقية في الفقرات السابقة.

التالي هو خطوة أخرى:

1. [2-1] مع الاحتمال p _{split s ، تنقسم} الجملة المولدة في اللغة الأصلية إلى كلمتين غير فارغتين ، بحيث يزيد العدد الإجمالي للكلمات بواحدة . احتمال أن تنفصل جملة الطول L _s إلى أجزاء من الطول L ₁ و L ₂ (أي L ₁ + L ₂ = L _s + 1) تتناسب مع P _s (L ₁ ) ⋅ P _s (L ₂ ).

2. [1-2] مع وجود الاحتمال p _{split t ، تنقسم} الجملة التي تم إنشاؤها في اللغة الهدف إلى جملتين غير فارغتين ، بحيث يزيد العدد الإجمالي للكلمات بحرف واحد. احتمال أن تنفصل جملة الطول L _t إلى أجزاء من الطول L1 و L2 (أي L ₁ + L ₂ = L _t + 1) تتناسب مع P _t (L ₁ ) ⋅ P _t (L ₂ ).

3. 3. [1-1] مع احتمال (1 - p _{split s} - p _{split t} ) ، لن يتحلل أي من الجمل المتولدة.

قرار

المهمة هي حالة خاصة من المحاذاة باستخدام نماذج Markov المخفية (محاذاة HMM). الفكرة الرئيسية هي أنه يمكنك حساب احتمال إنشاء زوج معين من المستندات باستخدام هذا النموذج وخوارزمية إعادة التوجيه : في هذه الحالة ، تكون الحالة عبارة عن بادئات من المستندات. وفقًا لذلك ، يمكن حساب الاحتمال المطلوب لمحاذاة زوج معين من الجمل المتوازية بواسطة خوارزمية الأمام والخلف .

الشريط من التوصيات

حالة

النظر في موجز للتوصيات لمحتوى غير متجانسة. يمزج الكائنات من أنواع مختلفة (الصور ومقاطع الفيديو والأخبار وما إلى ذلك). عادةً ما يتم ترتيب هذه الكائنات حسب صلتها بالمستخدم: كلما كان الكائن (المستخدم) الأكثر صلة بالموضوع ، كلما اقتربنا من أعلى قائمة التوصيات. ومع ذلك ، مع مثل هذا الترتيب ، تنشأ مواقف غالبًا تظهر فيها عدة كائنات من نفس النوع في قائمة التوصيات. يؤدي هذا إلى تفاقم التنوع الخارجي لتوصياتنا إلى حد كبير وبالتالي لا يحب المستخدمون ذلك. من الضروري تنفيذ خوارزمية ، وفقًا لقائمة التوصيات ، ستشكل قائمة جديدة ستكون خالية من هذه المشكلة وستكون ذات صلة.

اسمح بقائمة أولية من التوصيات: = [a ₀ ، a ₁ ، ...، _{n - 1} ] من الطول n> 0. كائن برقم _i كتبته بالرقم b _i 0 {0، ...، m - 1}. بالإضافة إلى ذلك ، يوجد كائن تحت الرقم i ذو صلة r (a _i ) = 2 _−i . النظر في القائمة التي تم الحصول عليها من القائمة الأولية عن طريق اختيار مجموعة فرعية من الكائنات والتقليب: x = [a _{i 0} ، _{i i 1} ، ...، _{i k - 1} ] من الطول k (0 ≤ k ≤ n). تُدعى قائمة مقبولة إذا لم يتزامن وجود كائنين متتاليين في النوع ، أي ، b _{i j} ≠ b _{i j + 1} للجميع j = 0 ، ... ، k - 2. يتم احتساب أهمية القائمة من خلال الصيغة $$$\ sum_ {j = 0} ^ {k-1} 2 _ {- j} r (a_ {i_j})$. تحتاج إلى العثور على قائمة الصلة القصوى بين جميع صالحة.

قرار

باستخدام حسابات رياضية بسيطة ، يمكن إثبات أن المشكلة يمكن حلها من خلال نهج "جشع" ، أي في القائمة المثلى للتوصيات ، كل عنصر لديه الكائن الأكثر صلة بكل ما هو صالح في بداية نفس القائمة. تنفيذ هذا النهج بسيط: نأخذ الأشياء على التوالي ونضيفها إلى الإجابة ، إن أمكن. عندما تتم مصادفة كائن غير صالح (يتزامن نوعه مع نوع العنصر السابق) ، فإننا نضعه جانباً في قائمة انتظار منفصلة ، نقوم بإدخاله في الاستجابة في أقرب وقت ممكن. لاحظ أنه في كل لحظة من الزمن ، سيكون لكل الكائنات في قائمة الانتظار نوع مطابق. في النهاية ، قد تبقى عدة كائنات في قائمة الانتظار ، ولن يتم تضمينها في الاستجابة.

  std::vector<int> blend(int n, int m, const std::vector<int>& types) { std::vector<int> result; std::queue<int> repeated; for (int i = 0; i < n; ++i) { if (result.empty() || types[result.back()] != types[i]) { result.push_back(i); if (!repeated.empty() && types[repeated.front()] != types[result.back()]) { result.push_back(repeated.front()); repeated.pop(); } } else { repeated.push(i); } } return result; } 

D. تجميع تسلسل الأحرف

هناك أبجدية محددة A = {a ₁ ، a ₂ ، ...، _{K - 1} ، a _K = S}، a ∈ {a، b، ...، z}، S هي نهاية السطر.

النظر في الطريقة التالية لإنشاء سلاسل عشوائية على الأبجدية A:

1. الحرف الأول x ₁ هو متغير عشوائي مع التوزيع P (x ₁ = a _i ) = q _i (من المعروف أن q _K = 0).
2. يتم إنشاء كل حرف تالي بناءً على الحرف السابق وفقًا للتوزيع الشرطي P (x _i = a _j || x _{i - 1} = a _l ) = p _jl .
3. إذا كانت x _i = S ، يتوقف الجيل وتكون النتيجة x ₁ × ₂ ... x _{i - 1} .

يتم توفير مجموعة من الخطوط الناتجة من مزيج من نموذجين الموصوفة مع معلمات مختلفة. من الضروري أن يعطي كل صف فهرس السلسلة التي تم إنشاؤه منها.

قرار

تم حل المشكلة باستخدام خوارزمية EM : من المفترض أن يتم إنشاء العينة المقدمة من خليط من اثنين من سلاسل Markov التي يتم استعادة المعلمات أثناء التكرار. تم وضع قيود بنسبة 80٪ من الإجابات الصحيحة بحيث لا تتأثر صحة الحل بأمثلة ذات احتمال كبير في كلتا السلسلتين. لذلك ، عند استعادة هذه الأمثلة بشكل صحيح ، يمكن تعيينها إلى سلسلة غير صحيحة من حيث الاستجابة التي تم إنشاؤها.

 import random import math EPS = 1e-9 def empty_row(size): return [0] * size def empty_matrix(rows, cols): return [empty_row(cols) for _ in range(rows)] def normalized_row(row): row_sum = sum(row) + EPS return [x / row_sum for x in row] def normalized_matrix(mtx): return [normalized_row(r) for r in mtx] def restore_params(alphabet, string_samples): n_tokens = len(alphabet) n_samples = len(string_samples) samples = [tuple([alphabet.index(token) for token in s] + [n_tokens - 1, n_tokens - 1]) for s in string_samples] probs = [random.random() for _ in range(n_samples)] for _ in range(200): old_probs = [x for x in probs] # probs fixed p0, A = empty_row(n_tokens), empty_matrix(n_tokens, n_tokens) q0, B = empty_row(n_tokens), empty_matrix(n_tokens, n_tokens) for prob, sample in zip(probs, samples): p0[sample[0]] += prob q0[sample[0]] += 1 - prob for t1, t2 in zip(sample[:-1], sample[1:]): A[t1][t2] += prob B[t1][t2] += 1 - prob A, p0 = normalized_matrix(A), normalized_row(p0) B, q0 = normalized_matrix(B), normalized_row(q0) trans_log_diff = [ [math.log(b + EPS) - math.log(a + EPS) for b, a in zip(B_r, A_r)] for B_r, A_r in zip(B, A) ] # A, p0, B, q0 fixed probs = empty_row(n_samples) for i, sample in enumerate(samples): value = math.log(q0[sample[0]] + EPS) - math.log(p0[sample[0]] + EPS) for t1, t2 in zip(sample[:-1], sample[1:]): value += trans_log_diff[t1][t2] probs[i] = 1.0 / (1.0 + math.exp(value)) if max(abs(x - y) for x, y in zip(probs, old_probs)) < 1e-9: break return [int(x > 0.5) for x in probs] def main(): N, K = list(map(int, input().split())) string_samples = [] alphabet = list(input().strip()) + [''] for _ in range(N): string_samples.append(input().rstrip()) result = restore_params(alphabet, string_samples) for r in result: print(r) if __name__ == '__main__': main() 

---

.