الشبكات العصبية والتعلم العميق ، الفصل 4: دليل مرئي على أن الشبكات العصبية يمكنها حساب أي وظيفة

في هذا الفصل ، أعطي شرحًا بسيطًا ومرئيًا في الغالب لنظرية الشمولية. لمتابعة المواد الموجودة في هذا الفصل ، لا يتعين عليك قراءة المواد السابقة. وهي منظمة كمقال مستقل. إذا كان لديك فهم أساسي لـ NS ، فيجب أن تكون قادرًا على فهم التفسيرات.


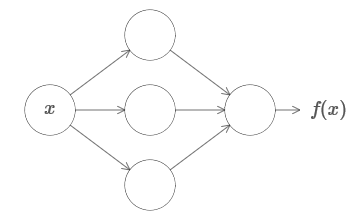
واحدة من أكثر الحقائق المدهشة حول الشبكات العصبية هي أنها تستطيع حساب أي وظيفة على الإطلاق. وهذا هو ، دعنا نقول أن شخصًا ما يعطيك نوعًا من الوظائف المعقدة والمتعرجة f (x):



وبغض النظر عن هذه الوظيفة ، هناك ما يضمن وجود هذه الشبكة العصبية التي بالنسبة لأي إدخال x فإن القيمة f (x) (أو بعض التقريب بالقرب منها) ستكون ناتج هذه الشبكة ، أي:



يعمل هذا حتى لو كانت دالة للعديد من المتغيرات f = f (x ₁ ، ... ، x _m ) ، ومع العديد من القيم. على سبيل المثال ، فيما يلي شبكة تحسب دالة ذات مدخلات m = 3 و n = 2 مخرجات:



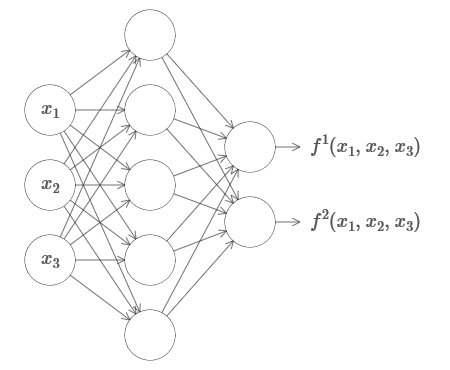
هذه النتيجة تشير إلى أن الشبكات العصبية لها عالمية معينة. بغض النظر عن الوظيفة التي نريد حسابها ، نعلم أن هناك شبكة عصبية يمكنها القيام بذلك.

علاوة على ذلك ، فإن نظرية الشمولية تظل قائمة حتى لو قصرنا الشبكة على طبقة واحدة بين الخلايا العصبية الواردة والصادرة - ما يسمى في طبقة واحدة خفية. لذلك حتى الشبكات ذات البنية البسيطة جدًا يمكن أن تكون قوية للغاية.

نظرية عالمية معروفة للناس الذين يستخدمون الشبكات العصبية. ولكن على الرغم من أن هذا هو الحال ، فإن فهم هذه الحقيقة ليس واسع الانتشار. ومعظم التفسيرات لهذا معقدة للغاية من الناحية الفنية. على سبيل المثال ، استخدمت إحدى الأوراق الأولى التي أثبتت هذه النتيجة نظرية هان-باناخ ، ونظرية تمثيل ريزز ، وبعض تحليلات فورييه. إذا كنت عالم رياضيات ، فمن السهل عليك فهم هذا الدليل ، لكن بالنسبة لمعظم الناس ، ليس بهذه السهولة. إنه لأمر مؤسف ، لأن الأسباب الأساسية للعالمية بسيطة وجميلة.

في هذا الفصل ، أعطي شرحًا بسيطًا ومرئيًا في الغالب لنظرية الشمولية. سنذهب خطوة بخطوة من خلال الأفكار الكامنة وراءه. سوف تفهم لماذا يمكن للشبكات العصبية حساب أي وظيفة بالفعل. سوف تفهم بعض القيود من هذه النتيجة. وسوف تفهم كيف ترتبط النتيجة مع NS العميق.

لمتابعة المواد الموجودة في هذا الفصل ، لا يتعين عليك قراءة المواد السابقة. وهي منظمة كمقال مستقل. إذا كان لديك فهم أساسي لـ NS ، فيجب أن تكون قادرًا على فهم التفسيرات. لكنني سأقدم أحيانًا روابط لمواد سابقة للمساعدة في سد الفجوات المعرفية.

غالبًا ما توجد نظريات العالمية في علوم الكمبيوتر ، لذلك في بعض الأحيان ننسى كم هي مدهشة. لكن الأمر يستحق تذكير نفسك: القدرة على حساب أي وظيفة تعسفية مدهشة حقًا. يمكن تقريبًا أي عملية يمكن تخيلها إلى حساب دالة. النظر في مهمة العثور على اسم التأليف الموسيقي على أساس مقطع قصير. يمكن اعتبار هذا حساب دالة. أو فكر في مهمة ترجمة نص صيني إلى الإنجليزية. وهذا يمكن اعتباره حساب دالة (في الواقع ، العديد من الوظائف ، نظرًا لوجود العديد من الخيارات المقبولة لترجمة نص واحد). أو فكر في مهمة إنشاء وصف لمؤامرة الفيلم وجودة التمثيل بناءً على ملف mp4. هذا ، أيضًا ، يمكن اعتباره بمثابة حساب لوظيفة معينة (الملاحظة الموجودة حول خيارات ترجمة النص صحيحة أيضًا هنا). العالمية تعني ، من حيث المبدأ ، أن NSs يمكنها أداء كل هذه المهام ، وغيرها الكثير.

بالطبع ، فقط من حقيقة أننا نعرف أن هناك NSs قادرة ، على سبيل المثال ، على ترجمة من الصينية إلى الإنجليزية ، لا يترتب على ذلك أن لدينا تقنيات جيدة لإنشاء أو حتى الاعتراف بهذه الشبكة. ينطبق هذا التقييد أيضًا على نظريات العالمية التقليدية لنماذج مثل المخططات المنطقية. ولكن ، كما رأينا بالفعل في هذا الكتاب ، لدى NS خوارزميات قوية لوظائف التعلم. مزيج من خوارزميات التعلم والتنوع هو مزيج جذاب. حتى الآن ، ركزنا في الكتاب على خوارزميات التدريب. في هذا الفصل ، سوف نركز على التنوع وماذا يعني ذلك.

اثنين من الحيل

قبل توضيح سبب صحة نظرية الشمولية ، أود أن أذكر حالتين واردة في البيان غير الرسمي "يمكن لشبكة عصبية حساب أي وظيفة".

أولاً ، هذا لا يعني أنه يمكن استخدام الشبكة لحساب أي وظيفة بدقة. يمكننا فقط الحصول على تقريب جيد كما نحتاج. عن طريق زيادة عدد الخلايا العصبية المخفية ، نقوم بتحسين التقريب. على سبيل المثال ، سبق لي أن أوضحت شبكة تقوم بحساب وظيفة معينة f (x) باستخدام ثلاث خلايا عصبية مخفية. بالنسبة لمعظم الوظائف ، باستخدام ثلاث خلايا عصبية ، يمكن الحصول على تقريب منخفض الجودة فقط. من خلال زيادة عدد الخلايا العصبية المخفية (على سبيل المثال ، ما يصل إلى خمسة) ، يمكننا عادة الحصول على تقريب محسّن:



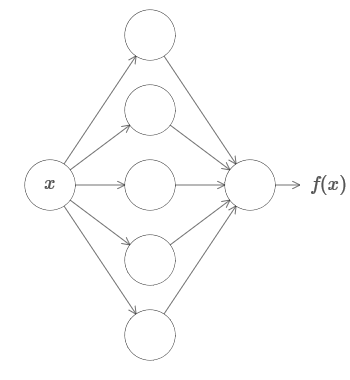
ولتحسين الموقف من خلال زيادة عدد الخلايا العصبية المخفية.

لتوضيح هذا البيان ، دعنا نقول أننا حصلنا على دالة f (x) ، والتي نريد حسابها ببعض الدقة اللازمة ε> 0. هناك ضمان بأنه عند استخدام عدد كافٍ من الخلايا العصبية المخفية ، يمكننا دائمًا العثور على NS يفي خرجه g (x) بالمعادلة | g (x) −f (x) | <ε لأي x. بمعنى آخر ، سيتم تحقيق التقريب بالدقة المطلوبة لأي قيمة إدخال ممكنة.

الصيد الثاني هو أن الوظائف التي يمكن تقريبها بالطريقة الموصوفة تنتمي إلى فئة مستمرة. إذا تمت مقاطعة الوظيفة ، فستحدث قفزات حادة مفاجئة ، في الحالة العامة سيكون من المستحيل التقريب بمساعدة NS. وهذا ليس مفاجئًا ، نظرًا لأن NSs لدينا يحسب الوظائف المستمرة لبيانات الإدخال. ومع ذلك ، حتى إذا كانت الوظيفة التي نحتاج فعلاً إلى حسابها غير متقطعة ، فغالبًا ما يكون التقريب مستمرًا تمامًا. إذا كان الأمر كذلك ، ثم يمكننا استخدام NS. في الممارسة العملية ، هذا القيد عادة ما يكون غير مهم.

نتيجة لذلك ، سيكون البيان الأكثر دقة لنظرية الشمولية هو أن NS مع طبقة مخفية واحدة يمكن استخدامها لتقريب أي وظيفة مستمرة بأي دقة مطلوبة. في هذا الفصل ، نثبت نسخة أقل صرامةً من هذه النظرية ، باستخدام طبقتين مخفيتين بدلاً من واحدة. في المهام ، سوف أصف بإيجاز كيف يمكن تكييف هذا الشرح ، مع تغييرات طفيفة ، لإثبات يستخدم طبقة مخفية واحدة فقط.

براعة مع إدخال واحد وقيمة الإخراج واحد

لفهم سبب صحة نظرية الشمولية ، نبدأ بفهم كيفية إنشاء دالة تقريبية NS مع إدخال واحد فقط وقيمة إخراج واحدة:



اتضح أن هذا هو جوهر مهمة العالمية. بمجرد أن نفهم هذه الحالة الخاصة ، سيكون من السهل جدًا توسيعها لتشمل العديد من قيم المدخلات والمخرجات.

لإنشاء فهم لكيفية إنشاء شبكة للحساب f ، نبدأ بشبكة تحتوي على طبقة مخفية واحدة مع اثنين من الخلايا العصبية المخفية ، ومع طبقة الإخراج التي تحتوي على الخلايا العصبية الإخراج واحد:



لتخيل كيف تعمل مكونات الشبكة ، نحن نركز على الخلية العصبية المخفية العليا. في المخطط في المقالة الأصلية ، يمكنك تغيير وزن الماوس بشكل تفاعلي من خلال النقر على "w" ونرى على الفور كيف تتغير الوظيفة المحسوبة بواسطة الخلية العصبية المخفية العليا:



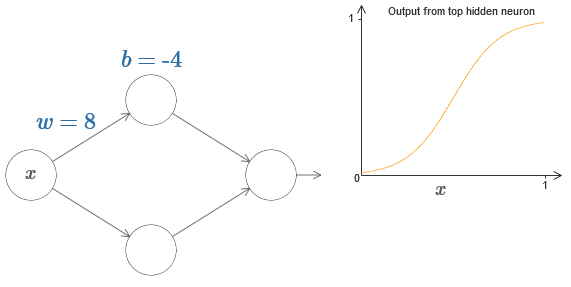
كما تعلمنا في وقت سابق من هذا الكتاب ، فإن عدد الخلايا العصبية المخفية هو σ (wx + b) ، حيث σ (z) ≡ 1 / (1 + e ^−z ) عبارة عن السيني . حتى الآن ، استخدمنا هذا الشكل الجبري في كثير من الأحيان. ومع ذلك ، لإثبات عالمية أنه سيكون من الأفضل إذا تجاهلنا تماما هذه الجبر ، وبدلاً من ذلك التلاعب ومراقبة الشكل على الرسم البياني. لن يساعدك ذلك على الشعور بشكل أفضل بما يحدث فحسب ، بل يمنحنا أيضًا دليلًا على الشمولية المطبقة على وظائف التنشيط الأخرى إلى جانب السيني.

بالمعنى الدقيق للكلمة ، النهج البصري الذي اخترته لا يعتبر تقليديًا دليلًا. لكنني أعتقد أن النهج البصري يوفر نظرة أكثر على حقيقة النتيجة النهائية من الدليل التقليدي. وبالطبع ، فإن هذا الفهم هو الهدف الحقيقي للبرهان. في الأدلة التي أقترحها ، ستظهر الفجوات بين الحين والآخر ؛ سأقدم أدلة بصرية معقولة ، ولكن ليس دائمًا. إذا كان هذا يزعجك ، ففكر في مهمتك لملء هذه الفجوات. ومع ذلك ، لا تغفل الهدف الرئيسي: فهم سبب صحة نظرية العالمية.

لتبدأ هذا الإثبات ، انقر على الإزاحة b في المخطط الأصلي واسحب إلى اليمين لتكبيره. سترى أنه مع زيادة الإزاحة ، ينتقل الرسم البياني إلى اليسار ، لكنه لا يغير الشكل.

ثم اسحبه إلى اليسار لتقليل الإزاحة. سترى أن الرسم البياني يتحرك إلى اليمين دون تغيير الشكل.

خفض الوزن إلى 2-3. سترى أنه كلما انخفض الوزن ، استقر المنحنى. حتى لا ينحني المنحنى عن الرسم البياني ، فقد تضطر إلى تصحيح الإزاحة.

أخيرًا ، ارفع الوزن إلى قيم أكبر من 100. سيصبح المنحنى أكثر انحدارًا ، ثم يقترب في النهاية من الخطوة. حاول ضبط الإزاحة بحيث تكون الزاوية في منطقة النقطة x = 0.3. يظهر الفيديو أدناه ما يجب أن يحدث:



يمكننا تبسيط تحليلنا إلى حد كبير من خلال زيادة الوزن بحيث يكون الإخراج تقريبًا جيدًا لوظيفة الخطوة. أدناه أنا بنيت إخراج الخلايا العصبية الخفية العليا للوزن ث = 999. هذه صورة ثابتة:



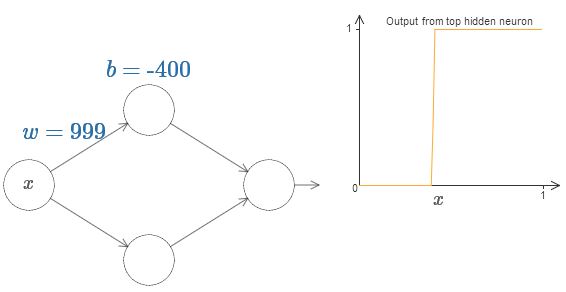
استخدام وظائف الخطوة أسهل قليلاً من السيني النموذجي. والسبب هو أن المساهمات من جميع الخلايا العصبية المخفية تضاف في طبقة المخرجات. من السهل تحليل مجموع مجموعة من الخطوات ، ولكن من الصعب التحدث عما يحدث عندما تتم إضافة مجموعة من المنحنيات في شكل السيني. لذلك ، سيكون من الأسهل بكثير افتراض أن الخلايا العصبية المخفية لدينا تنتج وظائف تدريجية. بتعبير أدق ، نقوم بذلك عن طريق تحديد الوزن عند قيمة كبيرة جدًا ، ثم تعيين موضع الخطوة خلال الإزاحة. بالطبع ، العمل مع الإخراج كدالة خطوة هو تقريبي ، لكنه جيد جدًا ، وحتى الآن سنتعامل مع هذه الوظيفة كدالة خطوة حقيقية. في وقت لاحق ، سأعود لمناقشة تأثير الانحرافات عن هذا التقريب.

ما قيمة x هي الخطوة؟ بمعنى آخر ، كيف يعتمد موضع الخطوة على الوزن والتشريد؟

للإجابة على السؤال ، حاول تغيير الوزن والإزاحة في المخطط التفاعلي. هل يمكنك فهم كيف يعتمد موضع الخطوة على w و b؟ من خلال الممارسة قليلاً ، يمكنك إقناع نفسك بأن موقعها يتناسب مع b ويتناسب عكسياً مع w.

في الواقع ، تكون الخطوة عند s = −b / w ، كما سنرى إذا قمنا بضبط الوزن والإزاحة على القيم التالية:



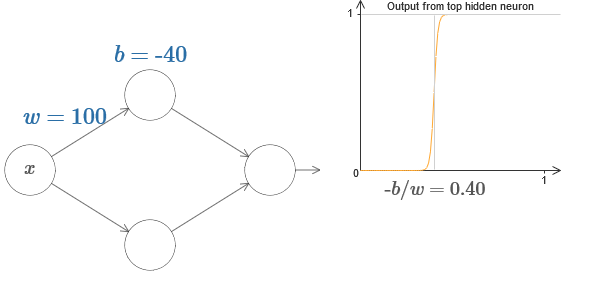
سيتم تبسيط حياتنا إلى حد كبير إذا وصفنا الخلايا العصبية المخفية مع معلمة واحدة ، ق ، وهذا هو ، من خلال موقف الخطوة ، ق = /b / ث. في المخطط التفاعلي التالي ، يمكنك ببساطة تغيير s:



كما هو مذكور أعلاه ، خصصنا بشكل خاص وزنًا عند الإدخال بقيمة كبيرة جدًا - كبيرة بما يكفي بحيث تصبح دالة الخطوة تقريبًا جيدًا. ويمكننا بسهولة تحويل الخلايا العصبية ذات المعلمات بهذه الطريقة إلى شكلها المعتاد من خلال اختيار التحيز b = −ws.

حتى الآن ، ركزنا على إخراج الخلايا العصبية الخفية المتفوقة فقط. لنلقِ نظرة على سلوك الشبكة بالكامل. لنفترض أن الخلايا العصبية المخفية تحسب وظائف الخطوة المحددة بواسطة معلمات الخطوتين s ₁ (الخلية العصبية العليا) و s ₂ (الخلية العصبية السفلى). الأوزان الخاصة بكل منها هي w ₁ و w ₂ . هنا شبكتنا:



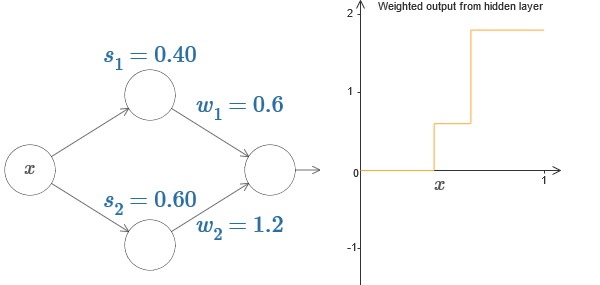
على اليمين يوجد رسم بياني للمخرجات المرجحة w ₁ a ₁ + w ₂ a ₂ للطبقة المخفية. هنا ₁ و ₂ هما مخرجات الخلايا العصبية الخفية العلوية والسفلية ، على التوالي. يتم الإشارة إليها بواسطة "a" ، حيث يطلق عليها غالبًا تنشيط الخلايا العصبية.

بالمناسبة ، نلاحظ أن إخراج الشبكة بالكامل هو σ (w ₁ a ₁ + w ₂ a ₂ + b) ، حيث b هو تحيز الخلايا العصبية للخرج. هذا ، بالطبع ، ليس هو نفسه الناتج المرجح للطبقة المخفية ، الرسم البياني الذي نبنيه. ولكن في الوقت الحالي ، سوف نركز على الإخراج المتوازن للطبقة المخفية ، وسنفكر فقط فيما بعد في كيفية ارتباطها بإخراج الشبكة بالكامل.

حاول زيادة وتقليل الخطوة _{1 من} الخلايا العصبية المخفية العليا على الرسم التخطيطي التفاعلي في المقالة الأصلية . انظر كيف يؤدي هذا إلى تغيير المخرجات المرجحة للطبقة المخفية. من المفيد بشكل خاص فهم ما يحدث عندما تتجاوز s ₁ s ₂ . سترى أن الرسم البياني في هذه الحالات يتغير شكله ، ونحن ننتقل من موقف يتم فيه تنشيط الخلايا العصبية المخفية العليا أولاً إلى موقف يتم فيه تنشيط الخلية العصبية السفلية المخفية أولاً.

بالمثل ، حاول معالجة الخطوة ₂ للخلية العصبية المخفية السفلية وانظر كيف يغير ذلك الناتج الكلي للخلايا العصبية المخفية.

محاولة لتقليل وزيادة الأوزان الإخراج. لاحظ كيف يقيس هذا مساهمة الخلايا العصبية الخفية المقابلة. ماذا يحدث إذا كانت إحدى الأوزان تساوي 0؟

أخيرًا ، حاول ضبط w من ₁ إلى 0.8 ثم من ₂ إلى -0.8. والنتيجة هي وظيفة "نتوء" ، مع بداية في s ₁ ، ونهاية في s ₂ ، وارتفاع 0.8. على سبيل المثال ، قد يبدو الإخراج الموزون كما يلي:



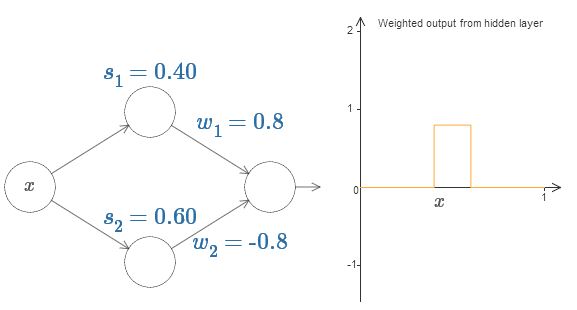
بالطبع ، يمكن توسيع النتوء إلى أي ارتفاع. دعنا نستخدم معلمة واحدة ، h ، تشير إلى الارتفاع. أيضًا ، من أجل البساطة ، سأتخلص من التدوين "s ₁ = ..." و "w ₁ = ...".



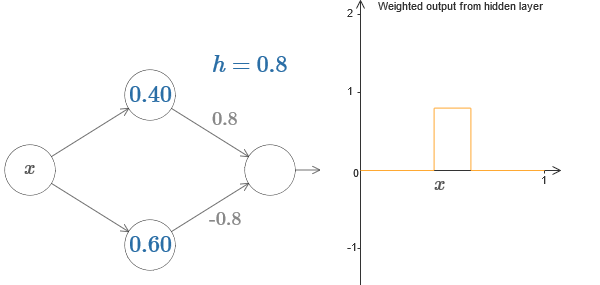
حاول زيادة وخفض قيمة h لمعرفة كيف يتغير ارتفاع البروز. محاولة لجعل ح سلبية. حاول تغيير نقاط الخطوات لمراقبة كيفية تغيير شكل البروز.

سترى أننا نستخدم خلايانا العصبية ليس فقط كبدائل رسومية ، ولكن أيضًا كوحدات أكثر دراية بالمبرمجين - شيء يشبه تعليمة if-if-else في البرمجة:

إذا الإدخال> = بداية الخطوة:
إضافة 1 إلى الناتج المرجح
آخر:
إضافة 0 إلى الناتج المرجح

بالنسبة للجزء الاكبر سألتزم بالرمز البياني. ومع ذلك ، قد يكون من المفيد في بعض الأحيان التبديل إلى طريقة العرض "if-then-else" والتفكير فيما يحدث في هذه الشروط.

يمكننا استخدام خدعة نتوء لدينا عن طريق لصق جزءين من الخلايا العصبية المخفية معًا على نفس الشبكة:



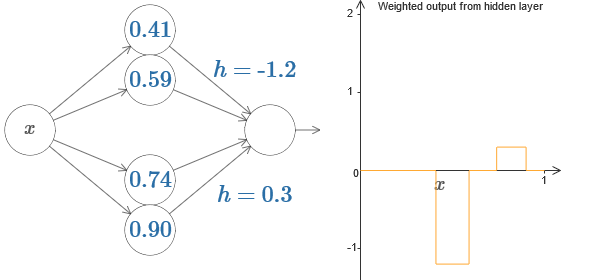
هنا أسقطت الأوزان ببساطة عن طريق كتابة قيم h لكل زوج من الخلايا العصبية المخفية. حاول اللعب بكلتا قيمتي h وشاهد كيف يغير الرسم البياني. حرك علامات التبويب ، وتغيير نقاط الخطوات.

في حالة أكثر عمومية ، يمكن استخدام هذه الفكرة للحصول على أي عدد مطلوب من القمم من أي ارتفاع. على وجه الخصوص ، يمكننا تقسيم الفاصل الزمني [0،1] إلى عدد كبير من الفواصل الفرعية (N) ، واستخدام أزواج N من الخلايا العصبية المخفية للحصول على قمم لأي ارتفاع مرغوب. دعونا نرى كيف يعمل هذا ل N = 5. هذا بالفعل الكثير من الخلايا العصبية ، لذلك أنا عرض تقديمي قليلاً. آسف للمخطط المعقد - يمكنني إخفاء التعقيد وراء تجريدات إضافية ، لكن يبدو لي أن الأمر يستحق القليل من العذاب مع التعقيد من أجل الشعور بشكل أفضل بكيفية عمل الشبكات العصبية.



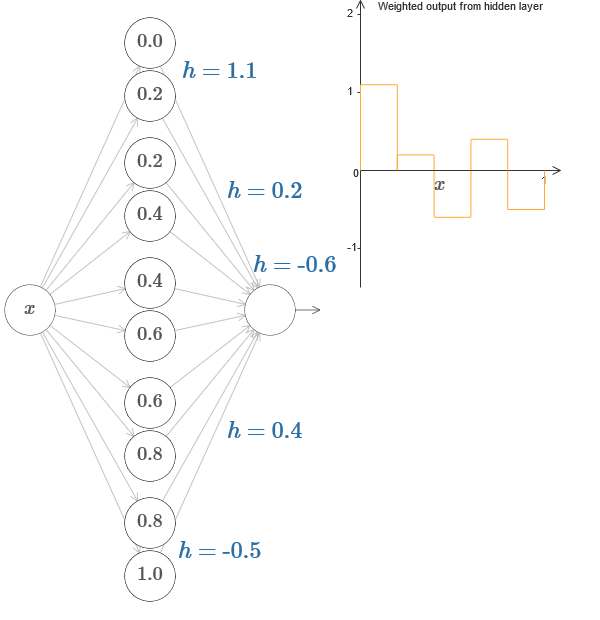
كما ترى ، لدينا خمسة أزواج من الخلايا العصبية المخفية. تقع نقاط خطوات الأزواج المقابلة في 0.1 / 5 ، ثم 1 / 5.2 / 5 ، وهكذا ، ما يصل إلى 4 / 5.5 / 5. هذه القيم ثابتة - نحصل على خمسة نتوءات متساوية العرض على الرسم البياني.

كل زوج من الخلايا العصبية له قيمة h المرتبطة به. تذكر أن اتصالات الخلايا العصبية الإخراج لها أوزان h و –h. في المقالة الأصلية على المخطط ، يمكنك النقر فوق قيم h ونقلها إلى اليسار. مع تغير في الطول ، يتغير الجدول أيضًا. من خلال تغيير أوزان المخرجات ، نقوم ببناء الوظيفة النهائية!

في المخطط ، لا يزال بإمكانك النقر على الرسم البياني ، وسحب ارتفاع الخطوات لأعلى أو لأسفل. عندما تقوم بتغيير ارتفاعه ، سترى كيف يتغير ارتفاع h المطابق. إخراج الأوزان + ح و- تغيير وفقا لذلك. بمعنى آخر ، نتعامل مباشرة مع دالة يظهر الرسم البياني بها على اليمين ونرى هذه التغييرات في قيم h على اليسار. يمكنك أيضًا الضغط باستمرار على زر الماوس في أحد النتوءات ، ثم سحب الماوس إلى اليسار أو اليمين ، وسوف يتم ضبط النتوءات على الارتفاع الحالي.

لقد حان الوقت لإنجاز المهمة.

أذكر الوظيفة التي رسمتها في بداية الفصل:



ثم لم أذكر هذا ، لكن في الحقيقة يبدو الأمر كما يلي:

$$

$$f (x) = 0.2 + 0.4 x ^ 2 + 0.3x \ sin (15 x) + 0.05 \ cos (50 x) \ tag {113}$$

يتم إنشاؤه لقيم س من 0 إلى 1 ، والقيم على طول المحور ص تختلف من 0 إلى 1.

من الواضح أن هذه الوظيفة غير بديهية. وعليك معرفة كيفية حسابها باستخدام الشبكات العصبية.

في شبكاتنا العصبية أعلاه ، قمنا بتحليل توليفة مرجحة w _j w _j of من مخرجات الخلايا العصبية المخفية. نحن نعرف كيفية الحصول على سيطرة كبيرة على هذه القيمة. ولكن ، كما أشرت سابقًا ، هذه القيمة لا تساوي ناتج الشبكة. إخراج الشبكة هو σ (∑ _j w _j a _j + b) ، حيث b هو إزاحة الخلايا العصبية الناتجة. هل يمكننا التحكم مباشرة في إخراج الشبكة؟

يكمن الحل في تطوير شبكة عصبية يتم فيها إعطاء الناتج الموزون للطبقة المخفية بالمعادلة σ ⁻¹ ⋅f (x) ، حيث σ ⁻¹ هي الوظيفة العكسية لـ σ. بمعنى ، نريد أن يكون الإخراج المرجح للطبقة المخفية كما يلي:



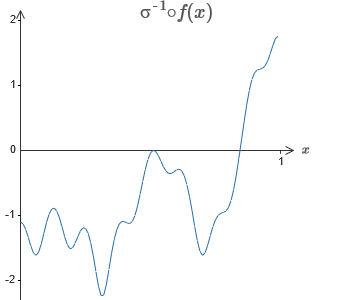إذا نجح ذلك ، فسيكون ناتج الشبكة بالكامل تقريبًا جيدًا لـ f (x) (قمت بتعيين إزاحة الخلايا العصبية الناتجة على 0).

ثم مهمتك هي تطوير NS تقريب الوظيفة الموضوعية الموضحة أعلاه. لفهم ما يحدث بشكل أفضل ، أوصي بأن تحل هذه المشكلة مرتين. لأول مرة في المقالة الأصلية ، انقر على الرسم البياني ، واضبط ارتفاعات النتوءات المختلفة مباشرةً. سيكون من السهل عليك الحصول على تقريب جيد للوظيفة الموضوعية. يتم تقدير درجة التقريب بواسطة متوسط ​​الانحراف ، والفرق بين الوظيفة الهدف والوظيفة التي تحسبها الشبكة. مهمتك هي جعل متوسط ​​الانحراف إلى الحد الأدنى للقيمة. تعتبر المهمة مكتملة عندما لا يتجاوز متوسط ​​الانحراف 0.40.



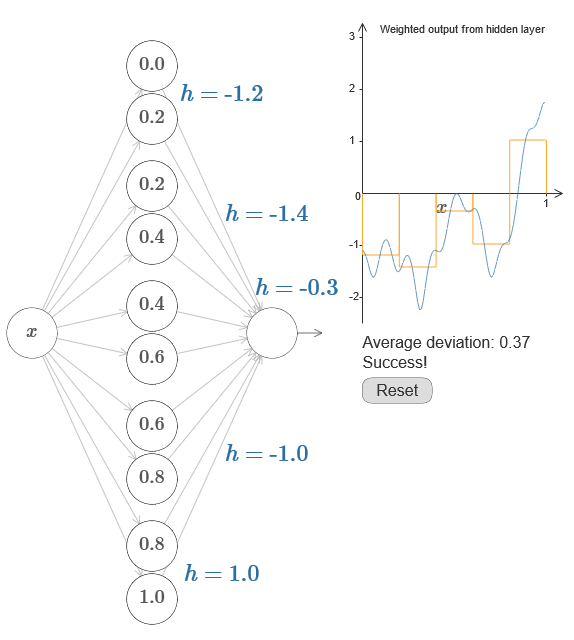بعد تحقيق النجاح ، اضغط على زر إعادة الضبط ، والذي يغير علامات التبويب بشكل عشوائي. في المرة الثانية ، لا تلمس الرسم البياني ، ولكن قم بتغيير قيم h على الجانب الأيسر من الرسم البياني ، في محاولة لجعل متوسط ​​الانحراف إلى قيمة 0.40 أو أقل.

وهكذا ، فقد وجدت جميع العناصر اللازمة للشبكة لحساب الدالة f (x) تقريبًا! تبين أن التقريب تقريبي ، لكن يمكننا بسهولة تحسين النتيجة ببساطة عن طريق زيادة عدد أزواج الخلايا العصبية المخفية ، مما سيزيد من عدد النتوءات.

على وجه الخصوص ، من السهل تحويل جميع البيانات التي تم العثور عليها مرة أخرى إلى طريقة العرض القياسية مع استخدام المعلمات NS. اسمحوا لي أن أذكرك بسرعة كيف يعمل هذا.

في الطبقة الأولى ، لكل الأوزان قيمة ثابتة كبيرة ، على سبيل المثال ، w = 1000.

يتم حساب تشريد الخلايا العصبية المخفية من خلال ب = −ws. لذلك ، على سبيل المثال ، بالنسبة للخلية العصبية الثانية المخفية ، يتحول s = 0.2 إلى b = 0001000 × 0.2 = −200.

يتم تحديد الطبقة الأخيرة من المقياس بواسطة قيم h. لذلك ، على سبيل المثال ، القيمة التي حددتها لأول h ، h = -0.2 ، تعني أن أوزان الخرج للخلايا العصبية المخفية العلوية هما -0.2 و 0.2 ، على التوالي. وهلم جرا ، لطبقة كاملة من الأوزان الإخراج.

أخيرًا ، إزاحة الخلايا العصبية الناتجة هو 0.

وهذا كل شيء: لقد حصلنا على وصف كامل لنظام NS ، الذي يحسب الوظيفة الموضوعية الأولية جيدًا. ونحن نفهم كيفية تحسين جودة التقريب من خلال تحسين عدد الخلايا العصبية المخفية.

بالإضافة إلى ذلك ، في وظيفتنا الهدف الأصلي f (x) = 0.2 + 0.4x ²+ 0.3sin (15x) + 0.05cos (50x) ليس شيئًا مميزًا. يمكن استخدام إجراء مماثل لأي وظيفة مستمرة على الفواصل الزمنية من [0،1] إلى [0،1]. في الواقع ، نحن نستخدم NS طبقة واحدة لإنشاء جدول بحث لوظيفة. ويمكن أن نأخذ هذه الفكرة كأساس للحصول على دليل عام على العالمية.

وظيفة العديد من المعلمات

نوسع نتائجنا إلى حالة مجموعة من متغيرات الإدخال. يبدو الأمر معقدًا ، ولكن يمكن بالفعل فهم جميع الأفكار التي نحتاجها للحالة باستخدام متغيرين واردين فقط. لذلك ، نعتبر الحالة مع اثنين من المتغيرات الواردة.

لنبدأ بالنظر إلى ما يحدث عندما يكون للخلية العصبية مدخلات اثنين: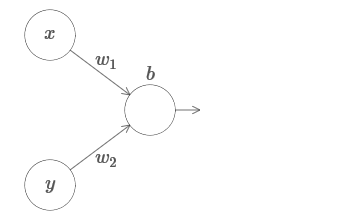



لدينا مدخلات x و y ، مع أوزان مقابلة w ₁ و w ₂ وتعويض b للخلايا العصبية. لقد حددنا وزن w ₂ إلى 0 ونلعب مع الأول ، w ₁ ، ونعوض b لنرى كيف تؤثر على إخراج الخلايا العصبية:



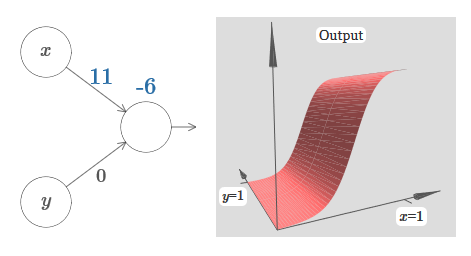كما ترون ، مع w ₂ = 0 ، لا يؤثر الإدخال y على إخراج الخلايا العصبية. كل شيء يحدث كما لو أن x هو الإدخال الوحيد.

بالنظر إلى هذا ، ماذا تعتقد أنه سيحدث عندما نزيد وزن w ₁ إلى w ₁ = 100 و ₂ w يترك 0؟ إذا لم يكن هذا الأمر واضحًا لك على الفور ، فكر قليلاً في هذه المشكلة. ثم شاهد الفيديو التالي ، والذي يوضح ما سيحدث:



كما كان من قبل ، مع زيادة في وزن الإدخال ، يقترب الإخراج من شكل الخطوة. الفرق هو أن وظيفة الخطوة لدينا تقع الآن في ثلاثة أبعاد. كما كان من قبل ، يمكننا نقل موقع الخطوات عن طريق تغيير الإزاحة. ستكون الزاوية عند النقطة s _x ≡ - b / w1.

دعنا نعيد الرسم البياني بحيث تكون المعلمة هي موقع الخطوة:



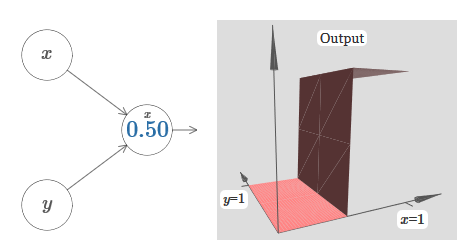نفترض أن وزن إدخال x له أهمية كبيرة - لقد استخدمت w ₁ = 1000 - والوزن w ₂ = 0. الرقم الموجود على الخلية العصبية هو موضع الخطوة ، ويذكّرنا x بالأعلى بأننا نحرك الخطوة على طول محور x. بطبيعة الحال ، من الممكن تمامًا الحصول على وظيفة خطوة على طول المحور y ، مما يجعل الوزن الوارد لـ y كبيرًا (على سبيل المثال ، w ₂= 1000) ، والوزن لـ x هو 0 ، w ₁ = 0:



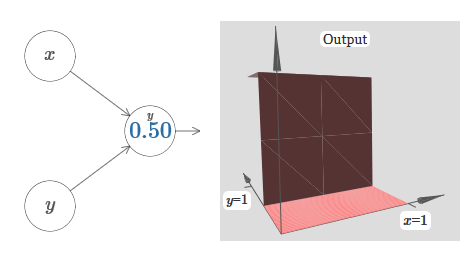يشير الرقم الموجود على الخلية العصبية ، مرة أخرى ، إلى موضع الخطوة ، ويذكّرنا y أعلاه بأننا نحرك الخطوة على طول محور y. يمكنني تحديد أوزان x و y مباشرةً ، لكنني لم أقم بذلك ، لأن ذلك سيؤدي إلى تناثر المخطط. لكن ضع في اعتبارك أن علامة y تشير إلى أن وزن y كبير ، وأن x هو 0.

يمكننا استخدام وظائف الخطوة التي صممناها للتو لحساب وظيفة protrusion ثلاثية الأبعاد. للقيام بذلك ، نأخذ اثنين من الخلايا العصبية ، كل منها سوف يحسب وظيفة خطوة على طول المحور س. ثم نجمع بين وظائف الدوال هذه مع الأوزان h و –h ، حيث h هو ارتفاع البروز المرغوب. كل هذا يمكن رؤيته في المخطط التالي:



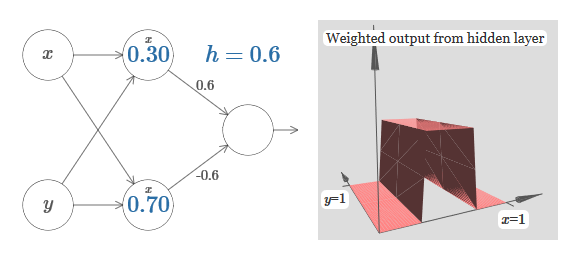حاول تغيير قيمة h. تعرف على كيفية ارتباطها بأوزان الشبكة. وكيف أنها تغير ارتفاع وظيفة نتوء على اليمين.

حاول أيضًا تغيير نقطة الخطوة ، حيث يتم تعيين القيمة إلى 0.30 في الخلية العصبية المخفية العليا. انظر كيف يغير شكل نتوء. ماذا يحدث إذا قمت بنقله إلى ما بعد نقطة 0.70 المرتبطة بالخلية العصبية السفلية المخفية؟

تعلمنا كيفية بناء وظيفة نتوء على طول المحور س. بطبيعة الحال ، يمكننا بسهولة إنشاء وظيفة البروز على طول المحور y ، باستخدام وظيفتين من الخطوات على طول المحور y. تذكر أنه يمكننا القيام بذلك عن طريق إنشاء أوزان كبيرة عند الإدخال y ، وتحديد الوزن عند الإدخال x. وماذا يحدث:



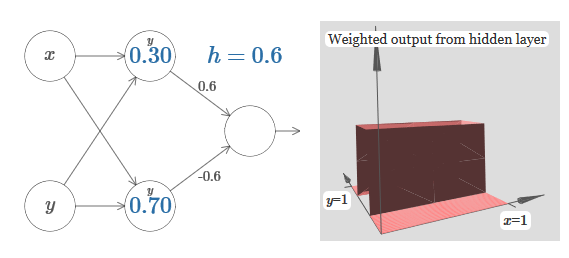يبدو متطابقة تقريبا إلى الشبكة السابقة! التغيير الوحيد المرئي هو علامات y الصغيرة على الخلايا العصبية المخفية. يذكرونهم بأنهم ينتجون وظائف خطوة لـ y ، وليس لـ x ، لذلك عند المدخلات y يكون الوزن كبيرًا للغاية وعند الإدخال x هو صفر ، وليس العكس. كما كان من قبل ، قررت عدم إظهارها مباشرة ، حتى لا تضرب الصورة.

دعونا نرى ما يحدث إذا قمنا بإضافة وظيفتين بارزتين ، إحداهما على طول المحور س ، والآخر على طول المحور ص ، وكلاهما بارتفاع h:



لتبسيط مخطط الاتصال بوزن صفري ، لقد حذفت. حتى الآن ، تركت علامات x و y صغيرة على الخلايا العصبية المخفية لأتذكر الاتجاهات التي تُحسب فيها وظائف البروز. في وقت لاحق سوف نرفضهم ، حيث يتم تضمينها بواسطة المتغير الوارد.

حاول تغيير المعلمة ح. كما ترون ، لهذا السبب ، تتغير أوزان المخرجات ، وكذلك أوزان كلتا الدالتين protrusion ، x و y.

إن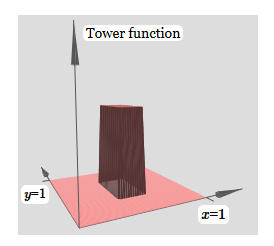



إنشاءنا يشبه إلى حد ما "وظيفة البرج": إذا استطعنا إنشاء مثل هذه الوظائف البرجية ، فيمكننا استخدامها لتقريب الوظائف التعسفية عن طريق إضافة أبراج ذات ارتفاعات مختلفة في أماكن مختلفة:



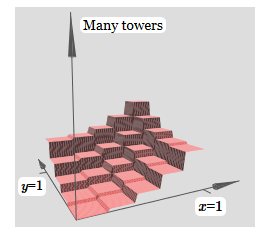بالطبع ، لم نصل بعد إلى إنشاء وظيفة برج تعسفية. حتى الآن ، قمنا ببناء شيء يشبه البرج المركزي للارتفاع 2 ساعة مع هضبة الارتفاع ح تحيط به.

ولكن يمكننا أن نجعل وظيفة البرج. تذكر أننا سبق أن أوضحنا كيف يمكن استخدام الخلايا العصبية لتنفيذ عبارة if-then-else:

if  >= :  1 else:  0 

وكان الخلايا العصبية المدخلات واحد. ونحن بحاجة إلى تطبيق فكرة مماثلة على الناتج المشترك للخلايا العصبية المخفية:

  if     >= :  1 else:  0 

إذا اخترنا العتبة الصحيحة - على سبيل المثال ، 3 ساعات / 2 ، يتم ضغطها بين ارتفاع الهضبة وارتفاع البرج المركزي - يمكننا سحق الهضبة إلى الصفر ، وترك برج واحد فقط.

تخيل كيف تفعل هذا؟ حاول تجربة الشبكة التالية. نحن الآن نرسم مخرجات الشبكة بالكامل ، وليس فقط المخرجات المرجحة للطبقة المخفية. هذا يعني أننا نضيف مصطلح الإزاحة إلى المخرجات المرجحة من الطبقة المخفية ، ونطبق السيني. هل يمكنك العثور على قيم h و b التي تحصل على برج لها؟ إذا واجهتك مشكلة في هذه المرحلة ، فإليك بعض النصائح: (1) للخلية العصبية المنتهية ولايتها لإظهار سلوك ما بعد ذلك ، نحتاج إلى أن تكون الأوزان الواردة (كل h أو h) كبيرة ؛ (2) تحدد قيمة b مقياس عتبة if-then-else.



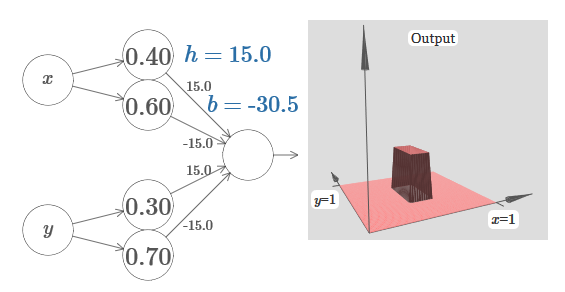
مع المعلمات الافتراضية ، يشبه الإخراج نسخة بالارض من الرسم البياني السابق ، مع برج وهضبة. للحصول على السلوك المطلوب ، تحتاج إلى زيادة قيمة h. هذا سوف يعطينا السلوك العتبة لـ if-then-else. ثانياً ، من أجل تعيين العتبة بشكل صحيح ، يجب على المرء أن يختار b ≈ h3h / 2.

إليك ما يبدو عليه بالنسبة إلى h = 10:


حتى بالنسبة للقيم المتواضعة نسبيًا لـ h ، نحصل على وظيفة برج جميلة. وبطبيعة الحال ، يمكننا الحصول على نتيجة جميلة بشكل تعسفي عن طريق زيادة h أكثر والحفاظ على التحيز عند المستوى b = h3h / 2.

دعونا نحاول لصق شبكتين معًا لحساب وظيفتي برج مختلفتين. لتوضيح أدوار كل من الشبكتين الفرعيتين ، أضعهما في مستطيلات منفصلة: كل منهما يحسب وظيفة البرج باستخدام التقنية الموضحة أعلاه. يوضح الرسم البياني الموجود على اليمين المخرجات المرجحة للطبقة المخفية الثانية ، أي المجموعة الموزونة لوظائف البرج.



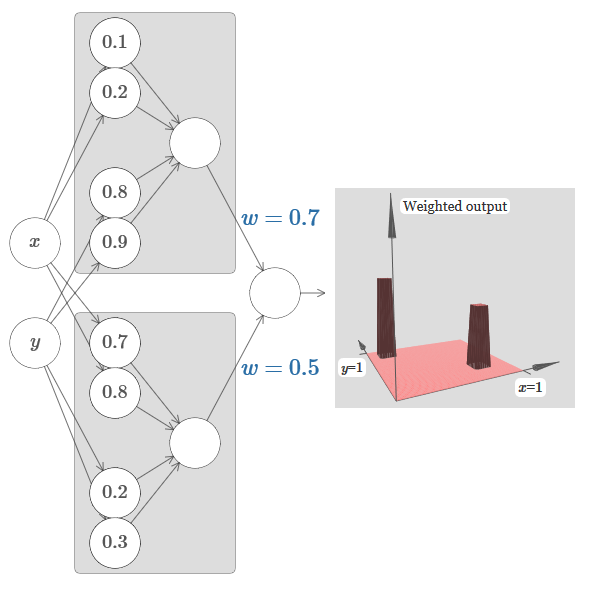
على وجه الخصوص ، يمكن ملاحظة أنه من خلال تغيير الوزن في الطبقة الأخيرة ، يمكنك تغيير ارتفاع أبراج الإخراج.

تتيح لك الفكرة نفسها حساب أكبر عدد تريده من الأبراج. يمكننا أن نجعلها نحيفة وطويلة التعسفي. نتيجة لذلك ، نحن نضمن أن الإخراج المرجح للطبقة المخفية الثانية يقارب أي وظيفة مطلوبة لمتغيرين:



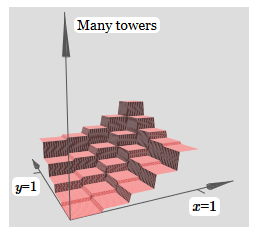
على وجه الخصوص ، من خلال جعل الناتج الموزون للطبقة المخفية الثانية تقريبًا σ ⁻¹ ⋅ جيدًا ، فإننا نضمن أن إخراج شبكتنا سيكون تقريبًا جيدًا للوظيفة المرغوبة f.

ماذا عن وظائف العديد من المتغيرات؟

دعونا نحاول أن نأخذ ثلاثة متغيرات ، × ₁ ، × ₂ ، × ₃ . هل يمكن استخدام الشبكة التالية لحساب وظيفة البرج بأربعة أبعاد؟



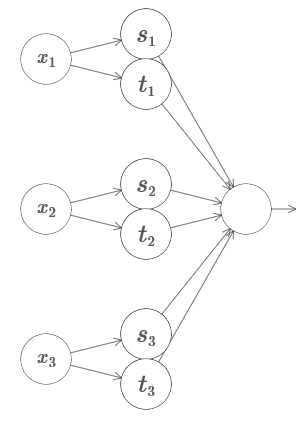
هنا x ₁ ، x ₂ ، x ₃ تدل على إدخال الشبكة. s ₁ ، t _{1 ،} وهكذا - نقاط خطوة للخلايا العصبية - أي أن جميع الأوزان في الطبقة الأولى كبيرة ، ويتم تعيين الإزاحات بحيث تكون نقاط الخطوات هي s ₁ ، t ₁ ، s ₂ ، ... الأوزان في الطبقة الثانية بديلة ، + h ، ،h ، حيث h عدد كبير للغاية. إزاحة الإخراج هو h5h / 2.

تحسب الشبكة وظيفة تساوي 1 في ظل ثلاثة شروط: × ₁ بين s ₁ و t ₁ ؛ × ₂ بين s ₂ و t ₂ ؛ × ₃ بين s ₃ و t ₃ . الشبكة هي 0 في جميع الأماكن الأخرى. هذا برج فيه 1 جزء صغير من مساحة المدخل ، و 0 هو كل شيء آخر.

عند الإلصاق بالكثير من هذه الشبكات ، يمكننا الحصول على أكبر عدد ممكن من الأبراج كما نحب ، وتقريب وظيفة تعسفية من ثلاثة متغيرات. نفس الفكرة تعمل في أبعاد م. يتم تغيير إزاحة الخرج (+m + 1/2) h فقط للضغط بشكل صحيح على القيم المطلوبة وإزالة الهضبة.

حسنًا ، نحن نعرف الآن كيفية استخدام NS لتقريب الوظيفة الحقيقية للعديد من المتغيرات. ماذا عن وظائف المتجه f (x ₁ ، ... ، x _m ) ∈ R ⁿ ؟ بالطبع ، يمكن اعتبار هذه الوظيفة مجرد وظائف حقيقية منفصلة n f1 (x ₁ ، ... ، x _m ) ، f2 (x ₁ ، ... ، x _m ) ، وهكذا. وبعد ذلك نحن فقط الغراء جميع الشبكات معا. لذلك من السهل معرفة ذلك.

مهمة

• لقد رأينا كيفية استخدام الشبكات العصبية ذات طبقتين مخفيتين لتقريب وظيفة تعسفية. هل يمكنك إثبات أن هذا ممكن مع طبقة واحدة مخفية؟ تلميح - حاول العمل باستخدام متغيري إخراج فقط ، وأظهر ما يلي: (أ) من الممكن الحصول على وظائف الخطوات ليس فقط على محاور س أو ص ، ولكن أيضًا في اتجاه تعسفي ؛ (ب) إضافة العديد من الإنشاءات من الخطوة (أ) ، من الممكن تقريب وظيفة جولة بدلاً من برج مستطيل ؛ © باستخدام الأبراج الدائرية ، من الممكن تقريب الوظيفة التعسفية. ستكون الخطوة © أسهل في استخدام المواد المعروضة في هذا الفصل أدناه بقليل.

تجاوز الخلايا العصبية السيني

لقد أثبتنا أن شبكة من الخلايا العصبية السيني يمكن حساب أي وظيفة. تذكر أنه في الخلايا العصبية السينية ، تتحول المدخلات x ₁ ، x ₂ ، ... عند الخرج إلى σ (∑ _j w _j x _{j j} + b) ، حيث w w هي الأوزان ، b هي الانحراف ، و σ هي السيني.



ماذا لو نظرنا إلى نوع آخر من الخلايا العصبية باستخدام وظيفة تنشيط مختلفة ، s (z):



أي أننا نفترض أنه إذا كانت الخلايا العصبية تحتوي على x ₁ و x ₂ و ... الأوزان w ₁ و w ₂ و ... والتحيز b ، فسيتم إخراج s (w _j w _j x _j + b).

يمكننا استخدام وظيفة التنشيط هذه للتخطي ، تمامًا كما في حالة السيني. حاول (في المقالة الأصلية ) في الرسم التخطيطي رفع الوزن إلى ، على سبيل المثال ، w = 100:





كما في حالة السيني ، لهذا السبب ، يتم ضغط وظيفة التنشيط ، ونتيجة لذلك تتحول إلى تقريب جيد للغاية لوظيفة الخطوة. حاول تغيير الإزاحة ، وسترى أنه يمكننا تغيير موقع الخطوة إلى أي. لذلك ، يمكننا استخدام نفس الحيل كما كان من قبل لحساب أي وظيفة مطلوبة.

ما هي الخصائص التي يجب أن تحتويها s (z) حتى تعمل؟ يجب أن نفترض أن s (z) معرّفة جيدًا على أنها z → −∞ و z → ∞. هذه الحدود هي اثنين من القيم المقبولة من قبل وظيفة خطوة لدينا. نحتاج أيضًا إلى افتراض أن هذه الحدود مختلفة. إذا لم يختلفوا ، فلن تنجح الخطوات ؛ سيكون هناك ببساطة جدول زمني ثابت! ولكن إذا كانت دالة التنشيط s (z) تفي بهذه الخصائص ، فإن الخلايا العصبية المستندة إليها مناسبة عالميًا لإجراء العمليات الحسابية.

المهام

• في وقت سابق من هذا الكتاب ، التقينا بنوع مختلف من الخلايا العصبية - الخلايا العصبية الخطية المستقيمة ، أو الوحدة الخطية المصححة ، ReLU. وضح سبب عدم تلبية هذه الخلايا العصبية للظروف اللازمة للعالمية. ابحث عن دليل على تعدد الاستخدامات يوضح أن ReLUs مناسبة عالميًا للحوسبة.
• لنفترض أننا نفكر في الخلايا العصبية الخطية ، مع وظيفة التنشيط s (z) = z. اشرح سبب عدم تلبية الخلايا العصبية الخطية لظروف العالمية. تبين أن مثل هذه الخلايا العصبية لا يمكن استخدامها للحوسبة العالمية.

إصلاح وظيفة الخطوة

في الوقت الحاضر ، افترضنا أن الخلايا العصبية لدينا تنتج وظائف خطوة دقيقة. هذا تقريب جيد ، ولكن فقط تقريب. في الواقع ، هناك فجوة ضيقة من الفشل ، كما هو موضح في الرسم البياني التالي ، حيث لا تتصرف الدالات على الإطلاق كدالة خطوة:



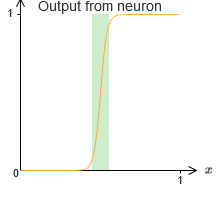
في فترة الفشل هذه ، لا يعمل تفسيري للعالمية.

الفشل ليس مخيف جدا. من خلال تحديد أوزان إدخال كبيرة بما فيه الكفاية ، يمكننا جعل هذه الفجوات صغيرة بشكل تعسفي. يمكننا أن نجعلها أصغر بكثير من على الرسم البياني ، غير مرئية للعين. لذلك ربما لا داعي للقلق بشأن هذه المشكلة.

ومع ذلك ، أود الحصول على طريقة لحلها.

اتضح أنه من السهل حلها. دعنا ننظر إلى هذا الحل لحساب وظائف NS مع إدخال وإخراج واحد فقط. نفس الأفكار سوف تعمل على حل المشكلة مع عدد كبير من المدخلات والمخرجات.

على وجه الخصوص ، لنفترض أننا نريد لشبكتنا حساب بعض الوظائف f. كما حدث من قبل ، نحاول القيام بذلك عن طريق تصميم الشبكة بحيث يكون الناتج المرجح للطبقة المخفية من الخلايا العصبية هو ⋅1 ⋅f (x):



إذا قمنا بذلك باستخدام التقنية الموضحة أعلاه ، فسوف نجبر الخلايا العصبية المخفية على إنتاج سلسلة من وظائف البروز:



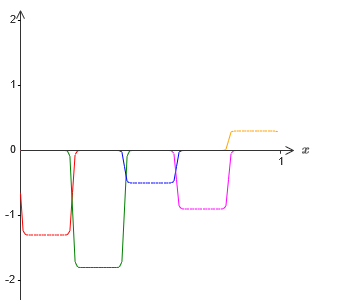
بالطبع ، بالغت في حجم فترات الفشل ، بحيث كان من السهل رؤيتها. يجب أن يكون من الواضح أننا إذا أضفنا كل هذه الوظائف من النتوءات ، فسوف نحصل على تقريب جيد إلى حد ما من σ1 ⋅f (x) في كل مكان باستثناء فترات الفشل.

ولكن لنفترض أنه بدلاً من استخدام التقريب الموصوف للتو ، فإننا نستخدم مجموعة من الخلايا العصبية المخفية لحساب تقريب نصف وظيفتنا الهدف الأصلية ، أي σ1 ⋅f (x) / 2. بالطبع ، سيبدو تمامًا كنسخة مصغرة لأحدث رسم بياني:



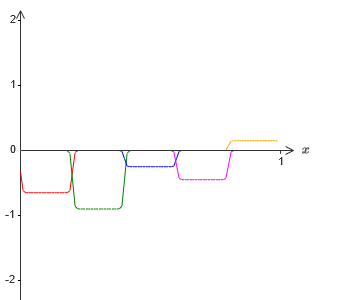
لنفترض أننا نجعل مجموعة أخرى من الخلايا العصبية المخفية تحسب التقريب إلى ⋅1 ⋅f (x) / 2 ، ومع ذلك ، في قاعدتها سيتم تحويل النتوءات بمقدار النصف بعرضها:



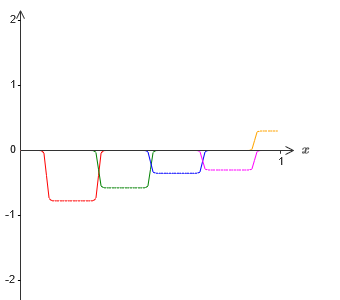
الآن لدينا تقريبان مختلفان لـ σ - 1⋅f (x) / 2. إذا أضفنا هاتين التقريبتين ، نحصل على تقريب عام إلى σ - 1⋅f (x). سيظل هذا التقريب العام يحتوي على معلومات غير دقيقة على فترات زمنية صغيرة. لكن المشكلة ستكون أقل من ذي قبل - لأن النقاط التي تقع في فترات فشل التقريب الأول لن تقع في فترات فشل التقريب الثاني. لذلك ، سيكون التقريب في هذه الفواصل الزمنية أفضل مرتين تقريبًا.

يمكننا تحسين الموقف عن طريق إضافة عدد كبير ، M ، لتقريب الوظيفة of - 1⋅f (x) / M. إذا كانت جميع الفواصل الزمنية للفشل ضيقة بما فيه الكفاية ، فسيكون أي تيار في واحدة منها فقط. إذا كنت تستخدم عددًا كبيرًا بشكل كافٍ من التقريبية المتداخلة لـ M ، فإن النتيجة تقريب عام ممتاز.

استنتاج

بالتأكيد لا يمكن أن يسمى تفسير الشمولية الذي تمت مناقشته هنا وصفًا عمليًا لكيفية حساب الوظائف باستخدام الشبكات العصبية! في هذا المعنى ، هو أشبه دليل على براعة بوابات المنطق NAND وأكثر من ذلك. لذلك ، حاولت بشكل أساسي جعل هذا التصميم واضحًا وسهل المتابعة دون تحسين تفاصيله. ومع ذلك ، فإن محاولة تحسين هذا التصميم يمكن أن تكون تمرينًا مثيرًا ومفيدًا لك.

على الرغم من أن النتيجة التي تم الحصول عليها لا يمكن استخدامها مباشرة لإنشاء NS ، إلا أنها مهمة لأنها تزيل مسألة قابلية حساب أي وظيفة معينة باستخدام NS. الإجابة على هذا السؤال ستكون دائما إيجابية. لذلك ، فمن الصحيح أن نسأل ما إذا كانت أي وظيفة قابلة للحساب ، ولكن ما هي الطريقة الصحيحة لحسابها.

يستخدم تصميمنا العالمي طبقتين مخفيتين فقط لحساب دالة تعسفية. كما ناقشنا ، من الممكن الحصول على نفس النتيجة بطبقة واحدة مخفية. بالنظر إلى ذلك ، قد تتساءل عن سبب حاجتنا إلى شبكات عميقة ، أي شبكات بها عدد كبير من الطبقات المخفية. ألا يمكننا استبدال هذه الشبكات بشبكات ضحلة لها طبقة خفية واحدة؟

على الرغم من أنه من الممكن ، من حيث المبدأ ، وجود أسباب عملية جيدة لاستخدام الشبكات العصبية العميقة. كما هو موضح في الفصل 1 ، فإن NSs العميقة لها هيكل هرمي يسمح لها بالتكيف بشكل جيد لدراسة المعرفة الهرمية ، والتي هي مفيدة لحل المشاكل الحقيقية. وبشكل أكثر تحديدًا ، عند حل المشكلات مثل التعرف على الأنماط ، من المفيد استخدام نظام لا يفهم فقط وحدات البكسل الفردية ، ولكن أيضًا المفاهيم المعقدة بشكل متزايد: من الحدود إلى الأشكال الهندسية البسيطة ، وما وراءها ، إلى المشاهد المعقدة التي تتضمن عدة كائنات. في الفصول اللاحقة ، سنرى دليلًا مؤيدًا لحقيقة أن NSs العميقة سيكونون أكثر قدرة على التعامل مع دراسة هذه التسلسلات الهرمية للمعرفة أكثر من تلك الضحلة. لتلخيص: العالمية تخبرنا أن NS يمكن حساب أي وظيفة. تشير الدلائل التجريبية إلى أن NSs العميقة تتكيف بشكل أفضل مع دراسة الوظائف المفيدة لحل العديد من مشكلات العالم الحقيقي.