طريقة تحليل الكتلة الجديدة

يتم اقتراح طريقة جديدة لتحليل الكتلة. ميزته في خوارزمية أقل تعقيدًا من الناحية الحسابية. تعتمد الطريقة على حساب الأصوات لحقيقة أن زوجًا من الكائنات موجود في نفس الفئة من معلومات حول قيمة الإحداثيات الفردية.

مقدمة

هناك حاجة كبيرة لتحليل البيانات وتطوير أساليب التصنيف الفعال. في مثل هذه الطرق ، يلزم تقسيم مجموعة الكائنات بأكملها إلى العدد الأمثل للفئات ، بناءً على معلومات حول قيمة المؤشرات الفردية فقط [Zagoruyko 1999].

تحليل الكتلة هو واحد من أكثر الطرق شعبية لتحليل البيانات والإحصاءات الرياضية. يسمح لك تحليل الكتلة بالعثور تلقائيًا على فئات من الكائنات ، وذلك باستخدام معلومات حول المؤشرات الكمية للكائنات فقط (تدريب بدون معلم). يمكن تعريف كل فئة من هذه الفئات بواحد من أكثر خصائصها المميزة ، على سبيل المثال ، المتوسط ​​من حيث المؤشرات. هناك عدد كبير من الأساليب والمناهج لتصنيف البيانات.

يتم إجراء البحوث الحديثة في مجال تحليل المجموعات لتحسين طرق تحديد فئات طبولوجيا معقدة [Furaoa 2007، Zagoruiko 2013] ، وكذلك لتحسين سرعة الخوارزميات في حالة البيانات الكبيرة.

في هذه الورقة ، نقترح طريقة تصنيف تستند إلى الحصول على الأصوات لزوج من الكائنات في نفس الفئة ، بناءً على معلومات حول قيمة المؤشرات الفردية. يُقترح مراعاة وجود زوج من الكائنات في نفس الفئة إذا كانت قيم المؤشرات الفردية في الفاصل الزمني بطول لا يتجاوز قيمة معينة.

طريقة K- يعني

طريقة k-الوسائل هي واحدة من أكثر طرق المجموعات شيوعًا. والغرض منه هو الحصول على مراكز البيانات هذه التي تتوافق مع فرضية الاكتناز لفئات البيانات مع توزيعها المتماثل الشعاعي. إحدى الطرق لتحديد مواقع مثل هذه المراكز ، نظرًا لعددهم \ textit {k} ، هي طريقة EM.

في هذه الطريقة ، يتم تنفيذ إجراءين بالتتابع.

1. تعريف لكل كائن البيانات$$ $ inline $ X_ {i} $ inline $ أقرب مركز$$ $ inline $ C_ {j} $ inline $ وتعيين تسمية فئة لهذا الكائن$$ $ inline $ X_ {i} ^ {j} $ inline $ . علاوة على ذلك ، بالنسبة لجميع الكائنات ، يصبح الانتماء لفئات مختلفة محددًا.
2. حساب الموقف الجديد لمراكز جميع الفئات.

بتكرار هذين الإجراءين من الموضع العشوائي الأولي لمراكز الفئات \ textit {k} ، يمكننا تحقيق فصل الكائنات إلى فئات تتوافق بشكل كبير مع فرضية الانضغاط الشعاعي للفئات.

ستتم مقارنة خوارزمية تصنيف المؤلف الجديد مع طريقة الوسائل k.

طريقة جديدة

تعتمد خوارزمية تحليل الكتلة الجديدة على أساس الأصوات للانتماء إلى مجموعات مختلفة من المعلومات حول قيم الإحداثيات الفردية لنقاط البيانات.

1. يتم تحديد القيمة d التي تميز طول الفاصل الزمني للمؤشرات التي يعتبر كائنين ينتميان إلى نفس الفئة.
2. المقياس المحدد$$ $ inline $ x_ {i} $ inline $ وتعتبر جميع أزواج من الكائنات$$ $ inline $ \ left \ {O_ {l} ، O_ {k} \ right \} $ inline $ حيث$$ $ inline $ l ، k = 1 \ ldots N $ inline $ .
3. إذا$$ $ inline $ \ left | x_ {i} ^ {l} -x_ {i} ^ {k} \ right | \ le d $ inline $ ثم الحجم$$ $ inline $ r_ {lk}: = r_ {lk} + 1 $ inline $ (صوت المضافة).
4. يتم تكرار الإجراءات 2) و 3) لجميع المؤشرات$$ $ inline $ i = 1 \ ldots M $ inline $ .
5. يتم تعيين القيمة p التي تميز الحد الأدنى لعدد الأصوات للانتماء إلى نفس الفئات.
6. باستخدام الطريقة الأساسية لأزواج القيم ، يتم تحديد جميع فئات الكائنات ، بحيث داخل فئة صوت واحدة لأزواج الكائنات من هذه الفئات > = p .
7. يتكرر على كل قيم d و p ويكرر البنود 1) - 6) للحصول على عدد الفئات الأقرب إلى عدد معين من الفئات g .

لتقليل تعقيد الخوارزمية إلى N ، يمكنك استخدام الفواصل الزمنية T للمؤشرات الفردية واستبدال الفقرة 2) و 3) في الخوارزمية بما يلي:

1. تم اختيار المؤشر$$ $ inline $ x_ {i} $ inline $ وتعتبر جميع الفواصل الزمنية$$ $ inline $ \ left [u_ {l}، w_ {l} \ right] $ inline $ حيث$$ $ inline $ l = 1 \ ldots T $ inline $ :

$$عرض $$ $$ u_ {0} = \ دقيقة (x_ {i}) ؛ u_ {0} = \ دقيقة (x_ {i}) ؛ $$ عرض $$

$$عرض $$ $$ w_ {T} = \ max (x_ {i}) ؛ عرض $$ $

$$عرض $$ $$ s_ {i} = w_ {T} -u_ {0} ؛ عرض $$ $

$$عرض $$ $$ u_ {l} = u_ {0} + l \ cdot s_ {i} ؛ عرض $$ $

$$عرض $$ $$ w_ {l} = u_ {l} + d ؛ $$ عرض $$

2. إذا$$ $ inline $ x_ {i} ^ {k} \ in \ left [u_ {j}، w_ {j} \ right] $ inline $ و$$ $ inline $ x_ {i} ^ {l} \ in \ left [u_ {j}، w_ {j} \ right] $ inline $ حيث$$ $ inline $ j = 1 \ ldots T $ inline $ ثم الحجم$$ $ inline $ r_ {lk}: = r_ {lk} + 1 $ inline $ (يضاف الصوت بمفتاح فريد l ، k لمؤشر i).

التجربة العددية

أخذت البيانات مع تصنيف بديهية للبشر والبيانات الأولية.

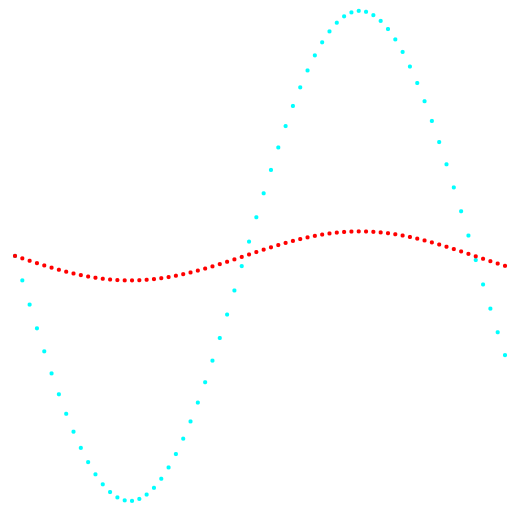
يوضح الشكلان 1 و 2 نتائج تصنيف طريقة k- وطريقة التصنيف الجديدة.


التين. 1. الإسقاط 1-2 وتصنيف البيانات.

على اليسار توجد طريقة k-mean ، على اليمين طريقة المؤلف.


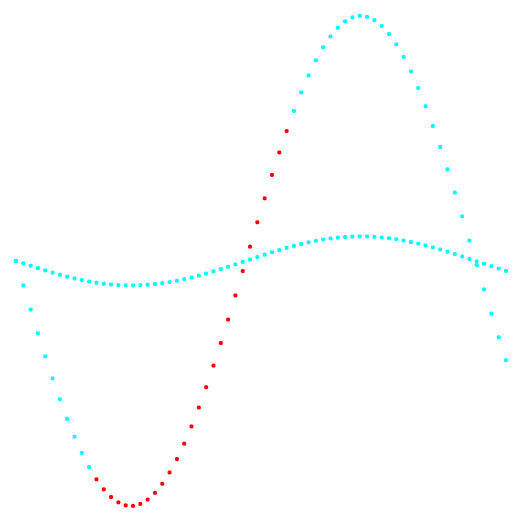
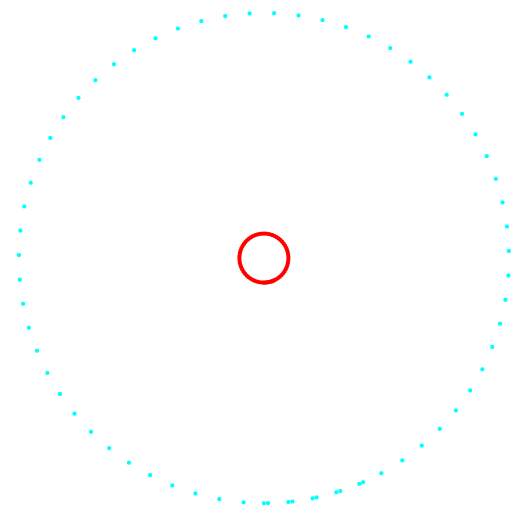
التين. 2. الإسقاط 2-3 وتصنيف البيانات.

على اليسار توجد طريقة k-mean ، على اليمين طريقة المؤلف.

تظهر نتيجة المقارنة بين الطريقتين الميزة الواضحة لطريقة المؤلف في قدرتها على اكتشاف مجموعات من الطوبولوجيا المعقدة.

تنفيذ البرامج

تم تطبيق طريقة التجميع k-mean برمجياً كتطبيق ويب. يتم تقديم جزء الحوسبة من التطبيق إلى خادم مكتوب بلغة PHP باستخدام إطار Zend. تتم كتابة واجهة التطبيق باستخدام HTML ، CSS ، JavaScript ، jQuery. التطبيق متاح على http://svlaboratory.org/application/klaster2 بعد تسجيل مستخدم جديد. يسمح لك التطبيق بتصور انتماء الكائنات إلى مجموعات مختلفة في مستوى إحداثيات محدد.

استنتاج

طريقة تصنيف جديدة مقترحة. تتمثل مزايا هذه الطريقة في التعرف على فئات الطوبولوجيا المعقدة ، والتوزيع غير الشعاعي ، بالإضافة إلى تعقيد الخوارزمية وإجراءات أقل ، وهو أمر مفيد بشكل خاص في حالة صفائف البيانات الضخمة.

المراجع (المراجع)

1. زاجورويكو ن. الأساليب المطبقة في تحليل البيانات والمعرفة. نوفوسيبيرسك: دار النشر لمعهد الرياضيات ، 1999.270 ص.
2. Zagoruyko N.G ، Borisova I.A.، Kutnenko O.A، Levanov D.A. الكشف عن الأنماط في صفائف البيانات التجريبية // التقنيات الحاسوبية. - 2013. المجلد 18. رقم S1. س 12-20.
3. Shen Furaoa ، Tomotaka Ogurab ، Osamu Hasegawab شبكة عصبية معززة ذاتية التنظيم للتعلم عبر الإنترنت بدون إشراف. مختبر هاسيغاوا ، 2007.