التجميع الهرمي للبيانات الفئوية في R

تم إعداد الترجمة لطلاب الدورة "التحليلات التطبيقية على البحث" .

---

كانت هذه أول محاولة لي لتجميع عملاء بناءً على بيانات حقيقية ، وقد أعطتني تجربة قيمة. هناك العديد من المقالات على الإنترنت حول التجميع باستخدام المتغيرات العددية ، ولكن إيجاد حلول للبيانات الفئوية ، وهو أمر أكثر صعوبة إلى حد ما ، لم يكن بهذه البساطة. أساليب التجميع للبيانات الفئوية لا تزال قيد التطوير ، وفي منشور آخر سأحاول استخدام طريقة أخرى.

من ناحية أخرى ، يعتقد الكثير من الناس أن تجميع البيانات الفئوية قد لا يؤدي إلى نتائج ذات معنى - وهذا صحيح جزئيًا (راجع المناقشة الممتازة حول CrossValidated ). عند نقطة ما ، فكرت: "ماذا أفعل؟ يمكن تقسيمها ببساطة إلى أفواج. " ومع ذلك ، لا يُنصح دائمًا بتحليل الأتراب ، خاصةً مع وجود عدد كبير من المتغيرات الفئوية مع عدد كبير من المستويات: يمكنك بسهولة التعامل مع 5-7 مجموعات ، لكن إذا كان لديك 22 متغيرًا ولكل منها 5 مستويات (على سبيل المثال ، استطلاع العملاء مع تقديرات منفصلة 1 و 2 و 3 و 4 و 5) ، وتحتاج إلى فهم المجموعات المميزة للعملاء الذين تتعامل معهم - ستحصل على 22 × 5 مجموعات. لا أحد يريد أن يكلف نفسه بهذه المهمة. وهنا يمكن أن تساعد المجموعات. لذلك في هذا المنشور سأتحدث عما أود معرفته بنفسي بمجرد أن بدأت التجميع.

تتكون عملية التجميع نفسها من ثلاث خطوات:

1. بناء مصفوفة من الاختلاف هو بلا شك أهم قرار في التكتل. تستند جميع الخطوات التالية إلى مصفوفة الاختلاف التي قمت بإنشائها.
2. اختيار طريقة التجميع.
3. تقييم الكتلة.

سيكون هذا المنشور نوعًا من المقدمة التي تصف المبادئ الأساسية للتجميع وتنفيذه في البيئة R.

مصفوفة الاختلاف

سيكون أساس التجميع هو مصفوفة التباين ، والتي تصف في المصطلحات الرياضية مدى اختلاف (إزالة) النقاط في مجموعة البيانات عن بعضها البعض. يسمح لك بمزيد من الجمع في المجموعات بين تلك النقاط الأقرب إلى بعضها البعض ، أو لفصل النقاط البعيدة عن بعضها البعض - هذه هي الفكرة الرئيسية للتجمع.

في هذه المرحلة ، تكون الاختلافات بين أنواع البيانات مهمة ، لأن مصفوفة التباين تعتمد على المسافات بين نقاط البيانات الفردية. من السهل تخيل المسافات بين نقاط البيانات العددية (مثال معروف هو المسافات الإقليدية ) ، ولكن في حالة البيانات الفئوية (العوامل في R) ، كل شيء غير واضح.

من أجل بناء مصفوفة الاختلاف في هذه الحالة ، يجب استخدام مسافة Gover المزعومة. لن أتطرق إلى الجزء الرياضي من هذا المفهوم ، سأقدم ببساطة روابط: هنا وهناك . لهذا ، أفضل استخدام daisy() مع metric = c("gower") من حزمة cluster .

 #-----   -----# #    ,       ,     ,   ,    library(dplyr) #     set.seed(40) #     #    ;   data.frame()     #    ,   200   1  200 id.s <- c(1:200) %>% factor() budget.s <- sample(c("small", "med", "large"), 200, replace = T) %>% factor(levels=c("small", "med", "large"), ordered = TRUE) origins.s <- sample(c("x", "y", "z"), 200, replace = T, prob = c(0.7, 0.15, 0.15)) area.s <- sample(c("area1", "area2", "area3", "area4"), 200, replace = T, prob = c(0.3, 0.1, 0.5, 0.2)) source.s <- sample(c("facebook", "email", "link", "app"), 200, replace = T, prob = c(0.1,0.2, 0.3, 0.4)) ##   —      dow.s <- sample(c("mon", "tue", "wed", "thu", "fri", "sat", "sun"), 200, replace = T, prob = c(0.1, 0.1, 0.2, 0.2, 0.1, 0.1, 0.2)) %>% factor(levels=c("mon", "tue", "wed", "thu", "fri", "sat", "sun"), ordered = TRUE) #  dish.s <- sample(c("delicious", "the one you don't like", "pizza"), 200, replace = T) #   data.frame()      synthetic.customers <- data.frame(id.s, budget.s, origins.s, area.s, source.s, dow.s, dish.s) #-----   -----# library(cluster) #       #   : daisy(), diana(), clusplot() gower.dist <- daisy(synthetic.customers[ ,2:7], metric = c("gower")) # class(gower.dist) ## ,  

مصفوفة الاختلاف جاهزة. بالنسبة لـ 200 ملاحظة ، تم إنشاؤها بسرعة ، ولكنها قد تتطلب مقدارًا كبيرًا جدًا من الحساب إذا كنت تتعامل مع مجموعة بيانات كبيرة.

في الممارسة العملية ، من المحتمل جدًا أنه سيتعين عليك أولاً تنظيف مجموعة البيانات ، وإجراء التحويلات اللازمة من الصفوف إلى عوامل ، وتتبع القيم المفقودة. في حالتي ، تحتوي مجموعة البيانات أيضًا على صفوف من القيم المفقودة التي تم تجميعها بشكل جميل في كل مرة ، لذلك بدا الأمر وكأنه كنز - حتى نظرت إلى القيم (للأسف!).

تجميع الخوارزميات

قد تعرف بالفعل أن التجميع هو الوسيلة الهرمية والتسلسل الهرمي . في هذا المنشور ، أركز على الطريقة الثانية ، نظرًا لأنها أكثر مرونة وتسمح بمختلف الطرق: يمكنك اختيار إما خوارزمية التجميع (من الأسفل إلى الأعلى) أو خوارزمية التجميع (من الأعلى إلى الأسفل).


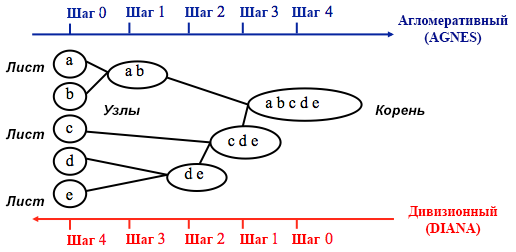المصدر: دليل برمجة جامعة كاليفورنيا للأعمال التحليلية

يبدأ التجميع التجميعي مع الكتل n ، حيث n هو عدد المشاهدات: من المفترض أن كل واحد منهم هو كتلة منفصلة. ثم تحاول الخوارزمية إيجاد وتجميع نقاط البيانات الأكثر تشابهًا فيما بينها - هكذا يبدأ تكوين الكتلة.

يتم تنفيذ تقسيم الأقسام في الاتجاه المعاكس - من المفترض في البداية أن جميع نقاط البيانات n التي لدينا مجموعة كبيرة واحدة ، ومن ثم يتم تقسيم النقاط الأقل تشابهًا إلى مجموعات منفصلة.

عند تحديد أي من هذه الطرق للاختيار ، يكون من المنطقي دائمًا تجربة كل الخيارات ، ومع ذلك ، بشكل عام ، يكون التجميع التكتل أفضل لتحديد المجموعات الصغيرة ويستخدمه معظم برامج الكمبيوتر ، وتقسيم الأقسام هو أكثر ملاءمة لتحديد المجموعات الكبيرة .

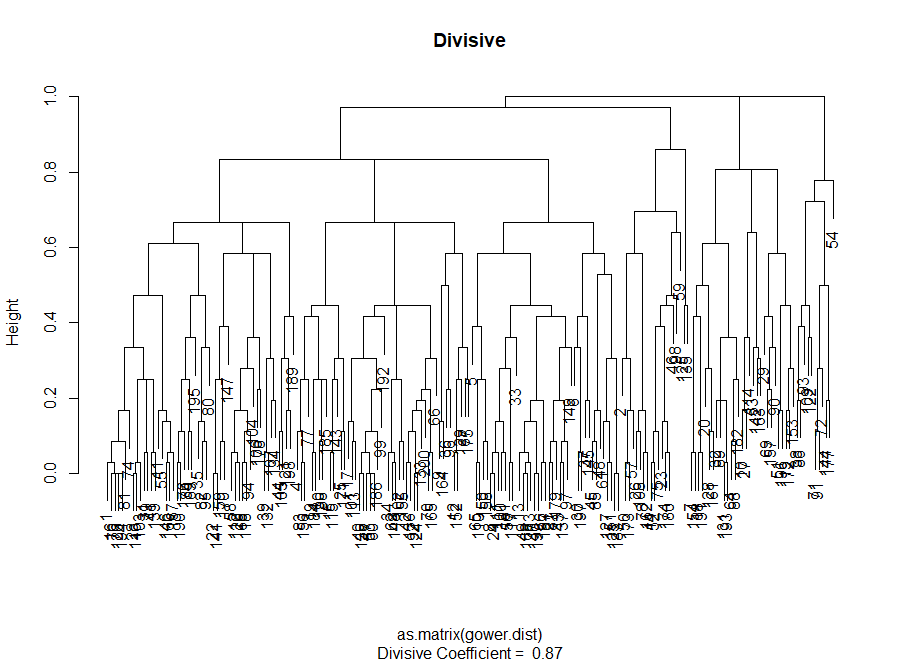
أنا شخصياً ، قبل تحديد طريقة الاستخدام ، أفضل النظر إلى dendrograms - وهو تمثيل رسومي للتجمع. كما سترى لاحقًا ، فإن بعض dendrograms متوازنة جيدًا ، بينما البعض الآخر فوضوي جدًا.

# الإدخال الرئيسي للرمز أدناه هو الاختلاف (مصفوفة المسافة)

 #             #            —         —    #------------  ------------# divisive.clust <- diana(as.matrix(gower.dist), diss = TRUE, keep.diss = TRUE) plot(divisive.clust, main = "Divisive") 

 #------------   ------------# #      #         —     ,      #    (complete linkages) aggl.clust.c <- hclust(gower.dist, method = "complete") plot(aggl.clust.c, main = "Agglomerative, complete linkages") 

تجميع تقييم الجودة

في هذه المرحلة ، من الضروري الاختيار بين خوارزميات التجميع المختلفة وعدد مختلف من المجموعات. يمكنك استخدام طرق مختلفة للتقييم ، دون أن تنسى أن تسترشد بالحس السليم . لقد سلطت الضوء على هذه الكلمات بالخط العريض والمائل ، لأن أهمية الاختيار مهمة للغاية - يجب أن يكون عدد المجموعات وطريقة تقسيم البيانات إلى مجموعات عملية من الناحية العملية. عدد مجموعات قيم المتغيرات الفئوية محدود (نظرًا لأنها منفصلة) ، ولكن لن يكون أي تفصيل يستند إليها مفيدًا. قد لا ترغب أيضًا في الحصول على مجموعات قليلة جدًا - في هذه الحالة ستكون معممة جدًا. في النهاية ، كل هذا يتوقف على هدفك ومهام التحليل.

بشكل عام ، عند إنشاء مجموعات ، تكون مهتمًا بالحصول على مجموعات محددة بوضوح من نقاط البيانات ، بحيث تكون المسافة بين هذه النقاط داخل الكتلة ( أو الاكتناز ) ضئيلة ، وتكون المسافة بين المجموعات (إمكانية الفصل ) هي أقصى حد ممكن. هذا سهل الفهم بشكل حدسي: المسافة بين النقاط هي مقياس لاختلافها ، تم الحصول عليها على أساس مصفوفة الاختلاف. وبالتالي ، يعتمد تقييم جودة التجميع على تقييم الاكتناز والانفصال.

بعد ذلك ، سأوضح طريقتين وأظهر أن أحدهما يمكن أن يعطي نتائج بلا معنى.

• طريقة الكوع : ابدأ بها إذا كان العامل الأكثر أهمية في تحليلك هو انضغاط المجموعات ، أي التشابه داخل المجموعات.
• طريقة تقييم الصور الظلية : يوضح الرسم البياني للصور الظلية المستخدم كمقياس لتناسق البيانات مدى قرب كل نقطة من النقاط داخل مجموعة واحدة من النقاط الموجودة في المجموعات المجاورة.

في الممارسة العملية ، غالبًا ما تعطي هاتان الطريقتان نتائج مختلفة ، والتي يمكن أن تؤدي إلى بعض الالتباس - الحد الأقصى للاكتناز وأوضح فصل سيتم تحقيقهما بعدد مختلف من المجموعات ، بحيث يلعب هذا الفهم السليم وفهم ما تعنيه البيانات حقًا دورًا مهمًا عند اتخاذ القرار النهائي.

هناك أيضًا عدد من المقاييس التي يمكنك تحليلها. سأضيفها مباشرة إلى الكود.

 #      ,        #      ,     ,   —   #     ,      ,         ,   ,     library(fpc) cstats.table <- function(dist, tree, k) { clust.assess <- c("cluster.number","n","within.cluster.ss","average.within","average.between", "wb.ratio","dunn2","avg.silwidth") clust.size <- c("cluster.size") stats.names <- c() row.clust <- c() output.stats <- matrix(ncol = k, nrow = length(clust.assess)) cluster.sizes <- matrix(ncol = k, nrow = k) for(i in c(1:k)){ row.clust[i] <- paste("Cluster-", i, " size") } for(i in c(2:k)){ stats.names[i] <- paste("Test", i-1) for(j in seq_along(clust.assess)){ output.stats[j, i] <- unlist(cluster.stats(d = dist, clustering = cutree(tree, k = i))[clust.assess])[j] } for(d in 1:k) { cluster.sizes[d, i] <- unlist(cluster.stats(d = dist, clustering = cutree(tree, k = i))[clust.size])[d] dim(cluster.sizes[d, i]) <- c(length(cluster.sizes[i]), 1) cluster.sizes[d, i] } } output.stats.df <- data.frame(output.stats) cluster.sizes <- data.frame(cluster.sizes) cluster.sizes[is.na(cluster.sizes)] <- 0 rows.all <- c(clust.assess, row.clust) # rownames(output.stats.df) <- clust.assess output <- rbind(output.stats.df, cluster.sizes)[ ,-1] colnames(output) <- stats.names[2:k] rownames(output) <- rows.all is.num <- sapply(output, is.numeric) output[is.num] <- lapply(output[is.num], round, 2) output } #     :      7 #     ,            stats.df.divisive <- cstats.table(gower.dist, divisive.clust, 7) stats.df.divisive 

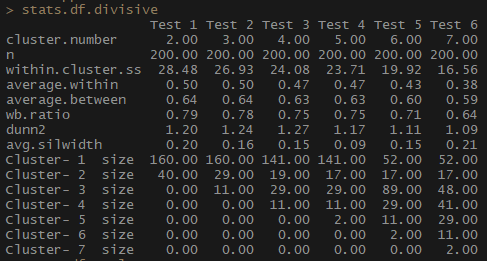
لذلك ، يتناقص مؤشر medium.within ، الذي يمثل متوسط ​​المسافة بين الملاحظات داخل الكتل ، كما يحدث داخل .cluster.ss (مجموع مربعات المسافات بين الملاحظات في كتلة). لا يتغير متوسط ​​عرض الصورة الظلية (avg.silwidth) بشكل لا لبس فيه ، ومع ذلك ، لا يزال من الممكن ملاحظة علاقة عكسية.
لاحظ كيف أحجام الكتلة غير متناسبة. لن أتسرع في العمل مع عدد لا يُضاهى من الملاحظات داخل المجموعات. أحد الأسباب هو أن مجموعة البيانات قد تكون غير متوازنة ، وأن مجموعة من الملاحظات ستتفوق على جميع الملاحظات الأخرى في التحليل - هذا ليس جيدًا وسيؤدي على الأرجح إلى أخطاء.

stats.df.aggl <-cstats.table(gower.dist, aggl.clust.c, 7) #

stats.df.aggl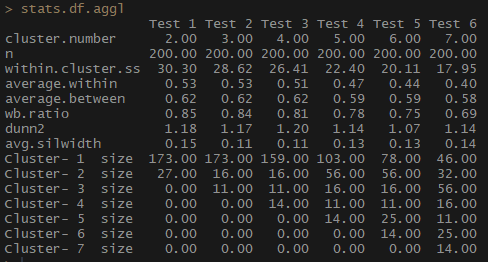



لاحظ مدى توازن عدد المشاهدات لكل مجموعة بشكل أفضل عن طريق التكتلات الهرمية التكتلية بناءً على طريقة الاتصال الكاملة.

 # ---------    ---------# #   «»       #    ,     7  library(ggplot2) #  #   ggplot(data = data.frame(t(cstats.table(gower.dist, divisive.clust, 15))), aes(x=cluster.number, y=within.cluster.ss)) + geom_point()+ geom_line()+ ggtitle("Divisive clustering") + labs(x = "Num.of clusters", y = "Within clusters sum of squares (SS)") + theme(plot.title = element_text(hjust = 0.5)) 

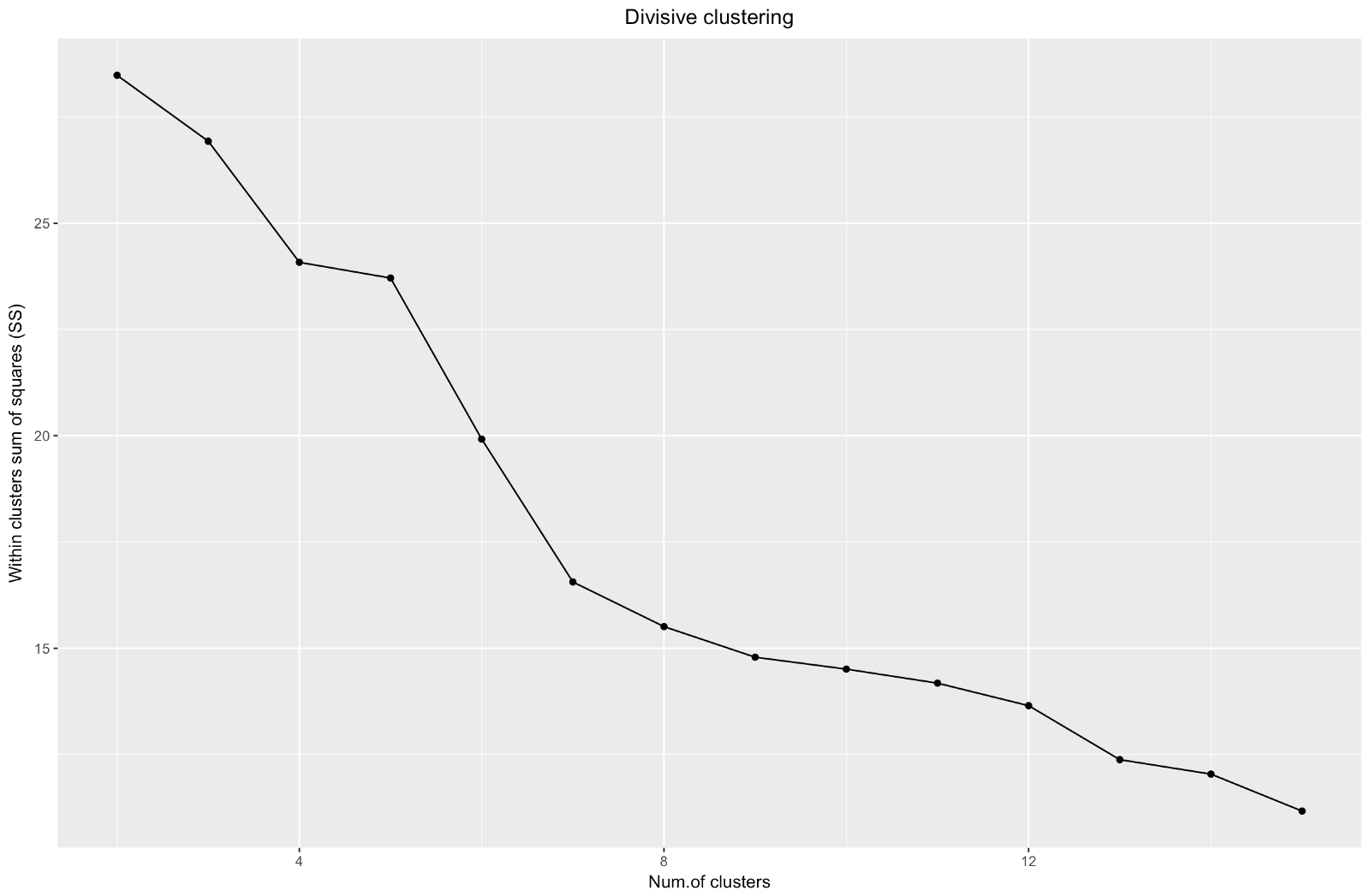
لذلك ، قمنا بإنشاء رسم بياني لل "الكوع". إنه يوضح كيف يتغير مجموع المسافات المربعة بين الملاحظات (نستخدمها كمقياس لقرب الملاحظات - كلما كانت أصغر ، كلما كانت القياسات داخل الكتلة لبعضها البعض) تختلف بالنسبة لعدد مختلف من المجموعات. من الناحية المثالية ، يجب أن نرى "منحنى الكوع" متميزًا عند النقطة التي تعطي فيها مجموعات أخرى فقط انخفاضًا طفيفًا في مجموع المربعات (SS). بالنسبة للرسم البياني أدناه ، أود التوقف عند حوالي 7. على الرغم من أنه في هذه الحالة ستتألف إحدى المجموعات من ملاحظتين فقط. دعونا نرى ما يحدث خلال التكتل التكتل.

 #       ggplot(data = data.frame(t(cstats.table(gower.dist, aggl.clust.c, 15))), aes(x=cluster.number, y=within.cluster.ss)) + geom_point()+ geom_line()+ ggtitle("Agglomerative clustering") + labs(x = "Num.of clusters", y = "Within clusters sum of squares (SS)") + theme(plot.title = element_text(hjust = 0.5)) 

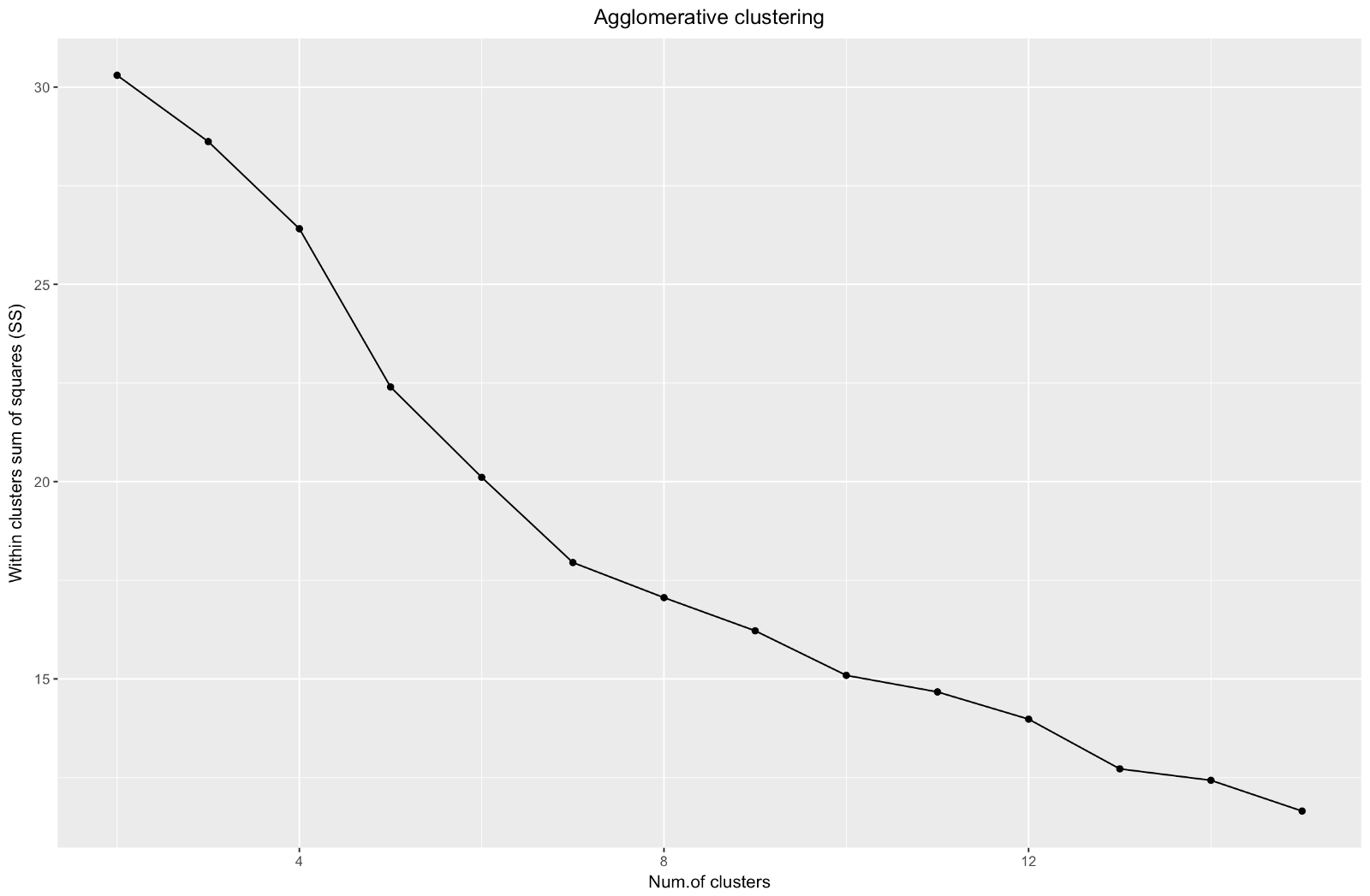
يشبه "الكوع" التجميعي التقسيم ، لكن الرسم البياني يبدو أكثر سلاسة - الانحناءات ليست واضحة جدًا. كما هو الحال مع المجموعات التقسيمية ، أود التركيز على 7 مجموعات ، ولكن عند الاختيار بين هاتين الطريقتين ، أحب أحجام المجموعات التي تم الحصول عليها بالطريقة التكتلية أكثر - من الأفضل أن تكون قابلة للمقارنة مع بعضها البعض.

 #  ggplot(data = data.frame(t(cstats.table(gower.dist, divisive.clust, 15))), aes(x=cluster.number, y=avg.silwidth)) + geom_point()+ geom_line()+ ggtitle("Divisive clustering") + labs(x = "Num.of clusters", y = "Average silhouette width") + theme(plot.title = element_text(hjust = 0.5)) 

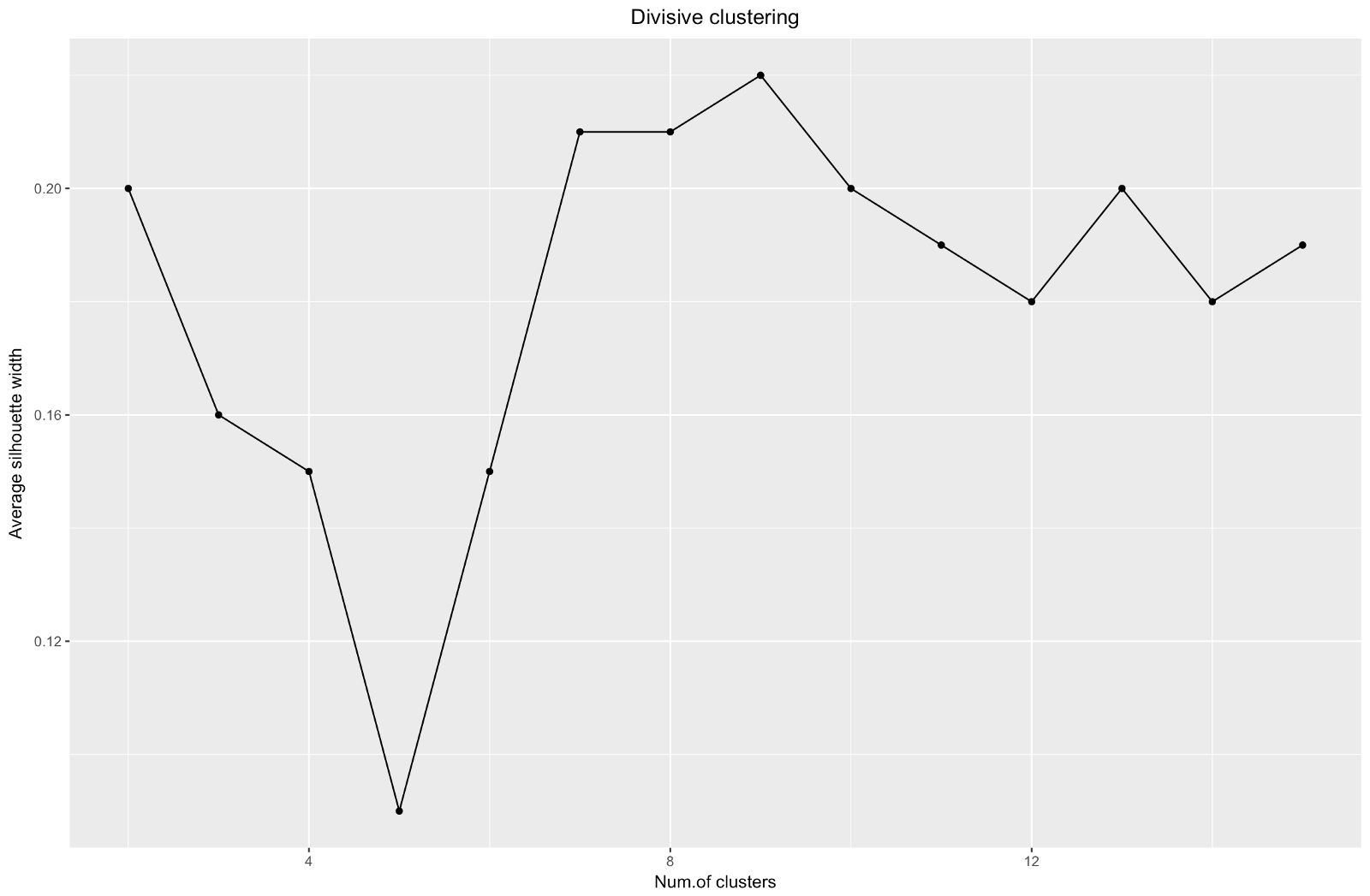
عند استخدام طريقة تقدير صورة ظلية ، يجب عليك اختيار الكمية التي تعطي الحد الأقصى لمعامل صورة ظلية ، لأنك تحتاج إلى مجموعات متباعدة بشكل كافٍ لتكون منفصلة.

يمكن أن يتراوح معامل الصورة الظلية بين -1 و 1 ، مع 1 يقابل الاتساق الجيد داخل المجموعات ، و -1 ليس جيدًا جدًا.
في حالة المخطط أعلاه ، يمكنك اختيار 9 مجموعات بدلاً من 5 مجموعات.

للمقارنة: في الحالة "البسيطة" ، يشبه الرسم البياني للصورة الظلية الرسم البياني أدناه. ليس تماما مثلنا ، ولكن تقريبا.


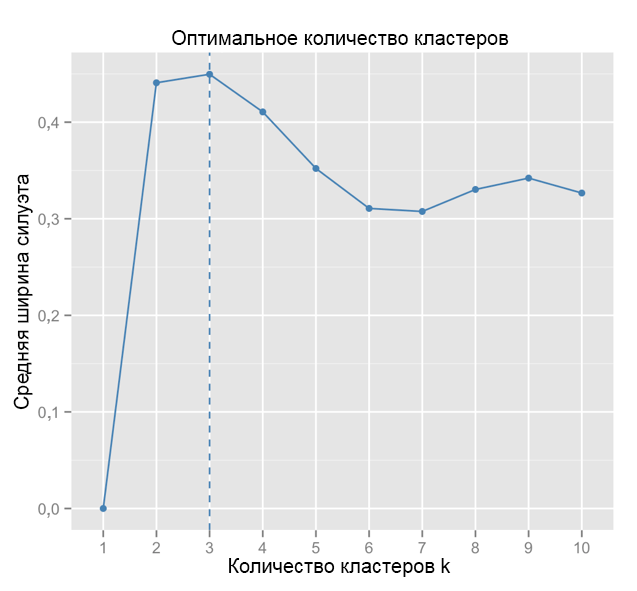المصدر: البحارة البيانات

 ggplot(data = data.frame(t(cstats.table(gower.dist, aggl.clust.c, 15))), aes(x=cluster.number, y=avg.silwidth)) + geom_point()+ geom_line()+ ggtitle("Agglomerative clustering") + labs(x = "Num.of clusters", y = "Average silhouette width") + theme(plot.title = element_text(hjust = 0.5)) 

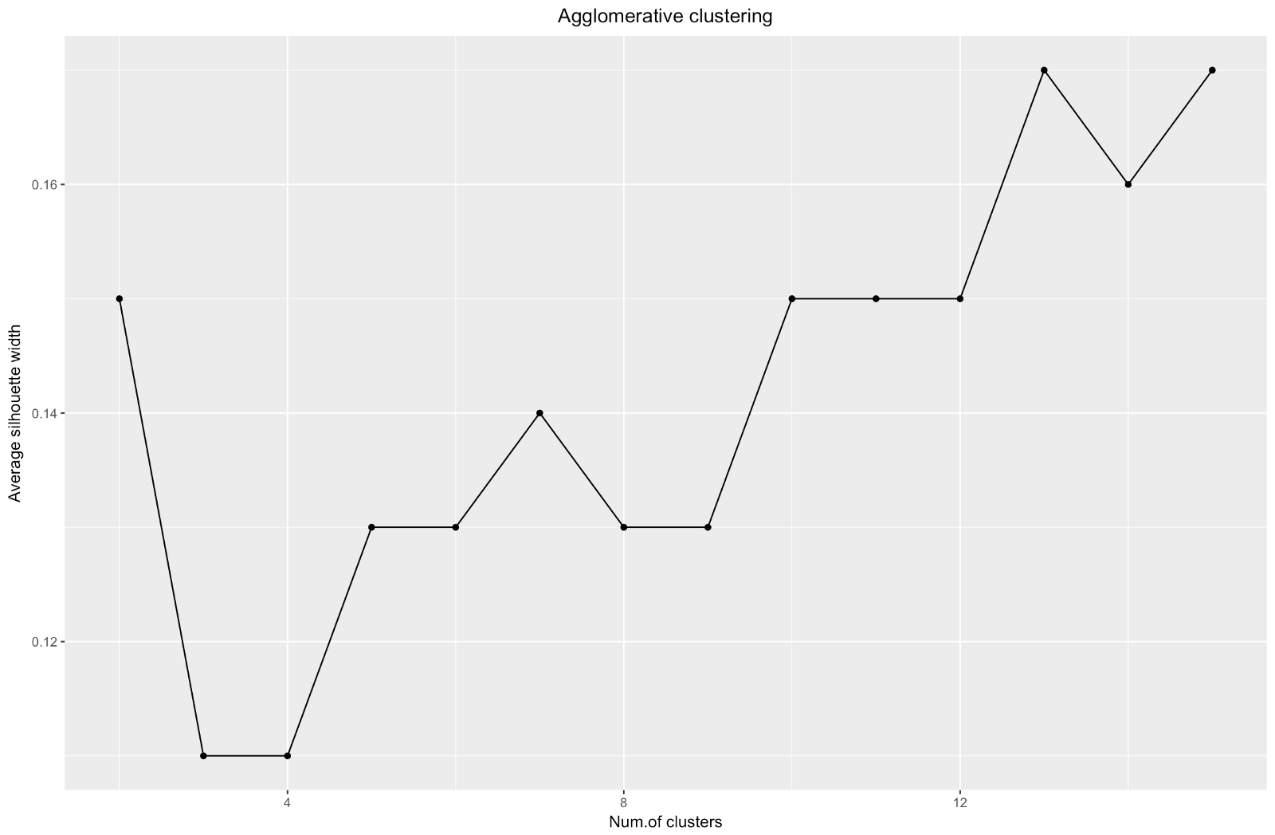
يخبرنا مخطط عرض الصور الظلية: كلما قسمتم مجموعة البيانات ، كلما أصبحت المجموعات أكثر وضوحًا. ومع ذلك ، في النهاية سوف تصل إلى نقاط فردية ، ولا تحتاج إلى ذلك. ومع ذلك ، هذا هو بالضبط ما ستراه إذا كنت تبدأ في زيادة عدد المجموعات k . على سبيل المثال ، بالنسبة إلى k=30 حصلت على الرسم البياني التالي:



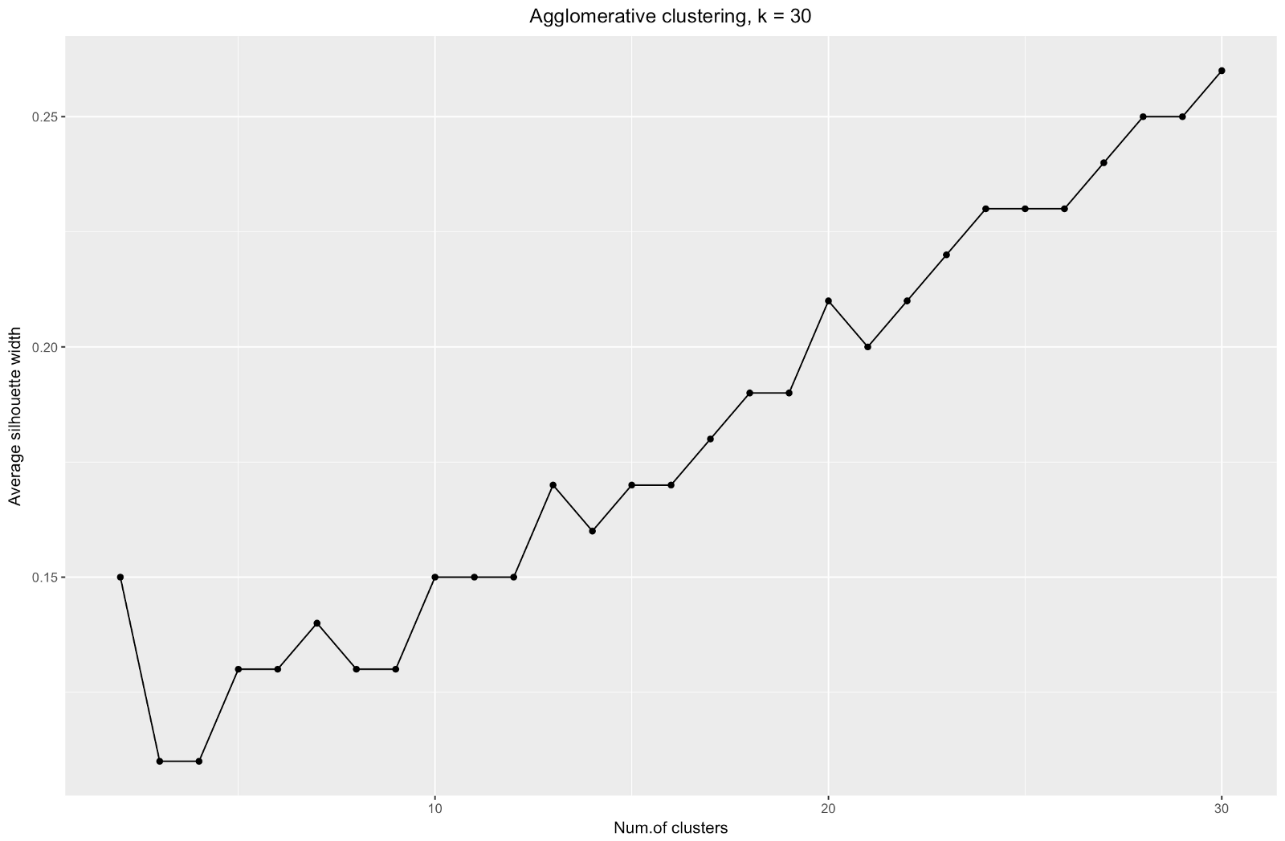
للتلخيص: كلما قمت بتقسيم مجموعة البيانات ، كان ذلك أفضل للمجموعات ، لكن لا يمكننا الوصول إلى نقاط فردية (على سبيل المثال ، في المخطط أعلاه ، حددنا 30 مجموعة ، ولدينا 200 نقطة بيانات فقط).

لذلك ، يبدو التكتل التجميعي في حالتنا أكثر توازنا: أحجام المجموعات قابلة للمقارنة إلى حد ما (انظر فقط إلى مجموعة من ملاحظتين فقط عند القسمة على طريقة التقسيم!) ، وأود أن أتوقف عند 7 مجموعات تم الحصول عليها بهذه الطريقة. دعونا نرى كيف تبدو وما هي مصنوعة من.

تتكون مجموعة البيانات من 6 متغيرات تحتاج إلى تصور ثنائي الأبعاد أو ثلاثي الأبعاد ، لذلك عليك أن تعمل بجد! تفرض طبيعة البيانات الفئوية أيضًا بعض القيود ، لذلك قد لا تعمل الحلول الجاهزة. أحتاج إلى: أ) معرفة كيفية تقسيم الملاحظات إلى مجموعات ، ب) فهم كيفية تصنيف الملاحظات. لذلك ، قمت بإنشاء أ) dendrogram لوني ، ب) خريطة حرارة لعدد المشاهدات لكل متغير داخل كل مجموعة.

 library("ggplot2") library("reshape2") library("purrr") library("dplyr") #    library("dendextend") dendro <- as.dendrogram(aggl.clust.c) dendro.col <- dendro %>% set("branches_k_color", k = 7, value = c("darkslategray", "darkslategray4", "darkslategray3", "gold3", "darkcyan", "cyan3", "gold3")) %>% set("branches_lwd", 0.6) %>% set("labels_colors", value = c("darkslategray")) %>% set("labels_cex", 0.5) ggd1 <- as.ggdend(dendro.col) ggplot(ggd1, theme = theme_minimal()) + labs(x = "Num. observations", y = "Height", title = "Dendrogram, k = 7") 

 #     ( ) ggplot(ggd1, labels = T) + scale_y_reverse(expand = c(0.2, 0)) + coord_polar(theta="x") 

 #  —   #    —       #    ,      clust.num <- cutree(aggl.clust.c, k = 7) synthetic.customers.cl <- cbind(synthetic.customers, clust.num) cust.long <- melt(data.frame(lapply(synthetic.customers.cl, as.character), stringsAsFactors=FALSE), id = c("id.s", "clust.num"), factorsAsStrings=T) cust.long.q <- cust.long %>% group_by(clust.num, variable, value) %>% mutate(count = n_distinct(id.s)) %>% distinct(clust.num, variable, value, count) # heatmap.c ,      — ,   ,     heatmap.c <- ggplot(cust.long.q, aes(x = clust.num, y = factor(value, levels = c("x","y","z", "mon", "tue", "wed", "thu", "fri","sat","sun", "delicious", "the one you don't like", "pizza", "facebook", "email", "link", "app", "area1", "area2", "area3", "area4", "small", "med", "large"), ordered = T))) + geom_tile(aes(fill = count))+ scale_fill_gradient2(low = "darkslategray1", mid = "yellow", high = "turquoise4") #            cust.long.p <- cust.long.q %>% group_by(clust.num, variable) %>% mutate(perc = count / sum(count)) %>% arrange(clust.num) heatmap.p <- ggplot(cust.long.p, aes(x = clust.num, y = factor(value, levels = c("x","y","z", "mon", "tue", "wed", "thu", "fri","sat", "sun", "delicious", "the one you don't like", "pizza", "facebook", "email", "link", "app", "area1", "area2", "area3", "area4", "small", "med", "large"), ordered = T))) + geom_tile(aes(fill = perc), alpha = 0.85)+ labs(title = "Distribution of characteristics across clusters", x = "Cluster number", y = NULL) + geom_hline(yintercept = 3.5) + geom_hline(yintercept = 10.5) + geom_hline(yintercept = 13.5) + geom_hline(yintercept = 17.5) + geom_hline(yintercept = 21.5) + scale_fill_gradient2(low = "darkslategray1", mid = "yellow", high = "turquoise4") heatmap.p 

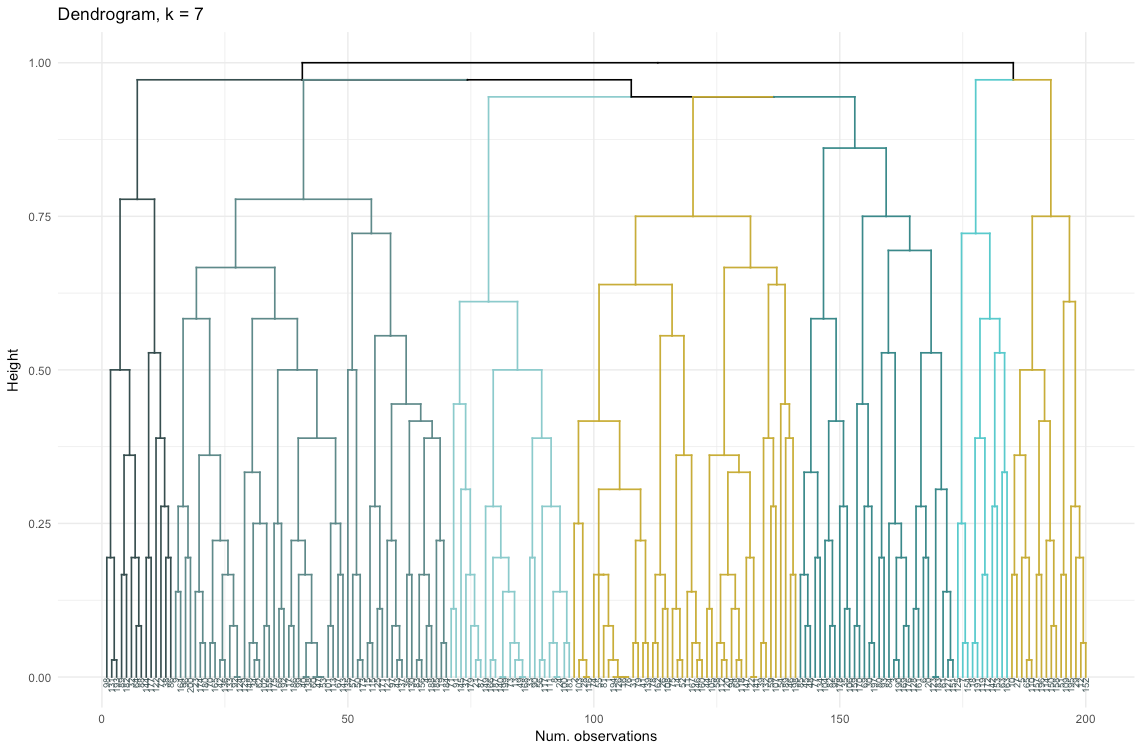
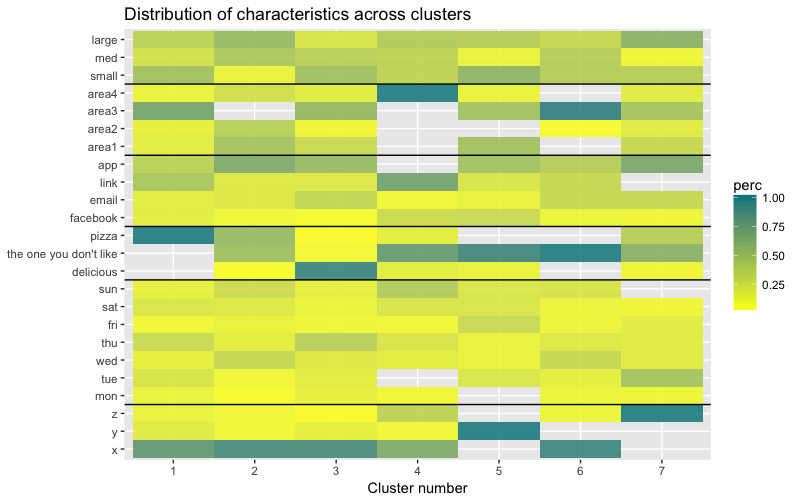
تُظهر خريطة الحرارة بيانياً عدد الملاحظات التي يتم إجراؤها لكل مستوى عامل للعوامل الأولية (المتغيرات التي بدأنا بها). يتوافق اللون الأزرق الغامق مع عدد كبير نسبيًا من الملاحظات داخل المجموعة. تُظهر خريطة الحرارة هذه أيضًا أن عدد العملاء في كل خلية هو نفسه تقريبًا ليوم الأسبوع (الشمس ، السبت ... الاثنين) وحجم السلة (كبير ، متوسط ​​، صغير) - وهذا قد يعني أن هذه الفئات ليست محددة للتحليل ، و ربما لا يحتاجون إلى أخذها في الاعتبار.

استنتاج

في هذه المقالة ، حسبنا مصفوفة التباين ، واختبرنا الطرق التكتل والقسمة للتجمعات الهرمية ، وتعرّفنا على أساليب الكوع والصورة الظلية لتقييم جودة المجموعات.

التكتل الهرمي للقسمة والتكتل هو بداية جيدة لدراسة الموضوع ، لكن لا تتوقف عند هذا الحد إذا كنت ترغب في إتقان تحليل الكتلة. هناك العديد من الأساليب والتقنيات الأخرى. الفرق الرئيسي من تجميع البيانات العددية هو حساب مصفوفة الاختلاف. عند تقييم جودة التجميع ، لن تقدم جميع الطرق القياسية نتائج موثوقة وذات مغزى - من المرجح جدًا أن تكون طريقة الظلية غير مناسبة.

وأخيرًا ، نظرًا لأن بعض الوقت قد مضى منذ أن قدمت هذا المثال ، أرى الآن عددًا من أوجه القصور في نهجي وسأكون سعيدًا بأي ملاحظات. لم تكن إحدى المشكلات المهمة في تحليلي متعلقة بالتكتل على هذا النحو - لم تكن مجموعة بياناتي متوازنة من نواح كثيرة ، وبقيت هذه اللحظة في عداد المفقودين. كان لهذا تأثير ملحوظ على التجميع: 70٪ من العملاء ينتمون إلى مستوى واحد من عامل "المواطنة" ، وهيمنت هذه المجموعة على معظم المجموعات التي تم الحصول عليها ، لذلك كان من الصعب حساب الاختلافات داخل مستويات أخرى من العامل. في المرة القادمة سأحاول تحقيق التوازن بين مجموعة البيانات ومقارنة نتائج المجموعات. ولكن المزيد عن ذلك في وظيفة أخرى.

أخيرًا ، إذا كنت ترغب في استنساخ الكود ، فإليك الرابط الخاص بـ github: https://github.com/khunreus/cluster-categorical
أتمنى أن تستمتعوا بهذا المقال!

المصادر التي ساعدتني:

دليل المجموعات الهرمية (إعداد البيانات ، التجميع ، التصور) - ستكون هذه المدونة ممتعة لأولئك المهتمين بتحليلات الأعمال في بيئة البحث والتطوير: http://uc-r.imtqy.com/hc_clustering و https: // uc-r. imtqy.com/kmeans_clustering

التجميع: http://www.sthda.com/english/articles/29-cluster-validation-essentials/97-cluster-validation-statistics-must-know-methods/

( k-): https://eight2late.wordpress.com/2015/07/22/a-gentle-introduction-to-cluster-analysis-using-r/

denextend, : https://cran.r-project.org/web/packages/dendextend/vignettes/introduction.html#the-set-function

, : https://www.r-statistics.com/2010/06/clustergram-visualization-and-diagnostics-for-cluster-analysis-r-code/

: https://jcoliver.imtqy.com/learn-r/008-ggplot-dendrograms-and-heatmaps.html

, https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5025633/ ( GitHub: https://github.com/khunreus/EnsCat ).