الشبكات العصبية والتعلم العميق ، الفصل 5: لماذا يصعب تدريب الشبكات العصبية العميقة؟

تخيل أنك مهندس ، وقد طُلب منك تطوير جهاز كمبيوتر من البداية. بمجرد أن تجلس في المكتب ، فإنك تكافح لتصميم دوائر منطقية ، وتوزيع صمامات AND ، OR ، وما إلى ذلك - وفجأة يأتي رئيسك ويخبرك بالأخبار السيئة. قرر العميل للتو إضافة متطلبات غير متوقعة للمشروع: يجب ألا يحتوي مخطط الكمبيوتر بالكامل على أكثر من طبقتين:



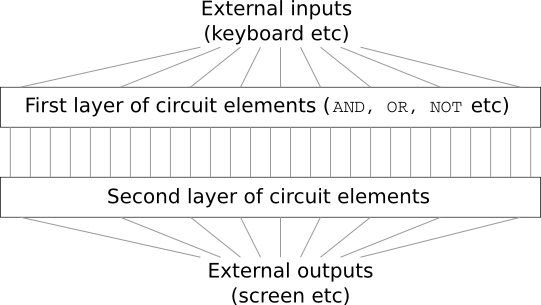
أنت مندهش وإخبر رئيسك: "نعم ، العميل مجنون!"

يجيب الرئيس: "أعتقد ذلك أيضًا. لكن يجب على العميل الحصول على ما يريد ".

في الواقع ، بمعنى ضيق ، العميل ليس مجنونًا تمامًا. افترض أنه مسموح لك باستخدام بوابة منطقية خاصة تسمح لك بتوصيل أي عدد من المدخلات من خلال AND. ويسمح لك باستخدام بوابة NAND مع أي عدد من المدخلات ، أي بوابة تضيف الكثير من المدخلات من خلال AND ، ثم تنعكس النتيجة. اتضح أنه مع هذه الصمامات الخاصة ، يمكنك حساب أي وظيفة باستخدام دائرة ثنائية الطبقة فقط.

ومع ذلك ، لا يعني مجرد القيام بشيء ما أنه يستحق القيام به. في الممارسة العملية ، عند حل المشكلات المرتبطة بتصميم الدوائر المنطقية (وجميع مشكلات الخوارزمية تقريبًا) ، نبدأ عادةً بحل المهام الفرعية ، ثم نجمع تدريجياً حلاً كاملاً. بمعنى آخر ، نحن نبني حلاً عبر العديد من مستويات التجريد.

على سبيل المثال ، لنفترض أننا قمنا بتصميم دائرة منطقية لضرب رقمين. من المحتمل أننا سنرغب في بنائها من دوائر فرعية تنفذ عمليات مثل إضافة رقمين. تتكون الدوائر الفرعية الإضافية ، بدورها ، من دوائر فرعية تضيف جزئين. بمعنى تقريبي ، سيبدو مخططنا كما يلي:



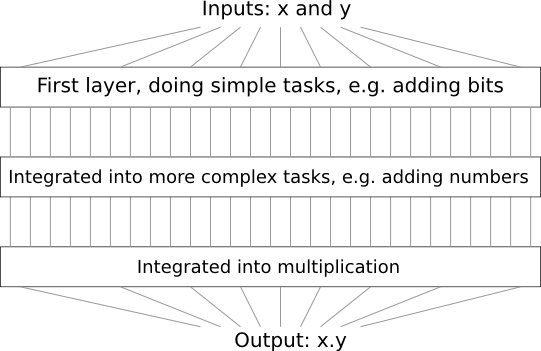
أي أن الدائرة الأخيرة تحتوي على ثلاث طبقات على الأقل من عناصر الدائرة. في الواقع ، من المحتمل أن تحتوي على أكثر من ثلاث طبقات عندما نقوم بتقسيم المهام الفرعية إلى مهام أصغر من تلك التي وصفتها. لكنك فهمت المبدأ.

لذلك ، تسهل المخططات العميقة عملية التصميم. لكنها تساعد ليس فقط في التصميم. هناك أدلة رياضية على أنه من أجل حساب بعض الوظائف في دوائر ضحلة جدًا ، يلزم استخدام عدد أكبر من العناصر بشكل كبير من تلك الموجودة في العناصر العميقة. على سبيل المثال ، هناك سلسلة مشهورة من الأعمال العلمية في الثمانينيات ، حيث تبين أن حساب تكافؤ مجموعة من البتات يتطلب عددًا أكبر من الأسيوية من البوابات بدائرة ضحلة. من ناحية أخرى ، عند استخدام المخططات العميقة ، يكون من الأسهل حساب التكافؤ باستخدام مخطط صغير: يمكنك ببساطة حساب تكافؤ أزواج البتات ، ثم استخدام النتيجة لحساب تكافؤ أزواج البتات ، وهكذا ، الوصول بسرعة إلى التماثل العام. لذلك ، يمكن أن تكون المخططات العميقة أقوى بكثير من المخططات الضحلة.

حتى الآن ، استخدم هذا الكتاب مقاربة الشبكات العصبية (NS) ، على غرار طلبات العميل المجنون. تحتوي جميع الشبكات التي عملنا معها تقريبًا على طبقة مخفية واحدة من الخلايا العصبية (بالإضافة إلى طبقات المدخلات والمخرجات):



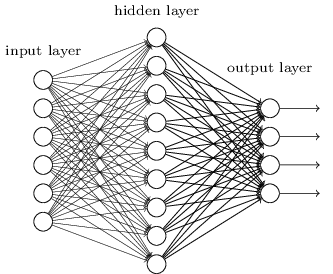
تبين أن هذه الشبكات البسيطة مفيدة للغاية: في الفصول السابقة استخدمنا هذه الشبكات لتصنيف الأرقام المكتوبة بخط اليد بدقة تتجاوز 98٪! ومع ذلك ، فمن الواضح بشكل حدسي أن الشبكات ذات الطبقات المخفية ستكون أقوى بكثير:



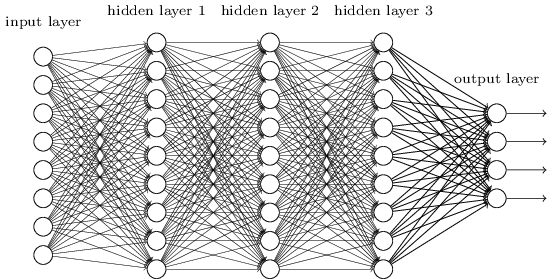
يمكن أن تستخدم هذه الشبكات الطبقات الوسيطة لإنشاء العديد من مستويات التجريد ، كما هو الحال في مخططات Boolean الخاصة بنا. على سبيل المثال ، في حالة التعرف على الأنماط ، يمكن أن تتعلم عصبونات الطبقة الأولى التعرف على الوجوه ، والخلايا العصبية من الطبقة الثانية - أشكال أكثر تعقيدًا ، مثل المثلثات أو المستطيلات التي تم إنشاؤها من الوجوه. عندها ستتمكن الطبقة الثالثة من التعرف على الأشكال الأكثر تعقيدًا. و هكذا. من المحتمل أن تمنح هذه الطبقات العديدة من التجريد الشبكات العميقة ميزة مقنعة في حل مشاكل التعرف على الأنماط المعقدة. علاوة على ذلك ، كما هو الحال في الدوائر ، هناك نتائج نظرية تؤكد أن الشبكات العميقة تتمتع بطبيعتها بقدرات أكثر من الشبكات الضحلة.

كيف ندرب هذه الشبكات العصبية العميقة (GNS)؟ في هذا الفصل ، سنحاول تدريب STS باستخدام عمود التشغيل لدينا بين خوارزميات التدريب - نزول الانتشار العشوائي التدريجي العشوائي. ومع ذلك ، سنواجه مشكلة - لن تعمل STS الخاصة بنا بشكل أفضل (إن تم تجاوزه على الإطلاق) من تلك الضحلة.

هذا الفشل يبدو غريبا في ضوء المناقشة أعلاه. ولكن بدلاً من الاستسلام لـ STS ، سوف نتعمق في المشكلة ونحاول أن نفهم سبب صعوبة تدريب STS. عندما نلقي نظرة فاحصة على المشكلة ، سنجد أن الطبقات المختلفة في STS تتعلم بسرعات مختلفة للغاية. على وجه الخصوص ، عندما يتم تدريب الطبقات الأخيرة من الشبكة بشكل جيد ، غالبًا ما تتعطل الأولى أثناء التدريب ولا تتعلم شيئًا تقريبًا. وانها ليست مجرد سوء الحظ. سوف نجد أسبابًا أساسية لإبطاء عملية التعلم المرتبطة باستخدام أساليب التعلم القائم على التدرج.

أثناء اختراق هذه المشكلة بشكل أعمق ، اكتشفنا أن الظاهرة المعاكسة قد تحدث أيضًا: يمكن أن تتعلم الطبقات المبكرة جيدًا ، بينما تتعثر الطبقات المتأخرة. في الواقع ، سوف نكتشف عدم الاستقرار الداخلي المرتبط بتدرب النسب التدريجي في NSs متعددة الطبقات العميقة. وبسبب هذا عدم الاستقرار ، غالبًا ما تتعثر الطبقات المبكرة أو المتأخرة في التدريب.

كل هذا يبدو غير سارة للغاية. لكن في ظل هذه الصعوبات ، يمكننا أن نبدأ في تطوير أفكار حول ما يجب القيام به من أجل التدريب الفعال لـ STS. لذلك ، ستكون هذه الدراسات إعدادًا جيدًا للفصل التالي ، حيث سنستخدم التعلم العميق لمعالجة مشكلات التعرف على الصور.

يتلاشى مشكلة التدرج

إذن ما الخطأ عندما نحاول تدريب شبكة عميقة؟

للإجابة على هذا السؤال ، نعود إلى الشبكة التي تحتوي على طبقة مخفية واحدة فقط. كالعادة ، سوف نستخدم مشكلة تصنيف أرقام MNIST كصندوق رمل للتعلم والتجريب.

إذا كنت ترغب في تكرار كل هذه الخطوات على جهاز الكمبيوتر الخاص بك ، يجب أن يكون لديك Python 2.7 مثبتًا ، ومكتبة Numpy ، ونسخة من الكود الذي يمكن أخذه من المستودع:

git clone https://github.com/mnielsen/neural-networks-and-deep-learning.git 

يمكنك الاستغناء عن git ببساطة عن طريق تنزيل البيانات والرمز . انتقل إلى الدليل الفرعي src ومن تحميل python shell تحميل البيانات MNIST:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() 

تكوين الشبكة:

 >>> import network2 >>> net = network2.Network([784, 30, 10]) 

تحتوي هذه الشبكة على 784 خلية عصبية في طبقة الإدخال ، تقابل 28 × 28 = 784 بكسل لصورة الإدخال. نحن نستخدم 30 من الخلايا العصبية المخفية وعطلة نهاية الأسبوع 10 ، الموافق عشرة خيارات التصنيف الممكنة للأرقام MNIST ('0' ، '1' ، '2' ، ... ، '9').

دعنا نحاول تدريب شبكتنا على 30 حقبة كاملة باستخدام مجموعات مصغرة من 10 أمثلة تدريب في وقت واحد ، وسرعة التعلم η = 0.1 ومعلمة التنظيم 5.0 = 5.0. أثناء التدريب ، سنتابع دقة التصنيف من خلال التحقق من الصحة:

 >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

نحصل على دقة تصنيف 96.48٪ (أو نحو ذلك - ستختلف الأرقام باختلاف عمليات الإطلاق) ، مقارنةً بنتائجنا السابقة مع إعدادات مماثلة.

لنقم بإضافة طبقة أخرى مخفية ، تحتوي أيضًا على 30 خلية عصبية ، وحاول تدريب الشبكة باستخدام نفس المعلمات الفائقة:

 >>> net = network2.Network([784, 30, 30, 10]) >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

دقة التصنيف تتحسن إلى 96.90 ٪. انها ملهمة - زيادة طفيفة في عمق يساعد. دعنا نضيف طبقة مخفية أخرى من 30 خلية:

 >>> net = network2.Network([784, 30, 30, 30, 10]) >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

لم يساعد. انخفضت النتيجة حتى 96.57 ٪ ، وهي قيمة قريبة من الشبكة الضحلة الأصلية. وإذا أضفنا طبقة أخرى مخفية:

 >>> net = network2.Network([784, 30, 30, 30, 30, 10]) >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

ثم سوف تنخفض دقة التصنيف مرة أخرى ، بالفعل إلى 96.53 ٪. من الناحية الإحصائية ، ربما يكون هذا الانخفاض ضئيلًا ، ولكن لا يوجد شيء جيد عنه.

هذا السلوك يبدو غريبا. يبدو بشكل حدسي أن الطبقات الإضافية المخفية يجب أن تساعد الشبكة على تعلم وظائف التصنيف الأكثر تعقيدًا ، والتعامل مع المهمة بشكل أفضل. بالطبع ، يجب ألا تتفاقم النتيجة ، لأنه في أسوأ الحالات ، لن تقوم الطبقات الإضافية ببساطة بأي شيء. ومع ذلك ، هذا لا يحدث.

إذن ما الذي يحدث؟ لنفترض أن الطبقات المخفية الإضافية يمكن أن تساعد من حيث المبدأ ، وأن المشكلة تكمن في أن خوارزمية التدريب لدينا لا تجد القيم الصحيحة للأوزان والإزاحة. نود أن نفهم ما هو الخطأ في خوارزمية لدينا ، وكيفية تحسينه.

لفهم الخطأ الذي حدث ، دعنا نتصور عملية تعلم الشبكة. في الأسفل ، قمت ببناء جزء من الشبكة [784،30،30،10] ، حيث يوجد طبقتان مخفيتان ، لكل منهما 30 خلية عصبية مخفية. على الرسم التخطيطي ، يحتوي كل خلية عصبية على شريط يشير إلى معدل التغير في عملية تعلم الشبكة. شريط كبير يعني أن الأوزان والتشريد من الخلايا العصبية تتغير بسرعة ، وقناة صغيرة تعني أنها تتغير ببطء. بتعبير أدق ، يشير الشريط إلى درجة الانحدار /C / ∂b للخلية العصبية ، أي معدل التغير في التكلفة فيما يتعلق بالإزاحة. في الفصل 2 ، رأينا أن هذه القيمة المتدرجة تتحكم ليس فقط في معدل تغيير النزوح أثناء التدريب ، ولكن أيضًا في معدل التغير في أوزان الخلايا العصبية المدخلة. لا تقلق إذا كنت لا تستطيع تذكر هذه التفاصيل: عليك فقط أن تضع في اعتبارك أن هذه الأشرطة تشير إلى مدى سرعة تغير أوزان وتشوهات الخلايا العصبية أثناء تدريب الشبكة.

لتبسيط المخطط ، وجهت ستة فقط من الخلايا العصبية العليا في طبقتين مخفيتين. لقد خفضت الخلايا العصبية الواردة لأنه ليس لديهم أوزان أو تحيزات. لقد حذفت أيضًا الخلايا العصبية الناتجة ، نظرًا لأننا نقارن طبقتين ، ومن المنطقي مقارنة الطبقات مع نفس عدد الخلايا العصبية. تم إنشاء المخطط باستخدام برنامج gener_gradient.py في بداية التدريب ، أي بعد تهيئة الشبكة مباشرةً.



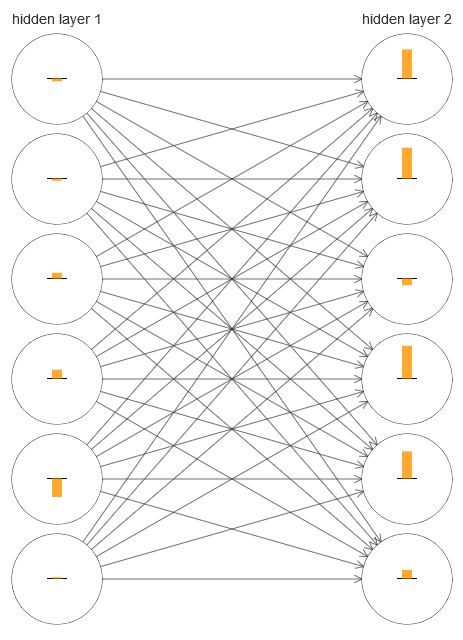
تمت تهيئة الشبكة عن طريق الصدفة ، لذلك هذا التنوع في سرعة تدريب الخلايا العصبية ليس مفاجئًا. ومع ذلك ، فإنه يلفت الأنظار على الفور إلى أنه في الطبقة الثانية المخفية ، تكون الشرائط أكثر بكثير من الطبقة الأولى. نتيجة لذلك ، سوف تتعلم الخلايا العصبية في الطبقة الثانية بشكل أسرع من الأولى. هل هذه صدفة أم أن الخلايا العصبية في الطبقة الثانية من المرجح أن تتعلم بشكل عام أسرع من الخلايا العصبية في الأولى؟

لمعرفة بالضبط ، سيكون من الجيد أن يكون هناك طريقة عامة لمقارنة سرعة التعلم في الطبقتين المخفية الأولى والثانية. للقيام بذلك ، دعونا نشير إلى التدرج اللوني على أنه δ ^l _j = ∂C / ∂b ^l _j ، أي أنه يمثل تدرج الخلايا العصبية No. j في الطبقة رقم l. في الفصل الثاني ، أطلقنا عليها "خطأ" ، ولكن هنا سأطلق عليها اسم "التدرج" بشكل غير رسمي. بشكل غير رسمي - نظرًا لأن هذه القيمة لا تتضمن صراحةً مشتقات جزئية من التكلفة حسب الوزن ، /C / ∂w. يمكن اعتبار التدرج δ ¹ متجهًا تحدد عناصره مدى سرعة تعلم الطبقة المخفية الأولى ، و ² كمتجه تحدد عناصره مدى سرعة تعلم الطبقة المخفية الثانية. نحن نستخدم أطوال هذه المتجهات كتقديرات تقريبية لسرعة تعلم الطبقات. هذا هو ، على سبيل المثال ، طول || || ¹ || يقيس سرعة التعلم من الطبقة الأولى المخفية ، وطول | δ ² || يقيس سرعة التعلم للطبقة الثانية المخفية.

مع هذه التعريفات وبنفس التهيئة المذكورة أعلاه ، نجد أن || || ¹ || = 0.07 و | δ ² || = 0.31. هذا يؤكد شكوكنا: الخلايا العصبية في الطبقة المخفية الثانية تتعلم أسرع بكثير من الخلايا العصبية في الطبقة المخفية الأولى.

ماذا يحدث إذا أضفنا المزيد من الطبقات المخفية؟ مع وجود ثلاث طبقات مخفية في الشبكة [784،30،30،30،10] ستكون سرعات التعلم المقابلة هي 0.012 و 0.060 و 0.283. مرة أخرى ، تتعلم الطبقات المخفية الأولى أبطأ بكثير من الأخيرة. إضافة طبقة أخرى مخفية مع 30 الخلايا العصبية. في هذه الحالة ، ستكون سرعات التعلم المقابلة هي 0.003 و 0.017 و 0.070 و 0.285. يتم الحفاظ على النمط: تتعلم الطبقات المبكرة ببطء أكثر من الطبقات اللاحقة.

لقد درسنا سرعة التعلم في البداية - مباشرة بعد تهيئة الشبكة. كيف تتغير هذه السرعة كما تتعلم؟ دعنا نعود وننظر إلى الشبكة بطبقتين مخفيتين. تتغير سرعة التعلم فيه كما يلي:



للحصول على هذه النتائج ، استخدمت نزول التدرج الدُفعي مع 1000 صورة تدريب وتدريب لـ 500 عصر. هذا يختلف قليلاً عن إجراءاتنا المعتادة - لم أستخدم الحزم الصغيرة والتقطت فقط 1000 صورة تدريب ، بدلاً من مجموعة كاملة من 50000 قطعة. لا أحاول خداعك وخداعك ، لكن اتضح أن استخدام النسب المتدرج العشوائي مع الحزم المصغرة يؤدي إلى إحداث ضوضاء أكبر بكثير على النتائج (ولكن إذا قمت بتقييم الضوضاء ، تكون النتائج متشابهة). باستخدام المعلمات التي اخترتها ، من السهل تحسين النتائج حتى نتمكن من رؤية ما يحدث.

في أي حال ، كما نرى ، تبدأ طبقتان في التدريب بسرعتين مختلفتين للغاية (وهو ما نعرفه بالفعل). ثم تنخفض سرعة كلتا الطبقتين بسرعة كبيرة ، وبعد ذلك يحدث انتعاش. ومع ذلك ، كل هذا الوقت ، تتعلم الطبقة المخفية الأولى أبطأ بكثير من الثانية.

ماذا عن الشبكات المعقدة؟ فيما يلي نتائج تجربة مماثلة ، ولكن مع شبكة بها ثلاث طبقات مخفية [784،30،30،30،10]:



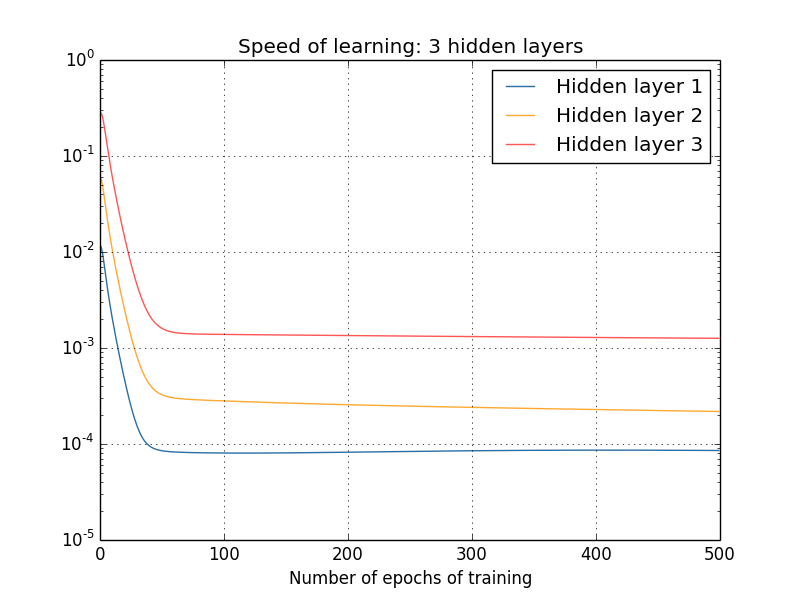
ومرة أخرى ، تتعلم الطبقات الأولى المخفية أبطأ بكثير من الأخيرة. أخيرًا ، دعونا نحاول إضافة طبقة مخفية رابعة (شبكة [784،30،30،30،30،10]) ، ونرى ما يحدث عندما يتم تدريبها:



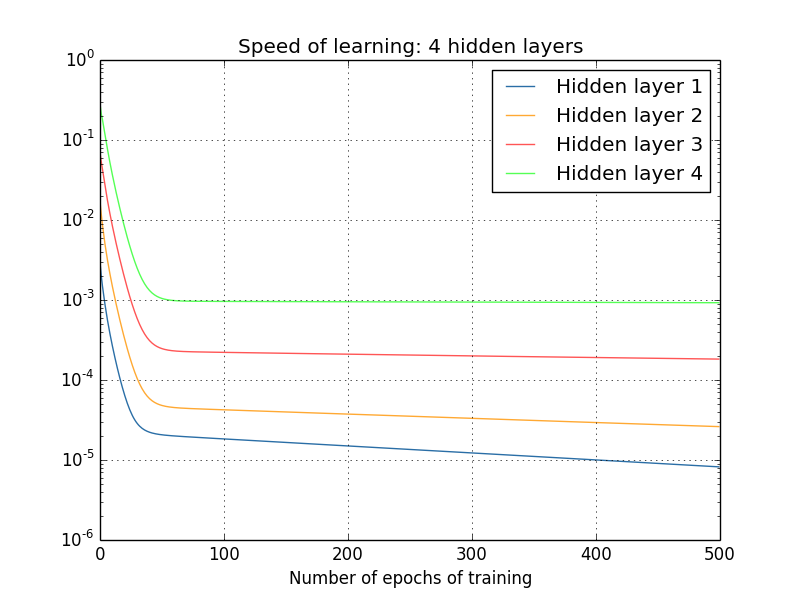
ومرة أخرى ، تتعلم الطبقات الأولى المخفية أبطأ بكثير من الأخيرة. في هذه الحالة ، تتعلم الطبقة الأولى المخفية حوالي 100 مرة أبطأ من الأخيرة. لا عجب أن لدينا مثل هذه المشاكل تعلم هذه الشبكات!

لقد قمنا بعمل ملاحظة مهمة: على الأقل في بعض شبكات GNS ، يتناقص التدرج عند التحرك في الاتجاه المعاكس على طول الطبقات المخفية. أي أن الخلايا العصبية في الطبقات الأولى يتم تدريبها ببطء أكثر بكثير من الخلايا العصبية في الماضي. وعلى الرغم من أننا لاحظنا هذا التأثير في شبكة واحدة فقط ، إلا أن هناك أسبابًا أساسية وراء حدوث ذلك في العديد من NS. تُعرف هذه الظاهرة باسم "مشكلة التدرج التلاشي" (راجع الأعمال 1 ، 2 ).

لماذا هناك مشكلة التدرج يتلاشى؟ هل هناك أي طرق لتجنب ذلك؟ كيف نتعامل معها عند تدريب STS؟ في الحقيقة ، سنعرف قريبًا أنه لا مفر منه ، على الرغم من أن البديل لا يبدو جذابًا لها: في بعض الأحيان يكون التدرج أكبر في الطبقات الأولى! هذه بالفعل مشكلة في نمو التدرج المتفجر ، وهي ليست أكثر نفعًا من مشكلة التدرج المختفي. بشكل عام ، اتضح أن التدرج في STS غير مستقر ، ويميل إما للنمو الهائل أو أن يختفي في الطبقات الأولى. يعد عدم الاستقرار هذا مشكلة أساسية لتدرج GNS المتدرج. هذا هو ما نحتاج إلى فهمه ، وربما حله بطريقة أو بأخرى.

أحد ردود الفعل على التدرج الخبو (أو غير المستقر) هو التفكير فيما إذا كانت هذه مشكلة خطيرة بالفعل؟ دعنا ننصرف لفترة وجيزة عن NS ، ونتخيل أننا نحاول تقليل العدد f (x) من متغير واحد إلى الحد الأدنى. ألن يكون لطيفًا إذا كانت المشتقة f ′ (x) صغيرة؟ ألا يعني هذا أننا قريبون بالفعل من أقصى الحدود؟ وبنفس الطريقة ، هل التدرج الصغير في الطبقات الأولى من GNS لا يعني أننا لم نعد بحاجة إلى ضبط الأوزان والتشريد بشكل كبير؟

بالطبع لا. أذكر أننا قمنا بتهيئة أوزان وإزاحة الشبكة بشكل عشوائي. من غير المرجح أن تؤدي الأوزان والمزيجات الأصلية الخاصة بنا بشكل جيد مع ما نريد من شبكتنا. كمثال محدد ، ضع في اعتبارك الطبقة الأولى من الأوزان في الشبكة [784،30،30،30،10] ، والتي تصنف الأرقام MNIST. التهيئة العشوائية تعني أن الطبقة الأولى تقوم بإخراج معظم المعلومات حول الصورة الواردة. حتى لو تم تدريب الطبقات المتأخرة بعناية ، فسيكون من الصعب للغاية تحديد الرسالة الواردة ، وذلك ببساطة بسبب نقص المعلومات. لذلك ، من المستحيل تمامًا تخيل أن الطبقة الأولى لا تحتاج ببساطة إلى التدريب. إذا كنا سنقوم بتدريب STS ، فنحن بحاجة إلى فهم كيفية حل مشكلة التدرج اللوني المختفي.

ما الذي يسبب مشكلة الانحدار التدريجي؟ تدرجات غير مستقرة في GNS

لفهم كيف تظهر مشكلة التدرج اللانهائي ، فكر في أبسط NS: مع خلية عصبية واحدة فقط في كل طبقة. هذه شبكة بها ثلاث طبقات مخفية:



هنا w ₁ ، w ₂ ، ... هي أوزان ، b ₁ ، b ₂ ، ... هي عمليات إزاحة ، C هي دالة تكلفة معينة. تمامًا كتذكير ، سأقول إن الخرج a _j من الخلايا العصبية No. j يساوي σ (z _j ) ، حيث σ هي وظيفة التنشيط السيني المعتادة ، و z _j = w _j a _{j - 1} + b _j هي المدخلات الموزونة للخلايا العصبية. قمت بتصوير وظيفة التكلفة في النهاية للتأكيد على أن التكلفة هي وظيفة ناتج الشبكة ، و ₄ : إذا كان الناتج الحقيقي قريبًا مما تريد ، فإن التكلفة ستكون صغيرة ، وإذا كانت بعيدة ، فستكون كبيرة.

نحن ندرس التدرج ∂C / ∂b ₁ المرتبط بأول خلية عصبية مخفية. نجد التعبير عن ∂C / ∂b ₁ ، وبعد دراسته ، سوف نفهم سبب ظهور مشكلة التدرج اللوني.

نبدأ بإظهار التعبير لـ ∂C / ∂b ₁ . يبدو منيعًا ، لكن في الحقيقة هيكله بسيط ، وسأصفه قريبًا. إليك هذا التعبير (في الوقت الحالي ، تجاهل الشبكة نفسها ولاحظ أن σ هو مجرد مشتق من الوظيفة σ):



بنية التعبير على النحو التالي: لكل خلية عصبية في الشبكة ، هناك مصطلح الضرب σ ′ (z _j ) ، لكل وزن يوجد w _j ، وهناك أيضًا المصطلح الأخير ، /C / 4a ₄ ، الموافق لوظيفة التكلفة. لاحظ أنني وضعت الأعضاء المقابلين فوق الأجزاء المقابلة من الشبكة. لذلك ، الشبكة نفسها هي قاعدة ذاكري للتعبير.

يمكنك أن تأخذ هذا التعبير عن الإيمان وتخطى مناقشته مباشرة إلى المكان الذي يتم فيه شرح كيفية ارتباطه بمشكلة التدرج الليلي. لا حرج في هذا ، لأن هذا التعبير هو حالة خاصة من مناقشتنا backpropagation. ومع ذلك ، من السهل شرح إخلاصه ، لذلك سيكون من المثير للاهتمام للغاية (وربما يكون مفيدًا) بالنسبة لك أن تدرس هذا الشرح.

تخيل أننا قمنا بإجراء تغيير بسيط في Δb ₁ على الإزاحة b ₁ . سيؤدي ذلك إلى إرسال سلسلة من التغييرات المتتالية عبر بقية الشبكة. أولاً ، سيؤدي ذلك إلى تغيير ناتج أول خلية عصبية مخفية 1a ₁ . هذا ، بدوره ، يجبر Δz ₂ على التغيير في المدخلات الموزونة على الخلية العصبية الثانية المخفية. ثم سيكون هناك تغيير في 2a ₂ في إخراج الخلايا العصبية المخفية الثانية. وهكذا ، ما يصل إلى تغيير في درجة مئوية في قيمة الإخراج. اتضح أن:

$$

$$\ frac {\ جزئية C} {\ جزئية b_1} \ approx \ frac {\ Delta C} {\ Delta b_1} \ tag {114}$$

يشير هذا إلى أنه يمكننا استنباط تعبير للتدرج ∂C / ∂b ₁ ، ومراقبة تأثير كل خطوة في هذه السلسلة بعناية.

للقيام بذلك ، دعونا نفكر في الكيفية التي يؤدي بها Δb ₁ إلى إخراج أحد الخلايا العصبية المخفية الأولى في التغيير. لدينا ₁ = σ (z ₁ ) = σ (w ₁ a ₀ + b ₁ ) ، لذلك

$$

$$\ Delta a_1 \ approx \ frac {\ جزئي \ sigma (w_1 a_0 + b_1)} {\ جزئي b_1} \ Delta b_1 \ tag {115}$$

$$

$$= \ sigma '(z_1) \ Delta b_1 \ tag {116}$$

يجب أن يبدو المصطلح σ ′ (z ₁ ) مألوفًا: هذا هو المصطلح الأول من تعبيرنا عن التدرج ∂C / ∂b ₁ . بشكل حدسي ، فإنه يحول التغيير في الإزاحة Δb ₁ إلى التغيير 1a _{1 في} تنشيط الخرج. يؤدي التغيير في ₁ causesa بدوره إلى حدوث تغيير في المدخلات الموزونة z ₂ = w ₂ a ₁ + b ₂ للخلايا العصبية المخفية الثانية:

$$

$$\ Delta z_2 \ approx \ frac {\ جزئي z_2} {\ جزئي a_1} \ Delta a_1 \ tag {117}$$

$$

$$= w_2 \ Delta a_1 \ tag {118}$$

عند الجمع بين التعبيرات لـ Δz ₂ و Δa ₁ ، نرى كيف ينتشر التغيير في الانحياز b ₁ عبر الشبكة ويؤثر على z ₂ :

$$

$$\ Delta z_2 \ approx \ sigma '(z_1) w_2 \ Delta b_1 \ tag {119}$$

ويجب أن يكون هذا أيضًا مألوفًا: هذه هي المصطلحين الأولين في تعبيرنا المعلن عن التدرج ∂C / ∂b ₁ .

يمكن الاستمرار في ذلك من خلال مراقبة كيفية نشر التغييرات في بقية الشبكة. في كل خلية عصبية نختار المصطلح _j (z _j ) ، ومن خلال كل وزن نختار المصطلح w _j . نتيجة لذلك ، يتم الحصول على تعبير يربط التغيير النهائي ΔC لدالة التكلفة بالتغيير الأولي Δb _{1 من} التحيز:

$$

$$\ Delta C \ approx \ sigma '(z_1) w_2 \ sigma' (z_2) \ ldots \ sigma '(z_4) \ frac {\ جزئي C} {\ الجزئي a_4} \ Delta b_1 \ tag {120}$$

بتقسيمه على Δb ₁ ، نحصل حقًا على التعبير المطلوب للتدرج:

$$

$$\ frac {\ جزئية C} {\ جزئية b_1} = \ sigma '(z_1) w_2 \ sigma' (z_2) \ ldots \ sigma '(z_4) \ frac {\ جزئية C} {\ جزئية a_4} \ tag { 121}$$

لماذا هناك مشكلة التدرج يتلاشى؟

لفهم سبب نشوء مشكلة التدرج اللوني ، دعنا نكتب بالتفصيل تعبيرنا بالكامل عن التدرج اللوني:

$$

$$\ frac {\ جزئية C} {\ جزئية b_1} = \ sigma '(z_1) \ w_2 \ sigma' (z_2) \ w_3 \ sigma '(z_3) \ ، w_4 \ sigma' (z_4) \ \ frac {\ جزئية C} {\ جزئية a_4} \ علامة {122}$$

بالإضافة إلى المصطلح الأخير ، فإن هذا التعبير هو نتاج مصطلحات النموذج w _j σ ′ (z _j ). لفهم كيف يتصرف كل منهم ، نلقي نظرة على الرسم البياني للدالة σ:



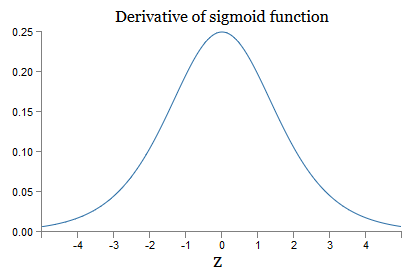
يصل الرسم البياني إلى الحد الأقصى عند النقطة σ ′ (0) = 1/4. إذا استخدمنا الطريقة القياسية لتهيئة أوزان الشبكة ، فسنختار الأوزان باستخدام التوزيع الغوسي ، أي يعني الجذر التربيعي الصفر المربع والانحراف المعياري 1. لذلك ، عادةً ما ترضي الأوزان عدم المساواة | w _j | <1. بمقارنة كل هذه الملاحظات ، نرى أن المصطلحات w _j σ ′ (z _j ) عادةً ما تلبي عدم المساواة | w _j σ ′ (z _j ) | <1/4. وإذا أخذنا منتج مجموعة من هذه الشروط ، فسوف ينخفض ​​بشكل كبير: كلما زادت الشروط ، كلما كان المنتج أصغر. يبدأ في الظهور كحل ممكن لمشكلة التدرج المختفي.

لكتابة هذا بشكل أكثر دقة ، نقارن التعبير عن ∂C / ∂b ₁ بتعبير التدرج فيما يتعلق بالإزاحة التالية ، على سبيل المثال ، /C / ∂b ₃ . بالطبع ، لم نكتب تعبيرًا مفصلاً عن ∂C / ∂b ₃ ، لكنه يتبع نفس القوانين الموضحة أعلاه لـ ∂C / ∂b ₁ . وهنا مقارنة بين تعبيرين:



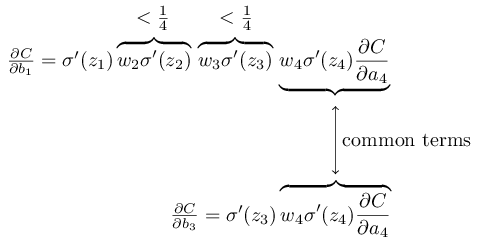
لديهم العديد من الأعضاء المشتركين. ومع ذلك ، فإن التدرج ∂C / ∂b ₁ يتضمن فترتين إضافيتين ، ولكل منهما شكل w _j σ ′ (z _j ). كما رأينا ، فإن هذه المصطلحات عادة لا تتجاوز 1/4. لذلك ، يكون التدرج ∂C / ∂b ₁ عادة 16 (أو أكثر) أصغر من ∂C / ∂b ₃ . وهذا هو السبب الرئيسي لمشكلة التدرج تختفي.

بالطبع ، هذا ليس دقيقًا ، لكنه دليل غير رسمي على المشكلة. هناك العديد من المحاذير. على وجه الخصوص ، قد يهتم المرء بما إذا كانت الأوزان w _j ستزداد أثناء التدريب. في حالة حدوث ذلك ، لن تلبي المصطلحات w _j σ ′ (z _j ) في المنتج عدم المساواة | w _j σ ′ (z _j ) | <1/4. وإذا تبين أنها كبيرة بما يكفي ، أكثر من 1 ، فلن نواجه مشكلة تدرج اللون. بدلاً من ذلك ، سينمو التدرج بشكل كبير أثناء العودة من خلال الطبقات. وبدلاً من مشكلة الانحدار التدريجي ، نواجه مشكلة نمو التدرج المتفجر.

مشكلة النمو التدريجي المتفجر

دعونا نلقي نظرة على مثال محدد للتدرج المتفجر. المثال سيكون مصطنعًا إلى حد ما: سوف أقوم بضبط معلمات الشبكة لضمان حدوث نمو هائل. ولكن على الرغم من أن هذا المثال مصطنع ، إلا أن إيجابته تكمن في أنه يوضح بوضوح أن النمو الهائل للتدرج ليس احتمالًا افتراضيًا ، لكن يمكن أن يحدث بالفعل.

لنمو التدرج المتفجر ، تحتاج إلى اتخاذ خطوتين. أولاً ، نختار الأوزان الكبيرة في الشبكة بالكامل ، على سبيل المثال ، w1 = w2 = w3 = w4 = 100. ثم نختار هذه التحولات بحيث تكون المصطلحات σ ′ (z _j ) ليست صغيرة جدًا. وهذا من السهل القيام به: نحتاج فقط إلى تحديد مثل هذه التشريدات بحيث تكون المدخلات الموزونة لكل خلية عصبية هي zj = 0 (ثم σ ′ (z _j ) = 1/4). لذلك ، على سبيل المثال ، نحتاج z ₁ = w ₁ a ₀ + b ₁ = 0. يمكن تحقيق ذلك عن طريق إعداد b ₁ = −100 ∗ a ₀ . يمكن استخدام نفس الفكرة لتحديد الإزاحات الأخرى. نتيجة لذلك ، سنرى أن كل المصطلحات w _j σ σ (z _j ) تتحول إلى 100 ∗ 14 = 25. ثم نحصل على نمو متدرج النمو.

مشكلة التدرج غير مستقرة

المشكلة الأساسية ليست مشكلة التدرج المختفي أو النمو الهائل للتدرج. هو أن التدرج في الطبقات الأولى هو نتاج أعضاء من جميع الطبقات الأخرى. وعندما يكون هناك العديد من الطبقات ، يصبح الوضع غير مستقر بشكل أساسي. والطريقة الوحيدة التي يمكن أن تتعلم بها جميع الطبقات بنفس السرعة تقريبًا هي اختيار هؤلاء الأعضاء من العمل الذي يحقق التوازن بين بعضهم البعض. وفي حالة عدم وجود آلية أو سبب لمثل هذا التوازن ، فمن غير المرجح أن يحدث هذا بالصدفة.باختصار ، المشكلة الحقيقية هي أن NS يعاني من مشكلة التدرج غير المستقر. وفي النهاية ، إذا استخدمنا تقنيات التعلم المعتمدة على التدرج القياسي ، فستتعلم طبقات مختلفة من الشبكة بسرعات مختلفة بشكل رهيب.

ممارسة

• في مناقشتنا لمشكلة التدرج التلاشي ، استخدمنا حقيقة أن | σ ′ (z) | <1/4. لنفترض أننا نستخدم وظيفة تنشيط مختلفة ، يمكن أن يكون مشتقها أكبر بكثير. هل سيساعدنا ذلك في حل مشكلة التدرج غير المستقر؟

لقد رأينا أن التدرج يمكن أن يختفي أو ينمو بشكل متفجر في الطبقات الأولى من الشبكة العميقة. في الواقع ، عند استخدام الخلايا العصبية السينيّة ، عادة ما يختفي التدرج اللوني. لفهم السبب ، ضع في اعتبارك مرة أخرى التعبير | wσ ′ (z) |. لتجنب مشكلة التدرج المختفي ، نحتاج إلى | wσ ′ (z) | ≥1. قد تقرر أنه من السهل تحقيق ذلك بقيم كبيرة جدًا من w. ومع ذلك ، في الواقع ليست بهذه البساطة. السبب هو أن المصطلح σ ′ (z) يعتمد أيضًا على w: σ σ (z) = σ ′ (wa + b) ، حيث a هو تنشيط الإدخال. وإذا جعلنا كبيرًا ، فيجب أن نحاول ألا نجعل wa ′ (wa + b) صغيرة على التوازي. وهذا تبين أن وجود قيود خطيرة. السبب هو أننا عندما نجعل w كبيرًا ، فإننا نجعل wa + b كبيرًا جدًا. إذا نظرت إلى الرسم البياني لـ σ ′ ، يمكن ملاحظة أن هذا يقودنا إلى "أجنحة" الوظيفة ′ ′ ،حيث يأخذ على قيم صغيرة جدا. والطريقة الوحيدة لتجنب ذلك هي الحفاظ على التنشيط الوارد في نطاق ضيق إلى حد ما من القيم. يحدث هذا في بعض الأحيان عن طريق الصدفة. ولكن في كثير من الأحيان هذا لا يحدث. لذلك ، في الحالة العامة ، لدينا مشكلة التدرج التلاشي.

• |wσ′(wa+b)|. , |wσ′(wa+b)|≥1. , , |w|≥4.
• , |w|≥4, , |wσ′(wa+b)|≥1.
• , , ,

  $$

  $$\frac{2}{|w|} \ln\left( \frac{|w|(1+\sqrt{1-4/|w|})}{2}-1\right) \tag{123}$$
• , |w|≈6.9, ≈0,45. , , , .
• . x, w ₁ , b w ₂ . , , , w ₂ σ(w ₁ x+b)≈x for x∈[0,1]. , , ( ). : x=1/2+Δ, , w ₁ , w ₁ Δ .

درسنا شبكات الألعاب مع خلية واحدة فقط في كل طبقة خفية. ماذا عن الشبكات العميقة الأكثر تعقيدًا التي تحتوي على العديد من الخلايا العصبية في كل طبقة مخفية؟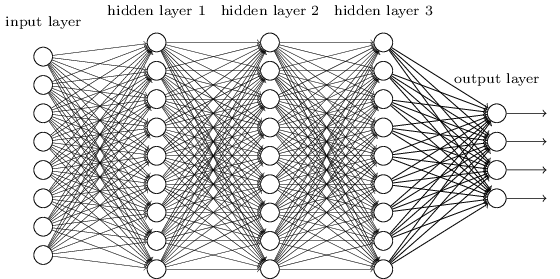



في الواقع ، يحدث نفس الشيء في مثل هذه الشبكات. في وقت سابق من الفصل المتعلق بالانتشار الخلفي ، رأينا أن التدرج في الطبقة #l من الشبكة ذات الطبقات L محدد على النحو التالي:

$$

$$\delta^l = \Sigma'(z^l) (w^{l+1})^T \Sigma'(z^{l+1}) (w^{l+2})^T \ldots \Sigma'(z^L) \nabla_a C \tag{124}$$

هنا Σ ′ (z ^l ) هي المصفوفة المائلة ، وعناصرها هي قيم σ ′ (z) للمدخلات الموزونة للطبقة رقم l. ث ^ل هي مصفوفات الوزن لطبقات مختلفة. و ∇ _a C هي ناقل للمشتقات الجزئية لـ C فيما يتعلق بتنشيط الخرج.

هذا التعبير هو أكثر تعقيدا بكثير من الحال مع خلية واحدة. ومع ذلك ، إذا نظرت عن كثب ، فسيكون جوهرها متشابهًا للغاية ، مع مجموعة من الأزواج من الشكل (w ^j ) ^T Σ ′ (z ^j ). علاوة على ذلك ، تحتوي المصفوفات Σ ′ (z ^j ) قطريًا على قيم صغيرة ، لا تزيد عن 1/4. إذا كانت مصفوفة الترجيح ث ^ي ليست كبيرة جدا، كل عضو إضافي (ث ^ي ) ^T Σ '(ض ^ل) يميل إلى تقليل متجه التدرج ، مما يؤدي إلى انحدار متدرج. في الحالة العامة ، يؤدي عدد أكبر من مصطلحات الضرب إلى تدرج غير مستقر ، كما في مثالنا السابق. في الممارسة العملية ، تجريبيا عادة في شبكات السيني ، تختفي التدرجات في الطبقات الأولى بسرعة كبيرة. نتيجة لذلك ، يتباطأ التعلم في هذه الطبقات. والتباطؤ ليس حادثًا أو إزعاجًا: إنه نتيجة أساسية لنهجنا المختار في التعلم.

عقبات أخرى أمام التعلم العميق

في هذا الفصل ، ركزت على تدرجات اللون الباهتة - وبشكل عام حالة التدرجات غير المستقرة - كعقبة أمام التعلم العميق. في الواقع ، التدرجات غير المستقرة ليست سوى عقبة واحدة أمام تطوير الدفاع المدني ، وإن كانت عقبة مهمة وأساسية. يحاول جزء كبير من البحث الحالي فهم المشكلات التي قد تنشأ في تدريس GO بشكل أفضل. لن أصف بالتفصيل كل هذه الأعمال ، لكنني أود أن أذكر بإيجاز بعض الأعمال لتعطيك فكرة عن بعض الأسئلة التي طرحها الناس.

كمثال أول في عام 2010تم العثور على أدلة على أن استخدام وظائف التنشيط السيني يمكن أن يؤدي إلى مشاكل في تعلم NS. على وجه الخصوص ، تم العثور على أدلة على أن استخدام السيني سيؤدي إلى حقيقة أن تنشيط آخر طبقة مخفية أثناء التدريب سيتم تشبعه في المنطقة 0 ، مما سيؤدي إلى إبطاء التعلم بشكل خطير. تم اقتراح العديد من وظائف التنشيط البديلة التي لا تعاني كثيرًا من مشكلة التشبع (انظر أيضًا ورقة مناقشة أخرى ).

كمثال أول ، في عام 2013 ، تمت دراسة تأثير التهيئة العشوائية للأوزان والرسم البياني للنبض في نزول تدرج عشوائي على أساس النبضة على GO. في كلتا الحالتين ، أثر اختيار جيد بشكل كبير على القدرة على تدريب STS.

تشير هذه الأمثلة إلى أن السؤال "لماذا يصعب تدريب STS؟" معقد جدا. في هذا الفصل ، ركزنا على عدم الاستقرار المرتبط بالتدرج التدريجي لنظام GNS. تشير نتائج الفقرتين السابقتين إلى أن اختيار وظيفة التنشيط ، وطريقة تهيئة الأوزان ، وحتى تفاصيل تنفيذ التدريب على أساس النسب المتدرجة تلعب أيضًا دورًا. وبالطبع ، سيكون اختيار بنية الشبكة وغيرها من المعلمات الفائقة أمرًا مهمًا. لذلك ، يمكن أن تلعب العديد من العوامل دورًا في صعوبة تعلم الشبكات العميقة ، وقضية فهم هذه العوامل هي موضوع البحث المستمر. لكن كل هذا يبدو كئيبًا إلى حد ما ويلهم التشاؤم. ومع ذلك ، فهناك أخبار جيدة - في الفصل التالي ، سنختم كل شيء لصالحنا ، وسنطور عدة نُهج في GO ،والتي سوف تكون قادرة إلى حد ما على التغلب على كل هذه المشاكل أو التحايل عليها.