الكم ، أو هناك والعودة: خوارزمية جديدة لدراسة الانتقال الكلاسيكية الكم

يعتقد الكثيرون أن فيزياء الكم فقط يمكن أن تكون أكثر تعقيدًا من الفيزياء الكلاسيكية. ومع ذلك ، من الأصعب بكثير دراسة الأنظمة التي ، إذا جاز التعبير ، عند تقاطع هذين العالمين. إذا تمت إضافة المزيد من الجزيئات إلى نظام الكم ، فسوف يبدأ في فقدان خصائصه الكمية ويتحول إلى خصائص أكثر كلاسيكية. وتسمى هذه العملية الانتقال الكم الكلاسيكية. لن تكون الحواسيب الكلاسيكية كافية لدراسة مثل هذا النظام ، لأن العلماء من مختبر لوس ألاموس الوطني قد اقترحوا خوارزمية خاصة بهم ، والتي ، إلى جانب الحواسب الكمومية من بضع مئات من البتات ، يمكنها حل أسرار التحول الكلاسيكي الكمومي. كيف تعمل الخوارزمية ، لماذا تعني الصيغ الأقل أفضل وأي تطبيق لهذه الخوارزمية في الممارسة؟ هذا وليس فقط نتعلم من تقرير مجموعة البحث. دعنا نذهب.

أساس الدراسة

يعتبر الانتقال الكلاسيكي الكمالي ، إذا تم المبالغة فيه ، عملية فك الارتباط عندما يفقد النظام الكمومي تماسكه ، أي اكتساب الخصائص الكلاسيكية. يمكن أن تحدث هذه العملية لعدد من الأسباب ، من بينها الأكثر وضوحا تفاعل النظام الكمومي والبيئة. ويعتقد أيضًا أن هذه العملية هي حجر تعثر عملية تحقيق الكمبيوتر الكمومي عليها.

هناك العديد من الطرق لمكافحة فك الارتباط ، إحداهما أكثر تسلية من الأخرى ، لكن بالإجمال يمكن تقسيمها إلى فئتين: العزلة والتنفيذ. في الحالة الأولى ، يحاول العلماء عزل النظام الكمومي عن البيئة ، باستخدام درجات حرارة منخفضة للغاية و / أو فراغ عالي. في الحالة الثانية ، يتم إدخال التصحيحات (الكود) في خوارزميات الحسابات الكمية ، والتي ستكون مقاومة للأخطاء الناشئة عن فك الارتباط. هذه الأساليب تعمل ، لا أحد ينكر هذا ، لكنها ليست قابلة للتطوير للغاية. يمكن للعلماء الاحتفاظ بالذرات في حالة تراكب لفترة من الوقت إذا تم تقليل التأثيرات البيئية. ومع ذلك ، على نطاق أوسع ، كل شيء ، كقاعدة عامة ، يذهب إلى الجحيم.

لذلك ، في حين أن بعض الأشخاص ذوي الذكاء في المعاطف البيضاء يبحثون عن طرق للتعامل مع عدم التسامح ، يبحث آخرون عن أدوات لدراستها. إذا كنت تريد هزيمة عدوك ، فاعرفه عن طريق البصر ، كما يقولون.

قبل أن نغرق في مجرى الصيغ والتفسيرات المتعلقة بالخوارزمية التي وضعها العلماء ، فإن الأمر يستحق القيام بقفزة قصيرة في الوقت المناسب. اقترح روبرت غريفيث ، عالم الفيزياء الأمريكي في جامعة كارنيجي ميلون ، نظرية القصص المتسلسلة (الأحداث) في عام 1984: الفيزياء الكلاسيكية قريبة من الميكانيكا الكمومية ، ويمكن للرياضيات الكمومية حساب احتمالات الظواهر واسعة النطاق ودون الذرية التي لا تتعلق بنتائج القياس ، ولكن حالة النظام. يقدم السيد غريفيث مثالًا على ذلك صورًا للجبال التي يمكن التقاطها من زوايا مختلفة ، ثم قم بعمل صورة لجبال حقيقي منها. في حالة فيزياء الكم ، من الممكن اختيار معلمة القياس ، لكن لن يعمل على الجمع بين قياسين لتكوين صورة كاملة للجسيم قبل القياس. قبل العملية الفعلية لقياس الموقف الحقيقي والزخم ، فإنه ببساطة غير موجود.


روبرت غريفيث

مرتبك وقليلًا ينزلق على السطح ، لكن هذا ليس كل شيء. في عام 1989 ، طرح موراي جيل مان وجيمس هارتل مفهومهما القائم على نظرية غريفيث. في رأيهم ، يمكن اعتبار الكون كله كنظام كم واحد دون بيئة خارجية. إذا كان الأمر كذلك ، فحينئذٍ يحدث فك الارتباط داخل النظام ، وتكون نتيجة نشاطه نطاقات كلاسيكية - مجموعات من التواريخ المتسلسلة التي يتعذر تمييزها على خلفية الحبوب الخشنة بسبب فك الارتباط.

ساعدت هذه النظريات في حل بعض المشاكل والمفارقات في ميكانيكا الكم ، ولكن ليس كلها. يعتقد الباحثون أن هذه الاستنتاجات من أسلافهم لا تستخدم على نطاق واسع بسبب حقيقة أن حسابات النظم غير التافهة (على سبيل المثال ، الأنظمة المنفصلة ذات الحجم الملحوظ أو الأنظمة المستمرة التي لا تسمح بالأوصاف التقريبية عن طريق تكاملات قابلة للحل بالضبط) معقدة للغاية. بمعنى آخر ، هذه النظريات جيدة ، ولكن فقط في حالات بسيطة.

في السنوات الأخيرة ، تسارعت وتيرة تطوير التقنيات الكمومية بشكل كبير ، وظهرت خوارزميات هجائية تقليدية كمومية ( VHQCA ) يمكنها أن تتكيف بشكل جيد مع المهام المختلفة (التخصيم ، البحث عن حالات الأرض ، إلخ).

في العمل الذي نفكر فيه اليوم ، يصف العلماء خوارزمية VHQCA الخاصة بهم للقصص المتسلسلة. وفقًا للباحثين ، فإن خوارزميةهم تتفوق على الطرق الكلاسيكية في العديد من المعلمات ، بما في ذلك حجم الأنظمة التي تمت دراستها.

ماراثون الصيغ (الأساس النظري)

لقد كان لدينا بالفعل استنباط تاريخي ، والآن يستحق الأمر بعض المعرفة بالقاعدة الحسابية للخوارزمية قبل النظر في نتائج عملها.

أساس التواريخ التسلسلية (CH) هو تاريخ Y ^α هو سلسلة من الخصائص في سلسلة من مثيلات الوقت t ₁ < t ₂ <... < t _k :



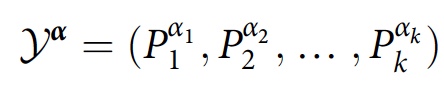
حيث يتم اختيار P α j j من مجموعة أجهزة العرض P j التي يتم جمعها في الوقت t j .

يقدم العلماء مثالًا توضيحيًا: فوتون يمر عبر عدة حواجز شبكية للحيود ثم ضرب الشاشة. في مثل هذه الحالة ، قد تكون القصة عبارة عن فوتون يمر عبر فتحة واحدة في الشبكة الأولى ، وشق آخر في الثانية ، إلخ. لذلك ، هناك بعض التدخل بين هذه القصص. ونظرًا لوجود عوائق ، من المستحيل بشكل تقليدي إضافة احتمالات مختلف القصص توقعًا للتنبؤ الصحيح للنقطة التي يضرب بها الفوتون على الشاشة.

يوفر إطار عمل CH أدوات لتحديد وقت تعرض عائلة القصة F = { Y ^α } للتداخل ، وهو أمر غير واضح دائمًا. كما أنه يحدد عامل الفصل:



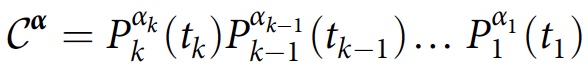
وهو منتج مرتب زمنياً لمشغلي الإسقاط في تاريخ Y ^α . إذا تم وصف النظام في البداية بمصفوفة كثافة ρ ، فإن درجة التداخل أو التداخل بين التاريخين Y ^α و Y ^{α ′} ستكون مساوية لـ:



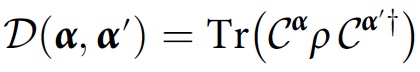
وتسمى هذه القيمة decoherence الوظيفية. ستبدو حالة الاتساق لعائلة القصة F في هذه الحالة كما يلي:



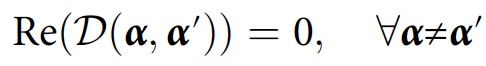
فقط إذا تم استيفاء هذا الشرط ، لتاريخ Y ^{α ، فإن} الاحتمال سيكون D ( α ، α ). لإجراء عمليات حسابية أكثر بساطة ، يمكن تطبيق شرط آخر:



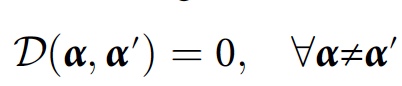
يقول العلماء أنه بالنسبة للخوارزمية العددية ، سيكون من المفيد للغاية مراعاة الاتساق التقريبي مع مراعاة التداخل البسيط:



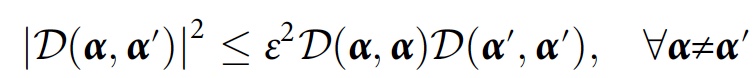
لدراسة الاتساق الذي ينشأ فقط من فك الارتباط (أي التسجيلات في البيئة) ، اقترح الباحثون طريقة تأخذ بدلاً من ذلك تتبعًا جزئيًا على E ، وهو نظام فرعي للبيئة:



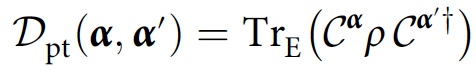
مع هذا التعديل ، ستبدو حالة التناسق كما يلي:



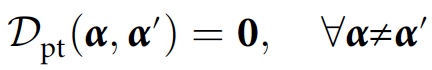
حيث 0 هي المصفوفة صفر. بدلاً من الإشارة إلى عدم وجود تدخل بيئي ، يشير الاتساق إلى وجود / عدم وجود تناقضات في سجلات القصص في البيئة.


الصورة رقم 1: مخطط المتفرعة قصة لخطوات الوقت ك.

بالنظر إلى ماراثون الصيغ وفهم القصص المتسلسلة ، يشير العلماء إلى دليل على أن المخططات العددية الكلاسيكية للميثان غير قادرة على التعامل مع المهمة.

تُظهر الصورة أعلاه مثالًا حيث توجد قصص عن العدد الإجمالي للجسيمات مع 1/2 تدور للخطوات الزمنية k . عدد القصص 2 ^nk ؛ لذلك ، هناك ~ ^{2 nk} العناصر الوظيفية للترابط. بالإضافة إلى ذلك ، يتطلب تقدير كل عنصر وظيفي من فك الارتباط D ( α ، α ' ) ما يعادل محاكاة هاميلتون للنظام ، أي ضرب مصفوفات 2 × 2 ^ن . هذا يعني أن المجموعات الحديثة ستحتاج إلى مئات السنين لحساب تناسق عائلة من القصص مع k = 2 خطوات زمنية و n = 10 يدور.

خوارزمية VCH الهجين

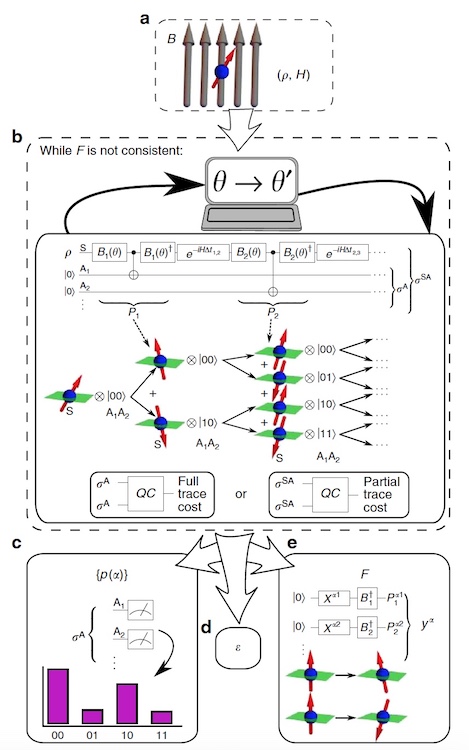الصورة رقم 2: مخطط كتلة VCH.

ودعا العلماء خوارزمية VHQCA VCH (قصص متتابعة متغيرة). تأخذ VCH كمدخلات للنموذج المادي (أي الحالة الأولية Hamilton و Hamiltonian H ) وبعض ansatz * لأنواع أجهزة العرض التي تحتاج إلى أخذها في الاعتبار.

Ansatz * هو حدس حول ما يجب أن يكون عليه حل المعادلة والشكل الذي ينبغي أن يكون عليه.

البيانات التالية متاحة باعتبارها البيانات الناتجة:

• عائلة من القصص F ، والتي (تقريبًا) تتبع كامل و / أو جزئي في شكل مشغلي إسقاط أعدوا على كمبيوتر الكم ؛
• احتمالات الأكثر احتمالا من قصص Y ^α في F (آسف للتورية) ؛
• تقدير معامل الاتساق ε .

تتضمن VCH دورة تحسين للمعلمات حيث يقوم الكمبيوتر الكمي بتقييم وظيفة التكلفة التي تحدد عدم تطابق الأسرة ، بينما يقوم المحسن الكلاسيكي بضبط الأسرة (أي تغيير معلمات جهاز العرض) لتقليل التكاليف.

لحساب التكاليف ، من الضروري مراعاة أن عناصر decoherence الوظيفية تشكل مصفوفة شبه نصف نهائية إيجابية. يتم استخدام هذه الخاصية في VCH لترميز D في الحالة الكمية σ ، عناصر المصفوفة الخاصة بها هي |α | | ^A | α ′ ⟩ = D ( α ، α ′ ).

يُظهر 2b دارة كمومية تستعد σ ^A بتحويل الحالة الأولية ρ ⊗ | 0〉 〈0 | في أنظمة SA (حيث تمثل S النظام المادي للفائدة و A نظامًا مساعدًا) للدولة σ ^SA ، التي تكون القيمة الحدية لها هي σ ^A.

من أجل اتساق التتبع الكامل للمصفوفة ، يتم تقديم مقياس عالمي للتناسق ، والذي يحدد كمياً المسافة من ^A إلى القطر ، والتي تعمل كدالة للتكاليف:



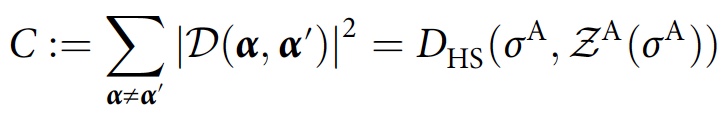
حيث D _HS هي مسافة Hilbert-Schmidt و Z ^A ( σ ^A ) خالية من الطور (جميع العناصر خارج القطر مضبوطة على الصفر) من σ ^A.

تميل هذه الكمية إلى الصفر إذا كانت F ثابتة. بالنسبة لحالة التتبع الجزئي ، يتم الحصول على دالة تكلفة مماثلة ، ولكن مع استبدال " ^A" بـ " ^SA" :



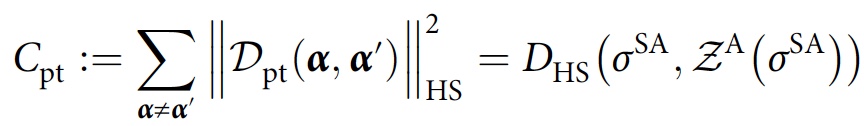
تؤدي دورة تحسين المعلمة إلى مجموعة متناسقة تقريبًا من القصص F ، حيث يتم تحديد معلمة التناسق from من الأعلى كجزء من التكاليف النهائية.

يُظهر 2c توليد الاحتمالات لأكثر القصص احتمالية من خلال إعداد repeatedlyA بشكل متكرر والقياس على أساس قياسي ، حيث تعطي ترددات القياس الاحتمالات.

يوضح 2e كيفية إعداد مجموعة من عوامل الإسقاط لأي تاريخ محدد في F.

نتائج التجربة

أجريت عدة تجارب مختلفة باستخدام خوارزمية VCH. سننظر في اثنين - تدور في مجال مغناطيسي وجزيء حلزوني.

تدور في المجال المغناطيسي

الصورة رقم 3

في التجربة الأولى ، درسنا تاريخين من الزمن لجسيم مع تدور 1/2 في المجال المغناطيسي Bz ، الذي هاميلتون هو H = - σBσ _z . تحتوي القصص التي ندرسها على خطوة زمنية بين الحالة الأولية وجهاز الإسقاط الأول ، وكذلك بين جهاز الإسقاط الأول والثاني. بالإضافة إلى ذلك ، تجدر الإشارة إلى أن أجهزة الإسقاط فقط على متن الطائرة xy من كرة Bloch تعتبر.

تُظهر الصورة أعلاه مخطط التكلفة لمعالج الكم ibmqx5 ، وكذلك لجهاز محاكاة ، الذي كانت دقته محدودة من خلال تداخل نفس الإحصاءات النهائية التي تم جمعها باستخدام معالج الكم. عدة مستويات منخفضة تم العثور عليها عند تشغيل VCH على ibmqx5 تتداخل مع المخطط. نظرًا لأن هذه الحدود الدنيا تتوافق تمامًا مع الأسر المتناسقة من الناحية النظرية ، فإن هذا يمثل نجاح VCH في الممارسة العملية.

جزيء Chiral

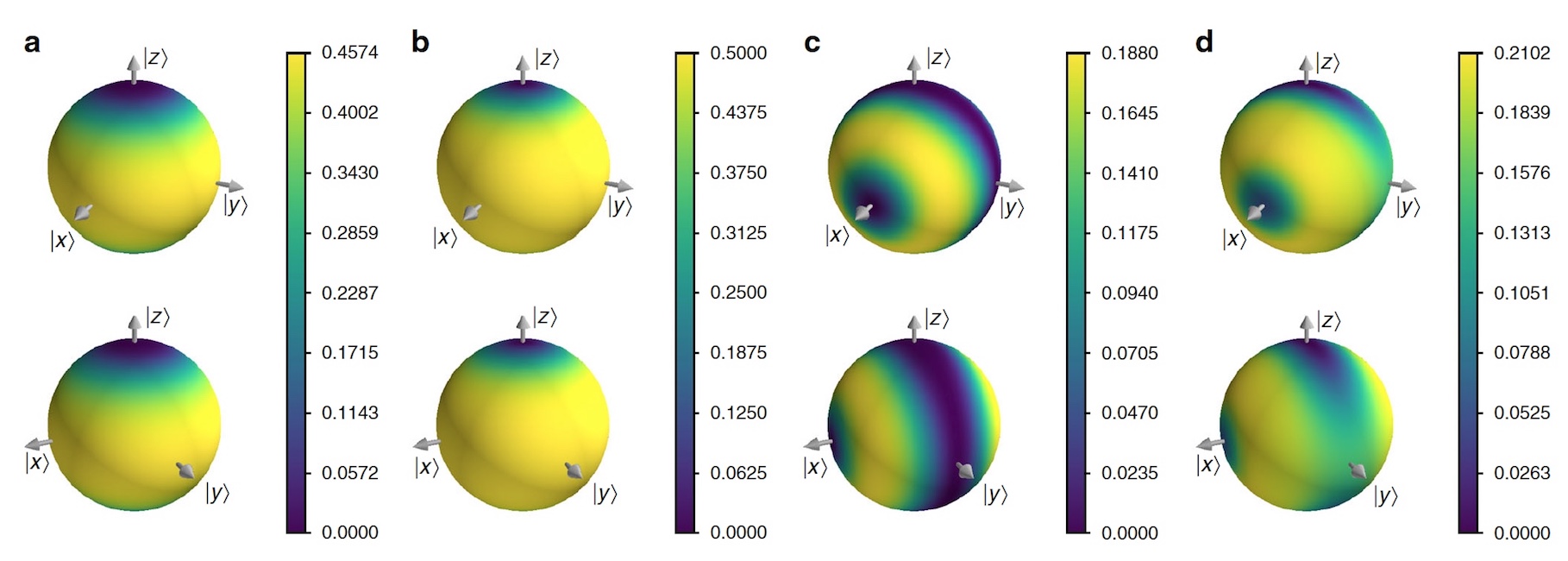الصورة رقم 4

تم اختيار جزيء chiral للتجارب العملية ، لأن هذه طريقة ممتازة لتحديد تطبيق VCH. تمت صياغة جزيء chiral كنظام من مستويين حيث يتم وصف حالات R | R اليمنى واليسرى | L〉 chirality كـ | R⟩ / | L⟩ = | +⟩ / | -⟩ = 1 / √2 * (| 0⟩ ± | 1⟩).

إنفاق جزيء كرومي معزول بين | R⟩ و | L⟩ ، لكن العلماء يتوقعون أنه في غاز ، حيث تنقل الاصطدامات مع جزيئات أخرى معلومات حول شرعية الجزيء إلى بيئته. يتم نمذجة نقل المعلومات هذا عن طريق الدوران من خلال زاوية _× حول المحور السيني للبتة المتوسطة التي تتحكم فيها شرعية النظام.

ثم يفكر العلماء في عائلات بسيطة من تاريخ ثابت ، حيث تتوافق مجموعة من أجهزة العرض مع نفس القاعدة كل خمس مرات (على سبيل بساطة النمذجة ، وجد أن الجزيء يصطدم بجزيئات أخرى 5 مرات). بافتراض أن الزاوية pre _z هي الزاوية المسبقة بسبب نفق الوقت بين الاصطدامات ، فمن الممكن التحقق من التنافس بين فك الارتباط والنفق. الصورة أعلاه توضح نتائج هذه المحاكاة.

يلاحظ العلماء حقيقة غريبة - هناك انتقال من نظام كمي حيث لا تكون التسلسلات التسلسلية لنظام كلاسيكي حيث تكون الخيوط متسلسلة ومستقرة مع مرور الوقت.

للتعرف أكثر تفصيلاً على الفروق الدقيقة في الدراسة ، أوصي بأن تنظر في تقرير العلماء ومواد إضافية إليه.

خاتمة

لقد أظهر هذا العمل خوارزمية جديدة ، والتي ، بالاقتران مع أجهزة الكمبيوتر الكمومية الحالية والمستقبلية ، يمكنها أن تصف بشكل أفضل هذه العملية المعقدة والمعقدة بأنها انتقال كلاسيكي الكم. تحظى دراسة هذه الظاهرة بأهمية كبيرة إذا أردنا أبدًا إنشاء كمبيوتر كمومي حقيقي وفعال وفعال ، لن يتأثر تشغيله بالترابط.

خوارزمية VCH في المرحلة الأولى من التطوير ، لكنها تُظهر بالفعل أدائها. في المستقبل ، ينوي العلماء تحسينه بشكل طبيعي. بصرف النظر عن ذلك ، فإن احتمالات التنفيذ المبكر للحوسبة الكمومية لا تظل عند نفس المستوى فحسب ، بل تنمو مع كل دراسة من هذا القبيل.

شكرا لك على اهتمامك ، ابقَ فضوليًا ولديك أسبوع عمل جيدًا يا شباب! :)

شكرا لك على البقاء معنا. هل تحب مقالاتنا؟ تريد أن ترى المزيد من المواد المثيرة للاهتمام؟ ادعمنا عن طريق تقديم طلب أو التوصية به لأصدقائك ، خصم 30 ٪ لمستخدمي Habr على تناظرية فريدة من خوادم الدخول التي اخترعناها لك: الحقيقة الكاملة حول VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1 جيجابت في الثانية من 20 $ أو كيفية تقسيم الخادم؟ (تتوفر خيارات مع RAID1 و RAID10 ، ما يصل إلى 24 مركزًا وما يصل إلى 40 جيجابايت من ذاكرة DDR4).

ديل R730xd 2 مرات أرخص؟ فقط لدينا 2 من Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6 جيجا هرتز 14 جيجا بايت 64 جيجا بايت DDR4 4 × 960 جيجا بايت SSD 1 جيجابت في الثانية 100 TV من 199 دولار في هولندا! Dell R420 - 2x E5-2430 سعة 2 جيجا هرتز 6 جيجا بايت 128 جيجا بايت ذاكرة DDR3 2x960GB SSD بسرعة 1 جيجابت في الثانية 100 تيرابايت - من 99 دولارًا! اقرأ عن كيفية بناء البنية التحتية فئة باستخدام خوادم V4 R730xd E5-2650d تكلف 9000 يورو عن بنس واحد؟