الضوضاء البيضاء توجه مربع أسود. الجزء 2. الحل

في المنشور الأول ، قيل أن هناك نظرية منسية لأر- رينيي ، والتي تتبع ذلك في سلسلة عشوائية بطول N ، مع احتمال قريب من 1 ، يوجد صف من القيم المتطابقة للطول $$$\ log_2 {N}$. يمكن استخدام الخاصية المشار إليها لمتغير عشوائي للإجابة على السؤال: "بعد معالجة البيانات الضخمة ، هل تمتثل السلسلة المتبقية لقانون الأعداد العشوائية أم لا؟"

لم يتم تحديد إجابة هذا السؤال على أساس اختبارات المراسلات إلى الحالة الطبيعية للتوزيع ، ولكن على أساس خصائص السلسلة المتبقية نفسها.

بحضور أو غياب أو تحول تردد العقود بنفس الحروف. حاولت النشر لإظهار إمكانات استخدام هذه الأداة ، على الرغم من أن العديد من الأسئلة قد أثيرت حول كيفية عمل ذلك في الواقع عند إجراء التحليل في البيانات الكبيرة. لكن المناقشة كانت مثمرة ، وحتى مستخدم VDG قدم مثالًا حقيقيًا: "... يمكن تمثيل الفروع التغصنية للخلايا العصبية كتسلسل بسيط. يتم تشغيل الفرع ، ثم العصبونات بأكملها ، عند تنشيط سلسلة من نقاط الاشتباك العصبي في أي من أماكنها. مهمة الخلايا العصبية هي عدم الاستجابة للضوضاء البيضاء ، على التوالي ، الحد الأدنى لطول السلسلة ، بقدر ما أتذكر مع Numenty ، هو 14 نقطة تشابك في العصبونات الهرمية مع 10 آلاف نقطة تشابك. وفقا للصيغة التي نحصل عليها: $\ log_2 {10000} = 13.287 دولا$. أي أن السلاسل التي يقل طولها عن 14 ستحدث بسبب الضوضاء الطبيعية ، ولكنها لن تنشط الخلايا العصبية. انها وضعت بشكل صحيح تماما . "

دعنا نحاول النظر في الآلية المعروضة في هذه المادة.

أثار المنشور الأول العديد من الأسئلة. دعونا نحاول توضيح آلية نظرية Erds-Renyi في هذه المقالة.

جاء الحل في اتصال مع مفارقة Penny Game . تتكون اللعبة فيما يلي - سيقوم لاعبان A و B برمي قطعة معدنية خمس مرات ، على سبيل المثال ، "eagle" - 1 ، "tails" - 0. يختار اللاعب A سلسلة من ثلاث قيم ويصوت بها ، افترض 001.

اختار اللاعب B تسلسله ، افترض 100. اللاعب الذي يقع تسلسله أولاً هو الفائز. لنفترض أن 01001 قد انخفض ، أي 0-100-1 ، وهو ما يتوافق مع اختيار B. مفارقة "Penny Game" هي أنه بغض النظر عن التسلسل الذي يختاره اللاعب A ، فإن اللاعب B لديه دائمًا فرصة لاختيار تسلسل ، الاحتمال أكبر منه من التسلسل الذي اختاره اللاعب A. تظهر المصفوفة الفائزة للاعب B في الشكل 1.


التين. 1. مصفوفة المردود للاعب B في "لعبة Penny" لمدة خمس طلقات.

إن تأثير هذه المفارقة هو أن السلسلة العشوائية ليست متعدية ، أي إذا كانت U> R و R> Q ، فهذا لا يعني أن Q> U.

نتيجة هذه المفارقة هي الأشياء العادية التالية ، إذا كان اللاعب يلعب وفقًا لقواعد نظرية الاحتمالات:

1. في المقامرة ، يفوز عادة ، الذي يكون أمين الصندوق أكثر - "سحق البنك".
2. في الكازينو ، يفوز الكازينو فقط.
3. عند اللعب في البورصة ، يحدد الحظ فقط كم من الوقت سوف يستمر التاجر حتى يفقد رأس ماله.

المعنى المادي لهذا القانون ، الذي تستند إليه مفارقة "لعبة بيني" ، هو أن الشخص الذي يمكنه مواصلة التسلسل العشوائي أكثر له ميزة. كما في المثال الأول - لاعب لديه المزيد من النقود. في الخيار الثاني - يلعب الكازينو بمئات التسلسلات في نفس الوقت ، وسيستمر اللعب بعد توقف أي من اللاعبين عن اللعب. لا تقارن أي لعبة ضد تبادل لاعب واحد ، بملايين العمليات في البورصة.

كما ترون ، تم وضع القانون الأول - يحدد BigData الموقف مقارنةً بالمعلومات المحلية.

اللحظة الحاسمة الثانية هي عدم وجود خاصية النقل التتابعي العشوائي. نتيجة هذا هو عدم القدرة على دحر الموقف.

فرضية إضافية في تحليل BigData:

1) فهم تطور الأحداث ممكن فقط على مثل هذا المجلد الذي يتم فيه تسجيل نتائج الأحداث قيد التحقيق. يمكن تمثيل آلية هذه العملية على النحو التالي. الحقل العشوائي هو حقل تحاول فيه عدة عمليات محتملة تحقيق نفسها. بعد تحقيق الذات ، تترك العملية تغييرات ، ونحن نحاول اكتشاف درجة الآثار من العمليات التي حدثت. يتم تحديد التبعيات بالفعل من خلال حجم حصة النتائج اليسرى. سأشرح لما ذكر أعلاه أنه ، في رأيي ، الطريقة التي تحدث بها التحولات ، في الوقت الحالي ، لا يمكن للعلم إعطاء تعريف رسمي. إذا كانت هذه التعريفات ، فستظل بعض مفارقات زينو بمثابة مفارقات ، ووحدة النضال والكفاح ضده ، فإن الجدليات المادية ستتوقف عن الافتراض.

أفترض أنه يجب عليك عدم كسر رماح البيانات التي إذا حددنا العملية بعد وقوعها ، فهذا تدريب لا معنى له ، لأن العملية التالية لن تكون متوقعة. يرى الشخص محليًا تمامًا ، وتستغرق عمليات BigData مليارات السنين ، لذلك لدينا الفرصة لرؤية آلية العملية من حقل BigData. يتم تقديم مواد مثيرة للاهتمام حول القيم العظمى للكون هنا .

2) الفرضية الثانية ، والتي يمكن استنتاجها من غياب خاصية النقل ، هي تأثير الفاصل الزمني والظروف على العملية قيد الدراسة. هذا ، من ناحية ، هناك تنسيق زمني يضع العملية قيد الدراسة ، وفرصة لتكرار الظروف التي تشكلت فيها عمليتنا ، وتلقى ملايين السجلات ، أمر شبه مستحيل. من ناحية أخرى ، لا يمكن تجاهل قوانين التوافقية. تخبرنا هذه القوانين أن احتمال حدوث مجموعة معينة يجب أن يكون دائمًا موجودًا. يوضح الشكل 2 توزيع متغيرات سلاسل إشارات N التي توجد فيها صفوف من الطلبات الفرعية ذات الطول k. المبلغ الإجمالي أكبر من $$$2 ^ N$، لأن السلاسل القصيرة يتم دمجها مع السلاسل الطويلة.


التين. 2. عدد متغيرات الترتيب الفرعي المحتملة للإشارات k المتطابقة ، في تسلسل قيم N.

بالنسبة للمتغيرات التي توجد فيها سلاسل أطول من N / 2 ، يتم ملؤها باللون الأصفر ، ويتم تحديد عددها بطريقة بسيطة إلى حد ما بواسطة الصيغة:



بمعنى أن الاحتمالات المقابلة للسلسلة التي تحتوي على سلاسل من القيم المتماثلة k> = N / 2 (لن نصف احتمال سلسلة من قيم N) سيتم تحديدها بواسطة الصيغة:



خلال المناقشة ، في الجزء الأول ، نشأت أسئلة ، جوهرها اختلط بما يلي: "أين هي حدود الضوضاء البيضاء؟" هنا ، بالنظر إلى جدول الشكل 2 ، تم تكوين فرضية للمناقشة ، وفقًا للمخطط التالي.

بناءً على نظرية Muavre-Laplace المتكاملة:



نحدد الفواصل الزمنية ل (1.96) = احتمال 95 ٪:



إذا نظرتم ، فإن الجدول في الشكل 2 يعكس الحقل الكامل للاحتمالات ، من ناحية أخرى ، تكون معلمات التوزيع في كل حالة محددة بشكل فريد ، ويتم عرضها في الشكل 3 ، حيث نعرضها كمثال لسلسلة من 9 قيم. منذ عدد الخيارات $$$2 ^ 9 {= 512}$، وبالنسبة لهذا العدد من الاختبارات ، سنجد ألفا.


التين. 3. حدود فترات الاحتمال للأوامر الفرعية للطول k لنفس الإشارات ، في تتابع من 9 قيم ، مع موثوقية 2 سيغما (95٪).

قدم الشكل 4 الفواصل الزمنية لمتغير عشوائي ، حيث الشكل 4 ب هو الشكل 4 أ المنقول.


التين. 4. فترات من حجم عشوائي لكل suborder ، مع موثوقية 95 ٪.

من أجل هيكلة الإجابات على الأسئلة حول مكان وجود الضوضاء البيضاء بطريقة ما ، قام بصياغة الأساليب الحالية على النحو التالي:

1. يتم التعرف على الضوضاء البيضاء من قبل المجتمع.
2. البيانات التي يمكن صياغتها مع التعبيرات التحليلية ؛
3. المعلومات التي تنظمها الشبكات العصبية ؛
4. Qubits ، أجهزة الكمبيوتر الكم ؛
5. BigData.
6. في حالة وجود بيانات كبيرة ، فمن الممكن وجود بيانات مفرطة.

بالنسبة للهيكل المقترح ، كانت الفكرة هي فكرة O. V. Filatov "تعريف التسلسل الثنائي العشوائي ككائن اندماجي. حساب شظايا متزامنة في تسلسل ثنائي عشوائي " حول سلوك شظايا تسلسل يشبه سلوك الجسيمات في العالم الصغير.

تعطي الكيبيتات ، التي لها بنية ثلاثية الأبعاد ، سببًا للاعتقاد بأن المخطط الهيكلي يجب أن يحتوي على نموذج ثلاثي الأبعاد. تتضمن العديد من الطبقات ، التي يعترف بها المجتمع ، طبقات النموذج ، والجمع بين كل هذا ، فإن المخطط الأكثر أناقة ممكن في شكل حلقي الشكل 5.


التين. 5. افتراض بنية البيانات في رسم خرائط للمتغيرات العشوائية على الفضاء (صور مأخوذة من الإنترنت).

بتطوير المنطق أكثر ، نلاحظ أنه في الشكل 3 ، كل الترددات أرقام. هذا هو نتيجة لتماثل البيانات "0-1". وينعكس تماثل البيانات العشوائية في مسلمات سليمان وولف غولومب في غولومب . بناء على البحث Filatova O.V. "اشتقاق الصيغ لمسلمات Golomb. طريقة لإنشاء تسلسل عشوائي شبه عشوائي من ترددات Mises. أساسيات "Combinatorics of Long Sequences" تستخدم مفهوم الموجة نصف. أعتقد أن هذا الجانب مهم في دراسة الضوضاء البيضاء ، لأنه يرتبط بمعلمات مثل طول الصف.

نظرًا لخصائص العمليات العشوائية ، يمكن لموجة الضوضاء البيضاء الحصول على خصائص متعددة ، بما في ذلك عدم وجود تناظر موجي وعدم احتمال الامتثال لنظرية Noether . ولكن هناك عمليات في العالم المادي مثل تكوين رغوة موجة الأمواج ، الشكل 6. لذلك ، لدينا كل الأسباب للسماح بمعلمات غير عادية لموجات الضوضاء البيضاء.


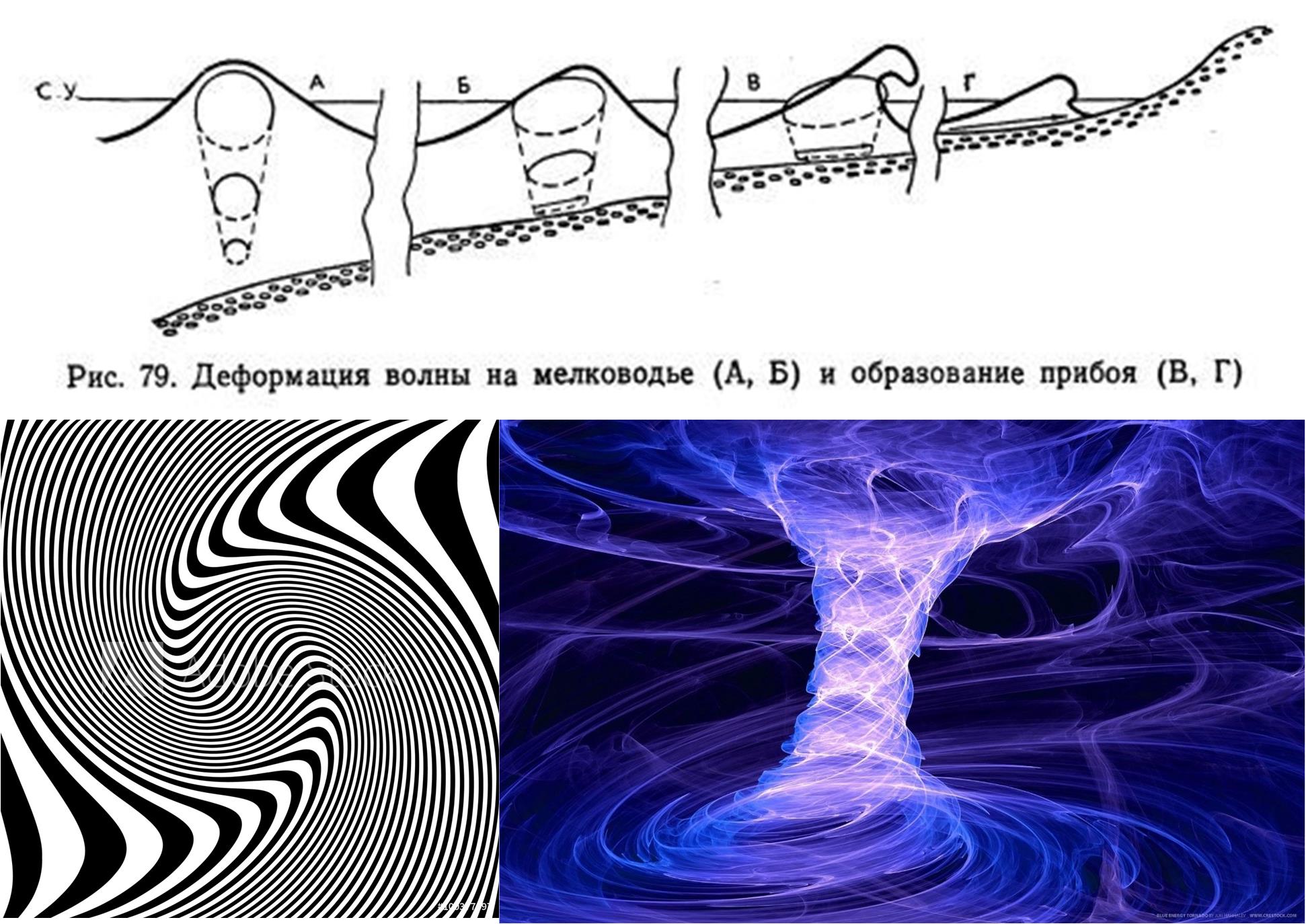التين. 6. آلية تشوه الموجة بالقرب من الساحل وأمثلة من العمليات التي ، عند إسقاطها على بعض الطائرات الفائقة ، في الفضاء المحلي ، قد تبدو وكأنها عملية عشوائية (صور مأخوذة من الإنترنت).

أنتقل إلى الجزء العملي ، وسأوجز النهج المقترحة عند التعامل مع الضوضاء البيضاء.

1. نقص خاصية النقل في عمليات عشوائية.
2. الافتراض بأن خصائص التماثل في الضوضاء البيضاء هي تحقيق خصائص التماثل للعمليات أعلى من العمليات في الوضع الحالي قيد النظر.
3. موقع العمليات العشوائية. لا يتم عرض هذا الافتراض بشكل صريح في المنشور ، ولكنه يناسب بشكل كافٍ في إطار الرياضيات البنّاءة. تستخدمها جميعًا (رياضيات بناءة) عند كتابة برنامج نصي يحدد المتطلبات للوصول إلى خلية ذاكرة وقراءة محتوياتها. نظرًا لأنك تعني افتراضيًا في هذه الخلية قيمة معينة 0 أو 1 ولا يمكن أن يكون هناك شيء آخر. يتم تقديم مواد جيدة للتعرف على مناهجها هنا: N.N. Nepeyvoda "الرياضيات البناءة: استعراض للإنجازات والضعف والدروس. الجزء الأول " .

الجزء العملي

في الجزء الأول ، تم فحص مسألة نظرية Erds-Renyi ، والتي تتألف من حقيقة أن هذه النظرية وجدت فقط في مصدر واحد ، وهو مترجم من المجرية ، وقد تم نشر هذا الكتاب مرة أخرى في الاتحاد السوفياتي ولم يتم العثور على دليل أو ذكر له. . نتيجة لهذه الحقيقة ، كان هناك عدم يقين بشكل عام حول وجودها ، وكذلك تطبيقه.

نتيجة لعمليات البحث ، تم العثور عليها في أعمال Filatov O.V. "اشتقاق الصيغ لمسلمات Golomb. طريقة لإنشاء تسلسل عشوائي شبه عشوائي من ترددات Mises. أساسيات "Combinatorics of long sequences" ص 15 فيما يلي ، الشكل 7 ، أقتبس الأصل من المادة.


التين. 7. الجزء الأصلي من منشور Filatova OV "اشتقاق الصيغ لمسلمات Golomb. طريقة لإنشاء تسلسل عشوائي شبه عشوائي من ترددات Mises. أساسيات "التوافقية من تسلسلات طويلة".

وضعت نظرية Erds-Renyi على النحو التالي:

عند رمي عملة معدنية N ، سلسلة من الجوانب المتساوية الساقطة لعملة واحدة في صف من الطول $$$\ log_2 {N}$لاحظ مع احتمال تميل إلى 1 ، مع N تميل إلى ما لا نهاية.
نكتب النظرية في تركيبات "مجموعات متوالية من سلاسل طويلة" لجانب واحد من العملة:



نقوم بتنفيذ الدليل:



كما ترون ترددات Mises في قطار يتكون من سلسلة من الإشارات متطابقة الطول $$$n = \ log_2 {N}$يتزامن مع استنتاجات نظرية أردوس ريني حول احتمالية وجود نفس السلسلة في حالة سلسلة عشوائية. حتى تتمكن من القضاء على الشك والاعتراف بوجودها وإمكانية التطبيق.

بما أن المنشور قد أوصى به المسوقون بالفعل ، فإن الاستمرار في الجزء التالي ، "الضوضاء البيضاء ترسم مربعًا أسود. الجزء 3. التطبيق. "

أجزاء أخرى: الجزء 1 ، الجزء 3 .