في الفصل الأخير ، تعلمنا أن الشبكات العصبية العميقة (GNS) غالبًا ما تكون أصعب في التدريب من الشبكات الضحلة. وهذا أمر سيئ ، لأن لدينا كل الأسباب للاعتقاد بأنه إذا تمكنا من تدريب STS ، فسيكونون أفضل بكثير في أداء المهام. ولكن على الرغم من أن الأخبار الواردة من الفصل السابق مخيبة للآمال ، فإنها لن تمنعنا. في هذا الفصل ، سنقوم بتطوير التقنيات التي يمكننا استخدامها لتدريب الشبكات العميقة وتطبيقها. سننظر أيضًا في الموقف على نطاق أوسع ، وسنتعرف بإيجاز على التقدم الأخير في استخدام GNS للتعرف على الصور والكلام والتطبيقات الأخرى. ونظر أيضًا بشكل سطحي في المستقبل الذي يمكن أن تتوقعه الشبكات العصبية ومنظمة العفو الدولية.
سيكون هذا فصلاً طويلاً ، لذا دعنا نذهب فوق جدول المحتويات قليلاً. أقسامه ليست مترابطة بشدة ، لذلك ، إذا كان لديك بعض المفاهيم الأساسية حول الشبكات العصبية ، يمكنك أن تبدأ بالقسم الذي يثير اهتمامك أكثر.
الجزء الرئيسي من الفصل هو مقدمة لواحد من أكثر أنواع الشبكات العميقة شعبية: شبكات الالتفاف العميقة (GSS). سنعمل مع مثال تفصيلي لاستخدام شبكة الالتفاف ، مع رمز وأشياء أخرى ، لحل مشكلة تصنيف الأرقام المكتوبة بخط اليد من مجموعة بيانات MNIST:
نبدأ في استعراضنا للشبكات التلافيفية مع الشبكات الضحلة ، والتي استخدمناها لحل هذه المشكلة في وقت سابق من هذا الكتاب. في عدة مراحل سنقوم بإنشاء شبكات أكثر وأكثر قوة. على طول الطريق ، سوف نتعرف على العديد من التقنيات القوية: التلافيق ، والتجميع ، واستخدام وحدات معالجة الرسومات لزيادة حجم التدريب بشكل كبير مقارنة بما قمنا به مع الشبكات الضحلة ، والتوسع الخوارزمي لبيانات التدريب (لتقليل التجاوز) ، باستخدام تقنية التسرب (أيضًا لتقليل إعادة التدريب) ، باستخدام مجموعات الشبكات ، وغيرها. نتيجة لذلك ، سنأتي إلى نظام تكون قدراته على المستوى الإنساني تقريبًا. من بين 10000 صورة تحقق من MNIST - والتي لم يراها النظام أثناء التدريب - ستكون قادرًا على التعرف على 9967 بشكل صحيح. وإليك بعض تلك الصور التي لم يتم التعرف عليها بشكل صحيح. في الزاوية اليمنى العليا هي الخيارات الصحيحة. يشار إلى ما أظهره برنامجنا في الزاوية اليمنى السفلى.
الكثير منهم يصعب تصنيفهم على البشر. خذ ، على سبيل المثال ، الرقم الثالث في السطر العلوي. يبدو لي أكثر مثل "9" من النسخة الرسمية من "8". قررت شبكتنا أيضًا أنها "9". على الأقل ، يمكن فهم مثل هذه الأخطاء تمامًا ، وربما الموافقة عليها. نختتم مناقشتنا للتعرف على الصور مع لمحة عامة عن التقدم الهائل الذي حققته الشبكة العصبية مؤخرًا (خاصة تلك التلافيفية).
يخصص الجزء المتبقي من الفصل لمناقشة التعلم العميق من وجهة نظر أوسع وأقل تفصيلاً. سننظر باختصار في نماذج NS الأخرى ، وعلى وجه الخصوص ، NSs المتكررة ، ووحدات الذاكرة قصيرة المدى طويلة الأجل ، وكيف يمكن استخدام هذه النماذج لحل المشاكل في التعرف على الكلام ، ومعالجة اللغة الطبيعية ، وغيرها. سنناقش مستقبل NS والدفاع المدني ، من الأفكار مثل واجهات المستخدم مدفوعة النية إلى دور التعلم العميق في الذكاء الاصطناعى.
يعتمد هذا الفصل على مواد من فصول سابقة من الكتاب ، باستخدام الأفكار المدمجة ودمجها مثل backpropagation ، والتنظيم ، و softmax ، وما إلى ذلك. ومع ذلك ، لقراءة هذا الفصل ، ليس من الضروري توضيح المواد الخاصة بكل الفصول السابقة. ومع ذلك ، لا يضر قراءة
الفصل 1 ، والتعرف على أساسيات الجمعية الوطنية. عندما أستخدم المفاهيم من الفصلين 2 إلى 5 ، سأقدم الروابط اللازمة للمواد حسب الضرورة.
تجدر الإشارة إلى أن هذا الفصل لا. هذه ليست مواد تدريبية على أحدث وأروع المكتبات للعمل مع NS. لن نقوم بتدريب STS بعشرات الطبقات لحل المشكلات من أحدث الأبحاث. سنحاول فهم بعض المبادئ الأساسية التي تقوم عليها GNS وتطبيقها على السياق البسيط والسهل الفهم لمهام MNIST. بمعنى آخر ، هذا الفصل لن يأخذك إلى مقدمة المنطقة. تتمثل رغبة هذا الفصل والفصول السابقة في التركيز على الأساسيات وإعدادك لفهم مجموعة واسعة من الأعمال المعاصرة.
مقدمة في الشبكات العصبية التلافيفية
في الفصول السابقة ، علمنا شبكاتنا العصبية أنه من الجيد التعرف على صور الأرقام المكتوبة بخط اليد:
لقد فعلنا ذلك باستخدام الشبكات التي تم توصيل الطبقات المجاورة بها تمامًا مع بعضها البعض. أي أن كل خلية عصبية في الشبكة كانت مرتبطة بكل خلية عصبية من الطبقة المجاورة:
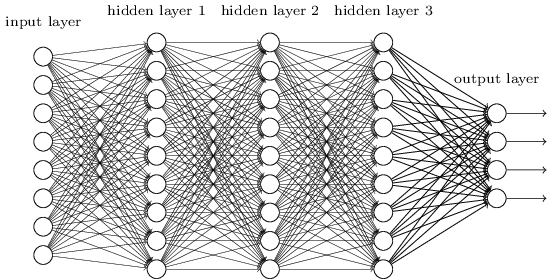
على وجه الخصوص ، قمنا بتشفير شدة كل بكسل في الصورة كقيمة للخلية العصبية المقابلة لطبقة الإدخال. بالنسبة للصور بحجم 28 × 28 بكسل ، فهذا يعني أن الشبكة سيكون بها 784 (= 28 × 28) خلايا عصبية واردة. بعد ذلك قمنا بتدريب الأوزان والإزاحات الخاصة بالشبكة بحيث حدد إخراج الشبكة (كان هناك هذا الأمل) الصورة الواردة بشكل صحيح: "0" أو "1" أو "2" أو ... أو "8" أو "9".
تعمل شبكاتنا المبكرة بشكل جيد: لقد حققنا دقة تصنيف أعلى من 98٪ باستخدام بيانات التدريب والاختبار من أرقام MNIST المكتوبة بخط اليد. ولكن إذا قمت بتقييم هذا الموقف الآن ، فمن الغريب استخدام شبكة ذات طبقات متصلة بالكامل لتصنيف الصور. والحقيقة هي أن هذه الشبكة لا تأخذ في الاعتبار الهيكل المكاني للصور. على سبيل المثال ، يتم تطبيقه تمامًا على وحدات البكسل الموجودة بعيدًا عن بعضها البعض ، وكذلك على وحدات البكسل المجاورة. من المفترض أن يتم إجراء استنتاجات حول مفاهيم البنية المكانية هذه بناءً على دراسة بيانات التدريب. ولكن ماذا لو بدلاً من بدء تشغيل بنية الشبكة من نقطة الصفر ، سوف نستخدم بنية تحاول الاستفادة من البنية المكانية؟ في هذا القسم ، أصف الشبكات العصبية التلافيفية (SNA). يستخدمون بنية خاصة ، مناسبة خاصة لتصنيف الصور. من خلال استخدام مثل هذه البنية ، تتعلم الحسابات القومية بشكل أسرع. وهذا يساعدنا على تدريب شبكات أعمق وأكثر طبقات تقوم بعمل جيد لتصنيف الصور. اليوم ، يتم استخدام نظام الحسابات القومية العميق أو بعض المتغيرات المماثلة في معظم حالات التعرف على الصور.
تعود أصول نظام الحسابات القومية إلى السبعينيات. لكن عمل البدء ، الذي بدأ توزيعه الحديث ، كان عام 1998 ، "
تدرج التعلم من أجل التعرف على المستندات ". أدلى Lekun بتصريح مثير للاهتمام حول المصطلحات المستخدمة في نظام الحسابات القومية: "إن ربط النماذج مثل الشبكات التلافيفية بعلم الأعصاب سطحي للغاية. لذلك ، أنا أسميها الشبكات التلافيفية ، وليس الشبكات العصبية التلافيفية ، وبالتالي نسميها عناصر العقد ، وليس الخلايا العصبية ". ولكن على الرغم من ذلك ، يستخدم نظام الحسابات القومية العديد من الأفكار من عالم NS التي درسناها بالفعل: الانتشار الخلفي ، والانحدار التدرج ، والتنظيم ، ووظائف التنشيط غير الخطية ، إلخ. لذلك ، سنتبع الاتفاقية المقبولة عمومًا ونعتبرها نوعًا من زمالة المدمنين المجهولين. سأدعو لهم كل الشبكات والشبكات العصبية ، والعقد الخاصة بهم - كل من الخلايا العصبية والعناصر.
يستخدم SNA ثلاثة أفكار أساسية: حقول الاستقبالات المحلية والأوزان الإجمالية والتجميع. دعونا نلقي نظرة على هذه الأفكار بدورها.
الحقول الاستقبالية المحلية
في طبقات الشبكة المتصلة بالكامل ، تتم الإشارة إلى طبقات الإدخال بخطوط رأسية من الخلايا العصبية. في نظام الحسابات القومية ، يكون أكثر ملاءمة لتمثيل طبقة الإدخال في شكل مربع من الخلايا العصبية ذات البعد 28 × 28 ، والتي تتوافق قيمها مع شدة البكسل في الصورة 28 × 28:
كالعادة ، نربط البكسلات الواردة مع طبقة من الخلايا العصبية المخفية. ومع ذلك ، فإننا لن نربط كل بكسل مع كل الخلايا العصبية المخفية. ننظم الاتصالات في مناطق صغيرة محلية من الصورة الواردة.
بتعبير أدق ، سيتم ربط كل خلية عصبية من الطبقة الأولى المخفية بجزء صغير من الخلايا العصبية الواردة ، على سبيل المثال ، منطقة 5 × 5 تقابل 25 بكسل واردة. لذلك ، بالنسبة لبعض الخلايا العصبية المخفية ، قد يبدو الاتصال كما يلي:
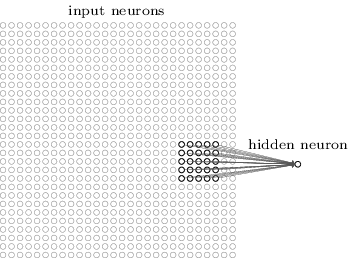
يسمى هذا الجزء من الصورة الواردة الحقل الاستقبالي المحلي لهذه الخلية العصبية المخفية. هذه نافذة صغيرة تبحث في وحدات البكسل الواردة. كل السندات يتعلم وزنه. أيضا ، الخلايا العصبية الخفية دراسات النزوح العام. يمكننا أن نفترض أن هذه الخلية العصبية الخاصة تتعلم تحليل مجالها الاستقبالي المحلي المحدد.
ثم نقوم بنقل حقل الاستلام المحلي خلال الصورة الواردة. يحتوي كل حقل تقبلا محلي على الخلية العصبية المخفية الخاصة به في الطبقة المخفية الأولى. للحصول على توضيح أكثر تحديدًا ، ابدأ بحقل الاستقبالات المحلي في الزاوية اليسرى العليا:
انقل الحقل التلقي المحلي بمقدار بكسل واحد إلى اليمين (خلية عصبية واحدة) لربطه بالخلية العصبية المخفية الثانية:
لذلك نحن نبني أول طبقة خفية. لاحظ أنه إذا كانت الصورة الواردة هي 28 × 28 وكان حقل الاستلام المحلي 5 × 5 ، فسيكون هناك 24 × 24 خلية عصبية في الطبقة المخفية. هذا لأنه لا يمكننا نقل حقل الاستقبالات المحلي إلا عن طريق 23 خلية عصبية إلى اليمين (أو لأسفل) ، وبعد ذلك سنواجه الجانب الأيمن (أو السفلي) من الصورة الواردة.
في هذا المثال ، تقوم حقول الاستلام المحلية بنقل بكسل واحد في كل مرة. ولكن في بعض الأحيان يتم استخدام حجم خطوة مختلفة. على سبيل المثال ، يمكننا نقل حقل الاستلام المحلي 2 بكسل إلى الجانب ، وفي هذه الحالة يمكننا التحدث عن حجم الخطوة 2. في هذا الفصل سوف نستخدم الخطوة 1 بشكل رئيسي ، لكن يجب أن تعلم أنه في بعض الأحيان يتم إجراء تجارب ذات خطوات من حجم مختلف . يمكنك تجربة حجم الخطوة ، كما هو الحال مع غيرها من المعلمات. يمكنك أيضًا تغيير حجم حقل الاستلام المحلي ، ولكن عادةً ما يتضح أن الحجم الأكبر لحقل الاستلام المحلي يعمل بشكل أفضل على صور أكبر من 28 × 28 بكسل.
مجموع الأوزان والإزاحة
ذكرت أن كل خلية عصبية مخفية لها إزاحة وأوزان 5 × 5 مرتبطة بحقلها الاستقبالي المحلي. لكنني لم أذكر أننا سنستخدم نفس الأوزان والتشريد لجميع الخلايا العصبية المخفية 24 × 24. بمعنى آخر ، بالنسبة للخلية العصبية المخفية j ، k ، سيكون الخرج مساوياً لـ:
هنا σ هي وظيفة التنشيط ، وربما السيني من الفصول السابقة. b هي القيمة الإجمالية للتعويض. w
l، m - مجموعة الأوزان الكلية 5x5. وأخيرًا ، تشير
x ، y إلى تنشيط الإدخال في الموضع x ، y.
هذا يعني أن جميع الخلايا العصبية في الطبقة الأولى المخفية تكتشف نفس العلامة ، الموجودة فقط في أجزاء مختلفة من الصورة. علامة الكشف عنها بواسطة خلية عصبية مخفية هي تسلسل وارد معين يؤدي إلى تنشيط الخلايا العصبية: ربما حافة الصورة ، أو شكل ما. لفهم سبب هذا الأمر ، افترض أن الأوزان والتشريدات لدينا تجعل الخلايا العصبية المخفية تتعرف ، على سبيل المثال ، على الوجه الرأسي في حقل تقريبي محلي معين. من المحتمل أن تكون هذه القدرة مفيدة في أي مكان آخر في الصورة. لذلك ، من المفيد استخدام كاشف الميزة نفسه على مساحة الصورة بأكملها. بشكل أكثر تجريدًا ، تم تكييف نظام الحسابات القومية بشكل جيد مع الثبات الترجمي للصور: نقل الصورة ، على سبيل المثال ، من القط ، قليلاً إلى الجانب ، وسيظل صورة القط. صحيح أن الصور من مشكلة تصنيف أرقام MNIST تتمركز جميعها وتطبيعها في الحجم. لذلك ، لدى MNIST ثبات أقل من الصور العشوائية. ومع ذلك ، من المحتمل أن تكون ميزات مثل الوجوه والزوايا مفيدة عبر كامل سطح الصورة الواردة.
لهذا السبب ، نشير في بعض الأحيان إلى تعيين طبقة واردة وطبقة مخفية كخريطة المعالم. الأوزان التي تحدد خريطة الخصائص ، نسميها مجموع الأوزان. والتحيز الذي يحدد خريطة المعالم هو التحيز العام. كثيرا ما يقال إن الأوزان الكلية والتشريد يحددان النواة أو المرشح. لكن في الأدب يستخدم الناس هذه المصطلحات أحيانًا لسبب مختلف قليلاً ، وبالتالي لن أتعمق في المصطلحات ؛ من الأفضل أن ننظر إلى بعض الأمثلة المحددة.
بنية الشبكة الموصوفة بواسطتي قادرة على التعرف على سمة محلية من نوع واحد فقط. للتعرف على الصور ، نحتاج إلى المزيد من خرائط الميزات. لذلك ، تتكون الطبقة التلافيفية النهائية من العديد من خرائط الميزات المختلفة:
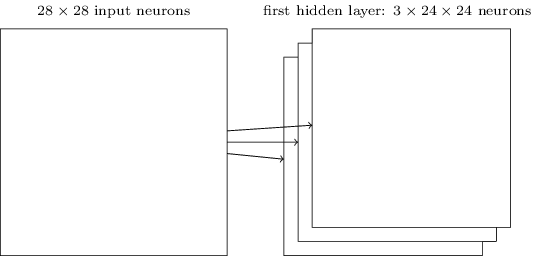
يوضح المثال 3 خرائط الميزات. يتم تحديد كل بطاقة بواسطة مجموعة من الأوزان الإجمالية 5 × 5 وإزاحة واحدة مشتركة. نتيجة لذلك ، يمكن لهذه الشبكة التعرف على ثلاثة أنواع مختلفة من العلامات ، ويمكن العثور على كل علامة في أي جزء من الصورة.
لقد وجهت ثلاث بطاقات سمة للبساطة. في الممارسة العملية ، يمكن استخدام SNA خرائط ميزة أكثر (ربما أكثر من ذلك بكثير). استخدمت واحدة من SNSs المبكرة ، LeNet-5 ، 6 بطاقات ميزة ، ارتبط كل منها بحقل تقريبي 5 × 5 ، للتعرف على أرقام MNIST. لذلك ، المثال أعلاه يشبه إلى حد كبير LeNet-5. في الأمثلة التي سنعمل على تطويرها بشكل مستقل ، سنستخدم الطبقات التلافيفية التي تحتوي على 20 و 40 بطاقة ميزات. دعونا نلقي نظرة سريعة على العلامات التي سنبحثها:
تتوافق هذه الصور 20 مع 20 خريطة سمات مختلفة (عوامل التصفية أو النواة). يتم تمثيل كل بطاقة بواسطة صورة 5 × 5 تقابل أوزان 5 × 5 في حقل الاستلام المحلي. البيكسلات البيضاء تعني الوزن المنخفض (عادة ما يكون أكثر سلبية) ، وتتفاعل خريطة المعالم مع البيكسلات المقابلة لها. البيكسلات الأغمق تعني وزنا أكبر ، وتتفاعل خريطة المعالم مع البيكسلات المقابلة لها. بشكل تقريبي ، تظهر هذه الصور تلك العلامات التي تستجيب لها الطبقة التلافيفية.
ما هي الاستنتاجات التي يمكن استخلاصها من خرائط السمات هذه؟ من الواضح أن الهياكل المكانية هنا لم تظهر بطريقة عشوائية - فهناك العديد من العلامات التي تظهر مناطق ناصعة ومظلمة. هذا يشير إلى أن شبكتنا تتعلم حقًا شيئًا متعلقًا بالهياكل المكانية. ومع ذلك ، إلى جانب هذا ، من الصعب إلى حد ما فهم هذه العلامات. من الواضح أننا لا ندرس ، على سبيل المثال ،
مرشحات غابور ، التي استخدمت في العديد من الأساليب التقليدية للتعرف على الأنماط. في الواقع ، يتم القيام بالكثير من العمل الآن من أجل فهم أفضل للعلامات التي يدرسها نظام الحسابات القومية بشكل أفضل. إذا كنت مهتمًا ، أوصي بالبدء من عام
2013 .
الميزة الكبيرة للأوزان والإزاحة العامة هي أن هذا يقلل بشكل كبير من عدد المعلمات المتاحة لنظام الحسابات القومية. لكل خريطة ميزة ، نحتاج إلى 5 × 5 = 25 إجمالي الأوزان وإزاحة واحدة مشتركة. لذلك ، هناك 26 معلمة مطلوبة لكل مخطط ميزة. إذا كان لدينا 20 خريطة للميزات ، فسنحصل إجماليًا على 20 × 26 = 520 معلمة تحدد طبقة الالتفاف. للمقارنة ، افترض أن لدينا طبقة أولى متصلة تمامًا مع 28 × 28 = 784 خلايا عصبية واردة و 30 خلية عصبية مخفية نسبياً - استخدمنا هذا المخطط في العديد من الأمثلة السابقة. اتضح 784 × 30 الأوزان ، بالإضافة إلى 30 إزاحة ، أي ما مجموعه 23،550 المعلمة. بمعنى آخر ، فإن الطبقة المتصلة بالكامل تحتوي على معلمات أكثر من 40 مرة أكثر من الطبقة التلافيفية.
بالطبع ، لا يمكننا مقارنة عدد المعلمات مباشرةً ، حيث يختلف هذان النموذجان بشكل جذري. ولكن بشكل بديهي ، يبدو أن استخدام الثقل التلافيفي التلافيفي يقلل من عدد المعلمات اللازمة لتحقيق الكفاءة المماثلة لتلك الموجودة في نموذج متصل بالكامل. وهذا بدوره سيسرع في تدريب النموذج التلافيفي ، ويساعدنا في النهاية على إنشاء شبكات أعمق باستخدام الطبقات التلافيفية.
بالمناسبة ، يأتي الاسم "التلافيفي" من العملية في المعادلة (125) ، والتي تسمى أحيانًا
الإلتواء . بتعبير أدق ، في بعض الأحيان يكتب الناس هذه المعادلة كـ
1 = σ (b + w ∗ a
0 ) ، حيث تشير
1 إلى مجموعة من تنشيطات الخرج لبطاقة ميزة واحدة ، و
0 - مجموعة من عمليات تنشيط الإدخال ، و * تسمى عملية الالتفاف. لن نتعمق في رياضيات التلفيق ، لذلك لا داعي للقلق خاصة بشأن هذا الاتصال. لكن الأمر يستحق أن تعرف من أين جاء الاسم.
تجمع طبقات
بالإضافة إلى الطبقات التلافيفية الموصوفة في نظام الحسابات القومية ، هناك أيضًا تجميع الطبقات. وعادة ما تستخدم مباشرة بعد تلافيفي. إنهم ملتزمون بتبسيط المعلومات من إخراج الطبقة التلافيفية.
هنا أستخدم عبارة "خريطة المعالم" ليس بمعنى الوظيفة المحسوبة بواسطة الطبقة التلافيفية ، ولكن للإشارة إلى تنشيط ناتج الخلايا العصبية المخفية. غالبًا ما يوجد مثل هذا الاستخدام المجاني للمصطلحات في الأدبيات البحثية.
تقبل طبقة التجميع إخراج كل خريطة ميزة لطبقة الالتفاف وتعد خريطة معالم مضغوطة. على سبيل المثال ، يمكن لكل عنصر في طبقة التجميع تلخيص قسم من الخلايا العصبية 2x2 من الطبقة السابقة ، على سبيل المثال. دراسة حالة: يُعرف إجراء التجميع الشائع باسم التجميع الأقصى. في أقصى تجمع ، يمنح عنصر التجميع أقصى تنشيط من قسم 2 × 2 ، كما هو موضح في الرسم التخطيطي:
نظرًا لأن ناتج الخلايا العصبية الطبقة التلافيفية يعطي قيمًا 24 × 24 ، وبعد الشد ، نحصل على 12 × 12 خلية عصبية.كما ذكر أعلاه ، فإن الطبقة التلافيفية عادةً ما تتضمن شيئًا أكثر من خريطة ميزة واحدة. نحن نطبق أقصى تجمع على كل خريطة ميزة على حدة. لذلك ، إذا كان لدينا ثلاث خرائط للميزات ، فستظهر طبقات الإلتفاف المدمجة وأقصى تجمع: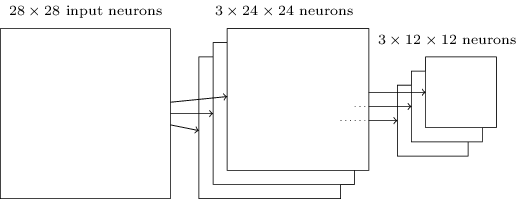
يمكن تخيل الحد الأقصى للسحب كطريقة للشبكة للسؤال عما إذا كانت هناك علامة معينة في أي مكان من الصورة. ثم تتجاهل معلومات حول موقعها بالضبط. من الواضح بشكل حدسي أنه عندما يتم العثور على علامة ، فإن موقعها الدقيق لم يعد بنفس أهمية موقعه التقريبي بالنسبة إلى العلامات الأخرى. الميزة هي أن عدد الميزات التي تم الحصول عليها باستخدام التجميع أصغر بكثير ، وهذا يساعد على تقليل عدد المعلمات المطلوبة في الطبقات التالية.Max pooling ليس تقنية التجميع الوحيدة. ومن المعروف أن هناك طريقة أخرى مشتركة تجمع L2. في ذلك ، بدلاً من أخذ أقصى تنشيط لمنطقة الخلايا العصبية 2x2 ، نأخذ الجذر التربيعي لمجموع مربعات تنشيط المنطقة 2x2. تختلف تفاصيل الأساليب ، لكنها تشبه بشكل حدسي أقصى تجمع: L2-pooling هو وسيلة لضغط المعلومات من طبقة تلافيفية. في الممارسة العملية ، وغالبا ما تستخدم كل التقنيات. في بعض الأحيان يستخدم الناس أنواعًا أخرى من التجميع. إذا كنت تكافح من أجل تحسين جودة الشبكة ، يمكنك استخدام البيانات الداعمة لمقارنة عدة طرق مختلفة للسحب واختيار أفضلها. لكننا لن تقلق بشأن هذا التحسين المفصل.تلخيص
الآن يمكننا جمع كل المعلومات معًا والحصول على نظام الحسابات القومية الكامل. إنه مشابه لهيكلنا الذي تمت مراجعته مؤخرًا ، لكنه يحتوي على طبقة إضافية من 10 خلايا عصبية مخرجة تقابل 10 قيم ممكنة لأرقام MNIST ('0' ، '1' ، '2' ، ..):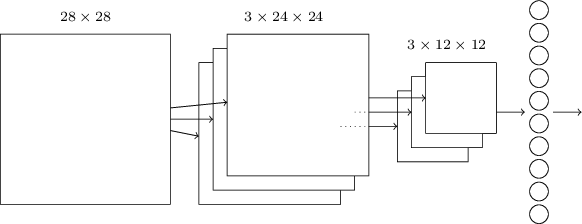
تبدأ الشبكة بخلايا عصبية مدخلات 28 × 28 مستعملة لتشفير شدة البكسل للصورة MNIST. بعد ذلك ، تأتي طبقة تلافيفية تستخدم خرائط المعالم المحلية 5x5 و 3. والنتيجة هي طبقة من الخلايا العصبية الصفات الخفية 3x24x24. الخطوة التالية هي طبقة التجميع القصوى المطبقة على مساحات 2 × 2 على كل من خرائط الميزات الثلاثة. والنتيجة هي طبقة من الخلايا العصبية الصفات الخفية 3x12x12.الطبقة الأخيرة من الاتصالات في الشبكة متصلة بالكامل. أي أنه يربط كل خلية عصبية من طبقة التجميع القصوى بكل خلية من الخلايا العصبية العشرة. استخدمنا بنية متصلة بالكامل سابقًا. يرجى ملاحظة أنه في الرسم البياني أعلاه ، استخدمنا سهمًا واحدًا للبساطة ، ولا أعرض جميع الروابط. يمكنك بسهولة تخيل كل منهم.هذا الهيكل التلافيفي يختلف اختلافًا كبيرًا عما استخدمناه من قبل. ومع ذلك ، فإن الصورة العامة متشابهة: شبكة تتكون من العديد من العناصر البسيطة ، والتي يتم تحديد سلوكها من خلال الأوزان والإزاحة. يبقى الهدف كما هو: استخدام بيانات التدريب لتدريب الشبكة في الأوزان والإزاحة بحيث تصنف الشبكة الأرقام الواردة جيدًا.على وجه الخصوص ، كما في الفصول السابقة ، سنقوم بتدريب شبكتنا باستخدام النسب التدرج العشوائي وانتشار الظهر. يذهب الإجراء نفسه كما كان من قبل. ومع ذلك ، نحتاج إلى إجراء بعض التغييرات على إجراء backpropagation. الحقيقة هي أن مشتقاتنا الخاصة بالانتشار الخلفي كانت مخصصة لشبكة ذات طبقات متصلة بالكامل. لحسن الحظ ، فإن تغيير المشتقات للطبقات التلافيفية والحد الأقصى للتجميع أمر بسيط للغاية. إذا كنت ترغب في فهم التفاصيل ، أدعوك لمحاولة حل المشكلة التالية. سأحذرك من أن الأمر سيستغرق الكثير من الوقت ، إلا إذا كنت قد فهمت تمامًا الأسئلة المبكرة المتمثلة في التمايز بين الارتجاع العكسي.مهمة
- . (BP1)-(BP4). , , - , . ?
ناقشنا الأفكار الكامنة وراء نظام الحسابات القومية. دعونا نرى كيف تعمل في الممارسة العملية عن طريق تطبيق بعض الحسابات القومية وتطبيقها على مشكلة تصنيف أرقام MNIST. سنستخدم برنامج network3.py ، وهو نسخة محسّنة من برامج network.py و network2.py التي تم إنشاؤها في الفصول السابقة. يستخدم برنامج network3.py أفكارًا من وثائق مكتبة Theano (على وجه الخصوص ، تطبيق LeNet-5 ) ، من تنفيذ الاستثناء من Misha Denil و Chris Olah . رمز البرنامج متاح على جيثب. في القسم التالي ، سنقوم بدراسة رمز برنامج network3.py ، وفي هذا القسم سنستخدمه كمكتبة لإنشاء نظام الحسابات القومية.تمت كتابة برامج network.py و network2.py في بيثون باستخدام مكتبة المصفوفة Numpy. لقد عملوا على أساس المبادئ الأولى ، وتوصلوا إلى التفاصيل الأكثر تفصيلاً حول انتشار الظهر ، نزول الانحدار العشوائي ، إلخ. ولكن الآن ، عندما نفهم هذه التفاصيل ، بالنسبة إلى network3.py ، سوف نستخدم مكتبة Theano لتعلم الآلات (انظر العمل العلمي مع وصفها). تعد Theano أيضًا أساس المكتبات الشعبية لـ NS Pylearn2 و Keras ، وكذلك Caffe و Torch .باستخدام Theano يسهل تنفيذ backpropagation في SNA ، لأنه يحسب تلقائيا جميع البطاقات. Theano هو أيضًا أسرع بشكل ملحوظ من الكود السابق (الذي تمت كتابته لتسهيل الفهم وليس للأعمال عالية السرعة) ، لذلك فمن المعقول استخدامه لتدريب شبكات أكثر تعقيدًا. على وجه الخصوص ، تتمثل إحدى ميزات Theano الرائعة في تشغيل التعليمات البرمجية على كل من وحدة المعالجة المركزية ووحدة معالجة الرسومات ، إن وجدت. يعمل الجرافيك على توفير زيادة كبيرة في السرعة ، ويساعد في تدريب شبكات أكثر تعقيدًا.للعمل بالتوازي مع الكتاب ، تحتاج إلى تثبيت Theano على نظامك. للقيام بذلك ، اتبع الإرشادات الموجودة على الصفحة الرئيسية للمشروع. في وقت كتابة وإطلاق الأمثلة ، كان Theano 0.7 متاحًا. لقد أجريت بعض التجارب على نظام التشغيل Mac OS X Yosemite بدون GPU. البعض على أوبونتو 14.04 مع GPU NVIDIA. والبعض هناك ، وهناك. لبدء network3.py ، قم بتعيين إشارة GPU في التعليمات البرمجية على True أو False. بالإضافة إلى ذلك ، قد تساعدك الإرشادات التالية على تشغيل Theano على وحدة معالجة الرسومات الخاصة بك . من السهل أيضًا العثور على مواد التدريب عبر الإنترنت. إذا لم يكن لديك وحدة معالجة الرسومات الخاصة بك ، يمكنك البحث عن Amazon Web Services EC2 G2. ولكن حتى مع GPU ، لن يعمل كودنا بسرعة كبيرة. سوف تستمر العديد من التجارب من بضع دقائق إلى عدة ساعات. سيتم تنفيذ أكثرها تعقيدًا على وحدة معالجة مركزية واحدة لعدة أيام. كما في الفصول السابقة ، أوصي ببدء التجربة ومواصلة القراءة والتحقق من عملها بشكل دوري. بدون استخدام GPU ، أوصي بأن تقلل من عدد مرات التدريب في أكثر التجارب تعقيدًا.للحصول على نتائج أساسية للمقارنة ، لنبدأ ببنية ضحلة بطبقة واحدة مخفية تحتوي على 100 خلية عصبية مخفية. سوف ندرس 60 عصرًا ، وسنستخدم سرعة التعلم η = 0.1 ، وحجم الحزمة المصغرة هو 10 ، وسندرس دون تنظيم.في هذا القسم ، قمت بتعيين عدد محدد من عصور التدريب. أفعل هذا من أجل الوضوح في عملية التعلم. في الممارسة العملية ، من المفيد استخدام نقاط التوقف المبكرة ، وتتبع دقة مجموعة التأكيد ، والتوقف عن التدريب عندما نكون مقتنعين بأن دقة التأكيد لم تعد تتحسن:>>> import network3 >>> from network3 import Network >>> from network3 import ConvPoolLayer, FullyConnectedLayer, SoftmaxLayer >>> training_data, validation_data, test_data = network3.load_data_shared() >>> mini_batch_size = 10 >>> net = Network([ FullyConnectedLayer(n_in=784, n_out=100), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(training_data, 60, mini_batch_size, 0.1, validation_data, test_data)
كانت أفضل دقة تصنيف 97.80 ٪. هذه هي دقة تصنيف test_data ، المقدرة من فترة التدريب ، والتي حصلنا على أفضل دقة تصنيف للبيانات من validation_data. يساعد استخدام التحقق من صحة البيانات في اتخاذ قرار بشأن تقييم الدقة في تجنب إعادة التدريب. ثم سنفعل ذلك. قد تختلف نتائجك قليلاً ، حيث تتم تهيئة أوزان الشبكة وإزاحاتها بشكل عشوائي.
دقة 97.80 ٪ هي قريبة جدا من دقة 98.04 ٪ التي تم الحصول عليها في الفصل 3 ، وذلك باستخدام بنية الشبكة مماثلة ومعلمات التدريب. على وجه الخصوص ، يستخدم كلا المثالين شبكات ضحلة ذات طبقة مخفية واحدة تحتوي على 100 خلية عصبية مخفية. تتعلم كلتا الشبكتين 60 عصرًا بحجم رزمة صغيرة يبلغ 10 ومعدل تعلُّم η = 0.1.
ومع ذلك ، كان هناك اختلافان في الشبكة السابقة. أولاً ، أجرينا عملية التنظيم للمساعدة في تقليل تأثير إعادة التدريب. يعمل تنظيم الشبكة الحالية على تحسين الدقة ، ولكن ليس كثيرًا ، لذلك نحن لا نفكر في الأمر في الوقت الحالي. ثانياً ، على الرغم من أن الطبقة الأخيرة من الشبكة المبكرة استخدمت تنشيطات السيني ودالة تكلفة الانتروبيا ، فإن الشبكة الحالية تستخدم الطبقة الأخيرة مع softmax ، وظيفة الاحتمال اللوغاريتمي كدالة تكلفة. كما هو موضح في الفصل 3 ، هذا ليس تغييرا كبيرا. لم أقم بالتبديل من واحدة إلى أخرى لسبب عميق - بشكل رئيسي لأن softmax ووظيفة الاحتمالية اللوغاريتمية تستخدم أكثر في الشبكات الحديثة لتصنيف الصور.
هل يمكننا تحسين النتائج باستخدام بنية شبكة أعمق؟
لنبدأ بإدخال طبقة تلافيفية ، في بداية الشبكة. سنستخدم حقل الاستقبالات المحلي 5 × 5 ، وهو طول الخطوة من 1 و 20 بطاقة ميزات. سنقوم أيضًا بإدراج طبقة تجمع أقصى تجمع بين الميزات باستخدام نوافذ التجميع 2 × 2. لذا ستبدو بنية الشبكة الشاملة مشابهة لتلك التي ناقشناها في القسم السابق ، ولكن مع طبقة إضافية متصلة بالكامل:
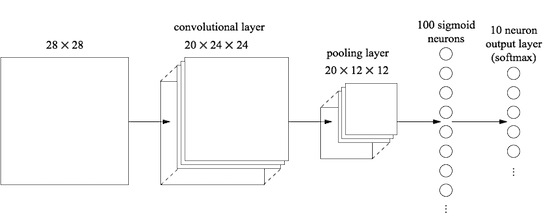
في هذه البنية ، يتم تدريب طبقات الالتفاف والتجميع على الهيكل المكاني المحلي المتضمن في صورة التدريب الواردة ، ويتم تدريب الطبقة الأخيرة المتصلة بالكامل على مستوى أكثر تجريدًا ، حيث يتم دمج المعلومات العالمية من الصورة بأكملها. هذا نظام شائع الاستخدام في SNA.
دعونا تدريب مثل هذه الشبكة ، ونرى كيف يتصرف.
>>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2)), FullyConnectedLayer(n_in=20*12*12, n_out=100), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(training_data, 60, mini_batch_size, 0.1, validation_data, test_data)
نحصل على دقة 98.78 ٪ ، وهو أعلى بكثير من أي من النتائج السابقة. قللنا الخطأ أكثر من الثلث - نتيجة ممتازة.
لوصف بنية الشبكة ، فكرت في الطبقات التلافيفية والتجميعية كطبقة واحدة. اعتبرها طبقات منفصلة ، أو كطبقة واحدة - مسألة تفضيل. يعتبر network3.py طبقة واحدة ، نظرًا لأن هذه الطريقة تكون الشفرة أكثر إحكاما. ومع ذلك ، فمن السهل تعديل network3.py بحيث يمكن تعيين الطبقات بشكل فردي.
ممارسة
- ما دقة التصنيف التي سنحصل عليها إذا قمنا بتخفيض الطبقة المتصلة بالكامل واستخدام طبقة الالتفاف / تجمع وطبقة softmax فقط؟ هل إدراج طبقة متصلة بالكامل يساعد؟
هل يمكننا تحسين النتيجة بنسبة 98.78 ٪؟
دعنا نحاول إدراج طبقة الالتفاف / التجميع الثانية. سنقوم بإدخاله بين الطبقات الحالية للإلتفاف / التجميع والطبقات المخفية المتصلة بالكامل. نستخدم مرة أخرى حقل الاستقبالات المحلي 5 × 5 والمسبح في أقسام 2 × 2. دعونا نرى ما يحدث عندما نقوم بتدريب شبكة لها نفس المعلمات تقريبًا كما كان من قبل:
>>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2)), ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12), filter_shape=(40, 20, 5, 5), poolsize=(2, 2)), FullyConnectedLayer(n_in=40*4*4, n_out=100), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(training_data, 60, mini_batch_size, 0.1, validation_data, test_data)
ومرة أخرى ، لدينا تحسن: لقد حصلنا الآن على دقة 99.06 ٪!
في الوقت الحالي ، يطرح سؤالان طبيعيان. أولاً: ما معنى استخدام طبقة الالتفاف / التجميع الثانية؟ يمكنك أن تفترض أنه في الطبقة الثانية من الإلتفاف / التجميع ، تأتي الصور "12 × 12" في الإدخال ، حيث تمثل "وحدات البكسل" وجود (أو عدم وجود) بعض الميزات المترجمة في الصورة الواردة الأصلية. وهذا يعني أنه يمكننا افتراض أن إصدارًا معينًا من الصورة الواردة الأصلية يأتي إلى إدخال هذه الطبقة. ستكون هذه النسخة أكثر تجريدًا وإيجازًا ، ولكن لا يزال لديها بنية مكانية كافية ، لذلك من المنطقي استخدام طبقة الالتواء / السحب الثانية لمعالجتها.
وجهة نظر ممتعة ، لكنها تثير سؤالاً ثانياً. عند الإخراج من الطبقة السابقة ، يتم الحصول على 20 KPs منفصلة ، وبالتالي تأتي مجموعات بيانات الإدخال 20 × 12 × 12 في طبقة الالتفاف / التجميع الثانية. اتضح أن لدينا 20 صورة منفصلة متضمنة في طبقة الالتفاف / التجميع ، وليس صورة واحدة ، كما كان الحال في الطبقة الأولى للالتفاف / التجميع. فكيف يجب على الخلايا العصبية من طبقة الالتواء / تجمع الثانية للرد على العديد من هذه الصور الواردة؟ في الواقع ، نحن نسمح ببساطة بتدريب كل خلية عصبية من هذه الطبقة على أساس جميع الخلايا العصبية 20 × 5 × 5 التي تدخل مجالها الاستقبالي المحلي. في لغة أقل رسمية ، فإن كاشفات المعالم في طبقة الالتفاف / التجمع الثانية سيكون لها حق الوصول إلى جميع ميزات الطبقة الأولى ، ولكن فقط داخل حقول الاستلام المحلية الخاصة بهم.
بالمناسبة ، قد تنشأ مثل هذه المشكلة في الطبقة الأولى ، إذا كانت الصور ملونة. في هذه الحالة ، سيكون لدينا 3 سمات إدخال لكل بكسل تتوافق مع القنوات الأحمر والأخضر والأزرق للصورة الأصلية. ومن ثم سنمنح كاشفات الإشارات حق الوصول إلى جميع المعلومات الملونة ، ولكن فقط في إطار حقل الاستلام المحلي.
مهمة
- باستخدام وظيفة التنشيط في شكل الظل الزائدي. لقد ذكرت في وقت سابق من هذا الكتاب أدلة عدة مرات على أن وظيفة التانه ، الظل المائل الزائد ، قد تكون أكثر ملاءمة لتكون وظيفة تنشيط أكثر من السيني. لم نفعل شيئًا مع هذا ، حيث أحرزنا تقدمًا جيدًا مع السيني. ولكن دعونا نجرب بعض التجارب مع tanh كوظيفة تنشيط. حاول تدريب شبكة تنشيط tang مع طبقات تلافيفية ومتصلة بشكل كامل (يمكنك تمرير activation_fn = tanh كمعلمة إلى فئتي ConvPoolLayer و FullyConnectedLayer). ابدأ بنفس المقاييس الفوقية التي كانت تمتلكها شبكة السيني ، لكن قم بتدريب شبكة من 20 حقبة ، وليس 60. كيف تتصرف الشبكة؟ ماذا سيحدث إذا واصلنا حتى العصر الستين؟ حاول أن تبني رسمًا بيانيًا لدقة تأكيد العمل من خلال الحقبات المظللة والجانبية ، حتى عصر الستين. إذا كانت نتائجك متشابهة مع نتائجي ، فستجد أن الشبكة القائمة على الظل تتعلم بشكل أسرع قليلاً ، لكن الدقة الناتجة عن كلتا الشبكتين هي نفسها. هل يمكن ان توضح لماذا يحدث هذا؟ هل من الممكن تحقيق نفس سرعة التعلم باستخدام السيني - على سبيل المثال ، عن طريق تغيير سرعة التعلم أو من خلال القياس (تذكر أن σ (z) = (1 + tanh (z / 2)) / 2)؟ جرب خمسة أو ستة معلمات تشعبية مختلفة أو بنى الشبكة ، ابحث عن المماس الذي يمكن أن يكون متقدمًا على السيني. ألاحظ أن هذه المهمة مفتوحة. شخصيا ، لم أجد أي مزايا جدية في التحول إلى الظل ، على الرغم من أنني لم أجرِ تجارب شاملة ، وربما ستجدها. على أي حال ، سنعثر قريبًا على ميزة التحول إلى وظيفة التنشيط الخطي المستقيم ، لذلك لن نتعمق في قضية الظل الزائدي.
باستخدام العناصر الخطية تقويمها
تعد الشبكة التي قمنا بتطويرها في الوقت الحالي أحد خيارات الشبكة المستخدمة في
العمل المثمر لعام 1998 ، حيث تم تقديم مهمة MNIST ، وهي شبكة تسمى LeNet-5. هذا هو أساس جيد لمزيد من التجارب ، لتحسين فهم القضية والحدس. على وجه الخصوص ، هناك العديد من الطرق التي يمكننا من خلالها تغيير شبكتنا للبحث عن طرق لتحسين النتائج.
أولاً ، دعنا نغير الخلايا العصبية لدينا حتى نستخدم العناصر الخطية المستقيمة (ReLU) بدلاً من استخدام وظيفة التنشيط السيني. بمعنى ، سوف نستخدم وظيفة التنشيط من النموذج f (z) ≡ max (0، z). سنقوم بتدريب شبكة من 60 عصور ، بسرعة 0.0 = 0.03. لقد وجدت أيضًا أنه من المريح قليلاً استخدام تنسيق L2 مع معلمة التنظيم 0.1 = 0.1:
>>> from network3 import ReLU >>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2), activation_fn=ReLU), ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12), filter_shape=(40, 20, 5, 5), poolsize=(2, 2), activation_fn=ReLU), FullyConnectedLayer(n_in=40*4*4, n_out=100, activation_fn=ReLU), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(training_data, 60, mini_batch_size, 0.03, validation_data, test_data, lmbda=0.1)
حصلت على تصنيف دقة 99.23 ٪. تحسن متواضع على نتائج السيني (99.06٪). ومع ذلك ، في جميع تجاربي ، وجدت أن الشبكات القائمة على ReLU كانت متقدمة على الشبكات القائمة على وظيفة التنشيط السيني مع ثبات يحسد عليه. على ما يبدو ، هناك مزايا حقيقية في التحول إلى ReLU لحل هذه المشكلة.
ما الذي يجعل وظيفة تنشيط ReLU أفضل من الظل السيني أو المائل الزائدي؟ في الوقت الحالي ، نحن لا نفهم هذا بشكل خاص. يقال عادة أن الدالة max (0، z) لا تشبع عند z كبيرة ، على عكس الخلايا العصبية السيني ، وهذا يساعد الخلايا العصبية ReLU على مواصلة التعلم. أنا لا أجادل ، لكن مثل هذا العذر لا يمكن اعتباره شاملاً ، إنه مجرد نوع من الملاحظة (أذكرك بأننا ناقشنا التشبع في
الفصل 2 ).
بدأت ReLU أن تستخدم بنشاط في السنوات القليلة الماضية. لقد تم تبنيها لأسباب تجريبية: حاول بعض الأشخاص "ReLU" ، وغالبًا ما يكون ذلك بناءً على حدس أو حجج إرشادية. لقد حصلوا على نتائج جيدة ، وانتشرت الممارسة. في عالم مثالي ، سيكون لدينا نظرية تخبرنا بالتطبيقات التي هي وظائف التنشيط الأفضل للتطبيقات. لكن في الوقت الحالي ، لا يزال أمامنا طريق طويل للذهاب إلى مثل هذا الموقف. لن أفاجأ على الإطلاق إذا كان يمكن الحصول على مزيد من التحسينات في تشغيل الشبكات عن طريق اختيار وظيفة تنشيط أكثر ملاءمة. وأتوقع أيضًا تطوير نظرية جيدة لوظائف التنشيط في العقود القادمة. ولكن اليوم علينا أن نعتمد على قواعد الإبهام والخبرة المكتسبة بشكل سيئ.
توسيع بيانات التدريب
هناك طريقة أخرى ربما تساعدنا في تحسين نتائجنا وهي توسيع بيانات التدريب بطريقة حسابية. تتمثل أسهل طريقة لتوسيع بيانات التدريب في تغيير كل صورة تدريبية بمقدار بكسل واحد أو أعلى أو أسفل أو اليمين أو اليسار. يمكن القيام بذلك عن طريق تشغيل برنامج
expand_mnist.py .
$ python expand_mnist.py
يحول إطلاق البرنامج 50000 صورة تدريبية لـ MNIST إلى مجموعة موسعة من 250000 صورة تدريبية. ثم يمكننا استخدام هذه الصور التدريبية لتدريب الشبكة. سوف نستخدم نفس الشبكة كما كان من قبل مع ReLU. في تجربتي الأولى ، قمت بتقليل عدد فترات التدريب - كان ذلك منطقيًا ، لأن لدينا بيانات تدريب أكثر 5 مرات. ومع ذلك ، فإن توسيع مجموعة البيانات يقلل بشكل كبير من تأثير إعادة التدريب. لذلك ، بعد إجراء العديد من التجارب ، عدت إلى عدد العصور 60. على أي حال ، دعنا ندرب:
>>> expanded_training_data, _, _ = network3.load_data_shared( "../data/mnist_expanded.pkl.gz") >>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2), activation_fn=ReLU), ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12), filter_shape=(40, 20, 5, 5), poolsize=(2, 2), activation_fn=ReLU), FullyConnectedLayer(n_in=40*4*4, n_out=100, activation_fn=ReLU), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(expanded_training_data, 60, mini_batch_size, 0.03, validation_data, test_data, lmbda=0.1)
باستخدام بيانات التدريب المتقدمة ، حصلت على دقة بلغت 99.37٪. مثل هذا التغيير تافهة تقريبا يوفر تحسنا كبيرا في دقة التصنيف. وكما ناقشنا سابقًا ، يمكن تطوير امتداد بيانات الخوارزمية بشكل أكبر. فقط لتذكيرك: في عام 2003 ، قام
Simard و Steinkraus و Platt بتحسين دقة شبكتهم إلى 99.6 ٪. كانت شبكتهم مماثلة لشبكتنا ، واستخدموا طبقتين تجمع / تجمع ، تليها طبقة متصلة بالكامل مع 100 الخلايا العصبية. تنوعت تفاصيل بنيانهم - لم تتح لهم الفرصة للاستفادة من ReLU ، على سبيل المثال - ومع ذلك ، فإن المفتاح لتحسين نوعية العمل هو توسيع بيانات التدريب. لقد حققوا ذلك من خلال تحويل صور تدريب MNIST ونقلها وتشويهها. كما طوروا عملية "التشويه المرن" ، محاكين الاهتزازات العشوائية لعضلات الذراع أثناء الكتابة. من خلال الجمع بين كل هذه العمليات ، زادوا بشكل كبير من الحجم الفعال لقاعدة بيانات التدريب الخاصة بهم ، ونتيجة لذلك ، حققوا دقة بلغت 99.6 ٪.
مهمة
- فكرة الطبقات التلافيفية هي العمل بغض النظر عن الموقع في الصورة. لكن قد يبدو غريباً أن شبكتنا مدربة بشكل أفضل عندما نقوم ببساطة بتحويل الصور المدخلة. هل يمكن أن توضح لماذا هذا هو في الواقع معقول جدا؟
إضافة طبقة إضافية متصلة بالكامل
هل من الممكن تحسين الوضع؟ أحد الاحتمالات هو استخدام نفس الإجراء بالضبط ، ولكن في نفس الوقت زيادة حجم الطبقة المتصلة بالكامل. قمت بتشغيل البرنامج مع 300 ومع 1000 الخلايا العصبية ، وحصلت على نتائج في 99.46 ٪ و 99.43 ٪ ، على التوالي. هذا مثير للاهتمام ، ولكنه ليس مقنعًا بشكل خاص مقارنة بالنتيجة السابقة (99.37٪).
ماذا عن إضافة طبقة متصلة بالكامل؟ دعنا نحاول إضافة طبقة إضافية متصلة بالكامل حتى يكون لدينا طبقتان مخبأتان متصلتان تمامًا من 100 خلية عصبية:
>>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2), activation_fn=ReLU), ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12), filter_shape=(40, 20, 5, 5), poolsize=(2, 2), activation_fn=ReLU), FullyConnectedLayer(n_in=40*4*4, n_out=100, activation_fn=ReLU), FullyConnectedLayer(n_in=100, n_out=100, activation_fn=ReLU), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(expanded_training_data, 60, mini_batch_size, 0.03, validation_data, test_data, lmbda=0.1)
وبالتالي ، لقد حققت دقة التحقق من 99.43 ٪. الشبكة الموسعة مرة أخرى لم تحسن كثيرا من الأداء. بعد إجراء تجارب مماثلة مع طبقات متصلة بالكامل من 300 و 100 خلية عصبية ، حصلت على دقة 99.48 ٪ و 99.47 ٪. ملهمة ، ولكن ليس مثل الفوز الحقيقي.
ما الذي يحدث؟ هل من الممكن أن لا تساعد الطبقات الموسعة أو الإضافية المتصلة بالكامل في حل مشكلة MNIST؟ أو هل يمكن لشبكتنا أن تحقق نتائج أفضل ، لكننا نعمل على تطويرها في الاتجاه الخاطئ؟ ربما يمكننا ، على سبيل المثال ، استخدام تشديد التنظيم للحد من إعادة التدريب. أحد الاحتمالات هو تقنية التسرب المذكورة في الفصل 3. تذكر أن الفكرة الأساسية للاستبعاد هي إزالة التنشيط الفردي عشوائيًا عند تدريب الشبكة. نتيجة لذلك ، يصبح النموذج أكثر مقاومة لفقدان الأدلة الفردية ، وبالتالي فمن غير المرجح أن يعتمد على بعض الميزات الصغيرة غير القياسية لبيانات التدريب. دعنا نحاول تطبيق الاستثناء على آخر طبقة متصلة بالكامل:
>>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2), activation_fn=ReLU), ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12), filter_shape=(40, 20, 5, 5), poolsize=(2, 2), activation_fn=ReLU), FullyConnectedLayer( n_in=40*4*4, n_out=1000, activation_fn=ReLU, p_dropout=0.5), FullyConnectedLayer( n_in=1000, n_out=1000, activation_fn=ReLU, p_dropout=0.5), SoftmaxLayer(n_in=1000, n_out=10, p_dropout=0.5)], mini_batch_size) >>> net.SGD(expanded_training_data, 40, mini_batch_size, 0.03, validation_data, test_data)
باستخدام هذا النهج ، نحقق دقة 99.60 ٪ ، وهو أفضل بكثير من السابق ، وخاصة تقييمنا الأساسي - شبكة مع 100 الخلايا العصبية المخفية ، والتي تعطي دقة 99.37 ٪.
جدير بالذكر أن هناك تغيرين يستحقان الإشارة هنا.
أولاً ، لقد خفضت عدد مرات التدريب إلى 40: الاستثناء يقلل إعادة التدريب ، ونتعلم بشكل أسرع.
ثانياً ، تحتوي الطبقات المخفية المتصلة تمامًا على 1000 خلية ، وليس 100 ، كما كان من قبل. بالطبع ، الاستثناء ، في الواقع ، يزيل العديد من الخلايا العصبية أثناء التدريب ، لذلك يجب أن نتوقع نوعا من التوسع. في الواقع ، أجريت تجارب على 300 و 1000 خلية عصبية ، وحصلت على تأكيد أفضل قليلاً في حالة 1000 خلية عصبية.
باستخدام فرقة الشبكة
تتمثل الطريقة السهلة لتحسين الكفاءة في إنشاء العديد من الشبكات العصبية ، ثم حملهم على التصويت للحصول على تصنيف أفضل. لنفترض ، على سبيل المثال ، أننا قمنا بتدريب 5 NS مختلفة باستخدام الوصفة أعلاه ، وحقق كل منهم دقة قريبة من 99.6 ٪. على الرغم من أن جميع الشبكات ستظهر دقة مماثلة ، فقد يكون لديها أخطاء مختلفة بسبب التهيئة العشوائية المختلفة. من المنطقي أن نفترض أنه في حالة التصويت 5 NA ، سيكون تصنيفها العام أفضل من تصنيف أي شبكة على حدة.
يبدو الأمر جيدًا جدًا بحيث لا يكون صحيحًا ، ولكن تجميع هذه المجموعات يعد خدعة مشتركة لكل من الجمعية الوطنية وتقنيات MO الأخرى. وفي الواقع يعطي تحسنا في الكفاءة: نحصل على دقة 99.67 ٪. بمعنى آخر ، يصنّف مجموعتنا بشكل صحيح جميع صور التحقق البالغ عددها 10000 ، باستثناء 33.
الأخطاء المتبقية مبينة أدناه. التصنيف الموجود في الركن الأيمن العلوي هو التصنيف الصحيح وفقًا لبيانات MNIST ، وفي الركن الأيمن السفلي هو الملصق الذي استلمته مجموعة الشبكة:
تجدر الإشارة إلى الصور. أول رقمين ، 6 و 5 هما الأخطاء الحقيقية لمجموعتنا. ومع ذلك ، يمكن فهمهم ، يمكن ارتكاب مثل هذا الخطأ من قبل الإنسان. هذا الرقم 6 يشبه إلى حد كبير الصفر ، و 5 يشبه إلى حد كبير 3. الصورة الثالثة ، من المفترض أن 8 ، تبدو في الحقيقة أكثر من 9. أقف مع مجموعة الشبكات: أعتقد أنه قام بالمهمة بشكل أفضل من الشخص الذي كتب هذا الرقم. من ناحية أخرى ، فإن الصورة الرابعة ، 6 ، مصنفة بشكل غير صحيح من قبل الشبكات.
و هكذا. في معظم الحالات ، يبدو حل الشبكة معقولًا ، وفي بعض الحالات يصنف الرقم بشكل أفضل من الشخص الذي كتبه. بشكل عام ، تُظهر شبكاتنا كفاءة استثنائية ، خاصةً إذا ذكرنا أنهم قاموا بتصنيف 9967 صورة بشكل صحيح ، والتي لا نقدمها هنا.
في هذا السياق ، يمكن فهم العديد من الأخطاء الواضحة. حتى الشخص الحذر يكون مخطئًا في بعض الأحيان. لذلك ، لا أتوقع نتيجة أفضل إلا من شخص دقيق ومنهجي للغاية. شبكتنا تقترب من الأداء البشري.لماذا طبقنا الاستثناء فقط على الطبقات المتصلة بالكامل
إذا نظرت عن كثب إلى الرمز أعلاه ، فسترى أننا طبقنا الاستثناء فقط على طبقات الشبكة المتصلة بالكامل ، ولكن ليس على الطبقات التلافيفية. من حيث المبدأ ، يمكن تطبيق إجراء مماثل على الطبقات التلافيفية. ولكن ليست هناك حاجة إلى ذلك: تتمتع الطبقات التلافيفية بمقاومة داخلية كبيرة لإعادة التدريب. وذلك لأن الأوزان الكلية تجعل المرشحات التلافيفية تتعلم عبر الصورة بأكملها دفعة واحدة. نتيجة لذلك ، يكونون أقل عرضة للتجول في بعض التشوهات المحلية في بيانات التدريب. لذلك ، ليست هناك حاجة خاصة لتطبيق أدوات ضبط أخرى عليها ، مثل الاستثناءات.المضي قدما
يمكنك تحسين كفاءة حل مشكلة MNIST أكثر. وضع رودريغو بينينسون لوحة إعلامية توضح التقدم المحرز على مر السنين ، وروابط للعمل. تستخدم العديد من الأعمال GSS بنفس الطريقة التي استخدمناها بها. إذا بحثت عن عملك ، فستجد العديد من التقنيات المثيرة للاهتمام ، وقد ترغب في تنفيذ بعض منها. في هذه الحالة ، سيكون من الحكمة بدء تنفيذها بشبكة بسيطة يمكن تدريبها بسرعة ، وسيساعدك ذلك على البدء بسرعة في فهم ما يحدث.بالنسبة للجزء الأكبر ، لن أحاول مراجعة العمل الحديث. لكنني لا أستطيع مقاومة استثناء واحد. إنه عن عمل واحد في عام 2010. أنا أحب بساطتها فيها. الشبكة متعددة الطبقات ، ولا تستخدم إلا طبقات متصلة بالكامل (بدون تلوينات). في أنجح شبكاتها ، هناك طبقات مخفية تحتوي على 2500 و 2000 و 1500 و 1000 و 500 خلية على التوالي. استخدموا أفكارًا مماثلة لتوسيع بيانات التدريب. لكن إلى جانب ذلك ، طبّقوا العديد من الحيل ، بما في ذلك عدم وجود طبقات تلافيفية: كانت أبسط شبكة من الفانيليا ، والتي كان من الممكن ، مع الصبر المناسب وتوافر إمكانات الكمبيوتر المناسبة ، أن تتعلم في الثمانينات (إذا كانت مجموعة MNIST موجودة آنذاك). لقد حققوا دقة تصنيف بنسبة 99.65٪ ، والتي تتوافق تقريبًا مع تصنيفنا. الشيء الرئيسي في عملهم هو استخدام شبكة كبيرة وعميقة للغاية ، واستخدام وحدات معالجة الرسومات لتسريع عملية التعلم. هذا سمح لهم لتعلم العديد من العصور. كما استفادوا من فترات التدريب الطويلة ،وخفضت تدريجيا سرعة التعلم من 10-3 إلى 10 -6 . محاولة تحقيق نتائج مماثلة مع بنية مثلها هي ممارسة مثيرة للاهتمام.لماذا نتعلم؟
في الفصل السابق ، رأينا عقبات أساسية أمام تعلم NS متعددة الطبقات العميقة. على وجه الخصوص ، رأينا أن التدرج يصبح غير مستقر للغاية: عند الانتقال من طبقة الإخراج إلى الطبقة السابقة ، يميل التدرج إلى الاختفاء (مشكلة التدرج المختفي) أو إلى النمو الهائل (مشكلة نمو التدرج المتفجر). بما أن التدرج هو الإشارة التي نستخدمها للتدريب ، فهذا يسبب مشاكل.كيف نجحنا في تجنبها؟الجواب ، بطبيعة الحال ، هو هذا: لم نتمكن من تجنبها. بدلاً من ذلك ، قمنا ببعض الأشياء التي سمحت لنا بمواصلة العمل ، على الرغم من هذا. على وجه الخصوص: (1) استخدام الطبقات التلافيفية يقلل بشكل كبير من عدد المعلمات الواردة فيها ، مما يسهل إلى حد كبير مشكلة التعلم ؛ (2) استخدام تقنيات تنظيم أكثر كفاءة (الاستبعاد والطبقات التلافيفية) ؛ (3) استخدام ReLU بدلاً من الخلايا العصبية السينيّة لتسريع التعلّم - تجريبيًا حتى 3-5 مرات ؛ (4) استخدام GPU والقدرة على التعلم مع مرور الوقت. على وجه الخصوص ، في التجارب الحديثة ، درسنا 40 عصور باستخدام مجموعة بيانات أكبر بخمس مرات من بيانات تدريب MNIST القياسية. في وقت سابق من هذا الكتاب ، درسنا بشكل رئيسي 30 عصور باستخدام بيانات التدريب القياسية. مزيج من العوامل (3) و (4) يعطي مثل هذا التأثير ،كما لو درسنا أطول 30 مرة من قبل.ربما تقول ، "هل هذا كل شيء؟" هل هذا كل ما يتطلبه الأمر لتدريب الشبكات العصبية العميقة؟ ولماذا اشتعلت النيران؟بالطبع ، استخدمنا أفكارًا أخرى: مجموعات بيانات كبيرة بما يكفي (للمساعدة في تجنب إعادة التدريب) ؛ دالة التكلفة الصحيحة (لتجنب تباطؤ التعلم) ؛ التهيئة الجيدة للأوزان (أيضًا لتجنب تباطؤ التعلم بسبب تشبع الخلايا العصبية) ؛ ملحق حسابي لمجموعة بيانات التدريب. ناقشنا هذه الأفكار وغيرها في الفصول السابقة ، وعادة ما أتيحت لنا الفرصة لإعادة استخدامها مع الملاحظات الصغيرة في هذا الفصل.من كل المؤشرات ، هذه مجموعة بسيطة من الأفكار. بسيطة ، ومع ذلك ، قادرة على الكثير عند استخدامها في المجمع. اتضح أن البدء بالتعلم العميق كان سهلاً للغاية!?
إذا نظرنا إلى طبقات الالتفاف / التجميع كطبقة واحدة ، فعندئذٍ في هيكلنا النهائي هناك 4 طبقات مخفية. هل تستحق مثل هذه الشبكة لقبًا عميقًا؟ بطبيعة الحال ، هناك 4 طبقات مخفية أكثر بكثير من الشبكات الضحلة التي درسناها سابقًا. تحتوي معظم الشبكات على طبقة مخفية واحدة ، وأحيانًا 2. ومن ناحية أخرى ، تحتوي الشبكات المتقدمة الحديثة في بعض الأحيان على عشرات الطبقات المخفية. التقيت أحيانًا بأشخاص اعتقدوا أنه كلما كانت الشبكة أعمق ، كلما كان ذلك أفضل ، وإذا كنت لا تستخدم عددًا كبيرًا بما فيه الكفاية من الطبقات المخفية ، فهذا يعني أنك لا تقوم بالفعل بالتعلم العميق. لا أعتقد ذلك ، على وجه الخصوص لأن هذا النهج يحول تعريف التعلم العميق إلى إجراء يعتمد على النتائج اللحظية. كانت هناك طفرة حقيقية في هذا المجال هي فكرة التطبيق العملي لتجاوز الشبكات مع طبقة أو طبقتين مخفيتين ،السائدة في منتصف 2000s. كان هذا إنجازًا حقيقيًا ، حيث فتح مجالًا من الأبحاث بنماذج أكثر تعبيراً. حسنًا ، هناك عدد محدد من الطبقات ليس ذا أهمية أساسية. يعد استخدام الشبكات العميقة أداة لتحقيق أهداف أخرى ، مثل تحسين دقة التصنيف.القضية الإجرائية
في هذا القسم ، انتقلنا بسلاسة من الشبكات الضحلة ذات الطبقة المخفية إلى شبكات الالتفاف متعددة الطبقات. كل شيء بدا سهلا جدا! لقد قمنا بإجراء تغيير وحصلنا على تحسن. إذا بدأت بالتجربة ، فأنا أضمن أن كل شيء عادة لن يتم بسلاسة. قدمت لك قصة تمشيط ، متجاهلة العديد من التجارب ، بما في ذلك التجارب غير الناجحة. آمل أن تساعدك هذه القصة الممشطة على فهم الأفكار الأساسية بشكل أفضل. لكنه يخاطر بنقل انطباع غير كامل. يتطلب الحصول على شبكة عمل جيدة الكثير من التجربة والخطأ ، تتخللها الإحباط. في الممارسة العملية ، يمكنك توقع عدد كبير من التجارب. لتسريع العملية ، يمكن أن تساعدك المعلومات الواردة في الفصل 3 فيما يتعلق باختيار معلمات الشبكة الفائقة ، وكذلك الأدبيات الإضافية المذكورة هناك.رمز لشبكات الإلتفاف لدينا
حسنًا ، دعنا الآن ننظر إلى رمز برنامج network3.py الخاص بنا. من الناحية الهيكلية ، يشبه network2.py ، الذي قمنا بتطويره في الفصل 3 ، ولكن التفاصيل تختلف بسبب استخدام مكتبة Theano. لنبدأ بفئة FullyConnectedLayer ، على غرار الطبقات التي درسناها سابقًا. class FullyConnectedLayer(object): def __init__(self, n_in, n_out, activation_fn=sigmoid, p_dropout=0.0): self.n_in = n_in self.n_out = n_out self.activation_fn = activation_fn self.p_dropout = p_dropout
تتحدث معظم طريقة __init__ عن نفسها ، لكن بعض الملاحظات يمكن أن تساعد في توضيح الكود. كالعادة ، نقوم بشكل عشوائي بتهيئة الأوزان والإزاحة باستخدام قيم عشوائية عادية مع انحرافات قياسية مناسبة. هذه الخطوط تبدو غير مفهومة قليلاً. ومع ذلك ، فإن معظم التعليمات البرمجية الغريبة تقوم بتحميل الأوزان والإزاحة إلى ما تسميه مكتبة Theano المتغيرات المشتركة. هذا يضمن أنه يمكن معالجة المتغيرات على وحدة معالجة الرسومات ، إن وجدت. لن نتعمق في هذه المشكلة - إذا كنت مهتمًا ، اقرأ الوثائق الخاصة بـ Theano. لاحظ أيضًا أن هذا التهيئة للأوزان والإزاحة خاص بوظيفة التنشيط السيني. من الناحية المثالية ، بالنسبة لوظائف مثل الظل الزائدي و ReLU ، سنقوم بتهيئة الأوزان والإزاحة بشكل مختلف. تمت مناقشة هذه المشكلة في المهام المستقبلية.تنتهي الطريقة __init__ بالعبارة self.params = [self.w، self.b]. هذه طريقة ملائمة لجمع كل معلمات التعلم المرتبطة بالطبقة. يستخدم Network.SGD فيما بعد سمات params لمعرفة المتغيرات في مثيل فئة الشبكة التي يمكن تدريبها.يتم استخدام طريقة set_inpt لتمرير الإدخال إلى طبقة وحساب الإخراج المقابل. أكتب inpt بدلاً من الإدخال ، لأن الإدخال عبارة عن وظيفة بيثون مدمجة ، وإذا كنت تلعب معهم ، فقد يؤدي ذلك إلى سلوك غير متوقع للبرنامج ويصعب تشخيص الأخطاء. في الواقع ، نقوم بتمرير الإدخال بطريقتين: من خلال self.inpt و self.inpt_dropout. يتم ذلك لأننا قد نرغب في استخدام استثناء أثناء التدريب. وسنحتاج بعد ذلك إلى إزالة جزء من الخلايا العصبية الذاتية. هذا ما تقوم به وظيفة dropout_layer في السطر قبل الأخير من الأسلوب set_inpt. لذلك ، يتم استخدام self.inpt_dropout و self.output_dropout أثناء التدريب ، ويتم استخدام self.inpt و self.output لجميع الأغراض الأخرى ، على سبيل المثال ، تقييم دقة بيانات التحقق من الصحة واختبارها.تتشابه تعريفات الفئة الخاصة بـ ConvPoolLayer و SoftmaxLayer مع FullyConnectedLayer. مشابه لدرجة أنني لن أقتبس الرمز. إذا كنت مهتمًا ، يمكن دراسة الرمز الكامل للبرنامج لاحقًا في هذا الفصل.تجدر الإشارة إلى بعض التفاصيل المختلفة. من الواضح ، في ConvPoolLayer و SoftmaxLayer ، نحسب تنشيطات الخرج بطريقة تناسب نوع الطبقة. لحسن الحظ ، Theano من السهل القيام به ، فإنه يحتوي على عمليات مدمجة لحساب الإلتواء ، وتجمع الحد الأقصى ووظيفة softmax.من غير الواضح كيفية تهيئة الأوزان والإزاحة في طبقة softmax - لم نناقش ذلك. ذكرنا أنه بالنسبة لطبقات الوزن السيني ، من الضروري تهيئة توزيعات عشوائية طبيعية ذات معلمات مناسبة. ولكن هذه الحجة ارشادية تنطبق على الخلايا العصبية السيني (و ، مع تصحيحات طفيفة ، لتانغ الخلايا العصبية). ومع ذلك ، لا يوجد سبب محدد لتطبيق هذه الوسيطة على طبقات softmax. لذلك ، ليس هناك سبب لتطبيق مسبق هذا التهيئة مرة أخرى. بدلاً من ذلك ، أقوم بتهيئة جميع الأوزان والإزاحة على 0. الخيار تلقائي ، لكنه يعمل بشكل جيد في الممارسة.لذلك ، لقد درسنا جميع فئات الطبقات. ماذا عن فئة الشبكة؟ لنبدأ باستكشاف طريقة __init__: class Network(object): def __init__(self, layers, mini_batch_size): """ layers, , mini_batch_size """ self.layers = layers self.mini_batch_size = mini_batch_size self.params = [param for layer in self.layers for param in layer.params] self.x = T.matrix("x") self.y = T.ivector("y") init_layer = self.layers[0] init_layer.set_inpt(self.x, self.x, self.mini_batch_size) for j in xrange(1, len(self.layers)): prev_layer, layer = self.layers[j-1], self.layers[j] layer.set_inpt( prev_layer.output, prev_layer.output_dropout, self.mini_batch_size) self.output = self.layers[-1].output self.output_dropout = self.layers[-1].output_dropout
معظم الكود يتحدث عن نفسه. يجمع السطر self.params = [param for layer in ...] جميع المعلمات لكل طبقة في قائمة واحدة. كما هو موضح سابقًا ، يستخدم أسلوب Network.SGD self.params لمعرفة المعلمات التي يمكن أن تتعلمها الشبكة. يحدد الأسطر self.x = T.matrix ("x") و self.y = T.ivector ("y") المتغيرات الرمزية Theano x و y. سوف يمثلون المدخلات والمخرجات المطلوبة للشبكة.هذا ليس برنامجًا تعليميًا حول استخدام Theano ، لذلك لن أتطرق إلى معنى المتغيرات الرمزية (انظر الوثائق وأيضًا من البرامج التعليمية)). يتحدثون تقريبًا ، وهم يشيرون إلى المتغيرات الرياضية ، وليس المتغيرات المحددة. معهم ، يمكنك تنفيذ العديد من العمليات العادية: إضافة ، طرح ، ضرب ، تطبيق الوظائف ، وهلم جرا. يوفر Theano العديد من الاحتمالات لمعالجة مثل هذه المتغيرات الرمزية والتلوين والسحب الأقصى وما إلى ذلك. ومع ذلك ، فإن الشيء الرئيسي هو إمكانية التمايز الرمزي السريع باستخدام شكل عام للغاية من خوارزمية backpropagation. هذا مفيد للغاية لتطبيق النسب التدرج العشوائي على مجموعة واسعة من بنيات الشبكة. على وجه الخصوص ، تحدد سطور التعليمات البرمجية التالية المخرجات الرمزية للشبكة. نبدأ بتعيين الإدخال إلى الطبقة الأولى: init_layer.set_inpt(self.x, self.x, self.mini_batch_size)
يتم إرسال بيانات الإدخال حزمة واحدة صغيرة في وقت واحد ، لذلك يشار إلى حجمها هناك. نقوم بتمرير إدخال self.x مرتين: الحقيقة هي أنه يمكننا استخدام الشبكة بطريقتين مختلفتين (مع أو بدون استثناء). الحلقة for ينشر المتغير الرمزي self.x عبر طبقات الشبكة. يتيح لنا ذلك تحديد إخراج السمات النهائية و output_dropout ، والتي تمثل رمزًا إخراج الشبكة.بعد التعامل مع تهيئة الشبكة ، دعنا ننظر إلى التدريب من خلال طريقة SGD. رمز تبدو طويلة ، ولكن هيكلها بسيط جدا. التفسيرات تتبع الكود: def SGD(self, training_data, epochs, mini_batch_size, eta, validation_data, test_data, lmbda=0.0): """ - .""" training_x, training_y = training_data validation_x, validation_y = validation_data test_x, test_y = test_data
الأسطر الأولى واضحة ، وهي تقسم مجموعات البيانات إلى مكونين x و y ، وتحسب عدد الحزم الصغيرة المستخدمة في كل مجموعة بيانات. الأسطر التالية أكثر إثارة للاهتمام ، وهي توضح السبب في أنه من الممتع للغاية العمل مع مكتبة Theano. سوف أقتبس منهم هنا:
في هذه السطور ، نقوم بتعريف دالة التكلفة المنظمة بطريقة رمزية استنادًا إلى دالة الاحتمال اللوغاريتمي ، وحساب المشتقات المقابلة في دالة التدرج ، وكذلك تحديثات المعلمات المقابلة. Theano يسمح لنا أن نفعل كل هذا في بضعة أسطر. الشيء الوحيد المخفي هو أن حساب التكلفة ينطوي على استدعاء طريقة التكلفة لطبقة المخرجات ؛ يقع هذا الرمز في مكان آخر في network3.py. لكنها قصيرة وبسيطة. من خلال تعريف كل هذا ، يكون كل شيء جاهزًا لتحديد وظيفة train_mb ، وهي الوظيفة الرمزية Theano التي تستخدم التحديثات لتحديث معلمات الشبكة بواسطة فهرس الحزمة المصغرة. وبالمثل ، فإن دالات validate_mb_accuracy و test_mb_accuracy تحسب دقة الشبكة في أي رزمة صغيرة محددة من بيانات التحقق أو التحقق. المتوسط على هذه الوظائف ،يمكننا حساب الدقة على كامل مجموعات التحقق من الصحة والتحقق.تتحدث بقية طريقة SGD عن نفسها - فنحن ببساطة نمر عبر الحلقات المتتالية ، ونقوم بتدريب الشبكة مرارًا وتكرارًا على حزم صغيرة من بيانات التدريب ، ونحسب دقة التأكيد والتحقق.نحن الآن نفهم أهم أجزاء الشبكة. دعنا نذهب لفترة قصيرة من خلال البرنامج بأكمله. ليس من الضروري أن تدرس كل شيء بالتفصيل ، ولكن قد ترغب في تجاوز القمم ، وربما الخوض في بعض المقاطع التي أعجبتني بشكل خاص. ولكن ، بطبيعة الحال ، فإن أفضل طريقة لفهم البرنامج هي تغييره ، وإضافة شيء جديد ، refactor تلك الأجزاء التي ، في رأيك ، يمكن تحسينها. بعد الرمز ، أقدم عدة مهام تحتوي على عدد من الاقتراحات الأولية حول ما يمكن القيام به هنا. هنا هو الرمز. """network3.py ~~~~~~~~~~~~~~ Theano . (, , -, softmax) (, , ReLU; ). CPU , network.py network2.py. , , GPU, . Theano, network.py network2.py. , . , API network2.py. , , . , , . Theano (http://deeplearning.net/tutorial/lenet.html ), (https://github.com/mdenil/dropout ) (http://colah.imtqy.com ). Theano 0.6 0.7, . """
المهام
- SGD . , . network3.py , .
- Network , .
- SGD , η ( , , , ).
- , . network3.py, . , , . .
- .
- – . , , , ? .
- ReLU , ( -) . . , ReLU ( ). , c>0 c L−1 , L – . , softmax? ReLU? ? , , . , ReLU.
- . , ReLU? , ? : «» . – , - - .