الرياضيات المنفصلة لنظام WMS: تجميع الأسهم

توضح المقالة كيف ، عند تقديم نظام WMS- ، واجهنا الحاجة إلى حل مشكلة التجميع غير القياسية ومع الخوارزميات التي حللناها. سنخبرك كيف طبقنا منهجًا علميًا منهجيًا لحل المشكلة ، والصعوبات التي واجهناها والدروس التي تعلمناها.

يبدأ هذا المنشور سلسلة من المقالات التي نشارك فيها تجربتنا الناجحة في تنفيذ خوارزميات التحسين في عمليات المستودعات. تهدف سلسلة المقالات إلى تعريف الجمهور بأنواع مهام تحسين عمليات المستودعات التي تنشأ في أي مستودع كبير وكبير تقريبًا ، فضلاً عن إخبارنا بتجربتنا في حل هذه المشكلات والمخاطر التي صودفت بهذه الطريقة. ستكون المقالات مفيدة لأولئك الذين يعملون في صناعة لوجستيات المستودعات ، وتطبيق أنظمة WMS ، وكذلك المبرمجين المهتمين بتطبيقات الرياضيات في الأعمال وتحسين العمليات في المؤسسة.

عنق الزجاجة عملية

في عام 2018 ، قمنا بعمل مشروع لإدخال نظام WMS في مستودع شركة LD Trading House في تشيليابينسك. عرض المنتج "1C-Logistics: Warehouse Management 3" لمدة 20 وظيفة: مشغلي WMS ، وأصحاب المتاجر ، وسائقي الرافعات الشوكية. تبلغ مساحة المستودع حوالي 4 آلاف متر مربع ، وعدد الخلايا هو 5000 وعدد SKU 4500. يتم تخزين الصمامات الكروية الخاصة بإنتاجنا ذي الأحجام المختلفة من 1 كجم إلى 400 كجم في المستودع. يتم تخزين المخزونات في المستودع في سياق الدُفعات بسبب الحاجة إلى اختيار البضائع وفقًا لـ FIFO والمواصفات "المضمنة" الخاصة بوضع المنتج (شرح أدناه).

عند تصميم مخططات الأتمتة لعمليات المستودعات ، واجهنا المشكلة الحالية المتمثلة في التخزين غير الأمثل للمخزونات. يحتوي تكديس الرافعات وتخزينها ، كما قلنا بالفعل ، على تفاصيل "الصف". أي أن المنتجات الموجودة في الخلية مكدسة في صفوف واحدة فوق الأخرى ، وغالباً ما تكون القدرة على وضع قطعة على قطعة غائبة (تسقط فقط ، والوزن ليس صغيراً). لهذا السبب ، اتضح أنه لا يمكن وضع سوى تسمية واحدة من دفعة واحدة في وحدة تخزين من قطعة واحدة ، وإلا فإن التسمية القديمة لا يمكن سحبها من تحت واحدة جديدة دون "التجريف" للخلية بأكملها.

تصل المنتجات إلى المستودع يوميًا وكل وصول عبارة عن مجموعة منفصلة. إجمالًا ، نتيجة لشهر واحد من تشغيل المستودع ، يتم إنشاء 30 وحدة منفصلة ، على الرغم من حقيقة أنه ينبغي تخزين كل منها في خلية منفصلة. غالبًا ما يتم اختيار البضائع ليس في المنصات بأكملها ، ولكن في القطع ، ونتيجة لذلك ، في منطقة اختيار القطعة ، يتم ملاحظة الصورة التالية في العديد من الخلايا: في خلية يزيد حجمها عن 1 متر مكعب ، توجد عدة قطع من الرافعات تشغل أقل من 5-10٪ من حجم الخلية (انظر الشكل 1). ).

الشكل 1. صورة لعدة قطع من البضائع في خلية

على وجه الاستخدام الأمثل لسعة التخزين. لتخيل حجم الكارثة ، يمكنني أن أذكر الأرقام: يوجد في المتوسط ​​ما بين 100 و 300 خلية من هذه الخلايا مع بقايا هزيلة في فترات مختلفة من تشغيل المستودع. نظرًا لأن المستودع صغير نسبيًا ، في مواسم التحميل للمستودع ، يصبح هذا العامل "رقبة ضيقة" ويمنع عمليات المستودع إلى حد كبير.

فكرة حل مشكلة

تم طرح الفكرة: لإحضار مجموعات الوحدات البنائية ذات التواريخ الأقرب إلى قطعة واحدة واحدة ووضع هذه الأرصدة مع مجموعة موحدة بشكل مضغوط معًا في خلية واحدة ، أو في عدة إذا لم تكن هناك مساحة كافية في واحدة لاستيعاب العدد الإجمالي للأرصدة.


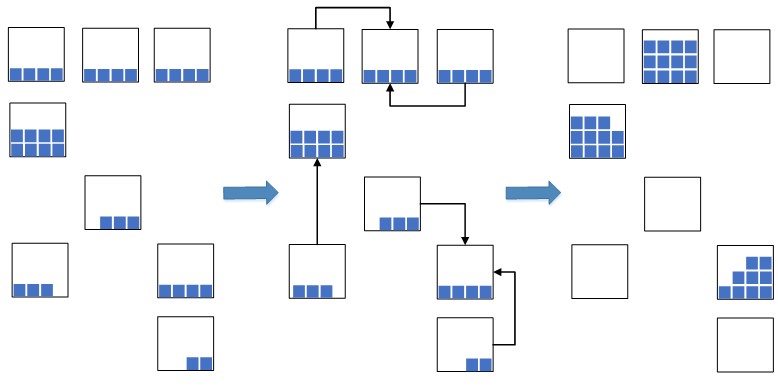الشكل 2. مخطط ضغط الخلية

يتيح لك ذلك تقليل مساحة المستودع المشغولة بشكل كبير ، والتي سيتم استخدامها للبضائع الموضوعة حديثًا. في حالة وجود سعة زائدة من المستودعات ، يكون هذا الإجراء ضروريًا للغاية ؛ وإلا ، فقد لا يكون هناك ببساطة مساحة حرة كافية لوضع سلع جديدة ، مما سيؤدي إلى توقف عمليات المستودعات الخاصة بالتنسيب والتجديد. في السابق ، قبل تنفيذ نظام WMS ، تم إجراء مثل هذه العملية يدويًا ، والتي لم تكن فعالة ، لأن عملية العثور على مخلفات مناسبة في الخلايا كانت طويلة جدًا. الآن ، مع إدخال أنظمة WMS ، قرروا أتمتة العملية وتسريعها وجعلها ذكية.

تنقسم عملية حل هذه المشكلة إلى مرحلتين:

• في المرحلة الأولى ، نجد مجموعات الأطراف قريبة من تاريخ الضغط ؛
• في المرحلة الثانية ، نحسب كل مجموعة من مجموعات الدُفعات أكثر المواضع المدمجة لمخلفات المنتجات في الخلايا.

في المقالة الحالية ، سنركز على المرحلة الأولى من الخوارزمية ، ونترك تغطية المرحلة الثانية للمقال التالي.

البحث عن نموذج رياضي للمشكلة

قبل أن نجلس لكتابة الرمز وابتكار دراجتنا ، قررنا التعامل مع هذه المشكلة بطريقة علمية ، وهي: صياغتها رياضيا ، وتقليلها إلى مشكلة التحسين المنفصلة المعروفة واستخدام الخوارزميات الحالية الفعالة لحلها ، أو أخذ هذه الخوارزميات الموجودة كأساس وتعديلها تحت تفاصيل المهمة العملية التي يتعين حلها.

نظرًا لأنه يستنتج بوضوح من بيان العمل للمشكلة التي نتعامل معها مع المجموعات ، فإننا نقوم بصياغة هذه المشكلة من حيث نظرية المجموعة.

سمح $$$P$ - مجموعة من كل الكثير من بقايا بعض البضائع في المخازن. سمح $$$C$ - ثابت معين من الأيام. سمح $$$K$ - مجموعة فرعية من الدُفعات حيث لا يتجاوز فارق التاريخ لجميع أزواج الدُفعات للمجموعة الفرعية الثابت $$$C$ . العثور على الحد الأدنى لعدد مجموعات فرعية disjoint $$$K$ بحيث أن جميع المجموعات الفرعية $$$K$ جماعيا سيعطي الكثير $$$P$ .

علاوة على ذلك ، نحن بحاجة إلى إيجاد ليس فقط الحد الأدنى لعدد المجموعات الفرعية ، ولكن حتى تكون هذه المجموعات الفرعية أكبر عدد ممكن. ويرجع ذلك إلى حقيقة أنه بعد تجميع الدُفعات ، سنقوم "بضغط" ما تبقى من الدُفعات الموجودة في الخلايا. دعونا توضيح مع مثال. افترض أن هناك العديد من الأطراف الموزعة على المحور الزمني ، كما في الشكل 3.
الشكل 3. خيارات متعددة التقسيم

من بين الخيارين لتقسيم المجموعة P بنفس عدد المجموعات الفرعية ، يكون القسم الأول (أ) مفيدًا جدًا لمهمتنا. نظرًا لأن عدد الأطراف سيكون في مجموعات ، تظهر مجموعات ضغط أكثر ، وبالتالي من الأرجح أن تجد الضغط الأكثر ضغطًا. بالطبع ، هذه القاعدة ليست أكثر من مجرد افتراض ارشادي وافتراضات مضاربة. على الرغم من أن التجربة الحسابية أظهرت أنه إذا تم أخذ شرط التعظيم هذا في الاعتبار ، فإن ضغط الانضباط اللاحق للمخلفات يصبح في المتوسط ​​5-10٪ أعلى من الضغط الذي تم إنشاؤه دون مراعاة مثل هذه الحالة.

بمعنى آخر ، باختصار ، نحتاج إلى إيجاد مجموعات أو مجموعات من أطراف متشابهة حيث يتم تحديد معيار التشابه بواسطة ثابت $$$C$ . هذه المهمة تذكرنا بمشكلة التكتل المعروفة. من المهم أن نقول أن المشكلة قيد النظر تختلف عن مشكلة التجميع حيث أنه في مشكلتنا يوجد شرط محدد بدقة لمعيار تشابه عناصر المجموعة ، يحدده الثابت $$$C$ ، وفي مشكلة المجموعات لا يوجد مثل هذا الشرط. يمكن العثور على بيان مشكلة المجموعات والمعلومات المتعلقة بهذه المهمة هنا.

لذلك ، تمكنا من صياغة المشكلة والعثور على المشكلة الكلاسيكية مع صيغة مماثلة. أنت الآن بحاجة إلى التفكير في خوارزميات معروفة لحلها ، حتى لا تعيد اختراع العجلة ، ولكن لأخذ أفضل الممارسات وتطبيقها. لحل مشكلة التجميع ، نظرنا في الخوارزميات الأكثر شيوعًا ، وهي: $$$ك$ -means، $$$ج$ ، خوارزمية لاختيار المكونات المتصلة ، الحد الأدنى لخوارزمية شجرة الامتداد. يمكن العثور على وصف وتحليل لهذه الخوارزميات هنا.

لحل مشكلتنا ، تجميع الخوارزميات $$$ك$ وسائل و $$$ج$ - لا تنطبق المواد على الإطلاق ، نظرًا لأن عدد المجموعات غير معروف أبدًا $$$ك$ وهذه الخوارزميات لا تأخذ في الاعتبار تقييد ثابت الأيام. تم التخلص من هذه الخوارزميات في البداية.
لحل مشكلتنا ، تعد خوارزمية اختيار المكونات المتصلة وخوارزمية شجرة الامتداد الدنيا أكثر ملاءمة ، ولكن كما اتضح ، لا يمكن تطبيقها "بشكل مباشر" على المشكلة التي يتم حلها والحصول على حل جيد. لتوضيح ذلك ، فإننا نعتبر منطق تشغيل هذه الخوارزميات كما هو مطبق على مشكلتنا.

النظر في الرسم البياني $$$G$ التي قمم هي الكثير من الأطراف $$$P$ ، والحافة بين القمم $$$p_1$ و $$$p_2 دولا$ له وزن يساوي اختلاف الأيام بين الدفعات $$$p_1$ و $$$p_2 دولا$ . في الخوارزمية لتحديد المكونات المتصلة ، يتم تحديد معلمة إدخال $$$R$ حيث $$$R \ leq C$ وفي الرسم البياني $$$G$ تتم إزالة جميع الحواف التي تمت إزالة وزنها $$$R$ . فقط أقرب أزواج الكائنات تبقى متصلة. معنى الخوارزمية هو تحديد هذه القيمة $$$R$ ، حيث "ينهار" الرسم البياني في العديد من المكونات المتصلة ، حيث تفي الأطراف المنتمية إلى هذه المكونات بمعيار التشابه ، الذي يحدده الثابت $$$C$ . المكونات الناتجة هي مجموعات.

تعتمد خوارزمية شجرة الامتداد الدنيا أولاً على رسم بياني $$$G$ الحد الأدنى لشجرة الامتداد ، ثم تزيل الحواف بأعلى وزن بالتتابع حتى "ينهار" الرسم البياني في العديد من المكونات المتصلة ، حيث تفي الكثير من المنتمين إلى هذه المكونات بمعايير التشابه. ستكون المكونات الناتجة مجموعات.

عند استخدام هذه الخوارزميات لحل المشكلة قيد النظر ، قد ينشأ موقف كما في الشكل 4.


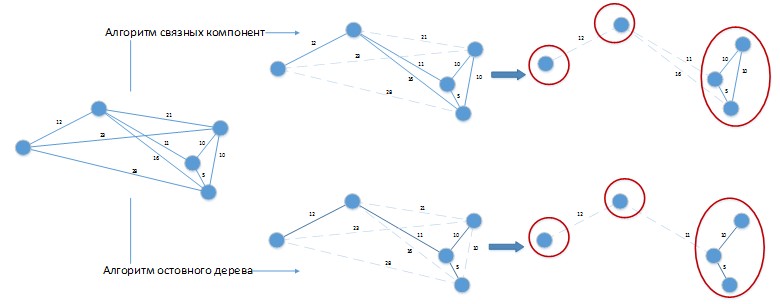الشكل 4. تطبيق خوارزميات التجميع للمشكلة التي يجري حلها.

لنفترض أن لدينا فرق ثابت في أيام الأطراف هو 20 يومًا. الايرل لقب انكليزي $$$G$ تم تصويره في شكل مكاني لراحة الإدراك البصري. قدمت كلتا الخوارزميات حلاً بثلاث مجموعات ، والتي يمكن تحسينها بسهولة من خلال الجمع بين الدفعات الموضوعة في مجموعات منفصلة فيما بينها! من الواضح أن هذه الخوارزميات تحتاج إلى مزيد من التطوير وفقًا لتفاصيل المشكلة التي يتم حلها وتطبيقها الخالص على حل مشكلتنا سوف يعطي نتائج سيئة.


لذلك ، قبل البدء في كتابة رمز خوارزميات الرسم البياني المعدلة لمهمتنا واختراع دراجتنا الخاصة (التي تم تخمينها بالفعل الخطوط العريضة للعجلات المربعة) ، قررنا مرة أخرى التعامل مع هذه المشكلة بشكل علمي ، وهي: محاولة للحد منها إلى مشكلة منفصلة أخرى التحسين ، على أمل أن الخوارزميات الموجودة لحلها يمكن تطبيقها دون تعديلات.

البحث التالي عن مشكلة كلاسيكية مماثلة كان ناجحاً! كان من الممكن العثور على مشكلة تحسين منفصلة ، يتزامن بيانها تقريبًا 1 في 1 مع بيان مشكلتنا. تحولت هذه المشكلة إلى أنها مشكلة تغطية المجموعة . نقدم بيان المشكلة كما هو مطبق على تفاصيلنا.

هناك مجموعة محدودة $$$P$ والعائلة $$$S$ جميع مجموعاتها الفرعية غير المترابطة للأطراف ، بحيث فرق التاريخ لجميع أزواج الأطراف في كل مجموعة فرعية $$$I$ من العائلة $$$S$ لا يتجاوز الثوابت $$$C$ . طلاء يسمى عائلة $$$يو$ أقل قوة عناصرها تنتمي $$$S$ بحيث اتحاد مجموعات $$$I$ من العائلة $$$يو$ يجب أن تعطي الكثير من جميع الأطراف $$$P$ .

ويمكن الاطلاع على تحليل مفصل لهذه المشكلة هنا وهنا. يمكن العثور على خيارات أخرى للتطبيق العملي لمشكلة التغطية وتعديلاتها هنا.

يتمثل الاختلاف الطفيف الوحيد بين المشكلة المدروسة والمشكلة الكلاسيكية المتمثلة في تغطية مجموعة في الحاجة إلى زيادة عدد العناصر في المجموعات الفرعية إلى الحد الأقصى. بالطبع ، يمكن للمرء أن يبحث عن المقالات التي تم فيها النظر في مثل هذه الحالة الخاصة ، وعلى الأرجح سيتم العثور عليها. ولكن من البحث التالي عن المقالات ، تم إنقاذنا من خلال حقيقة أن خوارزمية "الجشع" المعروفة لحل المشكلة الكلاسيكية المتمثلة في تغطية مجموعة تقوم بإنشاء قسم يأخذ في الاعتبار مجرد زيادة عدد العناصر في المجموعات الفرعية. لذلك ، ركضنا إلى الأمام قليلاً ، والآن كل شيء في محله.

الخوارزمية لحل المشكلة

لقد قررنا النموذج الرياضي للمشكلة المراد حلها. الآن نبدأ في النظر في الخوارزمية لحلها. فرعية $$$I$ من العائلة $$$S$ يمكن العثور عليها بسهولة ، على سبيل المثال ، من خلال مثل هذا الإجراء.

1. الخطوة 0. ترتيب دفعات من المجموعة $$$P$ بترتيب تصاعدي لتواريخها. نحن نعتقد أن جميع الأطراف لا يتم تمييزها على أنها تمت مشاهدتها.
2. الخطوة 1. ابحث عن الحفلة ذات التاريخ الأصغر من الأطراف التي لم يتم عرضها بعد.
3. الخطوة 2. بالنسبة إلى الطرف الذي تم العثور عليه ، والانتقال إلى اليمين ، ندرجه في المجموعة الفرعية $$$I$ جميع الأطراف التي تختلف تواريخها عن التواريخ الحالية بنسبة لا تزيد عن $$$C$ أيام. جميع الدفعات المدرجة في المجموعة $$$I$ بمناسبة كما ينظر إليها.
4. الخطوة 3. إذا ، عند الانتقال إلى اليمين ، لا يمكن تضمين الدفعة التالية في $$$I$ ، ثم انتقل إلى الخطوة 1.

مشكلة تغطية مجموعة $$$NP$ - صعب ، مما يعني أنه لا يوجد حل سريع (مع وقت تشغيل يساوي كثير الحدود من بيانات الإدخال) وخوارزمية دقيقة. لذلك ، لحل مشكلة تغطية المجموعة ، تم اختيار خوارزمية سريعة الجشع ، والتي بالطبع ليست دقيقة ، ولكن لها المزايا التالية:

• بالنسبة للمشاكل ذات البعد الصغير (وهذه هي حالتنا فقط) ، فهي تحسب الحلول القريبة بدرجة كافية إلى الحد الأمثل. مع نمو حجم المشكلة ، تتدهور جودة الحل ، ولكن لا يزال بطيئًا إلى حد ما ؛
• سهل التنفيذ
• سريع ، لأن تقدير وقت التشغيل هو $$$يا (مليون) دولا$ .

تحدد الخوارزمية الجشعة مجموعات تسترشد بالقاعدة التالية: في كل مرحلة ، يتم اختيار مجموعة تغطي الحد الأقصى لعدد العناصر التي لم تتم تغطيتها بعد. يمكن العثور هنا على وصف تفصيلي للخوارزمية ورمزها الزائف . يكون تنفيذ الخوارزمية بلغة 1C في المفسد أقل (حول سبب بدء تطبيقه باللغة "الصفراء" في الفصل التالي).


بطبيعة الحال ، فإن الأمثلية مثل هذه الخوارزمية هو أمر غير وارد - الاستدلال ، ليقول شيئا. يمكنك الخروج بمثل هذه الأمثلة التي قد تكون خاطئة مثل هذه الخوارزمية. تنشأ هذه الأخطاء عندما نجد ، في بعض التكرار ، عدة مجموعات لها نفس العدد من العناصر وتختار المجموعة الأولى التي تظهر ، لأن الاستراتيجية جشعة: لقد أخذت أول ما لفت انتباهي و "الجشع" راضٍ.

قد يكون هذا الخيار قد يؤدي إلى نتائج دون المستوى الأمثل عند التكرار اللاحق. لكن دقة مثل هذه الخوارزمية البسيطة لا تزال جيدة في معظم الحالات. إذا كنت ترغب في الحصول على حل للمشكلة بشكل أكثر دقة ، فأنت بحاجة إلى استخدام خوارزميات أكثر تعقيدًا ، على سبيل المثال ، كما هو الحال في العمل : خوارزمية الجشع الاحتمالية ، خوارزمية مستعمرة النمل ، إلخ. يمكن العثور على نتائج مقارنة هذه الخوارزميات على البيانات العشوائية التي تم إنشاؤها في العمل.

تنفيذ وتنفيذ الخوارزمية

تم تنفيذ هذه الخوارزمية بلغة 1C وتم تضمينها في معالجة خارجية تسمى "ضغط المخلفات" ، والتي كانت متصلة بنظام WMS . لم نطبق الخوارزمية في C ++ ونستخدمها من مكون أصلي خارجي ، والذي سيكون أكثر صحة ، لأن سرعة كود C ++ هي عدة مرات وفي بعض الأمثلة أسرع بعشر مرات من سرعة الكود المماثل في 1C . في 1C ، تم تنفيذ الخوارزمية لتوفير وقت التطوير وسهولة التصحيح على قاعدة عمل العميل. يظهر نتيجة الخوارزمية في الشكل 6.


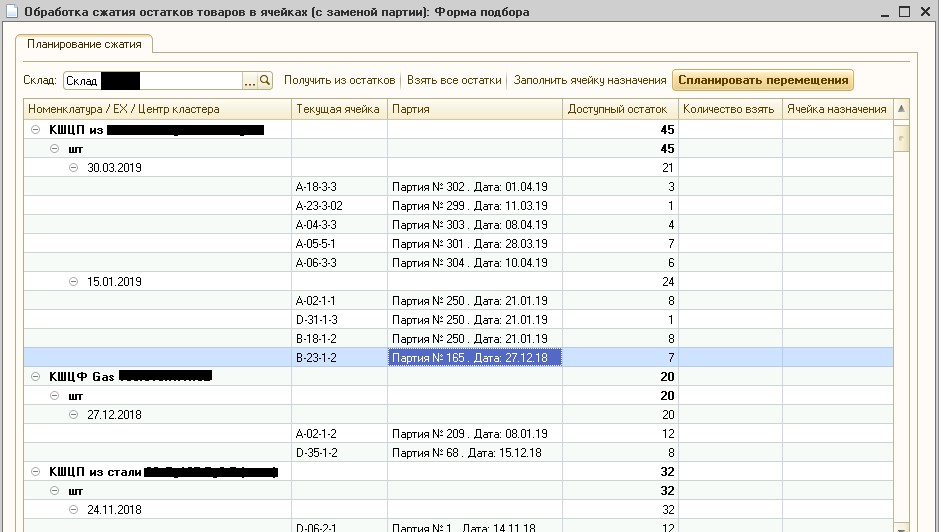الشكل 6. معالجة ضغط المخلفات

يوضح الشكل 6 أنه في المستودع المشار إليه ، تم تقسيم المخزون الحالي للبضائع في خلايا التخزين إلى مجموعات ، حيث تختلف تواريخ الشحنات بما لا يزيد عن 30 يومًا. نظرًا لأن العميل يصنع ويخزن صمامات الكرة المعدنية مع مدة صلاحية طويلة لسنوات ، يمكن إهمال فرق التاريخ هذا. لاحظ أن هذه المعالجة تستخدم حاليًا في الإنتاج بشكل منهجي ، وأن مشغلي WMS يؤكدون على الجودة الجيدة للتجميع الدفعي.

الاستنتاجات واستمر

تتمثل التجربة الرئيسية التي اكتسبناها من حل هذه المشكلة العملية في تأكيد فعالية استخدام النموذج: Mat. بيان المهمة $$$\ rightarrow$ حصيرة الشهيرة. النموذج $$$\ rightarrow$ الخوارزمية الشهيرة $$$\ rightarrow$ خوارزمية مع الأخذ بعين الاعتبار تفاصيل المهمة. هناك بالفعل أكثر من 300 عام من التحسين المنفصل ، وخلال هذه الفترة تمكن الأشخاص من التفكير في الكثير من المشاكل واكتساب الكثير من الخبرة في حلها. بادئ ذي بدء ، من المستحسن اللجوء إلى هذه التجربة ، وعندها فقط تبدأ في إعادة اختراع دراجتك.

من المهم أيضًا أن نقول إن حل مشكلة التكتل يمكن اعتباره غير منفصل عن حل مشكلة ضغط ما تبقى من الأطراف ، ولكن لحل هذه المشاكل معًا. أي لتحديد قسم من الأطراف في مجموعات من شأنه أن يعطي أفضل ضغط. لكن تم حل حل هذه المشكلات للأسباب التالية:

• ميزانية محدودة لتطوير الخوارزمية. تطوير مثل هذه الخوارزمية العامة ، وبالتالي أكثر تعقيدًا سيستغرق وقتًا أطول.
• تعقيد تصحيح الأخطاء والاختبار. سيكون من الصعب اختبار الخوارزمية العامة وتصحيحها في مرحلة القبول ، وسيكون الخلل فيها أكثر صعوبة ويطول التصحيح في العملية في الوقت الفعلي. على سبيل المثال ، حدث خطأ وليس من الواضح أين يجب الحفر: اللباد تسقيف نحو التجميع ، اللباد التسقيف نحو الضغط؟
• الشفافية وسهولة الإدارة. الفصل بين المهمتين يجعل عملية الضغط أكثر شفافية ، وبالتالي أكثر سهولة بالنسبة للمستخدمين النهائيين - مشغلي WMS. يمكنهم إزالة بعض الخلايا من الضغط أو تحرير الكمية القابلة للضغط لسبب ما.

في المقالة التالية ، سنستمر في مناقشة خوارزميات التحسين وننظر في الخوارزمية الأكثر إثارة للاهتمام والأكثر تعقيدًا: الخوارزمية المثلى لـ "ضغط" المخلفات في الخلايا ، والتي تستخدم مدخلات من خوارزمية تجميع الدُفعات كمدخلات.

أعدت مقالا
رومان شانجين ، مبرمج ، قسم المشاريع ،
أول شركة BIT ، تشيليابينسك