
في المقالة ، سنصف كيف قمنا بتطوير خوارزمية للضغط الأمثل للبضائع المتبقية في الخلايا. سنخبرك بكيفية اختيار metaheuristics اللازمة لبيئة حديقة حيوان الإطار: البحث في المحرمات ، الخوارزمية الجينية ، مستعمرة النمل ، إلخ.
سنقوم بإجراء تجربة حسابية لتحليل وقت التشغيل ودقة الخوارزمية. نحن نلخص ونلخص التجربة القيمة المكتسبة في حل مشكلة تحسين وتنفيذ "التقنيات الذكية" في العمليات التجارية للعميل.
ستكون هذه المقالة مفيدة لأولئك الذين يطبقون التقنيات الذكية ، ويعملون في المستودعات أو صناعة لوجستيات الإنتاج ، فضلاً عن المبرمجين المهتمين بتطبيقات الرياضيات في الأعمال وتحسين العمليات في المؤسسة.
الجزء التمهيدي
يستمر هذا المنشور في سلسلة المقالات التي نشارك فيها تجربتنا الناجحة في تنفيذ خوارزميات التحسين في عمليات المستودعات. المنشورات السابقة:
كيفية قراءة مقال. إذا قرأت المقالات السابقة ، فيمكنك المتابعة فورًا إلى الفصل "تطوير خوارزمية لحل المشكلة" ، إن لم يكن ، ثم وصف المشكلة التي يتعين حلها في المفسد أدناه.
وصف المشكلة المطلوب حلها في مستودع العميلعنق الزجاجة عملية
في عام 2018 ، قمنا بعمل مشروع لإدخال نظام
WMS في مستودع شركة LD Trading House في تشيليابينسك. عرض المنتج "1C-Logistics: Warehouse Management 3" لمدة 20 وظيفة: مشغلي
WMS ، وأصحاب المتاجر ، وسائقي الرافعات الشوكية. تبلغ مساحة المستودع حوالي 4 آلاف متر مربع ، وعدد الخلايا هو 5000 وعدد SKU 4500. يتم تخزين الصمامات الكروية الخاصة بإنتاجنا ذي الأحجام المختلفة من 1 كجم إلى 400 كجم في المستودع. يتم تخزين المخزونات في المستودع في سياق الدُفعات بسبب الحاجة إلى اختيار البضائع وفقًا لـ FIFO والمواصفات "المضمنة" الخاصة بوضع المنتج (شرح أدناه).
عند تصميم مخططات الأتمتة لعمليات المستودعات ، واجهنا المشكلة الحالية المتمثلة في التخزين غير الأمثل للمخزونات. يحتوي تكديس الرافعات وتخزينها ، كما قلنا بالفعل ، على تفاصيل "الصف". أي أن المنتجات الموجودة في الخلية مكدسة في صفوف واحدة فوق الأخرى ، وغالباً ما تكون القدرة على وضع قطعة على قطعة غائبة (تسقط فقط ، والوزن ليس صغيراً). لهذا السبب ، اتضح أنه لا يمكن وضع سوى تسمية واحدة من دفعة واحدة في وحدة تخزين من قطعة واحدة ، وإلا فإن التسمية القديمة لا يمكن سحبها من تحت واحدة جديدة دون "التجريف" للخلية بأكملها.
تصل المنتجات إلى المستودع يوميًا وكل وصول عبارة عن مجموعة منفصلة. إجمالًا ، نتيجة لشهر واحد من تشغيل المستودع ، يتم إنشاء 30 وحدة منفصلة ، على الرغم من حقيقة أنه ينبغي تخزين كل منها في خلية منفصلة. غالبًا ما يتم اختيار البضائع ليس في المنصات بأكملها ، ولكن في القطع ، ونتيجة لذلك ، في منطقة اختيار القطعة ، يتم ملاحظة الصورة التالية في العديد من الخلايا: في خلية يزيد حجمها عن 1 متر مكعب ، توجد عدة قطع من الرافعات تشغل أقل من 5-10٪ من حجم الخلية (انظر الشكل 1). ).
الشكل 1. صورة لعدة قطع في الخليةعلى وجه الاستخدام الأمثل لسعة التخزين. لتخيل حجم الكارثة ، يمكنني أن أذكر الأرقام: يوجد في المتوسط ما بين 100 و 300 خلية من هذه الخلايا مع بقايا هزيلة في فترات مختلفة من تشغيل المستودع. نظرًا لأن المستودع صغير نسبيًا ، في مواسم التحميل الخاصة بالمستودع ، يصبح هذا العامل "رقبة ضيقة" ويمنع إلى حد كبير عمليات القبول والشحن.
فكرة حل مشكلة
تم طرح الفكرة: لإحضار مجموعات الوحدات البنائية ذات التواريخ الأقرب إلى قطعة واحدة واحدة ووضع هذه الأرصدة مع مجموعة موحدة بشكل مضغوط معًا في خلية واحدة ، أو في عدة إذا لم تكن هناك مساحة كافية في واحدة لاستيعاب العدد الإجمالي للأرصدة. يظهر مثال على هذا "الضغط" في الشكل 2.
الشكل 2. مخطط ضغط الخليةيتيح لك ذلك تقليل مساحة المستودع المشغولة بشكل كبير ، والتي سيتم استخدامها للبضائع الموضوعة حديثًا. في حالة الحمولة الزائدة للمستودعات ، يعد هذا الإجراء ضروريًا للغاية ؛ وإلا ، فقد لا يكون هناك ببساطة مساحة حرة كافية لوضع سلع جديدة ، مما سيؤدي إلى توقف عمليات المستودعات الخاصة بالتنسيب والتجديد ، ونتيجة لذلك ، هناك سدادة للقبول والشحن. في السابق ، قبل تنفيذ نظام WMS ، تم إجراء مثل هذه العملية يدويًا ، والتي لم تكن فعالة ، لأن عملية العثور على بقايا مناسبة في الخلايا كانت طويلة جدًا. الآن ، مع إدخال أنظمة WMS ، قرروا أتمتة العملية وتسريعها وجعلها ذكية.
تنقسم عملية حل هذه المشكلة إلى مرحلتين:
- في المرحلة الأولى ، نجد أن مجموعات الأطراف القريبة في التاريخ مضغوطة (هذه هي المقالة الأولى لمهمة التفاني هذه) ؛
- في المرحلة الثانية ، نحسب كل مجموعة من مجموعات الدُفعات أكثر المواضع المدمجة لمخلفات المنتجات في الخلايا.
في المقالة الحالية ، ننتهي بوصف المرحلة الثانية من عملية الحل وننظر مباشرةً في خوارزمية التحسين نفسها.
تطوير خوارزمية لحل المشكلة
قبل الشروع في وصف مباشر لخوارزمية التحسين ، من الضروري أن نقول عن المعايير الرئيسية لتطوير مثل هذه الخوارزمية ، والتي تم تعيينها كجزء من المشروع لتنفيذ نظام
WMS .
- أولاً ، يجب أن تكون الخوارزمية سهلة الفهم . هذا مطلب طبيعي ، لأنه من المفترض أن الخوارزمية سيتم دعمها وتطويرها بواسطة خدمة تكنولوجيا المعلومات الخاصة بالعميل في المستقبل ، والتي غالبًا ما تكون بعيدة عن الدقة الحسابية والحكمة.
- ثانيا ، يجب أن تكون الخوارزمية سريعة . تشارك جميع البضائع الموجودة في المستودع تقريبًا في إجراء الضغط (هذا حوالي 3000 عنصر) ولكل منتج ، من الضروري حل مشكلة البعد التي تبلغ حوالي 10x100.
- ثالثًا ، يجب أن تحسب الخوارزمية الحلول القريبة من المستوى الأمثل .
- رابعًا ، يعد وقت تصميم الخوارزمية وتنفيذها وتصحيحها وتحليلها واختبارها داخليًا قليلًا نسبيًا. هذا مطلب أساسي ، لأن ميزانية المشروع ، بما في ذلك لهذه المهمة ، كانت محدودة .
تجدر الإشارة إلى أنه حتى الآن ، طور علماء الرياضيات العديد من الخوارزميات الفعالة لحل مشكلة مشكلة موقع مرفق ذي مصدر واحد. النظر في الأنواع الرئيسية من الخوارزميات المتاحة.
وتستند بعض الخوارزميات الأكثر كفاءة إلى نهج ما يسمى الاسترخاء لاغرانج. وكقاعدة عامة ، هذه خوارزميات معقدة إلى حد ما يصعب فهمها للشخص الذي لا ينغمس في التفاصيل الدقيقة للتحسين المنفصل. "الصندوق الأسود" مع خوارزميات معقدة ولكنها فعالة من الاسترخاء لاغرانج للعميل لا يناسب.
هناك metaheuristics فعالة جدا (ما هو metaheuristics تقرأ
هنا ، ما هي heuristics تقرأ
هنا ) ، على سبيل المثال ، الخوارزميات الجينية ، خوارزميات التلدين المحاكاة ، خوارزميات مستعمرة النمل ، خوارزميات البحث Tabu وغيرها (نظرة عامة على metaheuristics باللغة الروسية يمكن العثور عليها
هنا ). ولكن هذه الخوارزميات قد أرضت العميل بالفعل ، حيث:
- قادرة على حساب الحلول للمشاكل التي هي قريبة جدا من الأمثل.
- بسيطة بما يكفي لفهم ، مزيد من الدعم ، تصحيح وصقل.
- يمكنهم حساب بسرعة حل للمشكلة.
تقرر استخدام metaururistics. الآن بقي اختيار "إطار" واحد من بين "حديقة الحيوان" الكبيرة لعلم metaheuristics لحل مشكلة موقع التسهيلات ذات المصدر الواحد. بعد قراءة سلسلة من المقالات التي حللت فعالية مختلف metaururistics ، وقع اختيارنا على خوارزمية GRASP ، بالمقارنة مع metaheuristics الأخرى ، وأظهرت نتائج جيدة إلى حد ما على دقة الحلول المحسوبة للمشكلة ، كان واحدا من أسرع ، والأهم من ذلك ، كان أبسط ومنطق شفاف.
تم توضيح مخطط خوارزمية GRASP فيما يتعلق بمهمة مشكلة تحديد موقع مرفق ذي مصدر واحد بالتفصيل في
المقالة . المخطط العام للخوارزمية كما يلي.
- المرحلة 1. توليد بعض الحلول الممكنة لهذه المشكلة عن طريق خوارزمية عشوائية الجشع.
- المرحلة 2. تحسين الحل الناتج في المرحلة 1 باستخدام خوارزمية البحث المحلي في عدد من الأحياء.
- إذا تم استيفاء شرط الإيقاف ، فقم بإكمال الخوارزمية ، وإلا انتقل إلى الخطوة 1. الحل الذي يكون بأقل تكلفة إجمالية بين جميع الحلول الموجودة سيكون نتيجة الخوارزمية.
قد يكون شرط إيقاف الخوارزمية قيدًا بسيطًا على عدد التكرارات أو تقييدًا لعدد التكرارات دون أي تحسن في الحل.
رمز المخطط العام للخوارزميةint computeProblemSolution(int **aCellsData, int **aMatDist, int cellsNumb, int **aMatSolution, int **aMatAssignmentSolution) {
دعونا نفكر بمزيد من التفصيل في تشغيل
الخوارزمية العشوائية الجشعة في المرحلة الأولى. يُعتقد أنه في البداية لم يتم تحديد حاوية خلية واحدة.
- الخطوة 1. لكل خلية حاوية غير محددة حاليا ، يتم حساب القيمة F′i صيغة التكلفة
F′i= fracFiN،
حيث F′i - مقدار تكلفة اختيار الحاوية i والتكاليف الإجمالية لنقل البضائع من N الخلايا التي لم يتم إرفاقها بعد بأي حاوية في الحاوية i . مثل N يتم تحديد الخلايا بحيث لا يتجاوز إجمالي حجم البضائع فيها سعة الحاوية i . يتم تحديد الخلايا المانحة بالتسلسل للانتقال إلى حاوية حاوية i من أجل زيادة تكلفة نقل كمية البضائع إلى الحاوية i . يتم اختيار الخلية حتى يتم تجاوز سعة الحاوية. - الخطوة 2. مجموعة شكلت R حاويات ذات قيمة وظيفة F لا يتجاوز قيمة العتبة min(F) cdot(1+a) حيث دولا في حالتنا هو 0.2.
- الخطوة 3. عشوائيا من المجموعة R تم تحديد الحاوية i . N الخلايا التي تم اختيارها سابقا في الحاوية i في الخطوة 1 ، يتم تعيينهم أخيرًا إلى مثل هذه الحاوية ولا يشاركون أيضًا في حسابات الخوارزمية الجشعة.
- الخطوة 4. إذا تم تخصيص جميع الخلايا المانحة للحاويات ، فإن الخوارزمية الجشع تتوقف عن عملها ، وإلا فإنها تعود إلى الخطوة 1.
تحاول الخوارزمية العشوائية في كل تكرار بناء الحل بطريقة يكون هناك توازن بين جودة الحلول التي يبنيها ، وكذلك تنوعها. هذان الشرطان لبدء القرارات هما الشرطان الأساسيان للتشغيل الناجح للخوارزمية ، حيث:
- إذا كانت الحلول ذات نوعية رديئة ، فإن التحسين اللاحق في المرحلة 2 لن يحقق نتائج مهمة ، لأنه حتى في تحسين الحل السيئ ، فإننا في كثير من الأحيان نحصل على نفس الحلول ذات الجودة الرديئة ؛
- إذا كانت جميع الحلول جيدة ، ولكن نفس الحلول ، فإن إجراءات البحث المحلية سوف تتقارب مع نفس الحل ، فليس من الأمثل أن يكون الحل الأمثل. يسمى هذا التأثير بضرب الحد الأدنى المحلي ويجب تجنبه دائمًا.
خوارزمية عشوائية الجشع رمز void findGreedyRandomSolution(int **aCellsData, int **aMatDist, int cellsNumb, int **aMatSolutionIteration, int **aMatAssignmentSolutionIteration, int *aFreeContainersFitnessFunction, bool isOldSolution) {
بعد إنشاء حل "البدء" في المرحلة 1 ، تنتقل الخوارزمية إلى المرحلة 2 ، حيث يتم تنفيذ تحسين هذا الحل الموجود ، حيث يعني التحسين بطبيعة الحال تخفيض التكلفة الإجمالية. منطق
خوارزمية البحث المحلي في الخطوة 2 كالتالي.
- الخطوة 1. للحصول على الحل الحالي S يتم بناء جميع الحلول "المجاورة" وفقًا لنوع من الحي
 . N2 ، ... ،
. N2 ، ... ،  ولكل حل "مجاور" ، يتم حساب قيمة التكلفة الإجمالية.
ولكل حل "مجاور" ، يتم حساب قيمة التكلفة الإجمالية. - الخطوة 2. إذا كان من بين الحلول المجاورة كان هناك حل أفضل S1 من الحل الأصلي S ثم S يفترض المساواة S1 وتنتقل الخوارزمية إلى الخطوة 1. وإلا ، إذا لم يكن هناك حل أفضل من الحلول المجاورة من الحلول المجاورة ، فإن وجهة نظر الحي تتغير إلى حل جديد لم يتم بحثه مسبقًا ، وتنتقل الخوارزمية إلى الخطوة 1. إذا تم النظر في جميع طرق العرض المتاحة للمنطقة المجاورة ، ولكن فشلت إيجاد حل أفضل من الأصل ، الخوارزمية تنتهي عملها.
يتم تحديد طرق العرض المحيطة بالتتابع من المكدس التالي:

.
N2 .

.

.

. يتم تقسيم مشاهدات المنطقة المحيطة إلى نوعين: النوع الأول (الحي)

.
N2 .

) ، حيث لا تتغير العديد من الحاويات ، ولكن فقط خيارات إرفاق الخلايا المانحة تتغير ؛ النوع الثاني (الحي

.

) ، حيث لا تتغير خيارات ربط الخلايا بالحاويات فقط ، ولكن أيضًا العديد من الحاويات نفسها.
نحن نشير
|J| - عدد العناصر في المجموعة
J . توضح الأشكال أدناه خيارات
للأحياء من النوع الأول .
 التين. 7. الحي
التين. 7. الحي 
محيط

(أو
shift shift ): يحتوي على جميع الخيارات لحل المشكلة التي تختلف عن الأصل عن طريق تغيير مرفق خلية مانحة واحدة فقط في الحاوية. حجم الجوار لا أكثر
|J| خيارات.
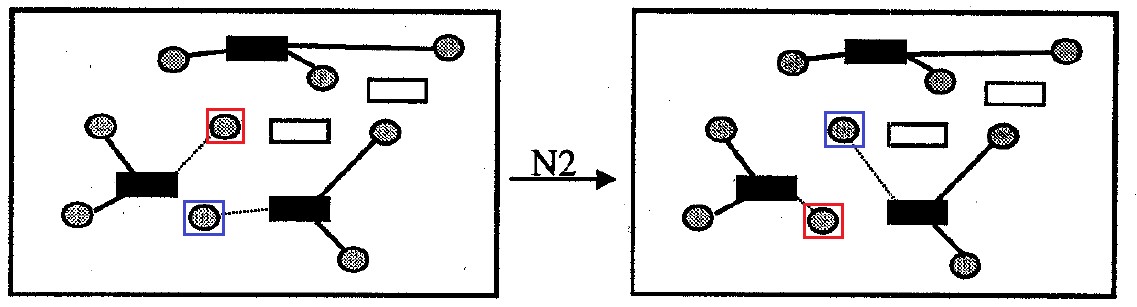 التين. 8. الحي N2
التين. 8. الحي N2رمز خوارزمية البحث المحلية في حي N1 void findBestSolutionInNeighborhoodN1(int **aCellsData, int **aMatDist, int cellsNumb, int **aMatSolutionIteration, int **aMatAssignmentSolutionIteration, int totalDemand, bool stayFeasible) {
محيط
N2 (أو حي
المبادلة ): يحتوي على جميع الخيارات لحل المشكلة التي تختلف عن المشكلة الأصلية عن طريق التبادل المتبادل للتعلق بالحاويات لزوج واحد من الخلايا المانحة. حجم الجوار لا أكثر
|J|2 خيارات.
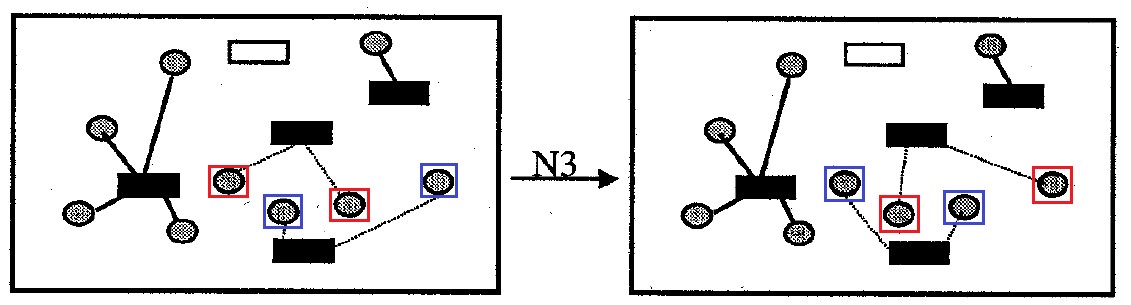 التين. 9. الحي
التين. 9. الحي 
محيط

: يحتوي على جميع الخيارات لحل المشكلة ، والتي تختلف عن الخيار الأصلي عن طريق الاستبدال المتبادل لمرفق جميع الخلايا لزوج واحد من الحاويات. حجم الجوار لا أكثر
|أنا| خيارات.
يعتبر النوع الثاني من الأحياء آلية "لتنويع" القرارات ، عندما يكون من المستحيل بالفعل الحصول على تحسينات من خلال البحث عن الأحياء "القريبة" من النوع الأول.
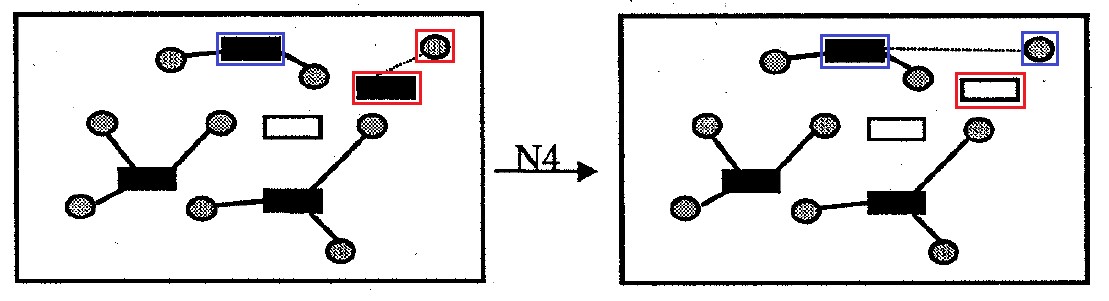 التين. 10. الحي
التين. 10. الحي 
محيط

: يحتوي على جميع الخيارات لحل المشكلة التي تختلف عن الأصل عن طريق إزالة خلية حاوية واحدة من الحل. يتم إرفاق الخلايا المانحة التي تم إرفاقها بهذه الحاوية التي تم إزالتها من الحل في حاويات أخرى من أجل تقليل مقدار تكاليف النقل وعقوبة تجاوز سعة الحاوية. حجم الجوار لا أكثر
|أنا| خيارات.
 التين. 11. الحي
التين. 11. الحي 
محيط

: يحتوي على جميع الخيارات لحل المشكلة التي تختلف عن الأصل عن طريق فصل الخلايا من حاوية واحدة وربط هذه الخلايا بحاوية فارغة أخرى لزوج واحد من الحاويات التعسفي. حجم الجوار لا أكثر
|I|2 خيارات.
يقول مؤلفو المقالة ، استنادًا إلى نتائج التجارب الحسابية ، إن الخيار الأفضل هو البحث أولاً عن الأحياء "القريبة" من النوع الأول ، ثم البحث عن الأحياء "البعيدة".
لاحظ أن واضعي المقالة يوصون بإجراء بحث في المنطقة المجاورة دون مراعاة القيود المفروضة على سعة كل حاوية. وبدلاً من ذلك ، إذا تم تجاوز سعة الحاوية ، فقم بإضافة بعض التكلفة الإيجابية للحل إلى مقدار "إيجابي" ، مما سيضعف من جاذبية هذا الحل مقارنة بالحلول الأخرى. يتم وضع التقييد الوحيد على إجمالي حجم الحاويات ، أي أن إجمالي حجم البضائع المنقولة من الخلايا المانحة يجب ألا يتجاوز إجمالي سعة الحاويات. تتم عملية إزالة القيود لأنه إذا تم أخذ القيود في الاعتبار ، فلن يحتوي الحي في كثير من الأحيان على حل واحد مقبول وستنتهي خوارزمية البحث المحلية من عملها فور بدايتها ، دون إجراء أي تحسينات. يوضح الشكل 12 مثالاً لعملية بحث محلية دون مراعاة القيود المفروضة على سعة كل حاوية.
التين. 12. أعمال البحث المحلي دون مراعاة القيود المفروضة على سعة كل حاويةفي هذا الشكل ، من المفترض أن بقايا الأحمر والأخضر من بعض الخلايا المانحة ليست مفيدة للانتقال إلى أي حاوية أخرى باستثناء الثانية. هذا يعني أن إجراء المزيد من التحسينات على الحل أمر مستحيل ، لأن أي حل ممكن ومجدي جديد للمشكلة ، حيث يتم احترام القيود المفروضة على السعة ، سيكون أسوأ من الأصل من حيث تكاليف النقل. كما ترون ، فإن الخوارزمية الخاصة بتكرارين تبني حلاً ممكنًا أفضل بكثير من الأصل ، على الرغم من أن التكرار الأول يبني حلاً غير صالح ذو سعة زائدة.
لاحظ أن هذا النهج المتمثل في إدخال "عقوبة" لعدم مقبولية الحل أمر شائع جدًا في التحسين المنفصل وغالبًا ما يستخدم في الخوارزميات مثل الخوارزميات الجينية ، والبحث في المحرمات ، إلخ.
بعد اكتمال خوارزمية البحث المحلية ، إذا كان الحل الذي تم العثور عليه لا يزال غير مقبول ، أي أنه تم تجاوز حدود سعة الحاوية في مكان ما ، يجب أن نجلب الحل الموجود في نموذج مقبول ، حيث يتم احترام جميع القيود المفروضة على سعة الحاوية. خوارزمية حل عدم مقبولية الحل هي كما يلي.
- الخطوة 1. إجراء بحث محلي على أحياء التحول والتبديل . في هذه الحالة ، يتم الانتقال فقط في تلك القرارات التي تقلل بدقة مقدار "الغرامة". إذا كان تخفيض العقوبة غير ممكن ، يتم اختيار حل بتكلفة إجمالية أقل. إذا لم يكن أي تحسين آخر من خلال البحث المحلي ممكنًا ، فانتقل إلى الخطوة 2 ، وإلا ، إذا كان الحل الناتج صالحًا ، فقم بإكمال الخوارزمية.
- الخطوة 2. إذا كان الحل لا يزال غير مقبول ، ثم من كل حاوية حيث كانت هناك سعة زائدة ، يتم فصل خلايا المانحين من أجل زيادة حجم البضائع حتى يتم تلبية قيود السعة. بالنسبة لهذه الخلايا المنفصلة ، يتم تكرار جميع خطوات الخوارزمية ، بدءًا من الأولى ، على الرغم من أن مجموعة الحاويات المحددة المتاحة وطريقة إرفاق الخلايا المتبقية بها ثابتة ولا يمكن تغييرها. لاحظ أن مثل هذه الخطوة 2 ، كما توضح التجربة الحسابية ، مطلوبة لتنفيذها بشكل نادر للغاية.
التجربة الحسابية وتحليل كفاءة الخوارزمية
تم تنفيذ خوارزمية GRASP من البداية في
C ++ ، حيث لم نعثر على الكود المصدري للخوارزمية الموضحة في
المقالة . تمت ترجمة رمز البرنامج باستخدام g ++ مع خيار التحسين -O2.
يتوفر رمز مشروع Visual Studio على
جيثب . الشيء الوحيد الذي طلبه العميل هو إزالة بعض إجراءات البحث المحلية الأكثر تعقيدًا لأسباب تتعلق بالملكية الفكرية والأسرار التجارية وما إلى ذلك.
في
المقالة التي تصف خوارزمية GRASP ، تم توضيح كفاءتها العالية ، حيث من المفترض أن الكفاءة بحسابها للحلول قريبة جدًا من المستوى الأمثل ، وأنها تعمل بسرعة كبيرة. من أجل التحقق من الفعالية الحقيقية لهذه الخوارزمية GRASP ، أجرينا تجربتنا الحسابية الخاصة. تم إنشاء بيانات إدخال المشكلة من قبلنا بشكل عشوائي مع توزيع موحد. تمت مقارنة الحلول المحسوبة بواسطة الخوارزمية مع الحلول المثالية ، والتي تم حسابها بواسطة الخوارزمية الدقيقة المقترحة في
المقالة . مصادر مثل هذه الخوارزمية الدقيقة متاحة بحرية على جيثب
بالرجوع إليها . يعني بُعد المهمة ، على سبيل المثال ، 10x100 أن لدينا 10 خلايا مانحة و 100 خلية حاوية.
تم إجراء العمليات الحسابية على جهاز كمبيوتر شخصي مع الخصائص التالية: وحدة المعالجة المركزية 2.50 جيجاهرتز ، Intel Core i5-3210M ، ذاكرة وصول عشوائي 8 جيجابايت ، نظام التشغيل Windows 10 (x64).
3. GRASP3, GRASP , . , GRASP , , 10100 0,5 . ,
.
, , , .
++ DLL,
1 Native. ,
1 1 . «1: 3» , . .
 .13. «» 1: 3
.13. «» 1: 3:
- : ( ) .
- , . . .
- , - , - , .
استنتاج
, .
- . : , , . - :
- , ;
- .
- ( ), , . «», - . , , . , , , - , .
- , ( ), . , , . , . . , .
- :
- .
- .
- . , .
- . , . , , , , .
- , . ( ) . , .
- .
, , . .
, . , « » .
, ERP, WMS, TMS .. . , . , , .
, ,
, .