دراسة نظام التحكم المغنطيسى المضنى

تم إنشاء هذه المادة في ضوء الدفاع السابق عن أعمال التأهيل النهائية للبكالوريوس ، مع مراعاة بعض التعليقات على عنصر التحكم. يتم إنشاء المادة كاحتياطي أولي لأطروحة الماجستير المحتملة حول نفس الموضوع.

أصبحت أنظمة الرفع المغنطيسي الحديثة تستخدم على نطاق واسع: قطارات الركاب عالية السرعة ، وعزل الآليات الحساسة للاهتزاز ، والمحامل المغناطيسية ، وترفيع المعدن المنصهر في أفران الحث ، وكذلك رفع قضبان المعدن. في الآونة الأخيرة ، يتم استخدام تأثير المغنطيسى أيضا في الأجهزة المنزلية.

ربما تم العثور على التطبيق الأكثر أهمية في القطارات مع نظام رفع على الموصلات الفائقة. ويرجع ذلك إلى مزايا مثل الموثوقية الأكبر (بسبب نقص الاحتكاك) ، وانخفاض استهلاك الطاقة نسبيًا ، والقدرة على تطوير السرعة العالية.

ومع ذلك ، بسبب المعادلات غير الخطية لحركة الكائن التي تصف دينامياتها ، من الصعب إعادة إنتاج عملية التحكم في الكائن. سيكون حول موقع (المسافة) للكائن بالنسبة إلى علامة الصفر.

باختصار ، يعد الإرتفاع المغنطيسي موقعًا ثابتًا لجسم ما على مسافة معينة في مجال الجاذبية ، عندما يتم ، كقاعدة عامة ، تعويض تسارع الجاذبية عن طريق تسارع الكائن ، الذي يتم إنشاؤه بواسطة حقل مغناطيسي. في هذه الحالة ، تنشأ قوة الرفع.

يتم تحقيق الإرتفاع المغنطيسي باستخدام diamagnetics ، وأنظمة التيار الدوامي والموصلات الفائقة ، وكذلك باستخدام آليات الحركة.

في المقالة الحالية (تحت القص) ، سننظر في التحكم المشروط لنظام الخطي للإرتفاع المغنطيسي ، وكذلك تطبيق التحكم المشروط لنموذج غير خطي للنظام.

نموذج رياضي

النظر في مخطط المغنطيسى البسيط.

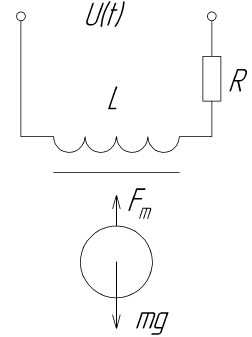
يُظهر هذا الرسم البياني مغناطيسًا كهربائيًا يتفاعل مع المجال المغناطيسي لكائن التحكم ، وهو مغناطيس دائم الكرة. من خلال التغيير في القوة الجذابة للمغناطيس الكهربائي ، سيتم تحقيق تأثير الرفع.

في العمل النهائي ، تم النظر في كائن من الدرجة الثانية ، حيث لم يتم تضمين عنصر مهم ، التيار في الملف ، في متجه الحالة. هذه المرة سيتم تقديم هذا المكون.

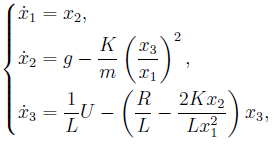
حيث $$$x_1$ - موضع الكائن ؛

$$$x_2 دولا$ - معدل تغيير موضع الكائن ؛

$$$g$ - تسارع الجاذبية.

$$$K$ ثابت

$$$م دولا$ - كتلة الجسم الكرة ؛

$$$x_3 دولا$ - الحالية في الملف.

$$$L$ - لفائف الحث.

$$$يو$ - مساهمة الجهد ؛

$$$R$ - المقاومة النشطة للملف.

يتم تلخيص قيم بعض المتغيرات أعلاه في جدول.

للحصول على نموذج خطي ، ينبغي للمرء أن خطي نظام المعادلات.

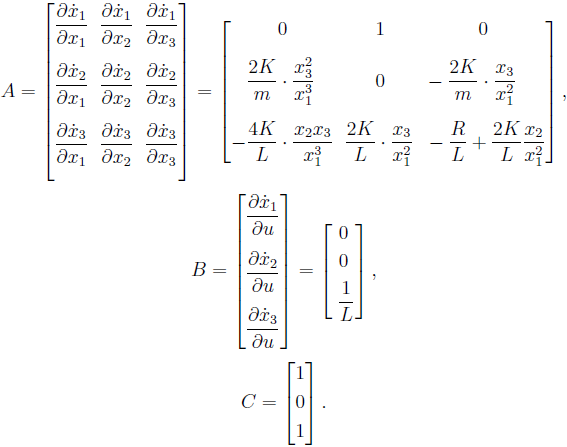
عرض المصفوفة $$$C$ يمكن تبريره من خلال حقيقة أن هذه المتجهات متجه الحالة كموقف ( $$$x_1$ ) والحالية ( $$$x_3 دولا$ ).

في هذا النموذج ، لا تزال المصفوفات الناتجة غير مناسبة للنمذجة. للقيام بذلك ، وضعنا الشروط الأولية.

$$

$$x_1 ^ {\ left \ {0 \ right \}} = 0.005 ، ~ x_2 ^ {\ left \ {0 \ right \}} = 0.$$

$$

$$g - \ frac {K (x_3 ^ {\ left \ {0 \ right \}}) ^ 2} {m (x_1 ^ {\ left \ {0 \ right \}}) ^ 2} = 0$$

$$

$$x_3 ^ {\ left \ {0 \ right \}} = \ sqrt {\ frac {gm} {K}} x_1 ^ {\ left \ {0 \ right \}} = 0.063 ~ \ text {A}.$$

استبدال الآن البيانات التي تم الحصول عليها و $$$x_3 ^ {\ left \ {0 \ right \}}$ للعثور على قيمة إشارة الدخل في الوقت الأولي:

$$

$$U ^ {\ left \ {0 \ right \}} = \ left (R - \ frac {2Kx_2 ^ {\ left \ {0 \ right \}}} {(x_1 ^ {\ left \ {0 \ right \ }}) ^ 2} \ right) x_3 ^ {\ left \ {0 \ right \}} = Rx_3 ^ {\ left \ {0 \ right \}} = 1.95 ~ \ text {B}.$$

تصميم

الآن يمكنك توليف التحكم. للبحث ، تم اختيار حزمة Matlab. فيما يلي رمز الحصول على معاملات المنظم حسب الحالة:

g = 9.81; K = 0.659*10^-3; m = 0.0106; L = 0.109; R = 31.1; x10 = 0.005; x20 = 0; x30 = sqrt(g*m/K)*x10; u = R*x30; A = [0 1 0; 2*K*x30^2/(m*x10^3) 0 -2*K*x30/(m*x10^2); -4*K*x20*x30/(L*x10^3) 2*K*x30/(L*x10^2) -R/L+2*K*x20/(L*x10^2)]; B = [0; 0; 1/L]; C = [1 0 0]; W = ctrb(A, B); %   detW = det(W); poles = [-10 -10 -10]; %  K = acker(A, B, poles); %  system = ss(A - B*K, B, C, 0); %   figure(1) step(system) %   km = 1/dcgain(system); %   system_m = ss(A - B*K, B*km, C, 0); figure(2) step(system_m) 

لفهم ما إذا كان من الممكن توليف التحكم في النظام الناتج ، فأنت بحاجة إلى معرفة مصفوفة إمكانية التحكم ، من خلال المحدد الذي تم التوصل إلى الاستنتاج:

 >> detW detW = -7.5351e+07 

المحدد هو غير صفري ؛ لذلك ، يمكن التحكم في النظام الخطي.

أقطاب المتجهات عبارة عن متجه يحتوي على الأقطاب المطلوبة للنظام المغنطيسي للإرتفاع المغنطيسي.

عند تطبيق تأثير الاختبار في شكل خطوة واحدة ، نحصل على النتيجة التالية:

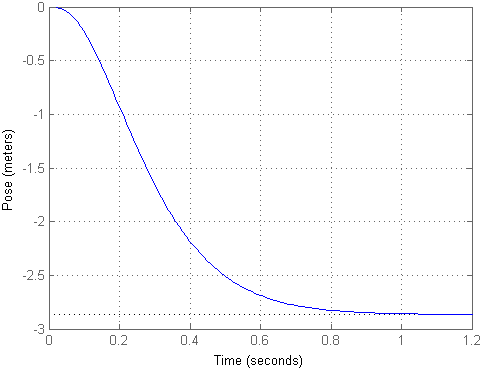
كما ترون ، اتضح أن الكائن قد طار مسافة كبيرة إلى حد ما مع تأثير ضئيل ، على الرغم من أنه ظل في نفس الموقف. لكي يتوافق المدخلات مع المخرجات ، يمكننا حساب عامل التحجيم km ومضاعفة إشارة الدخل به ، والتي تحققت في النموذج الثاني. ثم ستبدو عملية الانتقال هكذا:

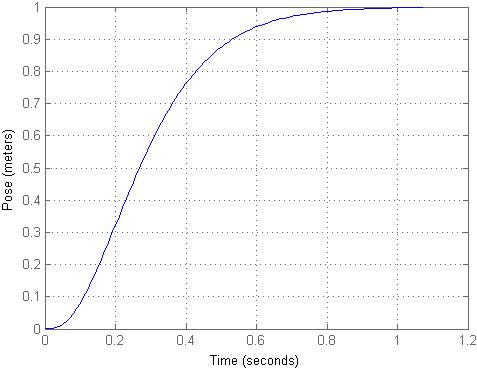
الموقف الناتج لا يزال كبيرا لمثل هذا التثبيت. الآن ، دعنا نتجاهل التيار ونذهب مباشرةً إلى طرز Simulink ، حيث نفكر في الأشياء المتبقية.

نقيس إشارة الدخل حتى يتم تمثيل قيم المخرجات بشكل ملائم بالسنتيمترات. نحن نطبق العديد من إجراءات الاختبار على المدخلات للتحقق من كيفية ظهور العابرين في النظام ، وكذلك التيار المتدفق.

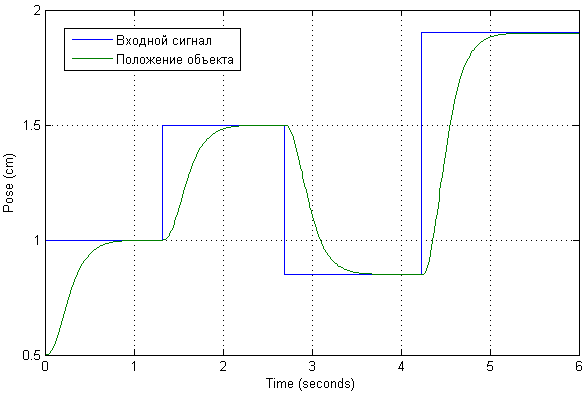
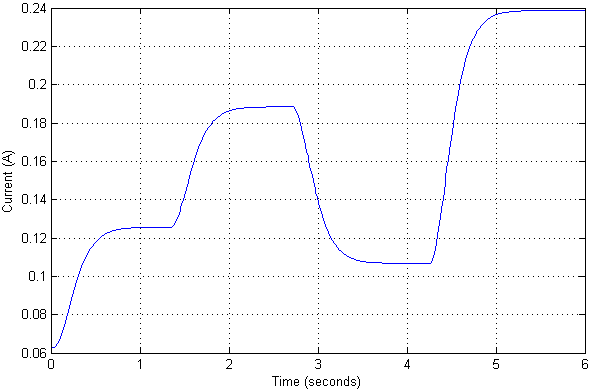
اتضح أن القيمة الحالية في مثل هذه المواضع من الكائن ليست كبيرة جدا. العابرون أنفسهم في موقفهم هم aperiodic في الطبيعة ، دون تجاوز الخطأ وخطأ ثابت. في الواقع ، تم ضبطه من قبل أعمدة النظام المعدل.

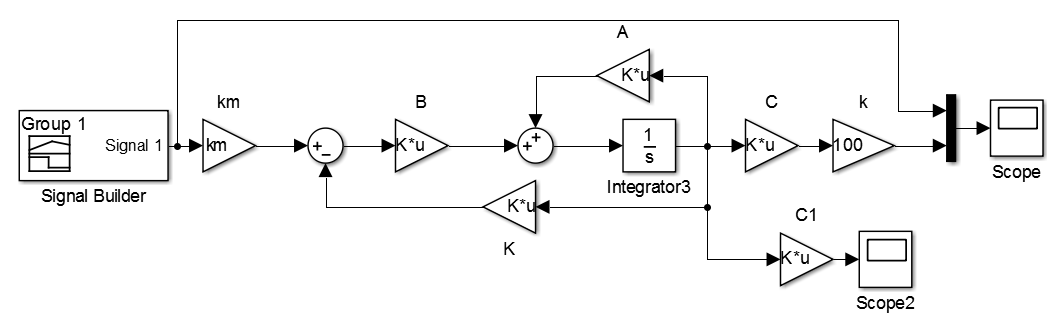
ومع ذلك ، قد لا يعمل هذا التقريب في نقطة التشغيل بشكل صحيح مع النموذج غير الخطي الأصلي. تحقق من ذلك. فيما يلي نموذج للنظام غير الخطي مزود بوحدة تحكم متصلة.

هذه هي النسخة النهائية المتبقية بعد كل التجارب. تم وضع قيود على جهد الدخل (0-12V) وموضع الكائن نفسه (0-4 سم). تم استبعاد المكون الثاني للجهة المنظمة ، حيث كانت عملية الانتقال غير مستقرة:

بعد التغييرات التي تطرأ على الدائرة ، يبدو المارة الآن كما يلي:

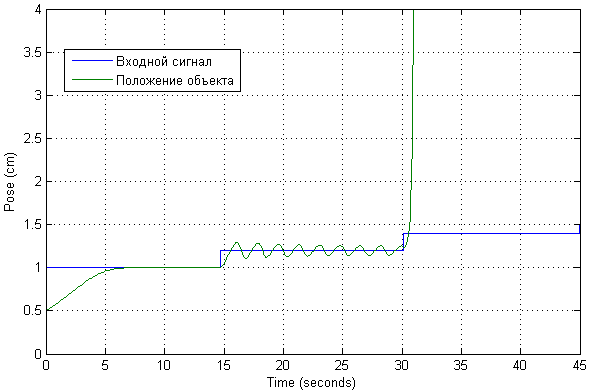
تم فحص النطاق المحتمل لتشغيل مثل هذا النظام على الفور. يمكنك أن ترى أن الموضع المطلوب سيتحقق بانحرافات طفيفة من نقطة البداية. في هذه الحالة ، يكون مظهر من مظاهر التذبذب الكبير ممكنًا.

في هذه الحالة ، تكون القيمة الحالية كما يلي:

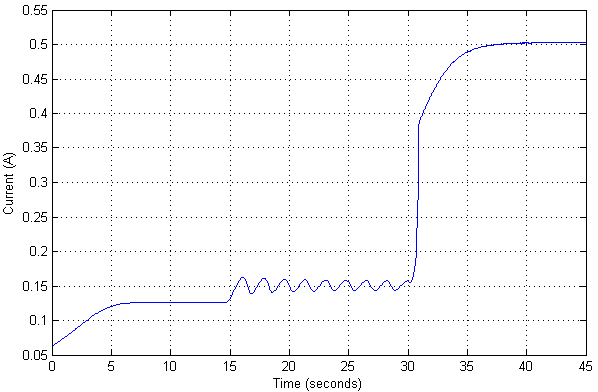
نظرًا لوجود فحص بالفعل لنموذج غير خطي لكائن ما ، يمكنك أيضًا الاطلاع على القيمة القصوى لقيمة الكائن التي لا يزال يفقد الاستقرار عندها.

بعد النمذجة مع إشارات الإدخال المختلفة ، لوحظ أن النموذج الخطي هو جيد جدا. سنقوم هنا بإظهار العابرين وفقًا لإشارة الدخل الأولية التي زادت بنسبة 10 مرات.

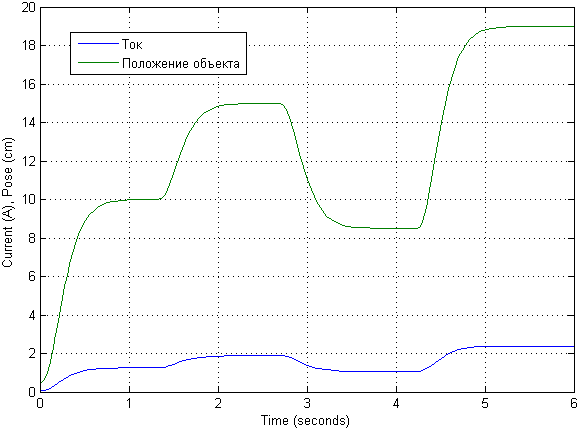
قد يبدو النموذج الرياضي نفسه مختلفًا بعض الشيء. الوصف مأخوذ من وصف النموذج الرياضي.

استنتاج

إن التحكم المشروط لهذا النموذج غير الخطي لنظام الرفع المغناطيسي ليس مناسبًا على الإطلاق لأي احتياجات عملية. يجب مراعاة التطبيقات الأخرى لنظام الرفع المغناطيسي.

بالنسبة لعمل البكالوريوس ، نفذ المؤلف تثبيتًا بسيطًا على الرفع ، والذي سيتم وصفه بشكل منفصل في المستقبل.