العثور على كشف الأشياء غير الخاضعة للرقابة

واحدة من أهم المهام في التعلم الآلي هي اكتشاف الأشياء. في الآونة الأخيرة ، تم نشر سلسلة من خوارزميات التعلم الآلي القائمة على التعلم العميق للكشف عن الكائنات. تشغل هذه الخوارزميات أحد الأماكن المركزية في تطبيقات رؤية الكمبيوتر العملية ، ولا سيما سيارات القيادة الذاتية الشائعة حاليًا. ولكن كل هذه الأساليب هي طرق التدريس مع المعلم ، أي يحتاجون إلى مجموعة بيانات ضخمة (مجموعة بيانات ضخمة). بطبيعة الحال ، هناك رغبة في الحصول على نموذج قادر على التعلم من البيانات "الأولية" (غير المخصصة). لقد حاولت تحليل الأساليب الحالية وأشير أيضًا إلى الطرق الممكنة لتطورها. أسأل كل من يرغب بالرحمة تحت القات ، سيكون الأمر ممتعًا.

الوضع الحالي للسؤال

بطبيعة الحال ، كانت صياغة هذه المشكلة موجودة لفترة طويلة (تقريبًا من الأيام الأولى لوجود التعلم الآلي) وهناك عدد كاف من الأعمال حول هذا الموضوع. على سبيل المثال ، واحد من الكائنات المفضلة غير المكشوف غير الثابت للكشف عن الكائنات مع الشبكات العصبية التلافيفية . باختصار ، يتدرب المؤلفون على أداة Variable Auto Encoder (VAE) ، لكن هذا النهج يثير عددًا من الأسئلة بالنسبة لي.

قليلا من الفلسفة

إذن ما هو الكائن في الصورة؟ للإجابة على هذا السؤال ، يجب علينا الإجابة على السؤال - لماذا نقسم العالم إلى أشياء؟ بعد قليل من التفكير في هذا السؤال ، كان لدي إجابة واحدة فقط على هذا السؤال (أنا لا أقول أنه لا يوجد غيرها ، لم أجدها فقط) - نحن نحاول إيجاد تمثيل للعالم يسهل علينا فهم مقدار المعلومات اللازمة لوصف العالم والتحكم فيه في سياق المهمة الحالية. على سبيل المثال ، بالنسبة لمهمة تصنيف الصور (التي يتم صياغتها بشكل غير صحيح بشكل عام - هناك صور نادرة جدًا لها كائن واحد. بمعنى ، نحن نحل المشكلة ليس ما هو موضح في الصورة ، ولكن أي كائن "رئيسي") ، نحتاج فقط إلى القول إن الصورة "سيارة" ، بدوره ، لمهمة اكتشاف الأشياء ، نريد أن نعرف الأشياء الموجودة "المثيرة للاهتمام" (نحن لسنا مهتمين بجميع الأوراق من الأشجار الموجودة في الصورة) ، وحيث توجد ، لمهمة وصف المشهد ، نريد الحصول على اسم العملية "المثيرة للاهتمام" يحدث هناك ، على سبيل المثال ، "غروب الشمس" ، إلخ.

اتضح أن الكائنات هي تمثيل مناسب للبيانات. ما الخصائص التي يجب أن يكون لها هذا التمثيل؟ يجب أن يحتوي العرض على أكبر قدر ممكن من المعلومات الكاملة حول الصورة. أي وجود وصف كائن ، نريد أن نكون قادرين على استعادة الصورة الأصلية بدرجة الدقة اللازمة.

كيف يمكن التعبير عن ذلك رياضيا؟ تخيل أن الصورة عبارة عن إدراك للمتغير العشوائي X ، وأن التمثيل سيكون إدراكًا لمتغير عشوائي Y. في ضوء ما ذكر أعلاه ، نريد أن يحتوي Y على أكبر قدر ممكن من المعلومات حول X. وبطبيعة الحال ، للقيام بذلك ، استخدم مفهوم المعلومات المتبادلة.

نماذج التعلم الآلي للحصول على أقصى قدر من المعلومات

يمكن اعتبار اكتشاف الكائنات نموذجًا عامًا ، يستقبل صورة عند الإدخال $$$x$، والإخراج هو تمثيل كائن من الصورة $$$ذ$.

لنتذكر الآن صيغة حساب المعلومات المتبادلة:

$$

$$I (x، y) = \ int p (x، y) log \ frac {p (x، y)} {p (x) p (y)} dxdy$$

حيث $$$p (x، y)$توزيع كثافة المفصل كذلك $$$p (x) ، p (y)$هامشية.

لن أعمق هنا لماذا تبدو هذه الصيغة هكذا ، لكننا نعتقد أنه داخليا من المنطقي للغاية. بالمناسبة ، استنادًا إلى الاعتبارات الموضحة ، ليس من الضروري اختيار معلومات متبادلة تمامًا ، يمكن أن تكون أي "معلومات" أخرى ، لكننا سنعود إلى هذا أقرب إلى النهاية.

لاحظوا بشكل خاص (أو أولئك الذين قرأوا كتبًا عن نظرية المعلومات) أن المعلومات المتبادلة ليست أكثر من اختلاف Kullback-Lebler بين التوزيع المشترك وعمل التوزيع الهامشي. يظهر هنا تعقيد بسيط - أي شخص قرأ على الأقل كتابين عن التعلم الآلي يعرف أنه إذا كان لدينا عينات من توزيعتين فقط (على سبيل المثال ، لا نعرف وظائف التوزيع) ، فهذا لا يعني حتى تحسينها ، ولكن حتى تقييم تباعد Kullback ، مهمة ليبلر غير تافهة للغاية. علاوة على ذلك ، وُلدت شبكات GAN الحبيبة الخاصة بنا على وجه التحديد لهذا السبب.

لحسن الحظ ، فإن الفكرة الرائعة المتمثلة في استخدام الحدود الأقل تباينًا الموضحة في On Variational Bounds of Mutual Information تأتي في عوننا. يمكن تمثيل المعلومات المتبادلة على النحو التالي:

$$

$$I (x، y) = \ int p (x) dx \ int p (y | x) log [q (x | y)] dxdy + \ int p (y) dy \ int p (x | y) log (\ frac {p (x | y)} {q (x | y)} dxdy$$

أو

$$

$$I (x، y) = \ int p (x) dx \ int p (y | x) log [q (x | y)] dxdy + KL [p (x | y) || q (x | y) ]$$

حيث $$$p (y | x)$- توزيع التمثيل لصورة معينة ، محدد من شبكتنا العصبية ومن هذا التوزيع ، يمكننا أخذ عينات ، لكننا لسنا بحاجة إلى أن نكون قادرين على تقدير كثافة أو احتمال عينة معينة (والتي عادة ما تكون نموذجية للعديد من النماذج التوليدية). $$$q (x | y)$هي دالة كثافة معينة محددة بواسطة الشبكة العصبية الثانية (في الحالة الأكثر شيوعًا ، نحتاج إلى شبكتين عصبيتين ، على الرغم من أنه في بعض الحالات يمكن تمثيلهما بواسطة الأولى) ، يجب هنا أن نكون قادرين على حساب احتمالات العينات الناتجة.

قيمة $$$LVB (x، y) = \ int p (x) dx \ int p (y | x) log [q (x | y)] dxdy$دعا السفلى المتغير.

الآن يمكننا حل النهج المتبع في مشكلتنا ، ألا وهو زيادة ليس المعلومات المتبادلة نفسها ، ولكن حدودها الأقل تنوعًا. إذا كان التوزيع $$$q (x | y)$تم اختيارها بشكل صحيح ، ثم عند الحد الأقصى من الحدود التبادلية والمعلومات المتبادلة سوف تتزامن ، ولكن في الحالة العملية (عند التوزيع $$$q (x | y)$لا أستطيع أن أتخيل بالضبط $$$p (x | y)$، ولكن تتكون من عائلة كبيرة إلى حد ما من الوظائف) ستكون قريبة جدًا ، مما يناسبنا أيضًا.

إذا كان شخص ما لا يعرف كيف يعمل هذا ، أنصحك أن تفكر بعناية في خوارزمية EM. هنا حالة مماثلة تماما.

ما الذي يحدث هنا؟ في الواقع ، حصلنا على وظيفة لتدريب التشفير التلقائي. إذا كانت Y هي نتيجة إخراج شبكة عصبية مع بعض الصور عند الإدخال ، فهذا يعني ذلك $$$p (y | x) = \ delta (enc (x))$حيث $$$enc (x)$وظيفة تحويل الشبكة العصبية. وتقريب التوزيع العكسي من قبل غاوسي ، أي $$$log [q (x | y)] = (x - dec (y)) ^ 2 - 2 * log (sigma)$حصلنا على:

$$

$$LVB (x، y) = \ int p (x) (x-dec (enc (x))) ^ 2dx + C$$

وهذه ميزة كلاسيكية للتشفير التلقائي.

التشفير التلقائي لا يكفي

أعتقد أن الكثيرين يرغبون بالفعل في تدريب جهاز التشفير التلقائي ، ونأمل أن يكون في طبقته المخفية خلايا عصبية تستجيب لكائنات محددة. بشكل عام ، هناك تأكيد لشيء مشابه واتضح بناء ميزات عالية المستوى باستخدام التعلم واسع النطاق بدون إشراف . ولكن لا يزال هذا غير عملي تماما. وقد لاحظ الأشخاص الأكثر اهتمامًا بالفعل أن مؤلفي هذه المقالة استخدموا التنظيم - فقد أضافوا مصطلحًا يوفر تباينًا في الطبقة المخفية ، وكتبوا باللونين الأبيض والأسود أن لا شيء من هذا القبيل يحدث بدون هذا المصطلح.

هل مبدأ تعظيم المعلومات المتبادلة كافٍ لتتعلم فكرة "ملائمة"؟ من الواضح ، لا ، لأنه يمكننا اختيار Y تساوي X (أي ، استخدام الصورة نفسها كتمثيل لها) أو أي تحول جذري ، تنتقل المعلومات المتبادلة إلى ما لا نهاية في هذه الحالة. لا يمكن أن يكون هناك أكثر من هذه القيمة ، لكن كما نعلم ، هذه فكرة سيئة للغاية.

نحتاج إلى معيار إضافي لـ "راحة" العرض التقديمي. واضع مؤلفو المقالة المذكورة أعلاه كذبة "راحة". هذا نوع من إدراك الفرضية القائلة بأنه يجب أن يكون هناك "أشياء مهمة" قليلة في الصورة. لكننا سنذهب إلى أبعد من ذلك - لا نريد فقط معرفة حقيقة أن مثل هذا الشيء موجود في الصورة ، ولكن نريد أيضًا معرفة مكانه ومدى تداخله وما إلى ذلك. السؤال الذي يطرح نفسه ، هو كيفية جعل الشبكة العصبية تفسر مخرجات الخلايا العصبية مثل ، على سبيل المثال ، تنسيق الكائن؟ الجواب واضح - يجب استخدام الإخراج من هذه الخلايا العصبية على وجه التحديد لهذا الغرض. وهذا يعني ، مع معرفة الفكرة ، يجب أن نكون قادرين على توليد صور "مماثلة" لتلك الأصلية.

تم استعارة الفكرة العامة من اللاعبين من Facebook.
سيبدو التشفير مثل هذا:

حيث $$$دولا$- بعض المتجهات التي تصف الكائن ، $$$x ، y$- إحداثيات الكائن ، $$$sx ، sy$- حجم الكائن ، $$$z$- موقع الكائن في العمق ، $$$ع$- احتمال وجود الكائن.

بمعنى أن الشبكة العصبية المدخلة تتلقى صورة ذات حجم محدد مسبقًا والتي نريد أن نجد لها كائنات وتصدر مجموعة من الأوصاف. إذا أردنا إنشاء شبكة تمريرة واحدة ، فسيكون حجم هذه المجموعة للأسف ثابتًا. إذا كنا نريد العثور على جميع الكائنات ، فسوف يتعين علينا استخدام شبكات التوظيف.

سيكون فك الترميز مثل هذا:


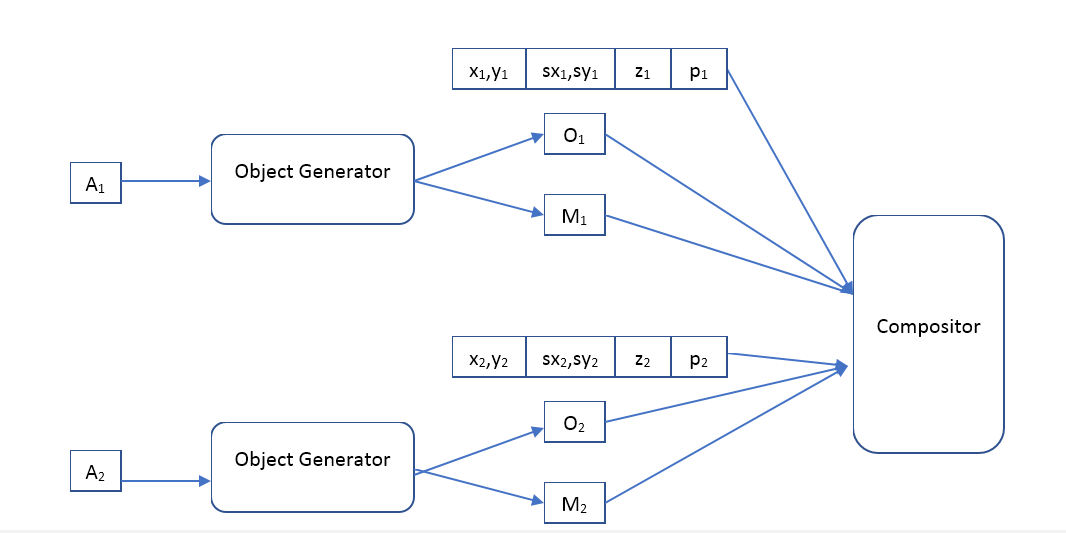
حيث Object Generator عبارة عن شبكة تستقبل متجه وصف الكائن عند الإدخال ويعطي $$$يا دولا$- صورة (بحجم قياسي معين) للكائن وقناع البكسلات غير الشفافة (قناع العتامة).
الملحن - يستقبل صورة الإدخال لجميع الكائنات ، والقناع ، والموضع ، والمقياس ، والعمق ، وتشكل صورة المخرجات ، والتي ينبغي أن تكون مشابهة للصورة الأصلية.

ما هو الفرق بين نهجنا و VAE؟

يبدو أننا نرغب في استخدام برنامج تشفير تلقائي له نفس البنية مثل مؤلفي المقال " اكتشاف الكائنات غير الخاضعة للرقابة المكانية المكانية مع الشبكات العصبية التلافيفية" ، لذا فإن السؤال هو ما هو الفرق. كل من هناك و autencoder ، فقط في الإصدار الثاني هو التغيير.

من الناحية النظرية ، الفرق كبير جدًا. VAE هو نموذج عام ومهمته هي جعل توزيعتين (صور أولية وتلك التي تم إنشاؤها) مماثلة قدر الإمكان. بشكل عام ، لا تقدم VAE أي ضمانات بأن الصورة التي تم إنشاؤها من "وصف" كائن تم إنشاؤه من الصورة الأصلية ستكون على الأقل شبيهة قليلاً بالأصل. بالمناسبة ، يتحدث مؤلفو Vae Auto-Encoding Variational Bayes أنفسهم عن هذا. فلماذا لا تزال تعمل؟ أعتقد أن البنية المختارة للشبكات العصبية و "الأوصاف" تساعد على زيادة المعلومات المتبادلة للصورة و "الوصف" ، لكن لم أجد أي دليل رياضي لهذه الفرضية. سؤال للقراء ، هل يمكن لشخص ما أن يشرح نتائج المؤلفين - صورتهم المستعادة تشبه إلى حد كبير الصورة الأصلية ، لماذا؟

بالإضافة إلى ذلك ، فإن استخدام مؤلفي VAE يفرض تحديد توزيع "الأوصاف" ، وطريقة تعظيم المعلومات المتبادلة لا يفرض أي افتراضات حول هذا. مما يمنحنا حرية إضافية ، على سبيل المثال ، يمكننا محاولة تجميع متجهات على نموذج تم تدريبه بالفعل $$$دولا$الأوصاف ، وننظر - ربما مثل هذا النظام سوف يتعلم فئات الكائنات؟ تجدر الإشارة إلى أن مثل هذه المجموعات باستخدام VAE لا معنى لها ، على سبيل المثال ، يستخدم مؤلفو المقال توزيعة غوسية لهذه المتجهات.

التجارب

لسوء الحظ ، يستغرق العمل الآن وقتًا كبيرًا ولا يمكن إكماله في فترة زمنية مقبولة. إذا أراد شخص ما كتابة عدة آلاف من الأسطر البرمجية ، وتدريب المئات من نماذج التعلم الآلي وإجراء العديد من التجارب المثيرة للاهتمام ، ببساطة لأنه (أو هي) يستمتع بها ، سأكون سعيدًا للانضمام إلى صفوفنا. اكتب بشكل شخصي.

مجال التجارب هنا واسع جدًا. لدي خطط للبدء بتدريب المشفر التلقائي الكلاسيكي (رسم الخرائط الحتمية للصور على الأوصاف وتوزيع غاوسي معكوس) ومعرفة ما يتعلمه. في التجارب الأولى ، سيكون استخدام الملحن الموصوف من قبل اللاعبين من فيسبوك كافياً ، لكن في المستقبل ، سيكون من الممتع للغاية اللعب مع ملحنين مختلفين ، ومن الممكن جعلها قابلة للتعلم أيضًا. قارن أدوات ضبط مختلفة: بدونها ، متفرق ، إلخ. قارن بين استخدام نماذج feedforward والعودية. ثم استخدم نماذج توزيع أكثر تقدماً للتوزيع العكسي ، على سبيل المثال ، تقدير الكثافة باستخدام Real NVP . تعرّف على مدى أفضل أو أسوأ مع نماذج أكثر مرونة. تعرف على ما سيحدث إذا كان عرض الصور على الأوصاف غير محدد (تم إنشاؤه من بعض التوزيع الشرطي). وأخيرًا ، حاول تطبيق طرق التجميع المختلفة لوصف المتجهات $$$دولا$وفهم ما إذا كان مثل هذا النظام يمكن أن يتعلم فئات الكائنات.

لكن الأهم من ذلك ، أريد حقاً مقارنة جودة النموذج بناءً على تعظيم المعلومات المتبادلة والنموذج باستخدام VAE.