👨‍🎨 👨🏾‍🌾 🖊️ هيلبرت ، ليبسج ... والفراغ 🤜🏿 👸🏾 🐧

تحت الخفض ، يتم بحث مسألة كيفية ترتيب خوارزمية فهرسة جيدة متعددة الأبعاد. والمثير للدهشة أنه لا يوجد الكثير من الخيارات.

المؤشرات أحادية البعد ، الأشجار ب

سيتم اعتبار مقياس نجاح خوارزمية البحث 2 حقائق -

يحدث حقيقة وجودها أو عدم وجود نتيجة لعدد لوغاريتمي (فيما يتعلق بحجم الفهرس) عدد من يقرأ صفحات القرص
تكلفة إصدار نتيجة تتناسب مع حجمها

وبهذا المعنى ، فإن الأشجار B ناجحة جدًا ويمكن اعتبار سبب ذلك استخدام شجرة متوازنة. ترجع بساطة الخوارزمية إلى البعد الواحد لمساحة المفتاح - إذا لزم الأمر ، قم بتقسيم الصفحة ، وهو ما يكفي لتقسيم نصف مجموعة العناصر المصنفة في هذه الصفحة إلى نصفين. عموما مقسوما على عدد من العناصر ، على الرغم من أن هذا ليس ضروريا.

لأن يتم تخزين صفحات الشجرة على القرص ، ويمكن القول أن الشجرة B لديها القدرة على تحويل مساحة مفتاح أحادية الأبعاد بكفاءة عالية إلى مساحة قرص أحادية البعد.

عند ملء شجرة بـ "الإدراج الأيمن" أكثر أو أقل ، وهذه حالة شائعة إلى حد ما ، يتم إنشاء الصفحات بترتيب نمو المفتاح ، من وقت لآخر بالتناوب مع الصفحات العليا. هناك فرص جيدة أنها ستكون على القرص أيضًا. وبالتالي ، وبدون أي جهد ، يتم تحقيق موقع البيانات العالي - البيانات القريبة القيمة ستكون في مكان قريب وعلى القرص.

بطبيعة الحال ، عند إدراج القيم في ترتيب عشوائي ، يتم إنشاء المفاتيح والصفحات بشكل عشوائي ، ونتيجة لذلك ما يسمى تجزئة المؤشر. هناك أيضا أدوات مكافحة التجزئة التي تستعيد مكان البيانات.

يبدو أنه في عصرنا من الأقراص RAID و SSD لا يهم ترتيب القراءة من القرص. لكن ، بدلاً من ذلك ، ليس له نفس المعنى كما كان من قبل. لا يوجد توجيه فعلي للرؤوس في SSD ، لذلك لا تنخفض سرعة القراءة العشوائية لمئات المرات مقارنة بالقراءة الصلبة ، مثل محرك الأقراص الصلبة. ومرة واحدة فقط كل 10 أو أكثر .

أذكر أن B- الأشجار ظهرت في عام 1970 في عصر الأشرطة المغناطيسية والطبول. عندما يكون الاختلاف في سرعة الوصول العشوائي للشريط والطبل المذكور أكثر دراماتيكية مقارنةً بمحرك الأقراص الصلبة ومحرك أقراص الحالة الصلبة.

بالإضافة إلى ذلك ، 10 مرات المسألة أيضا. وتشمل هذه الأوقات العشرة ليس فقط السمات المادية لمحرك أقراص الحالة الصلبة ، ولكن أيضًا النقطة الأساسية - إمكانية التنبؤ بسلوك القارئ. إذا كان من المحتمل جدًا أن يطلب القارئ الكتلة التالية لهذه الكتلة ، فمن المنطقي تنزيلها بشكل استباقي ، على افتراض. وإذا كان السلوك فوضويًا ، فكل محاولات التنبؤ لا معنى لها بل ومضرة.

فهرسة متعددة الأبعاد

علاوة على ذلك ، سوف نتعامل مع مؤشر النقاط ثنائية الأبعاد (X ، Y) ، لأنه ببساطة مناسب وبديهي للعمل معهم. لكن المشاكل هي في الأساس نفسه.

لا يمر خيار بسيط "غير متطور" مع مؤشرات منفصلة لـ X و Y وفقًا لمعايير النجاح لدينا. لا يعطي التكلفة اللوغاريتمية للحصول على النقطة الأولى. في الواقع ، للإجابة على السؤال ، هل هناك أي شيء على الإطلاق في المدى المرغوب ، يجب علينا

قم بالبحث في الفهرس X واحصل على جميع المعرفات من مدى الفاصل الزمني X
مماثلة ل Y
تتقاطع هاتين المجموعتين من معرفات

يعتمد العنصر الأول بالفعل على حجم المدى ولا يضمن اللوغاريتم.

لكي تكون "ناجحة" ، يجب ترتيب فهرس متعدد الأبعاد كشجرة أكثر أو أقل توازناً. هذا البيان قد يبدو مثيرا للجدل. لكن متطلبات البحث اللوغاريتمي تملي علينا مثل هذا الجهاز. لماذا لا أشجار أو أكثر؟ تعتبر بالفعل خيار "غير متطور" وغير مناسب مع شجرتين. ربما هناك منها مناسبة. لكن اثنين من الأشجار - وهذا هو ضعف أقفال (بما في ذلك في وقت واحد) ، أي ضعف التكلفة ، وفرص أكبر بكثير للوقوف في طريق مسدود. إذا تمكنت من الحصول على شجرة واحدة ، فيجب عليك بالتأكيد استخدامها.

بالنظر إلى كل هذا ، فإن الرغبة في اتخاذ تجربة B-tree الناجحة للغاية و "تعميمها" للعمل مع البيانات ثنائية الأبعاد أمر طبيعي تمامًا.

لذلك ظهرت شجرة آر.

R-شجرة

يتم ترتيب شجرة R على النحو التالي:
في البداية ، لدينا صفحة فارغة ، فقط أضف بيانات (نقاط) إليها.
ولكن هنا الصفحة ممتلئة ويجب تقسيمها.
في B-tree ، يتم ترتيب عناصر الصفحة بطريقة طبيعية ، وبالتالي فإن السؤال هو مقدار القطع. لا يوجد ترتيب طبيعي في شجرة آر. هناك خياران:

إحضار الطلب ، أي تقديم وظيفة ، بناءً على X&Y ، ستقدم قيمة وفقًا لعناصر الصفحة التي سيتم طلبها وتقسيمها وفقًا لذلك. في هذه الحالة ، يتحول المؤشر بالكامل إلى شجرة B منتظمة يتم إنشاؤها من قيم الوظيفة المحددة. بالإضافة إلى الإيجابيات الواضحة ، هناك سؤال كبير - حسنًا ، جيدًا ، لقد فهرست ، ولكن كيف تبدو؟ المزيد عن ذلك لاحقًا ، فكر أولاً في الخيار الثاني.
قسّم الصفحة حسب المعايير المكانية. للقيام بذلك ، يجب تعيين كل صفحة في نطاق العناصر الموجودة على / تحتها. أي الصفحة الجذر لها مدى الطبقة بأكملها. عند التقسيم ، يتم إنشاء صفحتين (أو أكثر) يتم تضمين نطاقاتها في مدى الصفحة الرئيسية (للبحث).

هناك عدم اليقين المطلق. كيف بالضبط لتقسيم الصفحة؟ أفقي أم عمودي؟ تابع من نصف المساحة أو نصف العناصر؟ ولكن ماذا لو شكلت النقاط مجموعتين ، لكن يمكنك فقط الفصل بينهما بخط مائل؟ وإذا كان هناك ثلاث مجموعات؟

مجرد وجود مثل هذه الأسئلة يشير إلى أن شجرة R ليست خوارزمية. هذه هي مجموعة من الأساليب البحثية ، على الأقل لتقسيم الصفحة أثناء الإدراج ، لدمج الصفحات أثناء الحذف / التعديل ، للمعالجة المسبقة للإدراج المجمع.

الاستدلال ينطوي على تخصص شجرة معينة على نوع بيانات معين. أي في مجموعات البيانات من نوع ما ، فإنها تخطئ في كثير من الأحيان. "الاستدلال لا يمكن أن يكون مخطئا تماما ، لأنه في هذه الحالة ، سيكون خوارزمية "©.

ماذا يعني الخطأ التجريبي في هذا السياق؟ على سبيل المثال ، سيتم تقسيم / دمج الصفحة دون جدوى وستبدأ الصفحات في التداخل جزئيًا مع بعضها البعض. إذا وقع نطاق البحث فجأة على مساحة التداخل في الصفحات ، فلن تكون تكلفة البحث لوغاريتمية بالفعل. بمرور الوقت ، عند إدراج / حذف ، يتراكم عدد الأخطاء ويبدأ أداء الشجرة في الانخفاض.

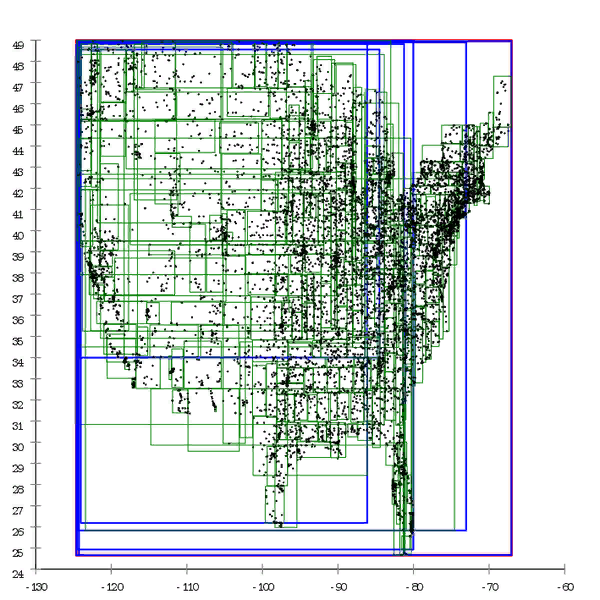الشكل 1 فيما يلي مثال لشجرة R * ، التي بنيت بطريقة طبيعية.

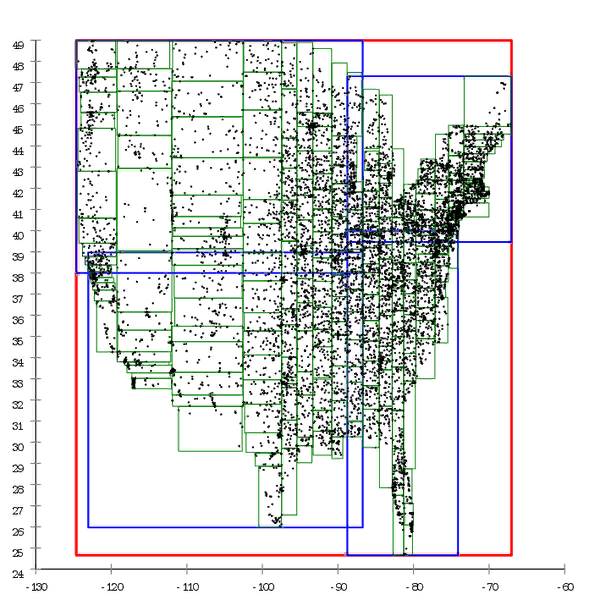الشكل 2 وهنا يتم تجهيز مجموعة البيانات نفسها مسبقًا ويتم بناء الشجرة عن طريق الإدراج الشامل

يمكننا القول أن الشجرة B تتحلل أيضًا بمرور الوقت ، لكن هذا تدهور مختلف قليلاً. ينخفض أداء B-tree بسبب حقيقة أن صفحاتها ليست متتالية. يتم التعامل مع هذا بسهولة عن طريق "استقامة" تجزئة الشجرة. في حالة شجرة R ، ليس من السهل التخلص منها ؛ بنية الشجرة نفسها "منحنى" لتصحيح الوضع ؛ يجب إعادة بنائها بالكامل.

إن تعميمات شجرة R إلى المساحات متعددة الأبعاد ليست واضحة. على سبيل المثال ، عند تقسيم الصفحات ، قللنا محيط الصفحات الفرعية. ما لتقليل في حالة ثلاثية الأبعاد؟ حجم أو مساحة السطح؟ وفي حالة الأبعاد الثمانية؟ الحس السليم لم يعد مستشارا.

قد تكون المساحة المفهرسة غير متناحية. لماذا لا تقوم فقط بفهرسة النقاط ، ولكن مواقعها في الوقت المناسب ، أي (س ، ص ، ر). في هذه الحالة ، على سبيل المثال ، الاستدلال على أساس محيط لا معنى له منذ ذلك الحين مداخن طول في فترات زمنية.

الانطباع العام لشجرة آر هو مثل القشريات الخيشومية . تلك لها مكانة بيئية خاصة بها يصعب عليها التنافس معها. ولكن في الحالة العامة ، ليس لديهم فرصة في المنافسة مع الحيوانات الأكثر تطوراً.

شجرة رباعية

في كل فصل ، تحتوي كل صفحة غير مطبوعة على أربعة أحفاد بالضبط ، والتي تقسم مساحتها بالتساوي إلى أرباع.

الشكل 3 الشكل 3. مثال على شجرة رباعية شيدت

هذا ليس تصميم قاعدة بيانات جيدة.

تضيق كل صفحة مساحة البحث لكل إحداثيات مرتين فقط. نعم ، يوفر هذا التعقيد اللوغاريتمي للبحث ، ولكن هذا هو اللوغاريتم الأساسي 2 ، وليس عدد العناصر في الصفحة ، (حتى 100) كما في شجرة B.
كل صفحة صغيرة ، ولكن خلفها لا يزال عليك الانتقال إلى القرص.
يجب أن يكون عمق الشجرة الرباعية محدودًا ، وإلا فإن عدم توازنها يؤثر على الأداء. نتيجة لذلك ، بناءً على البيانات شديدة التجميع (على سبيل المثال ، المنازل الموجودة على الخريطة - هناك الكثير من المدن في المدن ، والقليل منها في الحقول) يمكن أن تتراكم كمية كبيرة من البيانات على صفحات الأوراق. يصبح الفهرس الصادر من أحد الأعمدة ممتلئًا ويتطلب المعالجة اللاحقة.

يمكن أن يقلل حجم الشبكة الشبكي المحدد (عمق الشجرة) من الأداء. ومع ذلك ، أود أن أداء الخوارزمية لا تعتمد بشكل حاسم على العامل البشري.
تكلفة مساحة لتخزين نقطة واحدة كبيرة جدا.

ترقيم الفضاء

يبقى النظر في الإصدار المؤجل مسبقًا مع دالة تقوم ، على أساس مفتاح متعدد الأبعاد ، بحساب قيمة الكتابة في شجرة B عادية.

بناء مثل هذا المؤشر واضح ، والمؤشر نفسه لديه كل مزايا شجرة B. السؤال الوحيد هو ما إذا كان يمكن استخدام هذا الفهرس للبحث الفعال.

هناك عدد كبير من هذه الوظائف ، يمكن افتراض أن هناك عددًا قليلاً من "الجيد" ، وعدد كبير من "السيئ" وعدد كبير من "سيء جدًا".

العثور على وظيفة فظيعة ليس بالأمر الصعب - فنحن نسلسل المفتاح إلى سلسلة وننظر في MD5 منه ونحصل على قيمة غير مجدية تمامًا لأغراضنا.

وكيف تقترب من الخير؟ لقد قيل بالفعل أن فهرسًا مفيدًا يوفر "محلية" للبيانات - نقاط قريبة في الفضاء وغالبًا ما تكون قريبة من بعضها البعض عند حفظها على القرص. كما هو مطبق على الوظيفة المرغوبة ، فهذا يعني أنه بالنسبة للنقاط القريبة من الناحية المكانية ، فإنها تعطي قيمًا قريبة.

بمجرد دخول الفهرس ، ستظهر القيم المحسوبة على الصفحات "الفعلية" بترتيب قيمها. من وجهة نظر "المعنى المادي" ، يجب أن يؤثر مدى البحث على أقل عدد ممكن من صفحات الفهرس المادي. ما هو واضح عموما. من وجهة النظر هذه ، تكون منحنيات الترقيم التي "تسحب" البيانات "سيئة". وتلك التي "تخلط في الكرة" - أقرب إلى "الخير".

ترقيم ساذج

محاولة للضغط على مقطع في مربع (hypercube) مع البقاء في منطق الفضاء أحادي البعد ، أي مقطعة إلى قطع وملء مربع مع هذه القطع. يمكن أن يكون

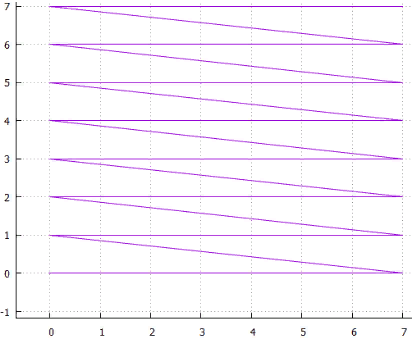4 خط المسح الضوئي

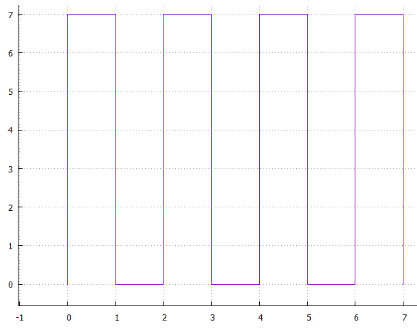5 المتداخلة

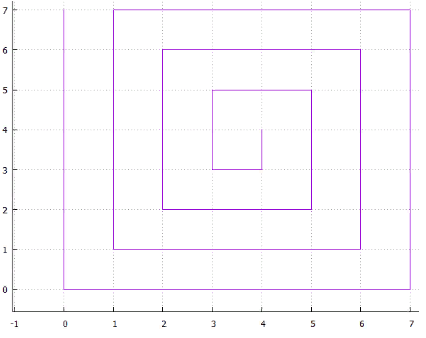التين .6 دوامة

أو ... يمكنك الخروج بالعديد من الخيارات ، جميعها لها عيبان

الغموض ، على سبيل المثال: لماذا يتم كرة لولبية في اتجاه عقارب الساعة وليس ضدها ، أو لماذا أول مسح أفقي على طول X ثم على طول Y
وجود قطع مستقيمة طويلة تجعل استخدام هذه الطريقة غير فعال للفهرسة متعددة الأبعاد (محيط صفحة كبيرة)

ميزات الوصول المباشر

إذا كانت المطالبة الرئيسية بالطرق "الساذجة" هي أنها تنشئ صفحات ممدودة جدًا ، فلننشئ الصفحات "الصحيحة" بمفردنا.

الفكرة بسيطة - فليكن هناك تقسيم خارجي للمساحة إلى كتل ، وتعيين معرف لكل كتلة وسيكون هذا هو مفتاح الفهرس المكاني.

اجعل إحداثيات X&Y 16 بت (للوضوح)
نحن ذاهبون لتغطية الفضاء مع كتل مربعة من 1024X1024
خشن الإحداثيات ، والتحول بنسبة 10 بت إلى اليمين
واحصل على معرف الصفحة ، قم بإلصاق البتات من X&Y. الآن في المعرِّف ، تكون الأرقام الستة الأدنى هي الأقدم من X ، والأرقام الستة التالية هي الأقدم من Y

من السهل أن ترى أن الكتل تشكل مسحًا خطيًا ، وبالتالي ، للعثور على البيانات الخاصة بمدى البحث ، سيتعين عليك إجراء بحث / قراءة في الفهرس لكل صف من الكتل الموجودة في هذا النطاق. بشكل عام ، تعمل هذه الطريقة بشكل رائع ، على الرغم من أن لها العديد من العيوب.

عند إنشاء فهرس ، يجب عليك اختيار حجم الكتلة الأمثل ، وهو أمر غير واضح تمامًا
إذا كانت الكتلة أكبر من طلب البحث المعتاد ، فسيكون البحث غير فعال منذ ذلك الحين يجب أن تقرأ وتصفية (postprocessing) أكثر من اللازم
إذا كانت الكتلة أصغر بكثير من استعلام نموذجي ، فسيكون البحث غير فعال منذ ذلك الحين سوف تضطر إلى القيام بالكثير من الاستفسارات صفًا تلو الآخر
إذا كان للكتلة بيانات كثيرة جدًا أو قليلة جدًا في المتوسط ، فسيكون البحث غير فعال
إذا تم تجميع البيانات (على سبيل المثال: في المنزل على الخريطة) ، فلن يكون البحث فعالًا في كل مكان
إذا نمت مجموعة البيانات ، فقد يتضح أن حجم الكتلة لم يعد مثاليًا.

جزئيًا ، يتم حل هذه المشكلات عن طريق بناء كتل متعددة المستويات. لنفس المثال:

لا تزال تريد كتل 1024X1024
ولكن الآن لا يزال لدينا كتل المستوى الأعلى من حجم كتل 8X8 أقل
المفتاح مرتب على النحو التالي (من الأقل إلى الأعلى):
3 أرقام - أرقام 10 ... 12 إحداثيات X
3 أرقام - أرقام 10 ... إحداثيات 12 Y
3 أرقام - أرقام 13 ... 15 إحداثيات X
3 أرقام - أرقام 13 ... إحداثيات 15 Y

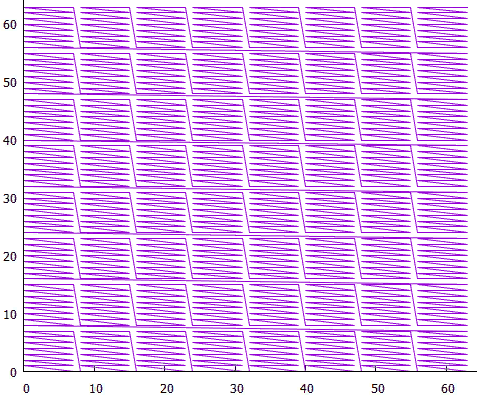7 كتل منخفضة المستوى تشكل كتل عالية المستوى

الآن بالنسبة للحالات الكبيرة لا تحتاج إلى قراءة عدد كبير من القطع الصغيرة ، يتم ذلك على حساب الكتل عالية المستوى.

ومن المثير للاهتمام ، أنه لم يكن من الممكن تقريب الإحداثيات ، ولكن بنفس الطريقة الضغط عليها في المفتاح. في هذه الحالة ، سيكون التصفية اللاحقة أرخص لأن سيحدث عند قراءة الفهرس.

يتم ترتيب فهارس GRID المكانية في MS SQL بطريقة مماثلة ؛ ويسمح بحد أقصى 4 مستويات كتلة فيها.

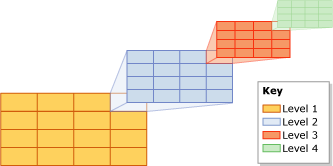الشكل 8 فهرس الشبكة

هناك طريقة أخرى مثيرة للاهتمام للفهرسة المباشرة وهي استخدام شجرة رباعية لتقسيم المساحة الخارجية.

شجرة رباعية مفيدة من حيث أنه يمكن أن تتكيف مع كثافة الكائنات منذ ذلك الحين عندما تفيض العقدة ، تنقسم. نتيجة لذلك ، حيث تكون كثافة الكائنات عالية ، فإن الكتل سوف تصبح صغيرة والعكس صحيح. هذا يقلل من عدد المكالمات فهرس فارغة.

صحيح أن الشجرة الرباعية عبارة عن بناء غير مريح لإعادة البناء أثناء الطيران ، من المفيد القيام بذلك من وقت لآخر.

من اللطيف ، عند إعادة بناء شجرة رباعية ، ليست هناك حاجة لإعادة بناء الفهرس إذا تم تحديد الكتل برمز مورتون وتم تشفير الكائنات باستخدامه. إليك الخدعة: إذا تم ترميز إحداثيات النقطة برمز Morton ، فإن معرف الصفحة هو بادئة في هذا الرمز. عند البحث عن بيانات الصفحة ، يتم تحديد جميع المفاتيح الموجودة في النطاق من [بادئة] 00 ... 00B إلى [بادئة] 11 ... 11B ، إذا تم تقسيم الصفحة ، فهذا يعني أن بادئة أحفادها فقط قد تم تمديدها.

ميزات تشبه نفسها

أول ما يتبادر إلى الذهن عند ذكر وظائف مشابهة للذات هو "منحنيات كاسحة". "منحنى ملحوظ هو رسم خرائط مستمر ، مجاله هو جزء الوحدة [0 ، 1] ، والمجال هو المساحة الإقليدية (أكثر صرامة ، الطوبوغرافية)." مثال على ذلك هو منحنى بيانو.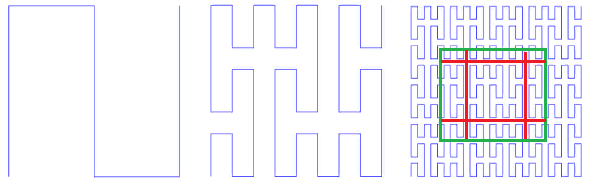

الشكل 9 التكرارات الأولى لمنحنى بيانو

في الزاوية السفلية اليسرى هي بداية منطقة التعريف (وقيمة الصفر للوظيفة) ، في الزاوية اليمنى العليا النهاية (و 1) ، في كل مرة ننتقل فيها خطوة واحدة ، أضف 1 / (N * N) إلى القيمة (شريطة أن N - درجة 3 ، بالطبع). نتيجة لذلك ، في الزاوية اليمنى العليا تصل القيمة إلى 1. إذا أضفنا واحدة في كل خطوة ، فإن هذه الوظيفة ببساطة ترقم الشبكة المربعة بالتسلسل ، وهو ما أردناه.

جميع المنحنيات تجتاح تشبه نفسها. في هذه الحالة ، يكون البسط البسيط 3 × 3. وفي كل تكرار ، تتحول كل نقطة من البساطة إلى البساطة نفسها ، لضمان الاستمرارية ، يجب عليك اللجوء إلى التعيينات (التقلبات).

تشابه الذات هو نوع مهم جدا بالنسبة لنا. يعطي الأمل لقيمة لوغاريتمية البحث. على سبيل المثال ، بالنسبة إلى 3x3 simplex ، ستكون جميع الأرقام التي تم إنشاؤها داخل كل من المربعات الابتدائية التسع بواسطة التكرار التالي من التفاصيل ضمن نفس النطاق. فقط لأن الرقم هو المسار الذي سافر من البداية. أي إذا قمت بتقسيم المدى إلى 9 أجزاء ، فيمكن الحصول على محتويات كل منها بواسطة مؤشر فهرس واحد. وهكذا بشكل متكرر ، يمكن الحصول على كل مربع من المربعات الفرعية التسعة لكل من المربعات من خلال استعلام واحد في الفهرس (ولو في نطاق أصغر). لذلك يمكن تقسيم مدى البحث إلى عدد صغير من الاستعلامات الفرعية المربعة ، إما قراءة كليًا أو باستخدام التصفية (حول المحيط). يوضح الشكل 9 مدى البحث باللون الأخضر ، مقسمًا بخطوط حمراء إلى استعلامات فرعية.

ومع ذلك ، فإن التشابه الذاتي لا يجعل منحنى الترقيم مناسبًا تلقائيًا لأغراض الفهرسة.

يجب أن يملأ المنحنى الشبكة المربعة. نقوم بفهرسة القيم في عقد الشبكة المربعة وفي كل مرة لا نريد البحث عن عقدة مناسبة في الشبكة ، على سبيل المثال ، عقدة ثلاثية. على الأقل لتجنب مشاكل التقريب. هنا ، على سبيل المثال ، مثل (الشكل 10)

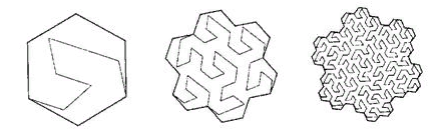
الشكل 10 بحيرة ثلاثية كوكا

المنحنى لا يناسبنا. على الرغم من أنه "يجسر" السطح تمامًا.
يجب أن يملأ المنحنى المساحة بدون فجوات ( البعد الكسري D = 2). ومن هنا (الشكل 11):

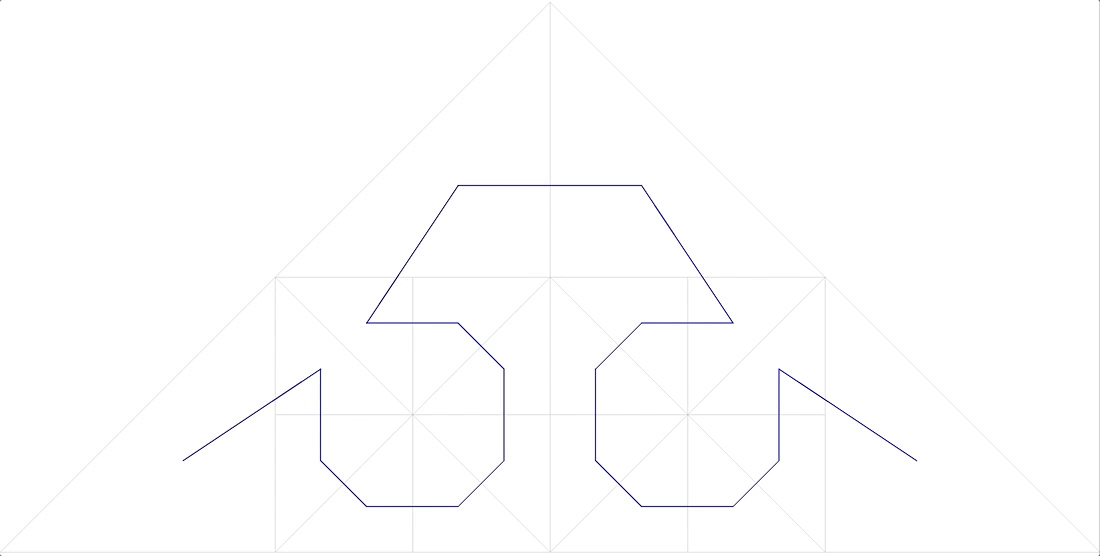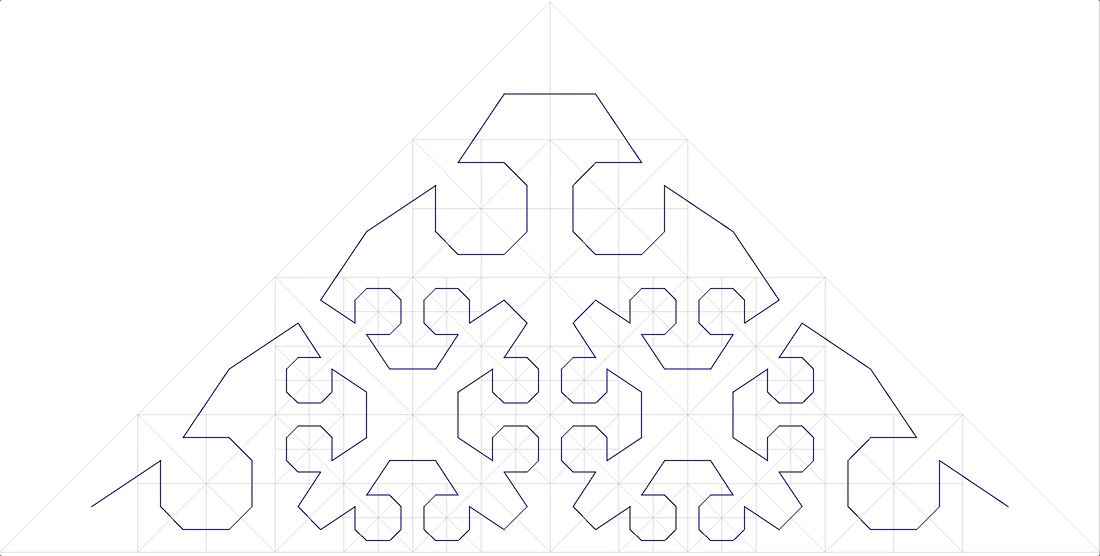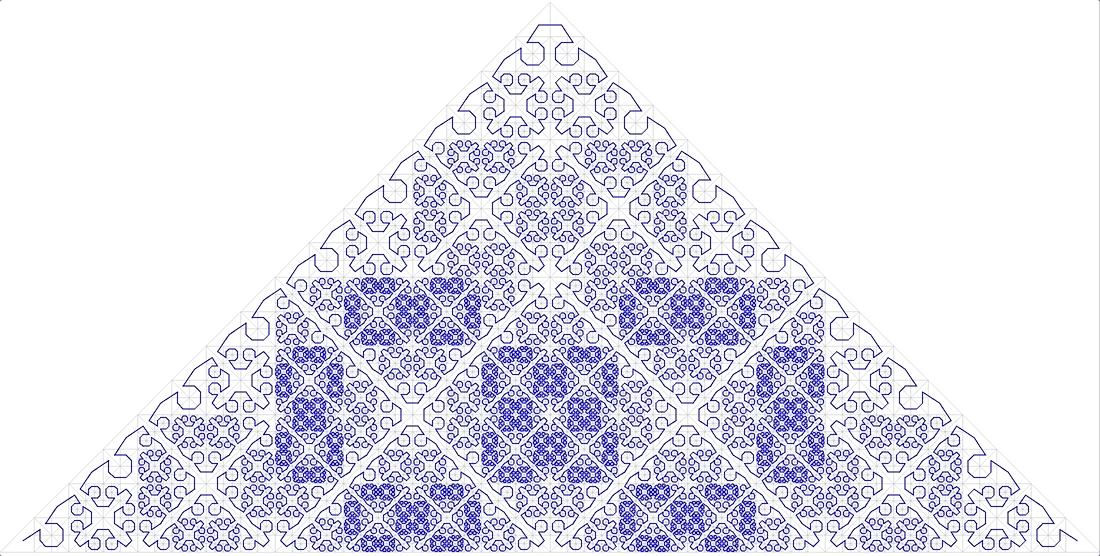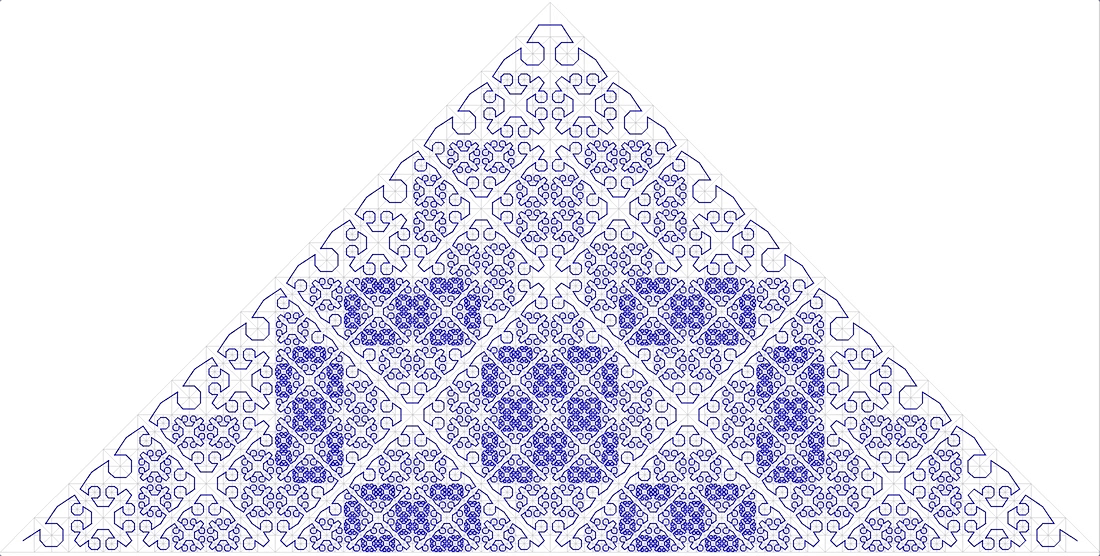
11 منحنى كسورية مجهول

أيضا لا يصلح.
يجب حساب قيمة وظيفة الترقيم (المسار الذي تم قطعه على طول المنحنى من البداية) بسهولة. يتبع ذلك أنه بسبب الغموض الناشئ ، لا تعد منحنيات اللمس الذاتي مناسبة ، مثل منحنى Sierpinski

الشكل. 12 منحنى Sierpinski

أو ، وهو نفسه (بالنسبة لنا) ، " اجتياز المثلث على طول سيزارو "

FIG. 13 مثلث سيزارو ، من أجل الوضوح ، يتم استبدال الزاوية اليمنى بزاوية 85 درجة
يجب ألا يكون هناك معلمات في وظيفة الترقيم ، يجب أن يكون المنحنى موحدًا (دقيقًا للتماثل). . : ( )

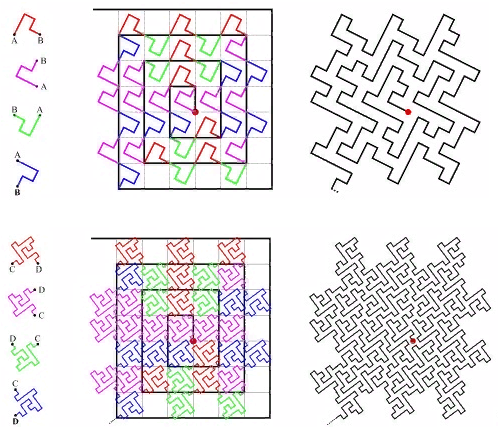
. 14 “A Plane Filling Curve for the Year 2017”

, ( ) .
, , , .

— . , . , N- N (N-1) . , , -.

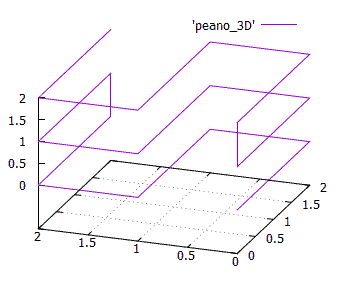. 15 3x3x3

, .

.

, . , ( ). , , . , .

.

,
( ) , . , . — . .
— , .. .
, . , , . , , — () 3...10% () Z-.

— , .

, () , ( ) .

, , - , . , , . , . .

, ? .

().

, , . , . , 3X3 3 X, 3 Y. . () 5X5, 5 . (ex: 2+3), .

- — , 5- 7- , . . , .

. 2 . 4 . .

, 33 22 , 3 > 2, 44 33, 88 55. , 22…

? . لأن , . 3X3 , 3 . 8x8 (.16), — 64 .

. 16 8x8

, , 2x2, , .

. 17 2x2

, , , “Z”, “” “”.
, “” , . 4 . 256 8- .

, ( “”), . .

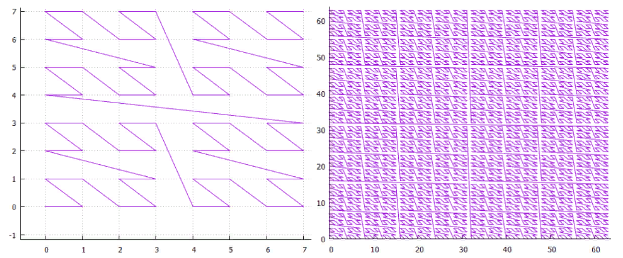. 18 Z-

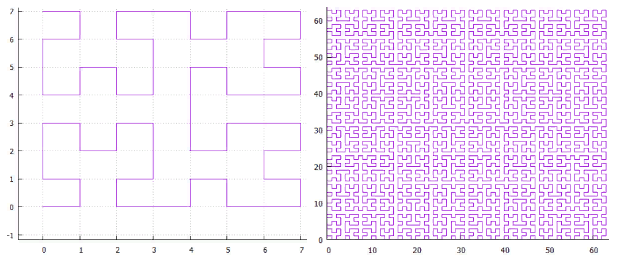. 19 “” —

, . .

, , .
—
- (KMin, KMax)
- ( ) KMin, KMax
- , SMin, , SMax
- . , , SMin, . .
- , , ( ).
- Z- . z- — , — ( ). , , .
- , , . ,
- , . — “ ” >= “ ” () , “ ”
  - “ ” > , ,
  - , ,
  - “ ” > , , ,
  - “ ” == ,
- - 0 1 —
  - 0 1 —
  - , , 1, 0. .

على منحنى Z ، يعمل مثل هذا:

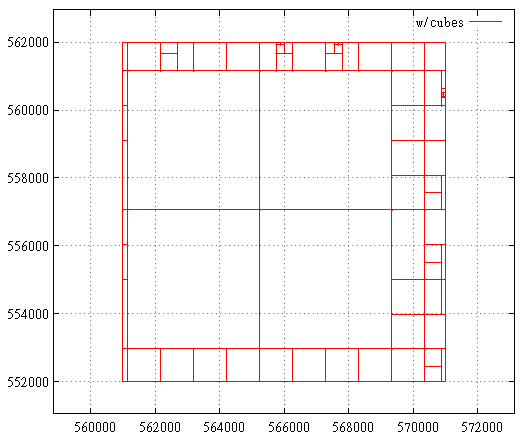FIG. 20 - تقسيم الاستعلام الفرعي في حالة منحنى Z

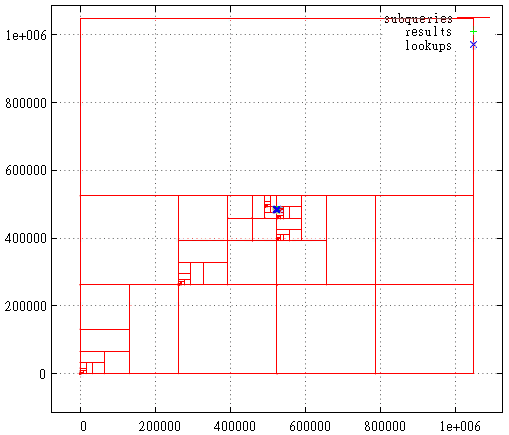FIG. 21 منحنى هيلبرت ، الحالة عندما يكون الحد الأقصى هو الحد الأقصى

تظهر المرحلة الأولى هنا - تقطع الطبقة الزائدة عن الحد الأقصى.

FIG. 22 Hilbert Curve ، منطقة استعلام البحث

وفي ما يلي تفاصيل الاستعلامات الفرعية والنقاط التي تم العثور عليها ومكالمات الفهرس في منطقة استعلام البحث. لا يزال هذا طلبًا فاشلاً للغاية من وجهة نظر منحنى هيلبرت. عادة ما يكون كل شيء أقل دموية.

ومع ذلك ، تشير إحصائيات الاستعلام إلى أنه (تقريبًا) على نفس البيانات ، يقرأ فهرس ثنائي الأبعاد يستند إلى منحنى Hilbert صفحات قرص أقل بنسبة 5٪ في المتوسط ، لكنه يعمل بشكل أبطأ. سبب التباطؤ أيضًا هو أن الحساب نفسه (المباشر والعاكس) لهذا المنحنى أصعب كثيرًا - 2000 دورة من المعالجات لـ Hilbert مقارنة بـ 50 لدورة منحنى Z.

من خلال التوقف عن دعم منحنى هيلبرت ، يمكن تبسيط الخوارزمية ؛ للوهلة الأولى ، هذا التباطؤ غير مبرر. من ناحية أخرى ، هذه مجرد حالة ثنائية الأبعاد ، على سبيل المثال ، في مساحة ذات ثمانية أبعاد أو أكثر ، يمكن أن تتألق الإحصاءات بألوان جديدة تمامًا. هذه المسألة لا تزال في انتظار التوضيح.

ملاحظة : يُسمى منحنى Z أحيانًا منحنى تشذير البتة بسبب الخوارزمية لحساب القيمة - تقع أرقام كل من الإحداثيات في القيمة الرئيسية من خلال إحداها ، وهي تقنية للغاية. لكن يمكنك ، على كل حال ، تشبيك التصريفات ليس بشكل فردي ، ولكن في عبوات 2.3 ... 8 ... قطعة. الآن ، إذا أخذنا 8 بتات ، فعندئذٍ على مفتاح 32 بت نحصل على تناظرية لمؤشر GRID ذي المستوى 4 من MS SQL. وفي الحالة القصوى - حزمة واحدة من 32 بت لكل - خوارزمية المسح الأفقي.

مثل هذا الفهرس (وليس بالأحرف الصغيرة ، بالطبع) يمكن أن يكون فعالًا للغاية ، بل وأكثر كفاءة من المنحنى Z في بعض مجموعات البيانات. لسوء الحظ ، بسبب فقدان العمومية.

PPS : الفهرس الموضح يشبه إلى حد بعيد العمل مع شجرة رباعية. الحد الأقصى هو صفحة الجذر لشجرة رباعية ، ويحتوي على 4 أحفاد ... وبالتالي ، يمكن أن تعزى الخوارزمية إلى "طرق الوصول المباشر".

الخلافات لا تزال أساسية.

لا يتم تخزين شجرة رباعية في أي مكان ، بل هو الظاهري ، جزءا لا يتجزأ من طبيعة الأرقام. لا توجد قيود على عمق الشجرة ؛ فنحن نحصل على معلومات عن عدد السكان المتحدرين من سكان الشجرة الرئيسية. علاوة على ذلك ، تتم قراءة الشجرة الرئيسية مرة واحدة ، نذهب من الأصغر إلى الأقدم. إنه أمر مضحك ، لكن الهيكل المادي للشجرة B يجعل من الممكن تجنب الاستعلامات الفارغة والحد من عمق العودية.

هناك شيء واحد آخر - في كل تكرار يظهر فقط سليلان - يمكن إنشاء 4 استعلامات فرعية منها ، ولا يمكن إنشاؤها في حالة عدم وجود بيانات تحتها. في الحالة ثلاثية الأبعاد ، سنتحدث عن 8 أحفاد ، في الحالة ذات الأبعاد الثلاثة - حوالي 256.

PPPS : في بداية هذه المقالة ، تحدثنا عن الانقسام عند البحث في فهرس متعدد الأبعاد - من أجل الحصول على القيمة اللوغاريتمية ، من الضروري تقسيم بعض الموارد المحدودة عند التكرار - إما مساحة القيمة الرئيسية أو مساحة البحث. في الخوارزمية المقدمة ، انهار هذا الانقسام - نشترك في الوقت نفسه في كل من المفتاح والفضاء.

"أنا أعيش في كلتا الساحتين ، وأشجاري أطول دائمًا" ( C )

PPPPS : بمجرد أن يطلقوا على المنحنى Z ، يوجد هنا ترتيب Z وتشذير البت ورمز / منحنى Morton. يُعرف أيضًا باسم منحنى Lebesgue ، لذا من أجل الحفاظ على التوازن ، قام المؤلف بعنوان المقال ، بما في ذلك تكريمًا لهنري ليون Lebesgue .

PPPPPS : في الرسم التوضيحي للعنوان ، فإن منظر Fedchenko Glacier جميل ببساطة ، وهناك ما يكفي من الفراغ. في الواقع ، أعجب المؤلف بكيفية تدفق الأفكار والأساليب المختلفة بسلاسة مع بعضها البعض ، ودمجها تدريجياً في خوارزمية واحدة. كما أن العديد من مصادر المياه الصغيرة التي تشكل مستجمعات المياه تشكل جريانًا واحدًا.

هيلبرت ، ليبسج ... والفراغ