لقد أثبت علماء الرياضيات أن العملية العشوائية عند تطبيقها على سطح عشوائي تؤدي دائمًا إلى ظهور أنماط معينة
في المقال الأصلي ، هذه صورة ثلاثية الأبعاد يمكن أن تكون ملتويةفي
فيلم البحث عن السفينة المفقودة ، كان على إنديانا جونز البحث عن غرفة سرية تختبئ
سفينة العهد الأسطورية. لتحديد موقعها بالضبط ، كانت إنديانا بحاجة إلى العثور على خريطة خاصة ، تكون مرئية فقط عندما تشرق الشمس من خلال بلورة خاصة في غرفة معينة في وقت معين من اليوم.
توجد فكرة مماثلة - وهي أن المعلومات الأكثر أهمية لا يمكن الكشف عنها إلا بالصدفة الدقيقة لظروف معينة - موجودة في العديد من الأساطير. يحدث في الرياضيات ، وأحيانا في مواقف غير متوقعة. الآن ،
أثبت ثلاثة علماء رياضيات أنه إذا تم ضبط نوع معين من العشوائية بدقة شديدة ، تظهر أشكال هندسية معقدة - مثل خريطة بها كنز في أرضية عادية.
هذه القطع تشبه خلايا الشطرنج المنتشرة على شبكات ، والتي بدورها يتم إنشاؤها بواسطة عملية عشوائية. قد يعتقد المرء أن تراكم العشوائية في العشوائية ، ونحن نحصل على الارتباك. لقد اتضح أنه ، كما هو الحال في رقاقات الثلج ، عندما يكون كل منها فريدًا ، ولكن في الوقت نفسه جميعها عبارة عن رقاقات ثلجية ، تتحول الفوضى إلى شكل عالمي - إذا تبين أن الظروف هي فقط حسب الحاجة.
نقطة تحول
يعلم الجميع أن علماء الرياضيات دراسة الأشكال. معظم هذه النماذج تتبع قواعد حتمية: إذا أعطيتك تعليمات لبناء كرة ، فستتلقى نفس الكرة في كل مرة.
لكن حتى علماء الرياضيات يدرسون النماذج التي يتم الحصول عليها نتيجة لعمليات عشوائية ، مثل ، على سبيل المثال ،
المشي العشوائي - مسار ، يتم اختيار اتجاه كل خطوة منها بشكل عشوائي. بالإضافة إلى المشي العشوائي ، هناك أنواع أخرى من الكائنات الهندسية العشوائية ، على سبيل المثال ، الأسطح ثنائية الأبعاد العشوائية (تخيل منظرًا طبيعيًا حيث تنتشر التلال والوديان عشوائيًا) وخرائط عشوائية (مجموعة من النقاط العشوائية المرتبطة بخطوط).
سطح عشوائي تم الحصول عليها عن طريق مثلثات الإلتصاقكل هذه الأشكال مختلفة عن بعضها البعض. ومع ذلك ، فقد وجد علماء الرياضيات أن هذه العمليات العشوائية تتلاقى مع أشكال قانونية معينة. على سبيل المثال ، جميع مسارات المشي العشوائية هي شكل من أشكال
الحركة البراونية مع السير لفترة طويلة إلى حد ما. في السنوات الأخيرة ، اكتشف علماء الرياضيات أشكالًا قانونية وعملية عشوائية أخرى - وحصلوا على أعلى الجوائز في هذا المجال.
يرتبط الدليل الجديد بفهم الخصائص الأساسية لعملية عشوائية أخرى.
يبدأ بإنشاء سطح عشوائي. تحتاج أولاً إلى لصق المثلثات معًا. بعد ذلك ، يجب أن تتم مواءمتها معًا بأي طريقة ، بحيث يتم إغلاق النموذج الناتج ، مثل الحزمة على هدية (لا تحتوي على ثقوب). إذا بدأت بعدد معين من المثلثات على يديك ، فستتاح لك العديد من الفرص. بعض هذه "التثليثات" ستنتج أسطحًا ناعمة تقريبًا تشبه الكرة. سيبدو معظمهم أكثر تشبهًا السطوح القاسية التي تشبه سلاسل الجبال.
قال
أوليفر برناردي ، عالم رياضيات من جامعة برانديز ، مؤلف مشارك للعمل ، شارك فيه
نيكولاس كوريان من جامعة باريس الجنوبية الجنوبية 11
وجريجوري مجيرمونت من المدرسة العليا العادية في ليون.
أوليفييه برناردي ونيكولاس كوريان وغريغوري ميرمونتأسس ميرمونت وعالم الرياضيات الآخر ،
جان فرانسوا لو غال ، العديد من خصائص هذه التثليثات العشوائية في أعمالهما السابقة. يذهب الدليل الجديد إلى أبعد من ذلك بإضافة طبقة ثانية من العشوائية إلى جانب التثليث العشوائي.
لإضافة عشوائية جديدة ، حدد كل نقطة تلتقي فيها المثلثات عند الزوايا - ما يسميه علماء الرياضيات قمة الرأس. تلوين الرؤوس عشوائياً باللون الأسود أو الأبيض. يمكنك القيام بذلك عن طريق رمي عملة معدنية ، على الرغم من أن العملة قد لا تكون صادقة تمامًا ، وتفوق على جانب واحد.
بعد رسم القمم ، يمكنك طرح أسئلة مختلفة حول النموذج الذي قمت بإنشائه. أحد العناصر الأساسية: إلى أي مدى يمكنك الذهاب على طول السطح باستخدام قمة سوداء واحدة فقط؟ وتسمى عملية التحرك على طول الرؤوس المتصلة من نفس اللون بالتسرب. هذه طريقة رياضية لدراسة ظاهرة فيزيائية تحمل نفس الاسم حيث يمر السائل عبر وسط مسامي.
سيكون من السهل التسلل (أو لا) ، اعتمادًا على كيفية توزيع وزن العملة: إذا كانت العملة تميل إلى إعطاء رؤوس سوداء ، يكون التسلل مضمونًا تقريبًا ؛ إذا لتسليم البيض ، فمن شبه المؤكد أن التسرب مستحيل.
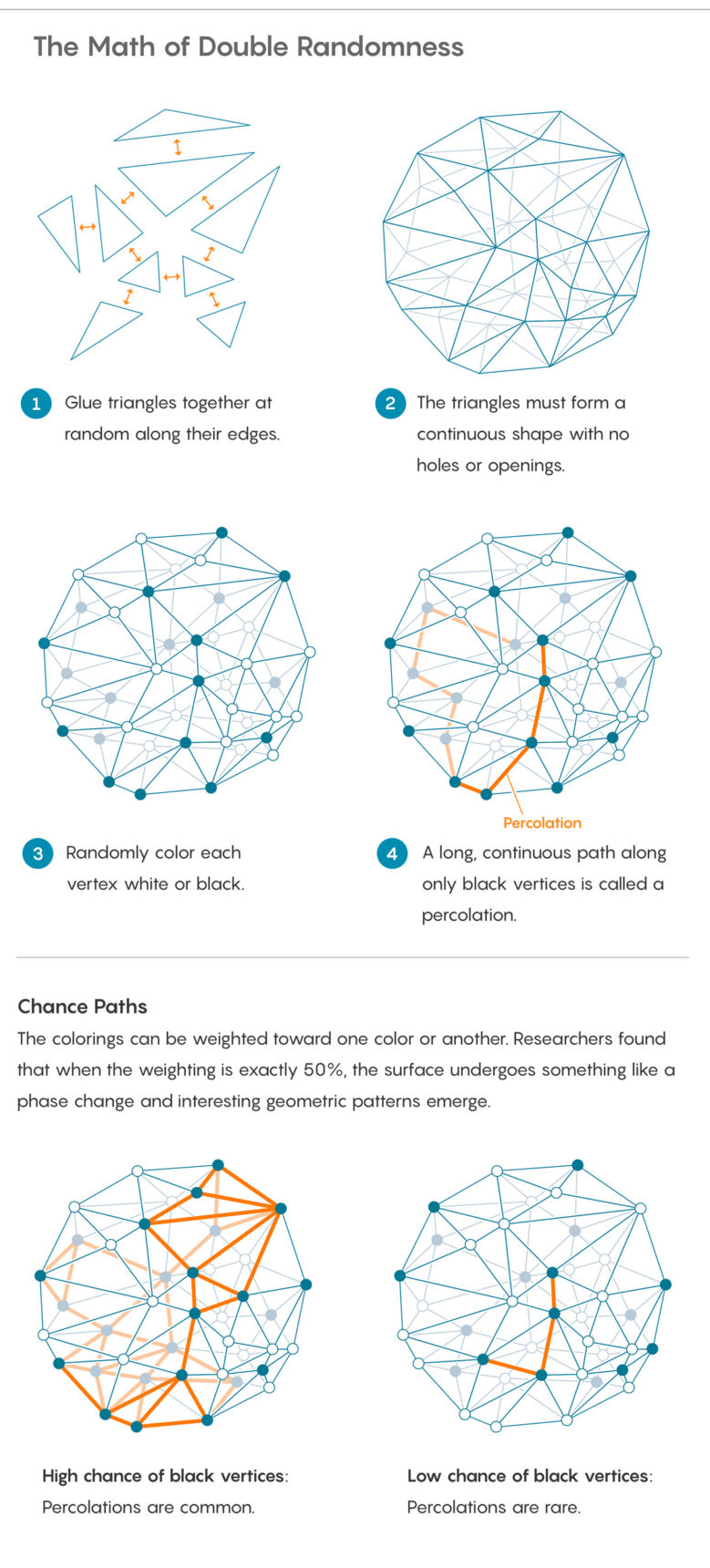
يقوم بيرناردي وكورين ومييرمونت بدراسة الحالات التي تقع بين هاتين الطائفتين - وهي نقطة تحول في التغير في وزن العملة ، عندما يتحول التسرب من ظاهرة شبه مستحيلة إلى ظاهرة مضمونة تقريبًا. يسمون هذه النقطة "عتبة حرجة". هذا مثال على انتقال المرحلة ، تلك اللحظة السحرية عندما يصبح الماء الساخن فجأة بخارًا.
وقال كوريان: "تعني العتبة الحرجة أنه إذا قمت بتغيير معلماتي قليلاً ، فإن سلوك نظامي سيتغير من دراماتيكي إلى دراماتيكي بعلامة مختلفة".
يهتم الفيزيائيون بتحولات الطور لأن العديد من الظواهر الطبيعية الأكثر أهمية تحدث فقط على وشك الوصول. يهتم علماء الرياضيات أيضًا بتحولات الطور ، نظرًا لأن الخصائص الرياضية المهمة تظهر غالبًا في هذه النقاط.
وقال
سكوت شيفيلد ، عالم الرياضيات في معهد ماساتشوستس للتكنولوجيا: "نعلم أن الماء يغلي عند 100 درجة ، مما يخلق كل هذه الأنماط المجنونة ، وأشكال البخار". "في بعض الأحيان يصبح هذا السلوك المجنون والبرّي ممتعًا للغاية. هذه المرحلة الانتقالية تدعونا لفهمها ".
في العمل الجديد ، يثبت ثلاثة علماء رياضيات أن مثل هذا السلوك المجنون يتجلى على وجه التحديد في انتقال المرحلة من التسرب. يظهرون أنه في هذه العتبة الحرجة ، يظهر شكل هندسي - فريد من نوعه وفي نفس الوقت عالمي.
ترتيب مخفي في فرصة
يحدد الجزء الأول من العمل كيفية تصحيح العملة المعدنية بحيث يقع تلوين القمم على العتبة بين وجود وغياب التسرب. يؤكد الحدس ، أنهم يثبتون أن العملة المثالية هي القيمة الحرجة - إعطاء فرصة بنسبة 50 ٪ للسقوط الأسود ، و 50 ٪ من السقوط الأبيض.
هذا هو الجزء الأول من العمل. وقال برناردي: "إننا نثبت أن النصف يحدث شيئًا مثيرًا للاهتمام".
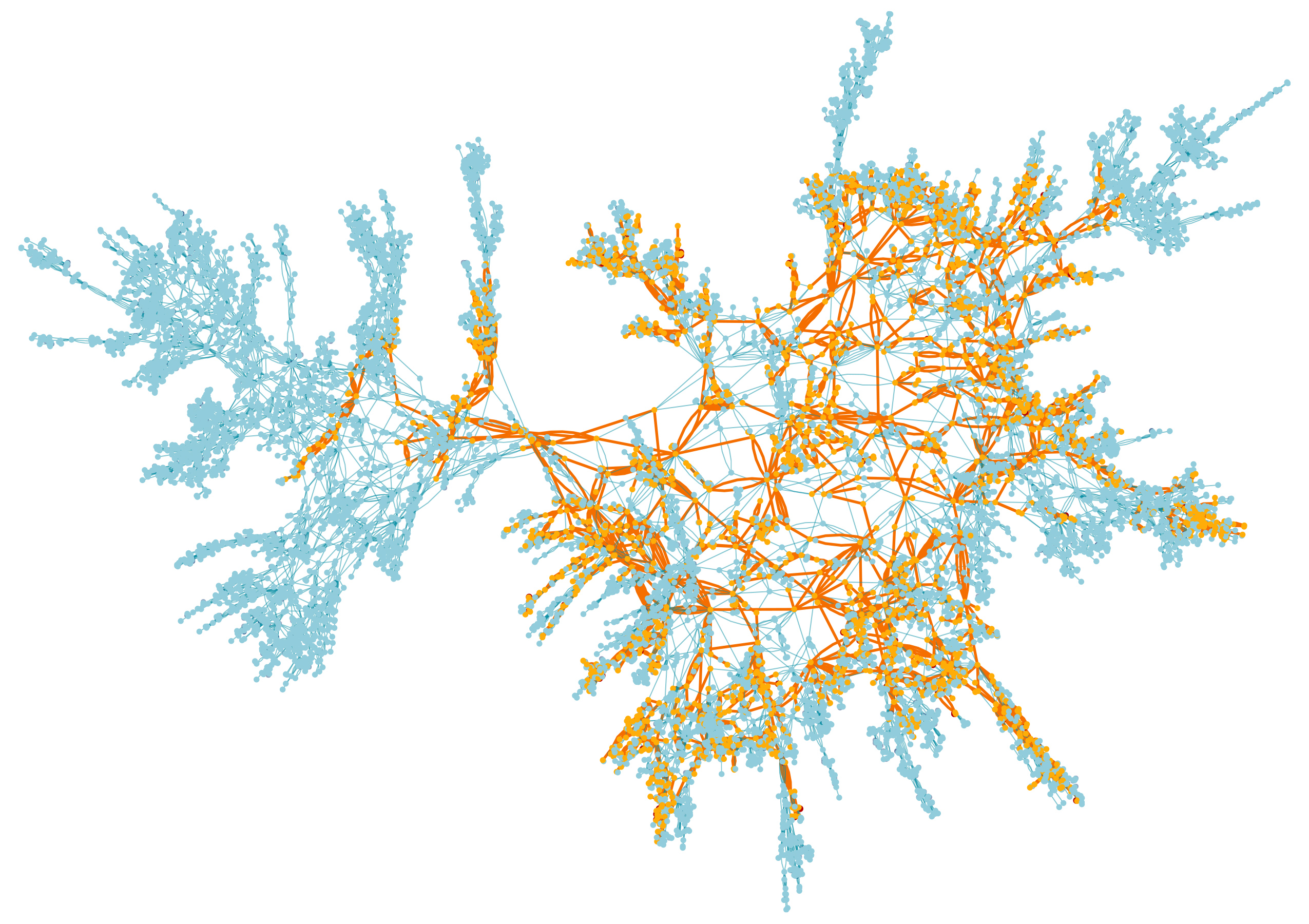خريطة قمم سطح عشوائي ، أكبر مجموعة باللون البرتقاليفي الجزء الثاني ، ندرس نفس الشيء الذي يحدث هناك. تلوين القمم بالأبيض والأسود بعملة معدنية عادلة ، تحصل على توازن جيد بين مجموعات القمم بالأبيض والأسود. تنمو المجموعات حول بعضها البعض ، مثل غابات الأعشاب التي تتنافس على مكان في حديقة متضخمة ، مما يخلق أشكالًا هندسية معقدة لا تظهر عندما تهيمن إحدى الزهور على القمم.
وقال شيفيلد "باختيار المعلمة الحرجة ، تكتشف مجموعات كبيرة". "ومع ذلك ، فهم لا يلونون الأمر برمته ، وهم ليسوا صغارًا".
نظرًا لأن السطح تم إنشاؤه عشوائيًا ، وعملية تلوين القمم تكون عشوائية أيضًا ، فإن المجموعة الكبيرة على سطح ما ستختلف دائمًا عن المجموعة الكبيرة على الجانب الآخر. لكن علماء الرياضيات أثبتوا أنه بالنسبة لجميع الأسطح وكل الطرق الممكنة لتلوين رؤوسهم ، فإن أكبر المجموعات سيكون لها نفس الخصائص. أول ما أثبتوه هو التوزيع الاحتمالي الدقيق لأحجام أكبر المجموعات السوداء على جميع الأسطح. وجدوا أن مجموعة من حجم وسيطة معينة تحدث في أغلب الأحيان ، وأن التردد الذي تظهر به المجموعات الكبيرة أو الأصغر يزداد أضعافا مضاعفة مع المسافة من هذا الوسيط.
يجادلون أيضًا بأن جميع المجموعات الكبيرة يمكن اختزالها إلى نفس الشكل الكنسي ، المعروف باسم "الخريطة الثابتة". تشير الخريطة المستقرة إلى هذه المجموعات بنفس طريقة الحركة البراونية إلى المشي العشوائي. هذا يعني أنه إذا كانت المجموعات الفردية مبعثرة قليلاً - بحيث تكون كل خطوة عشوائية داخل الكتلة أقل وضوحًا في هندسة الشكل ككل ككل - فإن المجموعات سوف تتحول تدريجياً إلى شكل مشترك. تبدو مثل رقاقات الثلج: تبدو فريدة من نوعها في المنطقة المجاورة ، لكن من الواضح أن قواسمها المشتركة مرئية من بعيد.
وقال شيفيلد "لقد وجدوا هذه الخريطة المستقرة ، والحد الطبيعي للتوسع".
يوسع العمل حدود المعرفة المتعلقة بالأشكال والعمليات العشوائية المتراكمة من قبل علماء الرياضيات في السنوات الأخيرة. إنه يكشف لنا أيضًا أنه في تلك اللحظة بالتحديد عندما يبدو النظام العشوائي أكثر فوضوية ، يبدأ ترتيب هندسي استثنائي من خلاله.