AntipovSN و MihhaCF
الجزء الثاني ، الذي فيه Athos لديه كل القواعد ، لكن الكونت دي لا فير ينقصه شيء
UPD الجزء الأول هنا
محدث الجزء الثالث هنا
مقدمة من المؤلفين:
مساء الخير نواصل اليوم سلسلة المقالات المكرّسة لتسجيل النقاط واستخدام نظرية الرسم البياني فيها. يمكنك التعرف على المقالة الأولى هنا .
تم تصميم جميع الرموز الهزلية ، وتدرج ، وما إلى ذلك لتخفيف السرد قليلا وعدم السماح لها الوقوع في محاضرة مملة. نعتذر لكل من لا يشارك في روح الدعابة لدينا
الغرض من هذه المقالة: في أكثر من 30 دقيقة ، لوصف الطرق الرئيسية لتخزين بيانات الرسم البياني ووصف قواعد ومبادئ بناء نموذجنا لتسجيل النقاط للمقترض.
المصطلحات والتعاريف:
- جدول التجزئة هو بنية بيانات تنفذ واجهة صفيف ترابطي ؛ فهي تسمح لك بتخزين الأزواج (المفتاح والقيمة) وتنفيذ ثلاث عمليات: عملية إضافة زوج جديد ، وعملية البحث ، وعملية حذف زوج بالمفتاح. البحث حسب جدول التجزئة ، في المتوسط ، يتم خلال O (1) الوقت.
واجه المدققون الذين عينتهم كورول ش.م.ع لتقييم الجدارة الائتمانية لـ One for All NPO بعض المشكلات. من ناحية ، من السهل جدًا وصف مخطط التفاعل بين 10-15 شركة وإجراء تقييم مبدئي للتفاعل بين الشركات ، وهو ما يكفي للحصول على ورقة وقلم في متناول اليد. ولكن ماذا لو كان لديك معلومات حول تفاعل عشرات أو مئات الآلاف من الشركات؟ على سبيل المثال ، إذا كنت بحاجة إلى وصف تفاعلات Aramis مع كل عواطفه أو D'artagnan مع كل من حارب معه؟
كيفية تخزين البيانات حول هذه التفاعلات؟
ما هياكل البيانات وأساليب الاستخدام؟
سيتعين على مراجعي الحسابات زرع مجموعة من الرهبان من الكتاب لهذا العمل.
لن نقوم بذلك وسنمنح مراجعي الحسابات لدينا معرفة وتقنيات المستقبل ( سنرسل إلى بروميثيوس في شكل T-800 لهم ، مما سيمنحهم ضوء المعرفة ).
حسنًا ، حسنًا ، لنبدأ بالإجابة على الأسئلة المطروحة. فليكن نور!
كما كتبنا ووجهنا هنا ، الرسم البياني هو نسبة مجموعتين - مجموعة من العقد ومجموعة من الحواف. ما هي أفضل طريقة لتخزين الرسم البياني؟
قبل الإجابة على سؤال حول كيفية تخزين الرسم البياني ، عليك أن تقرر بالضبط ما نريد تخزينه وبأي شكل.
وفقًا لنظرية الرسم البياني ، يمكن أن تكون عُقد الرسم البياني أي كائنات بها أي مجموعة من المعلمات (ستكون هذه الحقيقة مفيدة لنا لاحقًا ، بالنسبة للطرز المتقدمة / التكيفية لحساب كرة تسجيل).
إذن ماذا نحتاج إلى تخزين؟
كحد أدنى ، معرف العقدة ومعرفات جيرانها (الذين ترتبط بها). يسمح لك وجود هذه البيانات بالفعل بالبحث في العرض والعمق.
هل أحتاج إلى تخزين بيانات حافة الرسم البياني؟ نعم ، إذا كنا نتعامل مع رسم بياني مرجح. في حالتنا ، نحن نتعامل مع رسم بياني مرجح وفي المقالة الأولى قمنا برسم مثل هذا الرسم البياني.
هل هذه المعلومات كافية؟ لا.
من أين جاءت الضلوع؟ في الكتب المدرسية ، توجد هذه المعلومات ببساطة ، حيث قام شخص ما بجمعها ومعالجتها أمامنا. في القرون الوسطى المتأخرة (التي عاشها الفرسان فقط) ، لم يكلف أحد عناء حساب أوزان حواف الكونت. علينا أن نفعل ذلك بأنفسنا. في هذا المقال والمقال التالي ، لن نصف المنهجية المحددة لحساب وزن الحافة ؛ وسيتم ذلك في المادة 4. الآن من المهم بالنسبة لنا أن نقرر ما هي المعلومات حول الرسم البياني الذي سنخزنه.
لذلك ، في حالتنا ، هناك ثلاثة معايير رئيسية نحتاج إلى معرفتها من أجل حساب درجة التسجيل بشكل صحيح:
- تقييم داخلي للعقدة - يتكون من مؤشرات تميز العقدة (دوران ، دين ، غرامات ، إلخ). في مثالنا ، ستكون هذه:
- تقييم - عقدة جيدة أو سيئة فيما يتعلق NPO "واحد للجميع" ؛
- العقدة المرتبة - الملك لديه أعلى رتبة ، Bonacieux - أدنى ؛
- حجم الأموال ، وبعبارة أخرى ، الملاءة المالية.
- تقييم الأضلاع. في حالتنا ، سيكون تقييم الاتصال لكل عقدة - وهذا يعني أن علاقة Bonacieux - Constance قد لا تساوي اتصال Constance - Bonacieux ، لأن لديهم إمكانيات مختلفة للتأثير على بعضهم البعض.
- مستوى العقدة - لن يتم تخزينه ، لكنه مؤشر مهم.
لا تسأل من أين تأتي كل هذه الأرقام في النموذج ، يرى D'artanyan ذلك. في الحياة الحقيقية ، لن يتم حساب هذه المؤشرات من قبلنا (التجارة ، والديون ، والغرامات ، وما إلى ذلك ، التي نأخذها من المصادر الحالية ، لسنا في العصور الوسطى ، نوعا ما).
من كل ما سبق ، اتضح أنه بالإضافة إلى معرفات العقد ، يجب علينا تخزين معلمات كل عقدة وأوزان الحواف التي نحصل عليها بناءً على تجميع معلمات العقد.
المجموع ، المعلومات التالية خاضعة للتخزين:
- اسم العقدة
- معلمات العقدة
- عقدة الجيران
- وزن الضلع لكل جار.
! ممتاز اكتشفنا ما نحتاج إلى تخزينه. الآن - كيفية تخزين.
ومرة أخرى انحدار صغير.
كيف ستبدو عملية التسجيل لدينا في شكل مبسط:
- جمع بيانات الكائن ؛
- تكوين كائن يصف نموذج الرسم البياني. في هذا المرفق سنقوم بإجراء جميع عمليات التسجيل لدينا.
بناءً على هاتين الخطوتين ، لدينا ثلاثة خيارات:
- نقوم بتخزين بيانات حول كائن التسجيل على خادم SQL / NoSQL. يتم تنفيذ جميع العمليات المتعلقة بالحسابات والخوارزميات وغيرها على الخادم مباشرة ؛
- نقوم بتخزين بيانات حول كائن التسجيل على خادم SQL / NoSQL. بناءً على هذه البيانات ، نقوم بإنشاء كائن منفصل (على سبيل المثال ، جدول تجزئة) ننفذ به جميع الحسابات الأساسية ؛
- يتم تخزين البيانات حول كائن التهديف في ذاكرة الوصول العشوائي. استنادًا إلى هذه البيانات ، نقوم بإنشاء كائن منفصل (على سبيل المثال ، جدول تجزئة) ننفذ به جميع الحسابات الأساسية.
المتطلبات الأساسية لهذه العملية:
- سرعة العمل
- الموثوقية.
- التحقق.
الآن دعنا نتحدث. سنجلس ، مثل فرساننا على فنجان مما شربوه هناك ، الشاي ، على سبيل المثال. الشيء الرئيسي هو أننا لا نتدخل في كل أنواع الديوك مع الحراس.
إذا كانت هناك حاجة لتخزين طويل الأجل ، فيمكنك تحديد جدول مع الحقول المهمة المقابلة. في NoSQL أو RAM ، من الأفضل تخزين البيانات في شكل قائمة أو دليل (جدول التجزئة) للكائنات.
{ 'Id': 1, 'Title': ' ', 'Rang': 4, 'Type': '', 'Profit': 10000 }
مع قمم أكثر أو أقل وضوحا. ما هي أفضل طريقة لتمثيل أقواس / حواف الرسم البياني؟ للقيام بذلك ، تحتاج إلى فهم المبدأ الأساسي لأي عمليات تحليلية على الرسم البياني - يجب أن يحدث الوصول إلى أي قوس / حافة بسرعة كبيرة ، فمن المستحسن أن يكون وقت الوصول مساويا لـ O (1). تتبادر المصفوفة أو المصفوفة إلى الذهن فورًا - وهي بنية يمكن الوصول إليها بسرعة عن طريق الفهرس.
[i، j] - يشير عنصر المصفوفة إلى قوس الرسم البياني ، حيث i هو معرف الرأس الأولي ، j هو معرّف الرأس النهائي ، ويحدث الوصول إلى القمة الأولية واختيارها مباشرةً بواسطة معرف الرأس الأولي. تقاطع i و j يخزن وزن الحافة.
هناك العديد من العيوب لهذا العرض:
- غالبًا ما تكون البنية متكررة ، خاصةً إذا كان الرسم متناثرًا (عدد صغير من الحواف) ، فهناك العديد من القيم الفارغة التي تشير إلى عدم وجود اتصال.
- للعثور على جميع جيران قمة الرأس ، من الضروري الفرز من خلال مجموعة من جميع عناصر الصف إيث لمصفوفة العلاقة.
- لا يمكن تخزين مصفوفة بها العديد من الأعمدة في قاعدة البيانات.
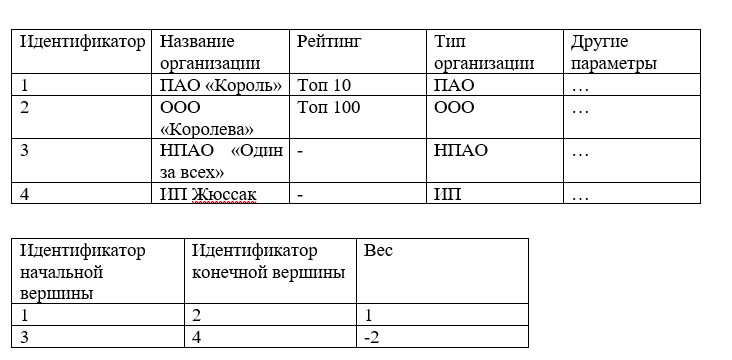
الخيار التالي لتخزين الأقواس / الحواف هو جدول ، أي مجموعة من الأعمدة والصفوف.
على سبيل المثال:

يمكن تخزين هذه البنية بسهولة في قاعدة بيانات علائقية وتحديد القيم اللازمة عند تنفيذ استعلامات SQL ، ولكن عندما يتعلق الأمر بذاكرة الوصول العشوائي (RAM) ، يزداد تعقيد العثور على جميع حواف قمة الرأس ويأخذ في الحالة العامة O (n) حيث n هو رقم كل حواف الرسم البياني.
هناك طريقة أخرى لتخزين الرسم البياني جيدة جدًا للاستخدام في جميع الأنظمة تقريبًا ، خالية من العيوب الموضحة أعلاه - هذا مرجع ذو قيمة مفتاح أو جدول تجزئة. يحدث الحصول على جميع حواف قمة الرأس المرغوبة بسرعة O (1).
هناك نقص كبير في أنه ليس كل لغات البرمجة تدعم هذا التصميم.
كيف يمكن للمرء أن يتخيل بنية مماثلة في أنظمة مختلفة؟
في قاعدة البيانات العلائقية ، يمكنك تطبيق علاقة جداول الكائنات والحواف (الفقرة السابقة)
NoSQL
{ 'Id': 1, 'Title': ' ', 'Rang': 4, 'Type': '', 'Profit': 10000, 'Relations': [{3,2}, {4,5}, … {n, -5}] }
عند الوصول إلى كائن بمفتاحه ، نحصل على الفور على مجموعة من اتصالاته. إذا كان لدينا رسم بياني غير مرجح ، فبدلاً من مجموعة من الكائنات ، يمكنك تمرير صفيف من معرفات العلاقات المجاورة: [3،4 ، ... n]. في شكل مرجع ، المفتاح هو القيمة ، يشبه هذا الخيار الخيار السابق. في الدليل ، المفتاح - القيمة ، يمكنك تخزين نفس الكائن كما في المثال السابق ، سيكون المفتاح ، بالطبع ، هو معرف الرأس (قد يكون هناك رقم ، قد يكون هناك سلسلة ، وما إلى ذلك ، مما يسمح بنظام تطوير معين). أيضًا في الدليل ، يمكنك فقط تخزين صفائف الروابط والمعلومات حول القمم في دليل آخر.
Graf[1] = { 'Id': 1, 'Title': ' ', 'Rang': 4, 'Type': '', 'Profit': 10000, 'Relations': [{3,2}, {4,5}, … {n, -5}] }
أو
graf['one_for_all'] = 'Relations': [{3,2}, {4,5}, … {n, -5}]
على سبيل المثال ، اخترنا خيار تخزين البيانات في ذاكرة الوصول العشوائي مع إنشاء جدول تجزئة لتسجيل البيانات. سيتم كتابة النتائج الوسيطة في ملف على الخادم.
لدينا هياكل تخزين ضعيفة وغير جيدة ، والآن حان الوقت لمعرفة أين نبدأ في بناء نموذجنا التحليلي. لنبدأ برسالة بسيطة - نحدد التفاعل مع أقرب الجيران وجيران الجيران (أصدقاء الأصدقاء).
وبالتالي ، من الممكن تحديد التفاعل مع جميع القمم المترابطة. وفقًا لملاحظاتنا ، فإن التفاعل مع الجيران بشكل أعمق من المستوى 2 أمر مهم فقط في الحالات الخاصة ويتم حسابه بطرق أخرى. تعقيد هذا الحساب كبير جدًا 0 (2 ^ n).
لحساب الكرة ، سوف نستخدم خوارزمية بحث عمق معدلة قليلاً.
سيكون التنقيح على النحو التالي:
- لا نحتاج إلى العثور على قمة محددة ، ولكن يجب الفرز عبر كل الرؤوس إلى عمق n ، لمهمتنا n = 2.
- لا ينبغي لنا تخزين المعلومات غير الضرورية ويجب أن نفترض أنه يمكن إجراء الحساب لأي عقدة في الرسم البياني ، وبالتالي لن يتم تخزين مستوى العقدة في الرسم البياني.
- إذا أدى مساران أو أكثر إلى الأعلى ، فسيتم تقييم جميع المسارات ، لأن نحن نتعامل مع الاتصالات ثنائية الاتجاه ومن الضروري إجراء تقييم كامل لتفاعل العقد.
- يجب أن تكون قادرًا على تحديد مستوى التعشيش لأي قمة لإجراء عملية حسابية محددة.
حسنًا ، حسنًا ، تم إجراء الحسابات النظرية الأساسية ، حتى لو بدت شخصًا بسيطًا وغير عادي. لكن بالنسبة إلينا Gascons ، كل هذا مهم ومثير للاهتمام ، مثله مثل دخول الفرسان الملكيين تقريبًا.
ننتقل إلى التنفيذ العملي. واحد للجميع والجميع لواحد!
سوف التقي بك! سنلتقي بالتأكيد! ربما في 10 سنوات أو 20! لكن قاء!
المقالة التالية قريبة!