حساب الفرضية الفارغة ، على سبيل المثال ، تحليل رواتب المبرمجين الأوكرانيين

قررت مشاركتها ، لكنني لن أنسى كيف يمكن استخدام الأدوات الإحصائية البسيطة لتحليل البيانات. على سبيل المثال ، استخدمنا استطلاعًا مجهولًا بخصوص الرواتب وطول مدة الخدمة ووظائف المبرمجين الأوكرانيين لعامي 2014 و 2019. (1)

خطوات التحليل

• معالجة البيانات الأولية والتحليل الأولي ( أي شخص مهتم بالكود هنا )
• تمثيل رسومي للبيانات. وظيفة كثافة التوزيع.
• نصوغ الفرضية الصفرية (H0) (2)
• اختيار مقياس للتحليل
• نستخدم طريقة bootstraping لتشكيل مجموعة بيانات جديدة.
• نحسب قيمة p (3) لتأكيد أو دحض الفرضية

معالجة البيانات مسبقا

بعد بعض التلاعب ( الرمز هنا ) ، نقدم البيانات في النموذج التالي:

#      ,  . display(data_14_1.head(), data_19_1.head()) print('  : \n \ {} .  14   {}  19 '.format(len(data_14_1), len(data_19_1))) 

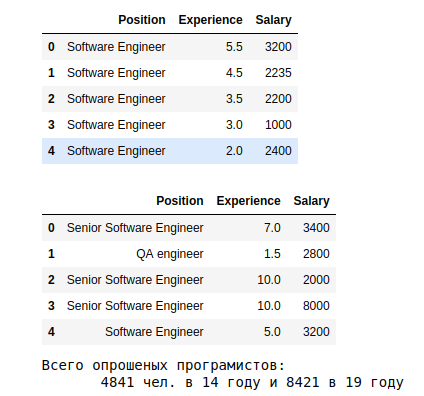
أكثر من ذلك بقليل مجموعات لمدة سنة واحدة (اسمحوا 19):

 # ,  19  display(pd.DataFrame(df.groupby(['Experience'])['Salary'].mean().sort_values(ascending=False)), \ pd.DataFrame(df.groupby(['Position'])['Salary'].mean().sort_values(ascending=False)), \ df.Position.value_counts()) 

التقديرات الأولى هي كما يلي.

أ. تظهر النتائج أنه في المتوسط ​​في عام 19 ، يحصل أولئك الذين كانوا يعملون لأكثر من 10 سنوات على أكثر من 3.5 ألف. الاعتماد على الخبرة -> zp

في. متوسط ​​s.p. في 19 عامًا ، بناءً على التخصص ، يظهرون انتشارًا 10 مرات - من 5k لـ System Architect ، إلى 575 لـ Junior QA.

أ. اللوحة الأخيرة توضح التوزيع حسب المهنة. معظم البيانات حول Software Engineer ، دون مؤهل.

نلفت الانتباه إلى ميزات السنة التاسعة عشرة: هناك خطأ ما في السنة التاسعة من الخبرة ولا يوجد تصنيف وفقًا لمستويات المبتدئين والمتوسطة والكبار. يمكنك فهم أفضل لأسباب نهاية العام التاسع. لكن بالنسبة لهذا التحليل ، نأخذها كما هي.

ولكن مع الفئات - الأمر يستحق الفرز. في 19 ، مهندس البرمجيات 2739 شخص (35 ٪ من الجميع) دون الإشارة إلى مستوى التأهيل. دعونا نحسب المتوسط ​​والانحرافات لأولئك الذين أشاروا.



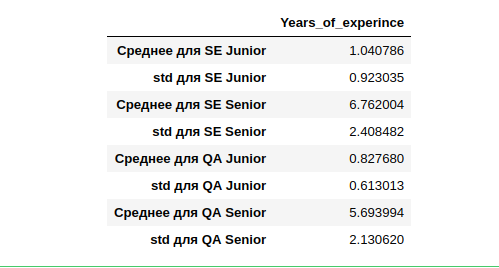
اتضح أن متوسط ​​خبرة العمل (الذي أشار إليها) لـ SE Junior هو عام ، مع انحراف واسع إلى حد ما لمدة سنة واحدة. تتمتع SE Senior بأكبر تجربة مع انحراف كبير مماثل خلال 2.4 عام.

إذا حاولنا حساب الأوسط واستخدام متوسط ​​تجربة أولئك الذين أشاروا إليه ، ثم لتصنيف الشخص الذي لم يشر إلى ذلك ، فقد لا نقوم بتجميع العينة بأكملها بشكل صحيح. سنرتكب أخطاء خاصة في التخصصات الأخرى (وليس SE و QA) ، أي القليل جدا من البيانات. علاوة على ذلك ، هناك عدد قليل منهم للمقارنة مع السنة 14th.

ماذا يمكنني أن استخدم؟

لنأخذ فقط مستوى الراتب كمؤشر موثوق لمستوى المهارة! (أعتقد أنه سيكون هناك معارضة).

أولاً ، نبني كيف يبدو توزيع الرواتب للسنة التاسعة عشرة.





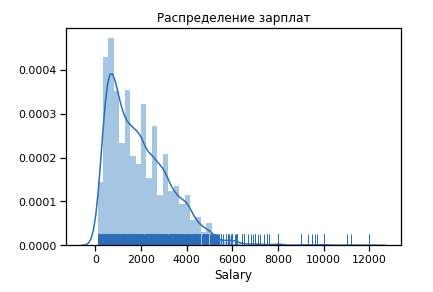
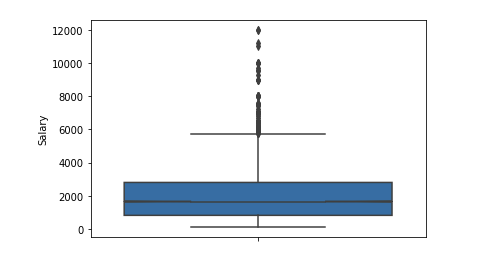
القيم المتطرفة عدد كبير بعد 6 دولار ك. نترك مجموعة من القيود [400 - 4000]. يجب أن يحصل أي مبرمج على أكثر من 400 :)

 df_new = data_19_1[(data_19_1['Salary'] > 400) & (data_19_1['Salary'] < 4000)] sns.distplot(df_new['Salary'], rug=True, norm_hist=True) 

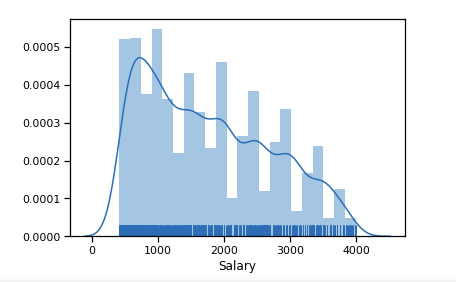
بالفعل أقرب قليلا إلى التوزيع الطبيعي.

نؤلف لمدة 19 سنة ، ومستويات المهارة اعتمادا على طلب تقديم العروض. 3600 دولار المدى يعطينا مقسم جيد إلى 3 فئات - 1200 دولار

 df_new.reset_index() df_new.loc['level'] = 0 df_new.loc[df_new.Salary <= 1200, 'level'] = 'Junior' df_new.loc[(df_new.Salary > 1200) & (df_new.Salary <= 2400), 'level'] = 'Middle' df_new.loc[df_new.Salary > 2401, 'level'] = 'Senior' 

رسم - فئة الكثافة لمدة 19 سنة.

 sns.set(style="whitegrid") fig, ax = plt.subplots() fig.set_size_inches(11.7, 8.27) plt.title('      19 ') sns.barplot(x='level', y='Salary', hue='Experience', hue_order=[1,3,5,7,10], palette='Blues', \ data=df_new, ci='sd') 

بإضافة مقدار الخبرة المحدد (الزاوية اليسرى) ، يمكنك رؤية الفروق الدقيقة المختلفة. على سبيل المثال ، يحصل Junior في المتوسط ​​على ما يصل إلى 1 كيلو مترًا وتجربة عمله 5 سنوات. أكبر مبعثر في sn في Senior (خط قصير أسود في الجزء العلوي من كل عمود) والعديد من التفاصيل الأخرى المثيرة للاهتمام.

هذا هو المكان الذي انتهت فيه المرحلتان الأوليان ، وننتقل إلى اختبار الفرضيات باستخدام أداة التمهيد.

نصوغ الفرضية الصفرية (H0)

في المراحل الأولى ، اكتشفنا أن خبرة العمل المحددة لا تعني بدقة مستوى التأهيل. ثم نشكل الفرضية الفارغة (تلك التي يجب دحضها)

هناك العديد من الخيارات (على سبيل المثال):

• اعتماد المرتب على الأقدمية في عام 14 هو نفسه كما في 19.
• لم تتغير رواتب المبتدئين منذ 14 سنة.

ومع ذلك ، نظرًا لأن التجربة المشار إليها تعد مؤشرًا سيئًا ، وقد يكون حساب بعض الفئات مربكًا ، فإننا نأخذ خيارًا بسيطًا وأكثر موضوعية: متوسط ​​مستوى sn عند 14 ، وهو نفس مستوى 19 ، هو فرضيتنا الخاوية H0 (2).

أي أننا نفترض أن الرواتب لمدة 5 سنوات لم تتغير.

لا الإخلاص للفرضية ، على الرغم من كل الوضوح ، يمكننا التحقق بدقة من خلال حساب القيمة P للفرضية الفارغة.

 #       (14  19 ),    95 % mean_salary_14 = np.mean(data_14_1['Salary']) conf_salary_14 = np.percentile(data_14_1['Salary'], [2.5, 97.5]) mean_salary_19 = np.mean(data_19_1['Salary']) conf_salary_19 = np.percentile(data_19_1['Salary'], [2.5, 97.5]) diff_mean_salary = mean_salary_19 - mean_salary_14 

متوسط ​​الراتب في عام 14 هو 1797 دولار ، حيث فاصل الثقة هو 95 ٪ [300.0 4000.0]
متوسط ​​الراتب في 19 هو 1949 دولار ، حيث فاصل الثقة هو 95 ٪ [300.0 5000.0]

الفرق في متوسط ​​الرواتب في 14 و 19: 152 دولار

متري للتحليل

من المنطقي اختيار القيم المتوسطة كمقياس لدينا. هناك خيارات أخرى ممكنة ، على سبيل المثال الوسيط ، والتي تتم غالبًا في حالة وجود عدد كبير من القيم المتطرفة. ومع ذلك ، فإن المتوسط ​​كتقدير سهل الفهم ويعطي فكرة جيدة أيضًا.

كتابة وظيفة bootstrapping.

 #   bootstraping def bootstrap(data, func): boots = np.random.choice(data, len(data)) return func(boots) def bootstrapping(data, func=np.mean, size=1): reps = np.empty(size) for i in range(size): reps[i] = bootstrap(data, func) return reps 

نحن نحسب إحصائياتنا.

 #  14  19   -       data = np.concatenate((data_14_1['Salary'].values, data_19_1['Salary'].values)) #     2  data_mean = np.mean(data) #      14  19 ,           data_14_shifted = data_14_1['Salary'].values - np.mean(data_14_1['Salary'].values) + data_mean data_19_shifted = data_19_1['Salary'].values - np.mean(data_19_1['Salary'].values) + data_mean #  10000     ,   data_14_bootsted = bootstrapping(data_14_shifted, np.mean, size=10000) data_19_bootsted = bootstrapping(data_19_shifted, np.mean, size=10000) #       .      . mean_diff = data_19_bootsted - data_14_bootsted #  P value               . p_value = sum(mean_diff >= diff_mean_salary) / len(mean_diff) print('p-value = {}'.format(p_value)) 

قيمة p = 0.0

تعتبر القيم P التي تصل إلى 0.05 غير ذات أهمية ، وفي حالتنا ، تساوي 0. مما يعني أن الفرضية الفارغة يتم دحضها - متوسط ​​قيم الراتب في العامين 14 و 19 مختلفان ، وهذه ليست نتيجة عرضية أو عدد كبير من القيم المتطرفة.

لقد أنشأنا 10 آلاف من هذه المصفوفات ، في المتوسط ​​، لم نتمكن من الحصول على ما مجموعه مزيد من هذه الانفصال من البيانات نفسها.

على الرغم من أننا قضينا الكثير من الاهتمام في المرحلتين الأوليين ، قمنا بصياغة الفرضية الصحيحة واخترنا المقياس الصحيح. في المهام الأكثر تعقيدًا ، مع وجود عدد كبير من المتغيرات ، بدون هذه الخطوات الأولية ، يمكن أن تؤدي التحليلات إلى تفسير غير صحيح. لا تخطيهم.

نتيجة لدراستنا لمستوى الرواتب لمدة 14 و 19 سنة ، توصلنا إلى الاستنتاجات التالية:

1. بناءً على بيانات المسح ، فإن التجربة المحددة ليست معيارًا مناسبًا تمامًا لتحديد مستوى الرواتب والمؤهلات.
2. من المرجح أن يستند التقسيم إلى مستوى المهارة إلى مستوى الرواتب.
3. ارتفعت رواتب المبرمجين من 14 إلى 19 (بمعدل 8.5 ٪) وهذه ليست نتيجة عرضية.

شكرا لاهتمامكم سأكون سعيدًا بالتعليقات والنقد.

مصادر

1. https://jobs.dou.ua/salaries/ (نتائج المسح)
2. https://en.wikipedia.org/wiki/Null_hypothesis
3. https://en.wikipedia.org/wiki/P-value