الوضع الحسابي: هزيمة نقطة عائمة في مجالها الخاص. الجزء 1

الجزء 2

من المترجم: كان موضوع تنسيق Posit موجودًا بالفعل على المحور هنا ، ولكن بدون تفاصيل تقنية مهمة. في هذا المنشور ، أوجه انتباهكم إلى ترجمة لمقال جون غوستافسون (مؤلف بوسيت) وإسحاق يونيموتو في تنسيق بوسيت.
بما أن المقال يحتوي على حجم كبير ، فقد قسمته إلى قسمين. قائمة الروابط في نهاية الجزء الثاني.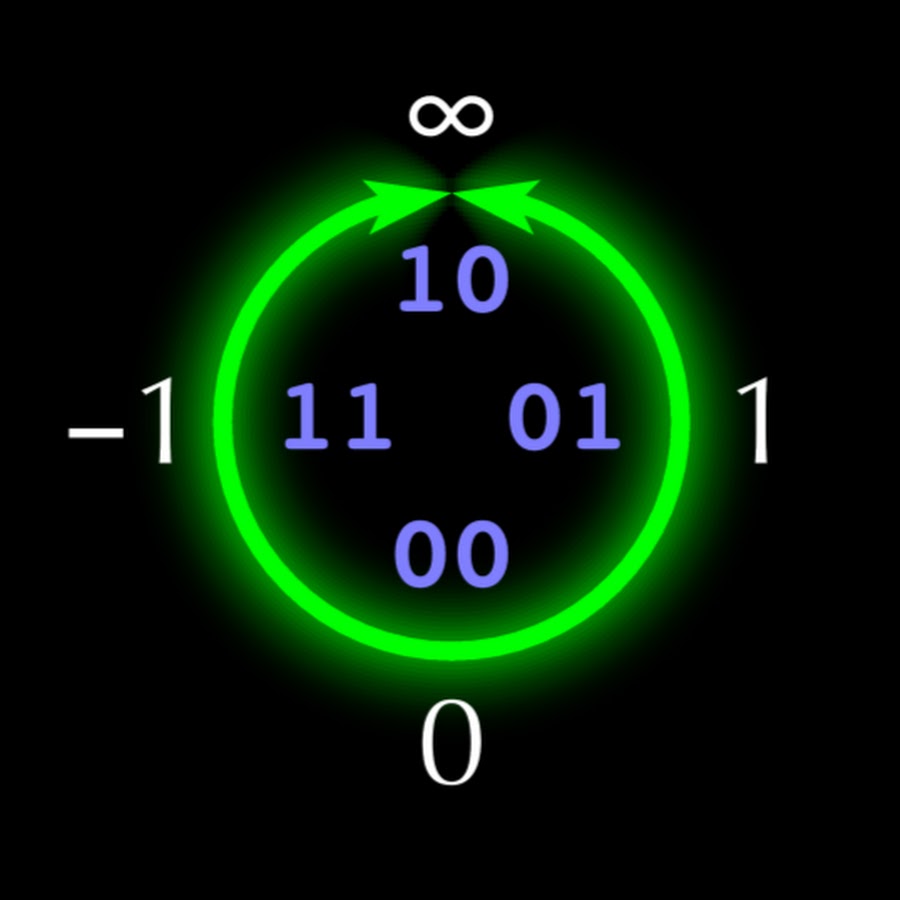



تم تصميم نوع البيانات الجديد ، المسمى posit ، كبديل مباشر لأرقام الفاصلة العائمة لمعيار IEEE 754. بخلاف النموذج السابق ، unum الحسابي ، لا يتطلب المعيار posit استخدام معاملات حسابية أو معاملات متغيرة الحجم ، مثل تطفو ، يتم تقريب الأرقام الافتراضية إذا كانت النتيجة لا يمكن تمثيلها بالضبط. لديهم مزايا لا يمكن إنكارها على التنسيق العائم ، بما في ذلك النطاق الديناميكي الأكبر ، والدقة الأكبر ، وتزامن حركة المرور بنتائج نتائج الحسابات على أنظمة مختلفة ، وأجهزة أبسط ودعم أبسط للاستثناءات. لا تتجاوز الأرقام المفترضة إما إلى ما لا نهاية أو إلى صفر ، و "ليس رقمًا" (ليس رقم ، NaN) هي أفعال وليست مجموعات بت. وحدة المعالجة الافتراضية أقل تعقيدًا من وحدة IEEE FPU. تستهلك طاقة أقل وتحتل مساحة أصغر من السيليكون ، لذلك يمكن للرقاقة إجراء عمليات أكثر بكثير على أرقام افتراضية في الثانية الواحدة من FLOPS ، مع نفس موارد الأجهزة. تستطيع وحدات معالجة الرسومات والمعالجات العميقة ، على وجه الخصوص ، إجراء مزيد من العمليات لكل واط من استهلاك الطاقة ، مما سيؤدي إلى تحسين جودة عملهم.

تم إجراء اختبارات شاملة لمقارنة الوضع المفترض والعائم من حيث دقة الحساب لمختلف دقة الوضع. تعد أرقام المواضع ذات الدقة المنخفضة هي الحل الأمثل لإجراء "عمليات حسابية تقريبية" في الحالات التي تكون فيها الدقة المنخفضة مقبولة. توفر الأرقام المفترضة عالية الدقة دقة أعلى من تعويم من نفس الحجم ؛ في بعض الحالات ، يمكن أن يستبدل الوضع الافتراضي 32 بت بأمان تعويم 64 بت. وبعبارة أخرى ، يفترض الوضع المفترض تعويم في لعبته الخاصة.

النظرية: Unums: النوع الأول والنوع الثاني

يحتوي إطار العمل الحسابي unum (أرقام عالمية ، u num ber) على عدة أشكال لتمثيل الأرقام. النموذج الأصلي هو "النوع الأول" ، وهو مجموعة شاملة من IEEE 754 ؛ إنها تستخدم ubit في نهاية الجزء الكسري للإشارة إلى أن الرقم الحقيقي دقيق أو في النطاق بين الأرقام الحقيقية المجاورة. على الرغم من أن Unum ، مثل float ، لها علامة ، وجزء أسي وجزئي ، فإن أطوال الجزء الأس والكسور تختلف تلقائيًا ، من بت واحد إلى قيمة معينة يحددها المستخدم. يعد Unum Type I طريقة مضغوطة لتمثيل الحساب الفاصل ولكن الأطوال المتغيرة تتطلب جهداً إضافياً. هذا النوع يمكن أن يكرر سلوك تعويم باستخدام وظيفة التقريب خاصة.

نموذج الرقم العالمي "النوع الثاني" [4] لا يتوافق مع تعويم IEEE ، وهو مفهوم نظيف وصارم رياضياً يستند إلى أرقام حقيقية إسقاطية x. الفكرة الأساسية هنا هي أن الأعداد الصحيحة الموقّعة في الكود الإضافي تعيّن بأناقة إلى أرقام حقيقية إسقاطية ، مع نفس خاصية التحويل من الأرقام الموجبة إلى السالبة ، وبنفس الترتيب على محور الأرقام. نقلا عن وليام كاهان [5]:
"إنها توفر مساحة الذاكرة لأنها لا تتلاعب بالأرقام ، لكنها تشير إلى القيم. وهذا يجعل من الممكن جعل الحساب سريعًا جدًا ".
يظهر هيكل unum 5 بت في الشكل. 1. إذا كانت كل وحدة من وحدات unum تحتوي على n bits ، فإن "u-شعرية" تملأ الربع العلوي الأيمن من الدائرة بمجموعة مرتبة من $$$2 ^ {n-3} -1$ أرقام حقيقية $$$x_i$ (ليس بالضرورة عقلاني). في الربع العلوي الأيسر سلبية $$$x_i$ ينعكس نسبة إلى المحور العمودي. يحتوي النصف السفلي من الدائرة على أرقام معاكسة لأرقام النصف العلوي ، تنعكس من المحور الأفقي ، مما يجعل عمليات الضرب والقسمة متماثلة مثل الجمع والطرح. كما هو الحال مع النوع الأول ، تنتهي أرقام unum من النوع II بالرقم 1 (ubit) ، والذي يمثل الفاصل الزمني المفتوح بين النقاط الدقيقة المتجاورة التي ينتهي unum بـ 0 .


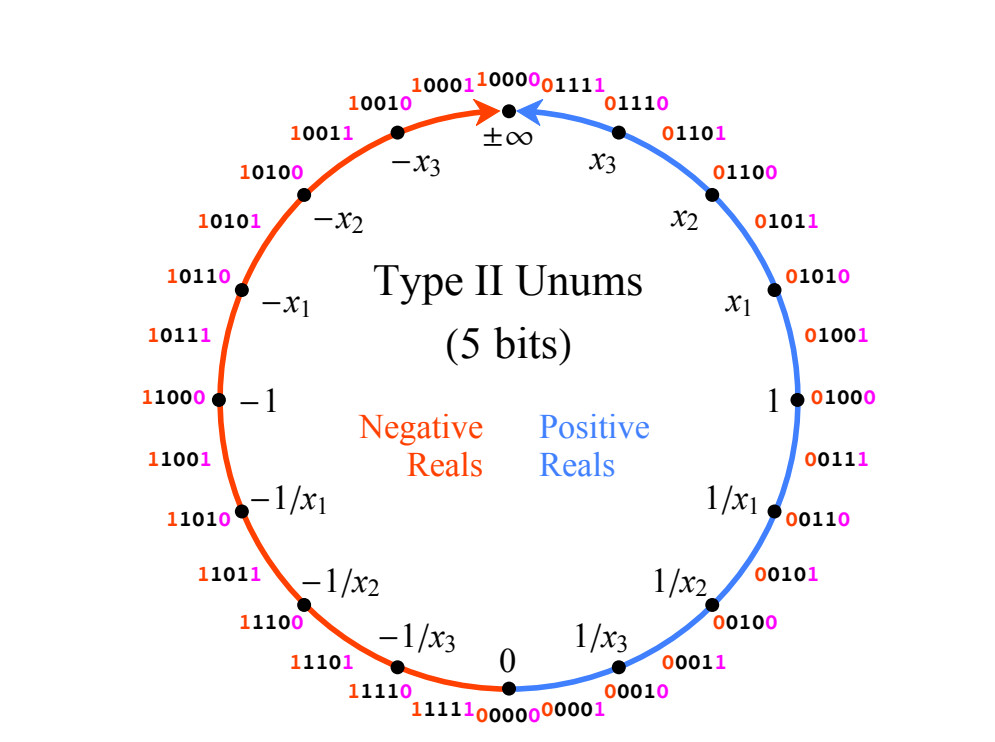التين. 1. سطر الأرقام الحقيقية الإسقاطية ، المعيّن إلى أعداد صحيحة في رمز إضافي يبلغ طوله 4 بتات.

تحتوي أرقام unum من النوع الثاني على العديد من الخصائص الرياضية المثالية ، ولكن تتم معظم العمليات باستخدام جداول البحث . إذا كانت هناك حاجة إلى وحدات بت الدقة n ، فسيكون الجدول (في أسوأ الحالات) $$$2 ^ {2n}$ قيم وظيفة الوسيطتين ، ولكن مع الأخذ في الاعتبار التماثلات والحيل الأخرى ، يمكن تقليل الجدول إلى حجم مقبول. يحد حجم الجدول من حجم هذا التنسيق فائق السرعة إلى 20 بت أو أقل لتكنولوجيا اليوم. النوع الثاني من أرقام unum أيضًا لا تفسح المجال لدمج العمليات. كانت أوجه القصور هذه بمثابة حافز للعثور على نسق يحتفظ بالعديد من خصائص أرقام النوع الثاني unum ، ولكنه أكثر "ملاءمة للأجهزة" ويمكن حسابه بواسطة دوائر منطقية مشابهة للوحدات FPU الحالية.

2. الأرقام Posit وصالحة

هناك طريقتان متعارضتان للحسابات بالأرقام الحقيقية:

• ليست صارمة ، ولكن رخيصة ، ومقبولة لعدد كبير من التطبيقات العملية
• صارمة رياضيا ، حتى على حساب الوقت والذاكرة

البيان الأول يتعلق بحساب حقيقي ، يكون فيه خطأ التقريب صغيرًا بدرجة كافية ، ويتعلق البيان الثاني بحساب الفاصل. يمكن أيضًا اعتبار أعداد Unum من النوعين الأول والثاني في سياق مشابه ، وهذا أحد أسباب كونها "أرقام عالمية". ومع ذلك ، إذا كنا سنستخدم دائمًا بعض الوظائف للتقريب بعد كل عملية ، فمن الأفضل عدم استخدام البت الأخير باعتباره جزءًا مهمًا من الجزء الكسري وليس كـ ubit. سيتم استدعاء الرقم unum من هذا النوع الرقم posit.

اقتباس من قاموس أوكسفورد الأمريكي الجديد ، الإصدار الثالث:

posit (اسم): بيان تم الإدلاء به على افتراض أنه سيصبح صحيحًا.

من أجل تبسيط تطبيق الأجهزة ، تضعف أرقام unum من النوع II إحدى القواعد: توجد القيم العكسية الدقيقة فقط لـ 0 ، $$$\ مساء \ infty$ ودرجات اثنين. هذا يسمح لنا بملء شبكة u بحيث تبقى الأرقام النهائية مماثلة للعوم ، وسيكون لها النموذج $$$m \ cdot2 ^ k$ حيث k و m أعداد صحيحة. لا توجد فواصل زمنية مفتوحة.

صالح هو زوج من الأرقام الافتراضية ذات الحجم المتساوي ، وينتهي كل منها بالرقم. تم تصميمها للاستخدام في تلك التطبيقات حيث من المهم تحديد الرقم في الفاصل الزمني بدقة ، على سبيل المثال ، عند تصحيح الخوارزميات الرقمية. القيم الصالحة أقوى من حساب الفاصل العادي وأقل عرضة للتوسع السريع في حدود الفاصل المتشائم المفرط [2 ، 4]. ومع ذلك ، فهي ليست موضوع هذا المنشور.

يوضح الشكل 2 بنية التمثيل الافتراضي n بت مع الأس الأس.


الشكل 2. الشكل العام المعمم لتتبع القيم غير الصفرية

تحتوي علامة الإشارة على 0 للأرقام الموجبة ، و 1 للأرقام السالبة. بالنسبة للأعداد السالبة ، ابحث عن الملحق 2 قبل فك تشفير النمط والجزء والكسور. لفهم بتات الوضع ، ضع في اعتبارك السلاسل الثنائية الموضحة في الجدول 1 ، حيث تعني k طول التسلسل البادئ ، و x في تدفق البتات تعني حالة غير مبالية.

الجدول 1. المدى البعيد يعني ك من بت النظام



نحن نسمي طول التسلسل القيادي وضع الأرقام. تبدأ السلاسل الثنائية بعدد معين من الأصفار أو تلك الموجودة في صف ، متبوعة بالبت المقابل ، أو يتم الوصول إلى نهاية السلسلة. يتم تمييز وحدات البت في وضع الكهرمان ، ويتم تمييز البت المعاكس باللون البني. اسمحوا m أن يكون عدد البتات المتطابقة في التسلسل ، إذا كانت هذه البتات صفراً ، ثم k = -m ، إذا كان 1 ، ثم k = m-1. يمكن لمعظم المعالجات العثور على الوحدة الأولى في كلمة أو الصفر الأول في كلمة في الأجهزة ، أي أن منطق فك الترميز متاح بالفعل. الوضع يعني عامل تحجيم يساوي $$$useed ^ k$ حيث $$$useed = 2 ^ {2 ^ {es}}$ . يوضح الجدول 2 مثال لقيم الاستخدام.

الجدول 2. useed كدالة es



البتات التالية (المظللة باللون الأزرق في الشكل) هي الأس ، والتي تشير إلى عدد صحيح غير موقَّع. لا يتم تغييره ، كما هو الحال في العوامات ، فهو يمثل التحجيم إلى $$$2 ^ e$ . قد يكون هناك ما يصل إلى es بت الأس ، وهذا يتوقف على عدد البتات التي يتم تركها إلى يمين بت الوضع. هذه طريقة مضغوطة لتغيير الدقة ؛ فالأرقام القريبة من 1 في القيمة المطلقة لها دقة أكبر من الأرقام الكبيرة جدًا أو الصغيرة جدًا ، والتي تعد أقل شيوعًا في العمليات الحسابية.

إذا بقيت بتات بعد الوضع وبت الأس ، فإنها تمثل الجزء الكسري ، f ، تمامًا مثل الجزء الكسري 1.f بالتنسيق العائم ، لكن البتة المخفية دائمًا 1. لا توجد أرقام غير معتدلة بها 0 مخفي ، على عكس التعويم.

النظام الذي وصفناه هو نتيجة طبيعية لملء شبكة u. لنبدأ بوضع بسيط 3 بت ، للتوضيح ، في التين. يوضح الشكل 3 فقط النصف الصحيح من الأرقام الحقيقية الإسقاطية. لذلك ، فإن الأرقام في التين. 3. إطاعة قواعد النوع الثاني. لا يوجد سوى قيمتين خاصتين: 0 (جميع البتات هي 0) و ± ∞ (وحدة متبوعة بجميع الأصفار) ، ولا يتبع تسلسل البتات الترميز الموضعي. بالنسبة للقيم الافتراضية الأخرى في الشكل 3. ، يتم تلوين البتات كما هو موضح أعلاه. لاحظ أن جميع القيم الموجبة في الشكل 3 هي قيم مفيدة في الدرجة k ممثلة بتات الوضع.


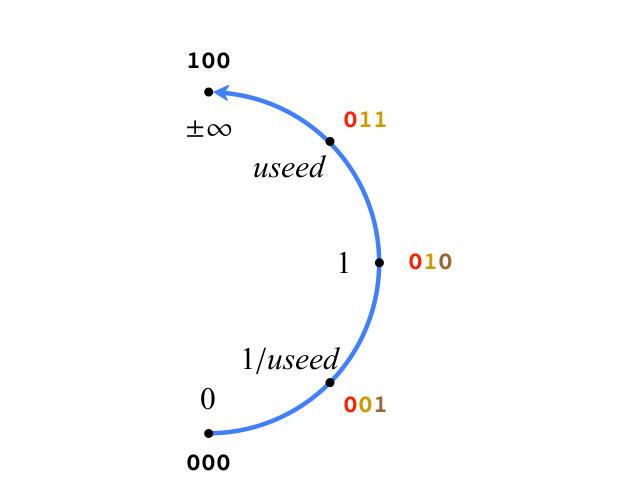الشكل 3. القيم الإيجابية لل 3 بت ايجابية

تزداد دقة أرقام Posit عند إضافة البتات ، وتبقى القيم في مكانها على الدائرة عند إضافة البتة 0. وعندما تتم إضافة 1 ، يتم إنشاء قيمة جديدة بين القيمتين الموجودين في الدائرة. ما القيمة العددية التي يجب أن نخصصها لهم؟ اجعل maxpos أكبر قيمة موجبة ويقلل أصغر قيمة موجبة على الدائرة المحددة بسلسلة البت. في الشكل 3 ، يتم استخدام maxpos ، و minpos هو 1 / useed. قواعد الاستيفاء هي كما يلي:

بين maxpos و ± ∞ ، القيمة الجديدة هي maxpos × useed ؛ بين 0 و minpos ، القيمة الجديدة هي minpos / useed (مع بت الوضع الجديد)
بين القيم الحالية $$$x = 2 ^ m$ و $$$y = 2 ^ n$ ، حيث يختلف m و n بأكثر من 1 ، ستكون القيمة الجديدة هي الوسط الهندسي ، $$$\ sqrt {x \ cdot y} = 2 ^ {(m + n) / 2}$ (مع بت الأس الجديد).
في حالات أخرى ، توجد القيمة الجديدة في الوسط بين x و y ، أي أنها حسابية ، $$$(س + ص) / 2 دولا$ (مع بت كسري جديد)

كمثال ، التين. يوضح الشكل 4 بناء الأعداد المفترضة من 2 إلى 5 بتات باستخدام المعادلة es = 2 ، وبالتالي تستخدم = 16.


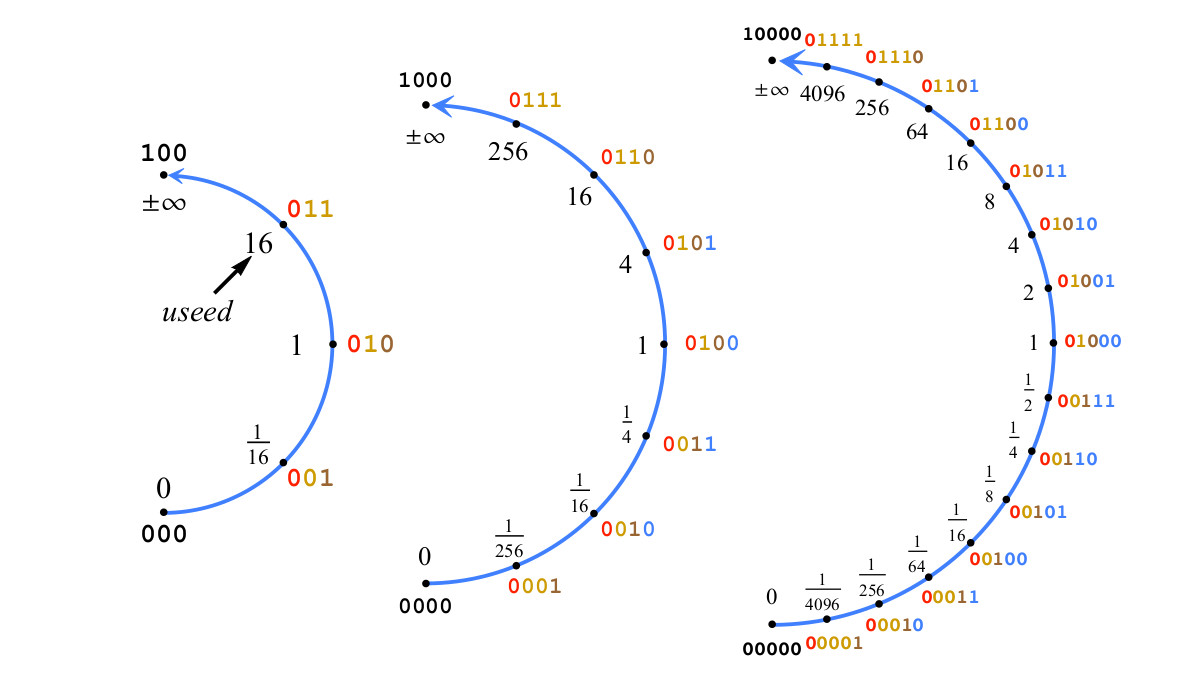التين. 4. بناء الموقف مع اثنين من القطع من الأس ، $$$es = 2 ، useed = 2 ^ {2 ^ {es}} = 16 دولارً$

إذا في التين. 4 أضف واحدًا إضافيًا للحصول على posit 6-bit ، إلى الأعداد المفترضة التي تمثل نطاقات القيم بين 1/16 و 16 ، سيتم إضافة جزء الجزء الكسري ، وليس بت الأس. ضع في اعتبارك سلسلة من البتات تمثل الرقم المفترض p كعدد صحيح موقّع ، يتراوح من $$$-2 ^ {n-1}$ إلى $$$2 ^ {n-1} -1$ . دع k يكون عددًا صحيحًا يمثل بتات الوضع ، e هو رقم غير موقّع يمثل بت الأس ، إذا كان موجودًا. إذا كانت مجموعة البت جزءًا بسيطًا $$$\ {f_1f_2 ... f_ {f_s} \}$ ربما فارغة ثم ترك f قيمة تمثل رقمًا $$$1 ، f_1f_2 ... f_ {f_s}$ . ثم يمثل ع

$$

$$x = \ start {cases} 0 & & p = 0، \\ \ pm \ infty، & p = -2 ^ {n-1}، \\ sign (p) \ times useed ^ k \ times 2 ^ e \ times f \، & \ text {any other} p \ end {cases}$$

يؤدي كل من الوضع وبت es نفس الوظيفة مثل البتات الأسية في التعويم القياسي ، حيث يحددان معًا عامل قياس مساوٍ لقوة اثنين ، وكل زيادة استخدام تعني تحولاً $$$2 ^ {es}$ الشيء. عدد maxpos هو $$$useed ^ {n-2}$ و minpos يساوي $$$useed ^ {2-n}$ . يوضح الشكل 5 مثالاً لفك تشفير الرقم المفترض (بقيمة "غير قياسية" لـ es ، من أجل البساطة).


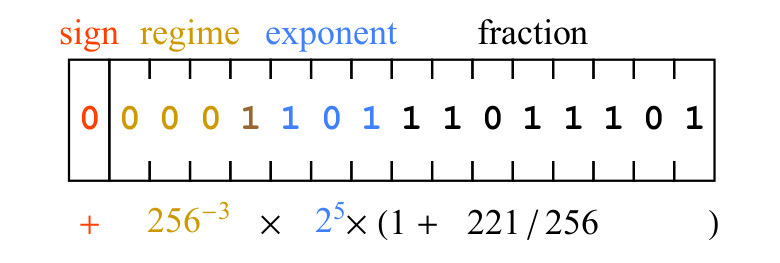التين. 5. مثال على سلسلة البت المفترضة ومعناها الرياضي

يعني القليل من علامة 0 أن القيمة موجبة. تحتوي بتات النمط 0001 على تسلسل من ثلاثة أصفار ، مما يعني أن k = -3 ، وبالتالي فإن عامل القياس الذي أدخلته بتات الوضع هو $$$256 ^ {- 3}$ . تمثل بت الأس ، 101 ، 5 كعدد صحيح ثنائي غير موقّع ، وعامل تحجيم الإدراج هو $$$2 ^ 5$ . أخيرًا ، تمثل أجزاء الجزء الكسري 11011101 الرقم 221 ، أي الجزء الكسري هو 1 + 221/256. التعبير المكتوب تحت bitfield في الشكل 5. يقودنا إلى النتيجة $$$477/134217728 \ approx3.55393 \ times10 ^ {- 6}$

2.2. 8 بت التدريب العصبي والشبكة العصبية

على الرغم من حقيقة أن معيار IEEE لا يحدد العوامات ذات 8 بتات ، فقد أثبتت الأعداد المفترضة من 8 بتات مع es = 0 فائدتها لبعض الأغراض ، فهي مفيدة للغاية لبناء الشبكات العصبية [3 ، 8]. حاليًا ، غالبًا ما يتم استخدام أرقام IEEE نصف الدقة (16 بت) لهذه الأغراض ، ولكن من المحتمل أن تتم معالجة الأرقام الافتراضية 8 بت بشكل أسرع مرتين إلى أربع مرات. وظيفة مهمة في الشبكات العصبية هي السيني ، الذي يحتوي على خط مقارب 0 لـ $$$x \ إلى- \ infty$ و 1 ل $$$x \ إلى \ infty$ . منظر عام لوظيفة السيني $$$1 / (1 + e ^ {- x})$ وهي مكلفة للحسابات ، ويمكن أن تتطلب بسهولة أكثر من مائة دورة من المعالج لاستدعاء الدالة exp (x) من المكتبة وبسبب الانقسام. باستخدام الأرقام المفترضة ، يمكنك ببساطة عكس البتة الأولى من الرقم الذي يمثل x ، وتحويل البتات رقم 2 إلى اليمين ، وملء البتات على اليسار بالأصفار ، ووظيفة البوزيت الناتجة ، الموضحة في الشكل 6. أرجواني ، بالقرب من السيني (كما هو موضح باللون الأخضر) ، وحتى لديه نفس الميل عند عبور المحور ص.


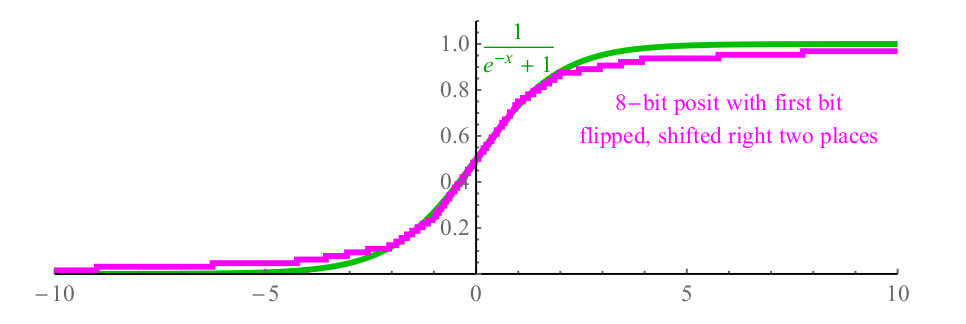التين. 6. وظيفة السيني السريع باستخدام التمثيل الافتراضي

2.3. يستخدم لتحقيق وتجاوز النطاق الديناميكي للطفو

نحدد النطاق الديناميكي لنظام الأرقام على أنه عدد الأوامر العشرية من الأصغر إلى القيمة النهائية الإيجابية الأكبر ، من minpos إلى maxpos. وهذا هو ، يتم تعريف النطاق الديناميكي كما $$$log_ {10} (maxpos) −log_ {10} (minpos) = log_ {10} (maxpos / minpos)$ . بالنسبة إلى poset ذي 8 بت مع es = 0 ، تكون minpos هي 1/64 و maxpos هي 64 ، وبالتالي فإن النطاق الديناميكي هو 3.6 ترتيب عشري. الأرقام الافتراضية المحددة بـ es = 0 أنيقة وبسيطة ، ولكن إصداراتها 16 و 32 بت لها نطاق ديناميكي أصغر من تعويم IEEE من نفس الحجم. على سبيل المثال ، يحتوي تعويم IEEE ذي 32 بت على نطاق ديناميكي من 83 عامًا ، لكن في الوضع 32 بت مع es = 0 سيكون له نطاق ديناميكي يبلغ 18 عامًا فقط.

يوجد أدناه جدول لقيم es التي تسمح للأرقام المفترضة بتجاوز النطاق الديناميكي للتعويم بأحجام 16 و 32 بت ، وتقترب منه بأحجام 64 و 128 و 256 بت.

الجدول 3. النطاقات الديناميكية للطفو والموجبة لعدد متساوٍ من البتات



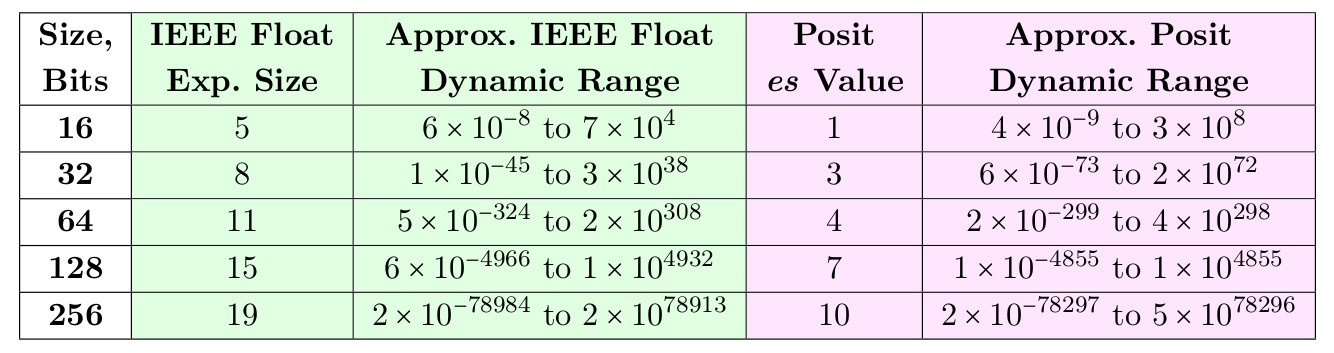
أحد أسباب اختيار es = 3 لـ posit 32 بت هو أنها في هذه الحالة يمكن أن تكون بديلاً بسيطًا ليس فقط لتعويم 32 بت ، ولكن أيضًا 64 بت. وبالمثل ، فإن النطاق الديناميكي الذي يبلغ 17 عامًا للوضع الافتراضي 16 بت يمهد الطريق أمامهم في التطبيقات التي تستخدم حاليًا العوامات 32 بت. نظهر أن البوزيت يمكن أن يتفوق على التعويم في النطاق الديناميكي والدقة بنفس حجم البت.

2.4. المقارنة النوعية لتنسيقات Float و Posit

لا يوجد "NaN" في التنسيق الافتراضي ، وبدلاً من ذلك ، تتم مقاطعة الحسابات ، ويجب على معالج المقاطعة الإبلاغ عن خطأ أو معالجة الخطأ بطريقة ما ومتابعة الحساب ، لكن الأرقام الافتراضية لا تسمح بتعيين قيمة معينة تشير إلى خطأ منطقي ، وهو ، بحكم التعريف ، هو الرقم. هذا يبسط إلى حد كبير الأجهزة. إذا رأى مبرمج الحاجة إلى استخدام قيم NaN ، فهذا يدل على أن البرنامج لم يكتمل بعد ، ويجب استخدام أرقام صالحة في بيئة تصحيح الأخطاء لإيجاد مثل هذه الأخطاء والقضاء عليها. أيضا ، ليس لديه افتراض $$$+ \ infty$ و $$$- \ infty$ ، مثل تعويم ، ومع ذلك ، أرقام صالحة تدعم فواصل زمنية مفتوحة $$$(maxpos ، + \ infty)$ و $$$(- \ infty ، - mpospos)$ ، التي تجعل من الممكن تمثيل قيمة غير محدودة لأي علامة ، والحاجة إلى اللانهاية الموقعة سيعني فقط أنه بدلاً من الأرقام المفترضة ، تحتاج إلى تطبيق قيم صالحة.

أيضًا في العرض الافتراضي ، لا يوجد "صفر سلبي" ، صفر سالبة ، وهذا عيب منطقي آخر موجود في معيار تعويم IEEE. مع الأرقام المفترضة ، إذا كانت a = b ، ثم f (a) = f (b). يقول معيار IEEE 754 أن الرقم المقلوب إلى -0 هو $$$- \ infty$ ، والرقم معكوس لـ +0 هو $$$+ \ infty$ ، ولكن يقول أيضًا أن -0 هي +0. لذلك ، من المفهوم ذلك $$$- \ infty = + \ infty$ ؟

تحتوي الأرقام العائمة على خوارزمية مقارنة متطورة a = b. إذا كان أي من (a ، b) NaN ، تكون نتيجة المقارنة سلبية دائمًا ، حتى لو كان تمثيل البت فيها هو نفسه. إذا كان تمثيل البت مختلفًا ، فلا يزال هناك احتمال أن تساوي a b ، بما أن الصفر السلبي يساوي الصفر الموجب! في posix ، يكون التحقق من المساواة هو نفسه بالنسبة للأعداد الصحيحة: إذا كانت البتات متساوية ، تكون الأرقام متساوية. إذا كان أي شيء مختلف ، فهي ليست متساوية. ترتبط الأعداد المفترضة بنفس العلاقة (a <b) مثل الأعداد الصحيحة الموقعة مثل الأعداد الصحيحة الموقعة ، يجب عليك التأكد من عدم وجود تجاوز في السعة مع تغيير في الإشارة ، لكنك لا تحتاج إلى إرشادات جهاز منفصلة لمقارنة البوزيت ، إذا كان لديك تعليمات لمقارنة الأعداد الصحيحة الموقعة.

في النسق المفترض ، لا توجد أرقام غير طبيعية ، أي أنه لا توجد مجموعة بت خاصة تُظهر أن البت المخفي يساوي 0 بدلاً من 1 . لا يستخدم Posit anti-overflow ، بدلاً من ذلك ، يتم استخدام انخفاض تدريجي في الدقة ، والذي يوفر وظيفة anti-overflow وحالة التماثل الخاصة به ، overflow (على عكس posit ، فإن float القياسي غير متماثل ، ويستخدم أنماط البت هذه لتمثيل مجموعة كبيرة وغير مجدية من قيم NaN).

يتميز التنسيق العائم بميزة واحدة على الوضع المفترض ، عند تطوير الأجهزة ، ترتيب ثابت لبت الأس والجزء الكسري يسمح بفك تشفيرها بالتوازي.في التنسيق الافتراضي ، تحتاج إلى اتباع بعض التسلسل ، أولاً فك تشفير بت الوضع ، ثم البتات المتبقية. هناك طريقة بسيطة للتغلب على هذا التقييد ، على غرار الخدعة المستخدمة لزيادة سرعة معالجة الاستثناء في الطفو: تتم إضافة عدة بتات إضافية إلى كل قيمة بحيث تخزن معلومات الحجم عند فك تشفير التعليمات.

3. التوافق bitwise والعمليات مجتمعة

أحد الأسباب التي لا تعطي IEEE float نتائج متطابقة على أنظمة مختلفة هو بسبب وجود وظائف أولية ، مثل $$$log(x)$ و $$$cos(x)$لا يتطلب IEEE الدقة حتى آخر جزء لأي إدخال ممكن. يجب على بيئة الوضع الافتراضي تقريب جميع نتائج العمليات الحسابية المدعومة بشكل صحيح. (بعض المبرمجين في مكتبة الرياضيات قلقون بشأن "معضلة جدول المعضلة" ، وهو أنه بالنسبة لبعض القيم قد يكون الأمر مكلفًا للغاية لتحديد التقريب الصحيح ، يمكن حذف ذلك باستخدام جداول الاستيفاء بدلاً من التقديرات متعددة الحدود.) قيمة غير صحيحة في الجزء الأخير من الوظيفة.$$$e^x$، على سبيل المثال ، قد يؤدي في النهاية إلى نظام كمبيوتر يخبرنا أن 2 + 2 = 5.

السبب الأكثر جوهرية لعدم تعويم IEEE نتائج مكررة على أنظمة مختلفة هو أن المعيار يسمح باستخدام الأساليب المحجبة لتجنب التدفق الزائد / مكافحة التدفق الزائد ، وزيادة دقة العمليات ، مثل تخزين بت حمل إضافي داخليًا للتسوية والكسرية جزء. يحظر الحساب الافتراضي مثل هذه الحيل الخفية.

يتضمن الإصدار الأخير (2008) من معيار IEEE 754 [7] عملية الجمع المضاعف المدمجة في المتطلبات. كان هذا تغييرًا مثيرًا للجدل ، ولم تتم الموافقة عليه من قبل العديد من أعضاء اللجنة. تؤدي العمليات المدمجة إلى تأخير عملية التقريب حتى تكتمل العملية الأخيرة في الحساب ، والتي تتضمن أكثر من عملية واحدة ، بعد الانتهاء من جميع العمليات ، بما في ذلك العمليات الصحيحة الصحيحة. الجمع بين العمليات ليس هو نفسه العمليات الحسابية ذات الدقة القابلة للتوسيع ، والتي يمكن أن تزيد من طول الأعداد الصحيحة حتى تصبح ذاكرة الكمبيوتر ممتلئة.

تتطلب البيئة الافتراضية وجود العمليات المدمجة التالية:

الجمع بين الضرب$$$(a\times b)+c$
الجمع بين الضرب $$$(a+b)\times c$
الجمع بين الضرب ، الضرب ، الطرح $$$(a\times b)-(c\times d)$
الجمع الجمع $$$\sum a_i$
الجمع العددية الضرب $$$\sum a_i b_i$

لاحظ أن جميع العمليات من القائمة أعلاه هي مجموعة فرعية من الضرب العددي المدمج [6] من حيث متطلبات أجهزة المعالج. أصغر رقم غير صفري يمكن الحصول عليه باستخدام الضرب العددي هو$$$minpos^2$ . أي منتج هو عدد صحيح مرات $$$minpos^2$ . إذا كنا نريد الحصول على منتج العددية من المتجهات $$$\{maxpos, minpos\}$ و $$$\{maxpos, minpos\}$ كعملية دقيقة في منطقة الصفر ، نحتاج إلى حجم كبير بما يكفي للتخزين $$$maxpos^2/minpos^2$ . أذكر ذلك $$$maxpos=useed^{n-2}$ و $$$minpos=1/maxpos$ . بهذه الطريقة $$$maxpos^2/minpos^2=useed^{4n-8}$ .مع الأخذ في الاعتبار وحدات النقل والتقريب حتى قدرة اثنين ، نحصل على القيم الموصى بها الواردة في الجدول 4.

جدول 4. الأحجام الدقيقة للبطارية لكل حجم مفترض ،



وفي بعض الحالات ، يكون حجم البطارية مماثلًا لحجم السجل ؛ وفي حالات أخرى ، يلزم وجود منطقة خدش مكافئة للذاكرة المؤقتة L1 أو L2. يمكن تنفيذ العمليات المدمجة مع برنامج أو جهاز ، ولكن يجب أن تكون متاحة للتنفيذ في بيئة افتراضية.