كيف سيساعد التشابك الكمومي في اكتشاف موجات الجاذبية

لقد أجرينا مؤخرًا تجربة لاختبار نهج جديد لتقليل الضوضاء الكمومية في LIGO وكتبنا مقالًا عنها ، انظر arXiv: "شرح لتحسين مقياس التداخل من خلال تشابك EPR" . وهنا سوف أخبرك ما هي الضوضاء الكمومية في LIGO ، وكيف يمكن تقليلها ، وما علاقة التشابك الكمي والضوء المضغوط به.

UPD مقالة نشرت في الطبيعة الضوئيات .

1. حساسية LIGO والضوضاء الكم

تحدثت عن كيفية عمل المكشاف والضوضاء الموجودة فيه بالتفصيل في المنشور الأخير عن تلسكوب أينشتاين . يحتوي الكاشف على مجموعة واسعة من الضوضاء: الزلزالية ، الحرارية ، الكم ، وغيرها - وكلها تتداخل مع تسجيل إشارة من موجات الجاذبية.


المساهمات الرئيسية في حساسية LIGO على ترددات مختلفة ، تطبيع إلى سعة GW (سلالة).

تكمن الصعوبة الكاملة في إنشاء كاشف لموجة الجاذبية في تقليل هذه الضوضاء. معظم هذه الضوضاء ليست أساسية ، ولكنها قيود تقنية. وتنشأ ضوضاء الكم فقط من الطبيعة ذاتها لجهاز القياس. سوف تصبح العقبة الرئيسية أمام تحسين الحساسية في أجهزة الكشف عن المستقبل ، لذلك سنتناولها بمزيد من التفصيل. هناك نوعان من الضوضاء الكمومية: ضوضاء النار وضوضاء ضغط الإشعاع.

تنشأ ضوضاء اللقطة بسبب الطبيعة الكمومية لليزر: تتكون حزمة الليزر من فوتونات تطير بتأخيرات عشوائية مختلفة بين بعضها البعض. عندما تقاس هذه الفوتونات على الثنائيات الضوئية ، تؤدي التقلبات في تدفق الفوتون إلى تقلبات التيار ، ونتيجة لذلك ، إلى الضوضاء في الإشارة التي نلاحظها.

ضجيج ضغط الإشعاع هو الجانب الثاني من الطبيعة الكمومية للضوء. كما هو معروف من الكهرومغناطيسية الكلاسيكية منذ زمن تجارب ليبيديف ، فإن الكائن الذي يضيء الضوء يتعرض له هو ضغط الضوء . من السهل أن نفهم ما إذا كنا نعتبر الفوتون كجسيم: كل جسيم يحمل دفعة ، والتي تنتقل إلى الجسم عند الاصطدام. أي عندما يضيء الليزر على مرآة متحركة ، تبدأ المرآة في التحول تحت تأثير ضغط الضوء. ونظرًا لأن الفوتونات يتم توزيعها بشكل عشوائي ، فإن المزيد من الفوتونات تصل في بعض الأحيان إلى المرآة خلال فترة زمنية معينة ، وأحيانًا تكون أقل ، وتكون قوة ضغط الضوء عشوائية أيضًا. لذا: تؤدي كمية الضوء إلى قوة عشوائية تعمل على المرايا في LIGO. تتسبب هذه القوة في حدوث تحول عشوائي للمرايا ، والتي يتم تسجيلها عند إخراج مقياس التداخل كإشارة زائفة.


شرح عن الضوضاء الكمومية. ينتج عن التوزيع العشوائي لعدد الفوتونات قوة عشوائية لضغط الإشعاع (يسار). من ناحية أخرى ، يؤدي التوزيع العشوائي للفوتونات في الوقت المناسب إلى تقلبات السعة على الكاشف الضوئي (يمين). كلا الضجيج يعتمد على الطول الموجي ، والطاقة الضوئية وطول الكتف. ضجيج الضغط الإشعاعي أقل ، كلما زادت كتلة المرايا. الائتمان: [1].

ضجيج الضغط الإشعاعي أقوى كلما زادت قوة الضوء الناتج عن المرايا (أي تدفق الفوتونات). تزداد الإشارة الصادرة عن GW أيضًا مع زيادة الطاقة الضوئية في المكشاف. ضجيج النار تطبيع إلى إشارة ينخفض. نتيجة لذلك ، اتضح أنه يمكنك زيادة الحساسية المحددة بضوضاء اللقطة عن طريق زيادة قوة الضوء ، ولكن سيتعين عليك دفع ثمنها بزيادة ضوضاء الضغط الإشعاعي. والعكس صحيح. لا توجد طريقة بالطريقة الكلاسيكية لقمع الضجيج الكمي في آن واحد. سوف تضطر إلى استخدام تكنولوجيا الكم.


اعتماد الحساسية على الطاقة الضوئية: تقل الضوضاء الصادرة (باللون الأزرق) ، ويزيد ضوضاء الضغط الإشعاعي (الأخضر) بشكل متناسب.

2. ضوء مضغوط

هناك مقال رائع عن حبري عن الضوء المضغوط من قبرتك . إذا كنت لا تعرف ما هو الضوء المضغوط ، فإنني أوصي بشدة أن تقرأ مقالته أولاً. سأكون موجزا.

إذا نظرت إلى الضوء على أنه موجة ، فلن تكون المعلمات المميزة هي تدفق الفوتون والتأخير بينهما ، ولكن سعة وطور الموجة. عادة ما يتحدثون عن تربيع الطور والسعة للضوء.

$$عرض $$ $ E = E_0 \ cos (\ omega_0 t + \ phi) = E_0 \ cos \ omega_0 t \ cos \ phi - E_0 \ sin \ omega_0 t \ sin \ phi = \\ = E_ {} \ sin \ omega_0 t + E_ {a} \ cos \ omega_0 t $$ عرض $$

إذا كانت الإشارة التي تهمنا موجودة في مرحلة الضوء ، وكانت صغيرة بدرجة كافية ، فيمكننا إجراء تقريب:

$$عرض $$ $$ E_ {f} = E_0 \ sin \ phi \ approx E_0 \ phi؛ \ quad E_ {a} = E_0 \ cos \ phi \ approx E_0 $$ عرض $$

لذلك ، القيمة$$ $ inline $ E_ {f} $ inline $ تسمى المرحلة التربيعية - تحتوي على معلومات حول المرحلة.

وفقًا لذلك ، فإن ضوضاء اللقطة هي تقلب في مرحلة الضوء ، وضوضاء الضغط الإشعاعي ناتج عن تقلبات السعة.

ترتبط حالة عدم اليقين في الطور وعدم اليقين في السعة بعلاقة Heisenberg:

$$عرض $$ $$ \ Delta ^ 2 E_ {f} \ Delta ^ 2 E_ {a} \ leq \ frac {1} {2} $$ عرض $$

في شعاع الليزر التقليدي ، تكون أوجه عدم اليقين هذه متساوية. ومع ذلك ، من الممكن ضغط عدم اليقين في المرحلة عن طريق زيادة عدم اليقين السعة - الشيء الرئيسي هو أن المنتج الخاص بهم يرضي علاقة عدم اليقين. هذا الضوء يسمى الضغط:

$$عرض $$ $$ \ Delta ^ 2 E_ {f} ^ {sqz} = e ^ {- 2r} \ Delta ^ 2 E_ {f} ، \ Delta ^ 2 E_ {a} ^ {sqz} = e ^ {2r } \ Delta ^ 2 E_ {a} \\ \ Delta ^ 2 E_ {f} ^ {sqz} \ Delta ^ 2 E_ {a} ^ {sqz} = \ Delta ^ 2 E_ {f} \ Delta ^ 2 E_ { a} \ leq \ frac {1} {2} ، عرض $$ $$

حيث r هي نسبة الضغط.

بشكل عام ، حتى في حالة عدم وجود حزمة قوية ، توجد تقلبات الفراغ دائمًا. يمكن أيضًا ضغطها للحصول على فراغ مضغوط: في المتوسط ​​، يكون عدد الفوتونات فيه صفرًا ، لكن تقلبات السعة والطور تكون مضغوطة.


إن تقلبات الفراغ التي تدخل الكاشف عبر منفذ الإشارة هي مصدر الضوضاء الكمومية في LIGO. لذلك ، إذا تم ضغط هذا الفراغ في الطور ، فإن هذا سوف يقلل من ضوضاء الرصاص في الكاشف.

لقد تم استخدام هذا النهج في كاشف GEO600 على مدار الأعوام الثمانية الماضية ، مما أدى إلى تقليل ضوضاء اللقطة بأربع مرات ، ومنذ هذا العام تم تطبيقه أيضًا في LIGO ، مما يقلل من ضوضاء اللقطة بمقدار النصف (مما يزيد من عدد الأحداث المسجلة بمقدار 8 مرات).



يسار: مثال على تحسين حساسية LIGO مع ضوء مضغوط. إلى اليمين: تم إنشاء أفضل ضغط حتى الآن في مجموعتنا منذ عدة سنوات: تم كبح تقلبات الفراغ بمقدار 15 ديسيبل.

ومع ذلك ، فإن كل شيء ليس بهذه البساطة: وفقًا لعلاقة عدم اليقين ، إذا ضغطنا المرحلة ، فإننا نزيد التقلبات في السعة. ويزيدون ضوضاء الضغط الإشعاعي. ومرة أخرى ، عليك اختيار الضوضاء التي تريد تقليلها بزيادة الضوضاء الأخرى. ولكن هل من الممكن للالتفاف حول هذا القيد بطريقة أو بأخرى؟

3. ضغط يعتمد على التردد

لحسن الحظ ، هناك ضجيجان كميان يحدان من حساسية الكاشف عند ترددات مختلفة: في حالة الضوضاء المنخفضة يكون ضغط الإشعاع أقوى بكثير من ضغط النار ، والعكس بالعكس. لذلك ، من الممكن تحضير ضغط صعب للضوء ، حيث يتم ضغط الضوء بترددات منخفضة في الترددات المنخفضة (وبالتالي يتم تقليل ضوضاء ضغط الإشعاع) ، وعلى ترددات عالية - في الطور (وبالتالي يتم تقليل ضوضاء الطلقة).


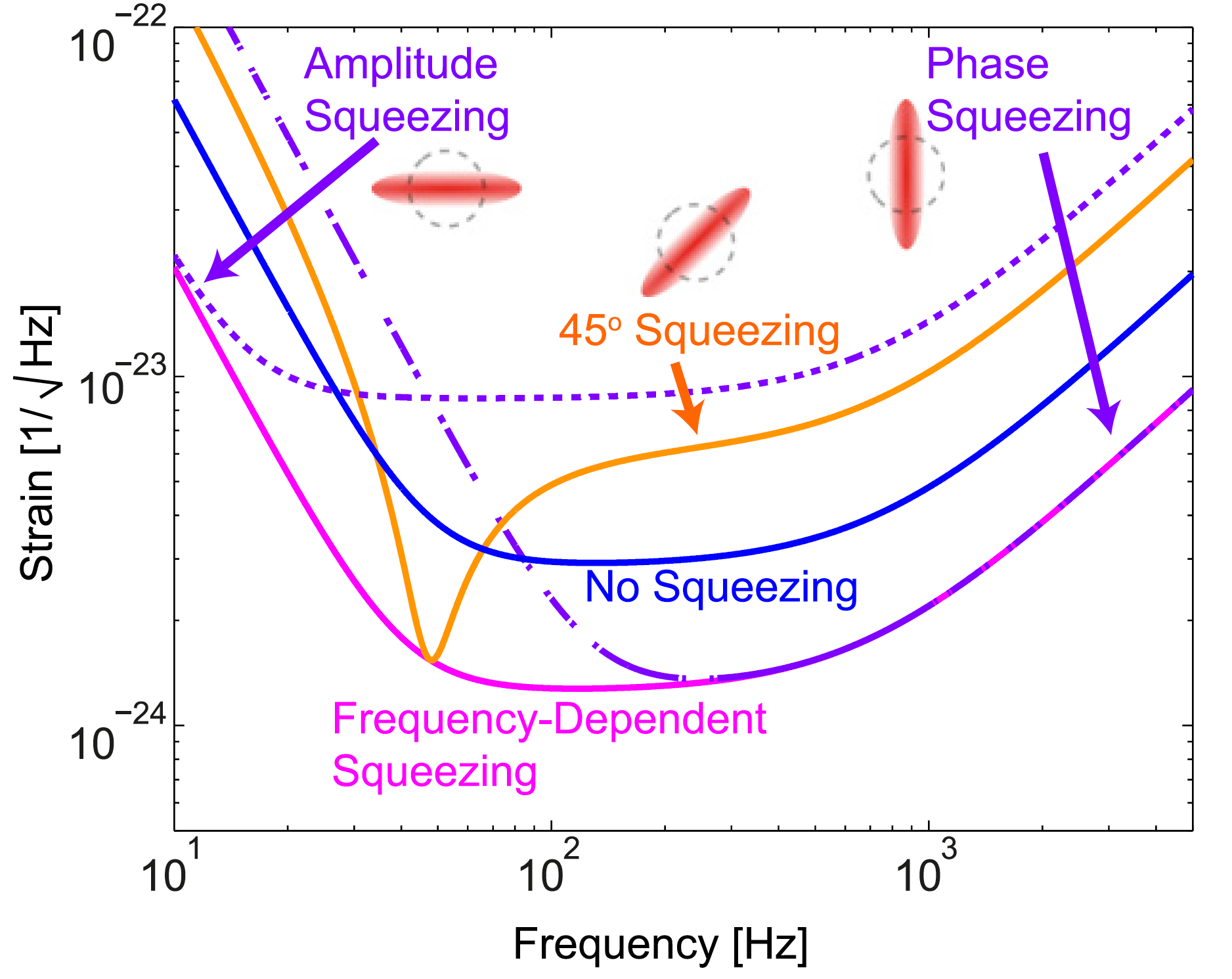الضغط المعتمد على التردد: في ترددات مختلفة ، يتم ضغط السعة أو الطور أو توليفة منها. نتيجة لذلك ، يتم تحسين الحساسية في جميع الترددات. [SSY Chua et al 2014 Class. جاذبية الكم. 31 183001]

في الأساس ، سبب الحاجة إلى الضغط المعتمد على التردد هو أن ضغط الإشعاع على المرايا يؤدي أيضًا إلى ضغط ضوئي ، ولكن في تربيع مختلف. يمكن ملاحظة ذلك في الصورة أدناه: إذا كنت تستخدم الضغط التقليدي عند الإدخال ، فسوف تحصل على اعتماد التردد في الإخراج بسبب ضغط الإشعاع. "لإلغاء" اعتماد التردد هذا ، تحتاج إلى تعيين الاعتماد العكسي للضغط عند الإدخال.


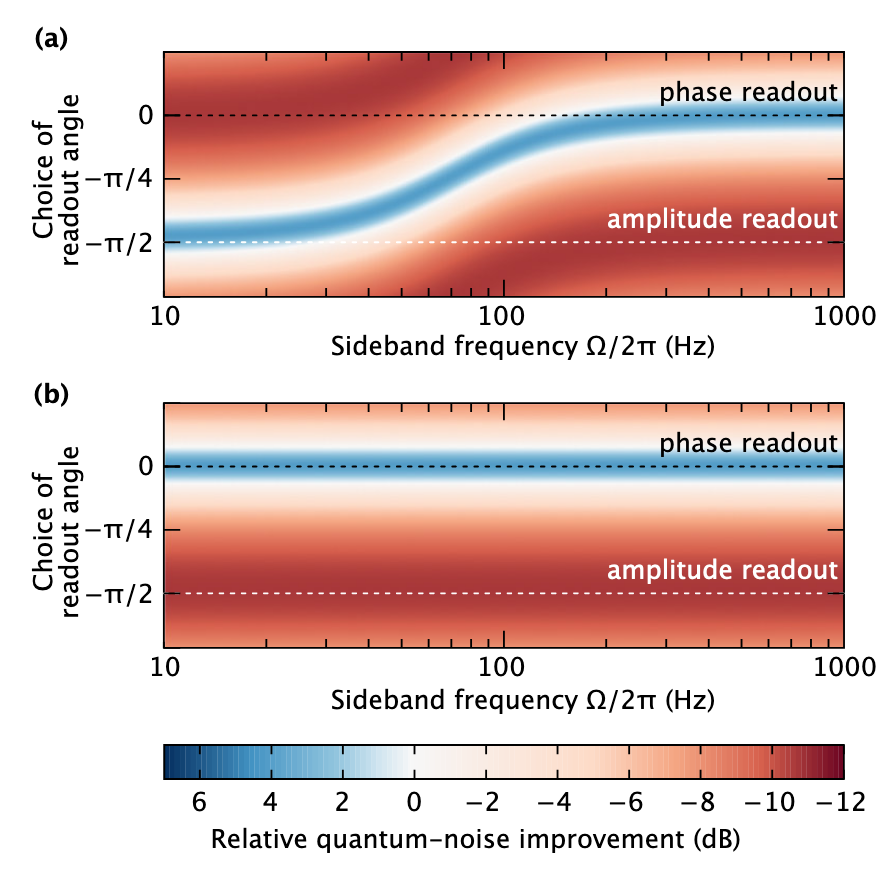مثال على المقال: الاعتماد على تحسين حساسية مقياس التداخل عند استخدام الانضغاط التقليدي كوظيفة تردد ومراحل قياس مختلفة أعلاه - الإشارة في تربيع المرحلة ، ويمكن ملاحظة أنه إذا زادت الحساسية عند ترددات عالية (اللون الأزرق) ، فسوف تتناقص عند الترددات المنخفضة ). يمكن أن يؤدي استخدام الضغط المعتمد على التردد إلى تحسين الحساسية في جميع الترددات.

لذلك ، نحن نحل من الناحية النظرية مشكلة الحد من الضوضاء الكمومية في جميع الترددات ، ويبقى السؤال: كيفية تنفيذ مثل هذا الاعتماد على التردد. للقيام بذلك ، تحتاج إلى معرفة كيفية تحويل المرحلة المضغوطة إلى سعة مضغوطة. في الواقع ، الأمر بسيط للغاية: إنتاج مرحلة التحول:

$$عرض $$ $$ E_ {f} ^ {sqz} = E_0 e ^ {- 2r} \ sin (\ phi) \ rightarrow E_0 e ^ {- 2r} \ sin (\ phi + \ pi / 2) = E_ { a} e ^ {- 2r} $$ عرض $$

عادةً ما تكون المرآة البسيطة كافية لتغيير الطور ، مما يؤدي إلى تغيير طول المسار الذي يسير فيه الضوء. ومع ذلك ، في هذه الحالة ، فأنت بحاجة إلى جهاز يقوم بإنشاء تحول طور معتمد على التردد: لا تقم بإزاحة الطور بترددات عالية ، ولكن عند انخفاض$$ $ inline $ \ pi / 2 $ inline $ .

في الوقت الحالي ، يتمثل المفهوم الرائد لإنشاء ضغط يعتمد على التردد في جميع تصميمات أجهزة الكشف المستقبلية في استخدام مرنانات ترشيح إضافية. إذا انعكس الفراغ المضغوط على مثل هذا الرنان عندما يتم فصله عن تردد الرنين ، فسيحصل على الاعتماد اللازم على التردد. ومع ذلك ، فإنه يواجه صعوبة كبيرة: من أجل إنشاء الاعتماد على التردد المطلوب ، يجب أن يكون الرنانات بطول عدة مئات من الأمتار في فراغ ، وهذا مكلف للغاية ويصعب التحكم فيه. لدينا فكرة أخرى.

والحقيقة هي أنه في الكاشف نفسه يوجد بالفعل العديد من الرنانات ذات الأحجام المناسبة ، والخسائر المنخفضة وبواسطة طريقة تحكم معروفة ، ولكن لا يمكن استخدامها مباشرة - للضغط المعتمد على التردد ، يعد الانفصال عن الرنين ضروريًا. لكن لكل مرنان ترددات رنانة كثيرة ، بينما يعمل الكاشف على واحد منها فقط. والفكرة هي استخدام رنين مختلف ، يعكس الضوء المضغوط من مقياس التداخل نفسه للحصول على الاعتماد اللازم على التردد. يبقى السؤال: كيفية استخدام اعتماد التردد الذي تم إنشاؤه على تردد مختلف عن تردد العمل الرئيسي لليزر. ومن ثم يأتي التشابك الكمومي للإنقاذ.

4. التشابك الكمي والمفارقة EPR

مسألة طبيعة التشابك تستحق بلا شك مقالة منفصلة. ناقشت موضوعًا أكثر تعقيدًا في مقال سابق عن Habré ، لذلك هنا سأصف بإيجاز خصائصه الرئيسية فقط. لنبدأ بتناقض EPR (أينشتاين-بودولسكي-روزن): لاحظ ثلاثة من السادة أن هناك مصيدة في ميكانيكا الكم. من ناحية ، هناك مبدأ عدم اليقين ، الذي يقول إنه من المستحيل قياس إحداثيات الزخم وجسيمه بدقة في نفس الوقت (وفي حالتنا ، سعة الضوء ومرحلة). من ناحية أخرى ، يمكن للمرء إجراء مثل هذه التجربة البسيطة: خذ حدث تحلل الجسيمات ، الذي يولد فيه جسيمان متطابقان. وفقا لقانون الحفاظ على الزخم ، فإنها سوف تنتشر في اتجاهين متعاكسين في نفس السرعة. إذا قمنا بقياس زخم جسيم واحد ، فسوف نعرف بالضبط زخم الثانية. إذا قمنا بقياس إحداثيات الجسيم الثاني ، فسوف نعرف في نفس الوقت بالضبط كل من الإحداثيات (قمنا بقياسها) والزخم (توقعنا ذلك من خلال قياس الجسيم الأول) ، وهو ما يبدو مستحيلًا بسبب علاقة عدم اليقين. يتم حل التناقض المرئي عن طريق إدخال مفهوم تشابك الجسيمات: جزيئان لا ينفصلان عن بعضهما البعض ، يتم وصفهما بوظيفة موجة واحدة. وظيفة الموجة هذه غير محلية: حتى لحظة القياس ، من المستحيل تحديد أي من الجزيئات التي طارت في أي اتجاه. بمعنى ما ، طار كلاهما في كلا الاتجاهين في وقت واحد ، وفقط في لحظة القياس كان هناك اختيار عشوائي للجسيم الذي تم قياسه. ترتبط إحداثياتها وزخمها بحيث لا تنطبق علاقة عدم اليقين على قيمتها النسبية. علاوة على ذلك ، إذا تم التعامل مع إحدى الجسيمات ، على سبيل المثال من خلال بعض القوة ، فإن الجسيم الثاني "يشعر" أيضًا بهذه القوة - سوف تتغير المعلمات المقاسة وفقًا لذلك.

بالنسبة لنا أهم شيء: إذا كان لدينا جزيئين ، فيمكننا التنبؤ بدقة بخصائص الجسيم الثاني من خلال قياس الأول. يمكننا وضع مصدر للتأثير على مسار جسيم واحد ، وسوف يعمل على اثنين في وقت واحد. بعد إجراء القياس الصحيح ، يمكننا أن نرى نتيجة لهذا التأثير.

كيف نستخدمها (تم اقتراحه لأول مرة في مقال في فيزياء الطبيعة [2]). يلعب دور الجسيمات في EPR بواسطة حزمتين من الفراغ المضغوط على ترددين: التردد الأساسي لمقياس التداخل وتكرار الرنين التالي للمرنان. نخلط بينها ، واحد منهم (التردد العالي) ينعكس من مرنان ضبطها وقياسها. انه يحصل على اعتماد التردد. نظرًا لأن الأشعة متشابكة ، يتم إرسال اعتماد التردد هذا أيضًا إلى الحزمة عند التردد الأساسي. بعد القياس ، يمكننا التنبؤ بالإشارات في الحزمة الرئيسية من الناحية المثالية بدقة كاملة. للقيام بذلك ، نقيس بشكل منفصل على كاشفين منفصلين ، ومعالجة البيانات على النحو الأمثل.


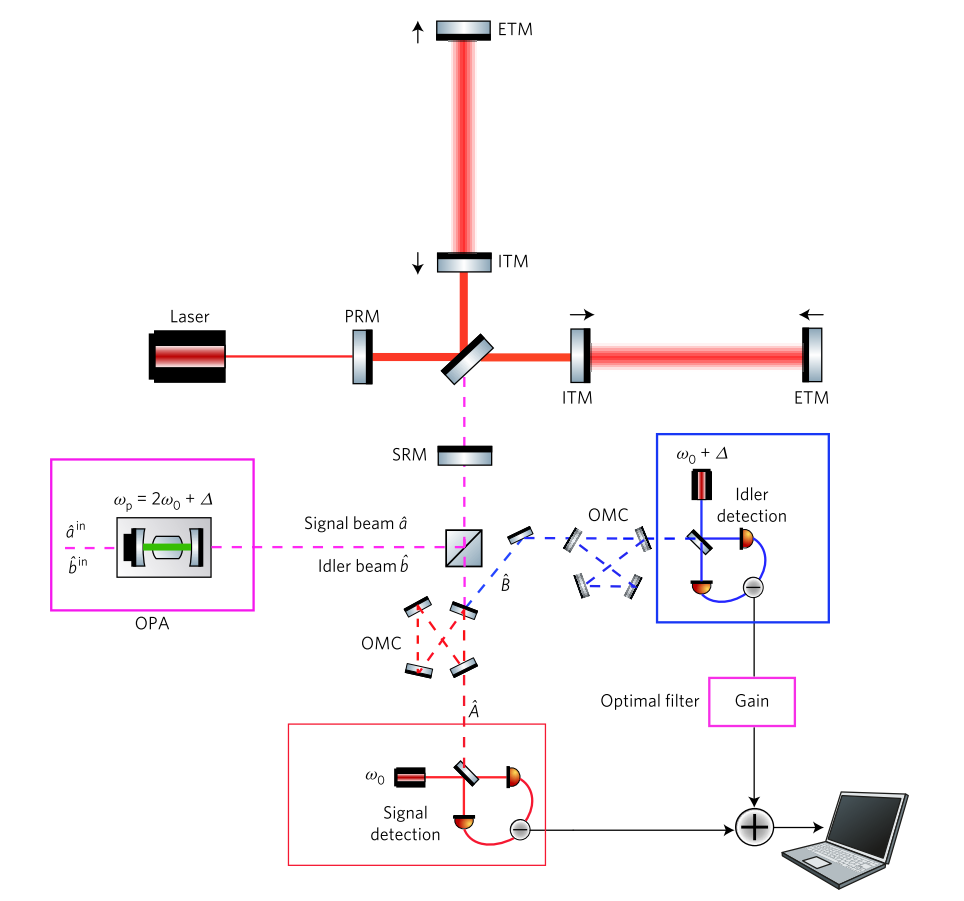نظام ضغط كامل يعتمد على التردد يعتمد على التشابك من [2]. تقوم OPA (مضخم بصري للمعلمات الضوئية) بإنشاء حزمين متشابكين من الفراغ المضغوط عند ترددات مختلفة ، يتم إرسال كلاهما إلى الكاشف. يتردد صدى الشعاع بتردد الموجة الحاملة في مقياس التداخل. يتم فك شعاع التردد العالي من أحد الأصداء الأعلى. في الخرج ، يتم فصل الأشعة والكشف عنها على اثنين من أجهزة الكشف المتجانسة المختلفة ، وبعد ذلك تتم معالجتها بالطريقة المثلى.

5. التجربة

لا تتضمن تجربتنا مقياس تداخل كامل مع مرايا متحركة. بدلاً من ذلك ، نحن نستكشف إمكانية الحصول على ضغط يعتمد على التردد باستخدام ضوء متشابك ينعكس من مرنان.


تصميم تجريبي مبسط. بدلاً من مقياس التداخل الكامل ، لدينا مرنان بصري واحد طوله 2.5 متر. بدلاً من اثنين من كاشفات homodyne المختلفة ، نستخدم كاشفًا واحدًا ، ولكن هناك حزمتان مرجعيتان لترددات مختلفة.

كما كتبت أعلاه ، في مقياس التداخل ، يخلق ضغط الإشعاع اعتمادًا على تردد الضوء المضغوط ، مما يفسد حساسية الكاشف. لإلغاء اعتماد التردد هذا ، نحتاج إلى إنشاء اعتماد تردد عكسي للضوء المضغوط. في تجربتنا ، لا تفسد حساسية الضغط الإشعاعي (ليس لدينا مرايا متحركة) ، ولكن تفكيك المكشاف من الرنين (انظر الصورة أدناه (أ)). عند القياس في تربيع الإشارة (قراءات الطور) ، يؤدي هذا إلى إفساد الحساسية عند الترددات المنخفضة (الأحمر).

لاستعادة الحساسية ، نقوم بإعادة إنشاء شعاع إضافي (العاطل) من الرنين في الاتجاه المعاكس. ثم بعد القياس ، يمكننا استعادة الحساسية بالكامل. بالنسبة إلى EPR - يمكننا التنبؤ بنتيجة قياس تربيع الطور بدقة أفضل باستخدام ضوء متشابك الكم.


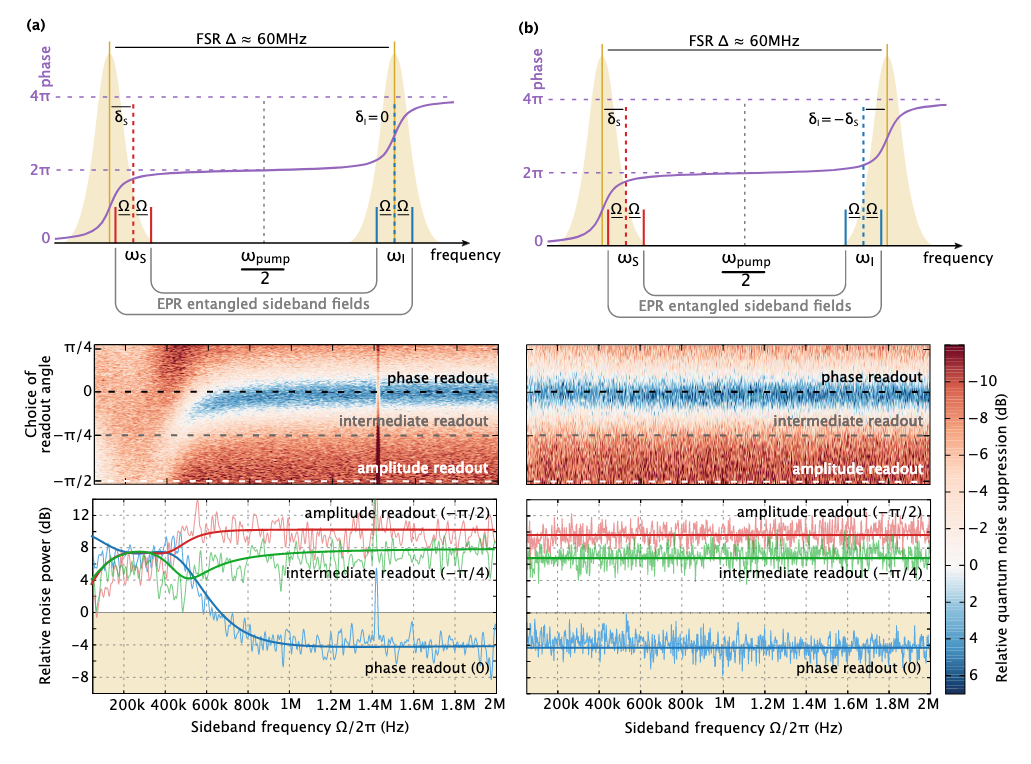تجربتان لمراقبة الضغط المعتمد على التردد. في الأول (أ) ، قمنا بضبط حزمة الإشارة من رنين الكاشف ، وبالتالي إفساد الحساسية في تربيع الطور (وخلق اعتماد تردد الضوء الخفيف). في الثانية ، أنشأنا اعتمادًا إضافيًا على التردد بالنسبة إلى الشعاع الثاني (العاطل) ، وبسبب التشابك الكمومي بين الأشعة ، تمكنت الإشارة والبلد من استعادة الحساسية التالفة عن طريق إلغاء اعتماد التردد الذي تم تقديمه في التجربة الأولى.

في الصورة أعلاه ، يكون اعتماد التردد في (أ) غير واضح. ويرجع ذلك إلى القيود في مرحلة ما بعد المعالجة: من الناحية المثالية ، هناك حاجة إلى اثنين من أجهزة الكشف عن متجانسة منفصلة ، والإشارات التي يمكن تصفية منها على النحو الأمثل. ومع ذلك ، في وضع آخر ، يمكننا الحصول على اعتماد تردد جميل للضوء المضغوط إذا قمنا بإعادة بناء كلا الأشعة من الرنين في اتجاه واحد. مثل هذا المخطط غير مناسب للكاشف ، لكنه يعطي فكرة عن خيارات التثبيت. حسنا ، مجرد بيانات تجريبية جميلة :)

6. الخاتمة

لتلخيص. تقلبات الكم من الضوء هي المصدر الرئيسي والأكثر أساسية للضوضاء في جميع أجهزة الكشف الحديثة والمستقبلية. لقمعها ، يمكن استخدام الارتباطات الكمومية - الضوء المضغوط. ومع ذلك ، من أجل تقليل الضوضاء في نطاق التردد الكامل للكاشف ، من الضروري ضغط تقلبات السعة عند ترددات منخفضة وتقلبات الطور بترددات عالية. يُقترح إجراء هذا الضغط المعتمد على التردد باستخدام مرنانات ترشيح خاصة. تقليديا ، هذه المرنانات غالية جدا ويصعب تنفيذها. البديل لدينا هو استخدام الكاشف نفسه كرنان للمرشح ، باستخدام ضوء متشابك الكم. أجرينا تجربة وأظهرنا أن التشابك الكمي يسمح في الواقع بإدراك هذه الفكرة.

هذا النهج ليس حلا سحريا ، للأسف: عليك أن تدفع من أجل الراحة. لكي يعمل المفهوم بالكامل ، من الضروري استخدام كاشفين متماثلين ، وهو أمر صعب للغاية من الناحية التجريبية. بالإضافة إلى ذلك ، يضيف الكاشف الثاني ضوضاء إلى الحساسية - وإن كان أقل بكثير مما يمكنك الحصول عليه من الضغط.

في هذا العمل ، تعاملنا مع التعقيدات والضوء المضغوط وأظهرنا كيف يمكننا استخدامها لتحسين حساسية كاشفات المستقبل. لكن هذه ، بالطبع ، ليست سوى الخطوة الأولى على طريق طويل لتنفيذ هذا النهج في كاشف حقيقي: تحتاج إلى التحقق من كيفية عمل كل شيء باستخدام مقياس تداخل حقيقي ، مع مرايا متحركة ، واثنين من متجانسة ، وما إلى ذلك. بشكل عام ، لا يزال العمل ممتلئًا.

للراغبين في التفاصيل ، انظر مقالتنا والمقالة التي تم فيها تقديم الفكرة لأول مرة [2].

[1] S. Hild Beyond 2nd Generation GW detector
[2] Y. Ma et al ، اقتراح لاكتشاف موجة الجاذبية يتجاوز الحد الكمي القياسي من خلال تشابك EPR ، Nature Physics المجلد 13 ، الصفحات 776-780 (2017)

7. متنوعة

والآن بعض الأخبار حول LIGO:

1. حاليًا ، سجلت LIGO 26 حدثًا خلال الأشهر الستة الأخيرة من العمل في دورة عمل O3. يمكن مراقبة الأحداث على https://gracedb.ligo.org/superevents/public/O3/ ، وهناك تطبيق كامل لجهاز iPhone.
2. ربما كان الحدث الأكثر إثارة للاهتمام هو الكشف الأخير عن انصهار ثقب أسود ونجم نيوتروني. يمكنك أن تقرأ ، على سبيل المثال ، N + 1 أو Scientific American . بشكل عام ، كل شيء مثير جدا للاهتمام.
3. 100 . , (c 55 130 ). , , .
4. LIGO , , , . . LIGO . , , . , , , , .

: , , : @hbar_universe .