الانحدار الخطي وطرق ترميمه

المصدر: xkcd

يعد الانحدار الخطي أحد الخوارزميات الأساسية للعديد من المجالات المتعلقة بتحليل البيانات. السبب في ذلك واضح. هذه خوارزمية بسيطة جدًا ومفهومة ، وقد ساهمت في استخدامها على نطاق واسع لعشرات السنين ، إن لم يكن مئات السنين. تتمثل الفكرة في أننا نفترض اعتمادًا خطيًا لمتغير واحد على مجموعة من المتغيرات الأخرى ، ثم حاول استعادة هذا الاعتماد.

لكن هذا المقال لا يتعلق بتطبيق الانحدار الخطي لحل المشكلات العملية. سنناقش هنا ميزات مثيرة للاهتمام لتطبيق الخوارزميات الموزعة لاستعادتها التي واجهناها عند كتابة وحدة تعلم الآلة في Apache Ignite . ستساعدك بعض الرياضيات الأساسية وأساسيات التعلم الآلي والحوسبة الموزعة على معرفة كيفية استعادة الانحدار الخطي ، حتى لو تم توزيع البيانات عبر آلاف العقد.

عن ماذا تتحدث

نحن نواجه مهمة استعادة الاعتماد الخطي. كمدخلات ، يتم تقديم العديد من المتجهات للمتغيرات المفترضة التي يُفترض أنها مستقلة ، يرتبط كل منها بقيمة معينة للمتغير التابع. يمكن تمثيل هذه البيانات في شكل مصففتين:

$$

$$\ تبدأ {pmatrix} a_ {11} & a_ {12} & a_ {13} & ... & a_ {1n} \\ a_ {21} & a_ {22} & a_ {23} & ... & a_ {2n} \\ ... \\ a_ {m1} & a_ {m2} & a_ {m3} & ... & a_ {mn} \\ \ end {pmatrix} \ تبدأ {pmatrix} b_ {1} \\ b_ {2} \\ ... \\ b_ {m} \\ \ end {pmatrix}$$

الآن ، بما أن التبعية مفترضة ، وإلى جانب كونها خطية ، نكتب افتراضنا في شكل منتج للمصفوفات (لتبسيط الترميز هنا وتحت ، يفترض أن المصطلح الحر للمعادلة مخفي وراء $$$x_n$ ، والعمود الأخير من المصفوفة $$$دولا$ يحتوي على وحدات):

$$

$$\ تبدأ {pmatrix} a_ {11} & a_ {12} & a_ {13} & ... & a_ {1n} \\ a_ {21} & a_ {22} & a_ {23} & ... & a_ {2n} \\ ... \\ a_ {m1} & a_ {m2} & a_ {m3} & ... & a_ {mn} \\ \ end {pmatrix} \ times \ تبدأ {pmatrix} x_ { 1} \\ x_ {2} \\ ... \\ x_ {n} \\ \ end {pmatrix} = \ start {pmatrix} b_ {1} \\ b_ {2} \\ ... \\ b_ {m} \\ \ end {pmatrix}$$

تشبه الى حد بعيد نظام المعادلات الخطية ، أليس كذلك؟ يبدو ، ولكن على الأرجح لن يكون هناك حلول لمثل هذا النظام من المعادلات. والسبب في ذلك هو الضوضاء الموجودة في أي بيانات حقيقية تقريبا. أيضا ، قد يكون السبب في عدم وجود علاقة خطية على هذا النحو ، والتي يمكنك محاولة القتال من خلال إدخال متغيرات إضافية تعتمد بشكل غير خطي على المصدر. النظر في المثال التالي:

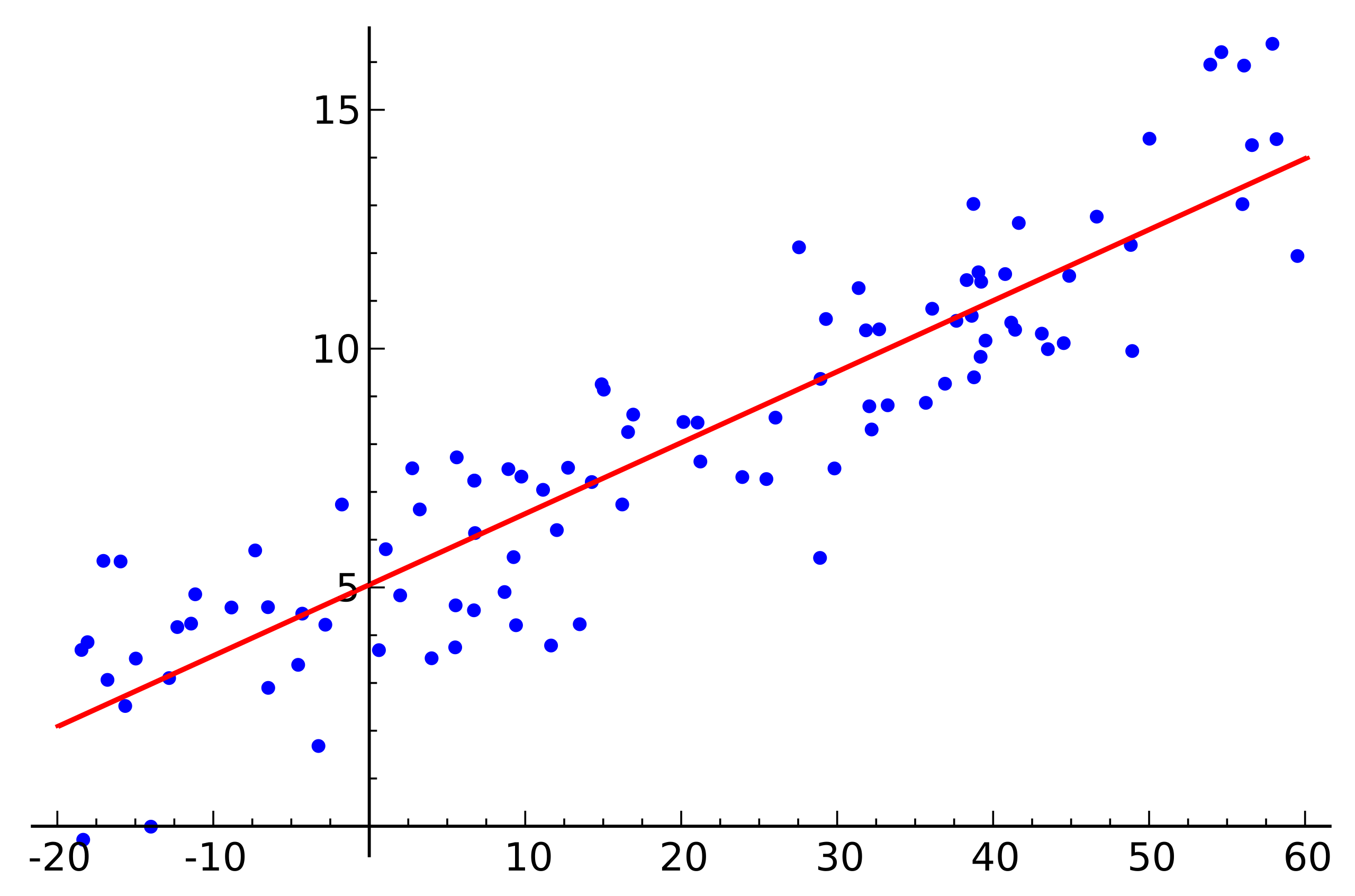المصدر: ويكيبيديا

هذا مثال بسيط على الانحدار الخطي يوضح اعتماد متغير واحد (على المحور) $$$ذ$ ) من متغير آخر (على طول المحور $$$x$ ). لكي يكون لنظام المعادلات الخطية المقابلة لهذا المثال حلاً ، يجب أن تقع جميع النقاط على خط مستقيم واحد. لكن هذا ليس كذلك. لكنهم لا يكذبون على خط مستقيم واحد على وجه التحديد بسبب الضوضاء (أو لأن افتراض وجود تبعية خطية كان خاطئًا). وبالتالي ، من أجل استعادة الاعتماد الخطي من البيانات الحقيقية ، عادة ما يكون من الضروري إدخال افتراض واحد آخر: تحتوي بيانات الإدخال على ضوضاء ويكون لهذا الضجيج توزيع عادي . يمكن للمرء أن يضع افتراضات حول الأنواع الأخرى من توزيع الضوضاء ، ولكن في الغالبية العظمى من الحالات ، يكون التوزيع الطبيعي هو الذي سيتم مناقشته لاحقًا.

طريقة الاحتمالية القصوى

لذلك ، افترضنا وجود ضوضاء عشوائية موزعة بشكل طبيعي. كيف تكون في مثل هذه الحالة؟ في هذه الحالة ، يوجد في الرياضيات ويستخدم طريقة الاحتمال القصوى على نطاق واسع. باختصار ، يكمن جوهرها في اختيار وظيفة الاحتمال وتعظيمها لاحقًا.

نعود إلى استعادة الاعتماد الخطي من البيانات مع الضوضاء العادية. لاحظ أن العلاقة الخطية المفترضة هي توقع رياضي $$$\ mu$ التوزيع الطبيعي المتاح. في الوقت نفسه ، فإن احتمال ذلك $$$\ mu$ يفترض قيمة واحدة أو أخرى ، رهنا بوجود ملحوظات $$$x$ ، يبدو كما يلي:

$$

$$P (\ mu \ mid X، \ sigma ^ 2) = \ prod_ {x \ in X} {\ frac {1} {\ sigma \ sqrt {2 \ pi}} \؛ e ^ {- \ frac {(x- \ mu) ^ 2} {2 \ sigma ^ 2}}}$$

نحن بديلا الآن بدلا من ذلك $$$\ mu$ و $$$X$ المتغيرات التي نحتاجها:

$$

$$P (x \ mid A، B، \ sigma ^ 2) = \ prod_ {i \ in [1، m]} {\ frac {1} {\ sigma \ sqrt {2 \ pi}} \؛ e ^ {- \ frac {(b_i-a_ix) ^ 2} {2 \ sigma ^ 2}}} ، a_i \ in A ، b_i \ in B$$

يبقى فقط للعثور على المتجه $$$x$ عند هذا الاحتمال هو الحد الأقصى. لتعظيم مثل هذه الوظيفة ، من الملائم prologarithm أولاً (ستصل لوغاريتم الوظيفة إلى الحد الأقصى عند نفس الوظيفة مثلها):

$$

$$f (x) = ln (\ prod_ {i \ in [1، m]} {\ frac {1} {\ sigma \ sqrt {2 \ pi}} \؛ e ^ {- \ frac {(b_i-a_ix ) ^ 2} {2 \ sigma ^ 2}}}) = \ sum_ {i \ in [1، m]} ln \ frac {1} {\ sigma \ sqrt {2 \ pi}} \؛ - \ sum_ {i \ in [1، m]} \ frac {(b_i-a_ix) ^ 2} {2 \ sigma ^ 2}$$

والتي بدورها تتلخص في تقليل الوظيفة التالية:

$$

$$f (x) = \ sum_ {i \ in [1، m]} (b_i-a_ix) ^ 2$$

بالمناسبة ، هذا يسمى طريقة المربعات الصغرى . في كثير من الأحيان ، يتم حذف جميع الأسباب المذكورة أعلاه ويتم استخدام هذه الطريقة ببساطة.

تحلل QR

يمكن العثور على الحد الأدنى من الوظيفة أعلاه إذا وجدت النقطة التي يكون فيها تدرج هذه الوظيفة مساويًا للصفر. وسيتم كتابة التدرج على النحو التالي:

$$

$$\ nabla f (x) = \ sum_ {i \ in [1، m]} 2a_i (a_ix - b_i) = 0$$

إن تحليل QR هو طريقة مصفوفة لحل مشكلة التصغير المستخدمة في طريقة المربعات الصغرى. في هذا الصدد ، نعيد كتابة المعادلة في شكل مصفوفة:

$$

$$A ^ T A x = A ^ Tb$$

لذلك ، نضع المصفوفة $$$دولا$ على المصفوفات $$$ف دولا$ و $$$R$ وإجراء سلسلة من التحويلات (لن يتم هنا النظر في خوارزمية تحلل QR نفسها ، بل استخدامها فقط فيما يتعلق بالمهمة):

$$

$$\ تبدأ {align} & (QR) ^ T (QR) x = (QR) ^ Tb؛ \\ & R ^ T Q ^ T Q R x = R ^ T Q ^ T b؛ \\ \ end {align}$$

قالب $$$ف دولا$ هو متعامد. هذا يسمح لنا بالتخلص من العمل. $$$Q Q ^ T$ :

$$

$$\ تبدأ {align} & R ^ T R x = R ^ T Q ^ T b؛ \\ & (R ^ T) ^ {- 1} R ^ T R x = (R ^ T) ^ {- 1} R ^ T Q ^ T b؛ \\ & R x = Q ^ T b. \ end {align}$$

وإذا كنت تحل محل $$$Q ^ T b$ في $$$z$ سوف تتحول $$$R x = z$ . بالنظر إلى ذلك $$$R$ هو المصفوفة الثلاثي العلوي ، يبدو مثل هذا:

$$

$$\ تبدأ {pmatrix} r_ {11} & r_ {12} & r_ {13} & r_ {14} & ... & r_ {1n} \\ 0 & r_ {22} & r_ {23} & r_ { 24} & ... & r_ {2n} \\ 0 & 0 & r_ {33} & r_ {34} & ... & r_ {3n} \\ 0 & 0 & 0 & r_ {44} & .. . & r_ {4n} \\ ... \\ 0 & 0 & 0 & 0 & ... & r_ {nn} \\ \ end {pmatrix} \ times \ تبدأ {pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ ... \\ x_n \ end {pmatrix} = \ تبدأ {pmatrix} z_1 \\ z_2 \\ z_3 \\ z_4 \\ ... \\ z_n \ end {pmatrix}$$

هذا يمكن حلها عن طريق طريقة الاستبدال. عنصر $$$x_n$ يشبه $$$z_n / r_ {nn}$ البند السابق $$$x_ {n-1}$ يشبه $$$(z_ {n-1} - r_ {n-1، n} x_n) / r_ {n-1، n-1}$ و هكذا.

تجدر الإشارة هنا إلى أن تعقيد الخوارزمية الناتجة من خلال استخدام تحليل QR هو $$$O (2 مليون ^ 2)$ . علاوة على ذلك ، على الرغم من أن عملية ضرب المصفوفة متوازنة بشكل جيد ، لا يمكن كتابة نسخة موزعة فعالة من هذه الخوارزمية.

نزول التدرج

عند الحديث عن التقليل من وظيفة معينة ، يجدر بك دائمًا تذكير طريقة الانحدار (stochastic) للإنحدار. هذه طريقة تصغير بسيطة وفعالة تستند إلى حساب تدرج دالة بشكل متكرر عند نقطة ما ثم تحويلها إلى الجانب المقابل للتدرج. كل خطوة من هذا القبيل يصل الحل إلى الحد الأدنى. يشبه التدرج نفسه:

$$

$$\ nabla f (x) = \ sum_ {i \ in [1، m]} 2a_i (a_ix - b_i)$$

هذه الطريقة أيضًا متوازنة وموزعة جيدًا بسبب الخواص الخطية لمشغل التدرج اللوني. لاحظ أنه في الصيغة أعلاه ، توجد مصطلحات مستقلة تحت علامة المجموع. بمعنى آخر ، يمكننا حساب التدرج بشكل مستقل لجميع المؤشرات $$$i$ من الأول إلى $$$ك$ ، بالتوازي مع هذا ، قم بحساب التدرج للمؤشرات بـ $$$ك + 1 دولا$ إلى $$$م دولا$ . ثم أضف التدرجات الناتجة. ستكون نتيجة الإضافة هي نفسها كما لو كنا نحسب التدرج اللوني للمؤشرات على الفور من الأول إلى $$$م دولا$ . وبالتالي ، إذا تم توزيع البيانات بين عدة أجزاء من البيانات ، فيمكن حساب التدرج بشكل مستقل على كل جزء ، ومن ثم يمكن تلخيص نتائج هذه العمليات الحسابية للحصول على النتيجة النهائية:

$$

$$\ nabla f (x) = \ sum_ {i \ in P_1} 2a_i (a_ix - b_i) + \ sum_ {i \ in P_2} 2a_i (a_ix - b_i) + ... + \ sum_ {i \ in P_k} 2a_i (a_ix - b_i)$$

من حيث التنفيذ ، وهذا يتناسب مع نموذج MapReduce . في كل خطوة من خطوات نزول التدرج ، يتم إرسال مهمة لحساب التدرج إلى كل عقدة بيانات ، ثم يتم جمع التدرجات المحسوبة معًا ، ويتم استخدام نتيجة الجمع لتحسين النتيجة.

على الرغم من بساطة التنفيذ والقدرة على التنفيذ في نموذج MapReduce ، فإن هبوط التدرج له أيضًا عيوبه. على وجه الخصوص ، فإن عدد الخطوات المطلوبة لتحقيق التقارب أكبر بكثير بالمقارنة مع الطرق الأخرى الأكثر تخصصًا.

LSQR

LSQR هي طريقة أخرى لحل المشكلة ، وهي مناسبة لإعادة بناء الانحدار الخطي ولحل أنظمة المعادلات الخطية. الميزة الرئيسية هي أنه يجمع بين مزايا أساليب المصفوفة والنهج التكراري. يمكن العثور على تطبيقات هذه الطريقة في مكتبة SciPy وفي MATLAB . لن يتم تقديم وصف لهذه الطريقة هنا (يمكن العثور عليه في مقالة LSQR: خوارزمية للمعادلات الخطية المتفرقة وأقل المربعات الصغرى ). بدلاً من ذلك ، سيتم توضيح طريقة لتكييف LSQR للتنفيذ في بيئة موزعة.

يستند الأسلوب LSQR إلى إجراء bidiagonalization. هذا إجراء تكراري ، يتألف كل تكرار من الخطوات التالية:


ولكن استنادا إلى حقيقة أن المصفوفة $$$دولا$ مقسمة أفقيا ، ثم يمكن تمثيل كل التكرار كخطوتين MapReduce. وبالتالي ، من الممكن تقليل نقل البيانات أثناء كل تكرار (فقط المتجهات ذات طول يساوي عدد المجهولين):



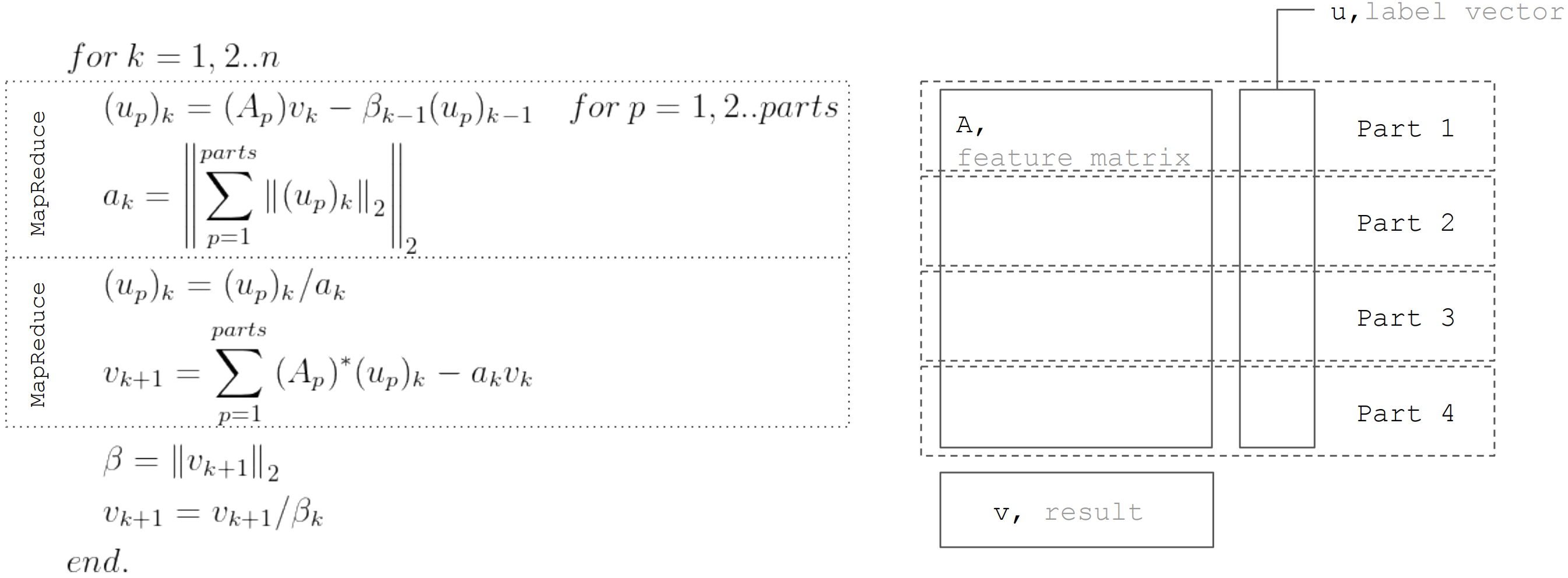
يتم استخدام هذا النهج عند تطبيق الانحدار الخطي في Apache Ignite ML .

استنتاج

هناك العديد من خوارزميات استرداد الانحدار الخطي ، ولكن لا يمكن تطبيقها جميعًا في أي ظروف. لذا يعد تحليل QR أمرًا رائعًا لحل دقيق على صفائف البيانات الصغيرة. يتم تطبيق تدرج النسب ببساطة ويسمح لك بالعثور بسرعة على حل تقريبي. وتجمع LSQR بين أفضل خصائص الخوارزميات السابقة ، حيث يمكن توزيعها ، وتتقارب بشكل أسرع مقارنة بنسب التدرج ، وتتيح أيضًا إيقاف مبكر للخوارزمية ، على عكس تحليل QR ، لإيجاد حل تقريبي.