في Habré ، كان هناك بالفعل العديد من المقالات المكرّسة للحسابات السريعة لعلم المثلثات عندما يكون ذلك ضروريًا للغاية ، لكنني أود أن أكملها بمذكرة صغيرة واحدة مع الإشارة إلى علم المثلثات المدرسي.
في بعض الأحيان قد لا يكون هناك تطبيق لجهاز علم المثلثات ، وأحيانًا قد تكون هناك أسباب أخرى لاختراع طرق لتسريع الحساب.
الرياضيات
دعنا نتذكر بعض الصيغ البسيطة من الدورة المدرسية.
لنبدأ بالأشياء البسيطة:
(1)
sin x = cos (90° - x)cos x = sin (90° - x)sin -x = -sin xcos -x = cos x- في الحالة العامة ،
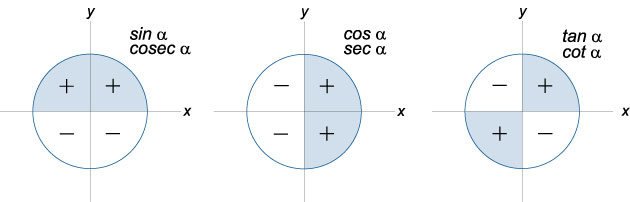
sin (90°N ± x) = ±cos x لـ odd N و ±sin x لـ متساوي. يتم أخذ العلامة بناءً على علامة الوسيطة في الربع المقابل من الدائرة.
التالي:
(2)
cos (x + y) = cos x cos y - sin x sin ysin (x + y) = sin x cos y + cos x sin y
وأيضا:
(3)
sin x = x - x^3/3! + x^5/5! - ...cos x = 1 - x^2/2! + x^4/4! - ...
يمكن تقليل جيب تمام / جيب أي زاوية إلى وسيطة في النطاق من 0 درجة إلى 45 درجة باستخدام صيغ المجموعة الأولى.
بالنسبة إلى الزوايا الصغيرة ، يمكن اختزال الدوال المثلثية إلى التوسعات غير المقاربة إذا تجاوزت المصطلحات المهملة عن عمد شبكة التصريف.
يمكن الحصول على جميع الزوايا الوسيطة من خلال تجميع الزوايا الكبيرة بخطوة معينة (ويمكن اعتبار علم المثلثات جدوليًا لها) ، والبقايا التي سوف تعطي إنحلالًا خطيًا عاجلاً أو آجلاً.
تطبيق
لنفترض أننا نعمل مع أرقام IEEE-754 ذات الدقة المفردة ، ولديها أسماء تطفو ، وحيدة ، إلخ. هناك 23 حرفًا في السرعوف ، وهذا يعني أننا بحاجة إلى الحصول على خطأ نسبي قدره 2^-23 .
لنقم بتقييم مدى عمق النزول لإنشاء جداول وسيطات.
من أجل الجيب ، سنتجاهل المصطلح التكعيبي ، لذلك نحتاج إلى أن تكون علاقته بالمصطلح الخطي أقل من الخطأ المسموح به ، مما يعني: 1 - (x - x^3/3!) / x = x^2/6 2/6 2 ^ -23 ، ومن ثم فإنه بالنسبة للحجج التي لا تزيد عن 0.000846 راديان ، فإن دقة الحساب التقريبي للجيب كافية بالنسبة لنا. بالنسبة لجيب التمام ، إذا قمت بإسقاط المصطلح التربيعي ، فأنت بحاجة إلى دقة أفضل بنحو مرتين - 0.000488 راديان.
لذلك ، لا نحتاج إلى وجود قيم جدولية للوسيطة التي تقل عن 0.000488 راديان.
لإنشاء الجدول ، أعد تنظيم وسيطة الإدخال بحيث تتطابق القيمة 0 مع زاوية 0 ° ، وقيمة 1 تقابل زاوية 45 ° ، أو pi/4=0.78539816 راديان. بعد ذلك ، سيتم تحويل الزاوية الدنيا التي تم الحصول عليها أعلاه إلى 0.0006217 راديان ، أو حوالي 1/1600 - وهذا أكثر من 1/2048 = 2^-11 .
بعد ذلك ، ستحتاج إلى اختيار خطوة الجداول بناءً على الطريقة التي نريد بها توزيع الحسابات ، وسنقوم بتقسيم الأس 11 على عدة أجزاء. على سبيل المثال ، يمكنك تقسيمها إلى جزأين: 11 = 6 + 5 ، ثم نحتاج إلى جدولين بحجم 64 و 32 إدخالات (إجمالي 96) ، أو ثلاثة أجزاء: 11 = 4 + 4 + 3 (حجم الجداول 16 + 16 + 8 = 40 إدخالات) ، ولكن سيكون هناك المزيد من عمليات الضرب - يعتمد الخيار المحدد على المهمة والموارد المتاحة.
ملاحظة: إدخال الجدول عبارة عن زوج من وسائط جيب التمام وجيب التمام. إذا تم تخزينه بدقة واحدة ، فسيكون حجم السجل 8 بايت.
مثال
لنأخذ التحلل 4 + 4 + 3 كمثال ، ثم نعمم.
لذلك ، المهمة: حساب قيمة sin x ل x التعسفي.
الخطوة 1. نأتي بالوسيطة x إلى مقياسنا ، ونقسمها على pi/4 الثابت (دعنا نسميها x' ).
الخطوة 2. اعتمادًا على قيمة الوسيطة x' باستخدام الصيغ (1) ، نختار الوظيفة المطلوبة بحيث تكون الوسيطة الخاصة بها في النطاق من 0 إلى 1 (ضمنيًا) (دعنا ندعو x'' . في هذه الخطوة ، ستحتاج أيضًا إلى وضع علامة على النتيجة. .
[لنفترض على سبيل المثال أن الجيب هو]
الخطوة 3. سوف نستخدم الجداول (سأذكرك بوجود 3 منها) ، في حين أن الأرقام القياسية في الجدول ستكون "حقول بت" في التمثيل الثنائي للوسيطة x'' - أول 4 بتات بعد العلامة العشرية ، ثم 4 أخرى ، و 3 أخرى ، والبقية للأعمال سوف يذهب البتات إلى الباقي.
يسمى جيب الجدول S1 ، S2 ، S3 ، جيب التمام الجدول C1 ، C2 ، C3.
بما أننا قسمنا الزاوية على pi/4 ، من أجل الحصول على الباقي في راديان ، يجب ضربها بنفس المقدار. يُشار إلى الباقي "bit" مضروب في pi/4 ب a. ثم جيبه سوف يساوي A ، وجيب التمام -1.
الخطوة 4. الجمع بين كل ما حدث:
C12 = C1 C2 - S1 S2 S12 = S1 C2 + C1 S2 C123 = C12 C3 - S12 S2 S123 = S12 C3 + C12 S3
|sin x| = S123 + C123 A |sin x| = S123 + C123 A (إذا حصلت على جيب في الخطوة 2)
|sin x| = C123 - S123 A |sin x| = C123 - S123 A (إذا تلقيت جيب التمام في الخطوة 2)
الخطوة 5. إذا اعتبرنا في الخطوة 2 أن النتيجة يجب أن تكون سالبة ، فيجب إدخال هذا الطرح في النتيجة.
استنتاج
يمكن استخدام نهج مشابه للحساب بالأرقام الحقيقية من أي حجم ، وعلى سبيل المثال ، لتنفيذ حساب النقطة الثابتة المتخصصة. في الواقع ، كانت المهمة الأخيرة التي دفعتني إلى الحفر في هذا الاتجاه في وقت واحد ، لكن ذلك كان منذ زمن طويل.