النمو. الوزن. ثلاثة جيران

بحثًا عن مجموعة بيانات مثيرة للاهتمام وبسيطة ، صادفت هذا الرجل الوسيم .

عن هذا الجمال

أنه يحتوي على بيانات عن نمو ووزن 10000 من الرجال والنساء . لا يوجد وصف لا شيء "لا لزوم لها". فقط الطول والوزن وعلامة الكلمة. أعجبتني هذه البساطة الغامضة.

حسنًا ، لنبدأ!

ما كان مثيرا للاهتمام بالنسبة لي؟

• ما هو نطاق الوزن والطول بالنسبة لمعظم الرجال والنساء؟
• أي نوع من الرجل "المتوسط" والمرأة "المتوسطة" هم؟
• هل يمكن أن يتنبأ نموذج تعلم آلة KNN البسيط من هذه البيانات بالوزن حسب الطول ؟

دعنا نذهب!

النظرة الأولى

أولا ، تحميل الوحدات اللازمة

#      import pandas as pd #     import matplotlib.pyplot as plt %matplotlib inline #    «  » from sklearn.neighbors import KNeighborsRegressor #         from sklearn.model_selection import train_test_split 

عندما وقفت المكتبات تمامًا - حان الوقت لتحميل DataSet نفسها وإلقاء نظرة على العناصر العشرة الأولى. هذا ضروري حتى تكون القناة الهضمية لدينا هادئة ، وقد حملنا كل شيء بشكل صحيح.

بالمناسبة ، لا تنزعج من أن الطول والوزن يختلفان عما اعتدنا عليه. هذا بسبب نظام قياس مختلف: البوصات والجنيه ، بدلاً من السنتيمترات والكيلوغرام .

 data = pd.read_csv('weight-height.csv') data.head(10) 

حسن! نرى أن المداخل العشرة الأولى هي "رجال". نرى طولهم والوزن . البيانات المحملة بشكل جيد.

الآن يمكنك إلقاء نظرة على عدد الصفوف في المجموعة.

 data.shape >> (10000, 3) 

عشرة آلاف سطر / سجلات. ولكل منها ثلاثة معايير . ما تحتاجه!

حان الوقت لإصلاح نظام القياس. الآن هنا سم و كيلوغرام.

 data['Height'] *= 2.54 data['Weight'] /= 2.205 #    data.head(10) 

الآن أصبح أكثر دراية. ويخبرنا السجل الأول عن رجل يبلغ ارتفاعه حوالي 190 سم ويزن حوالي 110 كجم. رجل كبير. دعنا ندعوه بوب.

ولكن كيف نفهم: هل هو كثير أو قليل مقارنة بالباقي؟ هل من الممكن أننا جميعا زائد أو ناقص الفول؟ هذا هو في وقت لاحق قليلا.

الآن لنكتشف مدى تناسق النوعين في مجموعة البيانات هذه؟

 data['Gender'].value_counts() >> Male 5000 Female 5000 Name: Gender, dtype: int64 

من الناحية المثالية منقسم بالتساوي. وهذا أمر جيد ، لأنه إذا كان هناك: 9999 رجل وامرأة واحدة ، فلن يكون هناك أي معنى في التظاهر بأن مجموعة البيانات هذه تكشف كلا الجنسين بشكل متساوٍ. في حالتنا ، كل شيء على ما يرام!

تقسيم وتعلم!

يشير الحدس الآن إلى أنه سيكون من الصحيح الفصل بين الجنسين واستكشاف كل منهما على حدة. في الواقع ، في كثير من الأحيان نرى أن الرجال والنساء لديهم طول زائد ووزن مختلفان أو ناقصان

 #  data_male = data[data['Gender'] == 'Male'].copy() #  data_female = data[data['Gender'] == 'Female'].copy() 

دعنا نلقي نظرة على الإحصاءات الوصفية الصغيرة التي توفرها لنا وحدة الباندا .

الرجال :

 data_male.describe() 

النساء :

 data_female.describe() 

نرى أنه في الرجال يبلغ المتوسط ​​والوسيط 175 سم و 85 كجم. وفي النساء : 162 سم ​​و 62 كجم. هذا يخبرنا أنه لا توجد انبعاثات قوية. أو أنها متناظرة على جانبي الوسيط. وهو نادر جدا.

لكن كلا الجنسين لديهما انحرافات طفيفة عن المتوسط ​​من المتوسط. لكنها غير ذات أهمية وأنها مرئية فقط على المئات. دعنا ننتقل!

Gistograma

هذا رسم بياني يرسم القيم من الحد الأدنى إلى الحد الأقصى في ترتيب النمو ، ويظهر عدد الحالات الفردية.

 fig, axes = plt.subplots(2,2, figsize=(20,10)) plt.subplots_adjust(wspace=0, hspace=0) axes[0,0].hist(data_male['Height'], label='Male Height', bins=100, color='red') axes[0,1].hist(data_male['Weight'], label='Male Weight', bins=100, color='red', alpha=0.4) axes[1,0].hist(data_female['Height'], label='Female Height', bins=100, color='blue') axes[1,1].hist(data_female['Weight'], label='Female Weight', bins=100, color='blue', alpha=0.4) axes[0,0].legend(loc=2, fontsize=20) axes[0,1].legend(loc=2, fontsize=20) axes[1,0].legend(loc=2, fontsize=20) axes[1,1].legend(loc=2, fontsize=20) plt.savefig('plt_histogram.png') plt.show() 

يتم توزيع البيانات على شكل جرس. تشبه الى حد بعيد التوزيع الطبيعي .

بالإضافة إلى الاختبارات الإحصائية للتوزيع الطبيعي ، هناك اختبار بصري. إذا كان التوزيع حسب النوع والمنطق طبيعيًا - فيمكننا افتراض بعض الافتراضات بأننا نتعامل معه.

يمكن للمرء القيام باختبار الحالة الطبيعية الإحصائية وتحديد قيمة p ، ولكن لا استطيع هذا هو خارج نطاق المقال.

تعلم العمل مع الأقلام

يمكن الباندا العد الكثير بالنسبة لنا. لكن عليك أن تحسب على الأقل بعض الإحصاءات بنفسك. الآن سوف أعرض كيفية حساب الانحراف المعياري .

دعونا نفعل ذلك على سبيل المثال من الرجال والسمة - النمو.

متوسط

الصيغة:

$$

$$M = \ frac {1} {N} \ sum \ limit_ {i = 1} ^ N n_i$$

حيث

• م - متوسط ​​القيمة
• N هو عدد الحالات
• ني - مثيل واحد

كود:

 mean = data_male['Height'].mean() print('mean:\t{:.2f}'.format(mean)) >> mean: 175.33 

متوسط ​​الارتفاع - 175 سم

الانحراف التربيعي

$$

$$d_i = (n_i - M) ^ 2$$

حيث

• دي - انحراف واحد
• ني - مثيل واحد
• م - المتوسط

كود:

 data_male['Height_d'] = (data_male['Height'] - mean) ** 2 data_male['Height_d'].head(10) >> 0 149.927893 1 0.385495 2 166.739089 3 47.193692 4 4.721246 5 20.288347 6 0.375539 7 2.964214 8 25.997623 9 200.149603 Name: Height_d, dtype: float64 

تشتت

الصيغة:

$$

$$D = \ frac {1} {N} \ sum \ limit_ {i = 1} ^ N d_i$$

حيث

• D هي قيمة التشتت
• دي - انحراف واحد
• N هو عدد الحالات

كود:

 disp = data_male['Height_d'].mean() print('disp:\t{:.2f}'.format(disp)) >> disp: 52.89 

تشتت - 53

الانحراف المعياري

الصيغة:

$$

$$std = \ sqrt {D}$$

حيث

• الأمراض المنقولة جنسيا - قيمة الانحراف المعياري
• D هي قيمة التشتت

كود:

 std = disp ** 0.5 print('std:\t{:.2f}'.format(std)) >> std: 7.27 

الانحراف المعياري - 7

فواصل الثقة

سنكتشف الآن نطاقات النمو والوزن 68٪ و 95٪ و 99.7٪ من الرجال والنساء .

هذا ليس بالأمر الصعب - تحتاج إلى إضافة وطرح الانحراف المعياري عن المتوسط. يبدو مثل هذا:

• 68 ٪ - زائد أو ناقص الانحراف المعياري
• 95 ٪ - زائد أو ناقص اثنين من الانحرافات القياسية
• 99.7 ٪ - زائد أو ناقص ثلاثة الانحرافات القياسية

نكتب وظيفة مساعدة من شأنها أن تنظر في هذا:

 def get_stats(series, title='noname'): #    print('= {} =\n'.format(title.upper())) #     pandas descr = series.describe() #   mean = descr['mean'] print('= Mean:\t{:.0f}'.format(mean)) #    std = descr['std'] print('= Std:\t{:.0f}'.format(std)) #    print('\n= = = =\n') #   ## 68% devi_1 = [mean - std, mean + std] ## 95% devi_2 = [mean - 2 * std, mean + 2 * std] ## 99.7% devi_3 = [mean - 3 * std, mean + 3 * std] #   print('= 68% is from\t\t{:.0f} to {:.0f}'.format(devi_1[0], devi_1[1])) print('= 95% is from\t\t{:.0f} to {:.0f}'.format(devi_2[0], devi_2[1])) print('= 99.7% is from\t\t{:.0f} to {:.0f}'.format(devi_3[0], devi_3[1])) 

حسنًا ، قم بتطبيقه على البيانات:

رجال | نمو

 get_stats(data_male['Height'], title='Male Height') >> = MALE HEIGHT = = Mean: 175 = Std: 7 = = = = = 68% is from 168 to 183 = 95% is from 161 to 190 = 99.7% is from 154 to 197 

رجال | الوزن

 get_stats(data_male['Height'], title='Male Height') >> = MALE WEIGHT = = Mean: 85 = Std: 9 = = = = = 68% is from 76 to 94 = 95% is from 67 to 103 = 99.7% is from 58 to 112 

النساء | نمو

 get_stats(data_male['Height'], title='Male Height') >> = FEMALE HEIGHT = = Mean: 162 = Std: 7 = = = = = 68% is from 155 to 169 = 95% is from 148 to 176 = 99.7% is from 141 to 182 

النساء | الوزن

 get_stats(data_male['Height'], title='Male Height') >> = FEMALE WEIGHT = = Mean: 62 = Std: 9 = = = = = 68% is from 53 to 70 = 95% is from 44 to 79 = 99.7% is from 36 to 87 

ومن هنا الاستنتاجات:

• معظم الرجال: 154 سم - 197 سم و 58 كجم - 112 كجم.
• معظم النساء: 141 سم - 182 سم و 36 كجم - 87 كجم.

الآن يبقى فقط تطبيق التعلم الآلي على هذه المجموعة ومحاولة التنبؤ بالوزن حسب الطول.

أقرب الجيران

الخوارزمية "إلى أقرب الجيران" بسيطة. يوجد لمهام التصنيف - لتمييز قطة عن كلب - وللمهام الانحدار - لتخمين الوزن بالطول. هذا هو ما نحتاجه!

بالنسبة إلى الانحدار ، يستخدم الخوارزمية التالية:

• يتذكر جميع نقاط البيانات
• عندما تظهر نقطة جديدة ، فإنها تبحث عن K المجاورة لها (يتم تعيين الرقم K من قبل المستخدم)
• المتوسطات النتيجة
• يعطي إجابة

تحتاج أولاً إلى تقسيم مجموعة البيانات إلى أجزاء التدريب والاختبار واختبار الخوارزمية

التجريب على الرجال

 X_train, X_test, y_train, y_test = train_test_split(data_male['Height'], data_male['Weight']) 

مقسمة ، لقد حان الوقت للمحاولة.

 #   knr3 = KNeighborsRegressor(n_neighbors=3) knr3.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr3.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.8298400793623182 #   knr5 = KNeighborsRegressor(n_neighbors=5) knr5.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr5.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.7958051642678619 #   knr7 = KNeighborsRegressor(n_neighbors=7) knr7.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr7.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.7769249318420969 

لن نذهب بعيدا ونتوقف عند ثلاثة جيران. لكن السؤال هو: هل يمكن لهذا النموذج تخمين وزني؟

 knr3.predict([[180]])[0, 0] >> 88.67596236265881 

88kg قريب جدا. هذا الثاني ، وزني هو 89.8kg

الرسم البياني التنبؤ للرجال

الوقت لبناء الجزء المفضل من العلوم هو الرسومات.

 array_male = [] #   99.7% xaxis = range(154, 198) for h in xaxis: ans = knr3.predict([[h]]) array_male.append(ans[0, 0]) plt.figure(figsize=(20,10)) plt.plot(xaxis, array_male, 'r-', linewidth=4) plt.title('Male heght-weight dependence', fontsize=30) plt.xlabel('Height', fontsize=30) plt.ylabel('Weight', fontsize=30) plt.grid() plt.savefig('plt_knn_male.png') plt.show() 

نموذج وتخطيط الرسم البياني للمرأة

 X_train, X_test, y_train, y_test = train_test_split(data_female['Height'], data_female['Weight']) knr3 = KNeighborsRegressor(n_neighbors=3) knr3.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr3.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.8135681584074799 

 array_female = [] #   99.7% xaxis = range(141, 183) for h in xaxis: ans = knr3.predict([[h]]) array_female.append(ans[0, 0]) plt.figure(figsize=(20,10)) plt.plot(xaxis, array_female, 'b-', linewidth=4) plt.title('Female heght-weight dependence', fontsize=30) plt.xlabel('Height', fontsize=30) plt.ylabel('Weight', fontsize=30) plt.grid() plt.savefig('plt_knn_female.png') plt.show() 

وبالطبع من المثير للاهتمام كيف تبدو هذه الرسوم البيانية معًا:

 #      xaxis = range(154, 183) plt.figure(figsize=(20,10)) plt.plot(xaxis, array_male[:-15], 'r-', linewidth=4) plt.plot(xaxis, array_female[13:], 'b-', linewidth=4) plt.title('Together heght-weight dependence', fontsize=30) plt.xlabel('Height', fontsize=30) plt.ylabel('Weight', fontsize=30) plt.grid() plt.savefig('plt_knn_together.png') plt.show() 

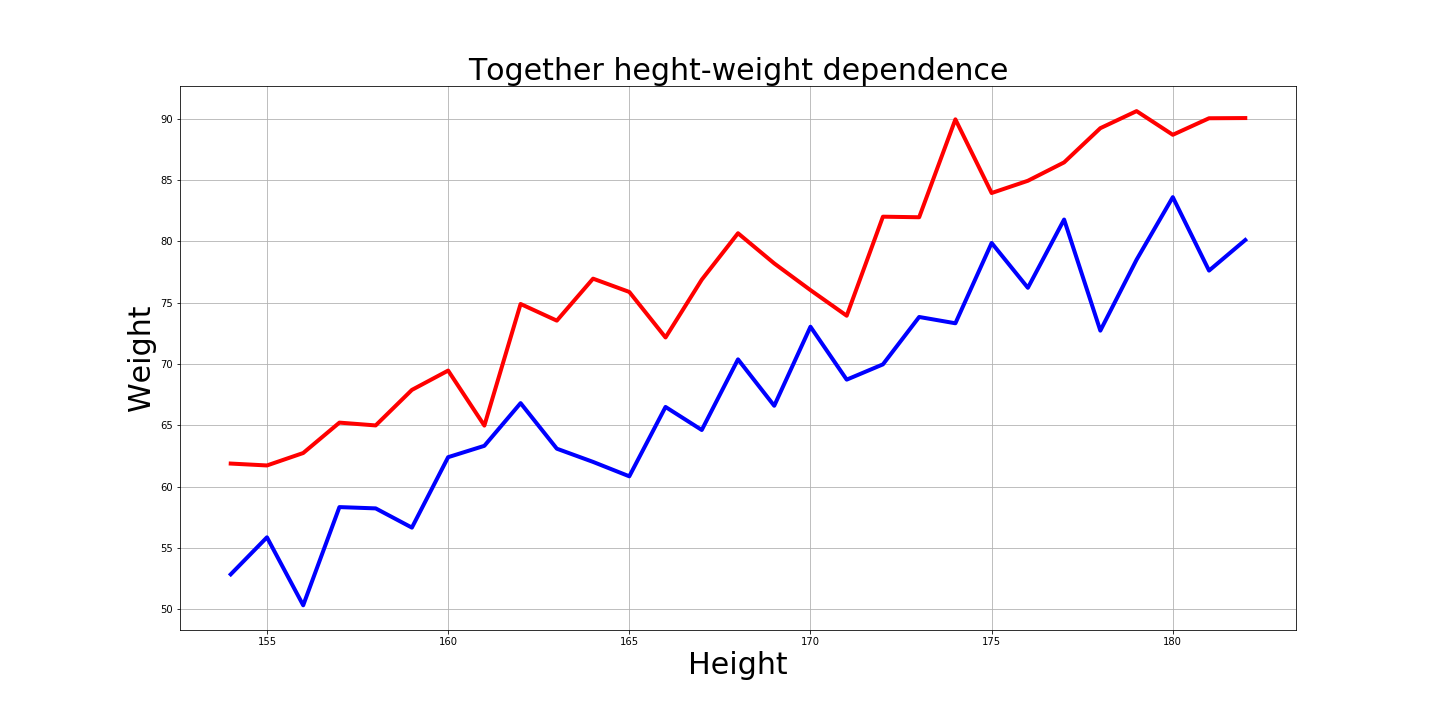
إجابات على الأسئلة

- ما هو نطاق الوزن والطول بالنسبة لمعظم الرجال والنساء؟

99.7٪ من الرجال: من 154 سم إلى 197 سم ومن 58 كجم إلى 112 كجم.
و 99.7٪ من النساء: من 141 سم إلى 182 سم ومن 36 كجم إلى 87 كجم.

- أي نوع من الرجل "المتوسط" والمرأة "المتوسطة" هم؟

الرجل المتوسط ​​هو 175 سم و 85 كجم.
و المرأة المتوسطة هي 162 سم ​​و 62 كجم.

- هل يتنبأ نموذج تعلم آلة KNN البسيط من هذه البيانات بالوزن حسب الطول؟

نعم ، توقع النموذج 88 كجم ، ولدي 89.8 كجم.

كل ما فعلته ، جمعت هنا

سلبيات المقال

• لا يوجد وصف لمجموعة البيانات. ربما كان العمر وعوامل أخرى في الناس مختلفة. لذلك ، لا يمكن للمرء أن يقبل ذلك على الإيمان ، ولكن من أجل التجربة - من فضلك.
• بطريقة جيدة - كان من الضروري إجراء اختبار لطبيعية التوزيع

خاتمة

مثل إذا كنت تصل إلى الفاصل 99.7 ٪