تواجه ClickHouse باستمرار مهام معالجة السلسلة. على سبيل المثال ، البحث ، وحساب خصائص سلاسل UTF-8 ، أو شيء أكثر غرابة ، سواء كان بحثًا حساسًا لحالة الأحرف أو بحثًا عن بيانات مضغوطة.
بدأ كل شيء بحقيقة أن مدير تطوير ClickHouse ، ليوشا ميلوفيدوف o6CuFl2Q ، جاء إلينا في كلية علوم الحاسب في المدرسة العليا للاقتصاد وقدم عددًا كبيرًا من الموضوعات لأوراق الفصل الدراسي والدبلومات. عندما رأيت "خوارزميات معالجة السلسلة الذكية في ClickHouse" (أنا ، شخص مهتم بخوارزميات متنوعة ، بما في ذلك تلك التجريبية) ، قمت على الفور بوضع خطط لكيفية الحصول على أفضل دبلوم. فرحي والتعبير يمكن وصفها على النحو التالي:

ClickHouse
ClickHouse بعناية مدروسة تنظيم تخزين البيانات في الذاكرة - في الأعمدة. في نهاية كل عمود يوجد حشوة من 15 بايت لقراءة آمنة من سجل 16 بايت. على سبيل المثال ، يخزن ColumnString سلاسل منتهية بقيمة خالية مع الإزاحة. أنها مريحة للغاية للعمل مع هذه المصفوفات.

هناك أيضًا ColumnFixedString و ColumnConst و LowCardinality ، لكننا لن نتحدث عنها بمثل هذه التفاصيل اليوم. النقطة الأساسية في هذه المرحلة هي أن تصميم القراءة الآمنة للذيول على ما يرام ، وأن موقع البيانات يلعب أيضًا دورًا في المعالجة.
البحث عن سلسلة فرعية
على الأرجح ، أنت تعرف العديد من الخوارزميات المختلفة للعثور على سلسلة فرعية في سلسلة. سنتحدث عن تلك المستخدمة في ClickHouse. أولاً نعرض تعريفين:
- كومة قش - الخط الذي نتطلع إليه ؛ عادة ما يتم الإشارة إلى الطول بواسطة n .
- إبرة - السلسلة أو التعبير المنتظم الذي نبحث عنه ؛ سيتم الإشارة إلى طول بواسطة م .
بعد دراسة عدد كبير من الخوارزميات ، يمكنني القول أن هناك نوعين (3 كحد أقصى) من خوارزميات البحث في السلسلة الفرعية. الأول هو إنشاء بنيات لاحقة بشكل أو بآخر. النوع الثاني هو خوارزميات تستند إلى مقارنة الذاكرة. هناك أيضًا خوارزمية Rabin-Karp ، التي تستخدم التجزئة ، لكنها فريدة من نوعها تمامًا. أسرع خوارزمية غير موجودة ، كل هذا يتوقف على حجم الأبجدية وطول الإبرة وكومة القش وتكرار حدوثها.
اقرأ عن الخوارزميات المختلفة هنا . وهنا الخوارزميات الأكثر شعبية:
- كنوت - موريس - برات ،
- بوير - مور ،
- بوير - مور - Horspool ،
- رابين - شبوط ،
- على الوجهين (يستخدم في glibc يسمى "memmem") ،
- BNDM.
القائمة تطول. لقد جربنا في ClickHouse بكل شيء بكل صدق ، لكن في النهاية استقرنا على إصدار أكثر استثنائية.
خوارزمية Volnitsky
تم نشر الخوارزمية على مدونة مبرمج ليونيد Volnitsky في أواخر عام 2010. إنه يشبه إلى حد ما خوارزمية Boyer-Moore-Horspool ، فقط نسخة محسنة.
إذا كانت m <4 ، فسيتم استخدام خوارزمية البحث القياسية. احفظ كل إبرة bigrams (2 بايت متتالية) من النهاية إلى طاولة تجزئة مع عنونة مفتوحة للحجم | Sigma | 2 عنصرا (في الممارسة ، هذه هي 2 16 عنصرا) ، حيث تكون إزاحة هذا bigram هي القيم ، وستكون bigram نفسها هي التجزئة والفهرس في نفس الوقت. سيكون الموقف الأولي في الموضع م -2 من بداية كومة القش. نتبع كومة قش بخطوة m - 1 ، وننظر إلى bigram التالي من هذا الموقف في كومة قش وننظر في جميع القيم من bigram في جدول التجزئة. ثم سنقارن قطعتين من الذاكرة مع خوارزمية المقارنة المعتادة. سيتم معالجة الذيل المتبقي بواسطة نفس الخوارزمية.
يتم اختيار الخطوة m - 1 بطريقة أنه إذا كان هناك إبرة في كومة قش ، فسننظر بالتأكيد في bigram من هذا الإدخال - وبالتالي التأكد من أننا نعيد موقف الإدخال في كومة قش. الحدث الأول مضمون من خلال حقيقة أننا نضيف فهارس من النهاية إلى جدول التجزئة بواسطة bigram. هذا يعني أنه عندما ننتقل من اليسار إلى اليمين ، سننظر أولاً في الحلقات الكبيرة من نهاية السطر (ربما تفكر مبدئيًا في ذلك في المقام الأول) ، ثم نقترب من البداية.
النظر في مثال. واسمحوا كومة قش سلسلة يكون abacabaac وإبرة تساوي aaca . سيكون جدول التجزئة {aa : 0, ac : 1, ca : 2} .
0 1 2 3 4 5 6 7 8 9 abacabaaca ^ -
نرى bigram ac . في الإبرة ، نحن بديل في المساواة:
0 1 2 3 4 5 6 7 8 9 abacabaaca aaca
لم تتطابق. بعد ac لا توجد إدخالات في جدول التجزئة ، نخطو الخطوة 3:
0 1 2 3 4 5 6 7 8 9 abacabaaca ^ -
لا توجد bigrams ba في جدول التجزئة ، تابع:
0 1 2 3 4 5 6 7 8 9 abacabaaca ^ -
هناك bigram ca في الإبرة ، ونحن ننظر إلى الإزاحة والعثور على الإدخال:
0 1 2 3 4 5 6 7 8 9 abacabaaca aaca
الخوارزمية لديها العديد من المزايا. أولاً ، لا تحتاج إلى تخصيص ذاكرة على الكومة ، و 64 كيلو بايت على المكدس ليست شيئًا متجاوزًا الآن. ثانيا ، 2 16 هو رقم ممتاز لاتخاذ modulo للمعالج. هذه مجرد تعليمات movzwl (أو ، كما نكتة ، "movsvl") والعائلة.
في المتوسط ، أثبتت هذه الخوارزمية أنها الأفضل. أخذنا البيانات من Yandex.Metrica ، طلبات حقيقية تقريبا. سرعة تيار واحدة ، أكثر أفضل ، KMP: خوارزمية Knut - Morris - Pratt ، BM: Boyer - Moore ، BMH: Boyer - Moore - Horspool.
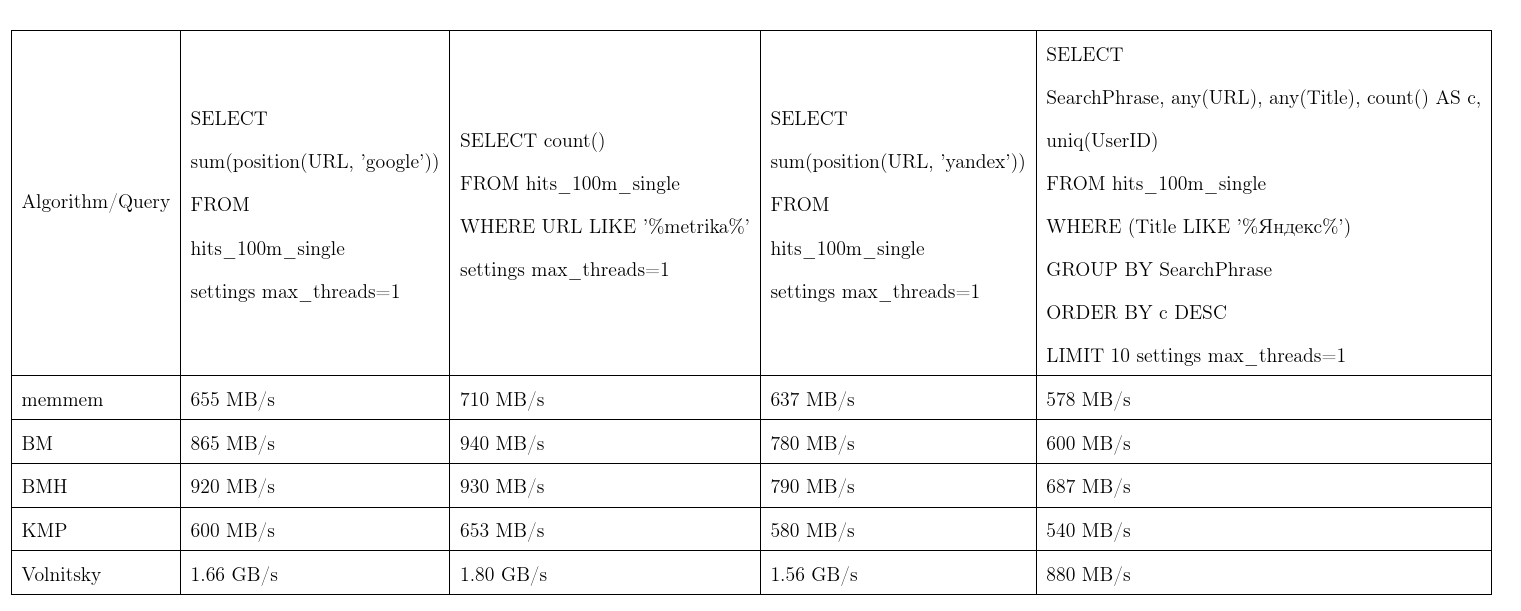
حتى لا تكون بدون أساس ، يمكن أن تعمل الخوارزمية وقتًا تربيعيًا:

يتم استخدامه في وظيفة position(Column, ConstNeedle) ، ويعمل أيضًا position(Column, ConstNeedle) لعمليات بحث التعبير position(Column, ConstNeedle) .
بحث التعبير العادي
سنخبرك كيف تقوم ClickHouse بتحسين عمليات البحث العادية عن التعبير. تحتوي العديد من التعبيرات العادية على سلسلة فرعية من الداخل ، والتي يجب أن تكون داخل كومة قش. حتى لا نبني جهازًا محددًا للدولة وفحصه ضده ، سنقوم بعزل مثل هذه الدعامات.
للقيام بذلك بسيط للغاية: أي أقواس فتح تزيد من مستوى التعشيش ، أي أقواس إغلاق تنخفض ؛ هناك أيضًا أحرف خاصة بالتعبيرات العادية (مثل "." ، "*" ، "؟" ، "\ w" ، إلخ). نحتاج إلى الحصول على جميع العناصر الفرعية في المستوى 0. فكر في مثال:
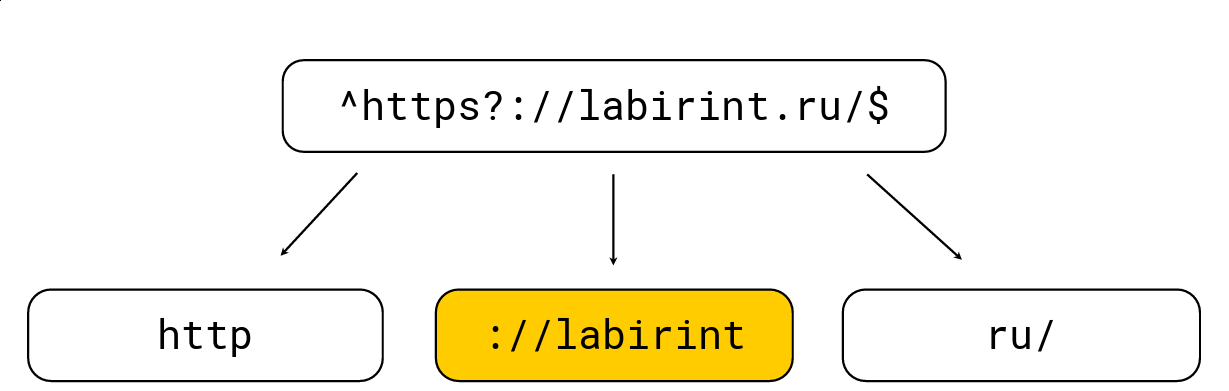
نحن نقسمها إلى تلك الأسس التي يجب أن تكون في كومة قش من التعبير العادي ، وبعد ذلك نقوم بتحديد الحد الأقصى للطول ، ابحث عن المرشحين عليها ثم تحقق مع محرك التعبير العادي المعتاد RE2. في الصورة أعلاه ، يوجد تعبير منتظم ، تتم معالجته بواسطة محرك RE2 المعتاد بسرعة 736 ميجابايت / ثانية ، وتمكّن Hyperscan (حوالي ذلك لاحقًا قليلاً) من 1.6 جيجابايت / ثانية ، وندير 1.69 جيجابايت / ثانية لكل نواة مع إلغاء الضغط LZ4. بشكل عام ، يكون هذا التحسين على السطح ويسرع بشكل كبير في البحث عن التعبيرات العادية ، ولكن في كثير من الأحيان لا يتم تنفيذه في الأدوات ، وهو ما يفاجئني إلى حد كبير.
تم تحسين الكلمة الرئيسية LIKE أيضًا باستخدام هذه الخوارزمية ، فقط بعد LIKE يمكن التعبير العادي المبسط للغاية من خلال ٪٪٪٪٪ (سلسلة فرعية تعسفية) و _ (حرف تعسفي).
لسوء الحظ ، ليست كل التعبيرات العادية تخضع لمثل هذه التحسينات ، على سبيل المثال ، من yandex|google من المستحيل صراحة استخراج سلاسل فرعية يجب أن تحدث في كومة قش. لذلك ، توصلنا إلى حل مختلف تماما.
البحث عن العديد من الدعامات
المشكلة هي أن هناك الكثير من الإبر ، وأريد أن أفهم ما إذا كان قد تم تضمين واحدة منها على الأقل في كومة قش. هناك طرق كلاسيكية تمامًا لمثل هذا البحث ، على سبيل المثال ، خوارزمية Aho-Korasik. لكنه لم يكن سريعًا جدًا لمهمتنا. سنتحدث عن هذا بعد قليل.
ليش يحب ClickHouse الحلول غير القياسية ، لذلك قررنا تجربة شيء مختلف ، وربما ، إنشاء خوارزمية بحث جديدة بأنفسنا. وفعلوا.
نظرنا إلى خوارزمية Volnitsky وقمنا بتعديلها بحيث بدأت في البحث عن العديد من المواد الفرعية في وقت واحد. للقيام بذلك ، تحتاج فقط إلى إضافة bigrams من جميع الصفوف وتخزين فهرس الصف في جدول التجزئة. سيتم اختيار الخطوة من على الأقل كل أطوال الإبرة مطروحًا منها 1 لضمان مرة أخرى على العقار أنه في حالة حدوث ذلك ، فسوف نشاهد حجمه الكبير. سينمو جدول التجزئة إلى 128 كيلو بايت (تتم معالجة الأسطر الأطول من 255 بواسطة الخوارزمية القياسية ، ولن ندرس أكثر من 256 إبرة). أنا كسول جدًا ، لذا إليك مثال من العرض التقديمي (اقرأ من اليسار إلى اليمين من أعلى إلى أسفل):


بدأنا في النظر في كيفية تصرف هذه الخوارزمية مقارنةً بالآخرين (يتم أخذ الصفوف من البيانات الحقيقية). وبالنسبة لعدد صغير من الخطوط ، يفعل كل شيء (تتم الإشارة إلى السرعة جنبًا إلى جنب مع التفريغ - حوالي 2.5 جيجابايت / ثانية).
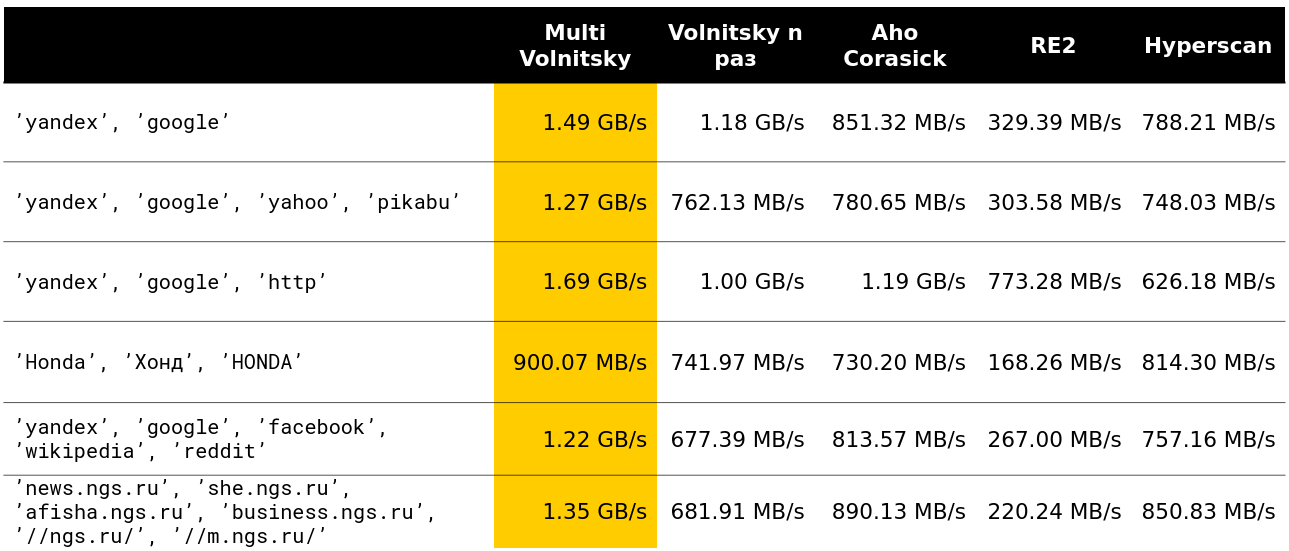
ثم أصبحت مثيرة للاهتمام. على سبيل المثال ، مع وجود عدد كبير من الشركات الكبيرة المماثلة ، نخسر بعض المنافسين. إنه أمر مفهوم - نبدأ في مقارنة العديد من أجزاء الذاكرة والتحلل.

لا يمكنك تسريع الكثير إذا كان الحد الأدنى لطول الإبرة كبيرًا بما يكفي. من الواضح ، لدينا المزيد من الفرص لتخطي قطع كاملة من كومة قش دون دفع أي شيء مقابل ذلك.

تبدأ نقطة التحول في مكان ما على الخطوط 13-15. حوالي 97٪ من الطلبات التي رأيتها على المجموعة كانت أقل من 15 صفًا:
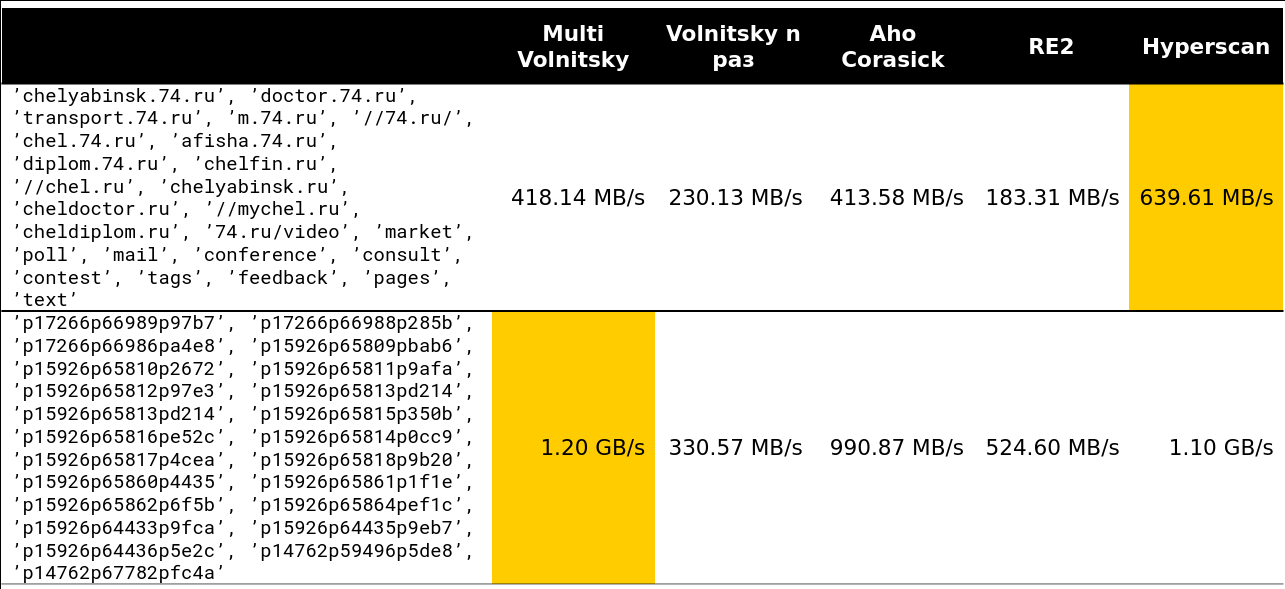
حسنًا ، صورة مخيفة جدًا - 41 سطرًا ، العديد من الشخصيات الكبيرة المتكررة:

نتيجة لذلك ، في ClickHouse (19.5) قمنا بتنفيذ الوظائف التالية من خلال هذه الخوارزمية:
- multiSearchAny(h, [n_1, ..., n_k]) - 1 ، إذا كان واحد على الأقل من الإبر في كومة قش.
- multiSearchFirstPosition(h, [n_1, ..., n_k]) - الموضع multiSearchFirstPosition(h, [n_1, ..., n_k]) للدخول في كومة قش (من واحد) أو 0 إذا لم يتم العثور عليه.
- multiSearchFirstIndex(h, [n_1, ..., n_k]) - مؤشر الإبرة في أقصى اليسار ، والذي تم العثور عليه في كومة قش. 0 إذا لم يتم العثور عليها.
- multiSearchAllPositions(h, [n_1, ..., n_k]) - جميع المواضع الأولى لجميع الإبر ، تقوم بإرجاع صفيف.
اللواحق هي -UTF8 (نحن لا نطبيع) ، -CaseInsensitive (نضيف 4 bigrams مع حالة مختلفة) ، -CaseInsensitiveUTF8 (هناك شرط أن الأحرف الكبيرة والصغيرة يجب أن يكون نفس عدد وحدات البايت). انظر التنفيذ هنا .
بعد ذلك ، تساءلنا عما إذا كان بإمكاننا فعل شيء مماثل مع العديد من التعبيرات العادية. ووجدوا حلاً قد أفسد بالفعل في المعايير.
البحث عن طريق العديد من التعبيرات العادية
Hyperscan هي مكتبة من Intel تقوم بالبحث الفوري عن العديد من التعبيرات العادية. يستخدم الاستدلال لعزل الكلمات الفرعية من التعبيرات العادية التي كتبنا عنها ، والكثير من بطاقات SIM للبحث عن غلوشكوف الآلي (يبدو أن الخوارزمية تسمى تيدي).
بشكل عام ، كل شيء في أفضل تقاليد الحصول على أقصى استفادة من البحث عن التعبيرات العادية. المكتبة حقا ما أعلن في وظائفها.

لحسن الحظ ، في الشهر الذي أمضيته في ClickHouse ، تمكنت من تجاوز التطوير لمدة 12 عامًا على فئة من الاستعلامات اللائقة وأنا مسرور جدًا بهذا.
في Yandex ، تستخدم مكتبة Hyperscan أيضًا في مكافحة البريد العشوائي. استنادا إلى المراجعات ، تعالج بهدوء الآلاف من التعبيرات العادية وتبحث بسرعة عنها.
المكتبة لديها العديد من العيوب. الأول هو مقدار الذاكرة غير المستهلكة المستهلكة وميزة غريبة يجب أن يكون كومة قش أقل من 32 بايت. الثاني - لا يمكنك إرجاع المواضع الأولى مجانًا ، ومؤشرات الإبرة الموجودة في أقصى اليسار ، وما إلى ذلك ، والثالث ناقص - هناك بعض الأخطاء من اللون الأزرق. لذلك ، في ClickHouse ، قمنا بتنفيذ الوظائف التالية باستخدام Hyperscan:
- multiMatchAny(h, [n_1, ..., n_k]) - 1 ، إذا تم التوصل إلى كومة من الإبر على الأقل.
- multiMatchAnyIndex(h, [n_1, ..., n_k]) - أي فهرس من الإبرة multiMatchAnyIndex(h, [n_1, ..., n_k]) كومة قش.
نحن مهتمون ، ولكن كيف يمكنك البحث ليس بالضبط ، ولكن تقريبًا؟ وجاءت مع العديد من الحلول.
البحث التقريبي
المعيار في البحث التقريبي هو المسافة Levenshtein - الحد الأدنى لعدد الأحرف التي يمكن استبدالها وإضافتها وإزالتها للحصول على سلسلة b بطول n من سلسلة a من الطول m. لسوء الحظ ، تعمل خوارزمية البرمجة الديناميكية الساذجة لـ O (mn) ؛ أفضل العقول من SHAD يمكن أن تفعل ذلك في O (مليون / سجل ماكس (ن ، م)) ؛ من السهل التفكير في O ((n + m) ⋅ alpha) ، حيث alpha هو الحل ؛ يمكن للعلم القيام بذلك من أجل O ((alpha - | n - m |) دقيقة (m ، n ، alpha) + m + n) (الخوارزمية بسيطة ، اقرأ على الأقل في ShAD) أو ، إذا كانت أوضح قليلاً ، لـ O (alpha ^ 2 + m + ن) . لا يزال هناك ناقص: من المستحيل على الأرجح التخلص من الوقت التربيعي في أسوأ الحالات متعدد الحدود - كتب بيتر إنديك مقالة قوية للغاية حول هذا الموضوع.
هناك تمرين: تخيل أنه لاستبدال شخصية في مسافة Levenshtein فإنك تدفع غرامة لا اثنين ، ولكن اثنين ؛ ثم الخروج بخوارزمية لـ O ((n + m) log (n + m)) .
ما زال لا يعمل ، طويل جدًا ومكلف. ولكن بمساعدة هذه المسافة ، قمنا بالكشف عن الأخطاء المطبعية في الاستعلامات.
بالإضافة إلى المسافة Levenshtein ، هناك مسافة Hamming. معه ، أيضًا ، كل شيء سيء جدًا ، لكنه أفضل قليلاً من مسافة ليفينشتاين. لا تأخذ في الحسبان إزالة الحروف ، ولكنها تأخذ بعين الاعتبار عدد الأحرف التي تختلف فيها فقط لخطين. لذلك ، إذا استخدمنا المسافة لسلاسل الطول m <n ، عندئذٍ فقط في البحث عن أقرب سلاسل فرعية.
كيفية حساب مثل هذا الصفيف من التناقضات (صفيف d من عناصر n - m + 1 ، حيث d [i] هو عدد الأحرف المختلفة في i-th من بداية التراكب ) لسجل O (| Sigma | (n + m) (n + m) ) ؟ أولا ، هل | سيغما | أقنعة بت تشير إلى ما إذا كان هذا الرمز مساوياً للرمز المعتبر. بعد ذلك ، نحسب الإجابة لكل من أقنعة Sigma ونضيف - نحصل على الإجابة الأصلية.
النظر في مثال. abba ، سلسلة فرعية ba ، الأبجدية الثنائية. نحصل على أقنعة 1001, 01 و 0110, 10 .
a 1001 01 - 0 01 - 0 01 - 1
b 0110 10 - 0 10 - 1 10 - 1
نحصل على المصفوفة [0 ، 1 ، 2] - هذه هي الإجابة الصحيحة تقريبًا. لكن لاحظ أنه بالنسبة لكل حرف ، فإن عدد التطابقات هو مجرد نتاج العددية لإبرة ثنائية ثابتة وجميع سلاسل التبطين. ولهذا ، بالطبع ، هناك تحول فورييه سريع!
بالنسبة لأولئك الذين لا يعرفون: يمكن لـ FFT مضاعفة متعددو الحدود من الدرجات m <n في وقت O (n log n) ، بشرط أن يتم تنفيذ العمل مع المعاملات لكل وحدة زمنية. تشابكات تشبه إلى حد كبير المنتجات العددية. يكفي تكرار معاملات متعدد الحدود الأولى ، وتوسيع واستكمال الثاني بالعدد المطلوب من الأصفار ، ثم نحصل على جميع المنتجات العددية لسلسلة ثنائية واحدة وجميع العناصر الفرعية الأخرى في O (n log n) - نوع من السحر! لكن صدقوني ، هذا حقيقي تمامًا ، وأحيانًا يفعله الناس.
ولكن ليس في ClickHouse. بالنسبة لنا ، العمل مع | Sigma | = 30 كبيرة بالفعل ، و FFT ليست الخوارزمية العملية الأكثر متعة للمعالج أو ، كما يقولون في عامة الناس ، "الثابت كبير."
لذلك ، قررنا أن ننظر إلى مقاييس أخرى. وصلنا إلى المعلوماتية الحيوية ، حيث يستخدم الناس مسافة ن غرام. في الواقع ، نحن نأخذ جميع غرامات الكومة والإبرة ، نأخذ بعين الاعتبار مجموعتين متعددتين مع هذه الغرامات n. ثم نأخذ الفرق المتماثل ونقسم على مجموع الكاردينيا لمجموعتين متعددتين مع n-gram. نحصل على رقم من 0 إلى 1 - كلما اقتربنا من 0 ، كلما كانت الخطوط متشابهة. النظر في مثال حيث ن = 4 :
abcda → {abcd, bcda}; Size = 2 bcdab → {bcda, cdab}; Size = 2 . |{abcd, cdab}| / (2 + 2) = 0.5
ونتيجة لذلك ، قطعنا مسافة 4 غرامات وتمسكنا بمجموعة من الأفكار من SSE هناك ، كما أضعفنا قليلاً في تنفيذ تجزئات crc32 مزدوجة البايت.
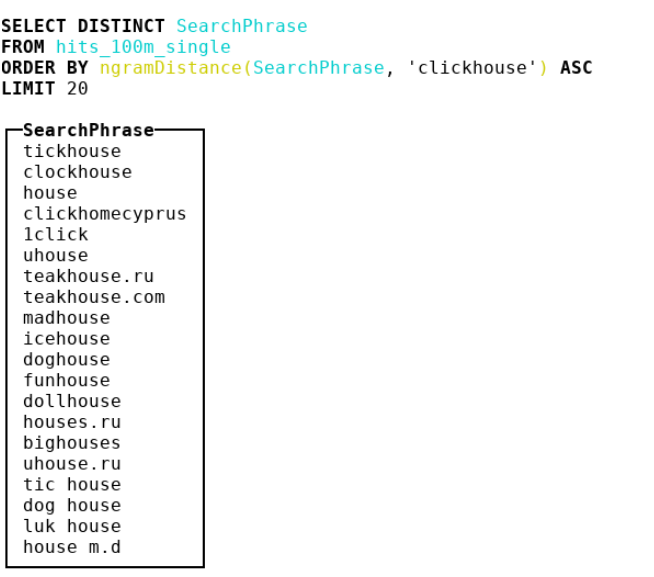
تحقق من التنفيذ . تحذير: رمز مقنن ومحسّن للغاية للمترجمين.
أنصحك بشكل خاص أن تنتبه إلى الاختراق القذر الذي يلقي ظلالاً صغيرة على نقاط ASCII والرموز الروسية.
- ngramDistance(haystack, needle) - إرجاع رقم من 0 إلى 1 ؛ أقرب إلى 0 ، والمزيد من خطوط تشبه بعضها البعض.
- -UTF8 ، -CaseInsensitive ، -CaseInsensitiveUTF8 (الاختراق القذر للروس و ASCII).
Hyperscan أيضًا لا يقف مكتوف الأيدي - لديه وظيفة للبحث التقريبي: يمكنك البحث عن الخطوط التي تبدو مثل التعبيرات العادية عن طريق المسافة المستمرة لـ Levenshtein. يتم إنشاء مسافة + 1 آليًا ، مترابطة عن طريق حذف حرف أو استبداله أو إدخاله ، بمعنى "جيد" ، وبعد ذلك يتم تطبيق الخوارزمية المعتادة لفحص ما إذا كان إنسان آلي يقبل سطرًا معينًا أم لا. في ClickHouse ، قمنا بتنفيذها تحت الأسماء التالية:
- multiFuzzyMatchAny(haystack, distance, [n_1, ..., n_k]) - تشبه multiMatchAny ، فقط مع المسافة.
- multiFuzzyMatchAnyIndex(haystack, distance, [n_1, ..., n_k]) - تشبه multiMatchAnyIndex ، فقط مع المسافة.
مع زيادة المسافة ، تبدأ السرعة في التدهور إلى حد كبير ، لكنها لا تزال عند مستوى لائق إلى حد ما.
الانتهاء من البحث والنزول إلى معالجة سلاسل UTF-8. كان هناك أيضا الكثير من الأشياء المثيرة للاهتمام.
تجهيز خط UTF-8
أعترف أنه كان من الصعب اختراق سقف التطبيقات الساذجة في السلاسل المشفرة UTF-8. كان من الصعب بشكل خاص المسمار SIMD. سوف أشارك بعض الأفكار حول كيفية القيام بذلك.
استذكر كيف يبدو تسلسل UTF-8 صالح:
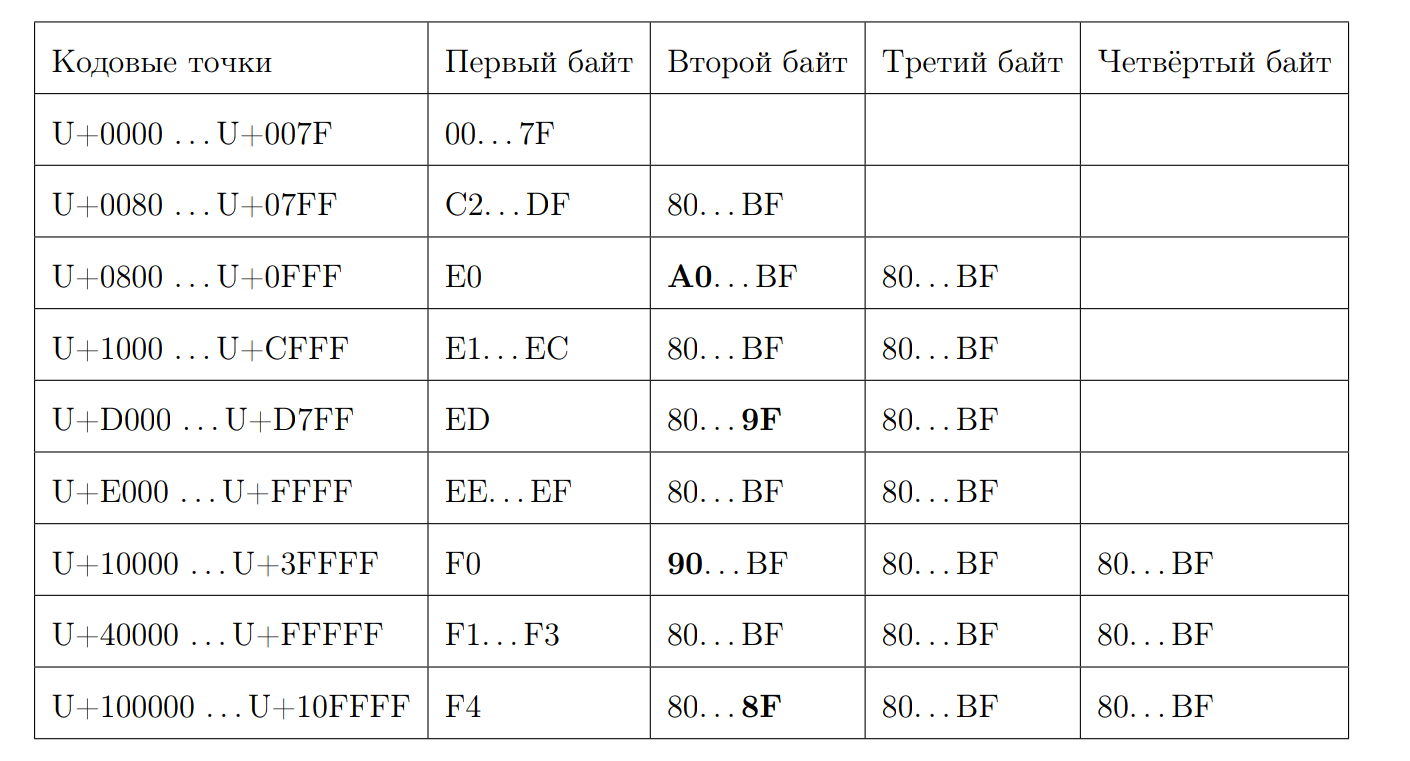
دعنا نحاول حساب طول نقطة الرمز بواسطة البايت الأول. هذا هو المكان الذي يبدأ السحر قليلا. مرة أخرى نكتب بعض الخصائص:
- بدءًا من 0xC وفي 0xD يكون لديك 2 بايت
- 0xC2 = 11 0 00010
- 0xDF = 11 0 11111
- 0xE0 = 111 0 0000
- 0xF4 = 1111 0 100 ، لا يوجد شيء أكثر من 0xF4 ، ولكن إذا كان هناك 0xF8 ، فلن يكون هناك قصة مختلفة
- الإجابة 7 ناقص موضع الصفر الأول من النهاية ، إذا لم يكن حرف ASCII
نحسب طول:
inline size_t seqLength(const UInt8 first_octet) { if (first_octet < 0x80u) return 1; const auto first_zero = bitScanReverse(static_cast<UInt8>(~first_octet)); return 7 - first_zero; }
لحسن الحظ ، لدينا في المخزون تعليمات التي يمكن أن تحسب عدد صفر بت ، بدءا من أهم منها.
f = __builtin_clz(val)
حساب bitScanReverse:
unsigned int bitScanReverse(unsigned int x) { return 31 - __builtin_clz(x); }
دعنا نحاول حساب طول سلسلة UTF-8 بنقاط الكود عبر SIMD. للقيام بذلك ، انظر إلى كل بايت كرقم موقّع ولاحظ الخصائص التالية:
- 0xBF = -65
- 0x80 = -128
- 0xC2 = -62
- 0x7F = 127
- جميع البايتات الأولى موجودة في [0xC2 ، 0x7F]
- جميع البايتات غير الأولى موجودة في [0x80 ، 0xBF]
الخوارزمية بسيطة للغاية. قارن بين كل بايت و -65 ، وإذا كان أكبر من هذا الرقم ، أضف واحدة. إذا أردنا استخدام SIMD ، فهذا هو الحمل المعتاد البالغ 16 بايت من دفق الإدخال. ثم هناك مقارنة بايت ، والتي في حالة وجود نتيجة إيجابية سوف تعطي البايت 0xFF ، وفي حالة سلبية - 0x00. ثم التعليمات pmovmskb ، والتي سوف تجمع بت عالية من كل بايت من السجل. ثم يزداد عدد popcnt السفلية ، نستخدم المضمنة في popcnt popcnt SSE4. يمكن توضيح مخطط هذه الخوارزمية بواسطة مثال:

اتضح أنه بالإضافة إلى تخفيف الضغط ، ستكون المعالجة لكل نواة حوالي 1.5 جيجابايت / ثانية.
تسمى الوظائف:
- lengthUTF8(string) - يُرجع طول سلسلة UTF-8 المشفرة بشكل صحيح ، يعتبر شيئًا غير صالح ، ولا يتم طرح استثناء.
ذهبنا أبعد من ذلك لأننا أردنا المزيد من الوظائف مع معالجة سلسلة UTF-8. على سبيل المثال ، التحقق من الصلاحية والإرسال إلى تعبير UTF-8 صالح.
للتحقق من الصلاحية ، أخذت https://github.com/cyb70289/utf8/ ، تم تكييفها من أجل ClickHouse (غيّرت بالفعل معالجة ذيول) وحصلت على سرعة 1.22 جيجابايت / ثانية مقارنة بـ 900 ميغابايت / ثانية للخوارزمية الساذجة . لن أصف الخوارزمية نفسها ، فهي معقدة للغاية بالنسبة للإدراك.
- isValidUTF8(string) - بإرجاع 1 إذا تم تشفير السلسلة بشكل صحيح مع UTF-8 ، وإلا 0.
- toValidUTF8(string) - يستبدل أحرف UTF-8 غير الصالحة بحرف U (U + FFFD). تنقسم كل الأحرف غير الصحيحة المتتالية إلى حرف بديل واحد. لا علم الصواريخ.
بشكل عام ، في خطوط UTF-8 ، نظرًا للخطة الثابتة غير السارة ، من الصعب دائمًا التوصل إلى شيء محسن جيدًا.
ما التالي؟
اسمحوا لي أن أذكرك أن هذه كانت رسالتي. بالطبع ، دافعت عنها لمدة 10/10. لقد ذهبنا معها بالفعل إلى Highload ++ Siberia (على الرغم من أنه بدا لي أنها لم تكن تهم أي أحد). مشاهدة العرض التقديمي . أحببت أن الجزء العملي من الأطروحة أدى إلى الكثير من البحوث المثيرة للاهتمام. وهنا هو الدبلوم نفسه. لديها الكثير من الأخطاء المطبعية ، لأنه لا أحد يقرأها. :)
كجزء من إعداد الدبلوم ، قمت بمجموعة من الأعمال المماثلة الأخرى (الروابط تؤدي إلى طلبات التجميع):
- محسن وظيفة concat 2 مرات ؛
- صنع أبسط شكل بيثون للطلبات ؛
- تسارع LZ4 بنسبة 4 ٪ .
- لقد قمت بعمل رائع على SIMD لنظام ARM و PPC64LE ؛
- ونصح اثنين من الطلاب من FCS مع الدبلومات في ClickHouse.
في النهاية ، اتضح ، في تجربتي ، كل شهر حاول ليشا أن يهتفوا لي ClickHouse هو النظام الأكثر متعة لكتابة التعليمات البرمجية عالية الأداء ، حيث يوجد وثائق وتعليقات ومطور ممتاز ودعم devops. ClickHouse رائع ، حقا. تعبت من تحويل صيغ JSON؟ تعال إلى ليشا واسأل عن مهمة من أي مستوى - سيقدمها لك ، وخلال عطلة نهاية الأسبوع ، ستشعر بسعادة غامرة من كتابة التعليمات البرمجية.
ولكن مع كل إنجازات ClickHouse وتصميمها ، فربما لا يتعلق الأمر بها. ليس في المقام الأول فيها.
مررت بأربع سنوات من الدراسات الجامعية في كلية الدراسات العليا ، في يونيو تخرجت من HSE مع مرتبة الشرف ، وعملت لمدة سنة ونصف في فريق رائع في ياندكس ، بعد أن ضخت جيدًا. بدون خبرة كاملة كل هذا الوقت والحديد لا شيء مكتوب في آخر قد عملت. FCN رائع جدًا ، إذا كنت تأخذ الحد الأقصى منه. بفضل Vana Puzyrevsky ivan_puzyrevskiy ، Ignat Kolesnichenko ، Gleb Evstropov ، Max Babenko maxim_babenko للقاءهم في مغامرتي المضحكة على FCN. وشكرًا أيضًا لجميع المعلمين الذين علموني شيئًا.