"إذا قرأت نقش" الجاموس "على قفص الفيل ، فلا تصدق عينيك" كوزما بروتكوف

في مقال سابق عن التصميم الموجه للنموذج ، تم توضيح سبب الحاجة إلى نموذج كائن ، وقد ثبت أنه بدون هذا النموذج للكائن يمكن للمرء أن يتحدث عن التصميم القائم على النموذج فقط باعتباره عاصفة ثلجية تسويقية بلا معنى ولا ترحم. ولكن عندما يظهر نموذج كائن ، يكون لدى المهندسين المؤهلين دائمًا سؤال معقول: ما الدليل على أن النموذج الرياضي لكائن يتوافق مع كائن حقيقي.

ويرد مثال على إجابة لهذا السؤال في مقال عن التصميم الموجه لنموذج لمحرك كهربائي. في هذه المقالة ، سننظر في مثال على إنشاء نموذج لأنظمة تكييف الهواء للطيران ، مع تخفيف الممارسة ببعض الاعتبارات العامة النظرية.

إنشاء نموذج موثوق للكائن. نظرية

حتى لا يتم سحب المطاط ، سوف أخبرك على الفور بالخوارزمية لإنشاء نموذج للتصميم الموجه للطراز. له ثلاث خطوات بسيطة فقط:

الخطوة 1. تطوير نظام المعادلات التفاضلية الجبرية التي تصف السلوك الديناميكي للأنظمة المحاكاة. إنها بسيطة إذا كنت تعرف فيزياء العملية. لقد طور العديد من العلماء بالفعل القوانين الفيزيائية الأساسية الخاصة باسم نيوتن وبرينولي ونافير ستوكس وشانتانجيلس أوف كومباس ورابينوفيتش.

الخطوة 2. في النظام الناتج ، عزل مجموعة من المعاملات التجريبية وخصائص الكائن المحاكاة التي يمكن الحصول عليها من الاختبارات.

الخطوة 3. تنفيذ اختبارات الكائن وضبط النموذج وفقًا لنتائج التجارب الميدانية ، بحيث يتوافق مع الواقع ، مع درجة التفاصيل اللازمة.

كما ترون ، ثلاثة فقط.

مثال عملي

نظام تكييف الهواء (SCR) في الطائرة متصل بنظام صيانة الضغط التلقائي. يجب أن يكون الضغط في الطائرة دائمًا أكبر من الضغط الخارجي ، في حين يجب أن يكون معدل تغيير الضغط بحيث لم ينزف الطيارون والركاب الأنف والأذنين. لذلك ، يعد نظام التحكم في تدفق الهواء الخارجي وتدفقه مهمًا للسلامة ، ويتم وضع أنظمة اختبار باهظة الثمن على الأرض لتطويره. إنها تخلق درجات حرارة وضغوط من ارتفاع الطيران ، وتعيد إنتاج أوضاع الإقلاع والهبوط في المطارات ذات الارتفاعات المختلفة. ومسألة تطوير وتصحيح أنظمة التحكم للعملة الصعبة ترتفع إلى أقصى إمكاناتها. كم من الوقت سنقود طاولة الاختبار للحصول على نظام تحكم مرضٍ؟ من الواضح ، إذا قمنا بضبط نموذج التحكم على طراز الكائن ، يمكن تقليل دورة العمل على طاولة الاختبار بشكل كبير.

يتكون نظام تكييف الهواء للطيران من نفس المبادلات الحرارية مثل أي نظام حراري آخر. البطارية - إنها أيضًا بطارية في إفريقيا ، وهي مكيفة فقط. ولكن نظرًا لتقييد كتلة الإقلاع وأبعاد الطائرة ، يتم تصنيع مبادلات الحرارة المدمجة قدر الإمكان وكفاءة قدر الإمكان من أجل نقل أكبر قدر ممكن من الحرارة من الكتلة السفلى. نتيجة لذلك ، تصبح الهندسة غريبة تمامًا. كما هو الحال في القضية قيد النظر. يوضح الشكل 1 مبادل حراري للوحة ، حيث يتم استخدام الغشاء بين الصفائح لتحسين نقل الحرارة. يتغير سائل التبريد الساخن والبارد في القنوات ، بينما يكون اتجاه التدفق مستعرضًا. يتم توفير مبرد واحد للقطع الأمامي ، والآخر في الجانب.

لحل مشكلة التحكم في SCR ، نحتاج إلى معرفة مقدار الحرارة التي يتم نقلها من وسط إلى آخر في مثل هذا المبادل الحراري لكل وحدة زمنية. يعتمد معدل التغير في درجة الحرارة على هذا الأمر الذي ننظمه.

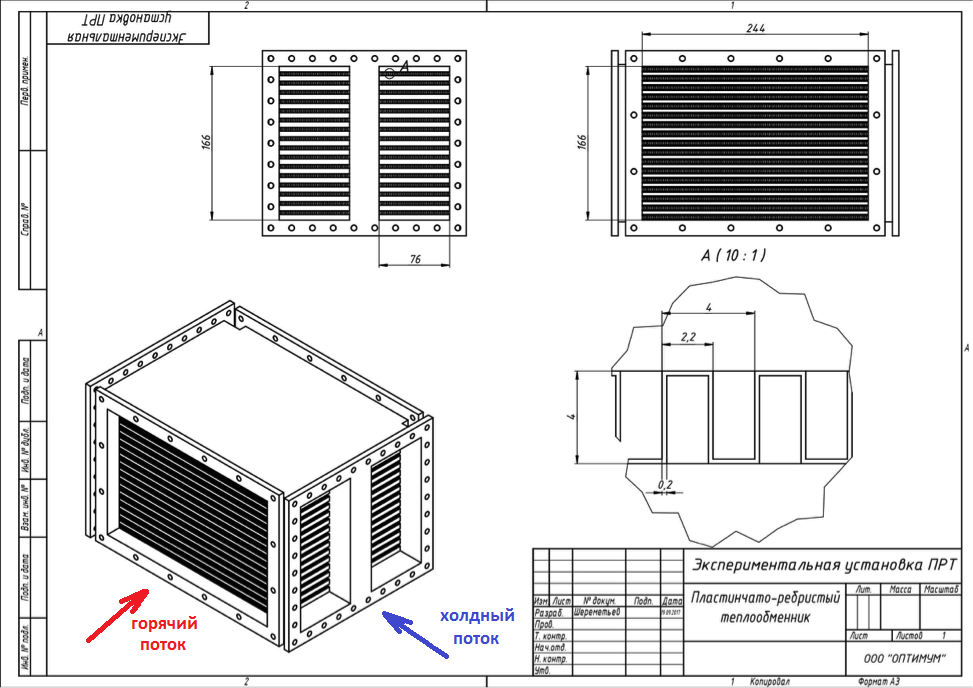
الشكل 1. مخطط مبادل حراري للطائرات.

مشاكل النمذجة. الجزء الهيدروليكي

للوهلة الأولى ، المهمة بسيطة للغاية ، فمن الضروري حساب تدفق الكتلة من خلال قنوات المبادل الحراري وتدفق الحرارة بين القنوات.
يتم حساب معدل التدفق الشامل لسائل التبريد في القنوات باستخدام صيغة برنولي:

حيث:
ΔP هو انخفاض الضغط بين نقطتين ؛
ξ هو معامل الاحتكاك من المبرد.
L هو طول القناة ؛
d هو القطر الهيدروليكي للقناة ؛
ρ هي كثافة سائل التبريد ؛
ω هي سرعة سائل التبريد في القناة.

لقناة ذات شكل اعتباطي ، يتم حساب القطر الهيدروليكي بواسطة الصيغة:

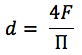
حيث:
F هي منطقة التجويف ؛
P - محيط قناة المبللة.

يتم حساب معامل الاحتكاك وفقًا للصيغ التجريبية ويعتمد على سرعة التدفق وخصائص المبرد. بالنسبة إلى الأشكال الهندسية المختلفة ، يتم الحصول على تبعيات مختلفة ، على سبيل المثال ، صيغة التدفق المضطرب في الأنابيب الملساء:

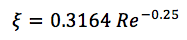
حيث:
Re هو رقم رينولدز.

للتدفق في القنوات المسطحة ، يمكن استخدام الصيغة التالية:

من صيغة Bernoulli ، يمكنك حساب انخفاض الضغط لسرعة معينة ، أو العكس ، لحساب سرعة سائل التبريد في القناة ، بناءً على انخفاض الضغط المحدد.

نقل الحرارة

يتم احتساب تدفق الحرارة بين المبرد والجدار بواسطة الصيغة:

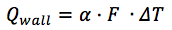
حيث:
α [W / (m2 × deg)] - معامل نقل الحرارة ؛
F هي منطقة التجويف.

فيما يتعلق بمشاكل تدفق المبردات في الأنابيب ، تم إجراء عدد كاف من الدراسات وهناك العديد من طرق الحساب ، وكقاعدة عامة ، يعود كل ذلك إلى الاعتماد التجريبي ، لمعامل نقل الحرارة α [W / (m2 × deg)]

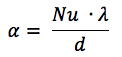
حيث:
نو هو رقم نسلت ،
λ هي الموصلية الحرارية للسائل [W / (م × درجة)]
d هو القطر الهيدروليكي (المكافئ).

تُستخدم تبعيات المعايير التجريبية لحساب رقم Nusselt (المعيار) ، على سبيل المثال ، تبدو صيغة حساب عدد Nusselt للأنبوب المستدير كما يلي:

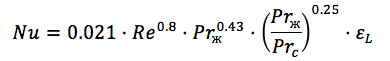
هنا نرى بالفعل عدد Reynolods ، وعدد Prandtl في درجة حرارة الجدار ودرجة حرارة السائل ، ومعامل عدم المساواة. ( المصدر )

بالنسبة للمبادلات الحرارية للصفائح المموجة ، تكون الصيغة متشابهة ( المصدر ):

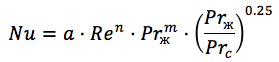
حيث:
ن = 0.73 م = 0.43 لتدفق مضطرب ،
يتراوح المعامل a بين 0.065 و 0.6 حسب عدد اللوحات ونظام التدفق.

لاحظ أنه يتم حساب هذا المعامل لنقطة واحدة فقط في الدفق. بالنسبة للنقطة التالية ، لدينا درجة حرارة سائل مختلفة (ارتفعت درجة حرارتها أو تبرد) ، ودرجة حرارة جدار مختلفة ، وبالتالي ، فإن جميع أرقام رينولدز وأرقام براندتل تطفو.

عند هذه النقطة ، سيقول أي عالم رياضيات أنه من المستحيل حساب النظام بالضبط الذي يتغير فيه المعامل 10 مرات ، وسيكون على صواب.

سيقول أي مهندس ممارس أن كل مبادل حراري يختلف في التصنيع وأنه من المستحيل حساب الأنظمة ، وسيكون ذلك أيضًا صحيحًا.

ولكن ماذا عن التصميم الموجه؟ هل ذهب كل شيء؟

سيقترنك بائعو البرامج الغربية المتقدمون في هذا المكان بنظم كمبيوتر فائق الحوسبة ثلاثية الأبعاد ، مثل "بدونه بأي شكل من الأشكال". وتحتاج إلى تشغيل الحساب ليوم واحد للحصول على توزيع درجة الحرارة لمدة دقيقة واحدة.

من الواضح أن هذا ليس خيارنا ، فنحن بحاجة إلى تصحيح نظام التحكم ، إن لم يكن في الوقت الفعلي ، ثم على الأقل في المستقبل المنظور.

كزة طريقة

يتم تصنيع المبادل الحراري ، ويتم إجراء سلسلة من الاختبارات ، ويتم تعيين جدول كفاءة درجة حرارة الحالة الثابتة بمعدلات التدفق المحددة. بسيطة وسريعة وموثوقة ، حيث أن البيانات التي تم الحصول عليها من الاختبارات.

عيب هذا النهج هو أنه لا توجد خصائص ديناميكية للكائن. نعم ، نحن نعرف حجم تدفق الحرارة الثابت ، لكننا لا نعرف كم من الوقت سيتم إنشاؤه عند التبديل من وضع تشغيل إلى آخر.

لذلك ، وبعد حساب الخصائص الضرورية ، أنشأنا نظام التحكم مباشرة خلال الاختبارات ، والتي نود تجنبها من البداية.

نموذج المنحى

لإنشاء نموذج لمبادل حراري ديناميكي ، من الضروري استخدام بيانات الاختبار ، للتخلص من أوجه عدم اليقين في صيغ الحساب التجريبية - رقم Nusselt والمقاومة الهيدروليكية.

القرار بسيط ، مثل كل عبقري. نحن نأخذ الصيغة التجريبية ، ونجري التجارب ونحدد قيمة المعامل a ، ومن ثم نتخلص من عدم اليقين في الصيغة.

بمجرد أن نحصل على قيمة معينة لمعامل نقل الحرارة ، يتم تحديد جميع المعلمات الأخرى بواسطة القوانين المادية الأساسية للحفظ. يحدد الاختلاف في درجة الحرارة ومعامل نقل الحرارة مقدار الطاقة المنقولة إلى القناة لكل وحدة زمنية.

مع العلم بتدفق الطاقة ، من الممكن حل معادلات الحفاظ على كتلة الطاقة وزخم سائل التبريد في القناة الهيدروليكية. على سبيل المثال ، هذا:

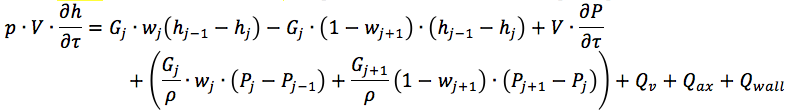
بالنسبة لحالتنا ، فإن تدفق الحرارة بين الجدار وسائل التبريد - Qwall - لا يزال غير محدد. مزيد من التفاصيل يمكن الاطلاع هنا ...

وكذلك معادلة المشتق الحراري لجدار القناة:

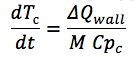
حيث:
wallQ _wall - الفرق بين التدفق الوارد والصادر إلى جدار القناة ؛
M هي كتلة جدار القناة ؛
ج _{الكمبيوتر} هو القدرة الحرارية للمواد الجدار.

دقة النموذج

كما ذكر أعلاه ، في المبادل الحراري لدينا توزيع درجة الحرارة على سطح اللوحة. بالنسبة لقيمة الحالة المستقرة ، يمكن للمرء أن يأخذ المتوسط ​​فوق الصفائح واستخدامه ، ويعرض مبادل حراري بالكامل كنقطة مركزية واحدة ، حيث يحدث انتقال الحرارة على كامل سطح المبادل الحراري في نفس فرق الحرارة. لكن بالنسبة إلى الأوضاع المؤقتة ، قد لا يعمل هذا التقريب. الطرف الآخر هو الحصول على مئات الآلاف من النقاط وتحميل Super Computer ، وهو ما لا يناسبنا أيضًا ، لأن المهمة تتمثل في تكوين نظام التحكم في الوقت الفعلي ، أو بشكل أفضل ، بشكل أسرع.

السؤال الذي يطرح نفسه ، ما هو عدد الأقسام التي تحتاجها لكسر المبادل الحراري للحصول على دقة وسرعة حساب مقبولة؟

كما هو الحال دائما عن طريق الصدفة ، كان لدي نموذج لمبادل حراري أمين في متناول اليد. المبادل الحراري عبارة عن أنبوب ، يتدفق وسط التسخين في الأنابيب ، ويتم تسخينه بين الحفر. لتبسيط المهمة ، يمكن تمثيل أنبوبة المبادل الحراري بالكامل كأنبوب واحد مكافئ ، ويمكن تمثيل الأنبوب نفسه على أنه مجموعة من خلايا الحساب المنفصلة ، حيث يتم حساب كل نموذج من نقاط نقل الحرارة. يظهر الرسم التخطيطي لطراز خلية واحدة في الشكل 2. يتم توصيل قناة الهواء الساخن وقناة الهواء البارد من خلال جدار يوفر نقل الحرارة بين القنوات.

الشكل 2. نموذج خلية مبادل حراري.

نموذج المبادل الحراري الأنبوبي قابل للتخصيص بسهولة. يمكنك تغيير معلمة واحدة فقط - عدد الأقسام على طول الأنبوب وإلقاء نظرة على نتائج الحساب لأقسام مختلفة. سنقوم بحساب عدة خيارات ، بدءًا من التقسيم إلى 5 نقاط في الطول (الشكل 3) وما يصل إلى 100 نقطة في الطول (الشكل 4).

الشكل 3. توزيع درجة حرارة ثابتة من 5 نقاط التصميم.

الشكل 4. توزيع درجة حرارة ثابتة من 100 نقطة التصميم.

نتيجة للحسابات ، اتضح أن درجة حرارة الحالة المستقرة عند القسمة على 100 نقطة هي 67.7 درجة. وعند تقسيمها إلى 5 نقاط محسوبة ، تكون درجة الحرارة 72 ، 66 درجة مئوية.

أيضا ، يتم عرض سرعة الحساب بالنسبة للوقت الحقيقي في الجزء السفلي من النافذة.
دعونا نرى كيف تتغير درجة حرارة الحالة المستقرة وسرعة الحساب اعتمادًا على عدد نقاط التصميم. يمكن استخدام الفرق في درجات حرارة الحالة المستقرة في العمليات الحسابية مع عدد مختلف من خلايا الحساب لتقييم دقة النتيجة.

الجدول 1. اعتماد درجة الحرارة وسرعة الحساب على عدد نقاط التصميم على طول المبادل الحراري.

تحليل هذا الجدول ، يمكننا استخلاص النتائج التالية:

• تتناقص سرعة الحساب بالتناسب مع عدد نقاط التصميم في نموذج المبادل الحراري.
• التغيير في دقة الحساب يحدث أضعافا مضاعفة. كلما زاد عدد النقاط ، تنخفض درجة الصقل في كل زيادة لاحقة.

في حالة المبادل الحراري للوحة مع ناقل حراري متدفق ، كما في الشكل 1 ، يكون إنشاء نموذج مكافئ من خلايا التصميم الأولي معقدًا بعض الشيء. نحن بحاجة إلى توصيل الخلايا بطريقة لتنظيم التدفق المتبادل. لمدة 4 خلايا ، ستبدو الدائرة كما هو موضح في الشكل 5.

ينقسم تدفق سائل التبريد إلى قناتين على امتداد الفرع الساخن والبارد ، وسوف يتم توصيل القنوات من خلال الهياكل الحرارية ، بحيث عندما يمر عبر القناة ، يتبادل سائل التبريد الحرارة مع قنوات مختلفة. بمحاكاة التدفق المتقاطع ، يتدفق حامل الحرارة الساخنة من اليسار إلى اليمين (انظر الشكل 5) في كل قناة ، حيث يتبادل الحرارة بالتتابع مع قنوات حامل الحرارة الباردة ، والذي ينتقل من الأسفل إلى الأعلى (انظر الشكل 5). توجد أعلى نقطة في الزاوية اليسرى العليا ، حيث يتبادل حامل الحرارة الساخنة الحرارة مع سائل التبريد المسخن بالفعل للقناة الباردة. والأبرد في أسفل اليمين ، حيث يتبادل المبرد البارد الحرارة مع المبرد الساخن الذي تم تبريده بالفعل في القسم الأول.

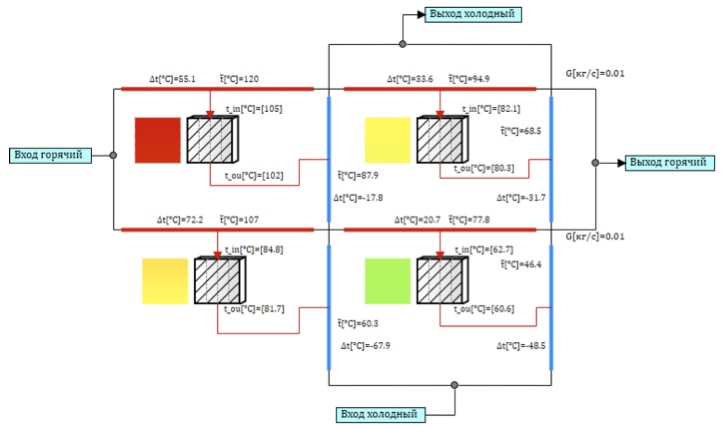
الشكل 5. نموذج عبر التدفق من 4 خلايا التصميم.

هذا النموذج لمبادل حراري للوحة لا يأخذ في الاعتبار انتقال الحرارة بين الخلايا بسبب التوصيل الحراري ولا يأخذ في الاعتبار خلط سائل التبريد ، حيث أن كل قناة معزولة.

ولكن في حالتنا ، لا يقلل القيد الأخير من الدقة ، حيث إن الغشاء المموج في تصميم المبادل الحراري يقسم التدفق إلى العديد من القنوات المعزولة على طول سائل التبريد (انظر الشكل 1). دعونا نرى ما يحدث مع دقة الحساب عند نمذجة مبادل حراري للوحة مع زيادة عدد خلايا التصميم.

لتحليل الدقة ، نستخدم خيارين لتقسيم المبادل الحراري إلى خلية التصميم:

1. تحتوي كل خلية مربعة على اثنين من التدفقات الهيدروليكية (الباردة والساخنة) وعنصر حراري واحد. (انظر الشكل 5)
2. تحتوي كل خلية مربعة على ستة عناصر هيدروليكية (ثلاثة أقسام في التدفقات الساخنة والباردة) وثلاثة عناصر حرارية.

في الحالة الأخيرة ، نستخدم نوعين من الاتصال:

• تدفق مضادة للتيارات الباردة والساخنة ؛
• تدفق المرتبطة الباردة والساخنة التدفق.

يزيد التيار الحالي من الكفاءة مقارنةً بالتدفق المتقاطع ، وينخفض ​​التيار المرتبط. مع وجود عدد كبير من الخلايا ، يحدث معدل تدفق التدفق ويصبح كل شيء قريبًا من التدفق العرضي الفعلي من حوله (انظر الشكل 6).

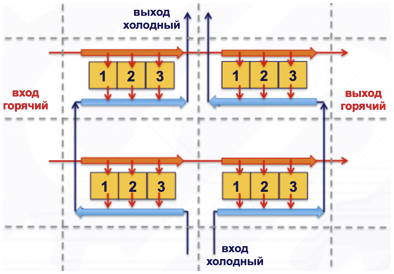
الشكل 6. نموذج عبر التدفق من أربع خلايا مع 3 عناصر.

يوضح الشكل 7 نتائج توزيع درجة حرارة ثابتة الحالة في المبادل الحراري عند توفير الهواء عند درجة حرارة 150 درجة مئوية على طول الخط الساخن ، و 21 درجة مئوية على طول الخط البارد ، للحصول على خيارات مختلفة لتقسيم النموذج. يعكس اللون والأرقام الموجودة في الخلية متوسط ​​درجة حرارة الجدار في الخلية.

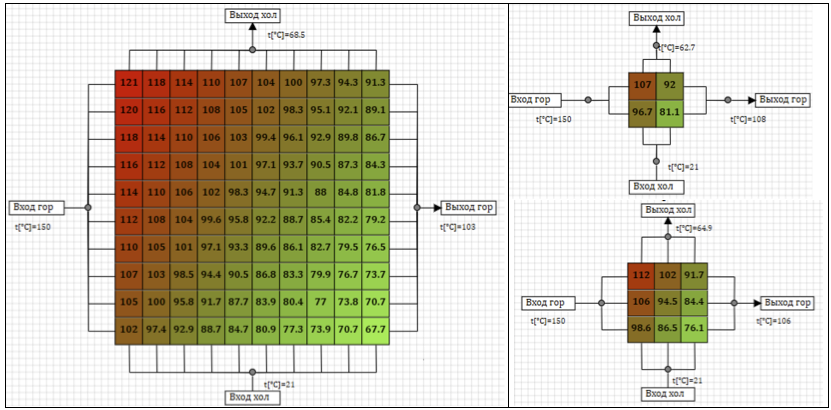
الشكل 7. درجات حرارة ثابتة للمخططات الحسابية المختلفة.

يوضح الجدول 2 درجة حرارة الحالة الثابتة للهواء المسخن بعد المبادل الحراري ، اعتمادًا على قسم نموذج المبادل الحراري إلى خلايا.

الجدول 2. اعتماد درجة الحرارة على عدد خلايا التصميم في المبادل الحراري.

مع زيادة عدد الخلايا الحسابية في النموذج ، تزداد درجة حرارة الحالة المستقرة النهائية. يمكن اعتبار الفرق بين درجة حرارة الحالة المستقرة عند أقسام مختلفة مؤشراً على دقة الحساب. يُلاحظ أنه مع زيادة عدد خلايا الحساب ، تميل درجة الحرارة إلى الحد الأقصى ، ولا تتناسب الزيادة في الدقة مع عدد نقاط الحساب.

السؤال الذي يطرح نفسه ، ولكن ما دقة النموذج الذي نحتاجه؟

تعتمد إجابة هذا السؤال على الغرض من نموذجنا. نظرًا لأن هذا المقال يدور حول التصميم الموجه للطراز ، فإننا نقوم بإنشاء نموذج لضبط نظام التحكم. هذا يعني أن دقة النموذج يجب أن تكون قابلة للمقارنة مع دقة أجهزة الاستشعار المستخدمة في النظام.

في حالتنا ، يتم قياس درجة الحرارة بواسطة الحرارية ، حيث دقة ± 2.5 درجة مئوية. أي دقة أعلى لغرض ضبط نظام التحكم لا طائل منه ، ونظام التحكم الحقيقي لدينا ببساطة "لن يرى". وبالتالي ، إذا افترضنا أن درجة الحرارة القصوى مع عدد لا حصر له من الأقسام هي 70 درجة مئوية ، فإن النموذج الذي يمنحنا أكثر من 67.5 درجة مئوية سيكون بدقة كافية. جميع الطرز التي تحتوي على 3 نقاط في خلية الحساب والنماذج أكبر من 5 × 5 بنقطة واحدة في الخلية. (مظللة باللون الأخضر في الجدول 2)

أوضاع التشغيل الديناميكية

لتقييم الوضع الديناميكي ، نقوم بتقييم عملية التغير في درجة الحرارة عند أكثر سخونة وأبرد نقطة في جدار المبادل الحراري لمختلف مخططات التصميم. (انظر الشكل 8)


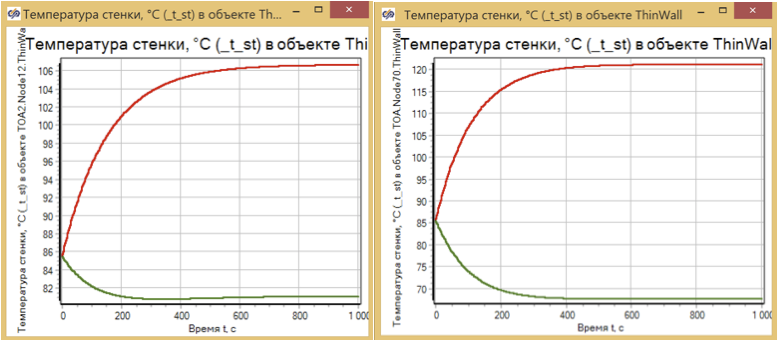
الرقم 8. مبادل حراري الاحماء. نماذج البعد 2x2 و 10x10.

يمكن ملاحظة أن وقت العملية الانتقالية وطبيعتها ذاتها ، لا يعتمد عملياً على عدد الخلايا المحسوبة ، ويتم تحديدها فقط من خلال كتلة المعدن المسخن.

وبالتالي ، فإننا نستنتج أنه من أجل المحاكاة الصادقة لمبادل الحرارة في الأوضاع من 20 إلى 150 درجة مئوية ، مع الدقة المطلوبة في نظام التحكم SCR ، فإن حوالي 10-20 نقطة محسوبة كافية.

تجربة إعداد نموذج ديناميكي

, , , , , .

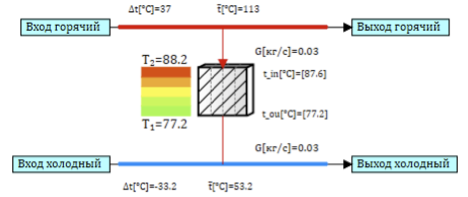
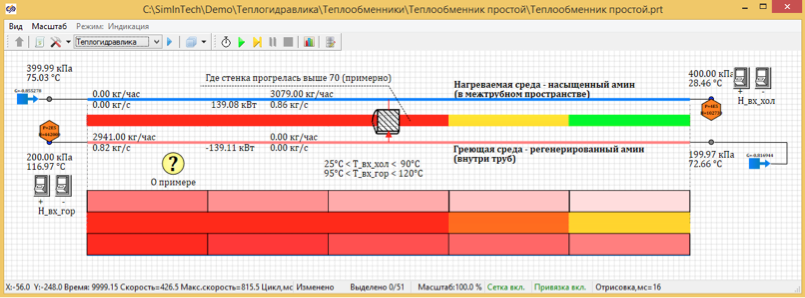
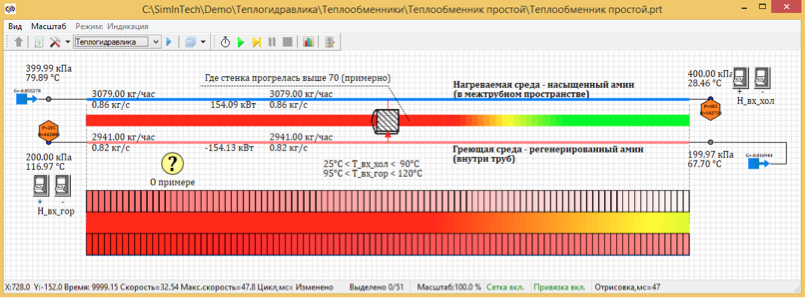
, , . 9 . , , , .

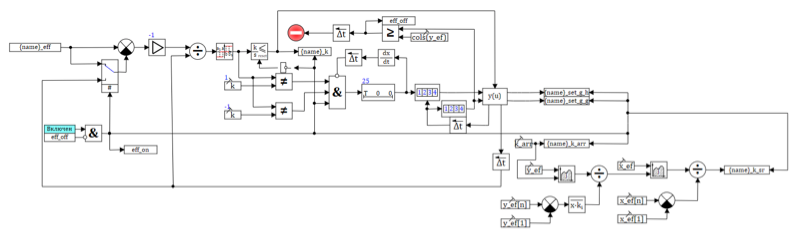
9. .

a . , ( ) . , 0.492 0.655

0.6, , , .

– :

:
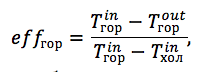
eff – ;
T ⁱⁿ – ;
T ^out – ;
T ⁱⁿ – .

3 .

3. %

. , , , , .

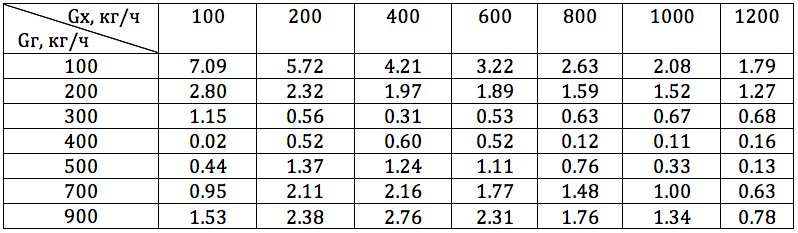
, 10 .

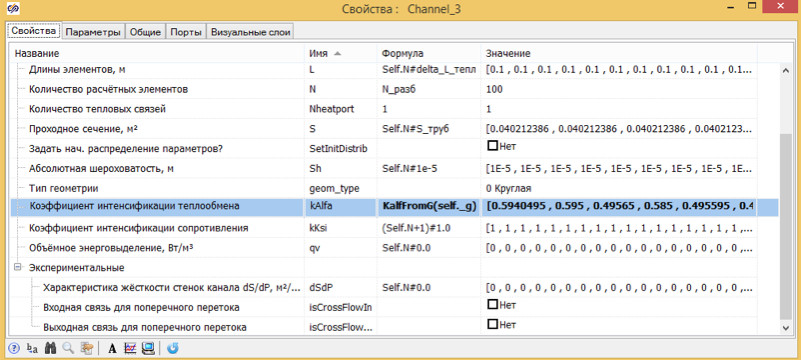
10. .

النتائج

• - .
  
• .
  
• .
  
• - !

. .