مثلث Pascal مقابل سلاسل من النوع "000 ... / 111 ..." في الصفوف الثنائية والشبكات العصبية

سلسلة "ضوضاء بيضاء ترسم مربعًا أسود"

يبدأ تاريخ دورة هذه المنشورات بحقيقة أنه في كتاب G.Sekey "التناقضات في نظرية الاحتمالات والإحصاء الرياضي" ( ص 43 ) ، تم اكتشاف البيان التالي:


التين. 1.

وفقًا للتحليل ، فإن التعليقات على المنشورات الأولى ( الجزء 1 ، الجزء 2 ) والمنطق اللاحق قد نضجت فكرة تقديم هذه النظرية في شكل بصري أكثر.

معظم أفراد المجتمع على دراية بمثلث باسكال ، نتيجة لتوزيع الاحتمالات ذات الحدين والعديد من القوانين ذات الصلة. لفهم آلية تشكيل مثلث Pascal ، سنقوم بتوسيعه بمزيد من التفصيل ، مع نشر تدفقات تشكيله. في مثلث Pascal ، يتم تشكيل العقد بنسبة 0 و 1 ، الشكل أدناه.


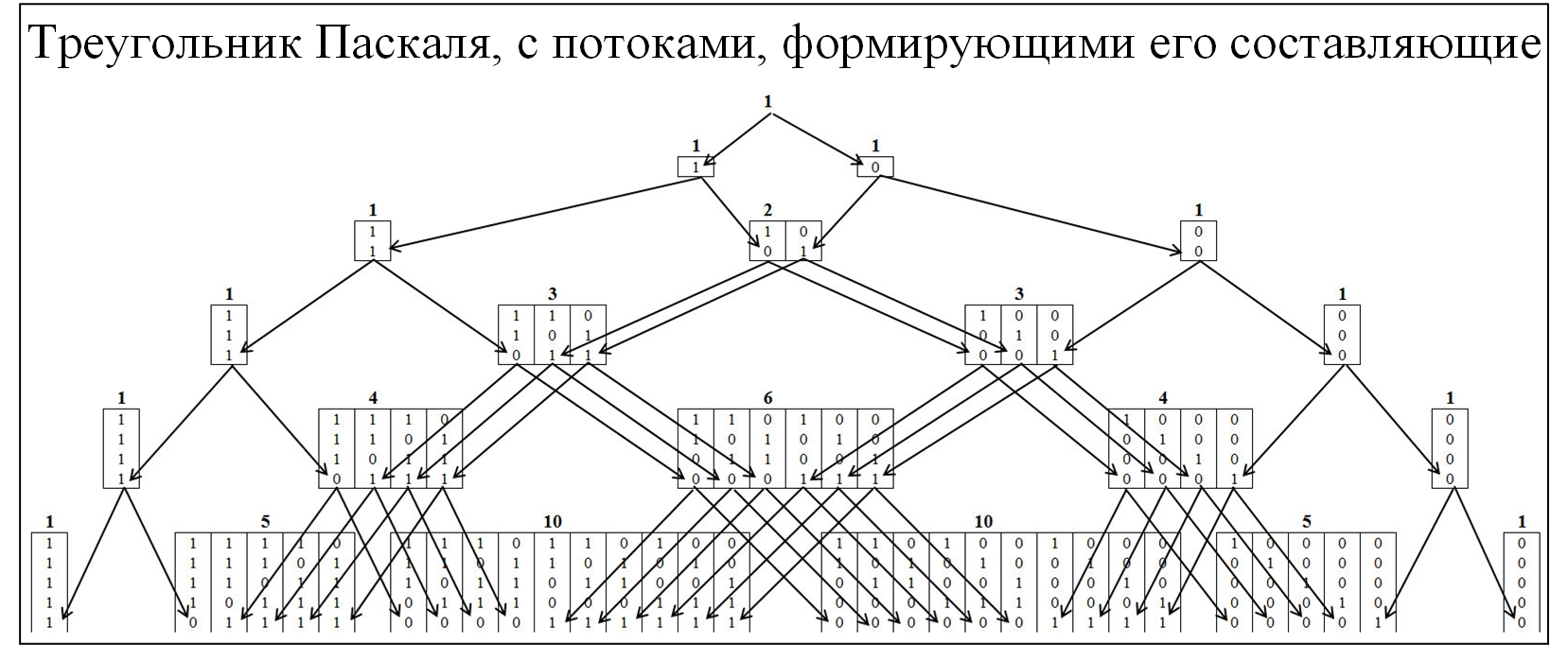
التين. 2.

لفهم نظرية Erds-Renyi ، سنقوم بتكوين نموذج مماثل ، ولكن سيتم تشكيل العقد من القيم التي توجد بها أكبر سلاسل ، والتي تتكون بالتتابع من نفس القيم. سيتم تنفيذ التجميع وفقًا للقاعدة التالية: السلاسل 01/10 ، إلى المجموعة "1" ؛ السلسلة 00/11 ، إلى المجموعة "2" ؛ سلاسل 000/111 ، إلى المجموعة "3" ، إلخ. في هذه الحالة ، سنقوم بتقسيم الهرم إلى مكونين متماثلين الشكل 3.


التين. 3.

أول ما يلفت انتباهك هو أن جميع الحركات تحدث من كتلة أقل إلى كتلة أعلى والعكس صحيح لا يمكن أن يكون. هذا أمر طبيعي ، لأنه إذا تشكلت سلسلة من الحجم j ، فلا يمكن أن تختفي بعد ذلك.

تحديد خوارزمية تركيز الأرقام ، تمكنا من الحصول على صيغة التكرار التالية ، والتي تظهر الآلية في الأشكال 4-6.

تشير إلى العناصر التي تتركز فيها الأرقام ، حيث n هو عدد الأحرف في الرقم (عدد البتات) ، وطول السلسلة القصوى هو m. وسيحصل كل عنصر على فهرس n ؛ mJ.
تشير إلى أن عدد العناصر التي تم تمريرها من n ؛ mJ إلى n + 1 ؛ m + 1J ، n ؛ mjn + 1 ؛ m + 1.


التين. 4.

يوضح الشكل 4 أنه من الصعب تحديد قيم كل صف بالنسبة إلى المجموعة الأولى. وهذا الاعتماد يساوي:


التين. 5.

نحدد للمجموعة الثانية ، مع طول السلسلة م = 2 ، الشكل 6.


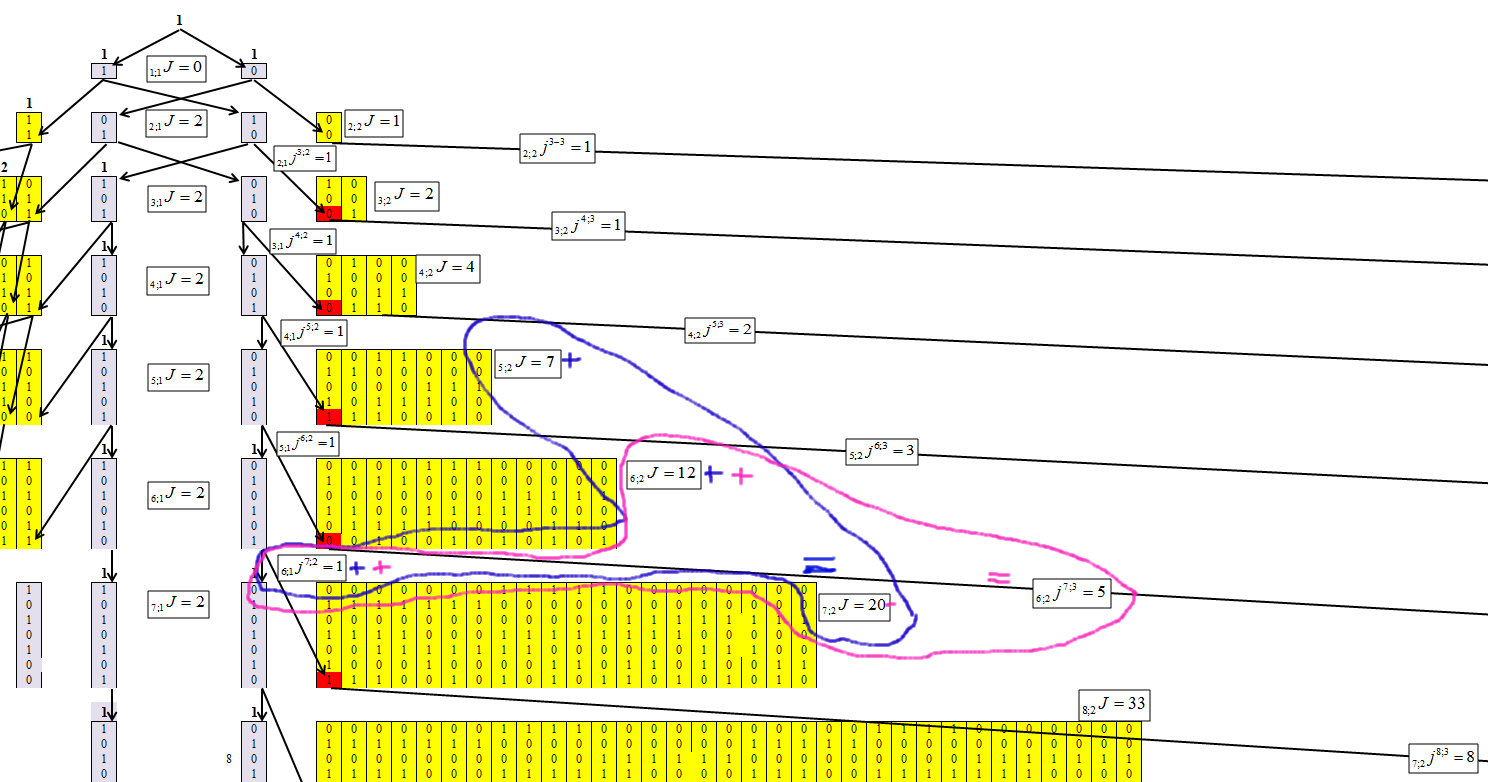
التين. 6.

يوضح الشكل 6 أن التبعية تساوي:


التين. 7.

نحدد للمجموعة الثالثة ، مع طول السلسلة م = 3 ، الشكل 8.


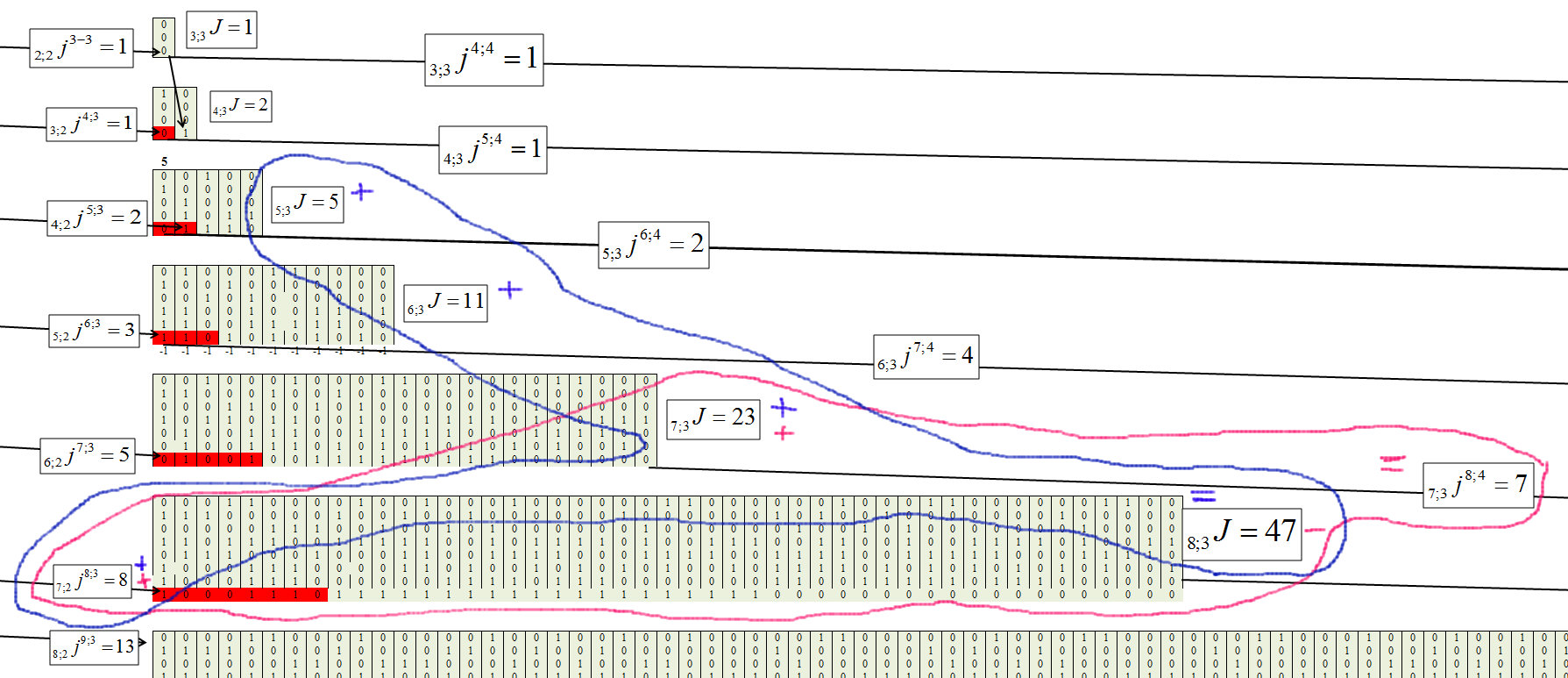
التين. 8.

التين. 9.

تأخذ الصيغة العامة لكل عنصر الشكل:


التين. 10.


التين. 11.

تحقق.

للتحقق ، نحن نستخدم خاصية هذا التسلسل ، الذي يظهر في الشكل 12. ويتكون في حقيقة أن آخر أعضاء السطر من موضع معين يأخذون قيمة واحدة لجميع الخطوط مع زيادة طول الخط.


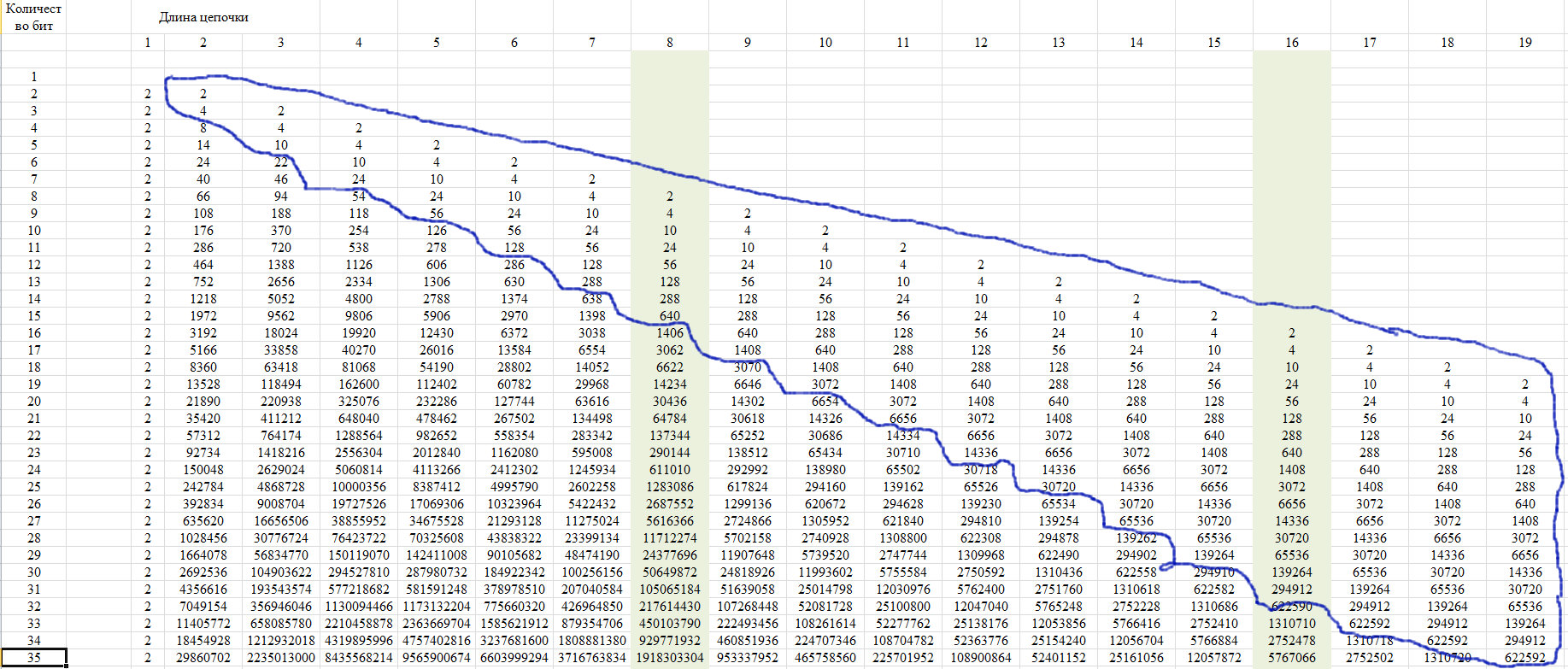
التين. 12.

يرجع هذا العقار إلى حقيقة أنه مع طول السلسلة لأكثر من نصف الصف بأكمله ، لا يمكن تحقيق سوى سلسلة واحدة من هذه السلسلة. نظهر هذا في الرسم البياني الشكل 13.


التين. 13.

وفقًا لذلك ، للحصول على قيم k <n-2 ، نحصل على الصيغة:


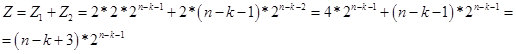
التين. 14.

في الواقع ، فإن قيمة Z هي العدد المحتمل للأرقام (الخيارات في سلسلة من البتات n) التي تحتوي على سلسلة من العناصر المتماثلة k. ووفقًا لمعادلة التكرار ، نحدد عدد الأرقام (الخيارات في سلسلة من البتات n) التي تكون فيها سلسلة العناصر المتطابقة k هي الأكبر. الآن ، أفترض أن القيمة Z هي قيمة افتراضية. لذلك ، في المنطقة n / 2 ، يمر إلى الفضاء الحقيقي. في الشكل 15 ، شاشة بها حسابات.


التين. 15.

دعونا نعرض مثالاً لكلمة 256 بت ، والتي يمكن تحديدها بواسطة هذه الخوارزمية.


التين. 16.

إذا تم تحديدها وفقًا لمعايير موثوقية 99.9٪ بالنسبة إلى GSPCH ، فيجب أن يحتوي المفتاح 256 بت على سلاسل متتالية من الأحرف المتطابقة مع الرقم من 5 إلى 17. وهذا ، وفقًا لمعايير GSPCH ، بحيث يلبي متطلبات تشابه العشوائية مع موثوقية 99.9٪ ، يجب على GSPCH ، في اختبارات عام 2000 (إصدار نتيجة على شكل رقم ثنائي 256 بت) أن تعطي فقط النتيجة التي يكون فيها الحد الأقصى لطول السلسلة بنفس القيم: إما أقل من 4 أو أكثر من 17.


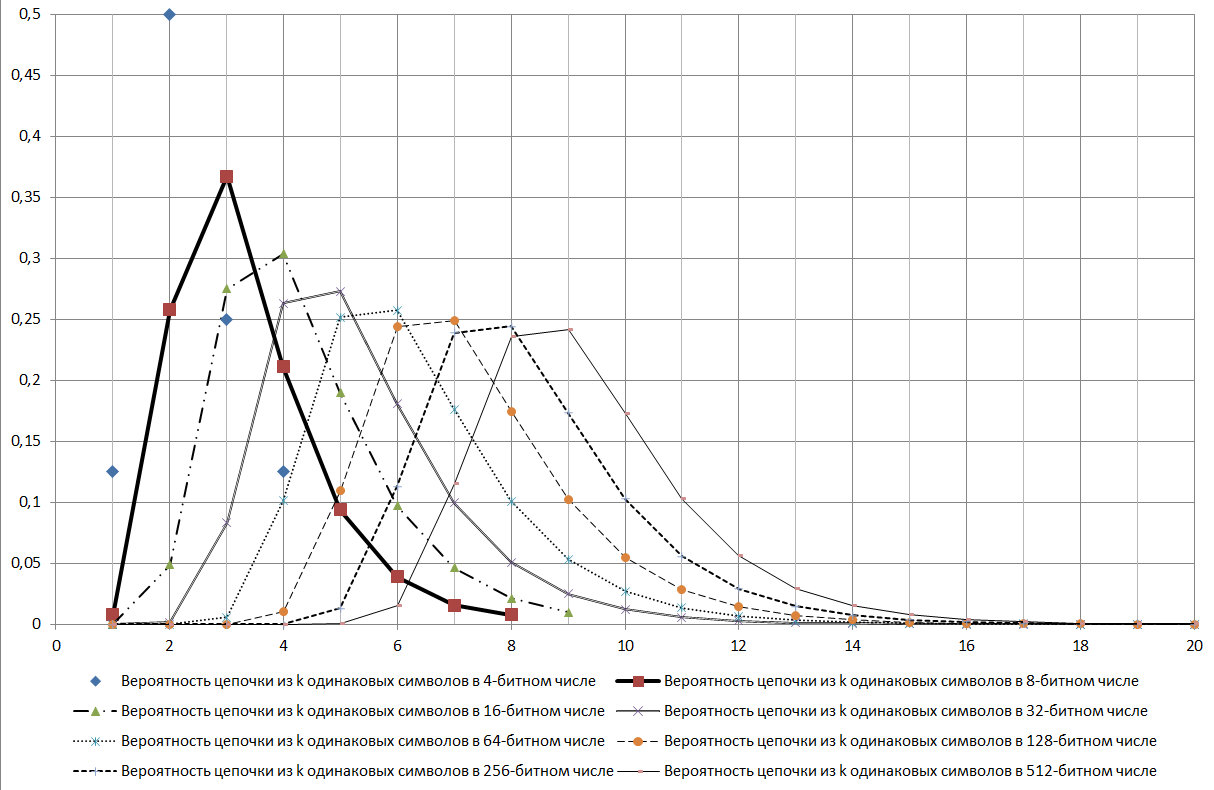
التين. 17.

كما يتضح من الشكل الموضح في الشكل 17 ، سلسلة log2N هي وسيلة للتوزيع قيد الدراسة.

خلال الدراسة ، تم العثور على العديد من علامات الخصائص المختلفة لهذا التسلسل. هؤلاء بعض منهم:

• يجب اختباره جيدًا وفقًا لمعيار chi-square ؛
• يعطي علامات على وجود خصائص كسورية ؛
• قد تكون معايير جيدة لتحديد العمليات العشوائية المختلفة.

والعديد من الاتصالات الأخرى.

تم التحقق مما إذا كان هذا التسلسل موجودًا أيضًا في موسوعة T he On-Line Encyclopedia of Integer Sequences (OEIS) (موسوعة عبر الإنترنت من Integer Sequences) في رقم التسلسل A006980 ، تتم الإشارة إلى المنشور JL Yucas ، Counting مجموعات خاصة من كلمات Lyndon الثنائية ، Ars Combin. ، 31 (1991) ، ص. 21-29 ، حيث يظهر التسلسل في الصفحة 28 (في الجدول). في المنشور ، يتم ترقيم الأسطر 1 أقل ، لكن القيم هي نفسها. بشكل عام ، فإن المنشور يدور حول كلمات ليندون ، أي أنه من الممكن أن يكون الباحث لم يشك حتى في أن هذه السلسلة كانت مرتبطة بهذا الجانب.

دعنا نعود إلى نظرية إردوس ريني. وفقًا لنتائج هذا المنشور ، يمكن القول أنه في الصيغة المقدمة ، تشير هذه النظرية إلى الحالة العامة التي تحددها نظرية Muavre-Laplace. والنظرية المشار إليها ، في هذه الصيغة ، لا يمكن أن تكون معيارًا لا لبس فيه لعشوائية السلسلة. لكن كسورية ، وفي هذه الحالة يتم التعبير عن أن السلاسل ذات الطول المشار إليه يمكن دمجها مع سلاسل ذات طول أطول ، لا تسمح لنا برفض هذه النظرية بشكل لا لبس فيه ، لأن عدم الدقة في الصياغة ممكن. مثال على ذلك هو أنه إذا كان هناك احتمال لوجود رقم 256 بت لعدد يبلغ الحد الأقصى لسلسلة 8 بتات هو 0.244235 ، فعندئذ ، بالاقتران مع تسلسلات أخرى أطول ، يكون احتمال وجود عدد من 8 بتات في عدد بالفعل - 0.490234375. هذا ، حتى الآن ، لا توجد فرصة لا لبس فيها لرفض هذه النظرية. لكن هذه النظرية تتناسب بشكل جيد مع جانب آخر ، والذي سيتم عرضه لاحقًا.

تطبيق عملي

دعونا نلقي نظرة على المثال الذي قدمه مستخدم VDG: "... يمكن تمثيل الفروع التغصنية للخلايا العصبية كتسلسل بسيط. يتم تشغيل الفرع ، ثم العصبونات بأكملها ، عند تنشيط سلسلة من نقاط الاشتباك العصبي في أي من أماكنها. مهمة الخلايا العصبية هي عدم الاستجابة للضوضاء البيضاء ، على التوالي ، الحد الأدنى لطول السلسلة ، بقدر ما أتذكر مع Numenty ، هو 14 نقطة تشابك في العصبونات الهرمية مع 10 آلاف نقطة تشابك. ووفقًا للصيغة التي نحصل عليها: Log_ {2} 10000 = 13.287. أي أن سلاسل بطول أقل من 14 ستحدث بسبب الضوضاء الطبيعية ، ولكنها لن تنشط الخلايا العصبية. انها وضعت بشكل صحيح تماما . "

سنقوم ببناء رسم بياني ، ولكن مع الأخذ في الاعتبار حقيقة أن Excel لا يعتبر قيمًا أكبر من 2 ^ 1024 ، سنقتصر على عدد عمليات المزامنة 1023 ، ومع أخذ ذلك في الاعتبار ، سنقوم بتحريف النتيجة بالتعليق ، كما هو موضح في الشكل 18.


التين. 18.

هناك شبكة عصبية بيولوجية تعمل عند تجميع سلسلة من m = log2N = 11. هذه السلسلة هي قيمة مشروطة ، ويتم الوصول إلى قيمة عتبة ، احتمال ، لنوع من التغيير في الوضع 0.78. واحتمال الخطأ هو 1- 0.78 = 0.22. لنفترض أن سلسلة من 9 أجهزة استشعار تعمل ، حيث يكون احتمال تحديد الحدث هو 0.37 ، على التوالي ، فإن احتمال الخطأ هو 1 - 0.37 = 0.63. وهذا يعني أنه من أجل تحقيق انخفاض في احتمال الخطأ من 0.63 إلى 0.37 ، من الضروري أن تعمل 3.33 سلسلة من 9 عناصر. الفرق بين 11 و 9 عناصر هو من الترتيب الثاني ، أي 2 ^ 2 = 4 مرات ، والتي إذا تم تقريبها إلى أعداد صحيحة ، حيث أن العناصر تعطي قيمة عدد صحيح ، ثم 3.33 = 4. نحن نتطلع إلى تقليل الخطأ عند معالجة إشارة من 8- عناصر ، نحتاج بالفعل إلى 11 سلاسل تشغيل من 8 عناصر. أفترض أن هذه آلية تسمح لك بتقييم الموقف واتخاذ قرار بشأن تغيير سلوك الجسم البيولوجي. في حدود المعقول والكفاءة ، في رأيي. ومع الأخذ في الاعتبار حقيقة أننا نعرف عن الطبيعة أنه يستخدم الموارد بشكل اقتصادي قدر الإمكان ، فإن الفرضية القائلة بأن النظام البيولوجي يستخدم هذه الآلية له ما يبرره. وعندما ندرب الشبكة العصبية ، فإننا في الواقع نحد من احتمالية الخطأ ، لأنه من أجل القضاء التام على الخطأ ، نحتاج إلى إيجاد علاقة تحليلية.

ننتقل إلى تحليل البيانات العددية. عند تحليل البيانات العددية ، نحاول تحديد تبعية تحليلية في النموذج y = f (xi). وفي المرحلة الأولى نجدها. بعد العثور عليها ، يمكن تمثيل السلسلة الحالية على أنها ثنائية بالنسبة إلى معادلة الانحدار ، حيث نخصص 1 للقيم الموجبة و 0 للقيم السالبة ، ثم نحلل على سلسلة من العناصر المتماثلة. نحدد أكبر ، على طول طول السلسلة ، وتوزيع سلاسل أقصر.

بعد ذلك ، ننتقل إلى نظرية Erdos-Renyi ، ويستنتج من ذلك أنه عند إجراء عدد كبير من الاختبارات ذات القيمة العشوائية ، يجب تشكيل سلسلة من العناصر المتطابقة في جميع سجلات الرقم الذي تم إنشاؤه ، أي m = log2N. الآن ، عندما ندرس البيانات ، لا نعرف حجم السلسلة بالفعل. لكن إذا نظرت إلى الوراء ، فإن هذه السلسلة القصوى تعطينا سببًا لنفترض أن R هي معلمة تميز حقل متغير عشوائي ، شكل 19


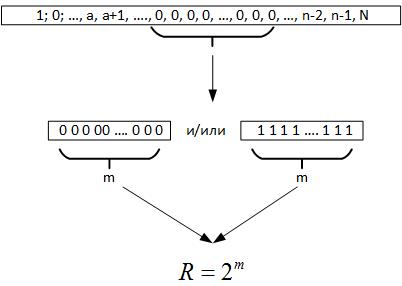
التين. 19.

وهذا يعني ، مقارنة بين R و N ، يمكننا استخلاص عدة استنتاجات:

1. إذا كانت R <N ، فسيتم تكرار العملية العشوائية عدة مرات على البيانات التاريخية.
2. إذا كانت R> N ، فإن العملية العشوائية لها بعد أعلى من البيانات المتاحة ، أو نحدد بشكل غير صحيح معادلة الدالة الهدف.

ثم في الحالة الأولى التي نقوم فيها بتصميم شبكة عصبية بأجهزة استشعار 2 ^ m ، أفترض أنه يمكننا إضافة زوج من أجهزة الاستشعار لالتقاط التحولات ، ونحن ندرب هذه الشبكة على البيانات التاريخية. إذا كانت الشبكة نتيجة التدريب غير قادرة على التعلم وستنتج النتيجة الصحيحة مع احتمال بنسبة 50 ٪ ، فإن هذا يعني أن الوظيفة الموضوعية التي تم العثور عليها هي الأمثل وأنه من المستحيل تحسينها. إذا تمكنت الشبكة من التعلم ، فسنقوم بتحسين الاعتماد التحليلي.

إذا كان بُعد السلسلة أكبر من بُعد متغير عشوائي ، فيمكن استخدام خاصية الكسر للمتغير العشوائي ، حيث أن أي سلسلة من الحجم m تحتوي على جميع المسافات الفرعية للأبعاد السفلية. أفترض أنه في هذه الحالة يكون من المنطقي تدريب الشبكة العصبية على جميع البيانات باستثناء السلاسل م.

قد تكون فترة التنبؤ هي طريقة أخرى لتصميم الشبكات العصبية.

في الختام ، يجب القول أنه في الطريق إلى هذا المنشور ، تم اكتشاف العديد من الجوانب التي يتقاطع فيها بعد متغير عشوائي وخصائصه المكتشفة مع مهام أخرى في تحليل البيانات. لكن في الوقت الحالي ، كل هذا في شكل خام للغاية وسيتم تركه للمنشورات المستقبلية.

الجزء السابق: الجزء 1 ، الجزء 2