الوضع الحسابي: هزيمة نقطة عائمة في مجالها الخاص. الجزء 2

الجزء 1

4. مقارنة كمية من النظم العددية

4.1. الدقة العشرية

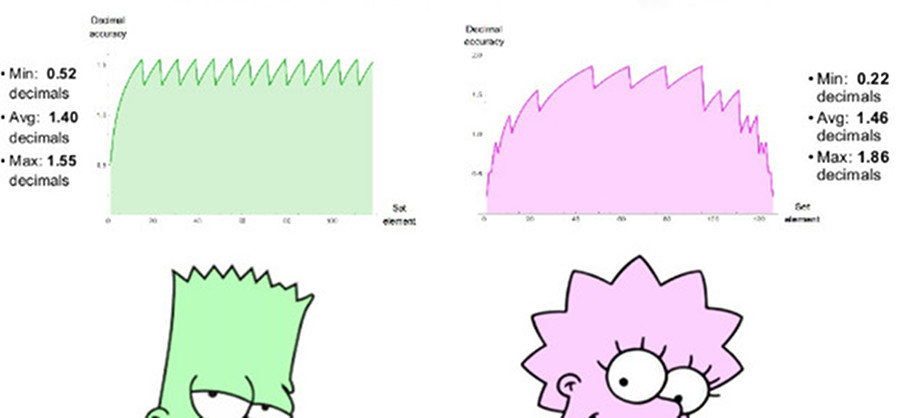
الدقة هي عكس الخطأ. إذا كان لدينا زوجان من الأرقام x و y (علامة غير صفرية وعلامة واحدة) ، فستكون المسافة بينهما مرتبة $$$\ mid log_ {10} (x / y) \ mid$ ترتيب عشري ، وهذا هو نفس المقياس الذي يحدد النطاق الديناميكي بين أصغر وأكبر عدد موجبة يمكن تمثيلها x و y. لن يكون التوزيع المثالي لعشرة أرقام بين 1 و 10 في نظام الأرقام الحقيقي توزيعًا متساويًا للأرقام بالترتيب من 1 إلى 10 ، ولكن الأسي: $$$1 ، 10 ^ {1/10} ، 10 ^ {2/10} ، ... ، 10 ^ {9/10} ، 10$ . هذا هو مقياس الديسيبل الذي يستخدمه المهندسون لفترة طويلة للتعبير عن العلاقات ، على سبيل المثال ، 10 ديسيبل هي نسبة عشرة أضعاف. 30db يعني معامل $$ . تبلغ نسبة 1db حوالي 1.26 ، إذا كنت تعرف القيمة بدقة 1db ، لديك دقة 1 منزلة عشرية. إذا كنت تعرف القيمة بدقة 0.1 ديسيبل ، فهذا يعني علامتي الدقة ، إلخ. صيغة الدقة العشرية هي $$$log_ {10} (1 / \ mid log_ {10} (x / y) \ mid) = - log_ {10} (\ mid log_ {10} (x / y) \ mid)$ ، حيث تمثل x و y قيمتين صالحتين يتم حسابهما باستخدام أنظمة التقريب ، مثل تلك المستخدمة في التنسيقات الطافية والموجبة ، أو الحدود العليا والسفلية في حالة استخدام أنظمة صارمة تستخدم فواصل زمنية ، أو قيم صالحة.

4.2. تحديد مجموعات المقارنة العائمة والموجودة

يمكننا إنشاء نماذج مصغرة للأرقام الطافية والموجبة لكل 8 بتات. تتمثل ميزة هذا النهج في أن 256 قيمة عبارة عن مجموعة صغيرة بما يكفي حتى نتمكن من اختبارها بشكل كامل ومقارنة كل شيء $$$256 ^ 2 دولا$ الحدوث في الجداول لعمليات الجمع والطرح والضرب والقسمة. تحتوي الأرقام الحقيقية بدقة 1/4 على بت إشارة واحدة ، وأربع بتات من الأس ، وثلاث بتات من الجزء الكسري ، وتلتزم بجميع قواعد IEEE 754. أصغر رقم موجب (غير طبيعي) هو 1/1024 ، وأكبر عدد موجب هو 240 ، والنطاق الديناميكي غير متماثل ومتساوي الطلبيات العشرية 5.1 - تمثل مجموعات 14 بت NaN.

يستخدم posit 8-bit للمقارنة es = 1 ، له مجموعة من الأرقام الموجبة من 1/4096 إلى 4096 ، وهو نطاق ديناميكي متماثل 7.2 أوامر عشرية. لا توجد قيم NaN. يمكننا رسم الرسوم البيانية الدقيقة العشرية من الأرقام الإيجابية في كلتا المجموعتين ، كما هو مبين في الشكل. 7. لاحظ أن القيم الممثلة بالأرقام المفترضة لها ترتيبان عشريان من حيث الحجم أكبر من النطاق الديناميكي العشري ، والدقة هي نفسها أو أكبر بالنسبة لجميع القيم باستثناء القيم التي تكون فيها الأعداد العائمة قريبة من التجاوز أو مكافحة التجاوز. المسافة البادئة من الرسوم البيانية لكلا النظامين هو تقريب لوغاريتمي للدالة الخطية قطعة. في أرقام التعويم ، تنخفض الدقة فقط على اليسار ، في المنطقة القريبة من مضاد للأفراد ، على اليمين ، تنقطع الوظيفة ، لأن ثم تأتي قيم NaN. تحتوي الأعداد المفترضة على وظيفة تناقص تناظرية أكثر حول الحواف.


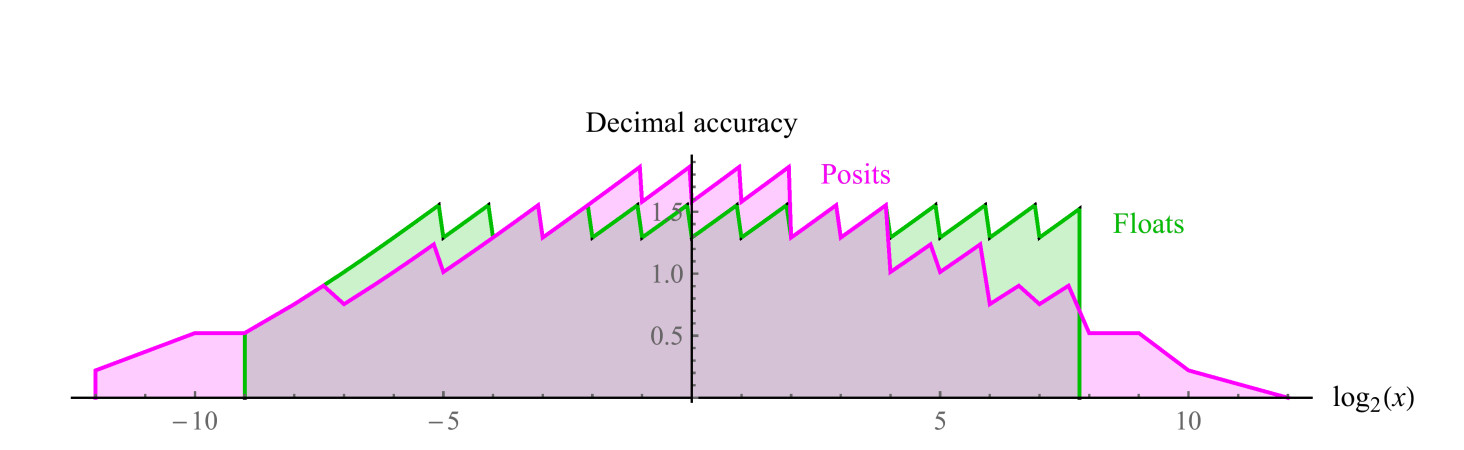
التين. 7. مقارنة الدقة العشرية للأرقام الطافية والموجبة

4.3. مقارنة عمليات وسيطة واحدة

4.3.1. قيمة عكسية

بالنسبة لكل قيمة إدخال x ممكنة لوظيفة 1 / x ، يمكن أن تتوافق النتيجة تمامًا مع قيمة أخرى في المجموعة المحددة ، أو يمكن تقريبها ، في هذه الحالة يمكننا قياس الخطأ العشري باستخدام الصيغة الواردة في القسم 4.1 ، بالنسبة للأرقام الطافية ، يمكن أن تؤدي النتيجة إلى تجاوز السعة أو NaN. انظر التين. 8.



التين. 8. المقارنة الكمية للأرقام الطافية والموجودة عند حساب القيمة المعكوسة

تُظهر المنحنيات على الرسم البياني الأيمن حجم الخطأ في حساب القيمة العكسية ، بينما يمكن أن تؤدي الأرقام الطافية إلى NaN. أرقام الوضعية أعلى من التعويم في عدد كبير من الحالات ، ويتم الحفاظ على هذا التفوق في جميع أنحاء النطاق. يؤدي حساب معكوس أرقام التعويم غير الطبيعية إلى حدوث تجاوزات ، مما يؤدي إلى قيمة خطأ لانهائية ، وبالطبع ، تعطي وسيطة NaN معكوس NaN. يتم إغلاق الأرقام المفترضة نسبة إلى حساب القيمة العكسية.

4.3.2. الجذر التربيعي

وظيفة الجذر التربيعي لا تؤدي إلى تجاوز أو مكافحة تجاوز. بالنسبة للحجج السلبية ، وبالنسبة إلى NaN ، ستكون النتيجة NaN. تذكر أن لدينا "نموذج مصغر" للأرقام الطافية والموجبة ، تزداد مزايا البوزيت مع زيادة دقة البيانات. بالنسبة إلى تعويم 64 بت ووضعيًا ، سيكون الخطأ المفترض حوالي 1/30 من الخطأ الطافي ، بدلاً من 1/2.

4.3.3. مربع

عملية شائعة أخرى هي $$$x ^ 2$ . الفيضانات والمضادات الفائضة شائعة عند تربيع العائمة. بالنسبة لنصف التعويم تقريبًا ، لا ينتج عن التربيع نتيجة مجدية ، بينما يؤدي تربيع الرقم المفترض في مربع دائمًا إلى إعطاء الرقم المفترض (مربع اللانهاية غير الموقَّعة لا نهائية غير موقعة).


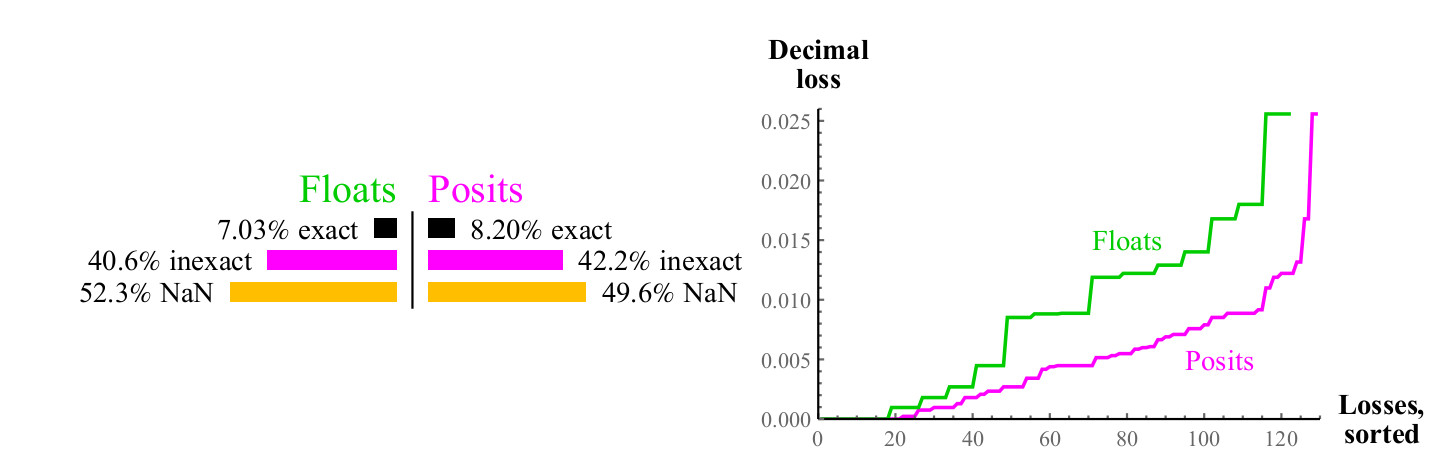
التين. 9. مقارنة كمية من الأرقام تعويم والافتراض عند حساب $$$\ sqrt x$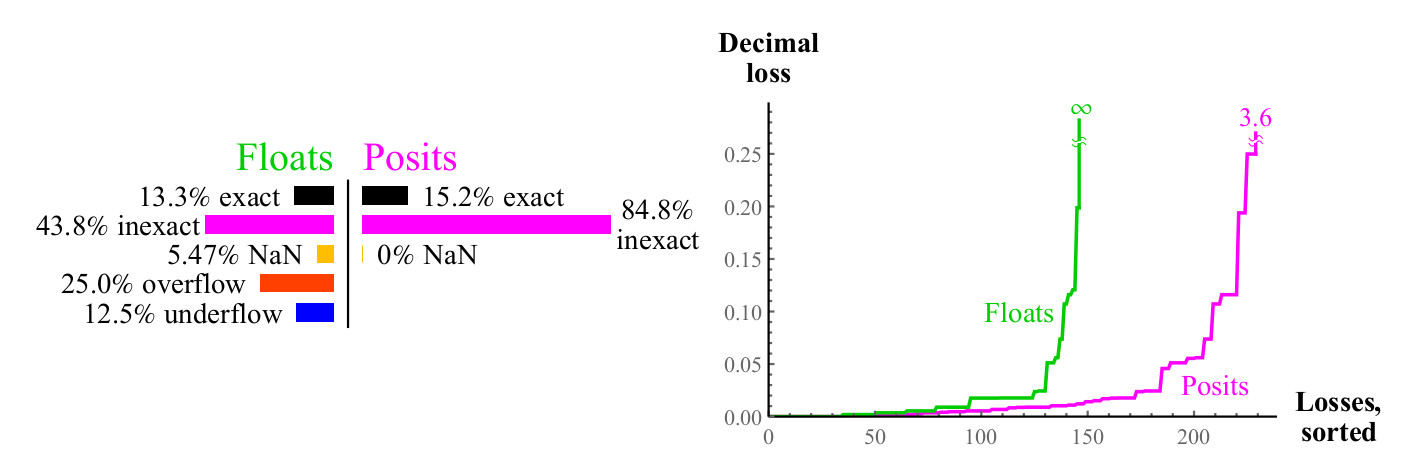


التين. 10. مقارنة كمية من الأرقام تعويم والافتراض عند حساب $$$x ^ 2$

4.3.4. قاعدة 2 لوغاريتم

لقد قمنا أيضًا بإجراء مقارنة لتغطية وظيفة اللوغاريتم الأساسي 2 ، أي النسبة المئوية للحالات التي $$ يمكن تمثيلها بدقة ، وإذا تعذر تمثيلها بدقة ، فكم عدد المنازل العشرية التي نخسرها. تتمتع أرقام الطفو بالميزة الوحيدة في هذه الحالة: يمكن استخدامها لتمثيلها $$$log_2 (0)$ كيف $$$- \ infty$ و $$$log_2 (\ infty)$ كيف $$$\ infty$ ، لكن هذا يقابله قاموس كبير يضم عددًا صحيحًا من الأعداد الصحيحة للعدد الصحيح.


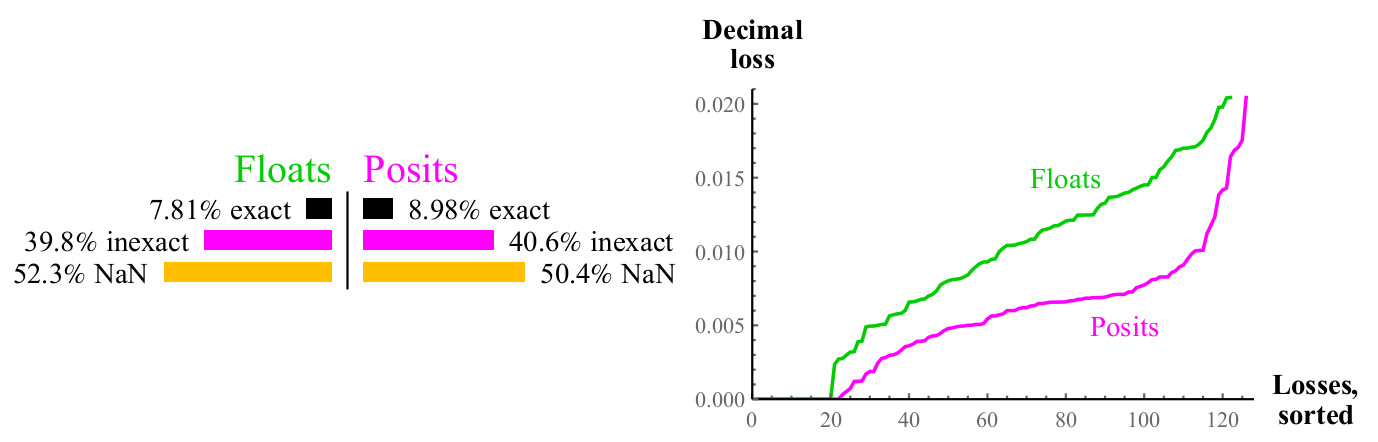
التين. 11. مقارنة كمية من الأرقام تعويم والافتراض عند حساب $$

يشبه الرسم البياني الرسم البياني للجذر التربيعي ، نصف الحالات تقريباً تعطي NaN في كلتا الحالتين ، لكن الأرقام المفترضة لها نصف فقدان الدقة العشرية. إذا كنت تستطيع حساب $$ ، تحتاج فقط إلى ضرب النتيجة بعامل تحجيم للحصول عليها $$$ln (x)$ أو $$$log_ {10} (x)$ أو لوغاريتم مع أي سبب آخر.

4.3.5. عارض $$$2 ^ x$

وبالمثل ، إذا كنت تستطيع حساب $$$2 ^ x$ ، يمكنك بسهولة استخدام عامل التحجيم للحصول عليه $$$e ^ x$ أو $$$10 ^ x$ إلخ أرقام المواضع لها استثناء واحد ، $$$2 ^ x$ يساوي NaN عندما تكون الحجة $$$\ مساء \ infty$ .


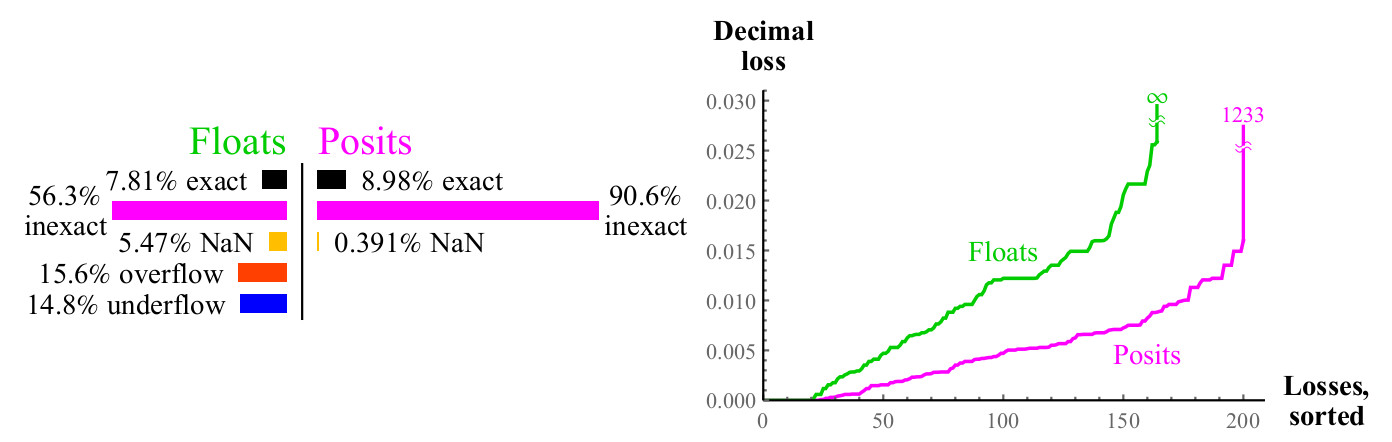
التين. 12. مقارنة كمية من الأرقام تعويم والافتراض عند حساب $$$2 ^ x$

قد يبدو الحد الأقصى للخسارة العشرية للأعداد المفترضة كبيرًا منذ ذلك الحين $$$2 ^ {maxpos}$ سيتم تقريب مرة أخرى إلى maxpos. في هذا المثال ، عدد صغير فقط من الأخطاء كبير $$$log_ {10} (24096) \ approx1233$ الطلبيات العشرية. حدد أيهما أفضل: تفقد أكثر من ألف أمر عشري ، أو تفقد عددًا لا حصر له من الطلبيات العشرية؟ إذا لم تتمكن من استخدام هذه الأرقام الكبيرة ، فلا تزال الأرقام المفترضة تربح ، لأن الأخطاء ذات القيم الصغيرة تكون أفضل بكثير. في جميع الحالات ، عندما تفقد عددًا كبيرًا من الطلبات العشرية عند استخدام أرقام افتراضية ، فإن وسيطة الإدخال تتجاوز إلى حد بعيد ما يمكن أن تعبر عنه الأرقام العائمة. توضح الرسوم البيانية مدى استقرار الأرقام المفترضة من حيث النطاق الديناميكي الذي تكون فيه النتيجة منطقية ، وتفوق في الدقة ضمن هذا النطاق.

للعمليات الأحادية العادية $$$1 / x ، \ sqrt x ، x ^ 2 ، log_2 (x)$ و $$$2 ^ x$ والأرقام المفترضة أكثر دقة ودقة من الأرقام الطافية التي لها نفس عدد البتات ، وتنتج نتائج ذات معنى في نطاق ديناميكي واسع. نحول انتباهنا الآن إلى أربع عمليات حسابية أولية تحتوي على وسيطين: الجمع والطرح والضرب والقسمة.

4.4. مقارنة عمليات حجتين

يمكننا استخدام نموذج المقياس لنظام الأرقام لدراسة العمليات الحسابية لوسيطتين ، مثل الجمع والطرح والضرب والقسمة. من أجل عرض نتائج 65536 ، نقوم بإنشاء "رسم بياني للتغطية" يبلغ 256 * 256 ، والذي يوضح بوضوح نسبة النتائج غير الدقيقة ، غير الدقيقة ، التي تسبب التدفق الزائد ، أو مكافحة التدفق الزائد ، أو NaN.

4.4.1. الجمع والطرح

ل $$$x - y = x + (- y)$ يعمل بشكل رائع لكلا التعويم والموضع ، ليست هناك حاجة لدراسة الطرح بشكل منفصل. لعملية الإضافة ، نحسب القيمة الدقيقة $$$z = x + y$ ، وقم بمقارنتها بالمبلغ المرتجع في كل نظام من أنظمة الأرقام. قد يحدث أن تكون النتيجة غير دقيقة ، ثم يجب تقريبها إلى أقرب رقم غير صفري محدد ، أو تجاوز سعة ، أو مكافحة تجاوز ، أو قد يحدث عدم اليقين في النموذج $$$\ infty- \ infty$ مما يؤدي إلى NaN. تتميز كل حالة من هذه الحالات بالألوان ، ويمكننا تغطية جدول الإضافة بالكامل في لمحة. في حالة تقريب النتائج ، يتغير اللون من الأسود (القيمة الدقيقة) إلى اللون الأرجواني (القيمة الدقيقة للوضع المفترض والعائم). التين. يُظهر الشكل 13 الشكل الذي يبدو عليه الرسم البياني للتغطية لأرقام التعويم والأرقام. كما هو الحال مع العمليات الأحادية ، ولكن مع وجود المزيد من النقاط ، يمكننا استخلاص استنتاجات حول قدرة كل نظام رقمي على تقديم إجابات مفيدة ودقيقة:


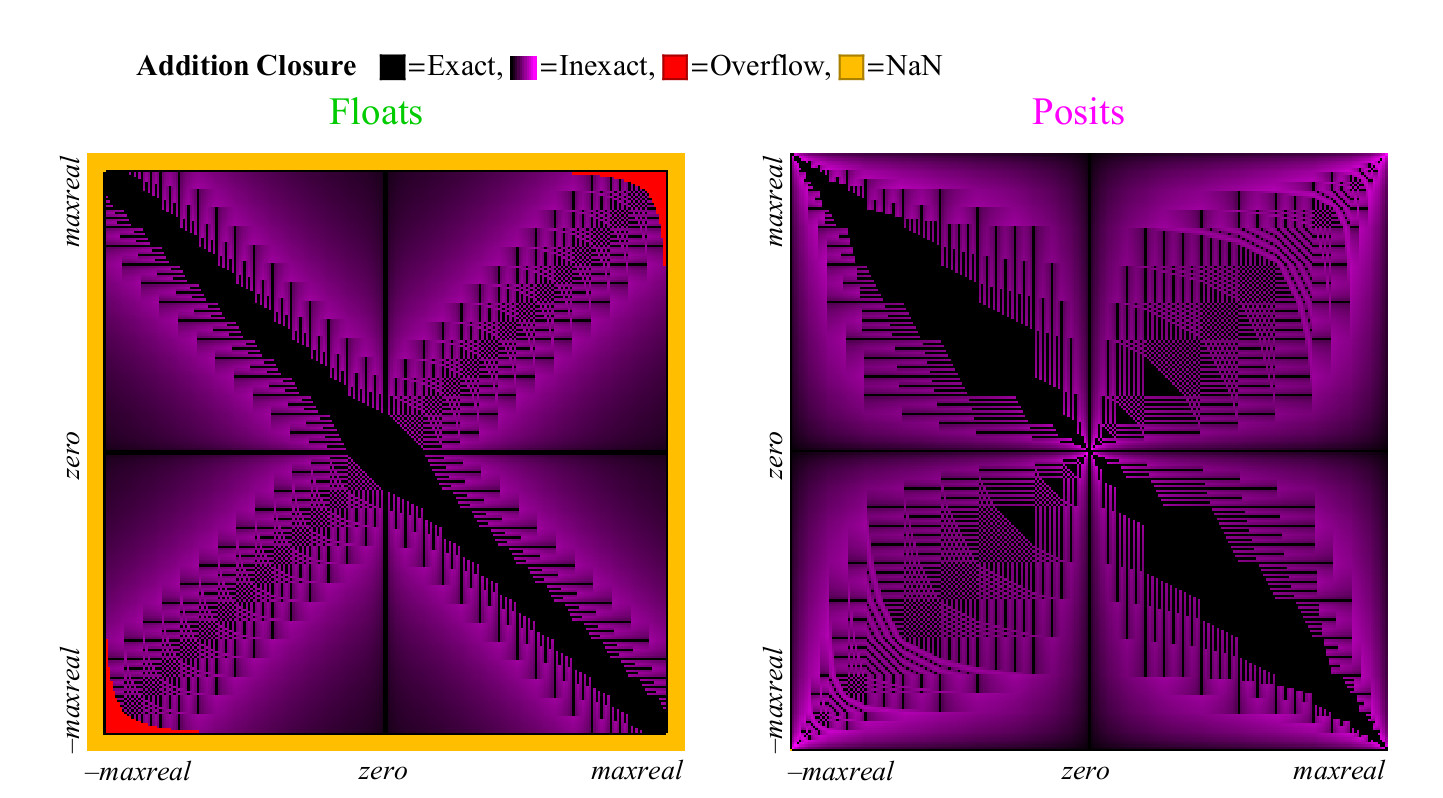
التين. 13. الرسم البياني التغطية الكاملة لإضافة أرقام تعويم والافتراض


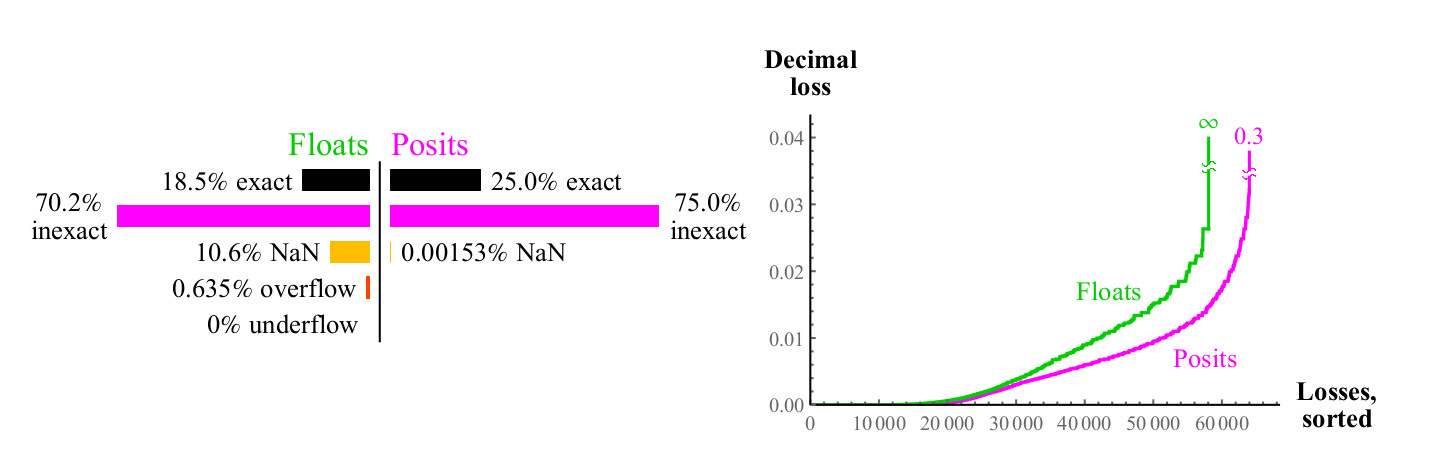
التين. 14. مقارنة كمية من الأرقام تعويم والافتراض للإضافة

للوهلة الأولى ، يصبح من الواضح أن posit لديه عددًا أكبر من النقاط في الرسم البياني للإضافة تكون فيه النتيجة دقيقة. الشريط القطري العريض الأسود على الرسم البياني للتغطية للطفو أوسع بكثير مما سيكون عليه لمزيد من الدقة ، لأنه يمثل منطقة أرقام غير طبيعية حيث يتم تباعد الأرقام العائمة على فواصل زمنية متساوية ، مثل أرقام النقطة الثابتة ، وتشكل هذه الأرقام نسبة كبيرة من العدد الإجمالي فقط في حالة أرقام 8 بت.

4.4.2. ضرب

نحن نستخدم نهجًا مماثلًا لمقارنة مدى تكاثر أعداد التعويم والوضع الافتراضي. على عكس الإضافة ، فإن الضرب يمكن أن يتسبب في زيادة عدد الأعداد العائمة. "التدريج المضاد للفيضان" ، المنطقة التي يمكنك رؤيتها في الوسط في الشكل 15. إلى اليسار. ( بمعنى الأرقام غير الطبيعية. الترجمة التقريبية. ) بدون هذه المنطقة ، سيكون لمنطقة مكافحة التجاوز الأزرق شكل ماسي. الرسم البياني للضرب للأعداد المفترضة هو أقل سخونة ، وهو أفضل. يتم تمييز وحدتي بكسل فقط على أنه NaN ، بالقرب من المكان الذي توجد فيه علامة الصفر للمحاور (تقع البيكسلات في أقصى اليسار في المركز رأسياً وأسفل في الوسط أفقيًا. تقريبًا. الترجمة. ) توجد نتائج الضرب $$$\ pm \ infty \ cdot 0 = NaN$ . تحتوي أرقام التعويم على المزيد من الحالات التي يكون فيها المنتج دقيقًا ولكن بسعر فظيع. كما هو مبين في الشكل 15 ، فإن ما يقرب من 1/4 من جميع المنتجات الطافية تؤدي إما إلى زيادة أو زيادة في التدفق ، ولا ينخفض ​​هذا الكسر بزيادة دقة الطفو.


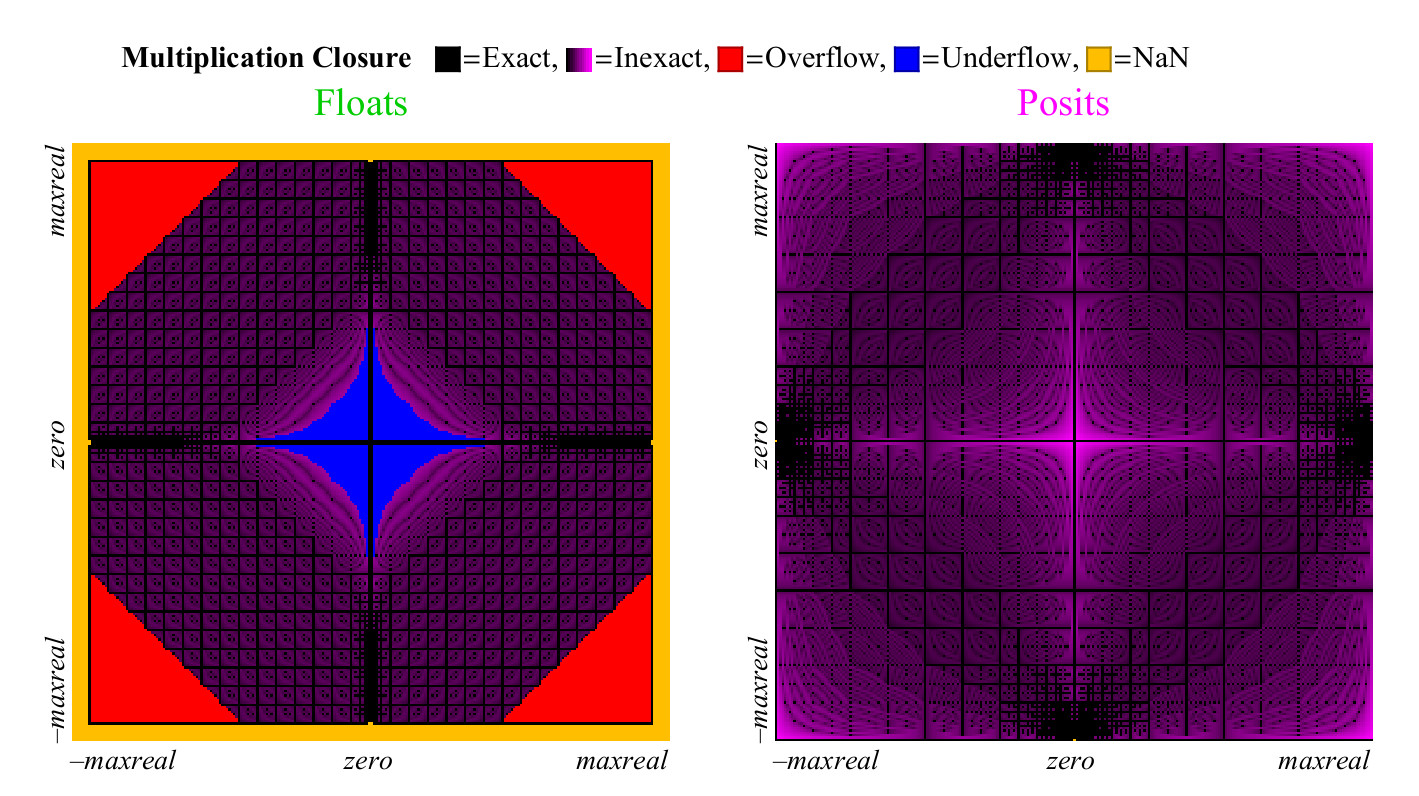
الشكل 15. الرسم البياني التغطية الكاملة لضرب أرقام تعويم والوضع الإيجابي

أسوأ حالة التقريب للأعداد المفترضة تحدث عندما $$$maxpos \ الأوقات maxpos$ الذي يتم تقريبه مرة أخرى إلى maxpos. في مثل هذه الحالات (نادر جدًا) ، يكون الخطأ هو 3.6 أوامر عشرية. كما الرسم البياني في التين. 16 ، أرقام افتراضية هي أفضل بكثير من تعويم ، تقليل خطأ الضرب.


التين. 16. مقارنة كمية من الأرقام تعويم والافتراض عن الضرب

يشبه الرسم البياني للتغطية لعملية القسمة الرسم البياني للضرب ، ولكن يتم تبديل المناطق لتوفير مساحة ، ولا يظهر هنا. المؤشرات الكمية للتقسيم هي نفسها تقريبا بالنسبة للضرب.

4.5. مقارنة بين أرقام التعويم والوضع الافتراضي لتقييم التعبيرات

4.5.1. اختبار "ميزانية الدقة 32 بت"

عادة ما يتم إجراء الاختبارات على أساس الحد الأدنى من وقت التشغيل ، وغالبًا لا تقدم صورة كاملة عن مدى دقة النتيجة. هناك نوع آخر من الاختبارات هو الذي نحدد فيه ميزانية الخطأ ، أي عدد البتات لكل متغير ، ونحاول الحصول على الدقة العشرية القصوى كنتيجة لذلك. فيما يلي مثال للتعبير الذي يمكننا استخدامه لمقارنة الأنظمة الرقمية بميزانية قدرها 32 بت لكل رقم:

$$

$$X = \ left (\ dfrac {27/10-e} {\ pi - (\ sqrt 2+ \ sqrt 3)} \ right) ^ {67/16} = 302.8827196 \ dotsb$$

القاعدة هي أننا نبدأ بأفضل تمثيل للأرقام $$$\ pi$ و $$$e$ ، ممكن في كل من الأنظمة العددية ، وتمثيل جميع الأعداد الصحيحة المشار إليها ، ونرى عدد الأرقام العشرية التي تتطابق مع القيمة الحقيقية لـ X بعد إجراء تسع عمليات في التعبير. سنسلط الضوء على الأرقام الخاطئة باللون البرتقالي .

على الرغم من أن أرقام تعويم IEEE ذات 32 بت لها دقة عشرية ، والتي تتراوح من 7.3 إلى 7.6 أوامر عشرية ، فإن تراكم أخطاء التقريب في حساب X يعطي إجابة 302. 912 صورة ، والتي تحتوي على ثلاثة أرقام صالحة فقط. هذا أحد الأسباب التي تجعل المستخدمين يشعرون بالحاجة إلى استخدام تعويم 64 بت في كل مكان ، نظرًا لأن التعبيرات البسيطة معرضة لخطر فقد الدقة إلى درجة أن النتيجة قد تكون عديمة الفائدة.

للأرقام الافتراضية ذات 32 بت الدقة العشرية المتغيرة ، والتي تتراوح بين 8.2 و 8.5 أوامر عشرية للأرقام بقيمة مطلقة حوالي 1. عند حساب X ، فإنها تعطينا إجابة قدرها 302.882 31 صورة ، والتي تحتوي على ضعف عدد الأرقام المهمة. لا تنس أيضًا أن الأرقام الافتراضية ذات 32 بت لها نطاق ديناميكي يزيد عن 144 منزلاً عشريًا ، وأن النطاقات ذات 32 بت لديها نطاق ديناميكي أصغر من 83 بت. لذلك ، لا يتم تحقيق الدقة الإضافية للنتيجة من خلال تضييق النطاق الديناميكي.

4.5.2. اختبار أربعة أضعاف: مشكلة المثلث الرقيق لجولدبرج

توجد مشكلة "مثلث رفيع" كلاسيكي [1]: ابحث عن مساحة المثلث ذي الجوانب a و b و c عندما يكون وجهان b و c 3 وحدات فقط من الرقم الأقل أهمية (الوحدات الموجودة في Last Place و ULP) أطول من نصف الطول الطويل الجانبين (الشكل 17).


التين. 17. غولدبرغ مشكلة مثلث رقيقة

تستخدم الصيغة الكلاسيكية للمنطقة A المتغير الوسيط s:

$$

$$s = \ frac {a + b + c} 2 ؛ A = \ sqrt {s (s-a) (s-b) (s-c)}$$

الخطر في هذه الصيغة هو أن s قريب جدًا من قيمة a ، والحساب $$$(s-a)$ يزيد من خطأ التقريب كثيرا. دعونا نجرب 128 بت (بدقة أربعة أضعاف) أرقام IEEE العائمة التي $$$a = 7 ، b = c = 7/2 + 3 \ times 2 ^ {- 111}$ . (إذا كنت تأخذ سنة ضوئية كوحدة قياس ، فإن الجانب القصير سيكون نصف الجانب الطويل فقط 1/200 من قطر البروتون. لكن هذا يجعل مثلث ارتفاع المدخل في الأعلى.) نحسب أيضًا قيمة A باستخدام أرقام افتراضية 128 بت ( وفاق = 7). فيما يلي النتائج:

$$عرض $$ $$ \ تبدأ {matrix} \ textrm {القيمة الحقيقية:} & 3.14784204874900425235885265494550774498 \ dots \ times 10 ^ {- 16} \\ \ textrm {128-bit IEEE float:} & 3. \ color {orange} { 63481490842332134725920516158057682788} \ dots \ times 10 ^ {- 16} \\ \ textrm {128-bit posit:} & 3.1478420487490042523588526549457744 \ colour {orange} {39} \ dots \ times 10 ^ {- 16} \ end {matrix $$ عرض $$

تحتوي أرقام المواضع على ما يصل إلى 1.8 رقمًا عشريًا من الدقة أكبر من أربعة أضعاف الدقة العائمة في نطاق ديناميكي واسع: من $$$2 \ times 10 ^ {- 270}$ إلى $$$5 \ times 10 ^ {- 269}$ . هذا يكفي لمنع العواقب الكارثية لزيادة الخطأ في هذه الحالة بالذات. ومن المثير للاهتمام أيضًا ملاحظة أن الإجابة بتنسيق الوضع الافتراضي ستكون أكثر دقة من التنسيق العائم ، حتى لو قمنا في النهاية بتحويلها إلى وضع 16 بت.

4.5.3. حل المعادلة التربيعية

هناك خدعة كلاسيكية مصممة لتجنب تقريب الأخطاء عند حساب الجذور $$$r_1$ . $$$r_2 دولا$ معادلة $$ باستخدام الصيغة المعتادة $$$r_1 ، r_2 = (- b \ pm \ sqrt {b ^ 2-4ac}) / (2a)$ عندما يكون b أكبر بكثير من a و c ، مما يؤدي إلى اختفاء الأرقام على اليسار ، منذ ذلك الحين $$$\ sqrt {b ^ 2-4ac}$ قريب جدا من ب . ولكن بدلاً من إجبار المبرمجين على حفظ الحيل الغامضة ، قد يكون من الأفضل للموضع أن يجعل الحساب آمنًا باستخدام صيغة بسيطة من البرنامج التعليمي. وضع $$$a = 3 ، b = 100 ، c = 2$ وقارن النتيجة في شكل تعويم 32 بت والموقع.

الجدول 5. حل المعادلة التربيعية


جذر غير مستقر عدديًا $$$r_1$ ، لكن لاحظ أن الوضع 32 بت يعطي 6 أرقام صحيحة بدلاً من 4 للعائم.

4.6. مقارنة بين العوامات وأنظمة Posit لاختبار LINPACK الكلاسيكي

لفترة طويلة ، كانت الطريقة الرئيسية لتقييم أجهزة الكمبيوتر العملاقة هي الحل $$$n \ مرة n$ نظم المعادلات الخطية $$$\ mathbf Ax = b$ . أي ، يملأ الاختبار المصفوفة A بأرقام عشوائية زائفة من 0 إلى 1 ، والناقل b بمبالغ الصفوف A. هذا يعني أن الحل x هو ناقل يتكون من وحدات. الاختبار يحسب معدل الخصم $$$\ | \ mathbf Ax-b \ |$ للتحقق من صحتها ، على الرغم من عدم وجود عدد ثابت من الأرقام التي يجب أن تكون صحيحة في الإجابة. يعتبر الفقد النموذجي لعدة أرقام من الدقة نموذجيًا للاختبار ، وعادةً ما يتم استخدام تعويم 64 بت (وليس بالضرورة IEEE). في البداية ، تم توفير الاختبار لـ n = 100 ، ولكن كان هذا الحجم صغيرًا جدًا بالنسبة لأسرع أجهزة الكمبيوتر العملاقة ، لذلك تمت زيادة n إلى 300 ، ثم إلى 1000 ، وأخيراً (من المؤلف الأول) ، أصبح الاختبار قابلاً للتطوير ويعطي عدد العمليات في الثانية ، بناء على حقيقة أن الاختبار يؤدي $$$\ frac {2} {3} n ^ 3 + 2n ^ 2$ عمليات الضرب والإضافة.

عند مقارنة الوضع المفترض والطفو ، لاحظنا وجود عيب بسيط في الاختبار: الإجابة في الحالة العامة ليست سلسلة من الوحدات ، بسبب أخطاء التقريب في المبالغ في الأسطر. يمكن التخلص من هذا الخطأ إذا وجدنا كيف أن الحوادث في A تساهم بت واحد ، والتي تقع خارج نطاق الدقة الممكنة ، وتعيين هذه البتة على 0. وهذا سيعطينا ثقة في أن مجموع السطر A يمكن تمثيله دون التقريب ، وأن الإجابة هي x هو في الواقع ناقل يتكون من وحدات. للإصدار الأصلي للمهمة ، بحجم 100 × 100 ، تعويم IEEE 64 بت يعطي إجابة من هذا النوع:

0.9999999999999 633626401873698341660201549530029296875
1.00000000000000 11102230246251565404236316680908203125
$$$\ vdots$
1.0000000000000 22648549702353193424642086029052734375

لا يوجد 100 رقم صحيح. إنها قريبة من 1 ولكن لا تساوي 1. مع الأرقام الافتراضية ، يمكننا أن نفعل شيئًا رائعًا. باستخدام أرقام افتراضية 32 بت ونفس الخوارزمية ، نحسب البقايا $$$r = \ mathbf Ax - b$ باستخدام عملية دمج هو منتج العددية. ثم تقرر $$$\ mathbf Ax '= r$ (باستخدام معالجتها بالفعل $$$\ mathbf A$ ) واستخدامها $$$x '$ لتصحيح: $$$x \ leftarrow x-x '$ . والنتيجة هي الإجابة الدقيقة غير المسبوقة لاختبار LINPACK: $$$\ {1 ، 1 ، ... ، 1 \}$ .هل يمكن لقواعد LINPACK أن تحظر استخدام نوع جديد من الأرقام 32 بت ، والذي يسمح باستخدامه بتحقيق نتيجة مثالية مع خطأ صفري ، أو الاستمرار في الإصرار على استخدام تعويم 64 بت ، والذي لا يسمح بذلك؟ سيتم اتخاذ هذا القرار من قبل المسؤولين عن هذا الاختبار. بالنسبة لأولئك الذين يحتاجون إلى حل أنظمة المعادلات الخطية لحل المشكلات الحقيقية ، بدلاً من مقارنة سرعة أجهزة الكمبيوتر العملاقة ، فإن posit تقدم مزايا مذهلة.

5. الخاتمة

Posit يهزم الطفو في لعبته: مع ذلك ، يمكنك إجراء العمليات الحسابية وتقليل أخطاء التقريب. تتميز أرقام المواضع بدقة أكبر ونطاق ديناميكي أكبر وتغطية أكبر. يمكن استخدامها للحصول على نتائج أفضل من تعويم بنفس عمق البت ، أو (التي يمكن أن تكون ميزة تنافسية أكبر) ، نفس النتائج مع عمق بت أقل. نظرًا لأن النطاق الترددي للنظام محدود ، فإن استخدام معاملات أصغر يعني سرعة أسرع واستهلاك أقل للطاقة.
نظرًا لأنهم يعملون كتعويم ، وليس كنظام زمني ، يمكن اعتبارهم كبديل مباشر للطفو ، كما هو موضح هنا. إذا نجحت الخوارزمية التي تستخدم العوامة في اجتياز الاختبارات ، وكان الوقت والاستقرار "جيدين بما فيه الكفاية" ، فسيعمل بشكل أفضل مع الوضع الافتراضي. توفر العمليات المنصهرة المتوفرة في الوضع الظاهري أداة قوية لمنع تراكم أخطاء التقريب ، وفي بعض الحالات تسمح لك باستخدام أرقام افتراضية 32 بت بأمان بدلاً من تعويم 64 بت في التطبيقات التي تتطلب أداءً عاليًا. بشكل عام ، سيزيد هذا من أداء التطبيق بنسبة 2-4 مرات ، ويقلل من استهلاك الطاقة ، ويوفر الطاقة ويقلل من تكلفة تخزين البيانات. سوف يعطينا موقف دعم الأجهزة ما يعادل خطوة أو خطوتين من قانون مور ،دون الحاجة إلى تقليل حجم الترانزستور أو زيادة التكلفة. بخلاف العوامة ، يوفر النظام المفترض استنساخًا تلو الآخر للنتائج على الأنظمة المختلفة ، مما يلغي العيب الرئيسي في معيار IEEE 754. الأرقام الافتراضية أكثر بساطة وأنيقة من العوامة ، وتقلل من كمية المعدات التي تدعمها. على الرغم من أن الأرقام الطافية أصبحت موجودة في كل مكان ، إلا أن الأرقام المفترضة قد تجعلها قديمة.

المراجع:

1. ديفيد جولدبيرج. ما يجب أن يعرفه كل عالم كمبيوتر عن حساب الفاصلة العائمة.
ACM Computing Surveys (CSUR)، 23 (1): 5–48، 1991. DOI: doi: 10.1145 / 103162.103163.
2. جون ل جوستافسون. The End of Error: Unum Computing، volume 24. CRC Press، 2015.
3. John L Gustafson. ما وراء النقطة العائمة: حساب الكمبيوتر من الجيل التالي. ندوة ستانفورد: https://www.youtube.com/watch؟v=aP0Y1uAA-2Y ، 2016. النسخ الكامل
متاح على http://www.johngustafson.net/pdfs/DebateTranscription.pdf .
4. جون ل جوستافسون. نهج جذري لحساب بأرقام حقيقية.
الحدود الفائقة للحوسبة والابتكارات ، 3 (2): 38-53 ، 2016. دوي: http://dx.doi.org/10.14529/jsfi160203.
5. جون ل جوستافسون. النقاش العظيم @ ARITH23. https://www.youtube.com/watch؟v=
KEAKYDyUua4 ، 2016. النسخ الكامل متاح على http://www.johngustafson.net/pdfs/
DebateTranscription.pdf .
6. أولريش دبليو كوليش وويلارد إل ميرانكر. منهج جديد للحساب العلمي ، المجلد 7. إلسفير ، 2014.
7. المزيد من المواقع. معيار IEEE للحساب الفاصلة العائمة. IEEE Computer Society ، 2008.
DOI: 10.1109 / IEEESTD.2008.4610935.
8. إسحاق يونيموتو. https://github.com/interplanetary-robot/SigmoidNumbers