مجرد تقسيم ، أو كيفية إنشاء نظرية رياضية وكسب 400 ألف دولار على ذلك

لقد حدث أن تطور العلم بشكل غير متساو ، وبالتالي في حياتنا اليوم ، إذا جاز التعبير ، هناك مكان للإنجاز. الانجاز ، بالطبع ، العلمية ، ولكن من هذا لا تقل أهمية. والآن ، أيها القراء ، يتم إعطاؤك الفرصة لرؤية مكان العمل الفذ ، والأسعار الرسمية للدفع (كما هو معتاد في البلدان التي تطلق على نفسها اسم المتحضرين) ، وتجرب حظك بنفسك. حسنًا ، في الوقت نفسه ، سوف يشعر بعضكم على الأقل بسحر العثور على اللؤلؤ في أشياء عادية جدًا.

علاوة على ذلك ، في العديد من المسلسلات ، ستتم متابعة قصة عن الأشياء التي يمكن الوصول إليها من قبل أي خريج في المدرسة الثانوية (وحتى العديد من أطفال المدارس). لن يكون هناك أي دليل ، حيث أنها غالبًا ما تكون واضحة ، وإذا تم تقديمها هنا فإنها لن تمدد فقط المجلد ، ولكنها ستخيف أيضًا العديد من القراء.

السلسلة الأولى

أولاً كان هناك نجوم. كانت هناك عملية لعب معهم ، والنظر والشعور ، والقذف ومراقبة طريق السقوط المشرق. كانت النجوم أنماط. وكانت الأرقام رمل. تحولت الأرقام في الجانب الجديد ، وظهر نجم آخر في الفجوات بينهما. ظهر إشراقها ، والأهم من ذلك كله ، أنها لم تحترق ، لكنها سمحت لنفسها باللمس والتقاطها ، ثم تلوحت بها لتترك أثراً متألقاً من صناعة النجوم. ولكن بعد ذلك أصبحت النجوم مألوفة وهناك وظيفة واحدة تركتها لفرزها. ثم جاءت فكرة.

كانت الفكرة بسيطة - يمكنك كسب المال عليها. ونعم ، هو الدافع حقا. لكنها لم تنمو معا. كان مسليا ، كان هناك النجوم العادية مشرقة بطريقة جديدة ، كان هناك متعة وكان هناك تقدم. في النهاية فقط نشأت غابة ، غابة متواصلة من الأشجار المتلألئة. وكنت ضعيفًا ، لم أتمكن من فرز هذا التايغا بحثًا عن ضوء حقيقي ، لأن هناك ملايين الأشجار ، وأنا وحدي. لذلك ، أقترح عليك أن تنظر إلى النجوم ، وإذا كانت مثيرة للاهتمام ، فيمكنك أن تكسب 400 ألف دولار ، ولكن الحقيقة هي أن هناك واحدًا "لكن" - في الغابة ، يجب أن تكون قادرًا على اختيار المسار الصحيح.

على النهج إلى النجوم

ما هو الرقم؟ من ناحية ، إنه نتاج عقولنا القاتمة ، غير الموجودة في الطبيعة. لكن من ناحية أخرى ، يسمح لنا هذا التجريد بنمذجة العديد من العمليات التي نلاحظها جميعًا بنفس الطبيعة. فقط النموذج لا يساوي الظاهرة الملاحظة. مرة أخرى ، نحن نتعامل مع التكيف مع قدراتنا المتواضعة لطرق وصف الطبيعة. هل هذا جيد؟ من حيث الدقة ، وصف ليست جيدة جدا. ليس لأن شخص ما قد لا يكون لديه عدد كافٍ من المنازل العشرية ، ولكن لأن ظاهرة غير دقيقة قد تفاجئنا كثيرًا عندما يتبين أن النموذج يفتقر إلى ميزة معينة أو أخرى موجودة في الواقع وقد يبدو مزعجًا في بعض الأحيان علماء الطبيعة الغائبين على الرأس.

في ضوء ما تقدم ، دعونا نحاول الاستفسار عن اكتمال أساس أي نمذجة - اكتمال فهم مفهوم الرقم. يبدو أن مجرد رقم ، مجرد معرفة به ، منذ الطفولة المبكرة - حسنًا ، ماذا يمكن أن يكون؟ ولكن هناك فقط يمكننا أن نجد الهاوية. نعم ، التي هي بلا قاع ، والتي هي مليئة بالنجوم.

لا توجد أرقام في الطبيعة. ولكن في الطبيعة تستطيع أن ترى العلاقة. السحابة أكبر (أطول / أوسع / أثخن / like_you_ else_will_be_becoming) السحابة الأخرى ، مما يعني وجود مكان للارتباط. لكن النسبة أيضا لا يوجد لديه أرقام. هناك اثنين فقط من السحب ، واحدة أخرى ، والآخر أقل ، وهناك نسبة. على الرغم من نعم ، اخترع الرجل النسبة أيضًا. لذلك ، قد يسأل المرء - ما هي الفائدة من ذلك؟ الفائدة هي هذا - مفهوم الارتباط هو خطوة واحدة إلى الأمام من مفهوم الرقم. في البداية كانت هناك نسبة ، وعندها فقط ظهر رقم. بتعبير أدق - الأعداد الكسرية. لذلك ، فهم العلاقة ، سوف نفهم الأرقام.

كيف يتم الحصول على الأرقام الكسرية؟ بسيط جدا - من الحاجة إلى نموذج الارتباط. في البداية كانت هناك نسب للخطوات وجوانب الأرض ، الأغنام من مالك إلى آخر من الأغنام ، وزن البطيخ إلى وزن الآخر. في كل هذه الحالات ، كانت هناك حاجة للتعبير عن الفرق بطريقة أو بأخرى. لكن الفرق لم ينقسم بدقة بعدد الخطوات أو حجم البطيخ المجاور. في البداية ، تعلموا التعبير عن الفرق من خلال تقسيمهم إلى وحدات قياس أصغر (تم إضافة المرفقين إلى الخطوات ، وأضيفت الأصابع إلى المرفقين). لكن العلم لم يقف ساكنا وطالب بمزيد من الدقة. ونتيجة لذلك ، وافق الجميع على التوحيد ، ونسيان الأصابع والمرفقين والخطوات وغيرها من الجنيهات الاسترليني. يتم التعبير عن التوحيد في العدد.

كيفية ربط شريحتين إذا كان أحدهما لا يتناسب مع عدد صحيح عدد المرات؟ يمكنك القياس بأصابعك ، لكن سيكون من الأصح أخذ شريحة أصغر كوحدة قياس وتقسيمها إلى أجزاء متطابقة. باستخدام هذه الأجزاء ، يمكنك قياس ذلك الجزء من شريحة أكبر لا تقاس بالجزء الأصغر بأكمله. ولكن بعد ذلك ينشأ جزء جديد من الجزء الأكبر ، والذي لم يعد قابلاً للقياس بواسطة الأجزاء المحددة. نحن نطبق العودية ونقطع مرة أخرى الأجزاء المكسورة بالفعل إلى مكونات أصغر. نقيسها سابقا لا حصر لها. ومرة أخرى نحصل على ما تبقى لا حصر له. تقسيم الأجزاء مرة أخرى ، وقياس مرة أخرى. مرة أخرى نحصل على الباقي. ولكن يمكنك أن تشعر بالملل!

نتيجة لذلك ، توصل الناس إلى فكرة التقريب وتوقفوا عن تقسيم وحدة القياس. وهذا هو ، وسجل الناس على دقة (يقولون أنها كافية). لكن الطبيعة لا تغفر عدم الدقة في النمذجة.

كيف يتم نمذجة النسب اليوم؟ يتم تصميمها باستخدام تصنيف الأرقام الكسرية. التصنيف هو هذا - هناك أعداد صحيحة وهناك أرقام كسرية. كلها لا تزال غير مستقرة ، ولكن تلك كسور تنقسم إلى كسور لانهائية وغير محدودة. في الوقت الحاضر ، ننسى أيضا تلك النهائية. تنقسم اللانهائية إلى عقلانية وغير عقلانية. ننسى عادة عن الجزء الأول. وتنقسم غير عقلانية إلى جبري ومتسامي. كل شيء ، لا مزيد من الانقسامات. ولكن من أجل الوضوح ، نعطي تصنيفًا في صورة:



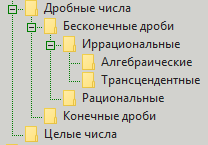
لماذا هذا التصنيف سيء؟ انها ليست سيئة للغاية. إنها ، كما اعتادت ويني ذا بوو ، أن تكون جيدة ، لكنها عرجاء بطريقة أو بأخرى ... أي أنه من الواضح أنه مع دقة التعبير عن القيم ، فهي ليست على ما يرام بسبب اللانهائية. ولكن هناك جانب آخر للعملة. يسمى هذا الجانب (في هذا السياق) "القسمة". لا يمكننا الفصل بدقة بين رقمين (واحد على الآخر) لأننا نقف أمام اللانهاية. لكن من ناحية أخرى ، نحن مهتمون بظواهر من عالم الأرقام مثل البساطة وعدد المقسومات التي تقضي على اللانهاية عند ظهورها. تشكل الأعداد الأولية أساس سلسلة الأعداد الصحيحة. وهذه الأرقام المهمة (بما في ذلك ، على سبيل المثال ، للراحة عند الدفع عن بعد للخدمات) تعتمد الأرقام إلى حد كبير على عملية التقسيم. وغالبا ما يعطينا الانقسام الكسور. والكسور تعطينا أرقام كسور. حسنًا ، بالنسبة إلى الأعداد الكسرية ، أعطانا شخص ما التصنيف المحدد سابقًا للمحدود ، اللانهائي ، العقلاني ، غير العقلاني ، الجبري والمتسامي. ولكن هل يتيح لنا هذا التصنيف الفرصة للعثور على إجابات لأسئلة حول الأرقام؟ على سبيل المثال ، عن نفس الأشياء البسيطة؟ أو كسور؟ يبدو أنه يعطي ، ولكن ليس بقدر ما نود.

خذ الأرقام الأولية. اليوم ، يتم البحث في الأساسيات الأولية القصوى. أي أنهم يأخذون رقم المرشح ، ثم يتحققون من أنه بسيط أم لا. يحصل المرشحون على الأرقام ببساطة - إذا كنت تعرف طريقة التحقق من البساطة لفئة معينة من الأرقام ، فإليك قائمة المرشحين في شكل ممثلين عن الفصل الذي يجتازونه بغباء في صف واحد ، والتحقق من كل رقم ، بدءًا من القيم الصغيرة بالطبع. وحتى الآن وصلوا إلى أعداد من اثنين إلى درجة ثمانين مليون غريب. هذا هو ما يقرب من خمسة وعشرين مليون المنازل العشرية. من حيث المبدأ ، يبدو رائعا. ولكن ما الذي يمنعنا من التذكير بشعار "أعلى ، أبعد ، أسرع"؟

في الأساس ، يعيقنا الافتقار إلى التفاهم. نعم ، نموذجنا للظاهرة المسماة "الرقم" غير مكتمل. ونعم ، جزء النموذج ، المسمى "القسمة" ، غير مكتمل إلى أقصى درجة. لذلك ، ثمانون مليون وحدة في ذاكرة الكمبيوتر هي الحد الأقصى للبشرية. لماذا الوحدات؟ لأنه يبدو وكأنه أكبر أعداد أولية. هذه هي وحدة واحدة ، ولكن في تدوين ثنائي. بالنسبة لهم ، يوجد اختبار Luc-Lemer ، والذي يوضح لنا رقمًا بسيطًا أو مركبًا. وهذا الاختبار يتطلب سنوات من العمل من معالج واحد الأساسية للتحقق من عدد مرشح واحد من ثمانين مليون وحدة ثنائية. فقط ثمانون ميغا بايت ، أو عشرة ميغا بايت ، والإنسانية لم تعد قادرة على المضي قدمًا. ما هو عشرة ميغابايت؟ هذا بنس ، هذا تافه ، إنه لا شيء تقريبًا لأجهزة الكمبيوتر الحديثة. لكن الاختبار مستمر منذ سنوات. لذلك ، يجب عليك تشغيله على ملايين أجهزة الكمبيوتر التي يقوم المتطوعون بتثبيت البرنامج المناسب عليها ، ونتيجة لذلك تحقق من رقم مرشح واحد لعدد معين من الثواني (وهذا إذا كان هناك الكثير من المتطوعين). لكن المشكلة تكمن في وجود عدد كبير من المرشحين ، وبالتالي فإن الأمر يستغرق عدة أشهر للعثور على الرقم الأول التالي. ومع مثل هذا المداولات ، يمكن للمرء أن يتوقع أن حركة ما يصل إلى مئات الملايين فقط من الوحدات الثنائية ستستغرق عشر سنوات.

هل من الممكن تسريع العملية؟ يمكنك ذلك. ولكن هناك حاجة إلى مزيد من التفاهم. على سبيل المثال - كيفية تقليل الوقت لاختبار كل رقم؟ حتى الآن ، يتم تحقيق هذا الانخفاض عن طريق تدليك الحديد. أو الخيار الثاني - يمكنك تقديم اختبار أسرع للبساطة. لكن مع هذا لمدة 100 عام ، لم يتغير شيء يذكر. ومع ذلك ، إذا اكتشفت ذلك ، فربما ستنجح معنا. تحتاج فقط إلى فهم من الأساسيات.

النجوم القريبة

بالتفكير في العلاقات ، يمكن للجميع المساهمة كثيرًا في العلوم. مجرد فضول يكفي. على سبيل المثال ، قد يتساءل المرء ، لماذا تصنيف الأعداد الكسرية بهذه الطريقة؟ وابحث عن الإجابة في تجربة فكرية لقياس نسبة الأجزاء نفسها. أولاً ، ترتبط الشرائح من 1 إلى 2. هذه النسبة مفهومة ، فهي تعطينا الرقم 2 ، والذي يوضح عدد مرات تجاوز الشريحة الأكبر للعدد الأصغر. والآن دعونا نطيل شريحة أصغر قليلاً. ماذا سيحدث؟ سوف تتوقف النسبة لتكون كاملة. الفائض الناتج من الإطالة يمنعنا من الحصول على إجابة بسيطة في المشكلة. ولكن يمكننا استخدامه كحاكم. إذا كان يناسب عددًا صحيحًا عدد المرات في نصف شريحة أكبر ، فيمكننا التعبير عن النسبة من خلال هذا العدد الصحيح. حتى نحصل على النسبة:

$$

$$(1 + 1 / N) / 2 دولا$$

حيث N هو عدد المرات اللازمة لتناسب الفائض من تمديد الطول الأصغر إلى نصف الطول الأكبر. لذلك لدينا عدد معقول. يتم تقديمها دائمًا بنسبة الأعداد الصحيحة. إذا قمنا الآن بتمديد الجزء الأصغر لفترة أطول قليلاً ، فبإمكاننا الحصول على موقف لا يهم فيه عدد العناصر الأصغر في عدد صحيح معين ، بغض النظر عن مقدارنا ، لا يمكننا الحصول على تطابق تام مع عدد معين من أطوال الجزء الأكبر. لذلك حصلنا على عدد غير منطقي يميز النسبة الجديدة. لاحظ أن التحول المجهري لحد القطعة يؤدي إلى عملية لا نهاية لها لتحديد نسبة الأطوال. خطوة واحدة للباحث المتواضع وتغيير كبير في نظرية الأعداد - عنصر جديد في التصنيف مطلوب. خطوة واحدة و- من الحجم الصغير إلى اللانهاية. من فئة واحدة من الأرقام إلى فئة جديدة تمامًا ، لا يتوافق بشكل أساسي مع الفئة السابقة. أليس هذا نجم؟

ولكن في الواقع ، لقد قمنا بتغيير شريحة واحدة قليلاً. من أين أتت الفئة الجديدة بشكل أساسي؟ بشكل عام ، يعتبر التصنيف مهمًا لقدرته على مطابقة الواقع تمامًا. لكن أي نوع من الدقة جاء مع أرقام غير عقلانية؟ إنها تتيح لك تصميم أي نسبة ، وليس فقط نسبة الأعداد الصحيحة ، لذلك من المنطقي حقًا فصل هذه الفئات. لكن هذا ليس كل الدقة ، لأنني أريد أن أفهم كل هذه اللانهاءات ، وكيف تظهر ، وماذا تعني ولماذا كانت موجودة على الإطلاق. صحيح ، مع اللانهاية ، ليس كل شيء سهلاً ، لكن الآن سنتعامل مع علاقات محدودة. يبدو أن كل شيء بسيط معهم ، خذ N ، وقسمه على M ، واحصل على رقم كسري. سيكون جيدًا للغاية إذا كان الرقم قصيرًا ، على سبيل المثال 2.5 أو 3.25. ولكن في كثير من الأحيان إلى العالم ، توجد علاقات من الشكل 4.12 (3456) ، أي مرة أخرى مع اللانهاية ، ولكن هذه هي اللانهاية "في الفترة". لاحظ فقط الأرقام المتكررة ، يمكنك بسهولة تسجيل رقم مضغوط من عدد لا حصر له من الأحرف. هكذا تعاملنا مع اللانهاية. أيضا النجمة الصغيرة. ولكن هذه ليست سوى لمحة سريعة.

الآن دعنا نشغل الفضول ونطرح الأسئلة. ولماذا بعض الأرقام الكسرية محدودة والبعض الآخر لا حصر له؟ ولماذا تكون بعض أنواع اللانهائي طويلة إلى ما لا نهاية ، بينما البعض الآخر مع فترة؟ ولماذا قبل الفترة في الرقم 4.12 (3456) نرى الأرقام 1 و 2؟ ولماذا توجد فترة تحضيرية؟ ولماذا في الفترة نرى الأرقام 3 و 4؟ ولماذا طول الفترة في هذا المثال يساوي أربعة؟ ولماذا عدد الأعداد قبل الفترة يساوي اثنين؟ ونحن فقط نلقي نظرة فضولية على رقم كسري واحد فقط. وبالنسبة للأرقام الأخرى ، ستكون الأسئلة أكثر إثارة للاهتمام.

دعنا نحاول الإجابة لماذا الأعداد الكسرية محدودة؟ بسيط للغاية - في الواقع ، هذا "خداع بصري". بتعبير أدق - استخدمنا خدعة واحدة. على سبيل المثال ، للحصول على الرقم 2.5 ، يمكنك تقسيم 5 على 2. ولهذا ، تعلمنا جميعًا في المدرسة طريقة تقسيم "الزاوية". ولكن دعونا نلقي نظرة فاحصة على هذه الطريقة. ثم نجد أن الفقير يتصرف على النحو التالي - إنه يضاعف العائد بواسطة ثابت يحتوي على المقسوم عليه ، أو عوامله. ثم يقلل بالضبط العوامل من الثابت إلى عوامل المقسوم عليها. يبدو مثل هذا:

$$

هذا كل المعجزات - يتم تقليل الشيطان من المقسم إلى الشيطان من الثابت $$ وهو يساوي $$ ، وظلت خمسة نتيجة لذلك ، والتي تتم كتابتها بعد الفاصل العشري. الرقم هو $$$1$لم يشارك $$ يتضاعف $$ من المبلغ $$ . لكننا لا نرى ذلك ، وذلك بفضل "الوهم البصري" الذي قمنا بتدريبه من المدرسة على الإبداع بشكل مستقل أثناء كل عملية تقسيم. حسنا ، أليس هذا نجم؟ كان على المرء فقط أن يدفع أوراق الشجر على التمثيل الصامت من وقت المدرسة الابتدائية ، عندما رأينا ضوء شيء جديد ، وليس عاديًا تمامًا ، لا يتم تدريسه في المدرسة (ولكن دون جدوى).

دعونا الآن نوضح "الوهم البصري" بمستوى أعلى قليلاً. لقد ترجمنا ببساطة نتيجة القسمة إلى تنسيق مناسب للتخزين والإدراك. الرقم نفسه لا يعتمد على التنسيق. وعدد الشخصيات في ذلك أيضا. لقد رأينا بالفعل إمكانية وضع أقواس حول فترة ما ، وبالتالي تقليل اللانهاية إلى طول الفترة واثنين من الأقواس. وهذا أيضًا تنسيق بيانات ، ولكنه يستخدم للكسور الدورية. ويخفي شكل الكسور المحدودة اللانهاية عن طريق تقليل العوامل من قاعدة نظام الأرقام العشرية. إذا أخذنا ، على سبيل المثال ، نظام الأعداد الثلاثية ، فإن تقسيم 5 في 2 سيبدو كما يلي:

$$

$$

$$= 2+ (1+ (1 + 1/2) / 3) / 3 = ... = 2.1 (1)$$

أي أننا حصلنا على ما لا نهاية في شكل كسر دوري ، لأننا استخدمنا الآن ثابتًا آخر لا يحتوي على عوامل يمكن تقليلها بالرقم 2. ولكن في النظام السداسي عشر ، ستصبح النتيجة مرة أخرى نهائية - 2.3. لكن الرقم نفسه يبقى في مكان ما في الظل ، وربما يكون أفضل سجل له هو 5/2 ، وكل شيء آخر هو مسألة اختيار تنسيق العرض التقديمي لهذا الرقم.

الآن عن الكسور لانهائية. يتم الحصول على تلك الدورية عن طريق تقسيم الأعداد الصحيحة ، ويتم الحصول على تلك غير المنطقية (مع طول الفترة اللانهائية) عن طريق حساب جذر من درجة ما من عدد صحيح. أي أن الناس استمدوا فئتين من التقسيم من تجريد الأعداد الصحيحة - بعوامل مختلفة وبنفس العوامل. يسمح لك الخيار الأول بتقسيم أي عدد صحيح إلى أي عدد صحيح آخر ، ولكنه في بعض الأحيان يعطي نتيجة كسرية. يسمح لك الخيار الثاني بتقسيم الأرقام فقط على تلك التي تساوي تمامًا نتيجة القسمة (بما في ذلك الأعداد المتعددة لجذور الدرجات الكبيرة). بشكل عام ، لدينا نفس التقسيم ، ولكن دون قيود على النتيجة ومع التقييد. يقودنا التقييد إلى خيارين: إما تقليل المقسوم بعامل من العائد (وبعد ذلك يمكنك الحصول على عدد صحيح يساوي المقسوم عليه) ، أو قسمة العائد غير القابل للاختزال على عدد معين. ماذا بعد ذلك يمكن أن يكون "عدد معين"؟ إذا كان عددًا صحيحًا ، فنتيجة لذلك نحصل على جزء صغير (العائد والمقسوم عليه غير قابل للاختزال) ، والذي لا يساوي العدد الصحيح. لذلك ، نظرًا لأن الأعداد الصحيحة لا تتناسب ، تحتاج إلى البحث عن كسر يساوي النتيجة. تختفي الكسور المحدودة أيضًا ، لأنها تمثل بالفعل عددًا من النموذج $$$N / M$التي ، عندما تضرب في حد ذاته ، من شأنها أن تعطينا جزء جديد من النموذج $$$N * N / (M * M)$، والذي يعطينا مرة أخرى جزءًا محدودًا أو دوريًا ، وليس عددًا صحيحًا.لذلك ، من الضروري تحديد الكسر الذي يقلل نسبة المربعات الخاصة بهم إلى عدد صحيح مع نمو لانهائي من N و M. لماذا لا حصر له الأعداد الصحيحة$$$N*N/(M*M)$يمكن أن تكون كاملة ، ولكن ليس للنهاية؟ لأن المزيد من الأرقام ، وأقل تأثير على النتيجة هو تقديرهم. العدد الصحيح الذي يتبع أي واحد مختار هو بالضرورة مختلف عنه. ولا تسمح لك هذه الوحدة بضبط النتيجة المرغوبة بدقة ، لأنه ، على سبيل المثال ، بين 1/1000 و 2/1000 يوجد عدد لا حصر له من الأرقام ، على سبيل المثال 11/10000 أو 145/100000 ، إلخ. لذلك ، بزيادة طول العدد ، من الممكن في اللانهاية الحصول على أي نتيجة بأي دقة. ثم اضربها بنفسها واحصل على عدد صحيح. وفي الوقت نفسه ، تصبح فترة هذا الكسر بلا حدود حقًا ، كما سنرى لاحقًا. والفترة اللانهائية هي خاصية عدد غير عقلاني ، والتي انتقلنا إليها من أرقام عقلانية تماما. هذا هو ضوء النجوم الذي يتحول بسلاسة إلى ظلام اللانهاية.

ولكن لماذا نحتاج إلى هذا التقاطع بين فئتين من الأرقام؟ ربما واحد يكفي؟ دعنا نحاول محاكاة. إذن ، لقد حصلنا على جذر عدد صحيح تمامًا ، ووجدنا عددًا صحيحًا كبيرًا يميلان إلى ما لا نهاية ، عندما يعطي كل منهما الآخر عددًا صحيحًا. الآن إضافة واحد إلى أي من هذه الأرقام الكبيرة بلا حدود. ماذا سيحدث بعد ذلك؟ بلغتنا المعتادة ، حصلنا على تعريف لعدد جديد ، وهو ليس دوريًا (لأنه يحتوي على فترة لانهائية) وفي نفس الوقت ليس جذر الكل. وهذا يعني أن الرقم الجديد لا يتناسب مع التصنيف الممنوح لنا من الأرقام المنطقية وغير المنطقية. والآن تم استدعاء جميع هذه الأرقام من قبل علماء الرياضيات التجاوزي ، لأنه يجب عليك وضعها في مكان ما. ولكن نقطة مثيرة للاهتمام - في البداية كانت هناك جذور الأعداد الصحيحة ، ودعا الأرقام غير المنطقية ،ثم ظهرت أرقام "أخرى". وهذا هو ، أولاً ، من أجل التقليد اليوناني القديم ، تم تقدير المبالغة في تقدير أهمية الأعداد الصحيحة على أساس طرق الحصول عليها من الأعداد الصحيحة. الطريقة الأولى كانت القسمة والأرقام المنطقية المستمدة منها. ثم اجتمع الناس مع الجذور. لذلك كان هناك أرقام غير عقلانية. بالإضافة إلى العقلاني وغير العقلاني ، نشأت فئة ثالثة. علاوة على ذلك ، كانت الفئة الثالثة في البداية ندرة رهيبة اكتشفها أويلر ، ولكن إلى جانب اكتشاف أويلر ، لم يكن هناك أشخاص آخرون مثل هذا. وقد تقرر تقسيم اللاعقلاني إلى فئتين - جبري (أي ، ينمو من الجذور) وتجاوزي (خاص ، رائع ، يتعدى ذلك ، لأن يولر هو الوحيد الذي وجدها). لكن في وقت لاحق ، أصبحت الأرقام التي لم تأت من جذور هائلة ، وحتى علماء الرياضيات قرروا أن هناك الكثير ،من الجبر. لذلك ، أصبح تجاوز (سمة) هذه الأرقام مجرد تكريم للتقليد. على الرغم من أننا إذا استذكرنا مفهوم الارتباط ، فإن كل هذه العناصر المنطقية وغير المنطقية والجبرية والمتسامية تصبح على الفور أسماء مصطنعة لتقسيم مشروط للغاية للأرقام ناتجة عن تحول بسيط في نهاية أحد المقارنات المقارنة. حسنًا ، من خلال هذا النهج ، تصبح الأرقام المتسلسلة ببساطة "البقية" ، أي أنه من علاقة القطاعات ، من أجل الحفاظ على تقليد استخراج الأعداد الصحيحة ، نختار الطبقات التي حصلت عليها عمليات تقسيم واستخراج الجذر من الأعداد الصحيحة ، نحصل على عقلانية وجبرية فقط الباقي متعال. وهذا هو ، في المجموع هناك ثلاث فئات فقط من الكسور لانهائية. لذلك ، يصبح اسم "متعالي" متوترًا إلى حد ما ،لا تجد؟ حسنًا ، حسنًا ، لأن التقاليد هي كل شيء لدينا ، حتى في مثل هذا العلم الدقيق مثل الرياضيات.

هذا كل شيء الآن. في السلسلة التالية ، دعنا نتحدث عن النجوم العقلانية.