كيفية تلوين كثير الحدود بشكل صحيح

كثيرات الحدود ليست مجرد تمارين في المسائل المجردة. فهي رائعة لاكتشاف الهياكل في أماكن غير متوقعة.

في عام 2015 ، ساعد جون هو ، وهو شاعر سابق أصبح عالم رياضيات ، في حل المشكلة التي نشأت منذ حوالي 50 عامًا. كان مرتبطًا بالأجسام الرياضية المعقدة ، و " matroids " ، والرسوم البيانية (مجموعات من النقاط والشرائح). وكان مرتبطًا أيضًا بالعديد من الحدود - التعبيرات المألوفة لنا من دروس الرياضيات ، والتي تتكون من مجموع المتغيرات التي تم رفعها بدرجات مختلفة.

في مرحلة ما من المدرسة ، من المحتمل أن تكون قد مررت بفتح الأقواس في كثير الحدود. على سبيل المثال ، قد تتذكر أن x ² + 2xy + y ² = (x + y) ² . خدعة جبرية مريحة ، لكن أين يمكن أن تكون مفيدة؟ اتضح أن كثيرات الحدود تساعد تمامًا على الكشف عن الهياكل الخفية - وقد استخدم هو هذه الحقيقة بنشاط في برهانه. هنا لغز بسيط يوضح هذا.

لنفترض أننا بحاجة إلى مقعد فريقين من اللاعبين على طاولة مربعة. لمنع الاحتيال ، يجب عليك التأكد من أن اللاعبين لا يجلسون بجانب اللاعبين الآخرين في فريقهم. كم عدد طرق الجلوس هناك؟

لنبدأ بمقاعد الفريق الأحمر والأزرق. دعنا نقول اللاعب الأحمر يجلس في الجزء العلوي من الرسم البياني:



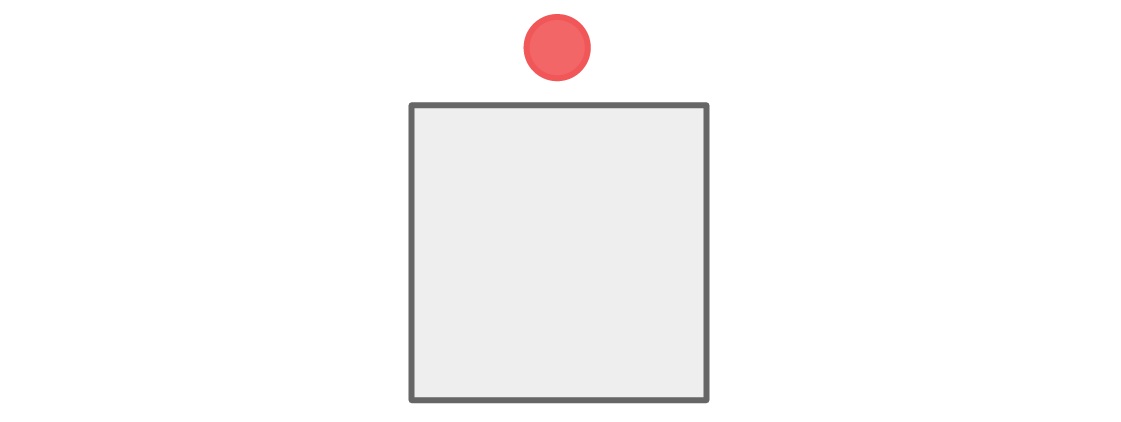
يوجد مكانان بالقرب من المكان العلوي - اليمين واليسار - ولتلبية القاعدة ، يجب أن يشغلها لاعبون أزرق هذه الأماكن.



المساحة أدناه مجاورة للاثنين الأزرق ، لذلك يجب أن يجلس اللاعب الأحمر هناك.



لم يجلس أي من اللاعبين بجانب أحد أعضاء فريقهم ، وتم استيفاء حالتنا.

يمكن أن نبدأ أيضًا باللاعب الأزرق في الأعلى. اعتبارات مماثلة تؤدي إلى الترتيب التالي:



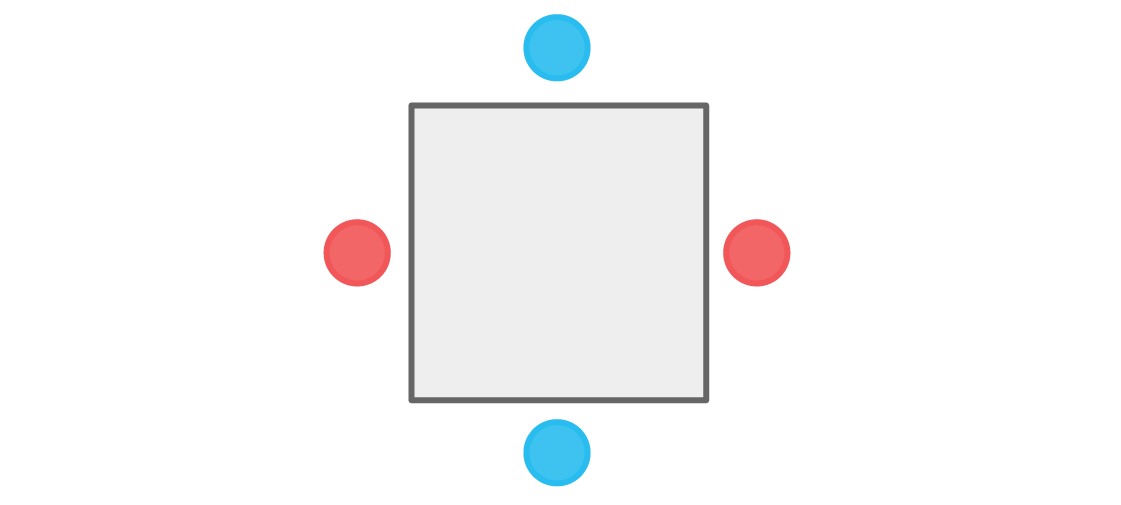
مرة أخرى ، لا يوجد لاعب يجلس بجوار أعضاء آخرين في فريقه. استوفيت حالتنا ، ومثل هذا الترتيب للجلوس مقبول. في الواقع ، هناك بالضبط نوعان من ترتيبات الجلوس هذه. بمجرد اختيار لون البقعة العليا ، يتم تعريف البقية بالكامل.

هناك طريقة لمعرفة أن هناك فقط ترتيبين محتملين للجلوس دون رسم كل هذه المخططات. لنبدأ من الأعلى: لدينا خياران ، الأحمر والأزرق. بعد هذا الاختيار ، يبقى هناك خيار واحد (لون مختلف) للمقاعد اليمنى واليسرى. وللمقعد السفلي هناك خيار واحد فقط اليسار - اللون الذي بدأنا به. باستخدام "المبدأ الأساسي للحساب" ، نعلم أن إجمالي عدد الفرص هو نتيجة ضرب عدد الفرص لكل خيار. هذا يعطينا 2 × 1 × 1 × 1 = 2 الشتلات ، كما حددنا من الرسوم البيانية لدينا.

أضف الآن الأمر الثالث باللون الثالث. تخيل أن لدينا لاعبين حمراء وزرقاء وصفراء. كم عدد ترتيبات الجلوس التي يمكن إجراؤها ، شريطة أن تكون الأماكن المجاورة بألوان مختلفة؟ للحصول على صورة لكل الاحتمالات ، سيكون عليك رسم مجموعة كاملة من الرسوم البيانية ، لذلك دعونا نحاول إجراء حسابات بدلاً من ذلك.

للحصول على المركز الأول ، لدينا الآن خيار من ثلاثة ألوان. بعد هذا الاختيار ، يمكننا اختيار أي من الألوان المتبقية للأماكن اليمنى واليسرى.

ماذا سيكون تحت الساحة؟ هناك إغراء بالإعلان أنه بالنسبة للمقعد الأخير ، سيكون هناك خيار واحد فقط ، لأنه بجوار المقعدين الأيسر والأيمن. ولكن هل تشعر بالعيوب في هذا المنطق؟



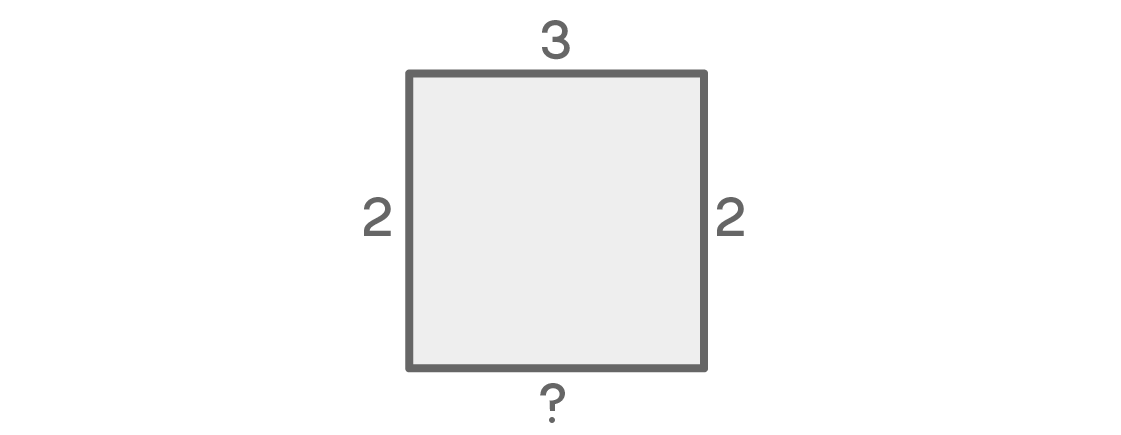
في الواقع ، إذا كانت الأماكن اليمنى واليسرى لها ألوان مختلفة ، فلن يكون هناك سوى خيار واحد للمكان السفلي. إذا كان على اليسار ، على سبيل المثال ، لونه أزرق وعلى اليمين أحمر ، فيجب أن يكون الجزء السفلي أصفر. ولكن ماذا لو كانت الألوان اليمنى واليسرى متشابهة؟ في هذه الحالة ، بالنسبة للمكان السفلي ، سيكون هناك خياران. يعتمد هذا الخيار الأخير على الخيارات السابقة ، مما يعقد حساباتنا.

علينا أن نفكر في حالتين مختلفتين: عندما تتزامن الألوان على اليسار وعلى اليمين ، وعندما تختلف.

إذا تزامنت الألوان الموجودة على اليسار وعلى اليمين ، فإن عدد الاحتمالات لكل مكان يبدو كما يلي:



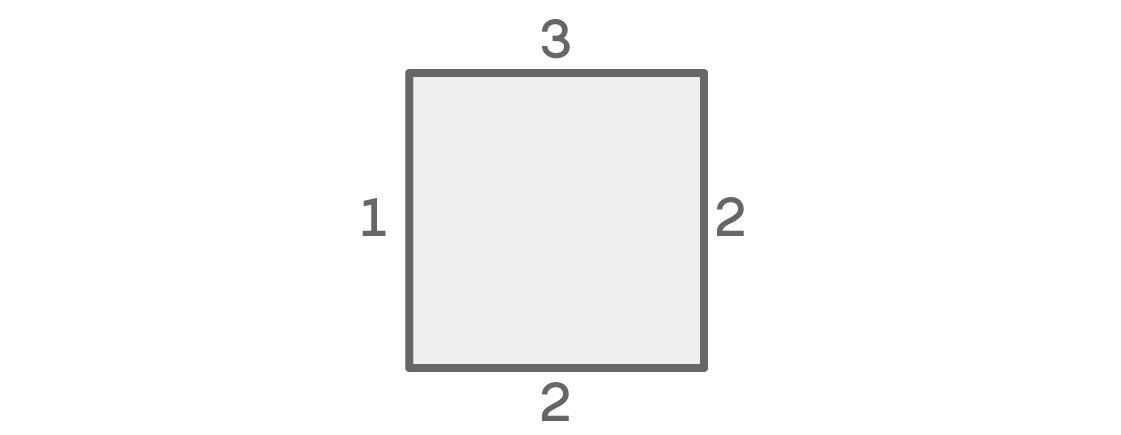
بالنسبة للمقعد العلوي ، لدينا ثلاثة خيارات. هناك اثنان اليسار لليمين. نظرًا لأننا نفترض أن الأماكن اليمنى واليسرى لها نفس اللون ، فلدينا فقط خيار واحد للمكان الأيسر: نفس لون اليمين. أخيرًا ، نظرًا لأن اللون هو نفسه على اليسار واليمين ، يمكننا اختيار أي من اللونين المتبقيين للمقعد السفلي. نتيجة لذلك ، حصلنا على 3 × 2 × 1 × 2 = 12 ترتيبات جلوس ممكنة.

الآن دعونا نلقي نظرة على هذه الاحتمالات عندما تكون الألوان على اليمين واليسار مختلفة:



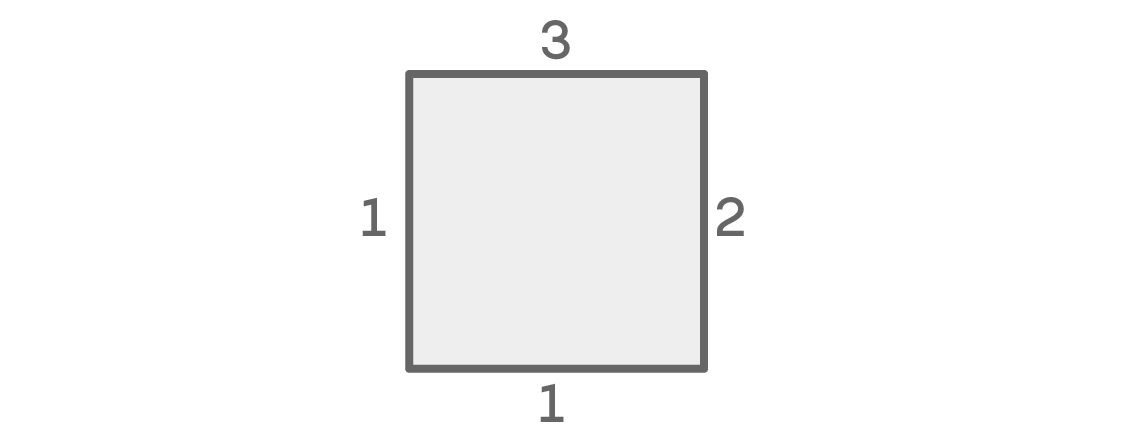
لدينا مرة أخرى ثلاثة خيارات للأعلى وخيارين للمكان المناسب. يوجد في المكان الأيسر مرة أخرى خيار واحد ، لكن لسبب مختلف: لا يمكن أن يكون هو نفسه الجزء العلوي ، المجاورة ، ولا يمكن أن يكون هو نفسه ، وفقًا لحالتنا. ونظرًا لأن الألوان الموجودة على اليمين واليسار مختلفة ، لا يوجد سوى خيار واحد متبقي للمكان السفلي (نفس الجزء العلوي). هذه الحالة تعطي 3 × 2 × 1 × 1 = 6 الترتيبات الممكنة.

نظرًا لأن هذين الخيارين يغطيان كل الاحتمالات ، فنحن نضيفهما ونحصل على 12 + 6 = 18 ترتيبات جلوس ممكنة.

إضافة لون ثالث تعقيد مهمتنا ، ولكن سيتم مكافأة عملنا الشاق. الآن يمكننا استخدام هذه الاستراتيجية لمدة 4 أو 5 أو أي عدد من الألوان المختلفة.

بغض النظر عن عدد الألوان ، سيكون لدينا دائمًا حالتان: اليسار واليمين سيكونان إما متماثلين أو مختلفين. لنفترض أن لدينا خيار من الألوان ف. فيما يلي مخطط يوضح عدد الخيارات لكل جانب ، في الحالة التي تكون فيها الألوان اليمنى واليسرى متماثلة:



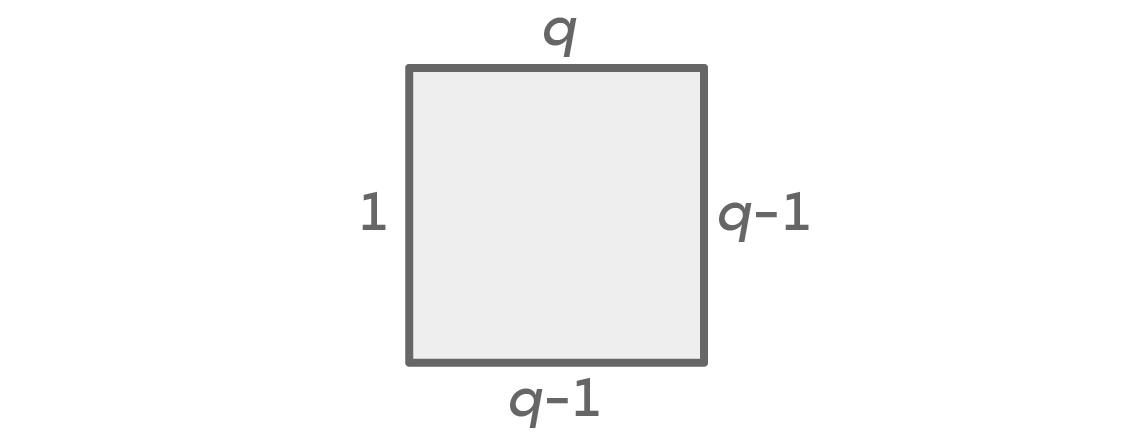
أولاً لدينا ألوان q للمقعد العلوي ، و q-1 لليمين. نظرًا لأننا افترضنا أن الألوان الموجودة على اليسار واليمين متشابهة ، فلدينا خيار واحد فقط للون الأيسر. هذا يترك خيارات q-1 للبقعة السفلية ، لأنه يمكن أن يكون أي لون آخر غير اللون الذي اخترناه للبقع اليمنى واليسرى. يعطينا المبدأ الأساسي للحساب q × (q - 1) × 1 × (q - 1) = q (q - 1) ² التخطيطات الممكنة.

إذا تم تلوين المكانين الأيمن والأيسر بشكل مختلف ، فيمكننا حساب الاحتمالات مثل هذا:



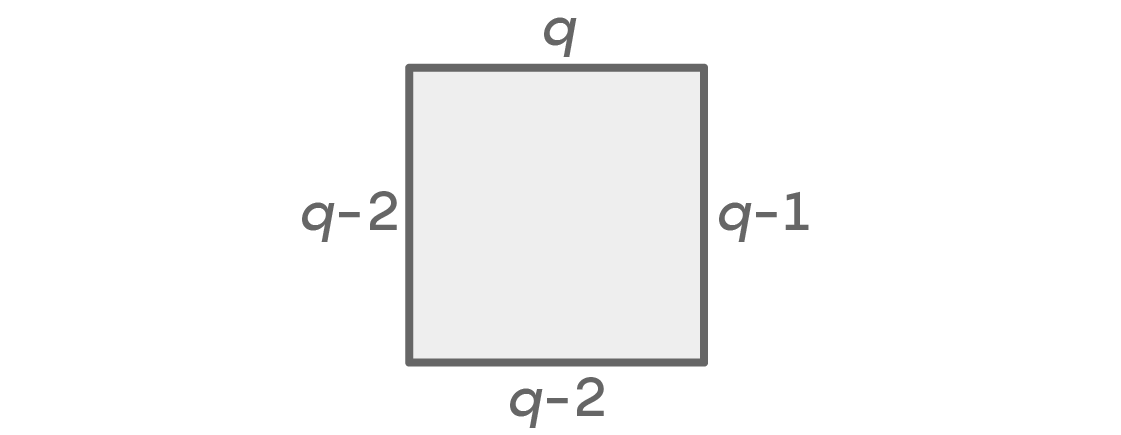
مرة أخرى ، لدينا خيارات q للأعلى و q-1 للأماكن المناسبة. لا يمكن أن يكون هناك نفس اللون على اليسار المحدد للأماكن العلوية واليمنى ، لذلك توجد خيارات q-2. يمكن أن يكون هناك أي لون أدناه ، باستثناء اللونين اللذين استخدمناهما في اليسار واليمين ، والذي يعطي خيارات q-2 مرة أخرى. نحصل على مجموع q × (q - 1) × (q - 2) × (q - 2) = q (q - 1) (q - 2) ² ترتيبات جلوس ممكنة. نظرًا لأن هاتين الحالتين تغطي جميع الخيارات ، فإننا كما سبق ، نضيفها ونحصل على العدد الإجمالي للترتيبات الممكنة: q (q - 1) ² + q (q - 1) (q - 2) ² .

قد يبدو مثل هذا التعبير إجابة غريبة على السؤال: "كم عدد ترتيبات الجلوس المختلفة لفرق مختلفة على المائدة المربعة ، بحيث لا يجلس عضوان من نفس الفريق جنبًا إلى جنب؟" ومع ذلك ، يحتوي هذا كثير الحدود على الكثير من المعلومات حول مشكلتنا. إنه لا يعطينا إجابة كمية فحسب ، بل يكشف أيضًا عن هيكل مهمتنا.

يُطلق على كثير الحدود اسم " متعدد الحدود لوني " لأنه يجيب على السؤال: ما عدد الطرق الموجودة لتلوين رؤوس الشبكة (أو الرسم البياني) بحيث يكون لأي زوج من الرؤوس المجاورة ألوان مختلفة؟

في البداية ، كانت مشكلتنا تتعلق بالجلوس حول الطاولة ، لكن يمكننا بسهولة تحويلها إلى سؤال حول تلوين رؤوس الرسم البياني. بدلاً من الأشخاص على الطاولة:



سوف نتخيلها في شكل قمم متصلة بحواف في الحالة عندما يجلسون بجانب:



الآن ، يمكن تمثيل أي تلوين لرؤوس الرسم البياني على أنه جلوس للأشخاص حول الساحة ، حيث يعني "الجلوس بجانب" على الطاولة "وجود حافة مشتركة" على الرسم البياني.

الآن ، بعد إعادة صياغة مشكلتنا في شكل رسم بياني ، نعود إلى كثير الحدود لوني. نحن نسميها ف (ف).

P (q) = q (q - 1) ² + q (q - 1) (q - 2) ²

من الخصائص المميزة لهذا كثير الحدود أنها تجيب على سؤال التلوين لأي عدد ممكن من الألوان. على سبيل المثال ، للإجابة على سؤال بثلاثة ألوان ، نضع q = 3 ، ونحصل على:

P (3) = 3 (3 - 1) ² + 3 (3 - 1) (3 - 2) ² = 3 × 2 ² + 3 × 2 × 1 ² = 12 + 6 = 18

هذا هو الجواب الذي تلقيناه في حالة ثلاثة فرق. وإذا وضعنا q = 2:

P (2) = 2 (2 - 1) ² + 2 (2 - 1) (2 - 2) ² = 2 × 1 ² + 2 × 1 × 0 ² = 2 + 0 = 2

يبدو مألوفا؟ هذا هو الجواب على اللغز الأول لدينا ، مع فريقين. يمكننا العثور على إجابات لأربعة أو خمسة أو حتى 10 فرق مختلفة ، ببساطة استبدال القيمة المطلوبة لـ q: P (4) = 84 و P (5) = 260 و P (10) = 6 570. اكتشف كثير الحدود اللوني بنية أساسية للمشكلة من خلال تلخيص استراتيجية العد لدينا.

يمكننا الكشف عن مزيد من التفاصيل عن الهيكل من خلال إجراء عمليات جبرية على متعدد الحدود P (q) = q (q - 1) ² + q (q - 1) (q - 2) ² :

= q (q - 1) (q - 1) + q (q - 1) (q - 2) ²
= q (q - 1) ((q - 1) + (q - 2) ² )
= q (q - 1) (q - 1 + q ² −4q + 4)
= q (q - 1) (q ² −3q + 3)

استخلصنا العامل q (q - 1) من كل جزء من المجموع ونجمع المصطلحات المتشابهة ، مما قلل كثير الحدود إلى شكل عامل. وفي هذا النموذج ، يمكن أن يخبرنا كثير الحدود عن الهيكل بمساعدة "جذوره".

جذور كثير الحدود هي قيم المدخلات التي يصبح عندها يساوي الصفر في الإخراج. من الأسهل العثور على الجذور في الشكل المعامل: بما أن الشكل متعدد الحدود يتم التعبير عنه كأجزاء مضروبة ، فإن أي قيمة يساوي فيها أحد العوامل صفر تعيد ضبط المنتج بالكامل.

على سبيل المثال ، لدينا متعدد الحدود P (q) = q (q - 1) (q ² - 3q + 3) لديه عامل (q - 1). إذا أخذنا q = 1 ، يصبح هذا العامل يساوي الصفر ، مثل النتيجة الكاملة للضرب. وهذا هو ، P (1) = 1 (1 - 1) (1 ² - 3 × 1 + 3) = 1 × 0 × 1 = 0. وبالمثل ، P (0) = 0 × (–1) × 3 = 0 لذلك ، q = 1 و q = 0 هي جذور متعدد الحدود. (قد تكون مهتمًا بالعامل (q ² - 3q + 3). نظرًا لأنه لا يساوي الصفر لأي q حقيقي ، فإنه لا يعطي جذور جديدة لعدد الحدود لوني لدينا.

هذه الجذور منطقية في إطار الرسم البياني لدينا. إذا كان لدينا خيار من نفس اللون ، فيجب أن يكون كل رأس من نفس اللون. لا يمكن تلوين الرسم البياني بحيث يكون لكل الرؤوس المجاورة ألوان مختلفة. هذا هو بالضبط ما يعني أن q = 1 هي جذر متعدد الحدود لوني. إذا كانت P (1) = 0 ، فهناك صفر طرق بالضبط لتلوين الرسم البياني بحيث تكون الرؤوس المجاورة ليست بنفس الألوان. وينطبق الشيء نفسه على الإصدار الذي يحتوي على عدد صفري من الألوان ، P (0) = 0. تخبرنا جذور متعدد الحدود اللونية لدينا عن بنية الرسم البياني لدينا.

تصبح القدرة على رؤية البنية من خلال الجبر أكثر وضوحًا إذا أخذنا في الاعتبار الرسوم البيانية الأخرى. دعونا نلقي نظرة على الرسم البياني الثلاثي:



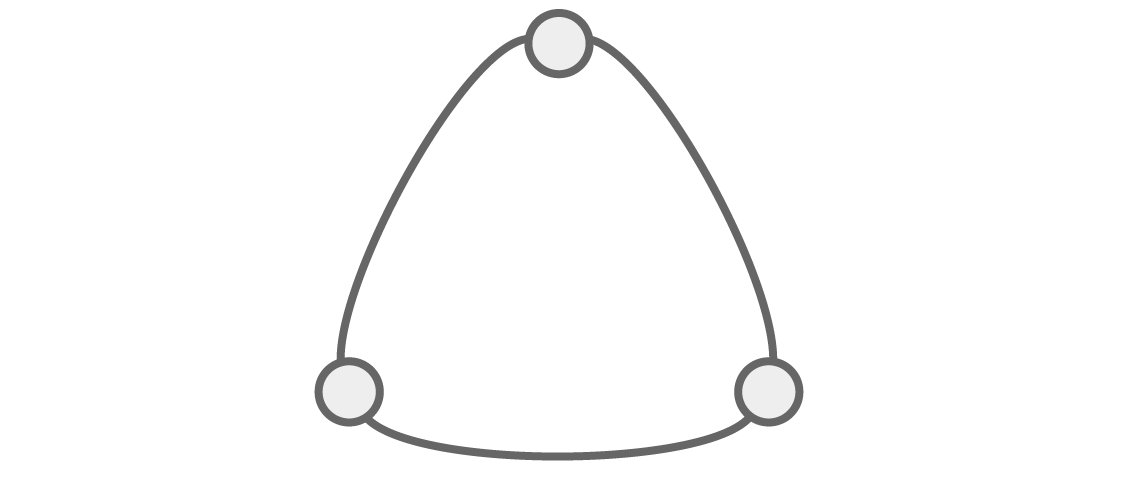
كم عدد الطرق لتلوين هذا الرسم البياني q بالألوان بحيث تكون الرؤوس المجاورة ليست بنفس الألوان؟

كالمعتاد ، توجد خيارات q و q-1 لأول قاريتين متجاورتين. ونظرًا لأن القمة الأخيرة متجاورة مع الأولين ، يجب أن تختلف في اللون عن كلاهما ، مما يترك لنا خيارات q-2. هذا يعطينا متعدد الحدود لوني لهذا الرسم البياني الثلاثي: P (q) = q (q - 1) (q - 2).

في هذا الشكل من العوامل ، يخبرنا كثير الحدود اللوني بشيء مثير للاهتمام: له جذر q = 2. وإذا كانت P (2) = 0 ، فيجب أن يكون من المستحيل تلوين هذا الرسم البياني بلونين بحيث لا يكون له رأسان متجاوران من نفس اللون. هل هذا صحيح؟

تخيل أننا نسير في دائرة في هذا المثلث ، ولون القمم على طول الطريق. إذا كان لدينا لونان فقط ، فسوف نحتاج إلى تبديلهما بعد كل قمة: إذا كان الأول أحمر ، فسيكون الثاني أزرق ، مما يعني أن اللون الثالث يجب أن يكون أحمر مرة أخرى. لكن القمم الأولى والثالثة متجاورتان ، ولا يمكن أن تكون باللونين الأحمر. لونان لا يكفيان ، كما توقع كثير الحدود.

باستخدام حجة متناوبة مماثلة ، يمكننا التوصل إلى تعميم مهم: يجب أن يكون لعدد الحدود اللونية لأي حلقة مغلقة برقم فردي من الرؤوس جذرًا يساوي 2. وبما أنك إذا قمت بالتبديل بين لونين وانتقلت على طول حلقة ذات طول فردي ، فستكون الرؤوس الملونة والأخيرة بنفس اللون . لكن بما أن هذه حلقة ، فستكون متاخمة. التلوين غير ممكن.

على سبيل المثال ، يمكننا استخدام تقنيات متنوعة لتحديد أنه في حلقة ذات خمسة رؤوس ، يكون كثير الحدود لوني كما يلي: P (q) = q ⁵ - 5q ⁴ + 10q ³ - 10q ² + 4q. مع أخذ هذا في الاعتبار ، نحصل على P (q) = q (q - 1) (q - 2) (q2 - 2q + 2). كما هو متوقع ، اتضح أن q = 2 هي الجذر ، و P (2) = 0. ومن المثير للاهتمام ، بمجرد أن نجد هذا الارتباط بين الرسوم البيانية ومتعدد الحدود ، تبدأ الأفكار في العمل في كلا الاتجاهين. يمكن أن تخبرنا كثيرات الحدود بمعلومات عن بنية الرسوم البيانية ، ويمكن أن تخبرنا الرسوم البيانية عن هيكل كثير الحدود.

كان البحث عن الهيكل هو ما دفع جون هو إلى إثبات فرضية ريد التي استمرت 40 عامًا فيما يتعلق بالعدد متعدد الحدود لوني. تنص الفرضية على أننا إذا عدّدنا معاملات كثير الحدود لوني ، متجاهلين علاماتهم ، فسيتم استيفاء الشرط التالي: يجب أن يكون مربع أي معامل ناتجًا على الأقل عن اثنين مجاورين. على سبيل المثال ، في كثير الحدود لوني لدينا حلقة الرؤوس الخمسة ، P (q) = q ⁵ - 5q ⁴ + 10q ³ - 10q ² + 4q ، نرى أن 5 ² ≥ 1 × 10 ، 10 ² ≥ 5 × 10 و 10 ² ≥ 10 × 4. من هذا ، على سبيل المثال ، يتبع أنه لا يمكن أن يكون كل متعدد الحدود لوني: كثير الحدود لوني المرتبطة بالرسوم البيانية لها بنية أعمق. علاوة على ذلك ، سمحت العلاقة بين هذه الحدود المتعددة والمجالات الأخرى لهو ومؤلفيه المشاركين بالإجابة على سؤال أوسع بكثير متعلق بفرضية روث ، بعد عدة سنوات من إثبات فرضية ريد.

ربما تشتهر كثيرات الحدود بأسوأ أشكالها - باعتبارها تمارين مجردة في التلاعب الرسمي بأشكال التعبير الجبري. لكن كثيرات الحدود وخصائصها - الجذور والمعاملات والأشكال المختلفة - تساعد على الكشف عن الهياكل في أماكن غير متوقعة ، وخلق روابط مع الجبر في كل ما يحيط بنا.

تمارين

1. الرسم البياني الكامل هو رسم بياني ، يتم توصيل كل زوج من القمم بحافة. أوجد متعدد الحدود لوني للرسم البياني الكامل المكون من خمسة رؤوس.


2. ابحث عن كثير الحدود لوني للرسم البياني التالي (استخدم معلومات حول كثير الحدود لوني من الرسوم البيانية الأبسط).




3. يسمى الرسم البياني على الوجهين إذا كانت رؤوسه يمكن تقسيمها إلى مجموعتين ، A و B ، بحيث تكون الرؤوس من A متجاورة فقط مع الرؤوس B ، وتكون الرؤوس B متجاورة فقط مع الرؤوس من A. افترض أن الرسم البياني G يحتوي على كثير لوني P (ف). ما الخاصية P (q) التي تسمح لك باستنتاج أن الرسم البياني G ذو اتجاهين؟