هناك العديد من المقالات على الإنترنت مع وصف لخوارزمية النسب التدرج. سيكون هناك واحد آخر.
في 8 يوليو 1958 ، كتبت صحيفة نيويورك تايمز : "يُظهر عالم نفسي جنينًا لجهاز كمبيوتر مصمم للقراءة وتصبح أكثر حكمة. تم تطويره بواسطة Navy ... تعلم الكمبيوتر 704 دولارات ، والذي تكلف مليوني دولار ، التمييز بين اليسار واليمين بعد خمسين محاولة ... ووفقًا للبحرية ، فإنهم يستخدمون هذا المبدأ لبناء أول آلة تفكير من فئة Perceptron ، والتي يمكنها القراءة والكتابة ؛ من المخطط الانتهاء من عملية التطوير في غضون عام ، بتكلفة إجمالية قدرها 100000 دولار ... يتوقع العلماء أنه في وقت لاحق سيتمكن Perceptrons من التعرف على الأشخاص والاتصال بهم بالاسم وترجمة الكلام الشفوي والكتابي على الفور من لغة إلى أخرى. قال السيد روزنبلات إنه من الممكن من حيث المبدأ بناء "أدمغة" يمكنها إعادة إنتاج نفسها على خط التجميع وستكون مدركة لوجودها "(مقتبسة ومترجمة من كتاب S. Nikolenko ،" التعلم العميق ، الانغماس في عالم الشبكات العصبية ").
آه ، هؤلاء الصحفيون يعرفون كيفية الدسيسة. من المثير للاهتمام للغاية معرفة ما هي آلة التفكير في فئة Perceptron حقًا.
ثنائي (ثنائي) تصنيف الكائنات ، الخلايا العصبية الاصطناعية من فئة Perceptron
ها هي الخلايا العصبية الاصطناعية لدينا ، وهي تقسم الكائنات إلى فئتين (تقوم بتصنيف ثنائي للأشياء):

لذلك لدينا:
- المدخلات: كائن أخذ العينات - متجه الفضاء الأبعاد س = ( س 1 ، . . . ، س م )
- معاملات الترجيح ث = ( ث 1 ، . . . ، ث م ) واحد لكل سمة من سمات كائن العينة (أيضًا ناقل m)
- في الداخل: الأفعى S U M = w 1 × 1 + . . . + w m x m = s u m m j = 1 w j x j - مجموع مرجح لمدخلات الخلايا العصبية
- التالي: التنشيط Φ(x،w)=Φ(SUM)
- لا يزال أبعد من ذلك: الكمي (العتبة) - θ [ثيتا]
- التنشيط + العتبة - التنبؤ بالتسمية الصفية لكائن بناءً على المبلغ المرجح لمدخلات الخلايا العصبية (سمات الكائن). يحدد هذا الجزء البنية المحددة للخلايا العصبية.
- الإخراج: تسمية فئة الكائن (واحد من اثنين) \ hat {y} = \ {1، -1 \}
التصنيف - لأن الخلايا العصبية تقوم بتعيين الفصل لكائن ، ثنائي ( ثنائي ) - لأنه يوجد فقط فئتان محتملتان.
haty [لعبة ذات غطاء] - سنشير إلى قيمة الفئة المتوقعة (المحسوبة) للكائن x
ذ [لعبة عادية بدون غطاء] - قيم فئة (معروفة) حقيقية لكائن x من مجموعة التدريب.
معنى x (هنا وأدناه x و w - هذه ليست قيم وحدة ، ولكن المتجهات) تختلف من كائن إلى كائن ، معاملات الوزن w (بمجرد تحديده) تظل كما هي. لمجموعة التدريب لكل كائن x تسمية فئة معروفة ذ . في مرحلة التدريب ، تحتاج إلى اختيار الأوزان w بحيث ينتج النموذج القيمة الصحيحة haty (يتزامن مع ذ ) للحصول على أكبر عدد ممكن من الكائنات في مجموعة التدريب. يعتمد افتراض فائدة الخلايا العصبية المدربة بهذه الطريقة على الأمل في أنها ستنتج القيمة الصحيحة مع المعاملات المحددة. haty لكائنات جديدة x قيمة الطبقة الحقيقية ذ التي لا يعرفها مسبقا.
المعنى الحدسي للمجموع المرجح لمدخلات الخلايا العصبية هو أن جميع سمات الكائن (كل من العلامات هي واحدة من مدخلات الخلايا العصبية) تؤثر على نتيجة تصنيف الكائن ، ولكن لا تتأثر جميع العلامات بالتساوي. إلى أي مدى - تحديد الوزن ؛ يؤدي التقليل من معامل معامل الترجيح إلى إلغاء مساهمة السمة المقابلة في المبلغ الإجمالي ، أي هذا بمثابة إزالة الميزة من الكائن.
الخطي التكيفي Neuron ADALINE
الخلايا العصبية ADALINE (الخلايا العصبية الخطية التكيفية) هي عصبون اصطناعي عادي مع وظيفة التنشيط هذه:
Φ(x،w)=Φ(SUM)=SUM
Phi(x(i)،w)= Phi( summj=1wjx(i)j)= summj=1wjx(i)j
فيما يلي مرتفع i بين قوسين سوف تدل i عنصر من مجموعة التدريب x(i) أو قيمة الطبقة الحقيقية y(i) أو قيمة الطبقة المتوقعة haty(i) بالنسبة له.
يمكننا القول أن مثل هذه الخلايا العصبية لا تحتوي ببساطة على وظيفة تنشيط ويتم تغذية قيمة المبلغ المرجح للمدخلات إلى مدخلات الكمي (العتبة). ولكن من أجل التناسق ، سيكون من المناسب أن نفترض أن قيمة المبلغ المرجح يتم اعتبارها تنشيط.
العتبة (الكمي) - تتوقع تسمية الفصل:
\ hat {y} ^ {(i)} = \ left \ {\ تبدأ {matrix} 1 ، \ Phi (x ^ {(i)} ، w) \ ge \ theta \\ - 1 ، \ Phi (x ^ {(i)} ، w) <\ theta \ end {matrix} \ right.
إذا كانت قيمة التنشيط أكبر من بعض قيمة العتبة θ [theta] ، فإن الكمي يحدد العلامة "1" للكائن ؛ وإذا كانت قيمة التنشيط أقل من العتبة θ ، فإن الكائن يستقبل التسمية "-1".
هنا يمكننا صياغة المشكلة في التقريب الأول : نحن بحاجة إلى تحديد معالم الخلايا العصبية
- عوامل الترجيح wj،j=1،..،m
- والعتبة the [ثيتا]
بحيث قيم الطبقة قبعةذ ، التي يعينها الخلايا العصبية إلى كائنات عينة التدريب ، تزامنت مع القيم الحقيقية للفصول ذ لنفس العناصر (أو ، على الأقل ، أعطت المعنى الصحيح للأغلبية).
نحن تحويل وظيفة العتبة قليلا ، ونأخذ القضية للفئة haty=1 ونقل العتبة إلى الجانب الأيسر من عدم المساواة:
تبدأالمجمعة Phi(x(i)،w) ge theta hfill summj=1wjx(i)j ge theta hfill− theta+ summj=1wjx(i)j ge0 hfill endتجمع
يرمز w0=− theta و x0=1دولا
تبدأالمجمعةw0x(i)0+ summj=1wjx(i)j ge0،w0=− theta،x0=1 hfill summj=0wjx(i)j ge0،x0=1 hfill endgathered
كما نرى ، تمكنا من التخلص من معامل منفصل θ ، وتقديمه تحت ستار معامل وزن جديد w0دولا تحت علامة المجموع ، بينما تضيف إلى وصف الكائن علامة وحدة وهمية جديدة x0=1دولا .
سنقوم بتصحيح صياغة المشكلة مع مراعاة الترميز الجديد.
المهمة ' : حدد معلمات عوامل ترجيح الخلايا العصبية wj،j=0،..،m .
x0=1دولا (علامة ثابتة) - الخلايا العصبية الوهمية ( الخلية العصبية للإزاحة )
بدءًا من هذا المكان ، نقوم بترقيم العلامات والأوزان c 0 ، وليس 1. حول المتجه w سوف نقول أنها تدور حول (m + 1) ، وليس الأبعاد. سهم التوجيه x وفقًا للسياق ، يمكننا مراعاة الأبعاد (m + 1) (في معظمها في الصيغ) ، ولكن تذكر أنه في الواقع م الأبعاد.
لماذا الخلايا العصبية ( في حالتنا ، مع ذلك ، ليست خلية عصبية ، ولكنها علامة على كائن أو مجرد إدخال ، ولكن في حالة وجود شبكة متعددة الطبقات تتحول إلى خلية عصبية وتسمى عادة بهذه الطريقة ) ، فهي وهمية - إنها واضحة الآن. لماذا هو أيضا النزوح سوف تصبح واضحة في وقت لاحق.
سيبدو التنشيط بالمبلغ الآن كما يلي:
Phi(x(i)،w)= Phi( summj=0wjx(i)j)= summj=0wjx(i)j،x(i)0=1 foralli
العتبة هي الآن 0 (صفر) دائمًا (يتم نقل القيمة الحقيقية إلى المعلمة w0دولا ):
\ hat {y} ^ {(i)} = \ left \ {\ تبدأ {matrix} 1 ، \ Phi (x ^ {(i)} ، w) \ ge 0 \\ - 1 ، \ Phi (x ^ {(i)} ، w) <0 \ end {matrix} \ right.
مرة أخرى نقوم بصياغة المشكلة بمعنى آخر (المعنى الهندسي للمشكلة)
إذا نظرنا بعناية إلى الصيغة الخاصة بوظيفة التنشيط ، فسوف نرى أنها طائرة تشعبية بارامترية في فضاء الأبعاد (m + 1) ، بينما تتعايش في أبعاد m الأولى مع نقاط عناصر العينة ، و (m + 1) - البعد الإلكتروني هو مساحة قيم الوظيفة ، منفصلة عن العناصر.
الآن ، إذا قمنا بربط قيمة التنشيط بالصفر (قيمة العتبة) ، فستكون هذه أيضًا طائرة تشعبية ، فقط بالفعل في الفضاء ذي البعد m ، أي تماما في مساحة قيمة العنصر x . هذا hyperplane سوف تفصل العناصر. x إلى مجموعتين منفصلتين.
عادة ما يقولون في هذا المكان أن مهمتنا هي تحديد قيم المعلمات w ، أي قم بإنشاء طائرة تشعبية متعددة الأبعاد في مساحة العناصر بحيث تكون عناصر التدريب التي تم تعيينها بالقيمة الحقيقية للفئة "1" على جانب واحد من الطائرة ، وعناصر مع الفئة الحقيقية "-1" على الجانب الآخر.
بالنسبة لأولئك الذين لا يفهمون تمامًا ما هو مكتوب هنا ، تابع القراءة - الآن سنرى جميعًا ، هذا أولاً. ثانياً ، سنرى أيضًا أن مثل هذا البيان للمشكلة ، رغم أنه صالح ، لم يكتمل تمامًا.
مساحة أحادية البعد (م = 1)
هذا هو المكان الذي يبدأ الرمز في الظهور. نقوم ببناء جميع الرسوم البيانية باستخدام مكتبة Matplotlib المعتادة ، لكنني هنا أيضًا استخدم مكتبة Seaborn في سطر واحد لضبط مساحة الرسم البياني ، لأن أنا أحب كيف تفعل ذلك ، ولكن من حيث المبدأ يمكنك الاستغناء عنها.
نأخذ الكثير من النقاط ذات الأبعاد والأجوبة عليها:
import numpy as np import math
لدينا هنا كل عنصر من عناصر الصفيف X1 - هذا هو العنصر رقم i (النقطة رقم 1) من نموذج التدريب (بشكل أكثر دقة ، السمة الأولى والوحيدة): x(i)=(X1[i]) . x(i)1=X1[i]
كل عنصر من عناصر الصفيف y هو الإجابة الصحيحة ، وهي تسمية حقيقية تتوافق مع العنصر رقم i من نموذج التدريب مع سمة واحدة X1 [i].
نحن نأخذ 5 نقاط فقط ، يتم تعيين الأولين في الفصل "-1" ، ويتم تعيين الثلاثة المتبقية في الفئة "1".
ارسم هذه النقاط على الخط:
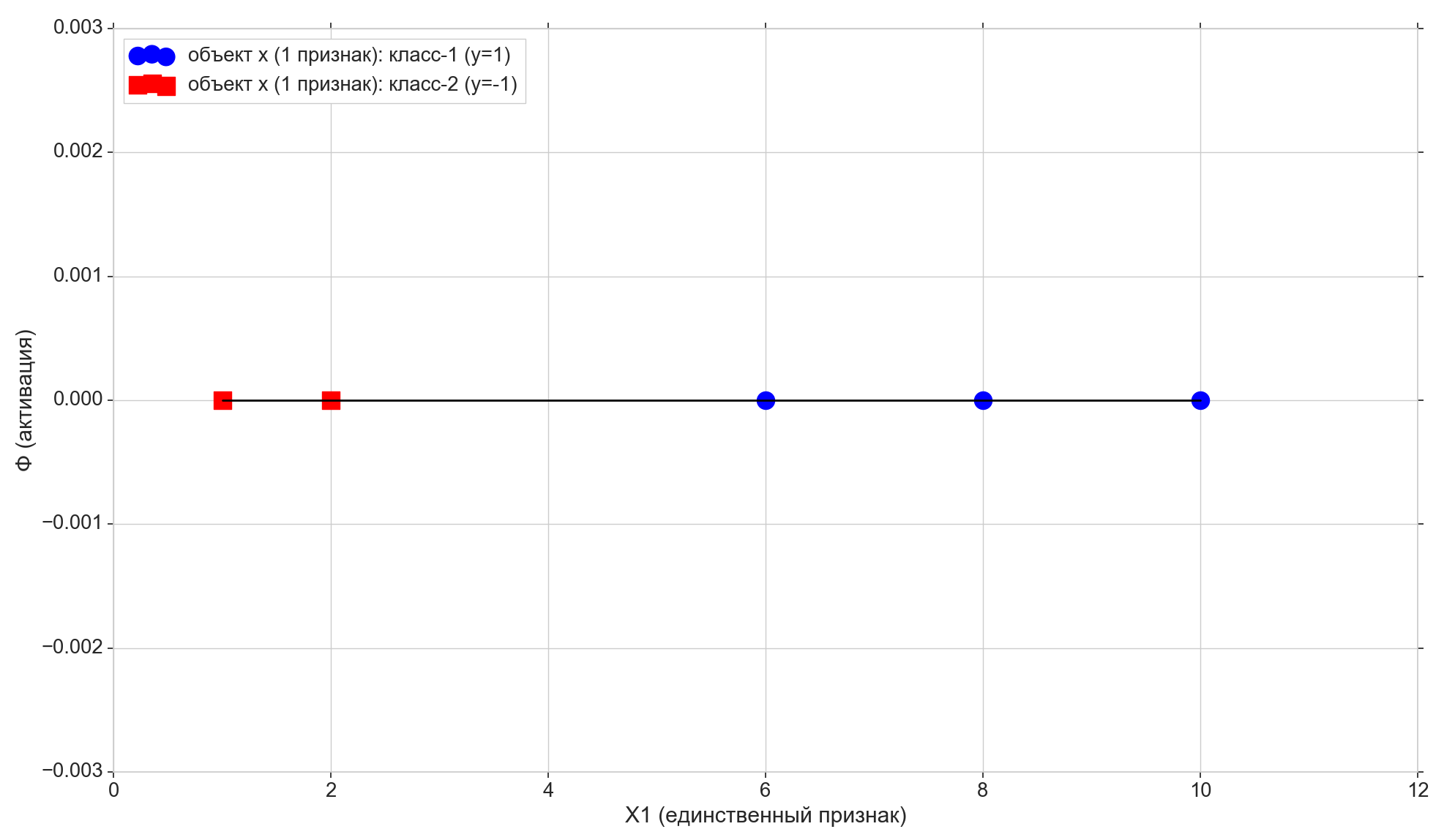
الآن دعونا نلقي نظرة على وظيفة التنشيط:
Phi=w0+w1x1
كما ترون ، هذا خط حدودي عادي على المستوى (في بعدين ، أي (م + 1) - الأبعاد):
- على المحور الأفقي لدينا نقاط العناصر (وهي أيضا قيم السمة X1)
- على قيم التنشيط العمودية لكل عنصر
- معلمة w1 - يحدد زاوية الميل ،
- و w0دولا - تحول على طول المحور العمودي (وهنا الجواب على الخلايا العصبية القص ).
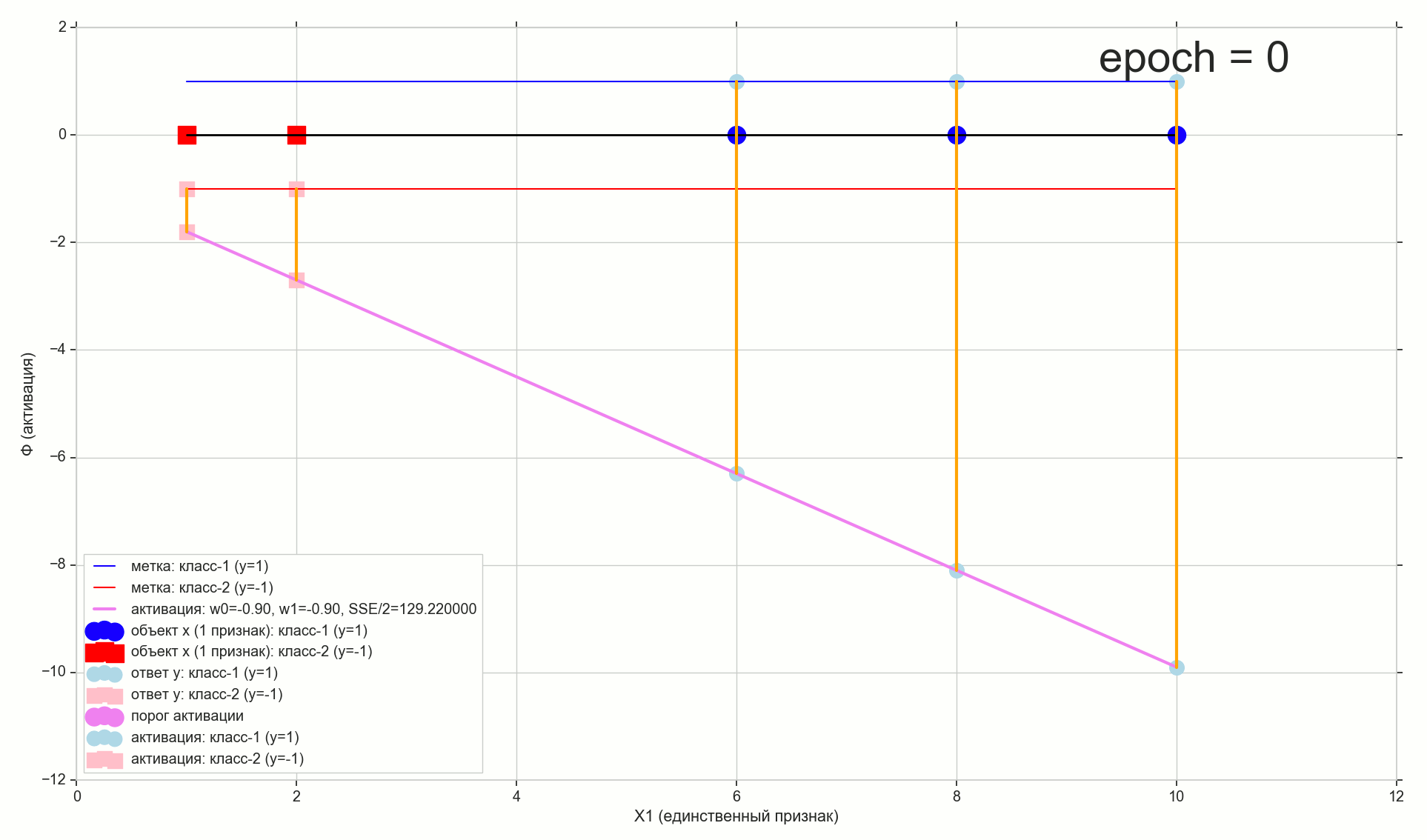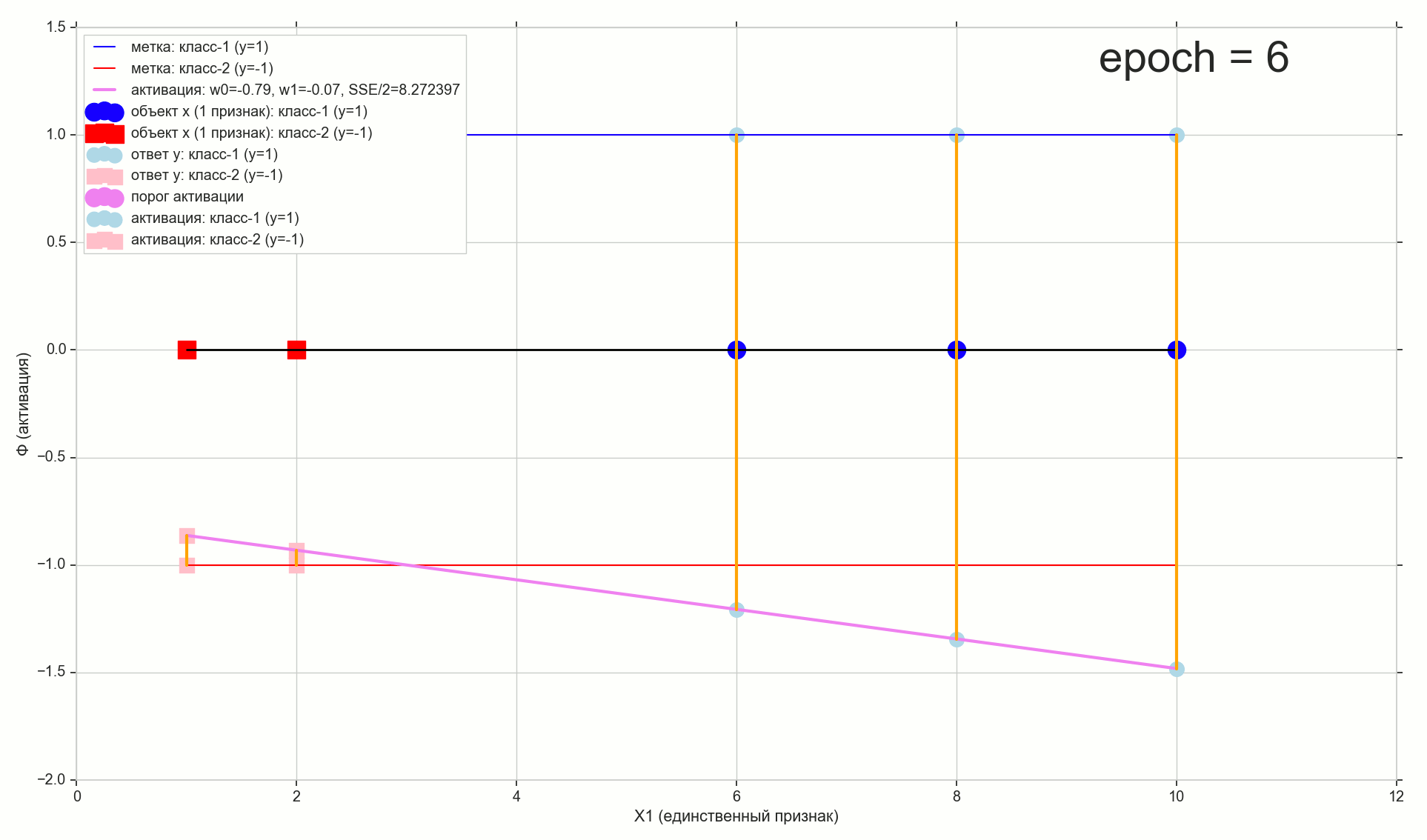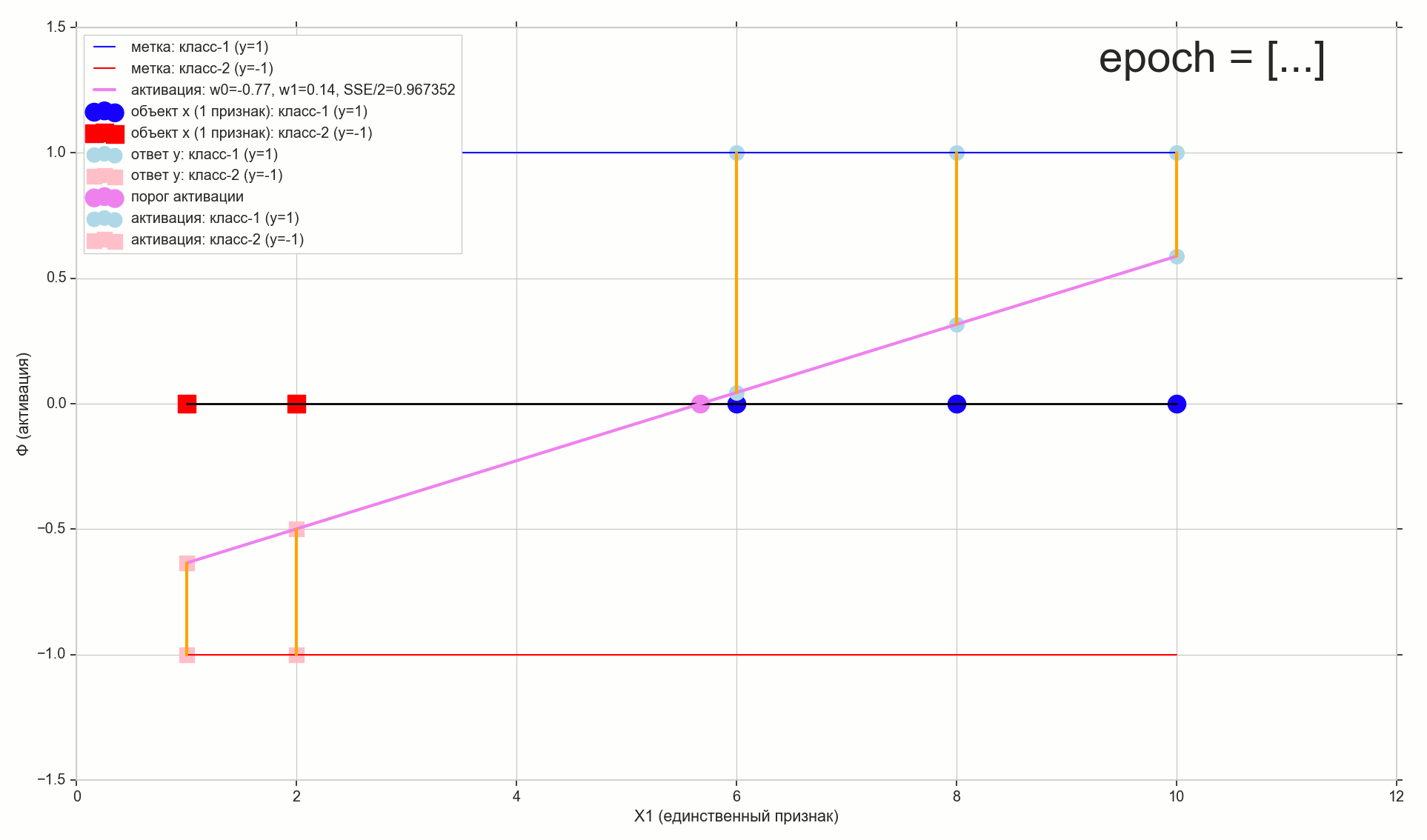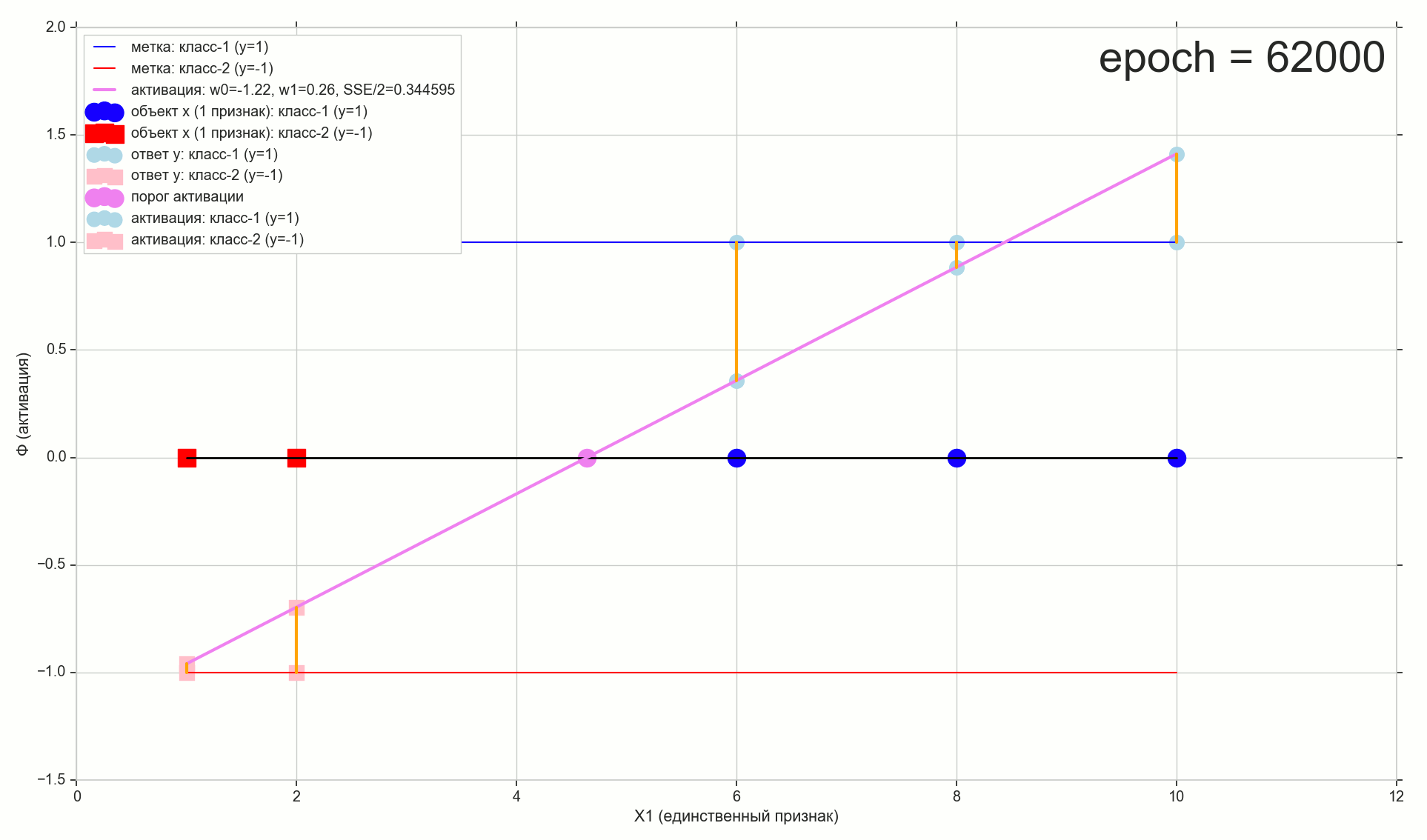
w0 = -1.1 w1 = 0.4

تذكر أيضًا أنه بعد تحويل صغير ، تحولت عتبة التنشيط إلى الصفر. وبالتالي ، إذا كان إسقاط عنصر ith على خط التنشيط أقل من الصفر ، فنحن نخصص الفئة -1 للعنصر ( haty=−1 ) ، إذا كانت أعلى من الصفر ، فسنخصص الفصل "1" ( haty=1 ).
نقطة أرجوانية - تقاطع خط التنشيط مع المحور Phi=0 ، بفصل العناصر عن الفئات المختلفة ، هذا هو المستوى الفائق للغاية (للمساحة أحادية البعد ، والنقطة هي الطائرة المفرطة) التي تم إنشاؤها في مساحة الميزة أحادية البعد (أي m-dimensional). كما ترون ، من أجل تقسيم العناصر إلى مجموعات ، فهذا يكفي ، ولكن لتخصيص فئات للمجموعات ، لم يعد كافياً. من أجل تخصيص فئات للعناصر ، نحتاج إلى تنشيط مباشر (ثنائي الأبعاد للطائرة الفائقة) مدمج في 2-d (أي ، في (m + 1) -d) الفضاء "علامات + التنشيط": اتجاه الانحراف التنشيط عن الاتجاه الرأسي سيحدد المحور الفئة لمجموعات العناصر ، لأن يعتمد ذلك على ما إذا كانت توقعات العناصر الموجودة على التنشيط أعلى أو أقل من الصفر.
تغيير المعلمات w0دولا و w1 سوف نتلقى خطوط تفعيل مختلفة. نحن بحاجة إلى بناء مثل هذا الخط التنشيط ، أي العثور على مثل هذا الجمع بين المعلمات w حيث يكون إسقاط النقطتين الأوليين من نموذج التدريب على خط التنشيط أقل من الصفر (بالنسبة لهما ، القيمة haty=y=−1 ) ، وإسقاط النقاط 3 المتبقية ستكون فوق الصفر (بالنسبة لهم haty=y=1 ).
من الواضح تمامًا أنه في حالتنا الخاصة ، لا يوجد شيء معقد في إنشاء مثل هذا الخط ، علاوة على ذلك ، يمكن بناء هذه الخطوط عمومًا بعدد غير محدود. لكننا سنحاول أن نبنيها بطريقة ترضي بعض معايير التحسين (يمكن أن تؤثر على جودة التنبؤات المستقبلية) ، بالإضافة إلى أنه ينبغي أن تكون هناك القدرة على مد الخوارزمية لتشمل الحالة متعددة الأبعاد.
نلاحظ هنا أيضًا أننا حددنا على وجه التحديد المجموعة الأولية من النقاط بحيث يمكن تقسيمها على هذا الخط (بالنسبة لـ 1-e: جميع عناصر المجموعة الأولى أصغر ، وجميع عناصر المجموعة الثانية أكبر من بعض القيمة الثابتة) ، أي العديد من نقاط التدريب قابلة للفصل خطياً .
أضف سطرين أفقيين آخرين إلى الرسم البياني المقابل للفئات {1 ، -1} ، واعرض العناصر عليهما.

نقاط مع فئة "-1" المشروع إلى بيت القصيد Phi=−1 ، يشير مع مشروع الفئة "1" إلى السطر العلوي Phi=1 .
دعنا ننتبه إلى فارق بسيط آخر. نرسم قيم التنشيط على طول المحور الرأسي ، ومساحة قيم التنشيط مستمرة. لكن نتيجة المصنف (وظيفة التنشيط التي مرت عبر العتبة) هي مجموعة منفصلة من عنصرين {-1 ، 1} ، وليس مقياسًا مستمرًا. هنا نأخذ مجموعة منفصلة من الطبقات ذ ووضعها على نطاق التفعيل المستمر Phi بحيث تصبح قيم الفئات المنفصلة نقاطًا عادية على مقياس التنشيط - حالات خاصة بقيم التنشيط يمكنها قبولها أو الاقتراب منها بشكل مباشر بما فيه الكفاية. بالمعنى الدقيق للكلمة ، يمكن أن نأخذ في البداية ليس القيم الرقمية كصفوف ، ولكن السلسلة تسمي "class-1" و "class-2" ، وفي هذه الحالة يجب أن نطابق تسميات السلسلة بالقيم الرقمية في مقياس التنشيط. لذلك ، في حالتنا ، يجب أن تؤخذ قيم الفئات "-1" و "1" بدلاً من ذلك كالتسميات الصفية كما هي ، ولكن كخريطة لفئات مميزة إلى مقياس التنشيط.
حان الوقت لإدخال قياس الخطأ

من الطبيعي أن نقبل أنه كلما كانت قيمة التنشيط للعنصر المحدد أقرب إلى قيمة الفئة للعنصر نفسه ، كلما تنبأت فئة التنشيط بهذا العنصر بشكل أفضل. وبالتالي ، بالنسبة للخطأ الخاص بالعنصر المحدد ، يمكنك أن تأخذ المسافة بين النقاط - الإسقاط العمودي للعنصر على خط التنشيط وإسقاط العنصر على الخط الأفقي للفئة المعروفة (صواب). على الرسم البياني: الأخطاء - خطوط برتقالية رأسية.
التكلفة (الخسارة) وظيفة
لدينا مقياس خطأ لكل عنصر على حدة. يمكننا الحصول منه على مقياس جودة لخط التنشيط بأكمله. من الطبيعي تمامًا أن نقبل ، على سبيل المثال ، أنه كلما كان مجموع أخطاء جميع عناصر عينة التدريب أصغر ، كان بناء خط التنشيط أفضل. لكل عنصر على حدة ، لن يكون الخطأ في حده الأدنى ، ولكن بالنسبة لعينة التدريب بأكملها ككل ، يمكنك الحصول على بعض الحلول الوسط.
لكن لا يمكنك أخذ مجموع الأخطاء البسيط ، ولكن مجموع الأخطاء المربعة ( مجموع الأخطاء المربعة ، مجموع الأخطاء المربعة ، SSE ). من الواضح تمامًا أنه كما في حالة مجموع الأخطاء العادية ، كلما اقترب خط التنشيط من النقاط التي تحتوي على فئات حقيقية للعناصر ، سيكون أصغر مجموع الأخطاء التربيعية ، ولكن في حالة الخطأ التربيعي ، ستتلقى العناصر الأكثر عن بُعد عقوبة أشد.
في الواقع ، ما يهمنا هنا ليس حجم الغرامة بالنسبة للعناصر البعيدة ، ولكن حقيقة أن الوظيفة التربيعية لها حد أدنى ويمكن تمييزها في كل مكان (سيكون المبلغ المعتاد كحد أدنى ، لكن في هذا الحد الأدنى لن يكون قابلاً للتمييز) ، انظر لماذا هذا ضروري. قليلا في وقت لاحق.
لذلك:
- خطأ - المسافة من قيمة تسمية الفئة إلى تنشيط hyperplane
- SSE - مجموع الأخطاء التربيعية لجميع عناصر عينة التدريب
- وظيفة التكلفة J(w) - قياس الجودة لخط التنشيط المحدد. كلما انخفضت القيمة ، كان التنشيط أفضل.
تأخذ كدالة ذات قيمة 1 أكثرمن2دولا SSE ، في الحالة العامة للخلايا العصبية الخطية ، سيبدو كما يلي:
تبدأالمجمعةJ(w)=1 over2SSE=1 over2 sumni=1( Phi( sum)j=0mwjx(i)j)−y(i))2=1 over2 sumni=1( summj=0wjx(i)j−y(i))2 endgathered
( 1 أكثرمن2دولا في المقام الأول ، لا تتداخل مع SSE ، وثانياً للراحة - سيتم تخفيضها بشكل جميل)
هنا i - رقم العنصر ، و ن - عدد العناصر في مجموعة التدريب. دعني أذكرك بذلك y(i) - الطبقة الحقيقية i عنصر من عينة التدريب ، أي الإجابة الصحيحة المعروفة مقدما.
كما نتذكر ، يتم تحديد موضع خط التنشيط من خلال العوامل - عوامل الترجيح w لذلك ناقلات w بمثابة المعلمة من وظيفة الخسارة.
لحالة 1-الأبعاد
J(w)=1 over2SSE=1 over2 sumni=1(w0+w1x(i)1−y(i))2
معنى x و ذ معروفة مسبقا (هذه مجموعة تدريب) ، وبالتالي فهي ثابتة. نختار المعلمات w ، أي w0دولا و w1 بحيث القيمة J(w) اتضح أن الحد الأدنى. دعونا نحاول رسم الرسم البياني كقيمة J(w) يعتمد على المعلمات w0دولا و w1

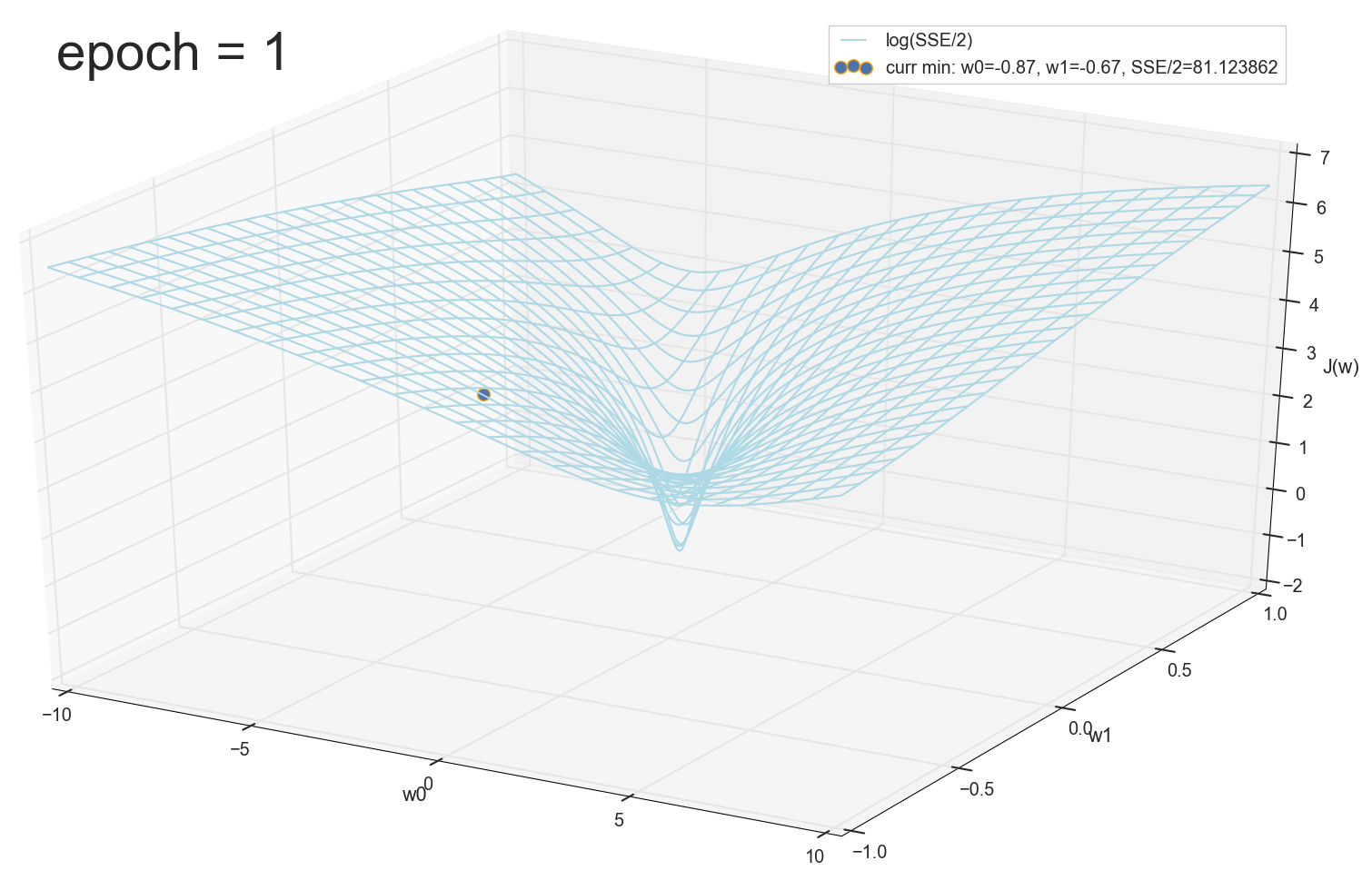
بشكل عام ، من الواضح هنا أن وظيفة الخسارة بها حد أدنى ، وموقعها تقريبًا. ولكن دعونا نفعل خدعة أخرى ونبني نفس الرسم البياني ، فقط بمقياس رأسي لوغاريتمي .

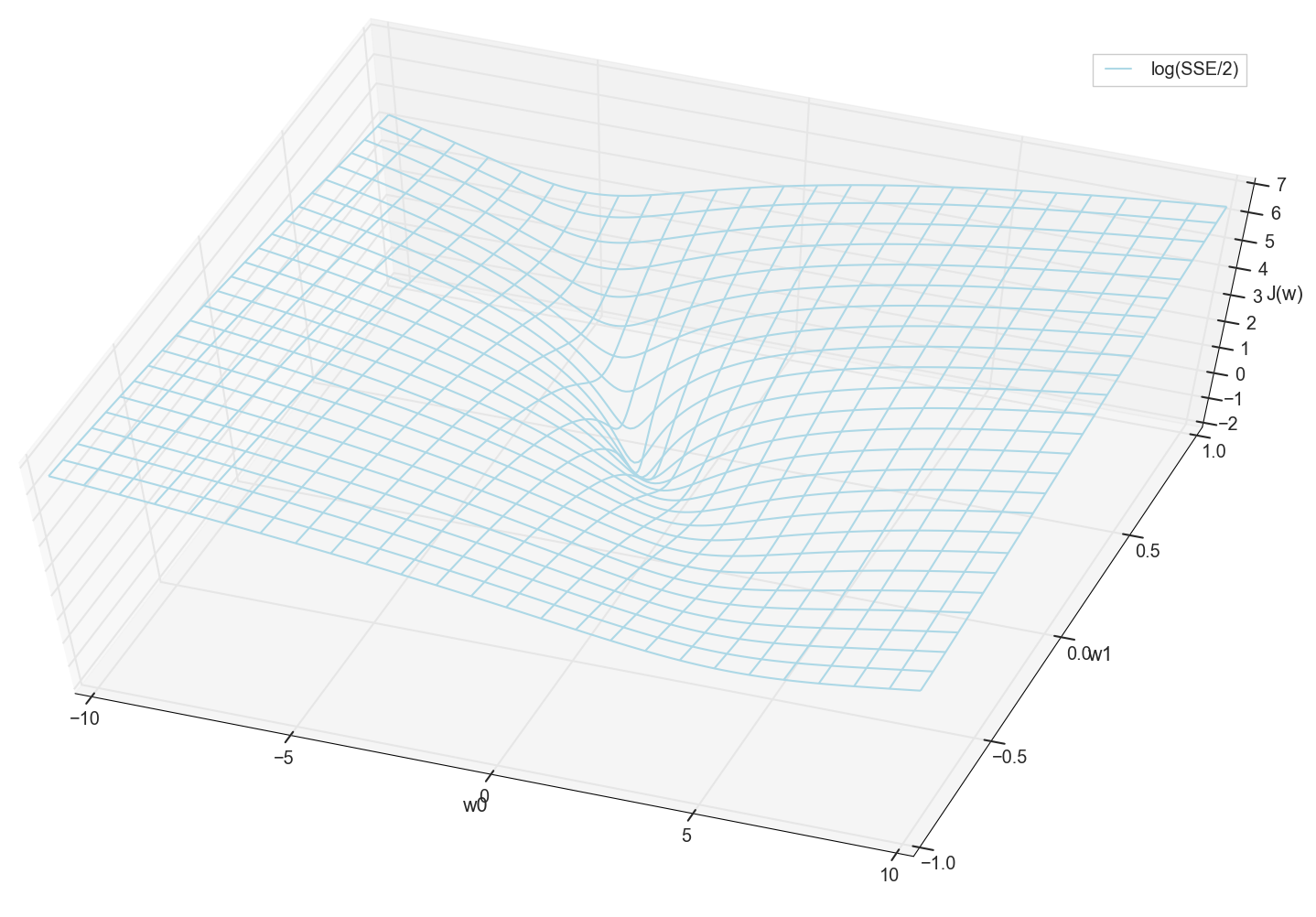
لا أعرف عنك ، لكنني شخصياً ، عندما رأيت هذا المخطط لأول مرة ، واجهت التنوير. هذا التجويف الطبيعي ليس مجرد تصور تصويري للتلال متعددة الأبعاد من مقال شائع على الشبكات العصبية ، إنه رسم بياني حقيقي.
مهمتنا هي اختيار هذه القيم w0دولا و w1 للوصول الى اسفل هذه الحفرة. نحصل على قيم الأوزان - نحصل على خلية عصبية مدربة.
نظرًا لأننا جميعًا قد رسمنا رسمًا بيانيًا ونلاحظ الحد الأدنى شخصيًا ، فلن يمنعنا أحد من العثور على إحداثياته باستخدام تعداد بسيط على الشبكة "يدويًا":

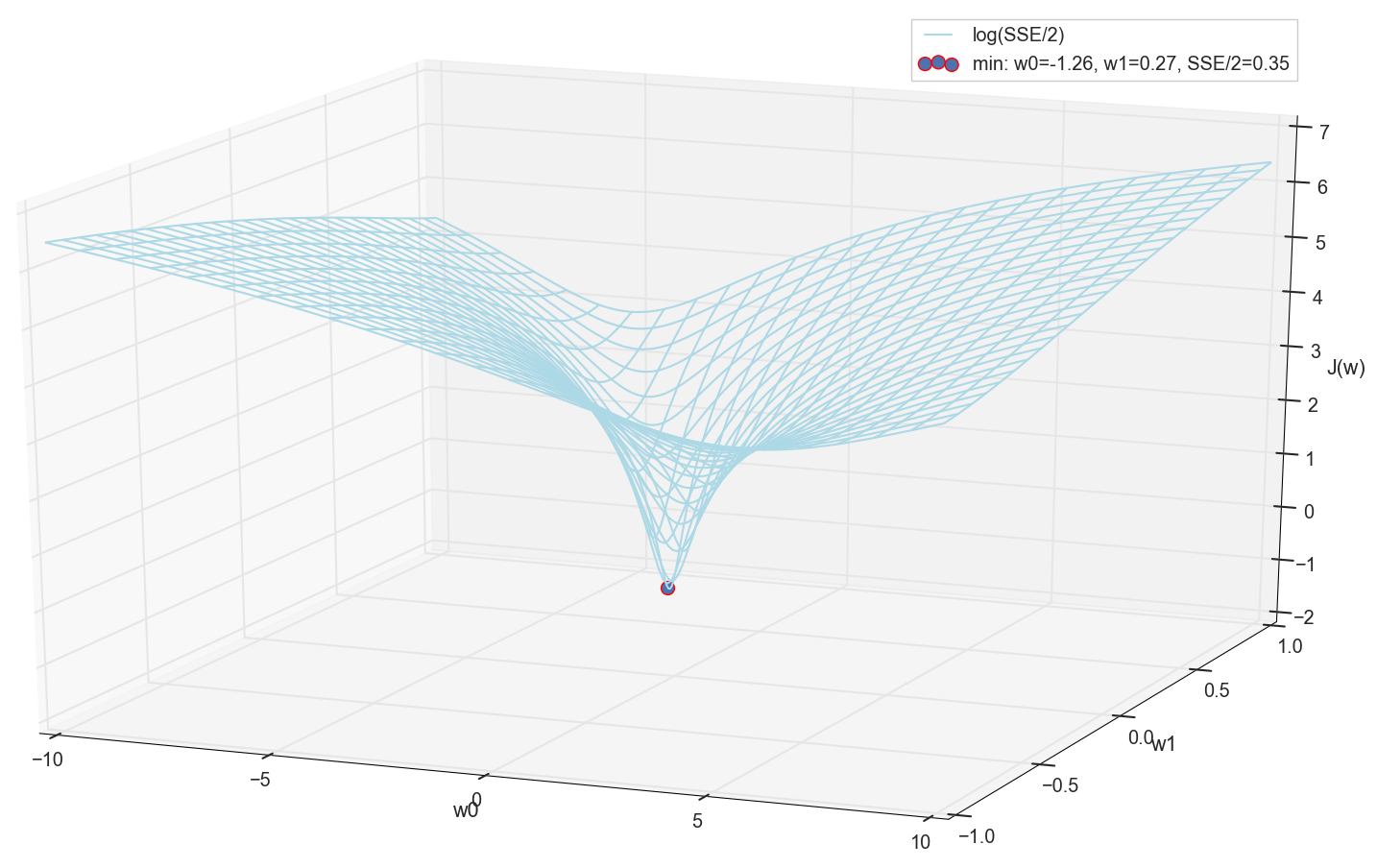
هذه هي القيم: w0=−1.26دولا و w1=0.27دولا ، مجموع الأخطاء المربعة من SSE هو 0.69 ، وظيفة التكلفة J(w)=SSE/2=0.35 (بتعبير أدق: 0.3456478371758288).
دعونا نرى كيف يبدو التنشيط مع هذه المعايير:

بالنسبة لي ، هذا طبيعي جدًا. تفصل نقطة التقاطع التنشيط مع عتبة الصفر العناصر عن فئات مختلفة ، ويقوم التنشيط نفسه بتعيين القيم الصحيحة لهم. في الوقت نفسه ، يبدو التنشيط في وضع مثالي.
قبل المضي قدمًا ، نعجب مرة أخرى الرسم البياني على الشبكة على نطاق أوسع:
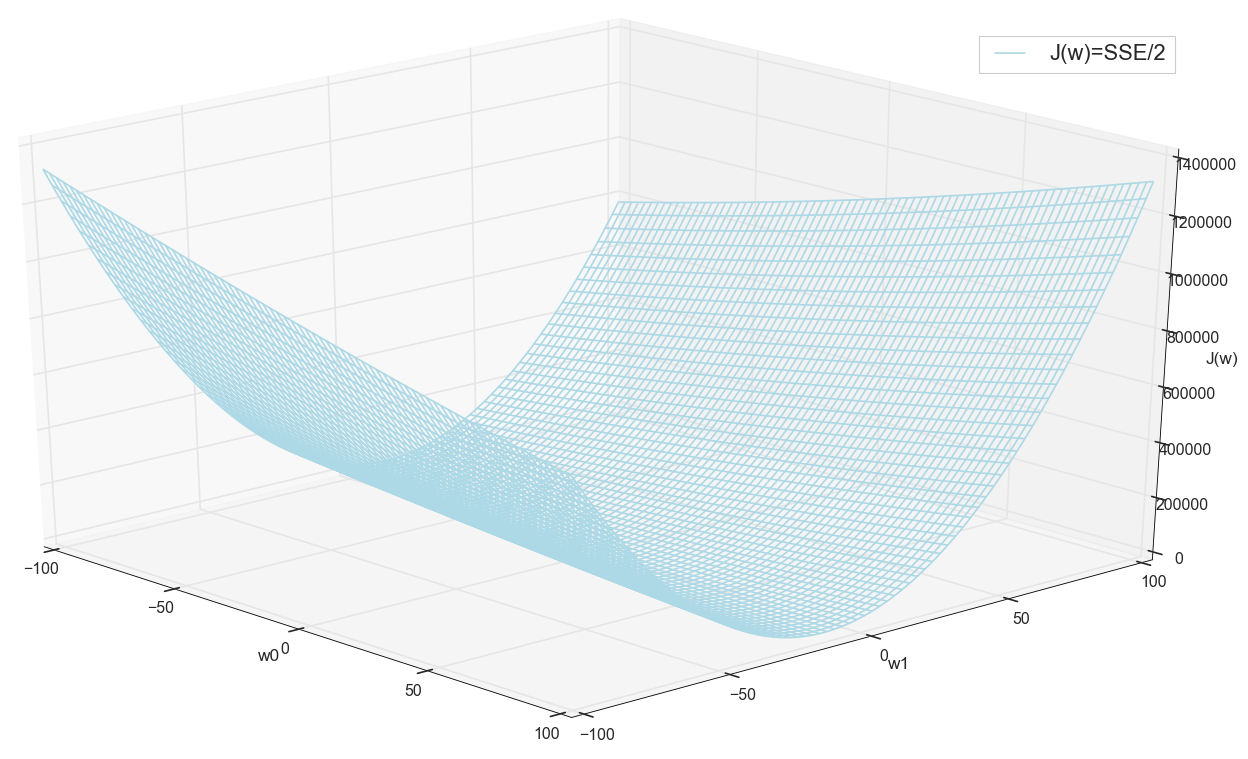
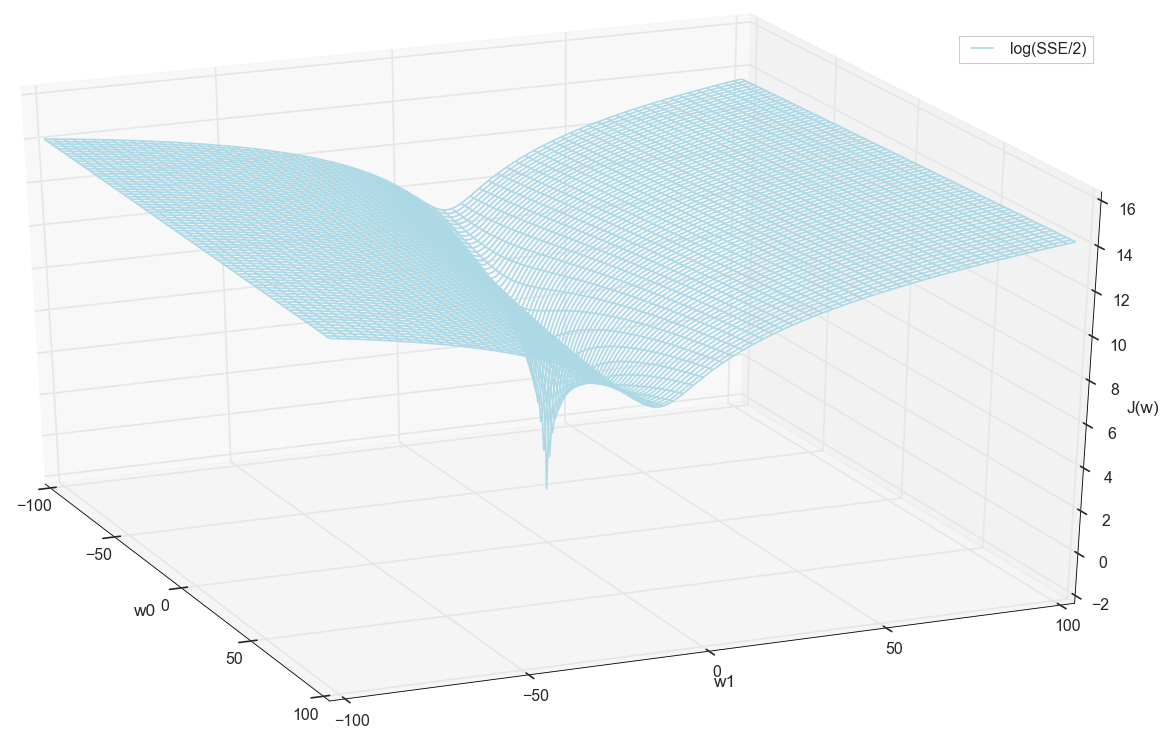
يبدو أنه لا توجد أدنى مستويات قريبة أخرى كانت تفكر.
الحد الأدنى من البحث
لذلك ، حصلنا على الأوزان - إحداثيات الحد الأدنى لقيمة الخطأ. ستكون هذه هي القيمة المثلى للأوزان في عينة التدريب. بشكل عام ، هذا هو بالضبط ما نحتاج إليه ، يمكننا أن نقول أن الخلايا العصبية مدربة. ربما هذا يمكن أن تكتمل؟
البحث عن الحد الأدنى: البحث عن طريق الشبكة
- الخيار للوهلة الأولى يعمل تمامًا (كما نرى)
- يجب أن تعرف مسبقًا المنطقة التي تبحث عنها كحد أدنى (يمكنك أن تأخذ حدودًا كبيرة جدًا ، ثم تضييق نطاق البحث - هذا فقط بالعين)
- لزيادة الدقة ، تحتاج إلى تقليل الخطوة → المزيد من النقاط (الحل: يمكنك تضييق نطاق البحث بشكل متكرر)
- عدد كبير جدًا من النقاط (بالنسبة إلى 2d ، قد يكون الأمر على ما يرام ، ولكن بالنسبة للحالات متعددة الأبعاد ، نواجه موارد بسرعة كبيرة)
- بالنسبة إلى MNIST (28 × 28 = 784 بكسل - نفس عدد المدخلات ، نفس عوامل الترجيح بالإضافة إلى الإزاحة ، شبكة من 100 خطوة لكل بُعد): 100 ^ 785 = 10 ^ 1570.
لذا ، إذا أردنا تدريب خلية عصبية واحدة (ولا حتى شبكة عصبية) في صورة تبلغ 28 × 28 = 784 بكسل من خلال البحث عن الحد الأدنى عن طريق التعداد المباشر على شبكة مكونة من 100 نقطة لكل قياس ، نحتاج إلى فرز مجموعات 10 ^ 1570. هذا كثير جدًا للتخزين والبحث (في الجزء المرئي من الكون لا يوجد سوى 10 ^ 80 ذرات ، الكون موجود لحوالي 4 * 10 ^ 17 ثانية = 4 * 10 ^ 26 نانو ثانية).
دعنا نحاول العثور على خيار أسرع.
الحد الأدنى للبحث: ثابت الخطوة النزول
دعونا نلقي نظرة على الرسم البياني لوظيفة الخسارة J(w) على متن الطائرة: الإصلاح w0دولا وتغير w1
def sse_(X, y, w0, w1): return ((w0+w1*X - y)**2).sum()
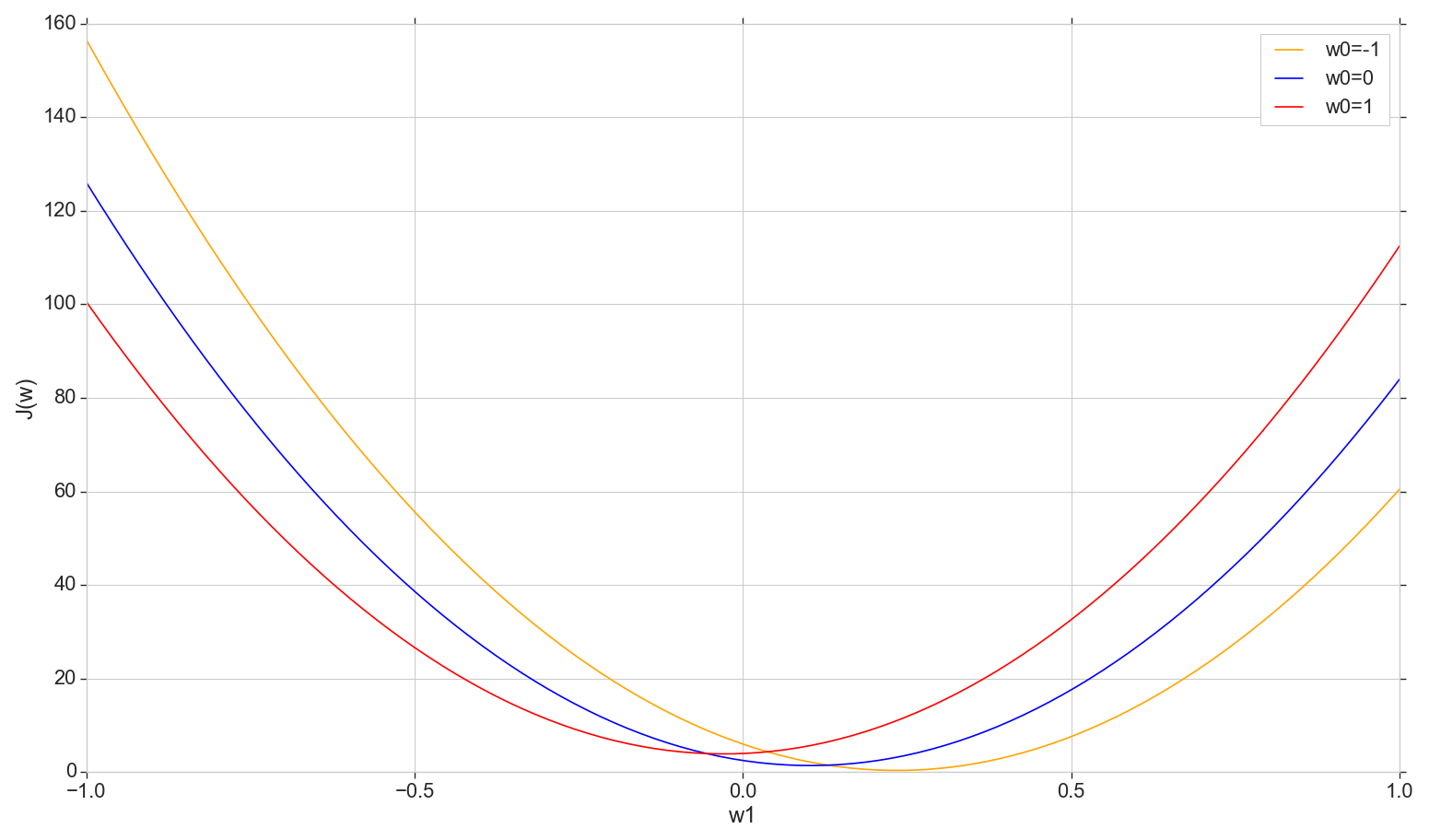
هذه عبارة عن قطع مكافئ عادي (بشكل أكثر دقة ، عائلة من القطع المكافئة - ستختلف قليلاً اعتمادًا على نوع القيمة المثبتة على w0دولا ). للعثور على الحد الأدنى من القطع المكافئ ، ليس من الضروري فرز جميع النقاط. يمكننا اختيار نقطة تعسفية على المحور الأفقي والتحرك نحو الحد الأدنى مع بعض الخطوة.
النظر في خيار الملعب ثابت
- إذا كانت الخطوة كبيرة جدًا ، فيمكنك التفويت وعدم بلوغ الحد الأدنى (يمكن تقليل الخطوة)
- إذا كانت صغيرة جدًا ، فسيكون هناك العديد من الخطوات (أكثر مما يمكن أن تكون)
- على أي حال ، لن نحقق الحد الأدنى بدقة ، لكن يمكننا تحقيق ذلك بدقة تعسفية عن طريق تغيير الخطوة بالقرب من الحد الأدنى غير الدقيق (الخطوة تتوقف عن أن تكون ثابتة)
- لا نعرف اتجاه الهبوط (من الممكن حل الخوارزمية: لا تتقدم في اتجاه الخطأ المتزايد)
- تم حل مشكلة العثور على النطاق (يمكنك النزول من أي مكان - عاجلاً أو آجلاً سننزل على أي حال)
- من حيث المبدأ ، فإن الخيار يعمل ، ولكن ربما هناك خيار أفضل؟
ملاحظة: عندما تحدثت عن مثل هذا الخيار من أصل إلى محاضرة ، سأل أحد الطلاب لماذا تحتاج إلى التحرك في خطوات إذا كان يمكنك أن تجد على الفور الحد الأدنى من القطع المكافئ باستخدام الصيغة؟ في البداية ، أجبت على شيء في الروح التي نحن مهتمون بها الآن للنظر في خيار التكرار ، بحيث يمكننا استخدامها في وقت لاحق ليس فقط مع القطع المكافئة ، ولكن أيضًا في المواقف الأخرى. بالإضافة إلى ذلك ، في الواقع ، لا نحتاج على الأقل إلى قطع مكافئ على وجه التحديد في هذا القسم - سننتقل إلى الحد الأدنى ليس في بعد واحد ، ولكن في جميع الأبعاد بطريقة ستحدث في كل تكرار جديد ، ليس على طول هذه القطع المكافئة ، ولكن في مكافئ مع شريحة جديدة مع قيمة مبدلة w0دولا . لكن التفكير لاحقًا ، أعتقد أنه ، من حيث المبدأ ، لا حرج إذا تحركنا في كل شريحة ، ليس في خطوات ، ولكن انتقلنا على الفور إلى الحد الأدنى للشريحة الحالية. لذلك ، مرة بعد مرة ، والقياس بالقياس ، لا يزال يتعين علينا الانزلاق إلى الحد الأدنى العالمي ، ويبدو أسرع من الخطوات. بالنسبة لخلية عصبية واحدة ، يجب أن تعمل ، وليس فقط مع القطع المكافئ. لكنني لم أبدأ بعد في تضييع الوقت في اختبار هذه النظرية ، لذلك نحن هنا ننتقل - وعدت بالتحدث عن نزول التدرج.
البحث عن الحد الأدنى: النسب التدرج
بشكل عام ، نحن نخطو الخطوات ، لكننا نفعل ذلك بشكل أكثر ذكاء. نستخدم مشتق منحنى التكلفة لتحديد الخطوة (هنا ، ليس منحنى التكلفة ، ولكن منحنى التكلفة ).
- لدينا عدة أبعاد ولكل منها منحنى خاص به: نقوم بإصلاح كل شيء wj يستثنى wk .
- J(wk) سيكون هناك منحنى خطأ في ك ال البعد
- جميعها (في حالتنا) هي مكافآت ، ولكن بشكل عام ، من المهم فقط أن تكون قابلة للتمييز في كل مكان ولديها حد أدنى
- لضبط الخطوة في كل قياس ، سنستخدم المشتق الجزئي لوظيفة الخطأ فيما يتعلق بهذا القياس (معامل متغير wk ).
- يسمى متجه هذه المشتقات الجزئية بتدرج.
كل هذا جيد ، لكن من أين يأتي المشتق؟ الآن دعنا نعرفها.
المعنى الهندسي للمشتق
بالنسبة لي ، بقي المشتق لفترة طويلة عبارة عن مجموعة من الصيغ والقواعد الخاصة لحسابه ، بالإضافة إلى شيء عن الزيادة والنقصان والتطرف. سيكون من المناسب هنا أن نتذكر أو تعرف ما هو المشتق بالفعل.
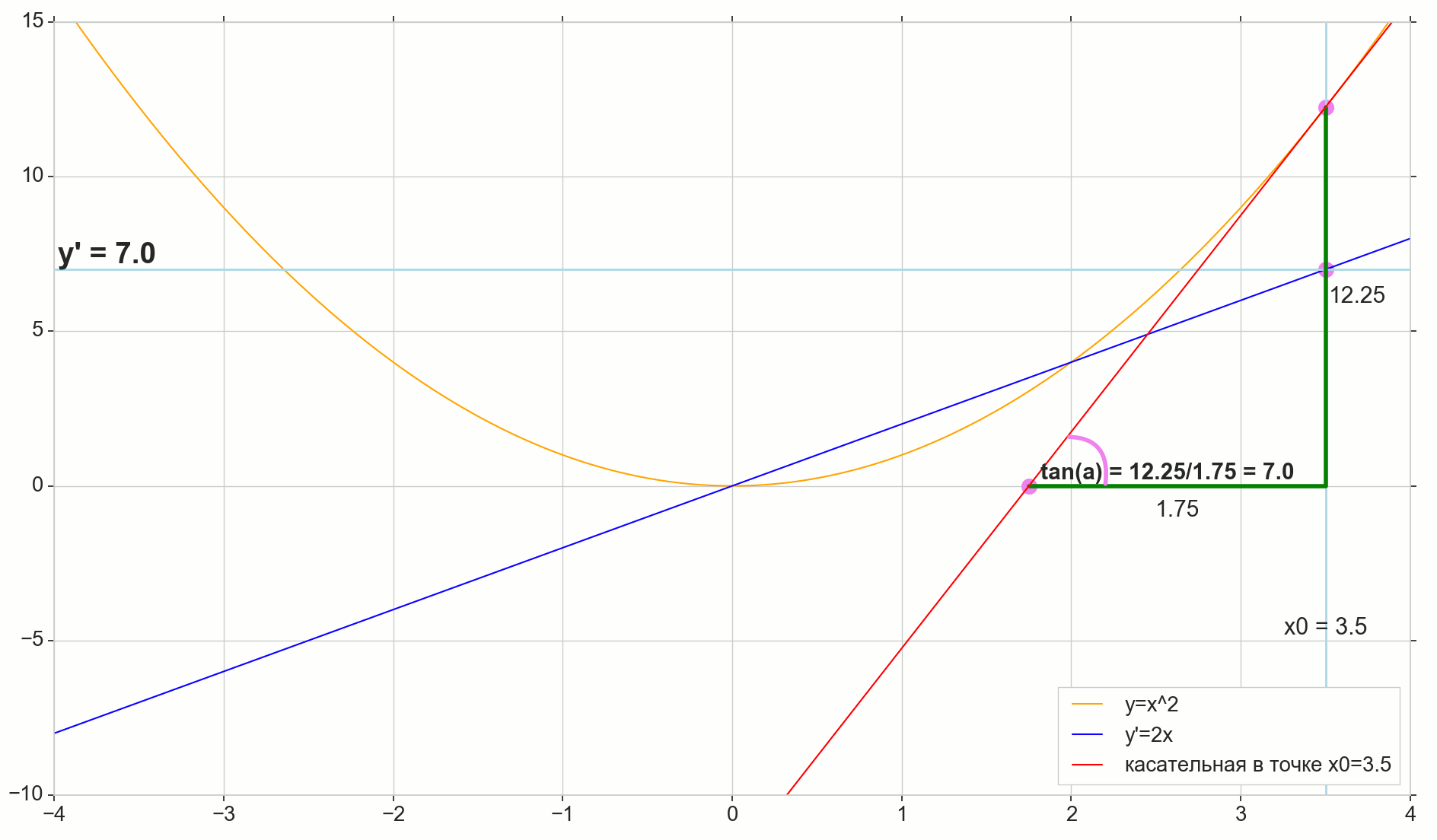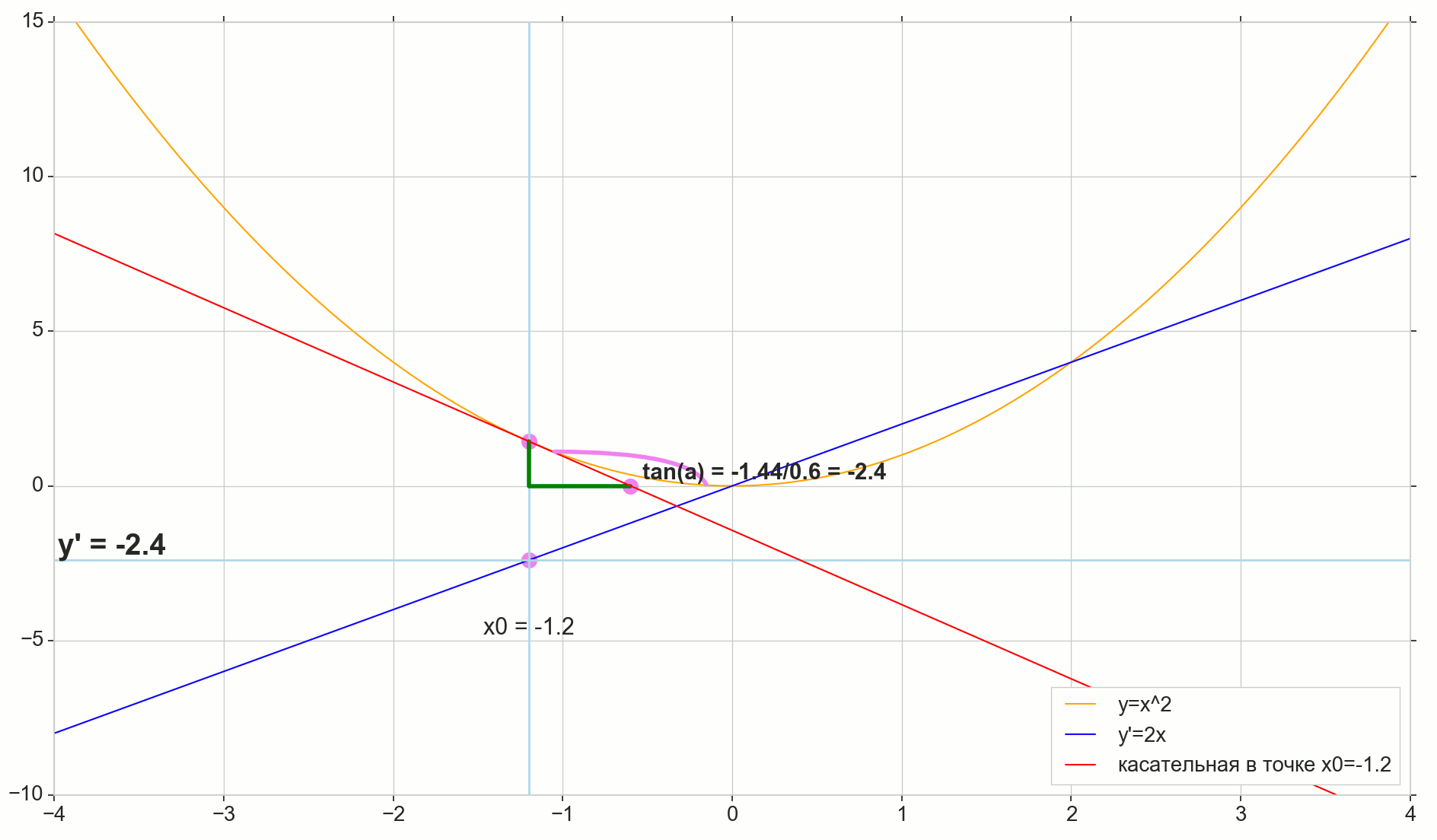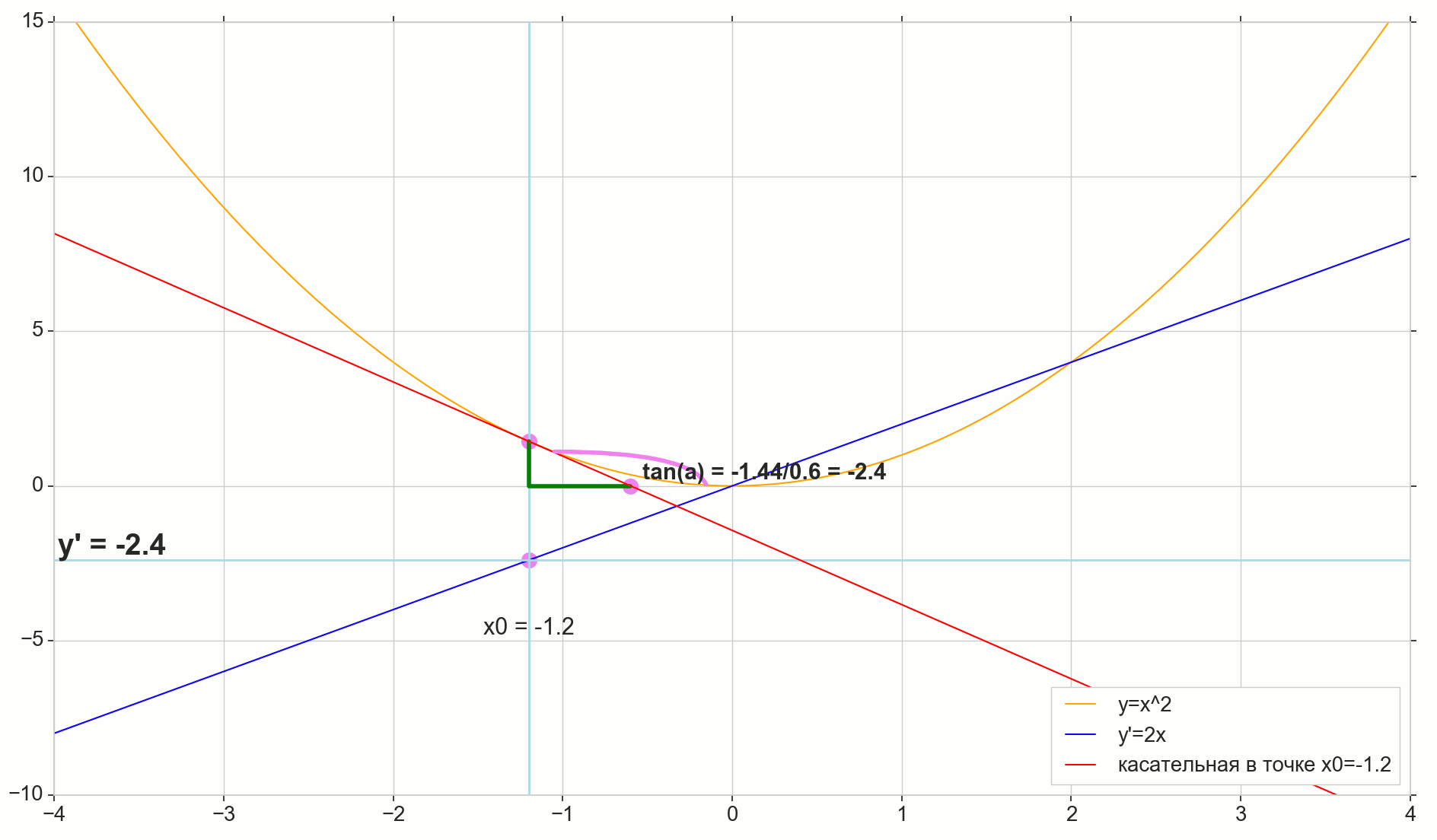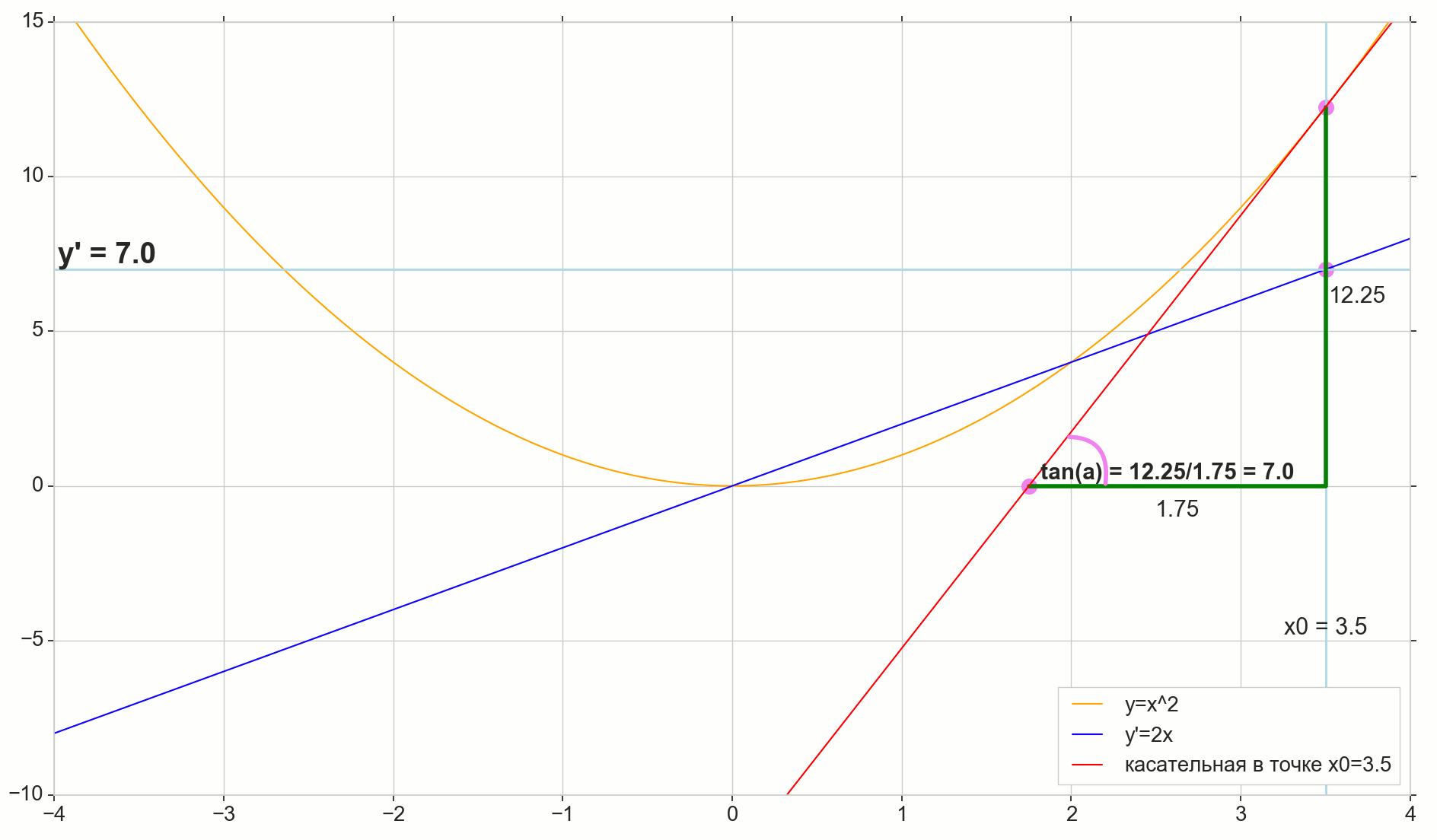
وظيفة مشتقة y(x) في هذه المرحلة x0دولا هو الحد الأقصى لنسبة الزيادة في الوظيفة دلتاذ للحجة الزيادة دلتا×دولا عند زيادة الحجة دلتا×دولا تميل إلى الصفر:
y′(x0)= lim Deltax to0 Deltay over Deltax، Deltay=y(x0+ Deltax)−y(x0)

النقطة في الصورة M(x0،y(x0))=(x0،y0) هي النقطة التي نريد عندها تحديد المشتق. نقطة N(x0+ Deltax،y(x0+ Deltax))=(x0+ Deltax،y0+ Deltay) - النقطة التي حصلت عليها بزيادة الحجة دلتا×دولا . مباشرة مليوندولا - عابر يمر عبر هاتين النقطتين.
نقطة دولا - تقاطع الثواني مليوندولا مع المحور الأفقي ص=0دولا .
النظر في اثنين من مثلثات الزاوية اليمنى: مثلث مثلثNPM مع قسم ثانوي مليوندولا باعتباره انخفاض ضغط الدم ومثلث  مع استمرار secant إلى المحور ص=0دولا - الجزء AM باعتباره انخفاض ضغط الدم. من الرسم البياني والهندسة المدرسية بالطبع فمن الواضح أن الزوايا الزاويةNMP و الزاويةMAB متساوون ، وبالتالي فإن ظلالهم متساوية:
مع استمرار secant إلى المحور ص=0دولا - الجزء AM باعتباره انخفاض ضغط الدم. من الرسم البياني والهندسة المدرسية بالطبع فمن الواضح أن الزوايا الزاويةNMP و الزاويةMAB متساوون ، وبالتالي فإن ظلالهم متساوية:
tan angleMAB= tan angleNMP=MB overAB=NP overMP= Deltay over Deltax
أضف إلى الصورة: MD - الظل إلى المنحنى الأولي في هذه النقطة M يعبر المحور ص=0دولا عند هذه النقطة D . مثلث مثلثMBD - مثلث الزاوية اليمنى مع انخفاض التوتر - قسم الكاسيت ، قطعة MD .
نحن نهدف إلى الزيادة دلتا×دولا إلى الصفر:
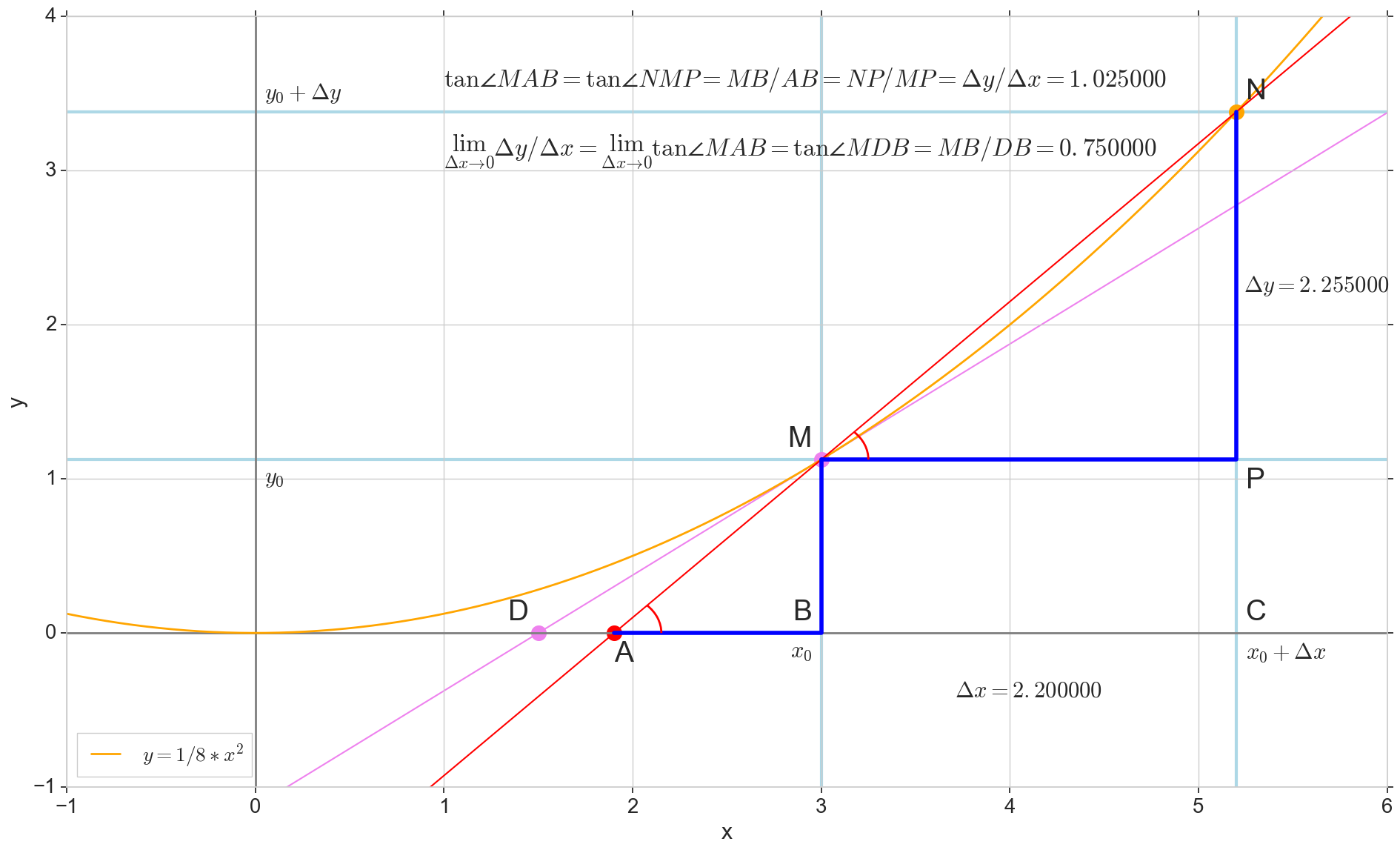
نقطة N الانتقال إلى هذه النقطة M حسب الوظيفة ، نقطة دولا تزحف إلى حد ما D على طول المحور ذ ، والانقسام مليوندولا يتحول إلى الظل MD مع نقطة اتصال M . مثلث المصدر مثلثNPM مع الساقين دلتا×دولا و دلتاذ يتقلص إلى حد ما ، ولكن مثلث مثل ذلك  يتحول إلى مثلث مثلثMBD الحفاظ على ليس فقط الأبعاد العيانية ، ولكن أيضًا مساواة الزوايا الزاويةMAB و الزاويةNMP .
يتحول إلى مثلث مثلثMBD الحفاظ على ليس فقط الأبعاد العيانية ، ولكن أيضًا مساواة الزوايا الزاويةMAB و الزاويةNMP .
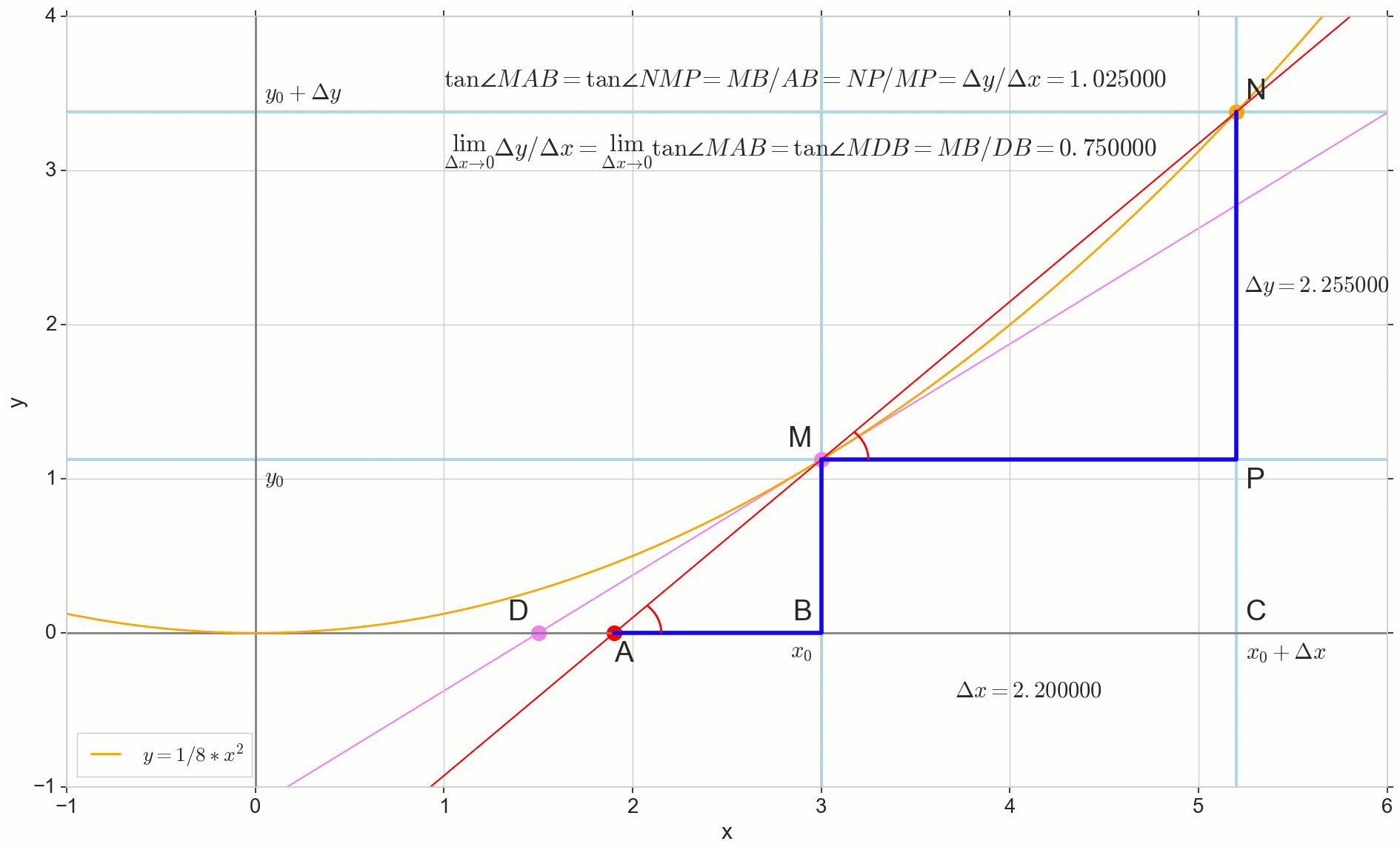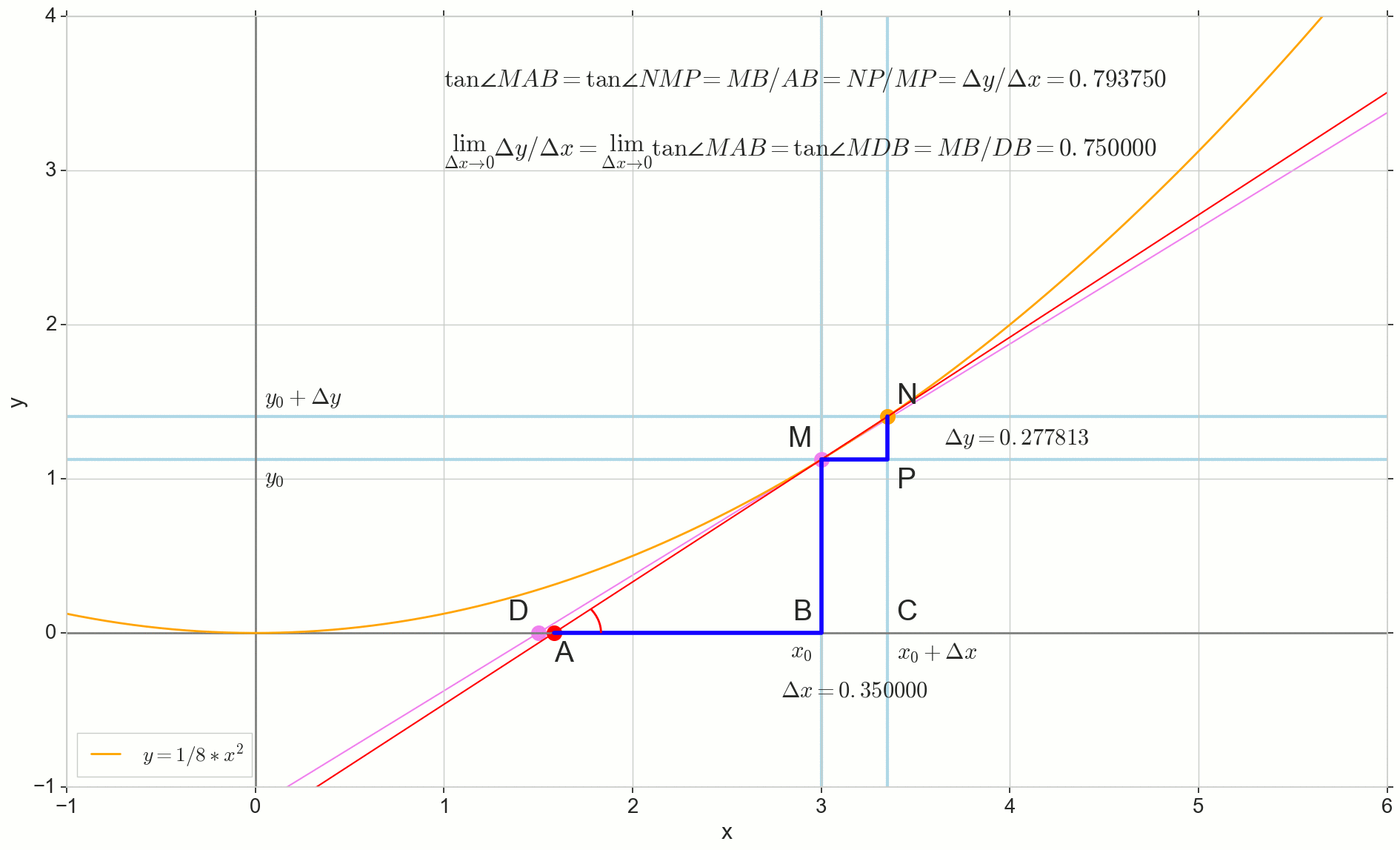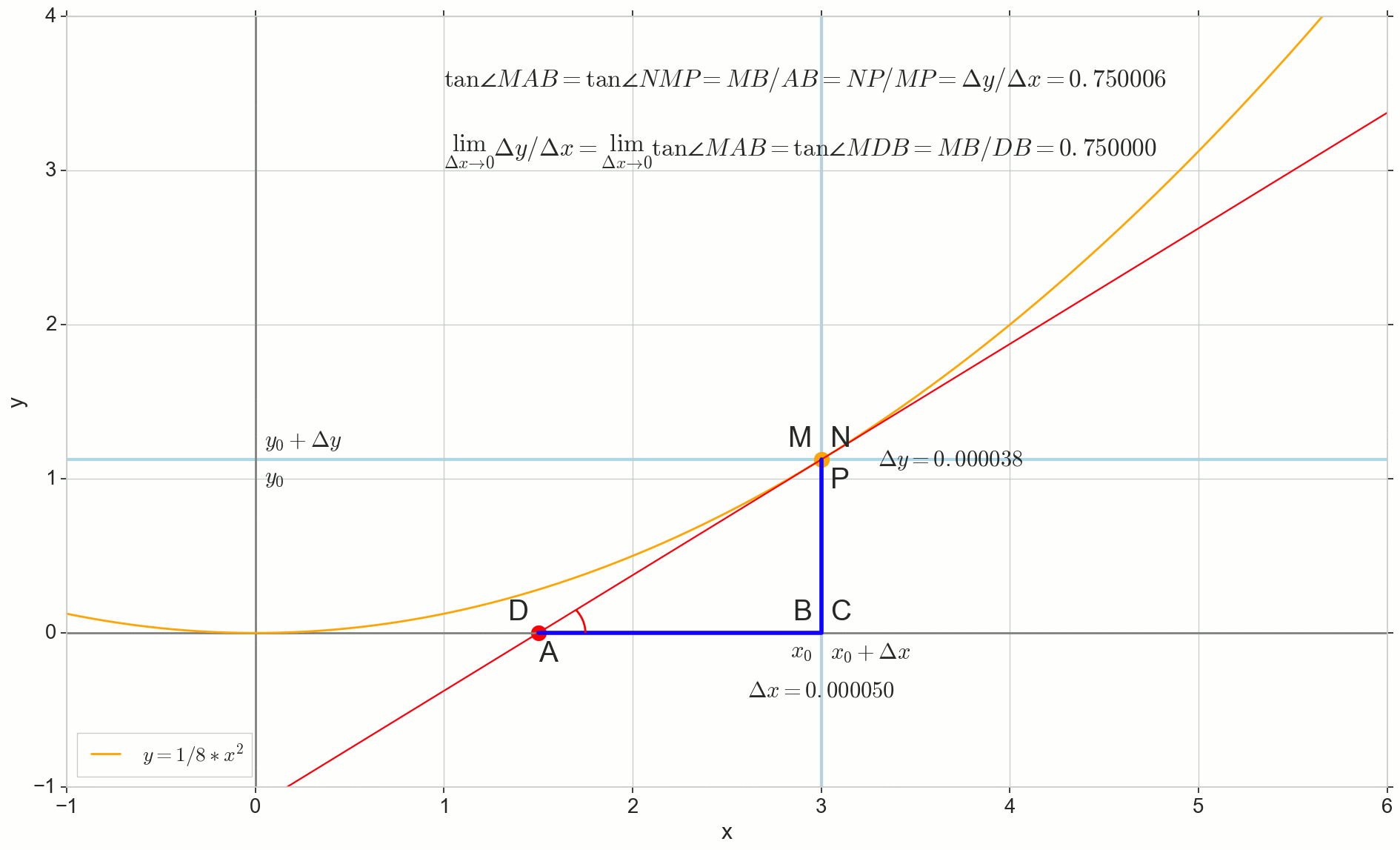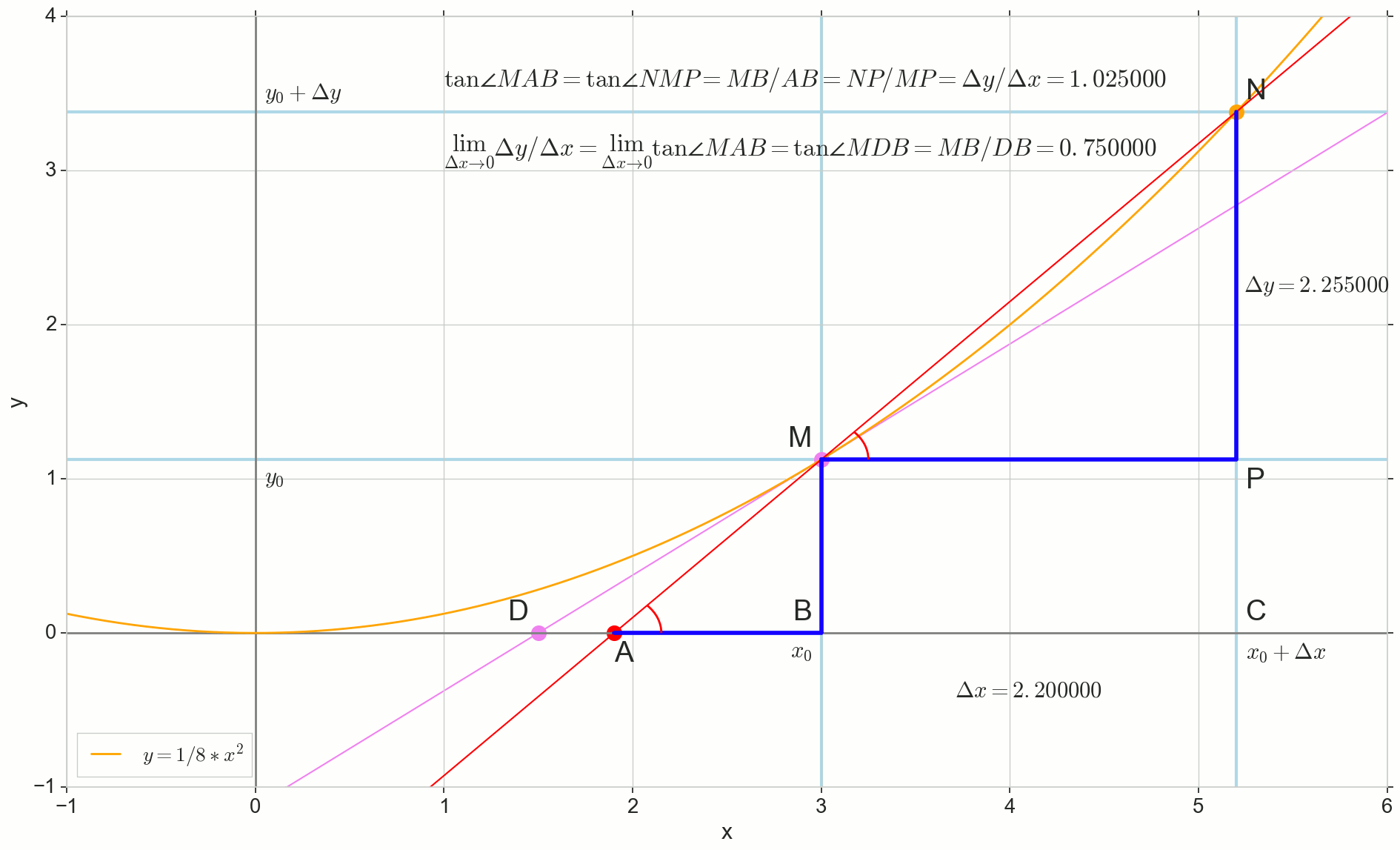
كيف الزيادة دلتا×دولا ، تقترب بلا حدود ، لن تصل أبدًا إلى الصفر ، وبالتالي فإن هذه النقطة N لم تصل إلى المكان بالضبط M ، وهذه النقطة دولا لن تصل إلى النقطة D مثلث  لن تتحول إلى مثلثMBD . , , «» lim .
لن تتحول إلى مثلثMBD . , , «» lim .
△MBA — △MBD , :
limΔx→0ΔyΔx=limΔx→0tan∠NMP=limΔx→0tan∠MAB=limΔx→0MBAB=MBDB=tan∠MDB
:
limΔx→0ΔyΔx=tan∠MDB
, , :
y′(x0)=limΔx→0ΔyΔx=tan∠MDB
, y=0 . .
, , , , , . , , , , .. ( , , ). : , (, — tangent line , , — ).
:
- x0 y=0
- — y(x0) — x0 y=0 y=0
- «» , ,
- — : — , —
- ( , , , Δy )
, , :

— , — x0 , — . — — . — y=0 , — .

, , , , . ( , ) (: y=0 , ).

( ): , (: y=0 , ).
, : (), «»/«» , . — . , , ? .
J(w) . , , , .
J(w)=12SSE=12n∑i=1(m∑j=0wjx(i)j−y(i))2
∂J(w)∂wk=∂∂wk12n∑i=1(m∑j=0wjx(i)j−y(i))2=12n∑i=1∂∂wk(m∑j=0wjx(i)j−y(i))2=12n∑i=12(m∑j=0wjx(i)j−y(i))∂∂wk(m∑j=0wjx(i)j−y(i))=122n∑i=1(m∑j=0wjx(i)j−y(i))∂∂wk((w0x(i)0+...+wkx(i)k+...+wmx(i)m)−y(i))=n∑i=1(m∑j=0wjx(i)j−y(i))x(i)k
, : , , , ( ) . , wk ( , ), . , , , 1/2 SSE .
:
∂J(w)∂wk=n∑i=1(m∑j=0wjx(i)j−y(i))x(i)k
— ( ∇ [], , .. []):
∇J(w)=(∂J(w)∂w0,...,∂J(w)∂wm),w=(w0,...,wm)
:
w:=w+Δw,Δw=−η∇J(w)
ك - :
wk:=wk+Δwk,Δwk=−η∂J(w)∂wk
:
, , , . , .
1- :
Φ(x,w)=w0+w1x1
( ):
∂J(w)∂w0=n∑i=1(w0+w1x(i)1−y(i))x(i)0=n∑i=1(w0+w1x(i)1−y(i))
∂J(w)∂w1=n∑i=1(w0+w1x(i)1−y(i))x(i)1
:
Δw0=−η∂J(w)∂w0=−ηn∑i=1(w0+w1x(i)1−y(i))
Δw1=−η∂J(w)∂w1=−ηn∑i=1(w0+w1x(i)1−y(i))x(i)1
, . .
( w1 )
w0=1 , J(w1)
X ( ) y w0 و w1 ( ):
def sse_(X, y, w0, w1): return ((w0+w1*X - y)**2).sum()
w1 -1.5 1.5.
, ( , , ):
plt.subplot(3,1,1)

, , δJ(w)δw1 — :
grad_w1 = [] for i in range(len(w1)): grad = ((w0 + w1[i]*X1 - y)*X1).sum() grad_w1.append(grad) plt.subplot(3,1,3) plt.plot(w1, grad_w1, label=u' ∂J(w)/∂w1') plt.xlim(-1.2, 1.2) plt.xlabel(u'w1') plt.ylabel(u'∂J(w)/∂w1') plt.legend(loc='upper left')

Δw1(w1) (, Δw1 w1 , .. , ):
eta = 0.001 delta_w1 = [] for i in range(len(w1)): grad = ((w0 + w1[i]*X1 - y)*X1).sum() delta = -eta*grad delta_w1.append(delta) plt.subplot(3,1,2) plt.plot(w1, delta_w1, color='orange', label=u'Δw1, η=%s'%eta) plt.xlim(-1.2, 1.2) plt.xlabel(u'w1') plt.ylabel(u'Δw1=-η*∂J(w)/∂w1') plt.legend(loc='upper right')

plt.show()

- : ,
- : — «» ( , «» ),
- : — ( ), η [] ( ),
: , 1000 .
, ,
w — - - . w0=1 , w1=0.9 . η=0.001 ( , ) 12:
:
w1 J(w1,w0=1) :
Δw1(w1)
plt.scatter(w1_epochs, delta_w1_epochs, color='blue', marker='o', s=size_epochs, label=u' , η=%s'%eta) plt.plot([w1_epochs, w1_epochs], [delta_w1_epochs, np.zeros(len(delta_w1_epochs))], color='orange')

, , ( ), . , , , .
: , , , «» , — , .
- — w1 , —
- , w1
- — : , —
- , —
- , ( ), , ( ) — , —
- ( , — ).
- : — , —
- ? — . .
- . w1 , . , «»/«» . , , . , , , « ». , : w1=0.9 200, , , , 1. , , , . — η . , 200 1. η=0.001 , w1=0.9 200*0.001=0.2 ( -1, -0.2) — .
- J(w1=0.9)=92.43 , 12 (, ) J(w1=0.03)=8.54
- , ,
, . , . , ( , ). η , .
: , , , .
, , , .
η
- η [] — ()
- ,
- «»: , , ,
- , J(w)
- : wk , η , wk
η=0.01

. , . 3- , 3- , , .. , .. . , , [] .
η J(w) η

: , , . , — , , .
:

:

.
η . , , .

, .
:
, ( ) w , , . , , , . , , .
,
, .
, :

— :
12 — , :

50 :

1767 — , :

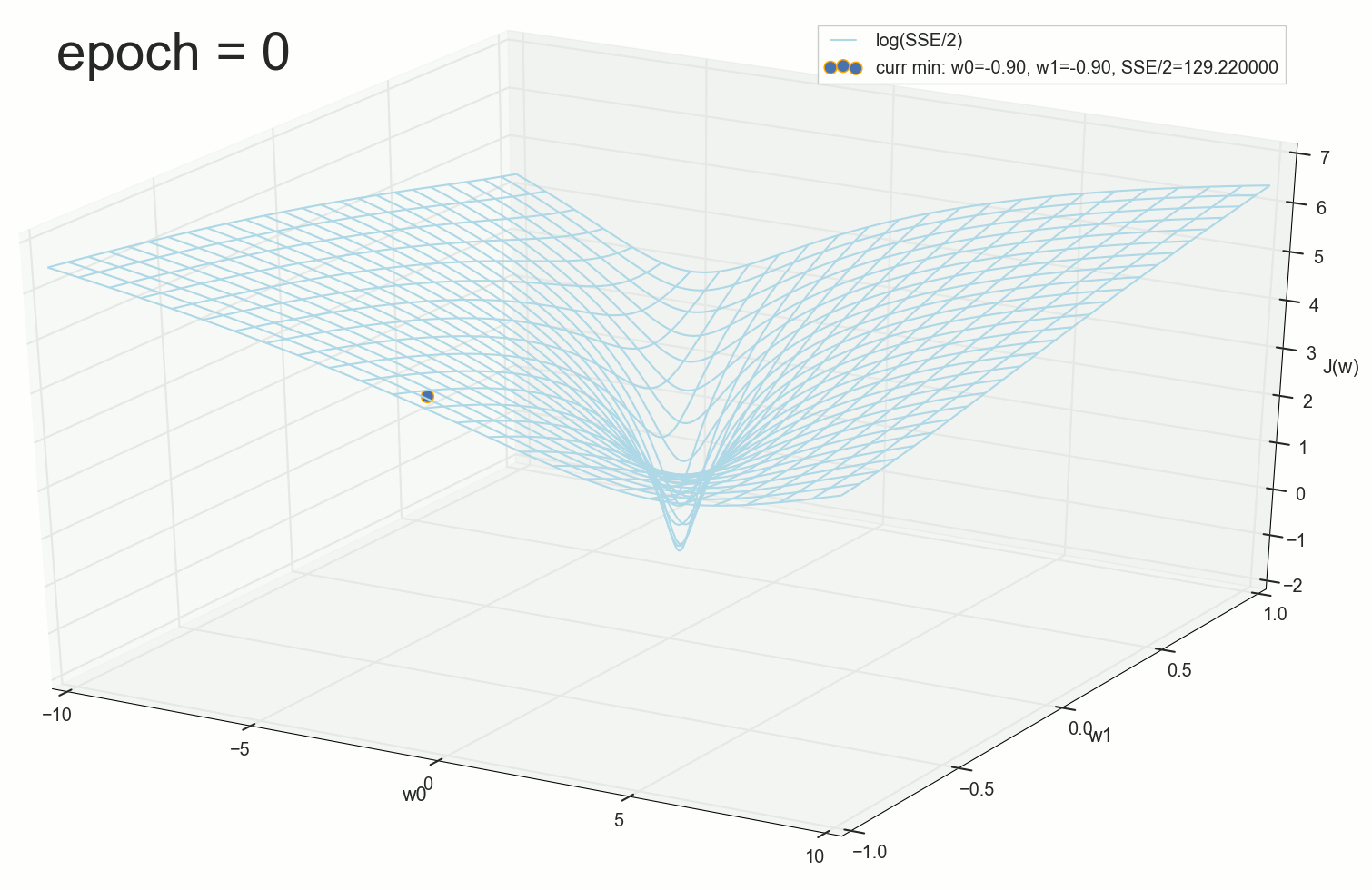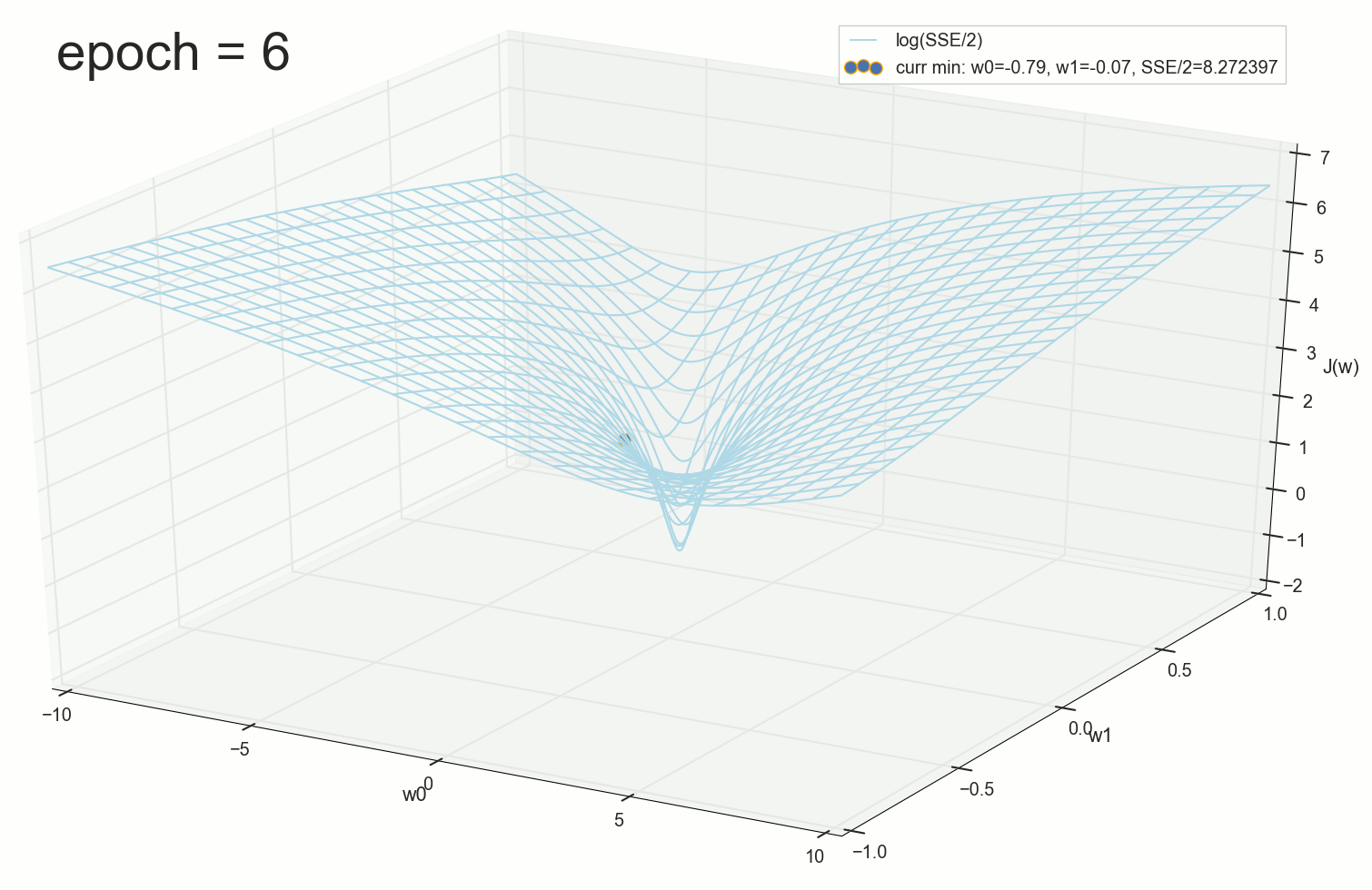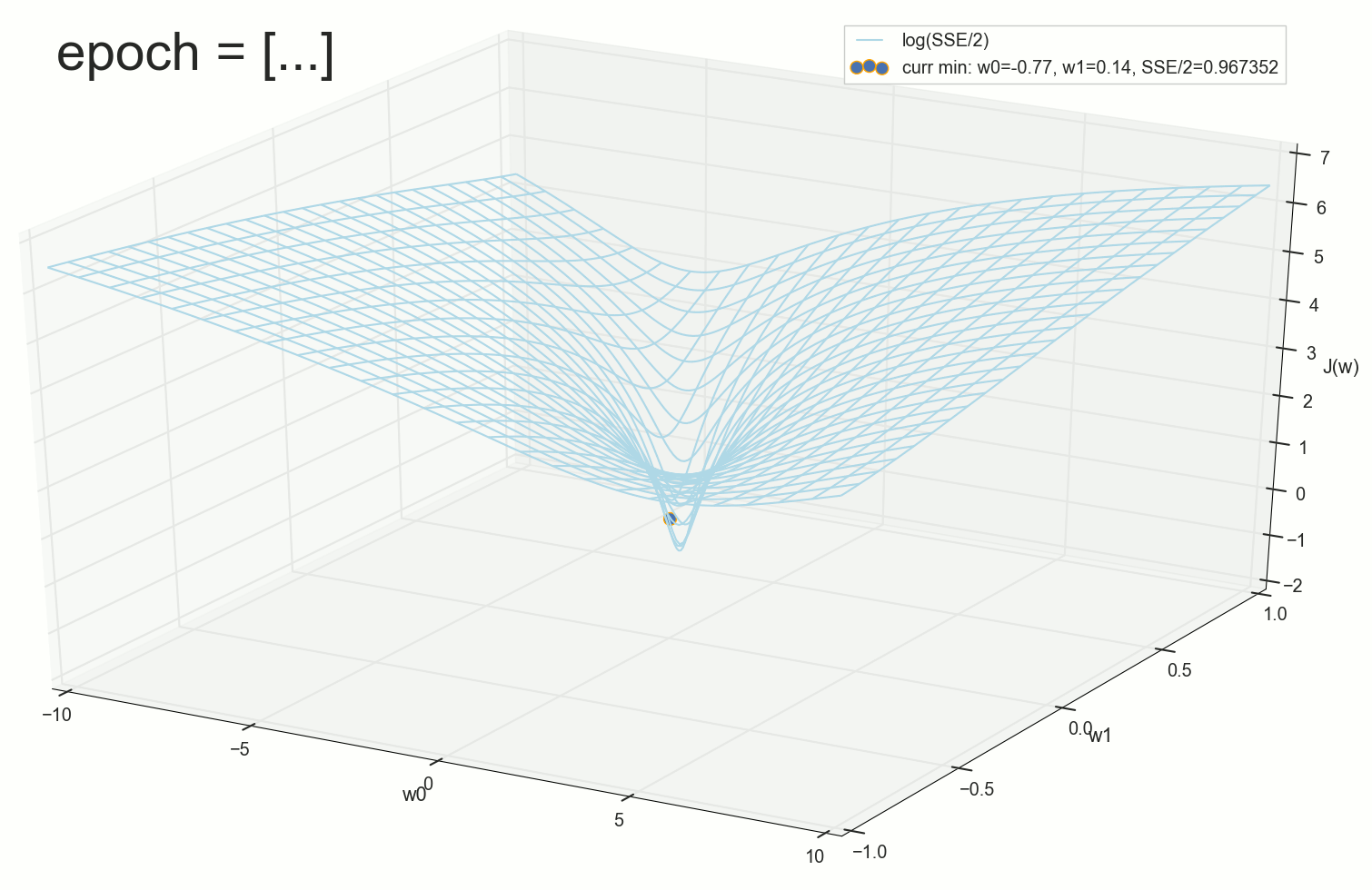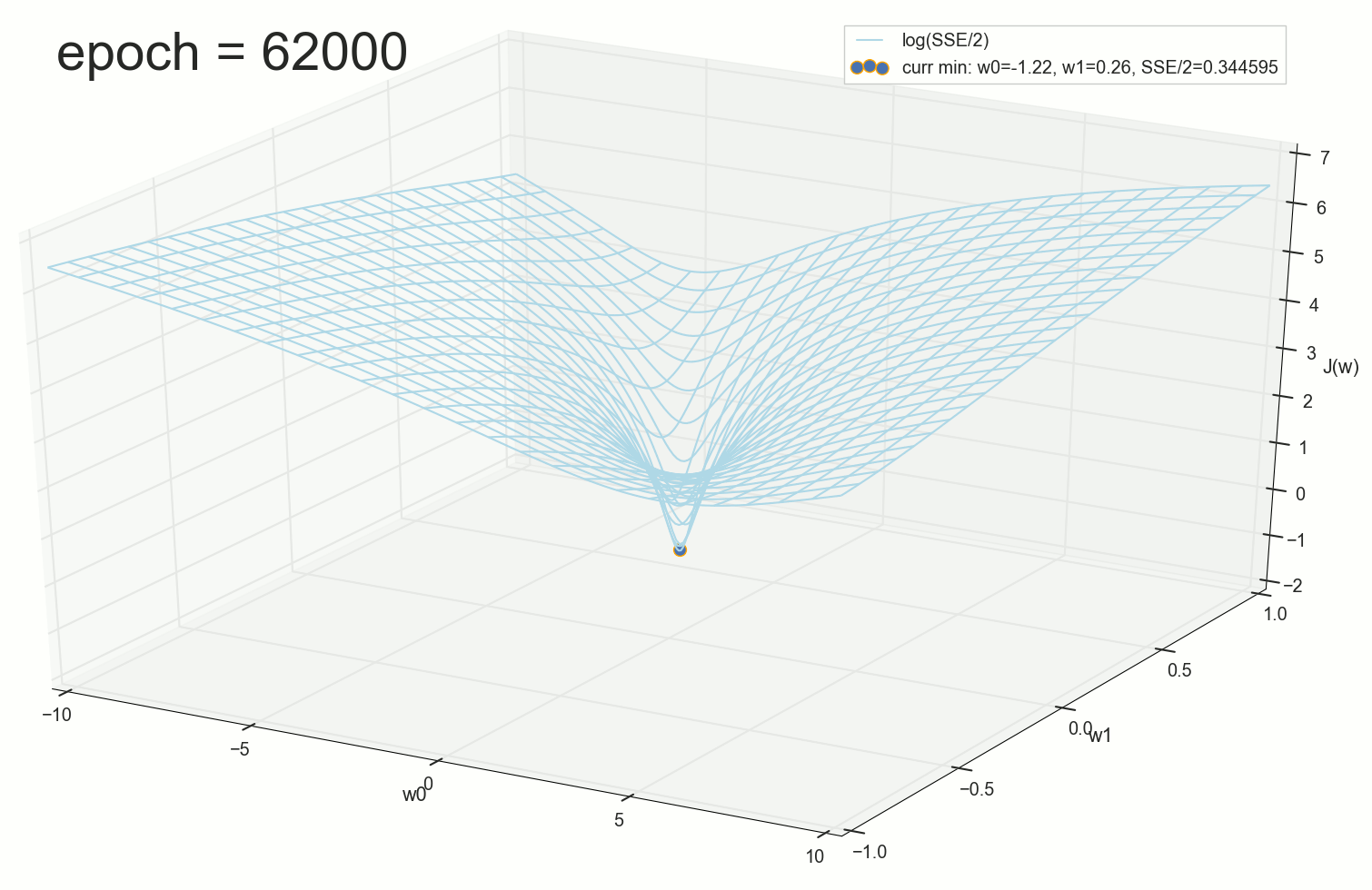
, 62000 :

:
. , : , , . , , , , , , . , , - .
, , - , - : , , , , , — . , , , , , , , — . ?
, . :
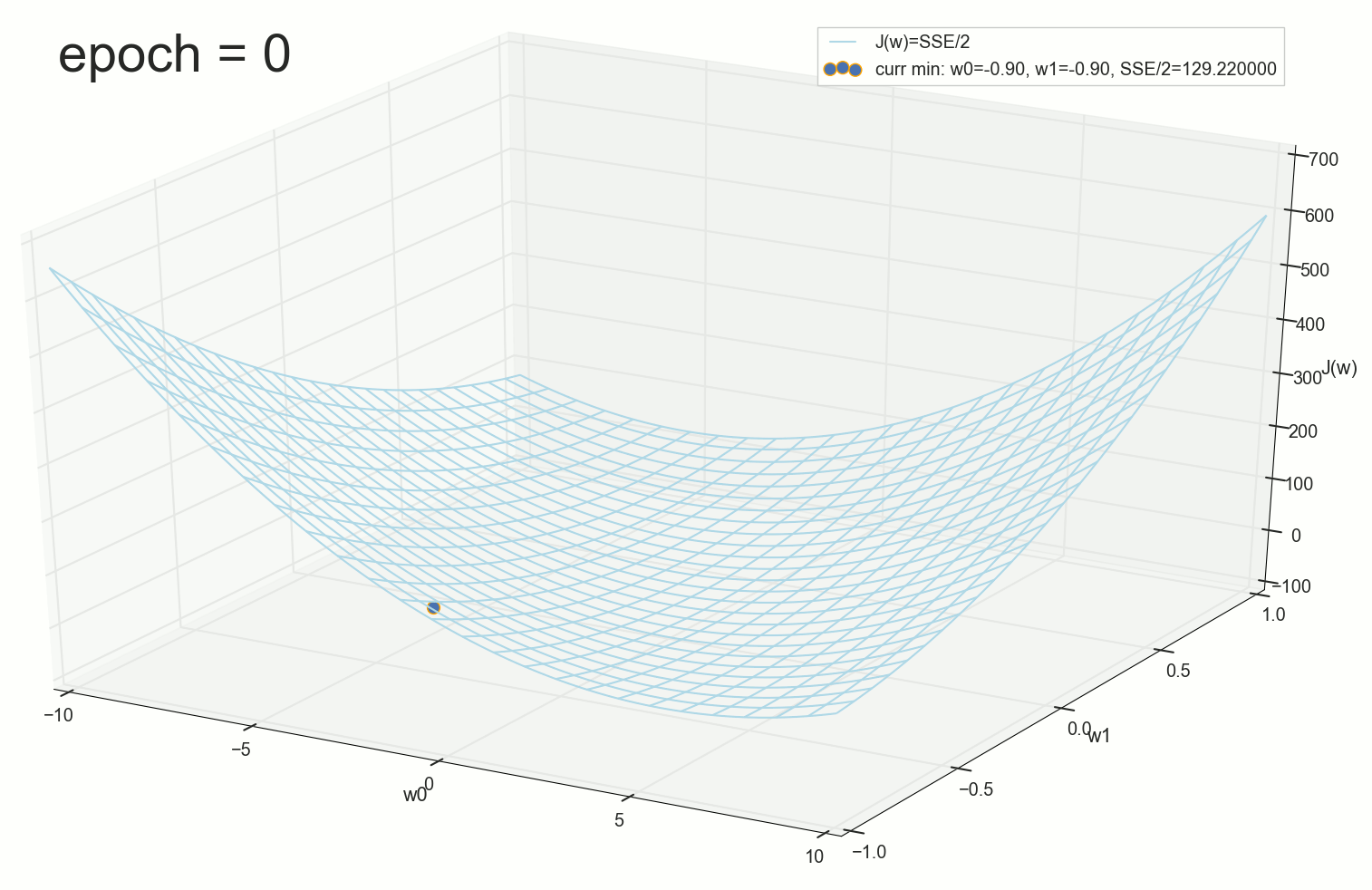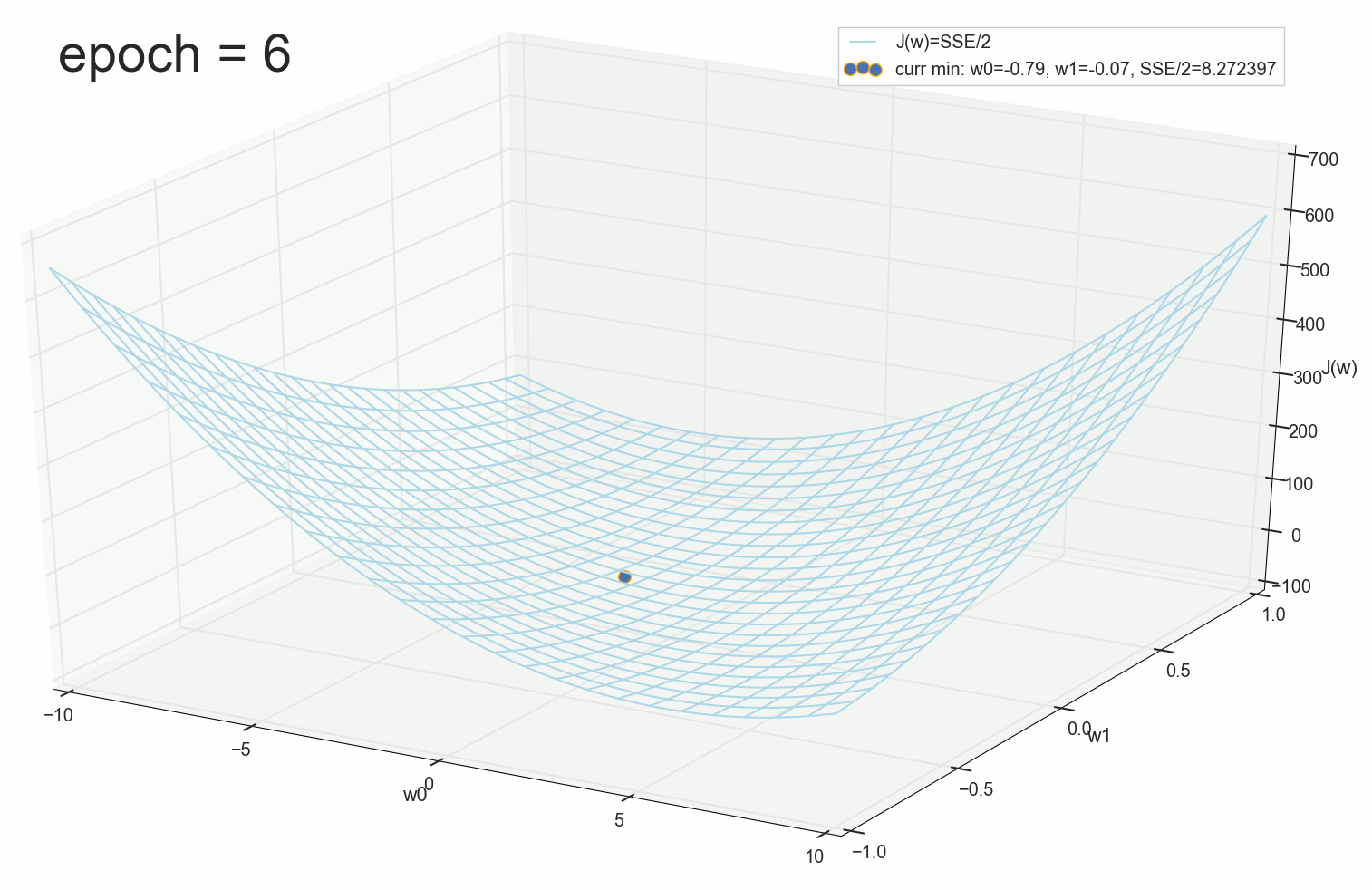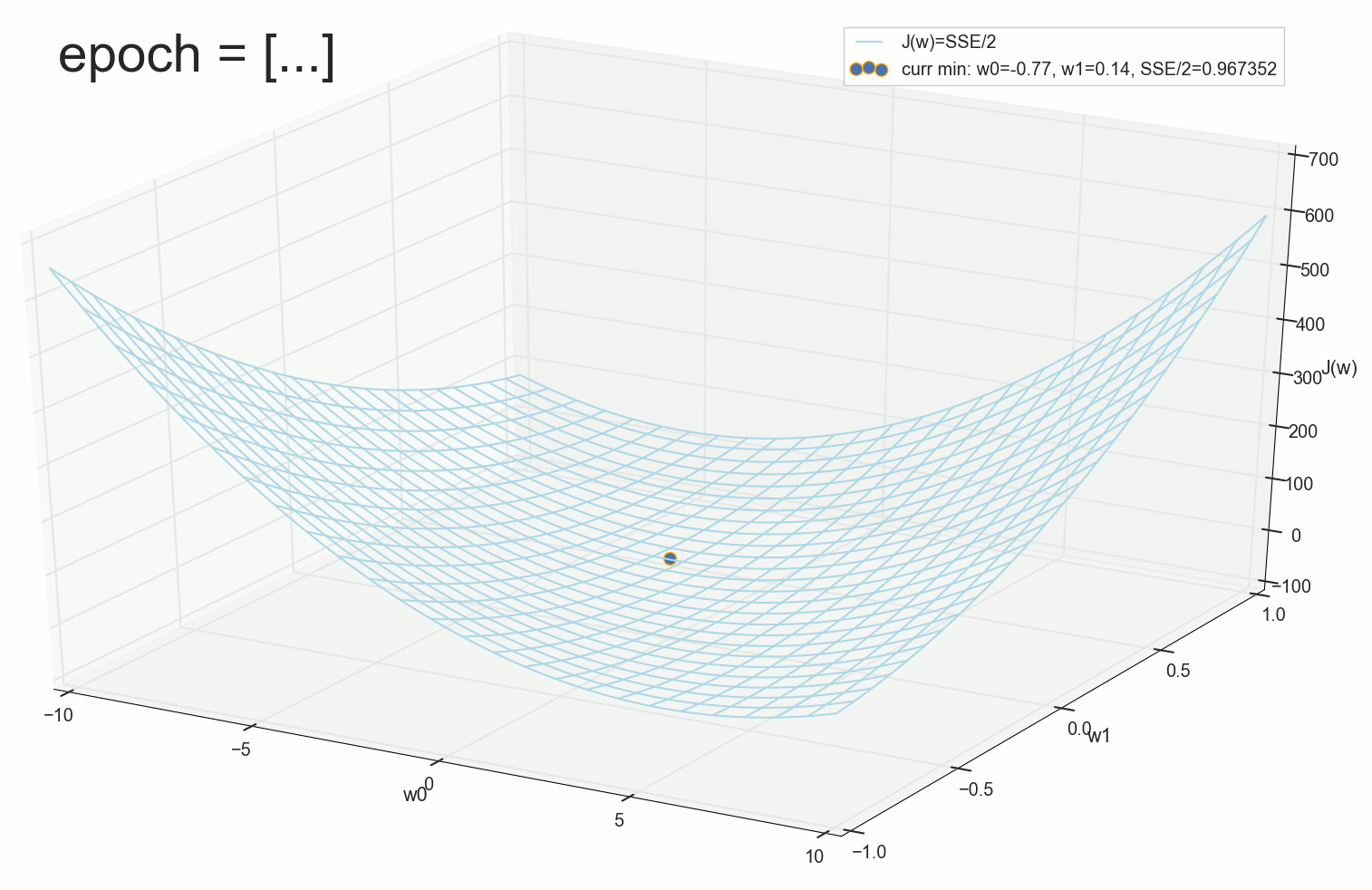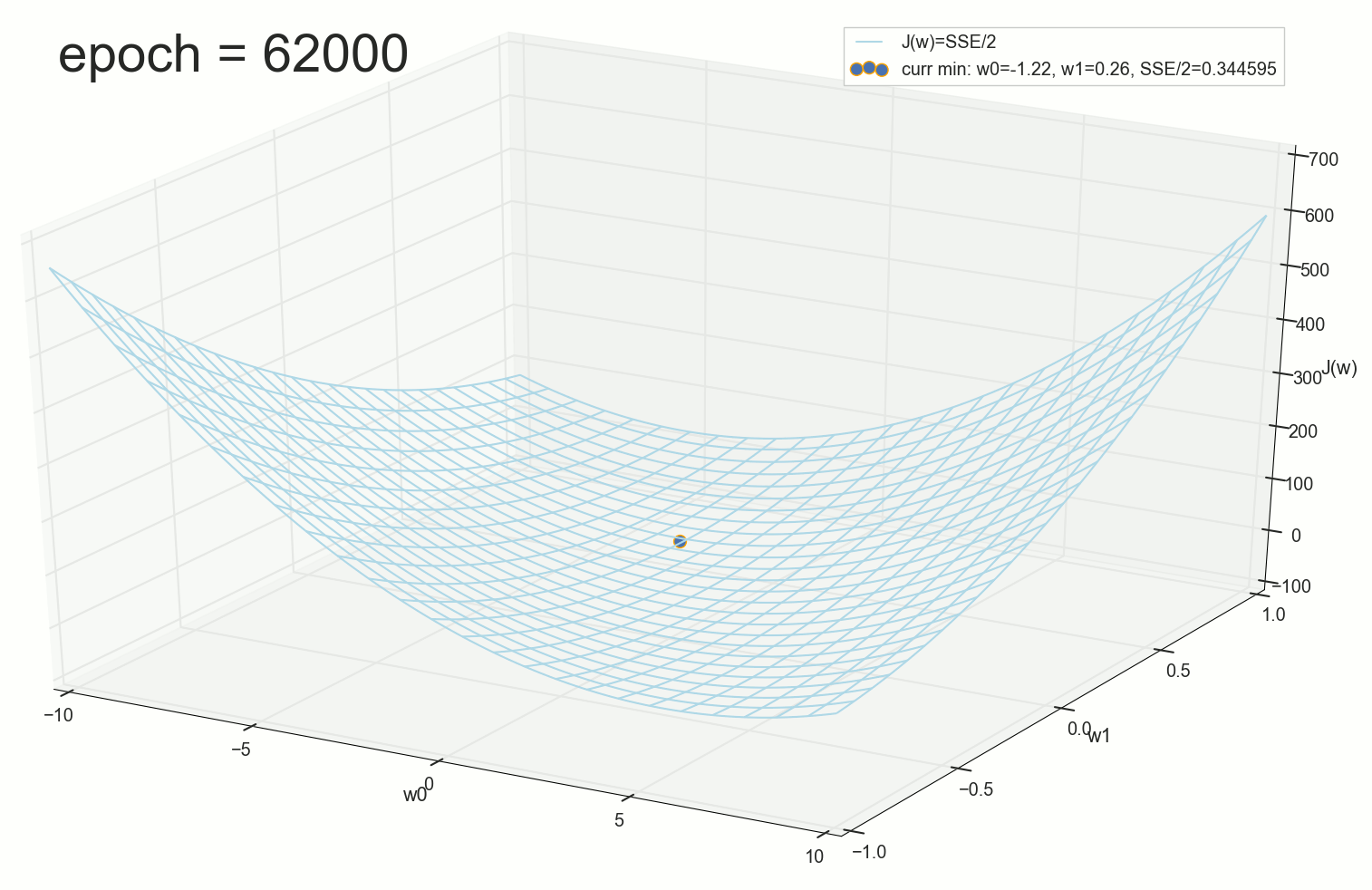
, , ( ). : , . , , .
. , .
. , , . , — .

— :

11- : , ; :

12- : , , :

50- : , 12-

1766: . J(w)=0.3456480221 — , , ( J(w)=0.3456478372 : 6- , , )

1767: J(w)=0.34564503 — , ( 6- , ). w0=−1.184831 . w1=0.258455 ( w0 2- : w0=−1.27 . w1=0.26 )

62000: J(w)=0.3445945 — , ( 2- ). :

:
. , , , , .
- η=0.001 , 10-12- ( )
- , , , (1767)
- — 60
- —
— ( , 1767): w0=−1.184831 . w1=0.258455 .
.
t(1)=(t(1)1)=(1.4) ( , t(i) — ). , .. , , ˆy=−1 , .. .
SUM=w0+w1∗t(1)1=−1.18+0.26∗1.4=−0.816
Φ(SUM)=SUM=−0.816
Φ(SUM)=−0.816<0⟹ˆy=−1
, .
: t(2)=(t(2)1)=(7)
Φ(SUM)=SUM=−1.18+0.26∗7=0.64⩾0⟹ˆy=1
ˆy=1 , .. . .
, ( «» ) 12 . , !
(m=2)
, , , . . , , .
— ( ). 2- .
- x=(x1,x2) ( , , )
- y={−1,1} ( , )
plt.scatter(X1[y == -1], X2[y == -1], s=400, c='red', marker='*', label=u': -1') plt.scatter(X1[y == 1], X2[y == 1], s=200, c='blue', marker='s', label=u': 1')

, .
Φ(x,w)=w0+w1x1+w2x2
, — , , 1- , 3-:

:

:

— :

() Φ(w)=0 (-). :

, , , , , ( , ). , . , , m=2, (m+1)=3: , — , , — , ( ).
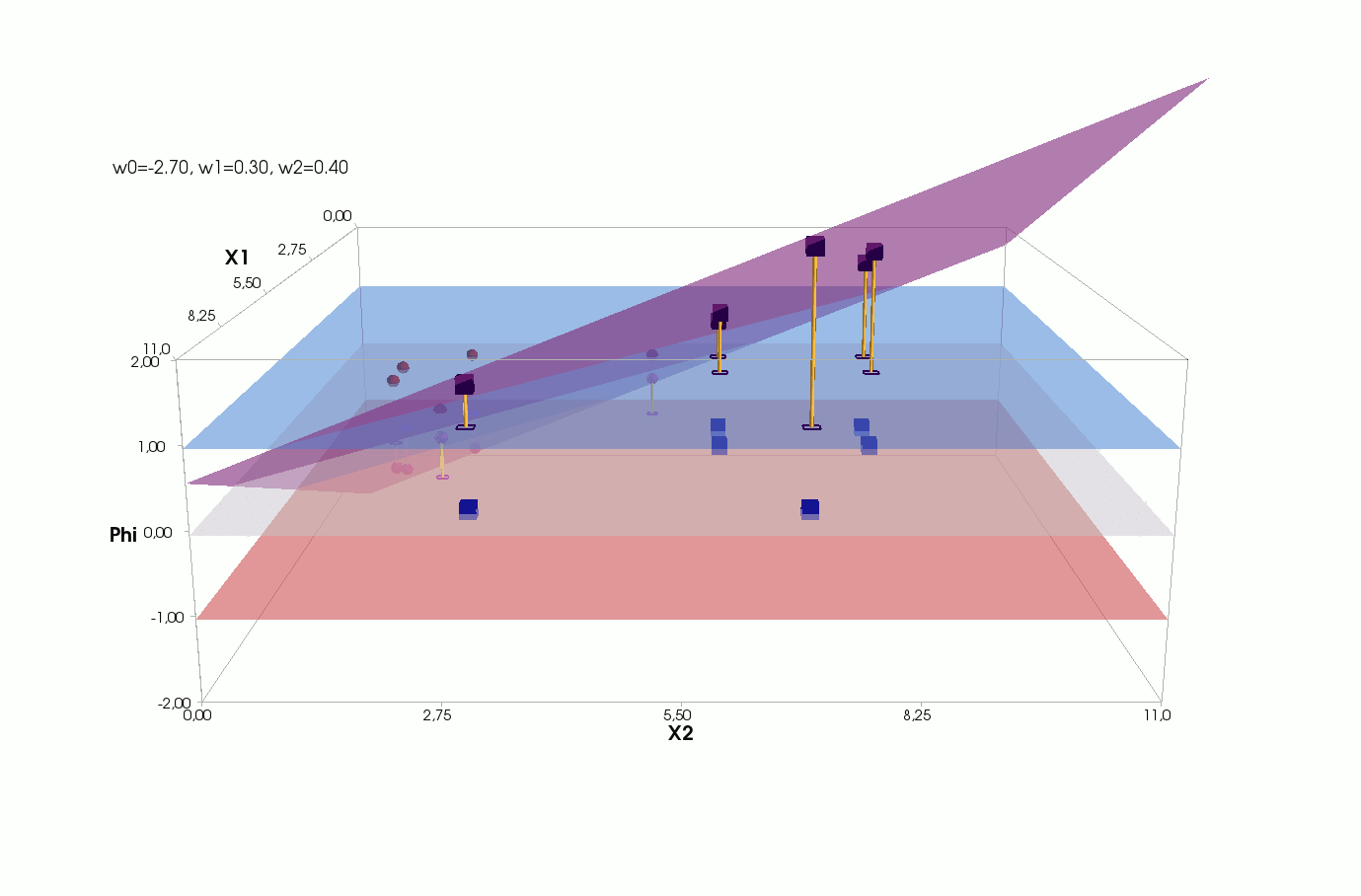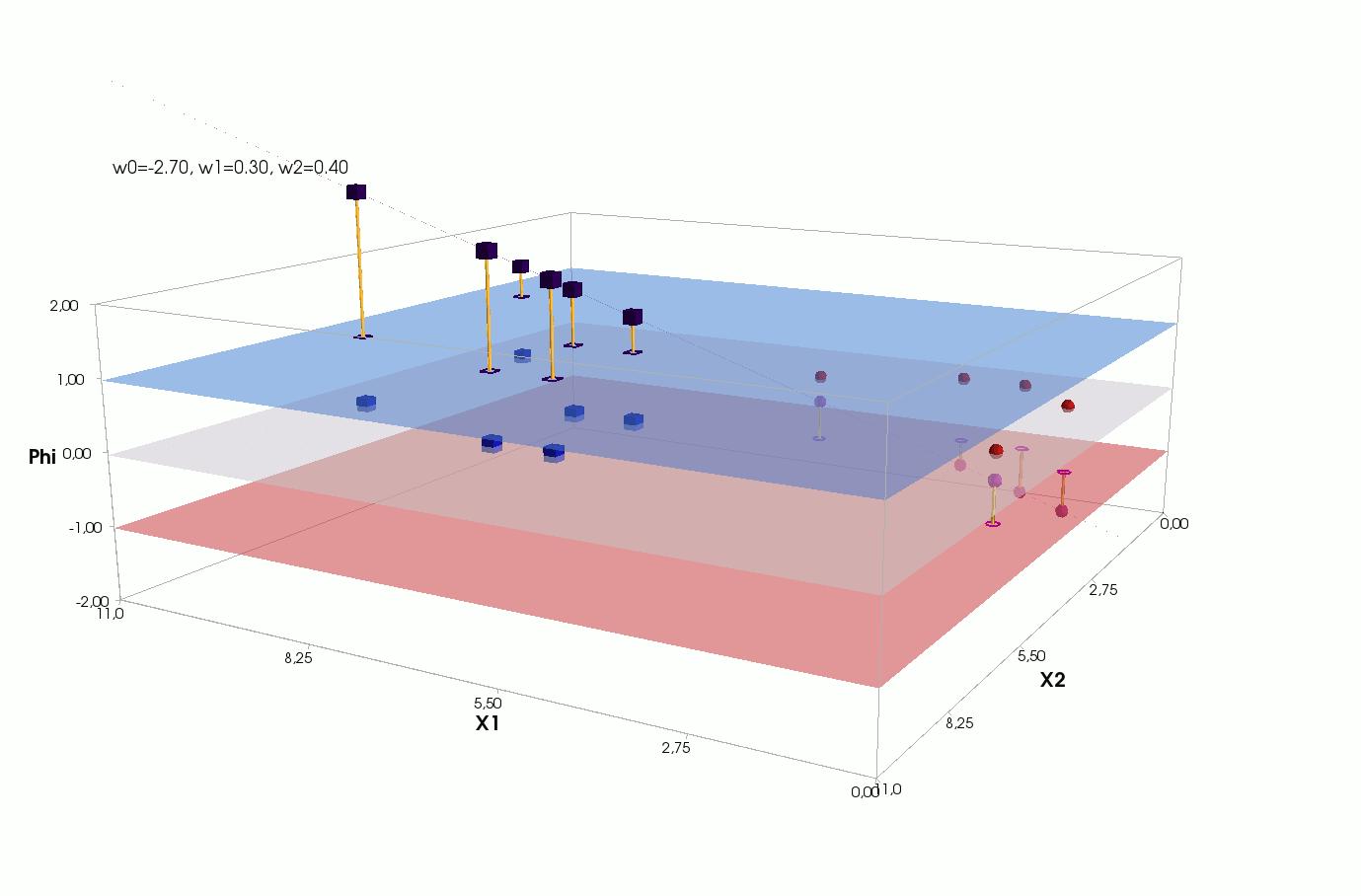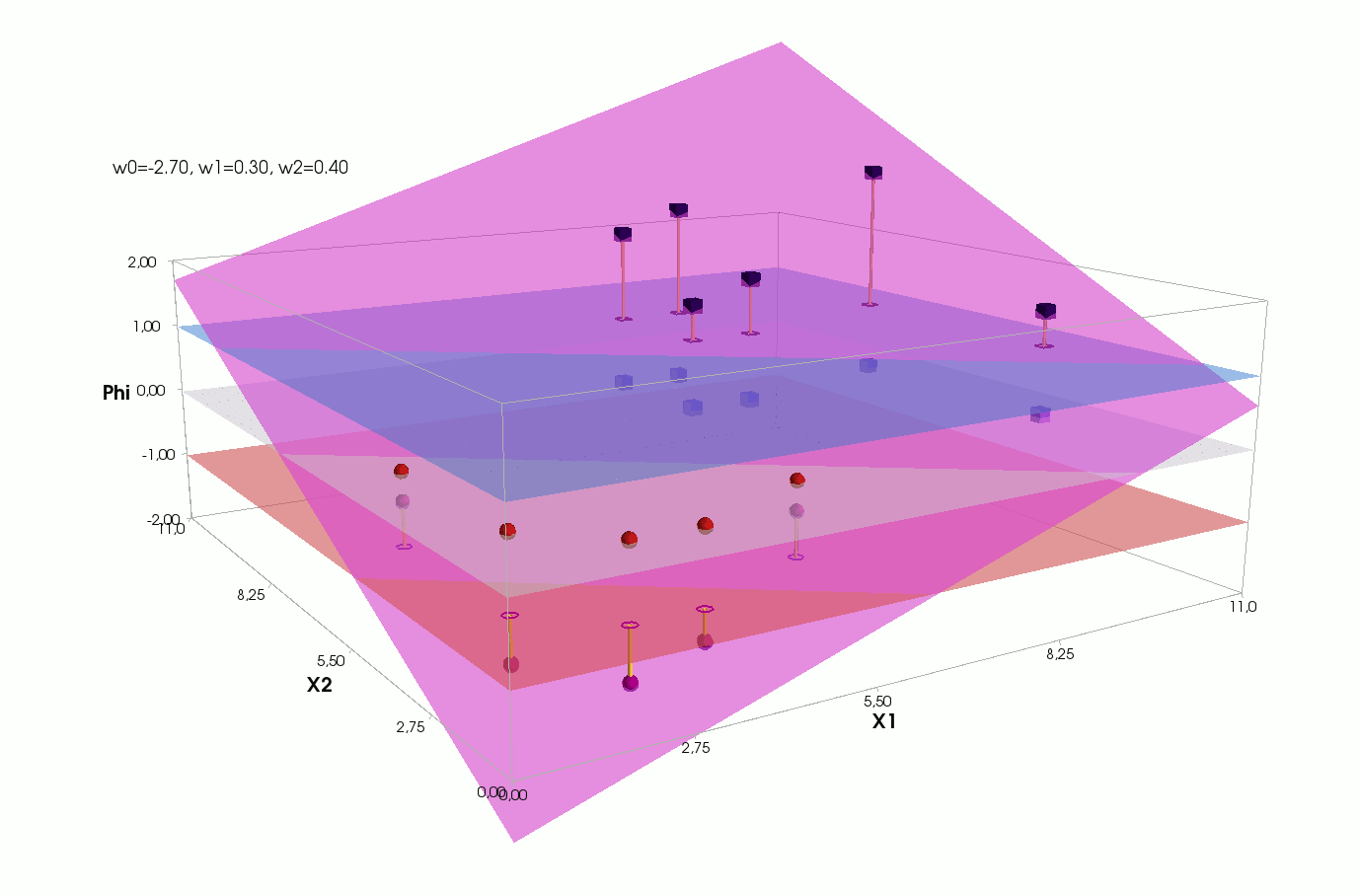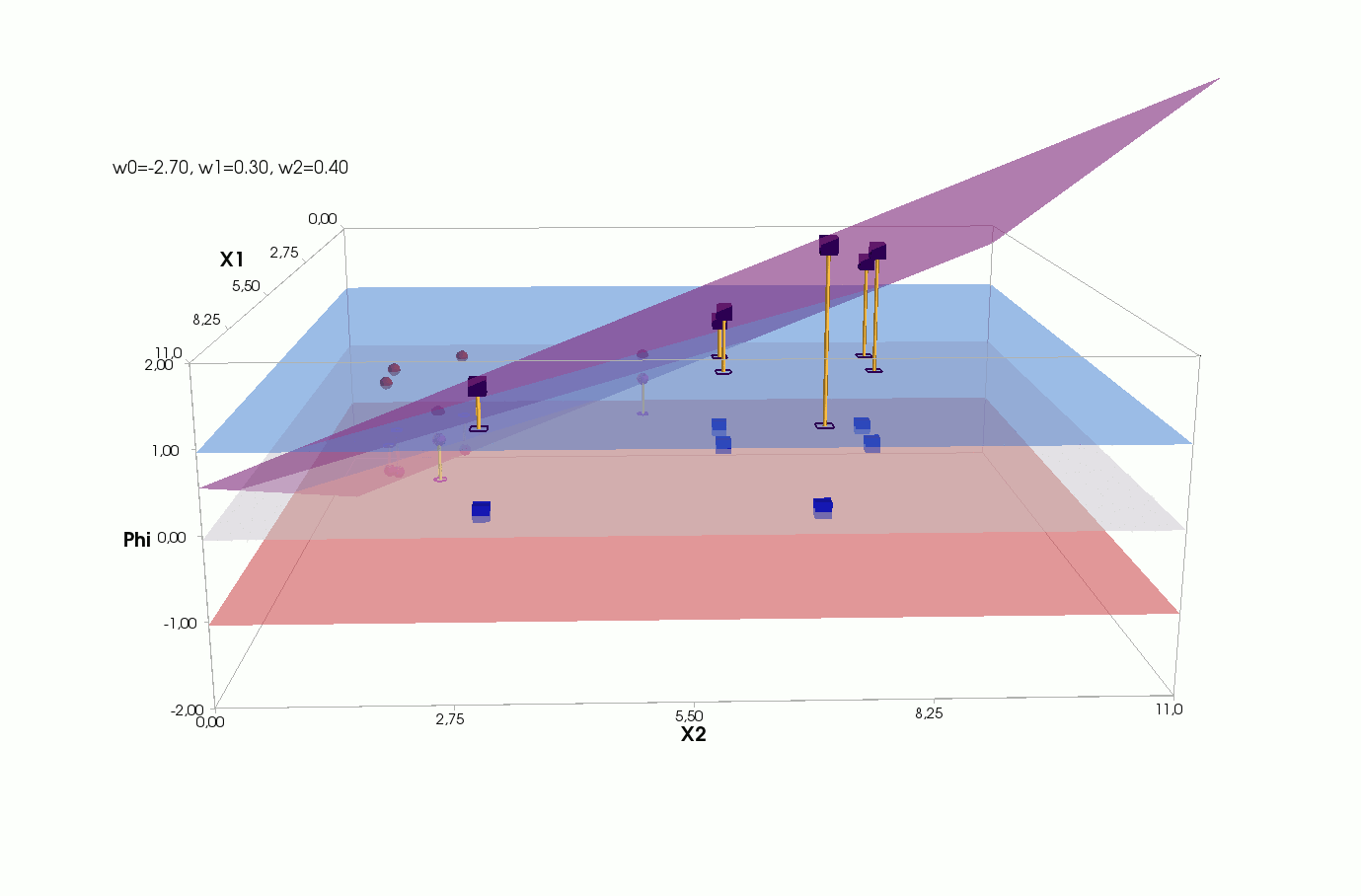
J(w)=12SSE=12n∑i=1(w0+w1x(i)1+w2x(i)2−y(i))2
() , .., , 3 + — 4 . , 2- 3- - 3-, , - 4- 3-, .
2- . , , 1- 2-.
∇J(w)=(∂J(w)∂w0,∂J(w)∂w1,∂J(w)∂w1),w=(w0,w1,w2)
( ):
∂J(w)∂w0=n∑i=1(w0+w1x(i)1+w2x(i)2−y(i))
∂J(w)∂w1=n∑i=1(w0+w1x(i)1+w2x(i)2−y(i))x(i)1
∂J(w)∂w2=n∑i=1(w0+w1x(i)1+w2x(i)2−y(i))x(i)2
:
Δw0=−η∂J(w)∂w0=−ηn∑i=1(w0+w1x(i)1+w2x(i)2−y(i))
Δw1=−η∂J(w)∂w1=−ηn∑i=1(w0+w1x(i)1+w2x(i)2−y(i))x(i)1
Δw2=−η∂J(w)∂w2=−ηn∑i=1(w0+w1x(i)1+w2x(i)2−y(i))x(i)2
3- ( 3- ), η=0.001 , w0=−0.9 . w1=−0.9 . w2=−0.9 .
— , , :


:

:

3- - :

4- :

60- — , :

70- , , :

200- — :

400- — :

:

, , w0 .
قانون
matplotlib ( mpl_toolkits.mplot3d.axis3d) ( , , 3). Mayavi .
import numpy from mayavi import mlab
, Mayavi , . , , , .
Mayavi, Matplotlib/axes3d, 3- OpenGL. , ( ) , Qt. mayavi . pip PyQt5 python-qt (, - , 'qt'). , , , , , :
env QT_API=pyqt python3 gradient-2d.py
— J(w)
def sse_(X1, X2, y, w0, w1, w2): return ((w0+w1*X1+w2*X2 - y)**2).sum()
12 :

70 :

, , : 6-12- , 70- — 70- , 30-, 40- 200-, , , , .
استنتاج
ADALINE (adaptive linear neuron — ) — . scikit-learn ADALINE ( - , ) , , - « 80-» (ADALINE 60-), .
«Python » ( scikit-learn) , - .
ADALINE .
-, — , : , , , .
-, () , , , ( , , y ) — , scikit-learn.
PS , ADALINE . , , , , ADALINE - , . , ADALINE . , - .