مرحبًا بك في المقالة التالية في
سلسلة من الألغاز التي طرحتها في مقابلات Google قبل حظرها بعد التسريب. منذ ذلك الحين ، توقفت عن العمل كمهندس برامج في Google وانتقلت إلى منصب مدير التطوير في Reddit ، لكن لا يزال لدي بعض الموضوعات الرائعة. لقد درسنا حتى الآن
البرمجة الديناميكية ،
ورفع المصفوفات إلى قوة ومرادفات الاستعلامات . هذه المرة سؤال جديد تماما.
لكن أولاً ، نقطتان. أولاً ، كان العمل في رديت رائعًا. على مدار الأشهر الثمانية الماضية ، قمت ببناء وقيادة فريق "صلة الإعلانات" الجديد وإنشاء مكتب تطوير جديد في نيويورك. بغض النظر عن مدى المتعة التي قد تكون ، لسوء الحظ ، وجدت أنه حتى وقت قريب لم يكن لدي وقت أو طاقة لمدونة. أخشى أن تخليت عن هذه السلسلة قليلاً. آسف على التأخير.
ثانياً ، إذا تابعت المقالات ، فبعد العدد الأخير ، قد تظن أنني سأبدأ في البحث في خيارات مرادف للاستعلامات. على الرغم من أنني أرغب في العودة إلى هذا الوقت ، يجب أن أعترف أنني فقدت الاهتمام الواجب بهذه المشكلة بسبب تغيير العمل وقررت حتى الآن تأجيلها. ومع ذلك ، البقاء على اتصال! أنا مدين لي ، وأعتزم إعادته. فقط ، كما تعلمون ، بعد قليل ...
إخلاء سريع: على الرغم من أن إجراء المقابلات مع المرشحين يعد أحد واجباتي المهنية ، إلا أن هذه المدونة تقدم ملاحظاتي الشخصية والقصص الشخصية والآراء الشخصية. من فضلك لا تأخذ هذا لأي بيان رسمي من جوجل ، الأبجدية ، رديت أو أي شخص أو مؤسسة أخرى.ابحث عن سؤال جديد
في
مقال سابق ، وصفت أحد أسئلتي المفضلة التي استخدمتها لفترة طويلة ، قبل التسرب المحتوم. كانت الأسئلة السابقة رائعة من وجهة نظر نظرية ، لكنني أردت اختيار مشكلة أكثر ارتباطًا بـ Google كشركة. عندما تم حظر هذا السؤال ، أردت العثور على بديل مع مراعاة التقييد الجديد: لجعل السؤال
أكثر بساطة .
الآن قد يبدو هذا مفاجئًا بعض الشيء نظرًا لعملية المقابلة الشائنة في Google. لكن في ذلك الوقت كانت المشكلة الأكثر بساطة منطقية. يتكون منطقي من جزأين. الأولى براغماتية: عادةً ما لم يتعامل المرشحون جيدًا مع الأسئلة السابقة ، على الرغم من التلميحات والتبسيط العديدة ، ولم أكن متأكدًا دائمًا من السبب. النقطة النظرية الثانية: يجب أن تقسم عملية المقابلة المرشحين إلى فئتي "تستحق التعيين" و "لا تستحق التعيين" ، وكنت فضولية إذا كان ذلك يمكن أن يكون أسهل مع السؤال.
قبل توضيح هاتين النقطتين ، أود أن أوضح ما
لا يعنيه. "لست متأكدًا دائمًا من سبب تعرض الشخص لمشاكل" لا يعني عدم جدوى الأسئلة وأردت تبسيط المقابلة لهذا السبب. حتى أصعب سؤال ، تعامل كثيرون بشكل جيد. أعني أنه عندما يواجه المرشحون مشاكل ، كان من الصعب علي أن أفهم ما الذي فقدوه.
المقابلات الجيدة تعطي صورة واسعة عن نقاط القوة والضعف في المرشح. لا يكفي أن تقول لجنة التوظيف ببساطة إنها "فاشلة": تحدد اللجنة ما إذا كان المرشح لديه صفات خاصة بالشركة التي يبحثون عنها. وبالمثل ، فإن كلمات "إنه لطيف" لا تساعد اللجنة على اتخاذ قرار بشأن مرشح قوي في بعض المجالات ، ولكن مشكوك فيه في مجالات أخرى. لقد وجدت أن القضايا الأكثر تعقيدًا تفصل المرشحين في هاتين الفئتين. في ضوء ذلك ، "لست متأكدًا دائمًا من سبب تعرض الشخص لمشاكل" ، يعني "عدم القدرة على التقدم بشأن هذه المسألة في حد ذاته لا يرسم صورة لقدرات هذا المرشح".
لا يعني تصنيف المرشحين على أنهم "يستحقون التوظيف" و "لا يستحق التوظيف" أن عملية المقابلة يجب أن تفصل بين المرشحين الأغبياء عن المرشحين الأذكياء. لا أستطيع أن أتذكر مرشحًا واحدًا لم يكن ذكيًا وموهوبًا ومتحمسًا. جاء الكثير منهم من جامعات ممتازة ، وكان الباقون متحمسين للغاية. إن اجتياز المقابلات الهاتفية يعد غربالًا جيدًا بالفعل ، وحتى الرفض في هذه المرحلة ليس علامة على نقص القدرة.
ومع ذلك ، يمكنني
أن أذكر الكثيرين الذين لم يكونوا مستعدين بما يكفي للمقابلة أو عملوا ببطء شديد ، أو طلبوا الكثير من الإشراف لحل المشكلة ، أو التواصل بطريقة غير واضحة ، أو لم يتمكنوا من ترجمة أفكارهم إلى كود ، أو شغلوا منصبًا ببساطة لن يؤدي نجاحه على المدى الطويل ، وما إلى ذلك. تعريف "يستحق التوظيف" غامض ويختلف حسب الشركة ، وعملية المقابلة هي تحديد ما إذا كان كل مرشح يفي بمتطلبات شركة معينة.
قرأت الكثير من التعليقات غير الرسمية تشكو من أسئلة المقابلة المفرطة التعقيد. كنت فضولية إذا كان لا يزال من الممكن تقديم توصية جديرة / لا تستحق لمهمة أكثر بساطة. كنت أظن أن هذا سيعطي إشارة مفيدة دون الصراخ بلا داع لأعصاب المرشح. سأخبرك عن استنتاجاتي في نهاية المقال ...
مع هذه الأفكار ، كنت أبحث عن سؤال جديد. في عالم مثالي ، هذا سؤال بسيط يكفي لحله في غضون 45 دقيقة ، ولكن مع أسئلة إضافية حتى يتمكن المرشحون الأقوى من إظهار مهاراتهم. يجب أن يكون أيضًا مضغوطًا في التنفيذ ، لأن العديد من المرشحين ما زالوا يكتبون على السبورة. ميزة إضافية كبيرة إذا كان الموضوع مرتبطًا بطريقة ما بمنتجات Google.
أخيرًا ، استقرت على سؤال وصفه بعض موظفي Google الرائعين بعناية وأدرجوه في قاعدة بيانات الأسئلة الخاصة بنا. لقد استشرت الآن مع زملائي السابقين وتأكدت من أن السؤال لا يزال محظورًا ، لذا لن يتم طرحك في المقابلة بالتأكيد. أقدمها بالشكل الذي يبدو لي أنه الأكثر فعالية ، مع اعتذار للمؤلف الأصلي.
السؤال
تحدث عن قياس المسافات.
Hand هي وحدة قياس أربعة بوصات شائعة الاستخدام في البلدان الناطقة باللغة الإنجليزية لقياس ارتفاع الخيل.
السنة الضوئية هي وحدة قياس أخرى تساوي المسافة التي يسافر بها جسيم (أو موجة؟) من الضوء في عدد معين من الثواني ، أي ما يعادل تقريبًا سنة أرضية واحدة. للوهلة الأولى ، لديهم القليل من القواسم المشتركة مع بعضها البعض ، إلا أنها تستخدم لقياس المسافة. لكن اتضح أن Google يمكنها تحويلها بسهولة تامة:
قد يبدو هذا واضحًا: في النهاية ، كلاهما يقيسان المسافة ، لذلك من الواضح أن هناك تحولًا. لكن إذا فكرت في الأمر ، فهذا غريب بعض الشيء: كيف قاموا بحساب معدل التحويل هذا؟ بوضوح ، لا أحد يحسب عدد الأيدي في السنة الضوئية. في الواقع ، لا تحتاج إلى أن تأخذ هذا مباشرة. يمكنك ببساطة استخدام التحويلات المعروفة:
- 1 يد = 4 بوصات
- 4 بوصات = 0.33333 قدم
- 0.33333 قدم = 6.3125e - 5 أميال
- 6.3125e - 5 أميال = 1.0737e - 17 سنة ضوئية
الهدف من المهمة هو تطوير نظام يقوم بهذا التحول. على وجه الخصوص:
في المدخلات لديك قائمة بعوامل التحويل (منسقة باللغة التي اخترتها) في شكل مجموعة من الوحدات الأولية للقياس والوحدات والعوامل النهائية ، على سبيل المثال:
قدم 12
ساحة القدم 0.3333333
ور. د.
بحيث ORIGIN * MULTIPLIER = DESTINATION. قم بتطوير خوارزمية تأخذ قيمتين اعتباطيتين وتعيد معامل التحويل بينهما.
المناقشة
أحب هذه المشكلة لأنها تحتوي على إجابة بديهية وواضحة: فقط قم بالتحويل من وحدة إلى أخرى ، ثم إلى أخرى ، حتى تجد الهدف! لا أستطيع أن أتذكر مرشحًا واحدًا واجه هذه المشكلة وكان في حيرة من طريقة حلها تمامًا. يتناسب هذا بشكل جيد مع متطلبات وجود مشكلة "أبسط" ، حيث كانت المشكلات السابقة تتطلب عادة دراسة مطولة وتفكير قبل العثور على نهج أساسي على الأقل للحل.
ومع ذلك ، فشل العديد من المرشحين في إدراك حدسهم كحل عملي دون تلميحات واضحة. واحدة من مزايا هذا السؤال هو أنه يختبر قدرة المرشح على صياغة المشكلة (لجعل تأطير) بحيث يفسح المجال للتحليل والترميز. كما سنرى ، هناك امتداد ممتع للغاية يتطلب قفزة مفاهيمية جديدة.
بالنسبة للسياق ، فإن تأطير هو فعل ترجمة مشكلة مع حل غير واضح إلى مشكلة معادلة ، حيث يتم استنتاج الحل بطريقة طبيعية. إذا كان هذا يبدو مجرّدًا وغير قابل للتحصيل تمامًا ، فأنا آسف ، لكنه كذلك. سأشرح ما أعنيه عندما أقدم الحل الأولي لهذه المشكلة. الجزء الأول من الحل سيكون تمرينًا في تطوير وتطبيق المعرفة الحسابية. الجزء الثاني سيكون تمرينًا لمعالجة هذه المعرفة من أجل الوصول إلى تحسين جديد وغير واضح.
الجزء 0. الحدس
قبل الحفر بشكل أعمق ، دعنا نستكشف الحل "الواضح" بالكامل. معظم التحويلات المطلوبة بسيطة ومباشرة. يعرف أي أمريكي سافر خارج الولايات المتحدة أن معظم العالم يستخدم الوحدة الغامضة "كيلومتر" لقياس المسافات. للتحويل ، تحتاج فقط إلى ضرب عدد الأميال بحوالي 1.6.
لقد صادفنا مثل هذه الأشياء لمعظم حياتنا. بالنسبة لمعظم الوحدات ، يوجد بالفعل تحويل محسوب مسبقًا ، لذلك تحتاج فقط إلى النظر إليه في الجدول المقابل. ولكن إذا لم يكن هناك تحويل مباشر (على سبيل المثال ، من الأيدي إلى السنوات الضوئية) ، فمن المنطقي إنشاء مسار تحويل ، كما هو موضح أعلاه:
- 1 يد = 4 بوصات
- 4 بوصات = 0.33333 قدم
- 0.33333 قدم = 6.3125e - 5 أميال
- 6.3125e - 5 أميال = 1.0737e - 17 سنة ضوئية
كان الأمر بسيطًا جدًا ، لقد توصلت للتو إلى مثل هذا التحول باستخدام مخيلتي وجدول تحويل قياسي! ومع ذلك ، تبقى بعض الأسئلة. هل هناك طريقة أقصر؟ ما مدى دقة المعامل؟ هل التحويل ممكن دائما؟ هل من الممكن لأتمتة ذلك؟ لسوء الحظ ، هنا ينهار النهج الساذج.
الجزء 1. قرار ساذج
من الجيد أن المشكلة لها حل بديهي ، ولكن في الواقع ، فإن هذه البساطة تشكل عقبة أمام حل المشكلة. لا يوجد شيء أصعب من محاولة فهم ما تفهمه بالفعل بطريقة جديدة - ليس أقله لأنك غالبًا ما تعرف أقل مما تعتقد. لتوضيح ذلك ، تخيل أنك جئت لإجراء مقابلة - ولديك هذه الطريقة البسيطة في رأسك. لكنه لا يسمح بحل عدد من المشاكل المهمة.
على سبيل المثال ، ماذا لو
لم يكن
هناك تحويل ؟ النهج الواضح لا يقول شيئًا ، هل من الممكن بالفعل التحويل من وحدة إلى أخرى. إذا أعطوني ألف معدل تحويل ، فسيكون من الصعب جدًا تحديد ما إذا كان ذلك ممكنًا من حيث المبدأ. إذا طُلب مني إجراء تحويل بين وحدات غير مألوفة (أو مخترعة) من
مؤشر و
jab ، فعندئذ ليس لدي أي فكرة من أين أبدأ. كيف نهج بديهية تساعد هنا؟
يجب أن أعترف أن هذا هو نوع من السيناريو المفترض ، ولكن هناك أيضًا سيناريو أكثر واقعية. ترى أن بياني للمشكلة يشمل فقط وحدات من المسافة. يتم ذلك عن قصد. ماذا لو طلبت من النظام التحويل من بوصة إلى كيلوغرام؟ أنت وأنا وأعلم أن هذا غير ممكن لأنهم يقيسون أنواعًا مختلفة ، لكن الإدخال لا يقول شيئًا عن "النوع" الذي تقيسه كل وحدة.
وهنا تسمح صياغة دقيقة للسؤال للمرشحين الأقوياء بإثبات أنفسهم.
قبل تطوير الخوارزمية ، يفكرون في الحالات القصوى للنظام. ومثل هذا البيان للمشكلة يعطيهم عن قصد الفرصة لتسألني ما إذا كنا سنترجم وحدات مختلفة. هذه ليست مشكلة كبيرة إذا حدثت في مرحلة مبكرة ، لكنها دائماً علامة جيدة عندما يسألني أحدهم مقدمًا: "ما الذي يجب أن يعود به البرنامج إذا كان التحويل غير ممكن؟" طرح السؤال بهذه الطريقة يعطيني فكرة عن قدرات المرشح قبل أن يكتب سطرًا واحدًا على الأقل من التعليمات البرمجية.
عرض الرسم البيانيمن الواضح أن النهج الساذج غير مناسب ، لذلك نحن بحاجة إلى التفكير في كيفية إجراء هذا التحويل؟ الجواب هو النظر في الوحدات على أنها رسم بياني. هذه هي قفزة التفاهم الأولى اللازمة لحل هذه المشكلة.
على وجه الخصوص ، تخيل أن كل وحدة هي عقدة في الرسم البياني ، وهناك حافة من العقدة
A إلى العقدة
B إذا كان من الممكن تحويل
A إلى
B :
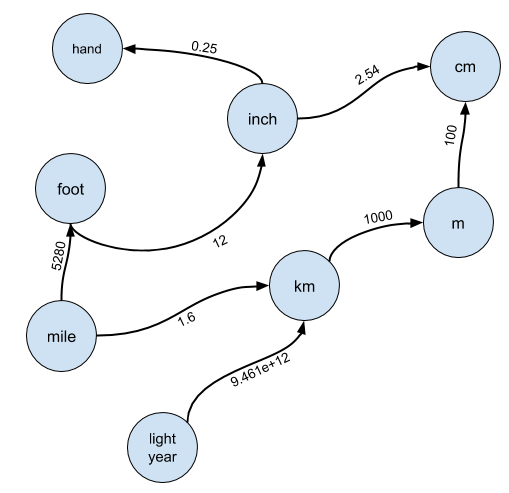
يتم تمييز الحواف بمعدل تحويل يجب عليك ضرب
A للحصول على
Bكنت أتوقع دائمًا أن يتوصل المرشح إلى مثل هذا الإطار ، ونادراً ما أعطى تلميحات خطيرة له. يمكنني أن أسامح المرشح الذي لا يلاحظ حل مشكلة استخدام مجموعات مفككة أو ليس على دراية كبيرة بالجبر الخطي لإدراك الحل الذي يقلل من إعادة رفع إلى قوة مصفوفة المجاورة ، ولكن يتم تدريس الرسوم البيانية في أي منهج أو دورة برمجة. إذا لم يكن لدى المرشح المعرفة المناسبة ، فهذه إشارة "لا توظيف".
في أي حال،تمثيل الرسم البياني يقلل من حل مشكلة البحث الرسم البياني الكلاسيكية. على وجه الخصوص ، هناك خوارزمتان مفيدتان هنا: البحث الواسع (BFS) والبحث العميق (DFS). عند البحث في العرض ، نقوم بفحص العقد وفقًا لبعدها عن الأصل:
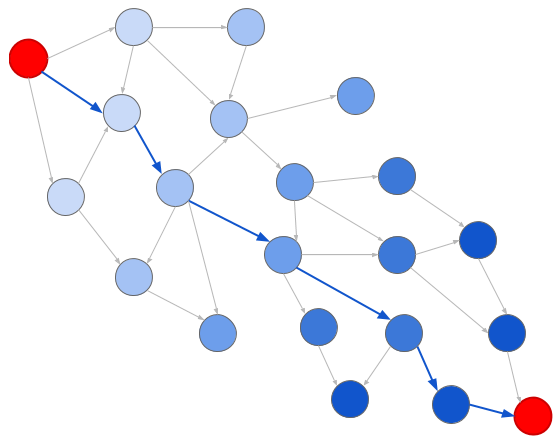البلوز الغامق يعني الأجيال اللاحقةوعند البحث بتعمق ، نقوم بفحص العقد بالترتيب الذي تحدث به:
البلوز الغامق يعني أيضًا الأجيال اللاحقة. يرجى ملاحظة أننا لا في الواقع زيارة جميع المواقعتحدد أي من الخوارزميات بسهولة ما إذا كان هناك تحويل من وحدة إلى أخرى ، وهو ما يكفي ببساطة للبحث في الرسم البياني. نبدأ من وحدة المصدر والبحث حتى نجد وحدة الوجهة. إذا لم تتمكن من العثور على وجهتك (كما لو كنت تحاول تحويل البوصات إلى كيلوغرامات) ، فإننا نعلم أنه لا توجد طريقة.
ولكن مهلا ، هناك شيء مفقود. لا نريد البحث عن طريقة ، نريد إيجاد معدل تحويل! هذا هو المكان الذي يجب أن يقوم فيه المرشح بالقفز: اتضح أنه يمكنك تعديل أي خوارزمية بحث لحساب معدل التحويل عن طريق حفظ الحالة الإضافية بمجرد تقدمك. هذا هو المكان الذي لم تعد فيه الرسوم التوضيحية منطقية ، لذلك دعونا نتعمق في الكود.
أولاً ، تحتاج إلى تحديد بنية بيانات الرسم البياني ، لذلك نستخدم هذا:
class RateGraph(object): def __init__(self, rates): 'Initialize the graph from an iterable of (start, end, rate) tuples.' self.graph = {} for orig, dest, rate in rates: self.add_conversion(orig, dest, rate) def add_conversion(self, orig, dest, rate): 'Insert a conversion into the graph.' if orig not in self.graph: self.graph[orig] = {} self.graph[orig][dest] = rate def get_neighbors(self, node): 'Returns an iterable of the nodes neighboring the given node.' if node not in self.graph: return None return self.graph[node].items() def get_nodes(self): 'Returns an iterable of all the nodes in the graph.' return self.graph.keys()
ثم دعونا نبدأ في DFS. هناك العديد من الطرق لتنفيذه ، لكن الأكثر شيوعًا هو الحل العودية. لنبدأ بهذا:
from collections import deque def __dfs_helper(rate_graph, node, end, rate_from_origin, visited): if node == end: return rate_from_origin visited.add(node) for unit, rate in rate_graph.get_neighbors(node): if unit not in visited: rate = __dfs_helper(rate_graph, unit, end, rate_from_origin * rate, visited) if rate is not None: return rate return None def dfs(rate_graph, node, end): return __dfs_helper(rate_graph, node, end, 1.0, set())
باختصار ، تبدأ هذه الخوارزمية بعقدة واحدة ، وتتكرر على جيرانها وتزور كل منهم فورًا ، وتجري مكالمة متكررة إلى الوظيفة. كل استدعاء دالة على المكدس يحفظ حالة التكرار الخاصة به ، لذلك عندما يتم إرجاع زيارة متكررة ، يستمر الوالد على الفور في التكرار. نتجنب زيارة الموقع نفسه مرة أخرى عن طريق الحفاظ على مجموعة من المواقع التي تمت زيارتها في جميع المكالمات. نحسب أيضًا المعامل بتعيين عامل تحويل بين كل عقدة والمصدر. وبالتالي ، عندما نواجه العقدة / الكتلة المستهدفة ، قمنا بالفعل بإنشاء معامل التحويل من العقدة المصدر ، ويمكننا ببساطة إرجاعه.
هذا تطبيق رائع ، لكنه يعاني من عيبين رئيسيين. أولا ، هو تكراري. إذا اتضح أن المسار المرغوب يتكون من أكثر من ألف القفزات ، فسوف نطير مع خلل. بالطبع ، هذا أمر غير مرجح ، لكن إذا كان هناك شيء غير مقبول لخدمة طويلة الأجل ، فهذا فشل. ثانياً ، حتى إذا أكملنا بنجاح ، فإن الإجابة لها بعض الخصائص غير المرغوب فيها.
أنا فعلا أعطى بالفعل تلميحا في بداية هذا المنصب. هل لاحظت كيف تعرض Google معدل التحويل من
1.0739e-17 ، لكن حسابي اليدوي يعطي
1.0737e-17 ؟ اتضح أن كل هذه مضاعفات الفاصلة العائمة تجعل المرء يفكر بالفعل في نشر الخطأ. هناك الكثير من الفروق الدقيقة لهذه المقالة ، ولكن خلاصة القول هي أنك تحتاج إلى تقليل مضاعفة الفاصلة العائمة لتجنب الأخطاء التي تتراكم وتتسبب في حدوث مشكلات.
DFS هو خوارزمية بحث كبيرة. إذا كان الحل موجودًا ، فسيجده. لكنه يفتقر إلى خاصية رئيسية: فهو لا يجد بالضرورة أقصر الطرق. هذا مهم بالنسبة لنا لأن المسار الأقصر يعني عدد أقل من القفزات والخطأ أقل بسبب مضاعفات الفاصلة العائمة. لحل المشكلة ، ننتقل إلى BFS.
الجزء 2. حل BFS
في هذه المرحلة ، إذا نجح المرشح في تنفيذ حل DFS تكراري وتوقف عنده ، عادةً ما أقدم توصية ضعيفة بشأن تعيين هذا المرشح. لقد فهم المشكلة ، واختار الإطار المناسب ونفذ حلاً فعالاً. هذا قرار ساذج ، لذلك أنا لا أصر على تعيينه ، لكن إذا تعامل مع مقابلات أخرى ، فلن أوصي بالرفض.
هذا يستحق التكرار: إذا كنت في شك ، فاكتب حلاً ساذجًا! حتى لو لم يكن الأمر مثاليًا تمامًا ، فإن وجود الشفرة على اللوحة يعد بالفعل إنجازًا ، وغالبًا ما يمكن العثور على الحل المناسب على أساسه. سأقول بشكل مختلف: لا تعمل أبدًا من أجل لا شيء. على الأرجح ، فكرت في حل ساذج ، لكنك لم ترغب في تقديمه ، لأنك تعلم أنه ليس الأمثل. إذا كنت مستعدًا لوضع أفضل حل في الوقت الحالي ، فهذا جيد ، ولكن إذا لم يكن كذلك ، فقم بتسجيل التقدم المحرز قبل الانتقال إلى أشياء أكثر تعقيدًا.
من الآن فصاعدًا ، دعنا نتحدث عن التحسينات على الخوارزمية. العيوب الرئيسية لحل DFS العودية هي أنه عودي ولا يقلل من عدد الضرب. كما سنرى قريبًا ، يقلل BFS من عدد الضرب ، كما أنه من الصعب جدًا تنفيذه بشكل متكرر. لسوء الحظ ، سيتعين علينا التخلي عن حل DFA العودي ، لأنه لتحسينه سنحتاج إلى إعادة كتابة الكود بالكامل.
بدون مزيد من اللغط ، أقدم نهجًا تكراريًا يعتمد على BFS:
from collections import deque def bfs(rate_graph, start, end): to_visit = deque() to_visit.appendleft( (start, 1.0) ) visited = set() while to_visit: node, rate_from_origin = to_visit.pop() if node == end: return rate_from_origin visited.add(node) for unit, rate in rate_graph.get_neighbors(node): if unit not in visited: to_visit.appendleft((unit, rate_from_origin * rate)) return None
يختلف هذا التطبيق من الناحية الوظيفية عن التطبيق السابق ، ولكن إذا نظرت عن كثب ، فستحدث نفس الشيء تقريبًا ، مع تغيير هام واحد: في حين أن DFS العودية يحفظ حالة المسار الآخر في مكدس الاستدعاءات ، مع تنفيذ مكدس LIFO بشكل فعال ، فإن الحل التكراري يقوم بتخزينه في قائمة الانتظار FIFO.
هذا يعني أن الخاصية "أقصر مسار / أقل عدد من الضرب". نزور العقد بالترتيب الذي تحدث به ، وبهذه الطريقة نحصل على أجيال من العقد. تدرج العقدة الأولى جيرانها ، ثم نزور هؤلاء الجيران بالترتيب ، حيث يتمسك بجيرانهم طوال الوقت وهكذا. تتبع خاصية أقصر مسار من حقيقة أن العقد قد تمت زيارتها بترتيب المسافة الخاصة بها من المصدر. لذلك ، عندما نواجه وجهة ، نعلم أنه لا يوجد جيل سابق يمكن أن يؤدي إليها.
في هذه اللحظة ، نحن على
وشك الانتهاء. تحتاج أولاً إلى الإجابة عن بعض الأسئلة ، وهم مضطرون للعودة إلى الصيغة الأصلية للمشكلة.
أولاً ، الشيء الأكثر تافهة الذي يجب القيام به إذا كانت الوحدة الأصلية غير موجودة؟ بمعنى ، لا يمكننا العثور على العقدة بالاسم المحدد. في الممارسة العملية ، تحتاج إلى القيام ببعض التطبيع للخيوط بحيث يشير الجنيه والباوند والرطل إلى نفس العقدة "الجنيه" (أو بعض التمثيل القانوني) ، ولكن هذا يتجاوز نطاق سؤالنا.
ثانيا ، ماذا لو لم يكن هناك تحويل بين الوحدتين؟ تذكر أنه في البيانات الأولية لا يوجد سوى تحويلات بين الوحدات ، ولا يعطي أي مؤشرات على ما إذا كان من الممكن الحصول على وحدة أخرى من وحدة معينة. هذا يتلخص في حقيقة أن التحويلات والمسارات متكافئة بشكل مباشر ، لذلك إذا لم يكن هناك مسار بين عقدتين ، فلن يكون هناك تحول. في الممارسة العملية ، ينتهي بك الأمر مع وجود جزر غير ذات صلة من الوحدات: واحدة للمسافات ، واحدة للأوزان ، واحدة للعملات ، إلخ.
أخيرًا ، إذا نظرت عن كثب إلى الرسم البياني أعلاه ، اتضح أنه لا يمكنك التحويل بين الأيدي والسنوات الضوئية باستخدام هذا الحل. اتجاه الاتصالات بين العقد يعني أنه لا توجد وسيلة من جهة إلى سنة ضوئية. ومع ذلك ، هذا سهل الإصلاح ، لأنه يمكن عكس التحويلات. يمكننا تغيير رمز تهيئة الرسم البياني الخاص بنا كما يلي:
def add_conversion(self, orig, dest, rate): 'Insert a conversion into the graph. Note we insert its inverse also.' if orig not in self.graph: self.graph[orig] = {} self.graph[orig][dest] = rate if dest not in self.graph: self.graph[dest] = {} self.graph[dest][orig] = 1.0 / rate
الجزء 3. التقييم
القيام به! إذا وصل المرشح إلى هذه النقطة ، فسوف أوصي به على الأرجح للتأجير. إذا درست علوم الكمبيوتر أو درست في الخوارزميات ، فقد تسأل: "هل هذا يكفي حقًا لإجراء مقابلة مع هذا الرجل؟" ، والذي سأجيب عليه: "بشكل أساسي ، نعم".
قبل أن تقرر أن السؤال بسيط للغاية ، دعنا ننظر إلى ما يجب على المرشح فعله للوصول إلى هذه النقطة:
- فهم السؤال
- بناء شبكة من التحولات في شكل رسم بياني
- نفهم أن المعاملات يمكن مقارنتها بحواف الرسم البياني
- انظر إمكانية استخدام خوارزميات البحث لتحقيق ذلك.
- اختر الخوارزمية المفضلة لديك وقم بتغييرها لتتبع الاحتمالات
- إذا قام بتنفيذ DFS كحل ساذج ، التعرف على نقاط ضعفه.
- تطبيق BFS
- للتراجع ودراسة الحالات القصوى:
- ماذا لو سُئلنا عن عقدة غير موجودة؟
- ماذا لو كان عامل التحويل غير موجود؟
- ندرك أن التحولات العكسية ممكنة وربما ضرورية
هذا السؤال أسهل من السابق ، لكنه صعب أيضًا. كما هو الحال في جميع الأسئلة السابقة ، يجب على المرشح إجراء قفزة ذهنية من سؤال تم إعداده بشكل تجريدي إلى خوارزمية أو بنية بيانات تفتح الطريق أمام الحل. الشيء الوحيد هو أن الخوارزمية النهائية أقل تقدماً من غيرها. خارج هذه المادة الحسابية ، تنطبق نفس المتطلبات ، خاصة فيما يتعلق بالحالات القصوى والصحة.
"لكن انتظر!" قد تسأل. - أليس Google مهووسًا بالتعقيد في وقت التشغيل؟ لم تسأل حتى عن التعقيد الزمني أو المكاني لهذه المشكلة. حسناً! قد تسأل أيضًا: "انتظر لحظة ، أعطيت التصنيف" أوصي بشدة بالتأجير "؟ كيف تحصل عليه؟ أسئلة جيدة جدا ، على حد سواء. هذا يقودنا إلى الجولة الإضافية الإضافية ...
الجزء 4. هل من الممكن أن تفعل أفضل؟
في هذه المرحلة ، أود أن أهنئ المرشح بإجابة جيدة وأن أوضح أن كل شيء آخر هو مجرد مكافأة. عندما يختفي الضغط ، يمكننا أن نبدأ في خلق.
فما هي صعوبة تشغيل BFS؟ في أسوأ الحالات ، يجب أن نأخذ بعين الاعتبار كل عقدة وحافة فردية ، والتي تعطي التعقيد الخطي
O(N+E) . هذا علاوة على نفس التعقيد في بناء الرسم البياني
O(N+E) . بالنسبة إلى محرك البحث ، قد يكون هذا جيدًا: فآلاف وحدات القياس كافية لمعظم التطبيقات المعقولة ، كما أن إجراء بحث عن الذاكرة لكل استعلام ليس زيادة في الحمل.
ومع ذلك ، يمكن للمرء أن يفعل أفضل. لتحفيز ، ضع في اعتبارك كيفية إدخال هذا الرمز في سلسلة البحث. تعد تحويلات بعض الوحدات غير القياسية أكثر شيوعًا قليلاً ، لذلك سنحسبها مرارًا وتكرارًا. في كل مرة يتم إجراء البحث ، يتم حساب القيم الوسيطة ، وما إلى ذلك.
غالبًا ما يُقترح ببساطة تخزين نتائج الحسابات مؤقتًا. عندما يتم حساب تحويل وحدة ، يمكننا دائمًا إضافة ميزة بين التحويلين. على سبيل المكافأة ، نحصل على التحول العكسي ، ومجانا! هل انتهيت
في الواقع ، سوف يمنحنا هذا وقتًا ثابتًا للبحث بدون تقارب ، لكنه سيكلف تخزين حواف إضافية. يصبح هذا بالفعل مكلفًا للغاية: بمرور الوقت ، سنسعى جاهدين للحصول على رسم بياني كامل ، حيث يتم حساب وتخزين جميع أزواج التحولات تدريجياً. عدد الحواف الممكنة في الرسم البياني هو نصف مربع عدد العقد ، لذا فإننا نحتاج إلى نصف مليون حافة لنحو ألف عقد. لعشرة آلاف عقد ، حوالي خمسين مليون ، إلخ.
إذا تجاوزنا نطاق محرك البحث ، للحصول على رسم بياني يضم مليون عقدة ، فإننا نسعى جاهدين لنحو نصف تريليون حواف. هذا المبلغ هو ببساطة غير معقول للتخزين ، بالإضافة إلى أننا ننفق الوقت في إدراج الحواف في الرسم البياني. يجب علينا أن نفعل ما هو أفضل.
لحسن الحظ ، هناك طريقة لتحقيق وقت ثابت للبحث عن المعاملات ، دون نمو مساحة التربيعية. في الواقع ، كل ما نحتاجه تقريبا تحت أنفنا.
الجزء 4. وقت ثابت
لذلك ، التخزين المؤقت الكلي هو في الواقع قريب من الحل الأمثل. في هذا النهج ، نحصل (في النهاية) على حواف بين جميع العقد ، وهذا يعني أن تحولنا إلى إيجاد حافة واحدة. ولكن هل من الضروري حقًا تخزين التحويلات من كل عقدة إلى كل عقدة؟ ماذا لو قمنا بحفظ عوامل التحويل من عقدة
واحدة إلى كل العناصر الأخرى؟
ألق نظرة أخرى على حل BFS:
from collections import deque def bfs(rate_graph, start, end): to_visit = deque() to_visit.appendleft( (start, 1.0) ) visited = set() while to_visit: node, rate_from_origin = to_visit.pop() if node == end: return rate_from_origin visited.add(node) for unit, rate in rate_graph.get_neighbors(node): if unit not in visited: to_visit.appendleft((unit, rate_from_origin * rate)) return None
دعونا نرى ما يحدث هنا: نبدأ من العقدة المصدر ، ولكل عقدة نواجهها ، نحسب معامل التحويل من المصدر إلى هذه العقدة. بعد ذلك ، بمجرد وصولنا إلى الوجهة ، نعيد المعامل بين نقطتي البداية والنهاية ونتجاهل المعاملات الوسيطة.
هذه النسب المتوسطة هي المفتاح. لكن ماذا لو لم نرميهم؟ ماذا لو نكتبهم بدلاً من ذلك؟ تصبح كل عمليات البحث الأكثر تعقيدًا وغير المفهومة أمرًا بسيطًا: للعثور على نسبة A إلى B ، أوجد أولاً نسبة X إلى B ، ثم قسّمها على نسبة X إلى A ، لقد انتهيت! بصريا ، يبدو مثل هذا:
لاحظ أنه بين أي عقدتين لا يزيد عن حافتيناتضح أنه لحساب هذا الجدول ، لا نحتاج إلى تغيير حل BFS:
from collections import deque def make_conversions(graph): def conversions_bfs(rate_graph, start, conversions): to_visit = deque() to_visit.appendleft( (start, 1.0) ) while to_visit: node, rate_from_origin = to_visit.pop() conversions[node] = (start, rate_from_origin) for unit, rate in rate_graph.get_neighbors(node): if unit not in conversions: to_visit.append((unit, rate_from_origin * rate)) return conversions conversions = {} for node in graph.get_nodes(): if node not in conversions: conversions_bfs(graph, node, conversions) return conversions
يتم تمثيل بنية التحويل بواسطة قاموس للوحدة A بقيمتين: الجذر للمكون المرتبط بالوحدة A ومعامل التحويل بين الوحدة الجذر والوحدة A. نظرًا لأننا ندرج وحدة في هذا القاموس في كل زيارة ، يمكننا استخدام مساحة المفتاح لهذا القاموس كمجموعة من الزيارات بدلاً من استخدام مجموعة مخصصة من الزيارات. لاحظ أنه ليس لدينا عقدة نهائية ، وبدلاً من ذلك نكررها عبر العقد حتى ننتهي.
خارج هذا BFS ، هناك وظيفة المساعد التي تتكرر عبر العقد في الرسم البياني. كلما واجهت عقدة خارج قاموس الترجمة ، يبدأ تشغيل BFS بدءًا من تلك العقدة. , .
, , :
def convert(conversions, start, end): 'Given a conversion structure, performs a constant-time conversion' try: start_root, start_rate = conversions[start] end_root, end_rate = conversions[end] except KeyError: return None if start_root != end_root: return None return end_rate / start_rate
« » . « » : , , BFS, , . , .
!
O(V+E) ( , ), . , , ó , . , :
O(V+E) , ,
O(V) , .
النتائج
, , , , - . - , . , .
( , , , ), « ». , : , , .
. , , , . — . , , Google ( , , ).
من ناحية أخرى ، لم يكن اختيار الخوارزمية مصدر إشارة مفيدًا بشكل خاص. الأشخاص الذين مروا بمرحلة تأطير عادة ما يصلون إلى الخوارزمية دون أي مشاكل. أظن أن هذا يرجع إلى حقيقة أن خوارزميات البحث يتم دائمًا تعليمها جنبًا إلى جنب مع الرسوم البيانية نفسها ، لذلك إذا كان شخص ما على دراية بواحد ، فإنهم يعرفون الآخر.لم يكن التنفيذ سهلاً. لم يكن لدى العديد من الأشخاص مشاكل في التنفيذ المتكرر لـ DFS ، لكن ، كما ذكرت أعلاه ، فإن هذا التنفيذ غير مناسب للإنتاج. لدهشتي ، لا يبدو أن تطبيقات تكراري BFS و DFS مألوفة جدًا للناس ، وحتى بعد تلميحات واضحة ، غالبًا ما يتم طرحها في هذا الموضوع.في رأيي ، فإن أي شخص دخل مرحلة التنفيذ قد أكسبني بالفعل توصية "توظيف" ، وكانت مناقشة المهلة الدائمة مجرد مكافأة. على الرغم من أننا نظرنا إلى الحل بالتفصيل في المقالة ، إلا أنه في الممارسة العملية ، عادة ما تكون المناقشة الشفوية بدلاً من كتابة التعليمات البرمجية أكثر إنتاجية. قلة قليلة من المرشحين يمكنهم اتخاذ قرار على الفور. غالبًا ما كان علي إعطاء أدلة مهمة ، وحتى ذلك الحين لم يتمكن الكثير من الناس من العثور عليه. هذا أمر طبيعي: كما هو متوقع ، يصعب الحصول على تصنيف موصى به للغاية.لكن مهلا ، هذا ليس كل شيء!
في الأساس ، درسنا المشكلة بأكملها ، ولكن إذا كنت مهتمًا بمزيد من الدراسة ، فهناك عدد من الامتدادات التي لن أتطرق إليها. أترك التدريبات التالية للقارئ:أولاً ، الاحماء: في الحل بالنسبة للوقت الثابت الذي حددته ، اخترت عقدة الجذر لكل مكون متصل بشكل تعسفي. على وجه الخصوص ، أستخدم عقدة المكون الأول التي نواجهها. هذا ليس مثاليًا ، لأنه بالنسبة لجميع القيم المعروفة ، اخترنا بعض العقدة ، على الرغم من أن بعض العقدة الأخرى قد تكون أقرب إلى المنتصف بمسارات أقصر من جميع العقد الأخرى. مهمتك هي استبدال هذا الاختيار التعسفي بخيار يقلل من عدد الضرب المطلوب ويقلل من انتشار خطأ الفاصلة العائمة.-, , , . — : — , A B — / . : , , , , , . .
أخيرًا ، جوهرة حقيقية: يتم التعبير عن بعض الوحدات كمزيج من الوحدات الأساسية المختلفة. على سبيل المثال ، يتم تعريف واط في نظام SI كـ kg • m² / s³. المهمة الأخيرة هي توسيع هذا النظام لدعم التحويل بين هذه الوحدات ، مع مراعاة فقط تعريفات وحدات SI الأساسية.إذا كان لديك أي أسئلة ، فلا تتردد في الاتصال بي على reddit .استنتاج
, , . : , , , . , , , , : , . , , , .
أتمنى أن تكون قد وجدت هذا المقال مفيدًا. أفهم أنه قد لا يكون هناك العديد من المغامرات مع الخوارزميات كما في بعض المقالات السابقة. في مقابلات المطورين ، من المعتاد مناقشة الخوارزميات بكثرة. ولكن الحقيقة هي أن صعوبات كبيرة تنشأ عند استخدام طريقة بسيطة ومعروفة. كل الشفرة في مستودع سلسلة المقالات هذه .