مجرد تقسيم ، أو كيفية إنشاء نظرية رياضية وكسب 400 ألف دولار على ذلك. السلسلة الثالثة ، النهائية

في السلسلة السابقة ، نظرنا إلى الأرقام الكسرية من عدة زوايا غير عادية. في هذه السلسلة ، بعد المقدمة وبعض الأسس النظرية ، سنحاول جمع كل شيء في شكل مناسب والاستفادة من المعلومات المتاحة.

البحث عن بسيط

بعد أن تحدثنا عن خصائص جدول المخلفات ، يمكننا محاولة تطبيق المعرفة حوله على الكسب. لذلك ، يجد الكثيرون في العالم أنه من المفيد البحث عن أعداد كبيرة من الأعداد الأولية. وحتى هناك منظمات مستعدة لتقديم الكثير من المال لشخص يجد عددًا أوليًا كبيرًا. لكن موضوع الحوسبة الكمومية يحظى أيضًا بشهرة واسعة في العالم. لماذا؟ لأنه يعد بإختراق نظام تشفير مشهور. هذا ، إذا جاز التعبير ، هو شعار الإعلان للحوسبة الكمية ، والذي يسمح بإقناع أي مدير لاتخاذ القرارات بتخصيص أموال لمثل هذا الدرس المثير للاهتمام. لذلك ، سنتحدث أيضًا عن هذا الموضوع.

أولاً سنريك كيف تبحث عن الأعداد الأولية. المشكلة الرئيسية هنا هي الكمية. بالنسبة للأعداد الكبيرة ، لا توجد ببساطة خوارزميات تسمح لك بالتحقق بسرعة من وجود رقم أولي أمامنا أو رقم مركب. لذلك ، يبلغ الحد الأقصى للتوقف لهذا اليوم أقل من 25 مليون منزلة عشرية. هذا فقط 10 ميجابايت ، على مثل هذه المصفوفات تظهر المعالجات الحديثة أوقات معالجة بالميللي ثانية ، ولكن للتحقق مما إذا كان الرقم الأولي في صفحتنا ، سيستهلك معالج حديث الكهرباء وينبض مع مروحة لعقود. هذا من الناحية الفنية ، لا يعد حجم المعالج جيدًا ، ولكن عدد العمليات في الخوارزميات المعروفة لهذه الأعداد الكبيرة هو ببساطة ضخم. لماذا هذا الوضع؟

بالنسبة لاختبارات البساطة ، على سبيل المثال ، يتم استخدام تعداد الفواصل. ولكن كم عدد المقسومات التي تحتاج إلى تكرارها لمدة عشرة ميغابايت؟ الجواب هو أنه حتى الذرات التي تحتوي على الإلكترونات في الكون بأكمله لن تكفي إلا لجزء صغير من هذه القيمة. هذا هو ، نحن بحاجة إلى أعداد هائلة من الأكوان ، فقط لوضع كل هذه المقسومات هناك. كثير جدا؟ لذلك ، يتم تطبيق تعداد المقسومات للأرقام التي تبلغ عشرة ميجابايت على نطاق محدود (نعم ، خذلنا الكون ...) ، لكن لحسن الحظ ، هناك خوارزميات أخرى. يمكننا التمييز بين الخوارزميات التي لا تستخدم تعداد المقسومات ، وفي الوقت نفسه مضمونة لإعطاء إجابة - بسيطة أمامنا أو مركب. ولكن هذه خوارزميات بطيئة للغاية. وهذا يعني ، بالطبع ، أنهم قادرون على طحن الأرقام مائة أو مائتي بت بهذه الطريقة ، ولكن عشرة ميغا بايت بالنسبة لهم هي الموت مرة واحدة. لذلك ، يجب عليك الخروج من الطرق الصعبة.

لكن المشكلة في كل الحيل هي أنهم لم يأتوا بعد بنظرية كاملة عن القسمة. بعد كل شيء ، إذا كان كاملاً ، فسنجد الإجابة بسرعة - أولية أم لا. بتعبير أدق ، ستمنحنا نظرية بسرعة خوارزمية للاختبار لن تبقينا في انتظار الموت الحراري للكون. لهذا السبب يمنحون مكافآت لأولئك الذين يتوصلون إلى خوارزمية بأسرع وقت ممكن ، والأهم من ذلك كله ، نظرية كاملة لتوفير الخوارزميات لجميع المناسبات.

في غضون ذلك ، لدينا تحت تصرفنا اختبار Luc-Lemer محدد ، والذي يستخدم اتصال أرقام Mersenne محددة للغاية مع تسلسل معين ، ولكن ليس بقية التقسيم ، كما لاحظنا مؤخرًا ، ولكن مجموع درجات بعض الأرقام غير المنطقية. وهذا يعني أن اختبار البساطة قد تم إجراؤه من الجانب ، دعنا نقول ، ليس واضحًا تمامًا ، على الرغم من أن البعض هنا يمكنهم إجراء مقارنات أكثر تعقيدًا. لكن لماذا اتضح أن درجات الأعداد غير المنطقية أقرب إلى اختبارات البساطة من جميع الإنجازات الأخرى لنظرية الأعداد؟ على ما يبدو لأن الرياضيات لا تعرف الحلول البسيطة. ونتيجة لذلك ، تم استخدام طريقة ، على الرغم من أنها ليست واضحة ولكنها لا تزال تعمل ، من المنطقة غير الأقرب إلى الحسابات الصحيحة ، تقريبًا كيف يساعد الانتقال من الإحداثيات الديكارتية إلى الإحداثيات القطبية على استخدام طرق إضافية يصعب تنفيذها في الإحداثيات الديكارتية.

بالإضافة إلى اختبار Luc-Lemer ، هناك أيضًا اختبارات احتمالية. أنها تساعد على التخلص من أرقام مركبة مضمونة. لذلك أحد الاختبارات الاحتمالية المستخدمة بنشاط هو اختبار يعتمد على صيغة فيرما ، التي تحدثنا عنها مؤخرًا. كيف يعمل؟ بسيط جدا - تذكر عمود الوحدات على اليمين في الجدول الباقي؟ هذه علامة مضمونة على بساطة الرقم. لشرح التحقق باستخدام صيغة Fermat ، يستخدم علماء الرياضيات مصطلحات محددة لا يفهمها سوى القليل من الناس إلى جانبهم ، لذلك نحن لا نذهب إلى هذه الأدغال الرياضية ، ولكننا نوضح كل شيء على الأصابع ، أو بالأحرى ، من جدول المخلفات. لفهم ما سيكون عليه الباقي في العمود الأخير ، يجب عليك إما التقسيم على عمود والوصول إلى الباقي في الموضع الذي يحتوي على 1 فيه ، أو حساب الباقي باستخدام صيغة تسمح لك بالحصول على الباقي من خلال رقم الموضع وقاعدة نظام الأرقام. سيتطلب الخيار الأول للأرقام التي يبلغ طولها عشرة ميغابايت وقتًا غير محدود تقريبًا ، لأن عرض الجدول هو N-1 ، مما يعني أنه بالنسبة لعدد من المليون ، سيتضمن الجدول مليون عمود على الأقل. لمليار ، مليار. للحصول على تريليون تريليون دولار. لكن تريليون ، هو فقط 12 منزلة عشرية. ونحن مهتمون بعدد أقل من 25 مليون حرف. حتى التريليونات المتخلفة عن طريق تقسيم العمود ، علينا أن نحسب بالكاد أقل من نصف ساعة ، وهذه ليست سوى 12 منزلة عشرية. مجموع! مقارنة بـ 25 مليون. هل تعتقد أن لديك ما يكفي من الوقت لانتظار النتيجة بهذه الطريقة؟ هذا هو السبب في أنه من الأفضل حساب القيمة المطلوبة فورًا باستخدام الصيغة. وفقط صيغة فيرما يتوافق مع صيغة لحساب الباقي في الموضع الأخير في الجدول. علاوة على ذلك ، إذا كانت الفترة أقصر من عرض الجدول ، فإن الرياضيات لا تعرف بعد كيفية حسابه ، مما يعني أنه في أي حال ، نحن بحاجة إلى اختيار العمود الأخير. يقوم علماء الرياضيات في الاختبار ببساطة بالتحقق مما إذا كان الباقي في العمود الأخير يساوي واحدًا في نظام الأرقام الذي اختاروه (على الرغم من أن علماء الرياضيات لا يستخدمون مفهوم نظام الأرقام ، فهناك فقط أساس يتم رفعه إلى القوة). إذا لم يكن الباقي مساويًا للرقم ، فسيكون العدد مضمونًا. كما رأينا في مثال الجدول للرقم 21 ، فإن عدم وجود وحدة في نهاية العديد من الأسطر يميزها عن جداول الأعداد الأولية. ولكن هناك مشكلة واحدة. في بعض الأسطر ، قد لا تزال هناك وحدات ، يمكننا التحقق منها أيضًا من خلال مثال الجدول رقم 21. ولهذا السبب يصف علماء الرياضيات الاختبار على أساس صيغة فيرمات الاحتمالية. أي أنهم لا يعرفون ما إذا كان الرقم أوليًا إذا وجد اختبار فيرما أن الباقي يساوي واحدًا ، لأن هذه الوحدات الخاطئة موجودة في الجدول للرقم 21 ، وفي العديد من الجداول الأخرى ، حتى بالنسبة لعشرة أرقام ميغا بايت. لذا ، عليك إما فحص كل الخطوط في صف واحد ، وهو وقت طويل للغاية ، لأن خطوط الرقم الذي يبلغ عشرة ميجابايت ، كما ذكرنا سابقًا ، أكثر بكثير من كل شيء في الكون الذي نعرفه ، أو نقول فقط - من المحتمل أن يكون هذا الرقم أولي. هذه هي الطريقة الأخيرة واختار علماء الرياضيات. لحسن الحظ ، هناك عدد قليل من الخطوط تنتهي بخط واحد في معظم الأرقام المركبة. صحيح ، هناك أيضًا ما يسمى بأرقام كارمايكل ، والتي تنتهي فيها جميع الأسطر ، باستثناء مضاعفات المقسومات في هذا العدد بواحد. لذلك ، على أرقام كارمايكل ، فإن الاختبار الاحتمالي من صيغة فيرما مضمون من الناحية العملية بأنه خاطئ ، لأن القضاء على الخطأ تحتاج إلى الدخول في مضاعفات مقسوم الأرقام ، ويمكن أن تحتوي عشرة ميغابايت من المقسومات على اثنين فقط ، ويمكن أن تكون قيمتها كبيرة جدًا ، وبالتالي فإن احتمالية الحصول عليها في مثل هذا الخط ، مع اختيار عشوائي لقاعدة نظام الأرقام ، يكون عملياً صفراً. لكن من ناحية أخرى ، فإن أعداد كارمايكل صغيرة نسبيا ، مما يسمح لنا بالأمل في اختبار احتمالي. فقط عند البحث عن الأعداد الأولية ، يتم استبعاد أمل الاحتمال. لهذا السبب ، بعد اختيار المرشحين لمرشحين بسيطين بمساعدة اختبارات الاحتمال ، يتم تطبيق اختبار Luc-Lemer مع ذلك.

أضف القليل عن أرقام كارمايكل. إنها رائعة ليس فقط لقدرتها على تقليد الأشياء البسيطة. لذلك ، لدى الشبكة موقع ويب حيث يمكنك معرفة تسلسلات مختلفة من الأرقام . إذا أدخلت الرقم 561 (الحد الأدنى لرقم كارمايكل) في حقل البحث ، فيمكنك أن تجد أنه يشارك في عدد كبير جدًا من التسلسلات. عن ماذا يتحدث هذا؟ على ما يبدو حول بعض الخصائص الهيكلية غير المعروفة لأرقام متشابهة شائعة جدًا في عالمنا. حقيقة مسلية جدا.

ولكن العودة إلى اختبارات البساطة. على الرغم من معامل التصفية الجيد مع الاختبارات الاحتمالية ، فإن البشرية تقضي سنوات في العثور على العدد الأولي التالي. لماذا؟ لأن اعتماد وقت تنفيذ الاختبار على حجم الرقم هو من الدرجة الثانية. وهذا يعني أنه بالنسبة للأعداد الصغيرة ، فكل شيء ينفجر بلا عناء ولا توجد مشاكل ، لكن عندما تزيد الأرقام مليون مرة ، يزداد وقت الحسابات بمقدار تريليون مرة. لذلك ، على أساس معالج واحد ، سننظر في اختبار Luc-Lemer لعقود. ولكن حتى في اختبار صيغة فيرما ، سننظر أيضًا في الأمر نفسه. وهذا هو ، في كلا النهجين ، بلغ عدد الحسابات حدود القدرات البشرية. عليك أن تفعل شيئا مع هذا ، أليس كذلك؟

ماذا يمكن أن تكون بدائل لمثل هذه النفايات الحوسبة المهدرة على تسخين الهواء لسنوات عديدة؟ بسيط جدًا - تحتاج إلى التنبؤ بالبساطة من خلال طبيعة الرقم وعضويته في فصل معين. لذلك أصبحت أعداد مرسين رائدة في الأحجام المحققة من الأعداد الأولية التي أثبتت جدواها على وجه التحديد بسبب انتمائهم إلى فئة معينة. يعمل اختبار Luke-Lemer على وجه التحديد لمثل هذه الفئة المحددة. أعداد الفئات الأخرى متأخرة بسبب عدم وجود اختبار باهظ مثل اختبار Luc-Lemer للأرقام التي تبلغ عشرة ميجابايت (على الرغم من أن هذا الاختبار يتم تكييفه بالنسبة للبعض). لذلك نحن بحاجة إلى تصنيف للأرقام يسمح لنا بالعثور على اختبارات بساطة بسيطة ، لذا سامحني الجنة لمثل هذه التورية.

كيفية إنشاء مثل هذا التصنيف؟ كما أنها ليست صعبة للغاية - تحتاج إلى دراسة أرقام مختلفة وتحديد الميزات المشتركة بينها. بشكل عام ، هذا هو بالضبط ما يحاول علماء الرياضيات القيام به ، لكن حتى الآن لم تخرج زهرة حجرية. لذلك ، سنحاول مساعدتهم.

يستكشف النهج الموصوف مسبقًا لتحليل الأرقام استنادًا إلى جداول البقايا أساسًا قابلية تقسيم أرقام النموذج 1000 ... 000. أي أن الأصفار الموجودة على اليمين يتم تعيينها باستمرار للوحدة ، وبالتالي ضربها على أساس كل نظام من أنظمة الأرقام الموجودة في الجدول الباقي. نتيجة للتحليل ، وجدنا أن الأرقام المختلفة تقسم أرقام النموذج 1000 ... بطرق مختلفة. لذلك لا يمكن تقسيم الأعداد الأولية بشكل عام على الأصفار. لكن المكونات ، وحتى ، على سبيل المثال ، من التوائم و / أو الأطفال ، مقسمة بالكامل. فيما يلي جدول الرقم 8:



كما ترون ، في السطور التي هي مضاعفات 2 ، بعد بعض الدخول من المخلفات غير الصفرية ، تبقى أصفارًا واحدة فقط. هذا هو بالضبط كيف تبدو جميع الأرقام المتعلقة بفئة المقسومات في الوحدات ذات الأصفار ، ويخبرنا وجود الأصفار بأي أنظمة أرقام سننجح. ولكن هنا تكمن المشكلة - من وجهة نظر العثور على الأعداد الأولية ، فإن الوحدة التي تحتوي على أصفار ليست مهمة بالنسبة لنا على الإطلاق ، لأنه من المضمون أن يتم تقسيمها على أساس نظام الأرقام ، والذي يعطينا كل هذه الأصفار بعد واحد. لذلك ، تحتاج إلى دراسة قسمة فئات أخرى من الأرقام. هل هو منطقي؟ هذا هو بالضبط ما سنفعله.

هل يمكننا تجربة نظرية القسمة؟

في وقت سابق ، تعرفنا على انتظام الجداول الباقية لعملية التقسيم المألوفة بالنسبة لنا. لقد تبين أن الأنماط مسلية ، لكنها لا تزال تواجه نفس المشكلة - فهي لا تعطينا خوارزمية سريعة لفحص البساطة. لمثل هذا الاختبار ، يتعين علينا ، كما هو الحال في الاختبار وفقًا لمعادلة Fermat ، رفع الأرقام إلى درجة كبيرة جدًا ، ومن ثم نجد ما تبقى من قسمة النتيجة على العدد قيد الدراسة. أو قم ببساطة بالتكرار على كل البقايا باستخدام طريقة "الزاوية" (قبل الموت الحراري للكون ، بالطبع). فيما يلي البيانات - تستغرق عملية الرفع إلى قوة مع العثور على الباقي 15 دقيقة على قلب واحد لأعداد الطلبات $$$2 ^ {100000}$. مع زيادة حجم العدد بمقدار 1000 مرة ، نحصل على زيادة تربيعية (بالإضافة إلى اللوغاريتمات ، لكن هذا ليس كثيرًا) على الأقل 1،000،000 مرة ، ولكن في الواقع - عدة ملايين من المرات. لنفترض ، نتيجة لذلك ، أننا نحصل على مليون ساعة لاختبار واحد. هذا هو ما يقرب من 40،000 يوما أو بشكل ملحوظ أكثر من مائة سنة. إذا قمنا بتحسين تنفيذ الاختبار إلى أذنيه ، فقم بإجراء ذلك مع مراعاة جميع ميزات بنية المعالج ، ثم ربما بدلاً من مائة عام نحصل على 10. في 10 مراكز - سنة واحدة. ل 1000 النوى - 4 أيام. ولكن هذا مجرد اختبار احتمالي ، لأن هناك حفلة تنكرية كأرقام مركبة بسيطة. لذلك لا تزال بحاجة إلى التحقق مرة أخرى. لكن الأهم من ذلك هو حقيقة أن أعداد المرشحين هي الملايين. بعد كل الترشيحات الممكنة ، سيكون هناك الكثير منها أيضًا. لذلك ، ما زال العالم يواصل العبث بعشرة أرقام ميغا بايت.

ولكن لدينا أداة. يعمل الجدول الباقي أيضًا مع أنواع أخرى من الأرقام. على سبيل المثال ، خذ أرقام مرسين. في ثنائي ، انها مجرد سلسلة من الوحدات. ما الذي يمنعنا من استكشاف سلسلة من الوحدات بدلاً من سلسلة من الأصفار؟ نعم ، لا شيء يمنع. واتضح أنه لمثل هذا التسلسل ، تعمل طريقتنا بشكل جيد ويتم الحفاظ على عدد من الأنماط المحددة مسبقًا فيه. هذه هي النتيجة للرقم 7:



كما نرى ، فإن الرقم الأول 7 في جميع أنظمة الأرقام (باستثناء المضاعفات السبعة) هو مقسوم على أرقام مرسين. أي أنه في كل سطر تقريبًا يوجد صفر يخبرنا عن قسمة أرقام النموذج 111 ... 111 (في النظام الثنائي) على 7. لذلك ، عند العمل مع نظام الأرقام الثنائية ، نرى أن الرقم 7 يقسم جميع أرقام مرسين ، طول وهو مضاعف 3. هذه النتيجة واضحة بدون جدول من المتبقيات - يتكون الرقم 7 في شكل ثنائي من ثلاث وحدات (111) ، لذلك سيتم تقسيم العدد الثنائي من ثلاث وحدات. وإذا كان هناك المزيد من الوحدات ، فإن التقسيم يبدو كما يلي:

111111 | 111 ------ 111 1001 111 111 111 

أي أننا ببساطة نضع سبعة (في شكل ثنائي) تحت الأرباح. وعدد المرات التي تناسبها السبعة - الكثير من الوحدات الثلاثية في عدد قابل للقسمة. إذا لم يكن عدد الوحدات فيه مضاعفًا للعدد ، فإن هذا العدد غير قابل للقسمة على 7. لكن هذا كله واضح فقط طالما ندرس الأرقام ذات بنية متطابقة (7 و 63 ، كما في المثال). وإذا كان هيكل الأرقام أكثر تعقيدًا ، فسيساعدنا جدول بقايا. لذلك ، على الرغم من بساطتنا ، نحصل على نتيجة مماثلة ، ولكن مع فترة تقسيم أطول قليلاً. يوجد أدناه مثال للرقم 11 (الرقم بالفعل في رقم عشري):



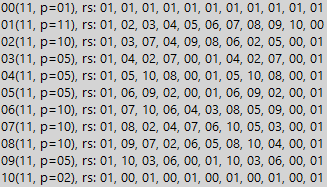
نرى أنه في النظام الثنائي ، تكون المسافة إلى الصفر (فترة القسمة) للرقم 11 هي 10. أي رقم مرسين يحتوي على 10 كيلو وحدة ، حيث k عدد صحيح أكبر من الصفر ، يكون بالضرورة قابلاً للقسمة على 11. يمكن إثبات بسهولة أن الباقي بسيط الأرقام تتصرف بالضبط نفس الشيء ، باستثناء حجم الفترة ، بالطبع. لكن بالنسبة للمركب ، فإن الوضع أقل انسجاما مرة أخرى. أدناه نرى مثال للرقم 8:



على ما يبدو ، 8 لا يمكن تقسيم أرقام مرسين في شكل ثنائي. هنا في فترة الثلاثية - من فضلك ، ولكن أرقام مرسين تتكون من وحدات فقط في شكل ثنائي. الموقف مشابه للأرقام المركبة الأخرى - لديهم كل شيء بطرق مختلفة. لا تتكرر الصورة النحيلة والمتماثلة للأعداد الأولية عن الصور المركبة. ولكن بالنسبة لنا ، فإن الأمر بسيط للغاية هو المهم ، لأنه إذا تم تقسيم العدد إلى علامة رئيسية ، فلن تكون هناك مشكلة على الإطلاق إذا ما كان سيتم تقسيمه أيضًا إلى مركب يتضمن هذا العنصر البسيط. ولكن إذا لم يتم تقسيم الرقم إلى رقم بسيط ، فسيكون من المستحيل تقسيمه إلى مركب بمثل هذا العدد البسيط. لذلك ، يجب أن نهتم فقط بالأعداد الأولية.

الآن دعونا نلخص. نحن نعلم أن أعداد مرسين مقسمة إلى أعداد أولية وأنه بالنسبة للقسمة ، تحتاج أرقام مرسين إلى عدد من الوحدات التي تعد مضاعفة لفترة القسمة للرقم قيد الدراسة. لكننا نعلم أيضًا أن المرشحين لأعداد Mersenne الأولية هم فقط أولئك الذين يكون عدد الوحدات أيضًا عددًا أوليًا. وهذا هو ، لا يتم تقسيم هذا المبلغ إلى أي شيء سوى وحدة ونفسها. ومن هنا الاستنتاج - نحتاج إلى مثل هذا العدد الأولي الذي تكون فترة القسمة مساوية لطول رقم مرسين. إذا لم نجد عددًا من المقسومات لفترة زمنية مناسبة ، فسيكون لدينا رقم Mersenne. يبدو بسيطا.

لكن المزيد من الصعوبات تبدأ. كيف تجد الرقم الذي تتزامن فترته مع طول رقم مرسين؟ للإجابة على هذا السؤال ، تحتاج إلى حل مهمة متواضعة - لإيجاد طريقة عن طريق وسيلة بسيطة لمعرفة الفترة للحصول على رقم أولي تعسفي. في الوقت الحالي ، يمكننا فقط مشاركة زاوية أو كزة في مكان معين باستخدام صيغة ذات درجات كبيرة. ولكن إذا استطعنا حساب الفترة دون الحاجة إلى عمليات حسابية طويلة ، فسنجد بسرعة المقسوم الصحيح ، أو نتأكد من عدم وجود شيء في الطبيعة. بالضبط نفس المهمة المتواضعة تنتظرنا في حالة دراسة قسمة أرقام النموذج 1000 ... 000. لذا فإن فترة القسمة مهمة جداً من جميع النواحي.

كيف تجد فترة؟

هنا ، تسرع الحواسيب الكمومية لمساعدتنا. ذات مرة ، في وقت ما سحيق ، اقترح بعض خبراء الفيزياء الكمومية باسم Shor ، العثور على هذه الفترة بدقة بمساعدة جهاز كمبيوتر الكم. في الواقع ، يعطي الكمبيوتر الكمي قيمة وسيطة فقط ، يستقبل منها الكمبيوتر العادي فترة ، لكن النقطة ليست كذلك ، ولكن بدون الكمبيوتر الكمي ، لن تكون الرياضيات قادرة على حساب الفترة. لكن عند حساب الفترة ، سنحصل على فرصة لحساب قيمة الباقي بدقة في منتصف الفترة. لماذا هذا مطلوب؟ لحقيقة أنه من خلاله يمكنك الحصول على العوامل التي تحتوي بالضرورة على قيمة معينة والتي هي مضاعف مقسوم الرقم قيد الدراسة. يتم ذلك عن طريق إضافة إلى ما تبقى من الوحدة وطرح الوحدة. يمكن تخطي الرقمين الناتج من خلال خوارزمية سريعة للعثور على أكبر مقسوم مشترك مع العدد قيد الدراسة. في حالة واحدة على الأقل ، نحصل على مقسوم الرقم قيد التحقيق. صحيح ، ليس كل شيء مثاليًا ، لأنه كما رأينا في مثال جدول الأعداد الأولية ، غالبًا ما توجد في منتصف الصف إضافة إلى العدد الذي يتم التحقيق فيه (N-1) ، في هذا النموذج نحصل على:

$$

$$N-1 + 1 = N$$

$$

$$N-1-1 = N-2$$

ويترتب على ذلك أنه في حالة واحدة لدينا الرقم المدروس نفسه ، وليس من المنطقي حساب العامل المشترك الأكبر ، وفي الحالة الثانية ، أكدنا أنه لا يوجد به مقسومات مشتركة مع الرقم المدروس. لا توجد مقسومات شائعة لأن هذا الرقم هو فقط 2 أقل من العدد الذي تم التحقيق فيه ، مما يعني أنه بغض النظر عن العدد المناسب لعدد الأعداد الصحيحة التي تمت دراستها (سيكون المقسوم عليها) ، وطرحه من العدد المدروس نحصل على ضمان أقل قيمة من $$$N-2$أو باستخدام الصيغ:

$$

$$N / x = k$$

$$

$$(N-x) / x = k-1$$

$$

$$N-x <N-2 \ Rightarrow x> 2 \؛ \ & \؛ (N-2) / x \ ne m$$

هنا N هو رقم اختبار فردي (فردي لأن مضاعفات اثنين قابلة للقسمة على اثنين ، ونحن بحاجة إلى عدم القسمة على أي شيء) ، x مقسوم على N ، k هو النتيجة الكاملة للتقسيم $$$N / x$، م هي النتيجة الكاملة للانقسام $$$(N-2) / x$. بمعنى أنه يتعين علينا أحيانًا تغيير نظام الأرقام ونطلب من الكمبيوتر الكمي العثور على فترة جديدة ، على أمل أن يكون هناك في الوسط عدد أكثر ملاءمة. القيد الزائد هو التكافؤ الإلزامي لقيمة طول الفترة. لكن هذا ليس مخيفًا للغاية ، لأنه على أي حال ، فإن الكمبيوتر الكمومي يحسب الطول الذي نحتاجه (أو عدة أطوال) أسرع بكثير من حدوث الموت الحراري للكون ، على عكس الخوارزميات الأخرى.

على الرغم من أن حساب الفترة الزمنية للحصول على مقسومات الأرقام مهمة مختلفة قليلاً عن العثور على مقسومات بسيطة. ومع ذلك ، يمكننا إضافة شيء هنا باستخدام الجداول المتبقية. لذلك ، توضح الجداول أن منتصف الصفوف ذات الطول الزوجي عادة ما يكون رقمًا يفي بالشروط التالية:

$$

$$r ^ 2 \ pmod N = 1$$

هنا r هو الباقي المطلوب ، و N هو الرقم قيد التحقيق. وهكذا ، اتضح أنه ليست هناك حاجة للبحث عن فترة للحصول على مقسومات الرقم ، لأنه يتم البحث في فترة للعثور على الباقي r ، ثم إضافة وطرح واحدة منه. وهذا هو ، يمكنك أن تجد على الفور ما تبقى يرضي الشرط المذكور أعلاه. صحيح أن البحث عن مثل هذه القيمة هو أمر غير بديهي أيضًا. ولكن ربما يمكن حبس كمبيوتر الكم لمثل هذا الشيء؟ يحتاج الخبراء في مجال الحوسبة الكمومية إلى فهم عدد البتات المطلوبة لهذا (البتات هي الببغاوات التي تقيس "قوة" الكمبيوتر الكمومي). رغم أنه ، ربما ، يمكنك الاستغناء عن كمبيوتر الكم. للقيام بذلك ، تحتاج فقط إلى فهم ما الأنماط سوف تأتي في متناول اليدين. بعض الأنماط مرئية في جداول البقايا ، حسناً ، وسيتعين على بقية القراء اكتشافها بأنفسهم ، ومن ثم ستقوم بالتأكيد بتشفير التشفير القائم على RSA. صحيح أن هناك بعض الصعوبات - فأنت تحتاج أولاً إلى العثور على هذه الأنماط المفيدة ، ثم ، ثم ... قد لا يدفعون لك المال. أولاً ، تمنح الجوائز جوائز أولية كبيرة ، وليس عن قرصنة RSA. وثانياً - حسنًا ، فكر بنفسك في عدد المنظمات الجادة في العالم المهتمة باعتراض بيانات الأشخاص الآخرين بهذه الطريقة؟ واكتشف بعض FSB (CIA ، Mossad ، Mi-5 ، فقط المافيا) أنك تعرف شيئًا ما. خمن ماذا سيحدث لك؟ لذلك ، أنت تتصرف فقط على مسؤوليتك وحدك.

صحيح أن الموضوع الكمومي بحد ذاته مثير للاهتمام لأنه يحتوي على حالة من عدم اليقين الكمي وتقلبات الفراغ وغيرها من الداروينية الكمومية. كيف يمكن تفسير كل هذا؟ لأكون صادقًا ، لا أعرف ، لكنني أرى تشابهًا مع الجداول الباقية. على سبيل المثال ، عندما يلاحظ شخص ما القيم في الجدول المتبقي ولا يعرف الأنماط المذكورة سابقًا ، فبالنسبة له لا يوجد سوى بعض الضوضاء في الجدول حيث تتغير الأرقام بعضها بعضًا بطريقة عشوائية ، مثل بعض التقلبات في الفراغ. لكن إذا فهمت أننا نطبق الخوارزمية نفسها على أزواج مختلفة من "التسلسل - الرقم قيد التحقيق" ، يصبح كل هذا العصيدة المغلي من الأرقام مفهوما على الفور. وبنفس الطريقة ، يصبح من الواضح لماذا ، ضمن المجموعة الضخمة من القيم المحتملة لملء الجدول ، فقط تلك المحددة بدقة لا تزال موجودة فيها. ولكن حتى نحصل على "تفاعل" التسلسل مع العدد المدروس ، لا يمكننا التنبؤ بمحتويات الجدول. بتعبير أدق ، أي ملء لها سيكون محتملاً بنفس الدرجة. ولكن بعد "التفاعل" - سيصبح كل شيء منطقيًا تمامًا ، ومن المحتمل أيضًا أن يولد احتمال واحد لخيار واحد فقط. ليس لأن بعض الداروينية تعمل ، ولكن فقط بسبب تطبيق خوارزمية معينة على بيانات إدخال محددة. إذا كنت لا تعرف الخوارزمية ، فقد يبدو أن الصفوف الموجودة في الجدول هي بالفعل على طراز داروين. وإذا كنت تعرف - كل شيء بسيط للغاية. ربما في الفيزياء الكمومية من الضروري البحث ليس فقط عن الجسيمات ، ولكن أيضًا عن خوارزمية عن "الانقسام"؟

ومرة أخرى عن هذه الفترة

ومع ذلك ، فإن الفترة مهمة للغاية بالنسبة لنا. نعم ، هذه هي الطريقة التي سوف يجيبون بها على الخط الساخن على المشاكل الساخنة للرياضيات. كما هو موضح أعلاه ، فإن معرفة الفترة تجعل من الممكن فهم ما إذا كان هناك عدد من المقسومات أو بطريقة أخرى ما إذا كان العدد أوليًا. لذلك ، نواصل هذه الفترة. حتى الآن ، نحن نعرف عددًا من خصائص الفترة (تفرد القيم ، التماثل بطول زوجي ، وما إلى ذلك) ، لكننا لا نعرف كيفية تحديد طولها. على الرغم من وجود حد أعلى وأسفل - لا يمكن أن تكون الفترة أطول من العدد قيد التحقيق ناقصًا واحدًا ، وكذلك لا يمكن أن تكون الفترة أقصر من فترة نمو قاعدة نظام الأرقام حتى يتم تجاوز الرقم قيد الدراسة (لمدة سبعة هو 3 ، و 11 هو 4 ، وما إلى ذلك. ) .. يمكنك محاولة تطبيق القوانين المعروفة من الجداول التي تمت دراستها واستنباط قوانين جديدة ، ولكن حتى الآن توجد بعض التوجيهات القليلة ، والتي لا تؤدي معظمها إلى النجاح ، على الرغم من أنه حتى لا تجرب كل ذلك ، لن تعرف.

لذلك ، فإن الطريقة الواعدة هي خلق نظرية محسنة للتقسيم. بناءً على التسلسلات المميزة للمخلفات ، من الممكن الكشف عن قوانين القسمة للعديد من فئات الأرقام. حتى الآن ، تم عرض فئتين فقط (أرقام وأرقام مرسين تساوي درجات نظام الأرقام) ، ولكن في الواقع هناك عدد لا حصر له منها. كيفية معالجة المعرفة على جميع فئات الأرقام؟ فقط في العمل الموازي الهائل ، وليس في شكل سخانات الهواء الحديد ، ولكن في شكل أشخاص يعملون معا في هذه المهمة الكبيرة. ستكون النتيجة المثالية هي إنشاء نظرية عامة للتقسيم لجميع فئات الأرقام. هذا بالنسبة للمبتدئين ، ومن ثم فإن قسمة كثير الحدود وغيرها من الجبر سوف تذهب. لكن هل يجب أن نتوقع حشدًا رائعًا من العقول البشرية حول مهمة إيجاد الأعداد الأولية؟ لا أظن ذلك. لذلك ، للأسف ، نحتاج مرة أخرى إلى طرق أخرى.

من الناحية النظرية ، هناك مثل هذه الطريقة

إذا درسنا تسلسلات بديلة قابلة للقسمة ، بما في ذلك قيم مختلفة ، نجد أن فترة تقسيم هذه التسلسلات تنمو بمضاعفات طول الأجزاء المتكررة من التسلسلات. فيما يلي مثال على تسلسل قابل للقسمة من النموذج 1010 ... 1010 ، حيث يتغير صفر وواحد بشكل دوري. ينقسم التسلسل المحدد دائمًا إلى قاعدة نظام الأعداد ، ولكن في هذه الحالة ، تعد بساطة مثال دراسة أرقام الفصل الدوري مهمة بالنسبة لنا فقط ، لذلك نحن لا ننتبه إلى القسمة "بالبناء".





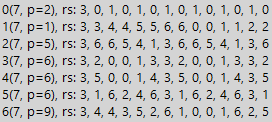
هنا نرى جدولين للرقم 7 والتسلسل أعلاه ، أحدهما عادي ، والجدول الثاني مضروب في 3. من الأنماط المحددة سابقًا في هذا المثال ، يوجد أقل ، لكن مع ذلك ، بالنسبة لأنظمة الأرقام على الأساسين 1 و 6 ، نرى زيادة طول الفترة ل $$$2 * N-2$. وللمضاعفة على 3 جداول ، نرى فقدان قابلية القسمة لقواعد نظامي الأرقام 2 و 5 ، وهو أمر ترفيهي بحد ذاته (لقد تغيرت خاصية القسمة من الضرب). ولكن أكثر أهمية من ذلك. من المهم أن نفهم إمكانية تطبيق جداول القسمة على أي تسلسل. ولكن لماذا نحتاج إلى أي تسلسل؟ على سبيل المثال ، لزيادة الحد الأدنى لفترة القسمة.

إذا كان بالإمكان إطالة الفترة الدنيا ، فهذا يتيح لنا المضي قدمًا في بناء الأعداد الأولية. نعم ، لا يمكن حساب الأعداد الأولية ، ولكن يتم إنشاؤها رياضيا. عندما تكون الفترة طويلة ، يقسم عدد صغير رقمًا كبيرًا ، مما يعني أنه إذا كانت كل الأرقام لها فترات كبيرة ، فيمكن أن تكون المقسومات بالنسبة للأعداد الكبيرة مجرد أرقام صغيرة. ماذا يعطي؟ هذا يجعل من الممكن العثور على جميع المقسومات على عدد كبير من خلال بحث بسيط. نظرًا لأن الأرقام الصغيرة تقسم الأرقام الكبيرة ، فإن حجم هذه الأرقام الصغيرة يساعد أجهزة الكمبيوتر لدينا على حل المشكلة التي لا يمكن حلها باستخدام المقسومات الكبيرة. لذلك ، يصبح الاتجاه الإضافي للبحث عن الأعداد الأولية واضحًا - نحتاج إلى إيجاد تسلسل يمنحنا فترات زمنية دنيا كبيرة. لماذا الدنيا؟ نظرًا لأننا ما زلنا لا نعرف كيفية حساب فترة ما دون تعداد كل البقايا أو الرفع إلى قوة ، وبالتالي لا يمكننا ببساطة العثور على فترة طويلة بما يكفي إذا كانت أكبر من الحد الأدنى ، حسنًا ، نحن نعرف الحد الأدنى للفترة ببساطة من تحليل الجداول الباقية ، أي أننا لا نحتاج إلى حسابها . حسنًا ، عندما نعثر على التسلسل الذي نحتاج إليه (ولهذا الغرض فقط يمكننا استخدام تحليل العديد من فئات هذه التسلسلات) ، ببساطة نختار طول التسلسل الذي لا يصلح في أي من الفترات الدنيا المعروفة لنا. وهذا هو ، ونحن سوف التقاط مثل هذا العدد الكبير ، والذي من الواضح أنه لا يوجد لديه المقسومات. وإذا كان حجمها كبيرًا ، تنتظرنا جائزة. في الوقت نفسه ، لن نكون مهتمين بأكثر من الفترات الدنيا ، لأنها تقسم بالفعل أعدادًا كبيرة جدًا ، والتي سنصلها في وقت لاحق.

كل ما تبقى هو العثور على التسلسل الصحيح. من سيأخذه؟ ولكن حتى لو لم نتمكن من العثور عليه ، فبالنسبة للتشفير المذكور سابقًا ، سيمكّن العمل باستخدام تسلسلات بديلة من إضافة مصطلح آخر إلى الشفرة يزيد من قوة التشفير - الآن ستحتاج مفرقعات التشفير الآن إلى تخمين التسلسل الذي اخترناه ، والذي يمكن أن يكون غير محدود في العدد. بالإضافة إلى ذلك ، لإنشاء تسلسلات عشوائية زائفة ، نحصل على تكرار القيم في سلسلة المتبقيات ، وليس فقط في سلسلة فترة الكسر.

وأخيرا - الجوائز!

مؤسسة الحدود الإلكترونية على استعداد لدفع أي شخص أولاً 150 ألف دولار ، ثم 250 ألف دولار أخرى. في المجموع - 400 ألف دولار . لن يزعجك ذلك؟ ثم إلى هذه النقطة! لكن الأمر بسيط - تحتاج إلى العثور على عدد أولي من مائة مليون منزلة عشرية. هذا هو حوالي 300 مليون بت ، أو 40 ميغابايت. غادر لتجاوز الرقم القياسي الحالي 4 مرات. ثم تحتاج إلى مليار رقم عشري طويلة. هذا بالفعل 400 ميغابايت. وكل شيء ، لعددين - 400 ألف دولار أخضر إلى الأبد.

في الواقع ، هذه ليست هذه الشخصيات الرهيبة. الآن ، إذا استطعنا الابتعاد عن حساب ما تبقى من قسمة الدرجات الكبيرة على العدد قيد الدراسة ... للحصول على تسلسلات بسيطة من النموذج 100 ... 00 و 111 ... 111 ، تكون الشهادة حاضرة بالضرورة. ولكن ربما يكون هناك تسلسلات من أجلها ستكون صيغة حساب العضو "إيث" في سلسلة من البقايا أبسط؟ أو يمكنك حقًا العثور على تسلسل مع فترة دنيا كبيرة. بعد كل شيء ، ما هي الفترة التي نحتاجها؟ 300 مليون فقط (في شكل ثنائي). إذا أعطانا تسلسل معين فترة لا تقل عن النموذج 100 * N ، حيث N هو الرقم قيد التحقيق ، فسيكون عدد يصل إلى 3 ملايين رقم كافياً لإيجاد رقم قيمته 150 ألف دولار. وتصل إلى 30 مليون دولار لعدد 250 ألف دولار. والآن ، عندما يمكن أن تحدث فترة قصيرة بأعداد كبيرة جدًا (للتسلسلين 100..00 و 111 ... 111) ، ليس لدينا أي إمكانيات بسيطة للعثور عليه. ولكن هناك أمل وكل هذا يتوقف على الاختيار الناجح لاتجاه البحث. من الواضح أن التكرار خلال التسلسل واحد في كل مرة ليس واقعيًا بالنسبة لشخص واحد ، ولكن يمكنك تجربة الحشد.

حسنًا ، عندما تجد الأرقام المطلوبة ، تنتظرك القليل من البيروقراطية. أولاً ، سيتعين عليك نشر مقال في مجلة رياضية بالولايات المتحدة الأمريكية أو إنجلترا أو كندا أو أستراليا ، ويجب أن تكون المجلة من القائمة التي أشارت إليها مؤسسة الحدود الإلكترونية (EFF) (هذه مجلات محترمة جدًا). في المقالة ، يجب أن تثبت أن طريقتك تجعل من الممكن حقًا العثور على الرقم الأولي المطلوب. ثم ترسل خطاب السعادة إلى EFF (على عنوان محدد) ، حيث تشير إلى المقالة المنشورة ثم تنتظر الأوامر من EFF. قد تتعلق الطلبات بالتحقق من كل ما قمت به للعثور على الرقم. لا ينبغي أن يكون هناك أي أسرار ، ولا أي أعمال غير قانونية أو مشكوك فيها. وهذا كل شيء ، بعد ذلك - جائزتك.

ما هي الكمائن التي يمكن أن تنتظرك في طريقك؟ حسنًا ، بالنسبة للمبتدئين - العثور على رقم أولي وعدم ارتكاب الأخطاء عند البحث عنه. القادمة تحتاج إلى الكتابة في مجلة قوية. بما أن المجلة قوية ، فإن رد الفعل المعتاد للمحررين على خطاب المخترع التالي لآلة الحركة الدائمة هو:

- ماذا؟ غريب آخر؟ إلى السلة!

ولكن من الممكن أن يكون لديك خبرة في كتابة المقالات ويمكنك التعامل بسهولة مع هذه المشكلة. وبعد ذلك سوف تجد الاختيار. لا أعرف ما الذي ستدرسه EFF دليلك ، لكنهم يكتبون أنهم قد يهتمون بكل شيء ، أي شيء. سيكون من المثير للاهتمام بشكل خاص إذا كانت أهداف EFF لا تتوافق مع النتيجة التي تقدمها. لذلك يعلنون عن هدف تطوير طرق لاستخدام أجهزة الكمبيوتر الشخصية لوضعها في الاستخدام عن بُعد المؤقت للحوسبة الخارجية.تم منح الجائزة السابقة فقط لإنشاء البرنامج والترويج له ، والذي قام المتطوعون بتنزيله ، وبالتالي قاموا بتوفير اللوحات الجرافيكية اللازمة لطحن الأعداد الأولية. كيف ترتبط EFF بحساب البرايم بدون الترافعات الجماعية - لا أعرف. من الناحية النظرية ، لا توجد قيود على متطلباتهم ، لذلك النجاح ممكن تمامًا.

هذا كل شيء ، بعد أن مررت بمرحلتين من المراحل المشار إليها (وعدم نسيان العثور على الأرقام اللازمة في مرحلة الصفر) ، فأنت تشير إلى البنك ورقم الحساب حيث تنخفض الجائزة إليك. مبلغ واحد كبير. أنت تتعامل مع الضريبة على نفقتك الخاصة.

بدلا من خاتمة

ذات مرة ، اكتشف بيير فيرما ، وليس عالم الرياضيات ، العديد من الأنماط لنظرية الأعداد. كان الرجل يتساءل فقط ، حسناً ، كان هناك وقت فراغ في متناول اليد. وهنا لديك الإنجازات التي لا تزال تتذكر. مثال آخر هو إيفاريست جالوا. لقد درس الرياضيات في سن 16 ، وتوفي في سن العشرين في مبارزة. لمدة 4 سنوات ، حاول الاهتمام بالعديد من علماء الرياضيات مع اكتشافاته ، لكنه لم ينجح. بعد موته ، تم تقدير عمله ومع ذلك نحن مدينون بإنشاء هذا الفرع من الرياضيات كنظرية المجموعة ، وكذلك تطور الجبر. مرة أخرى - كان من المثير للاهتمام أن يجد الشخص النجوم ، لكن ترتيب الأعمال وفقًا للقواعد لم يكن يناسبه. ولكن لحسن الحظ ، تم إضفاء الطابع الرسمي على عمله من قبل الآخرين. ومثال آخر - جورج كانتور ، الذي انعكس على المفاهيم المعروفة للمجموعة وعنصرها ، استنتج أحدهما النظرية في نهاية القرن التاسع عشر ،الذي اتفق علماء الرياضيات المعلقة على اعتباره جديراً بأن يصبح أساسًا لملكة العلوم.

لماذا كل هذه القصص؟ كما اعتاد السيد أوباما أن يقول ، "يمكنك!" نعم ، هذا الشعار الأمريكي مناسب تمامًا للأشخاص المتحمسين. على الرغم من تطور العلم اليوم ، فهو غير مكتمل ، إنه غير مثالي ، وهناك أماكن فيه لم تتقدم قدم عالم حقيقي. لذا فلنشغل فضولنا ونحاول البحث عن مثل هذه المسارات غير المربوطة ، وماذا لو نجحت؟