الدليل الجديد يحل تقريب الأرقام مثل pi

كان اليونانيون القدماء مهتمين بما إذا كان من الممكن التعبير عن الأرقام غير المنطقية تقريبًا في الكسور. لإثبات فرضية دوفن شافير القديمة ، أعطى اثنان من علماء الرياضيات إجابة شاملة.

الترميز الثنائي inf غير محدود. ولكن يمكن لعدد لا حصر له من الكسور تقترب من هذا الرقم مع زيادة الدقة باستمرار.

الانخفاضات العميقة على خط الأرقام ليست مستحيلة كما قد يبدو. هذا هو واحد من عواقب أدلة جديدة ذات معنى لكيفية أن الأرقام المعقدة تتناسب مع التقديرات البسيطة.

يثبت الدليل مشكلة ما يقرب من 80 عامًا ، والمعروفة باسم فرضية Duffin-Shaffer. وبالتالي ، فإنه يعطي الجواب النهائي الذي احتل علماء الرياضيات منذ العصور القديمة: تحت أي ظروف من الممكن تمثيل الأرقام غير المنطقية التي تدوم طويلاً بلا حدود - مثل pi - مع الكسور البسيطة من النوع 22/7؟ يثبت الدليل أن الإجابة على هذا السؤال العام قد وجدت كنتيجة لعملية حسابية واحدة.

وقال جيمس ماينارد من جامعة أكسفورد ، وهو مؤلف مشارك للدليل الذي قدمه مع ديميتريس كوكولوبولوس من جامعة مونتريال: "هناك معيار بسيط لمعرفة ما إذا كان يمكنك تقريب أي عدد تقريبًا أو عدم وجود أي رقم تقريبًا".

كان علماء الرياضيات يشككون منذ عدة عقود ، وهذا المعيار البسيط أساسي لفهم متى يمكن الحصول على تقريب جيد - لكنهم لم يتمكنوا من إثبات ذلك. لم يتمكن كوكولوبولس وماينارد من القيام بذلك إلا بعد إعادة صياغة مشكلة الأرقام هذه من حيث الارتباطات بين نقاط وخطوط الرسم البياني - تغيير أساسي في المنظور.

وقال جيفري والير من جامعة تكساس في أوستن ، الذي كان له يد في النتائج المبكرة المتعلقة بفرضية دوفن شافير: "أود أن أقول إنهم كانوا واثقين بما يكفي (وكان من الواضح أن ذلك له ما يبرره) لاتخاذ المسار المختار". "وظيفة رائعة."

الأثير الحسابي

مع الأرقام المنطقية ، كل شيء بسيط. وهي تتضمن أرقامًا لحساب العناصر وكافة الأرقام الأخرى التي يمكن كتابتها بالكسور.

نظرًا لهذه القدرة على الكتابة ، فإن الأرقام المنطقية معروفة لنا. ومع ذلك ، من بين جميع الأرقام الحقيقية ، فإن الأرقام المنطقية هي في الواقع قليلة جدا. معظم الأرقام غير منطقية ، مع تدوين عشري لانهائي ، ولا يمكن كتابتها في كسور. تبين أن بعضها مهم بما يكفي لتدوين الرموز الرمزية - pi، e، √2. الباقي لا يمكن حتى أن يسمى. إنها موجودة في كل مكان ، ولكن لا يمكن الوصول إليها - مثل الأثير الحسابي.

ربما ، لذلك ، سيكون من الطبيعي التفكير - إذا لم نتمكن من التعبير بدقة عن الأرقام غير المنطقية ، فكم مدى قربنا منها؟ هذا مجال تقريب عقلاني. أدرك علماء الرياضيات في العصور القديمة أن نسبة المراوغة من المحيط إلى القطر يمكن تقريبها جيدًا باستخدام الكسر 22/7. في وقت لاحق ، اكتشف علماء الرياضيات تقريبًا مضغوطًا أكثر دقة تقريبًا تقريبًا لـ pi: 355/113.

وقال بن جرين من جامعة أوكسفورد: "الكتابة بي صعبة للغاية". "حاول الناس العثور على التقريب الأكثر دقة ل pi ، وكانت إحدى الطرق الشائعة للقيام بذلك استخدام الأرقام المنطقية".



في عام 1837 ، اكتشف عالم الرياضيات بيتر غوستاف ليجون من ديريتش قاعدة تخبرنا بمدى دقة تقريب الأرقام غير المنطقية باستخدام الأرقام المنطقية. من السهل العثور على التقريب إذا لم تقم بتعيين القيمة الصحيحة للخطأ. لكن ديريتشيت أثبت وجود علاقة واضحة بين الكسور والأعداد غير المنطقية والأخطاء التي تفصل بينها.

لقد أثبت أنه لأي عدد غير عقلاني ، هناك عدد لا حصر له من الكسور تقترب منه أكثر فأكثر. بتعبير أدق ، لن يكون خطأ كل كسر أكثر من 1 مقسومًا على مربع المقام. على سبيل المثال ، يعبر الكسر 22/7 تقريبًا عن pi بدقة 1/7 ² أو 1/49. الكسر 355/113 ليس أبعد من pi من 1/113 ² ، أو 1/12 769. أثبت Dirichlet أن هناك العديد من الكسور بلا حدود ، تقترب وتقترب من pi مع قاسم متزايد.

وقال أندرو جرانفيل من جامعة مونتريال: "الشيء المدهش والرائع هو القدرة على التعبير عن العدد الحقيقي تقريبًا من خلال كسر بسيط ، مع وجود خطأ لا يتجاوز الرقم مقسومًا على مربع المقام".


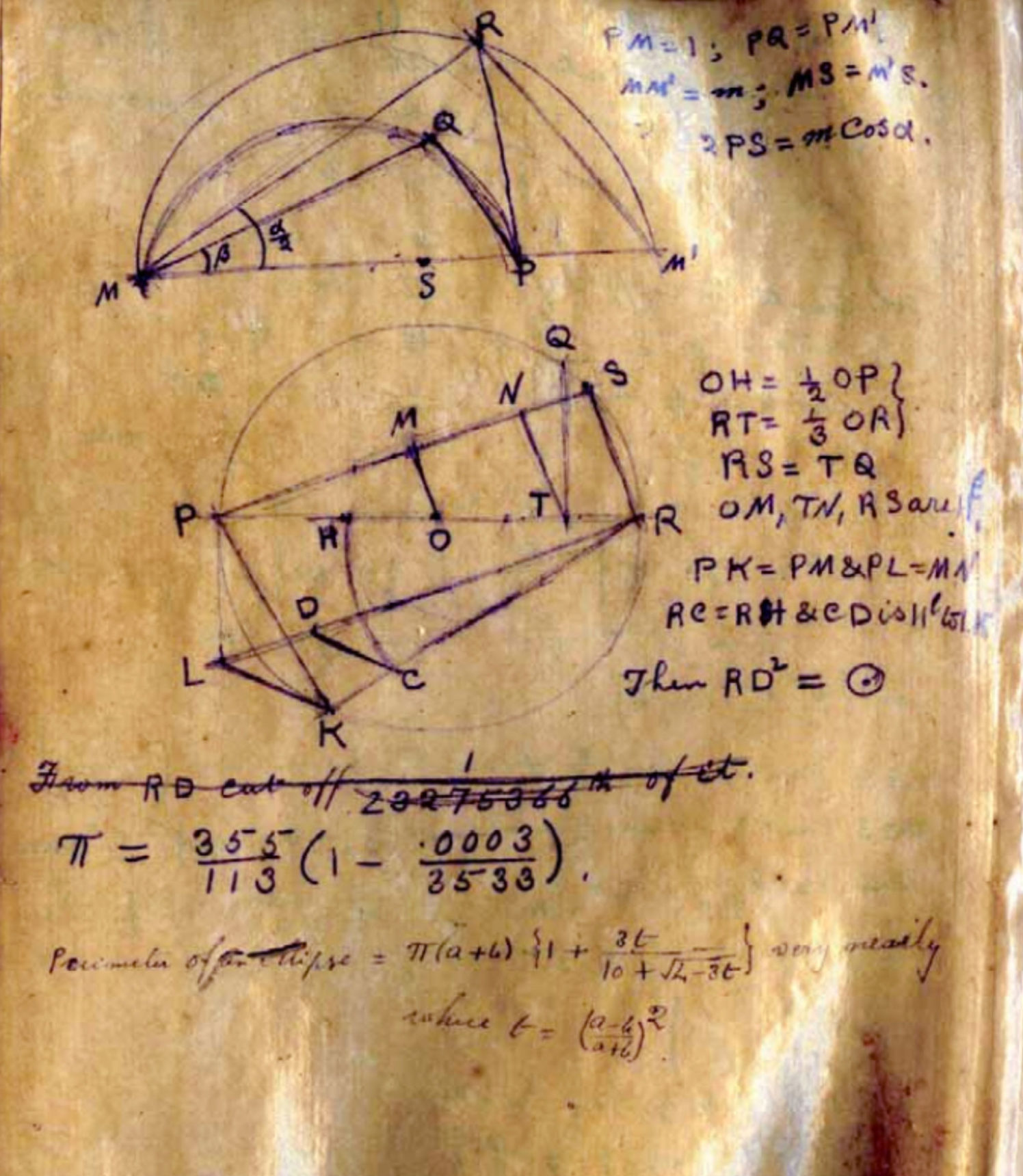في مخطوطة عام 1913 ، استخدم عالم الرياضيات سرينيفاسا رامانوجان آينجور الكسر 355/113 كتقريب منطقي ل pi.

كان اكتشاف ديريتشيت بمثابة بيان محدود حول التقريب العقلاني. تشير إلى أنه بالنسبة لأي رقم غير منطقي ، يمكنك العثور على عدد لا نهائي من الكسور التي تقترب منه ، إذا كنت تستطيع استخدام أي عدد صحيح كقاسم ، وكنت راضيًا عن الخطأ في حجم المربع العكسي. ولكن ماذا لو كنت تريد أن تنتمي القواسم إلى مجموعة فرعية (لا نهائية) من الأعداد الصحيحة ، على سبيل المثال ، إلى مجموعة الأعداد الأولية ، أو لمجموعة المربعات الكاملة ؟ ماذا لو كنت تريد أن يكون خطأ التقريب 0.00001 ، أو أن يكون لديك أي قيمة أخرى؟ هل ستكون قادرًا على العثور على عدد لا حصر له من الكسور التقريبية بالتحديد في مثل هذه الظروف؟

فرضية Duffin-Shaffer هي محاولة لإنشاء النظام الأساسي الأكثر تعميماً للتعامل مع التقديرات المنطقية. في عام 1941 ، عالم الرياضيات R.D. Duffin و A.S. قدم Schafer السيناريو التالي. أولاً ، اختر قائمة لا تنتهي من القواسم. يمكن أن يكون كل ما تريده: الأرقام الفردية والأرقام قابلة للقسمة على 10 والأعداد الأولية.

ثم ، لكل رقم في القائمة ، حدد مدى الدقة التي تحتاجها لتقريب الرقم غير المنطقي. يخبرنا Intuition أننا إذا اخترنا أخطاء كبيرة بما فيه الكفاية ، فستكون لدينا المزيد من الفرص للتقريب. إذا اخترت حجم خطأ صغير ، فسيكون الأمر أكثر صعوبة. وقال كوكولوبولوس "أي تسلسل سيؤدي في حالة ترك مساحة كافية".

الآن ، بالنظر إلى المعلمات المحددة - سلسلة من الأرقام وخطأ معين - السؤال الذي يطرح نفسه: هل من الممكن العثور على عدد لا حصر له من الكسور تقريب جميع الأرقام غير المنطقية؟

توفر الفرضية وظيفة رياضية لتقييم هذا السؤال. المعلمات الخاصة بك بمثابة المدخلات. يمكن أن تكون النتيجة واحدة من خيارين. اقترح Duffin and Schaffer أن هذين الخيارين يتوافقان بدقة مع ما إذا كان التسلسل الخاص بك يمكن تقريبًا تقريبًا لجميع الأرقام غير المنطقية بالدقة المطلوبة ، أو عملياً لم يتم ذكر أيٍّ منهما (عمليًا) لأن أي مجموعة من القواسم سيكون هناك دائمًا عدد صغير الأرقام غير المنطقية المعزولة التي يمكن أو لا يمكن تقريبها بشكل جيد بما فيه الكفاية).

"تحصل على كل شيء تقريبًا أو لا شيء تقريبًا. لا توجد خيارات وسيطة.

كان هذا بيانًا عامًا للغاية ، حيث حاول وصف التقريب بالأرقام المنطقية على طول وعبر. بدا المعيار الذي اقترحه دوفن وشافير صحيحًا لعلماء الرياضيات. ومع ذلك ، لإثبات أن الناتج الثنائي للوظيفة يحتوي على كل ما تحتاجه لفهم ما إذا كان التقريب الخاص بك يعمل أم لا ، كان من الصعب للغاية القيام به.

العد المزدوج

والدليل على فرضية Duffin-Schaffer هو فهم الفائدة التي تحصل عليها من كل من القواسم المتاحة لك. لكي تشعر بهذا ، سيكون من المفيد التفكير في إصدار أصغر من هذه المهمة.

افترض أنك تريد تقريب جميع الأرقام غير المنطقية على قطعة من 0 إلى 1. تخيل أن جميع الأرقام الطبيعية من 1 إلى 10. متوفرة كمقامين. قائمة الكسور المحتملة كبيرة جدًا. أول 1/1 ، ثم 1/2 و 2/2 ، ثم 1/3 ، 2/3 و 3/3 ، وهكذا ، حتى 9/10 و 10/10. ومع ذلك ، ليس هناك فائدة منها.

على سبيل المثال ، 2/10 هو نفس 1/5 ، و 5/10 هو نفس 1/2 و 2/4 و 3/6 و 4/8. قبل ظهور فرضية Duffin-Schaffer ، صاغ عالم الرياضيات السوفيتي ألكسندر ي. كينشين فرضية تقريب عقلاني مماثل في العرض. ومع ذلك ، فإن نظريته لم تأخذ في الاعتبار حقيقة أن الكسور المعادلة ينبغي أن تحسب مرة واحدة فقط.


ديميتريس كوكولوبولوس (يسار) وجيمس ماينارد أثناء تقديم أدلته في مؤتمر في إيطاليا

وقال جرانفيل: "عادة ، لا يجب أن تؤثر الرياضيات للصف الأول على حل المشكلات". "لكن في هذه الحالة ، من المدهش أنها تأثرت".

لذلك ، تتضمن فرضية Duffin-Shaffer مصطلحًا يحسب عدد الكسور الفريدة (أو الكسور المخفضة) لكل قاسم. يُطلق على هذا العضو وظيفة ul Euler تكريما لمخترعها ، عالم الرياضيات في القرن الثامن عشر ، Leonard Euler. φ (10) هي 4 ، لأنه بين 0 و 1 لا يوجد سوى أربعة كسور مخفضة مع مقام 10: 1/10 ، 3/10 ، 7/10 و 9/10.

والخطوة التالية هي حساب عدد الأرقام غير المنطقية التي يمكن تقريبها باستخدام كل من الكسور المقدمة. ذلك يعتمد على حجم الخطأ الذي كنت على استعداد لقبوله. تتيح لنا فرضية Duffin-Shaffer اختيار خطأ لكل من القواسم. على سبيل المثال ، بالنسبة للكسور ذات المقام 7 ، يمكنك أن تأخذ الخطأ المسموح به وهو 0.02. بالنسبة للمقام 10 ، يمكنك أن تأخذ الخطأ 0.01.

بعد تحديد القواسم وشروط الأخطاء ، حان الوقت لوضع الشبكات على أرقام غير عقلانية. قم ببناء الكسور على خط رقم بين 0 و 1 ، وارسم الأخطاء في شكل شبكات تمتد من الكسر على كل جانب. يمكننا أن نقول أن جميع الأرقام غير المنطقية التي تقع في الشبكة "تقارب بشكل مرض" للشروط المحددة. والسؤال هو: كم عدد الأرقام غير المنطقية التي اشتعلتها؟



في أي فاصل زمني من خط الأرقام يحتوي على عدد لا حصر له من الأرقام غير المنطقية ، لذلك لا يمكن كتابة العدد الدقيق للأرقام غير المنطقية التي تم اكتشافها. بدلاً من ذلك ، يتحدث علماء الرياضيات عن نسبة إجمالي عدد الأرقام غير المنطقية التي يتم صيدها بواسطة كل جزء. يقومون بتقييم هذه النسب باستخدام مفهوم مثل "قياس" مجموعة فرعية من الأرقام - إنه شيء مثل تقدير عدد الأسماك التي يتم صيدها بالوزن بدلاً من الكمية.

تقترح فرضية Duffin-Schaffer إضافة كافة مقاييس مجموعات فرعية من الأرقام غير عقلانية اشتعلت كل من الكسور التقريبية. إنها تمثل هذا الرقم كمجموع حسابي كبير. ثم تقوم بعمل تنبؤها الرئيسي: إذا ذهب هذا المبلغ إلى ما لا نهاية ، فأنت تقريبًا تقريبًا جميع الأرقام غير المنطقية ؛ إذا كانت تعطي القيمة النهائية فقط ، بغض النظر عن عدد الإجراءات التي لخصتها ، فلن تتمكن من تقريب أي رقم غير منطقي تقريبًا.

هناك سؤال مشابه ، ما إذا كان مجموع "يتحول" إلى ما لا نهاية أو "يتقارب" إلى قيمة محدودة ، ينشأ في العديد من مجالات الرياضيات. البيان الرئيسي لفرضية Duffin-Shaffer هو أنه إذا كنت تريد أن تفهم ما إذا كان يمكنك تقريب جميع الأرقام غير المنطقية تقريبًا باستخدام مجموعة معينة من القواسم والأخطاء ، فأنت بحاجة فقط إلى معرفة شيء واحد: هل تتباعد مجموعة التدابير اللانهائية إلى ما لا نهاية ، أو تتقارب إلى القيمة النهائية.

"في النهاية ، بصرف النظر عن كيفية تقييمك لتقريب كل قاسم ، فإن نجاحك يعتمد كليا على شيء واحد فقط: سواء كان التسلسل اللانهائي يتباعد أم لا" ، قال والر.

صنع القرار

قد تتساءل: ماذا لو تقاربت الأرقام بكسر واحد مع أرقام تقريبية بآخر؟ ألا نأخذها في الاعتبار مرتين عند حساب التدابير؟

بالنسبة لبعض تسلسل التقريب ، لا يهم الحساب المزدوج. أثبت علماء الرياضيات منذ عدة عقود أن هذه الفرضية تحمل تتابعات تقريبية تتكون من الأعداد الأولية. ولكن بالنسبة للعديد من متواليات التقريب الأخرى ، يعد الحساب المزدوج مشكلة. لذلك ، لم يستطع علماء الرياضيات التعامل مع هذه الفرضية لمدة 80 عامًا.

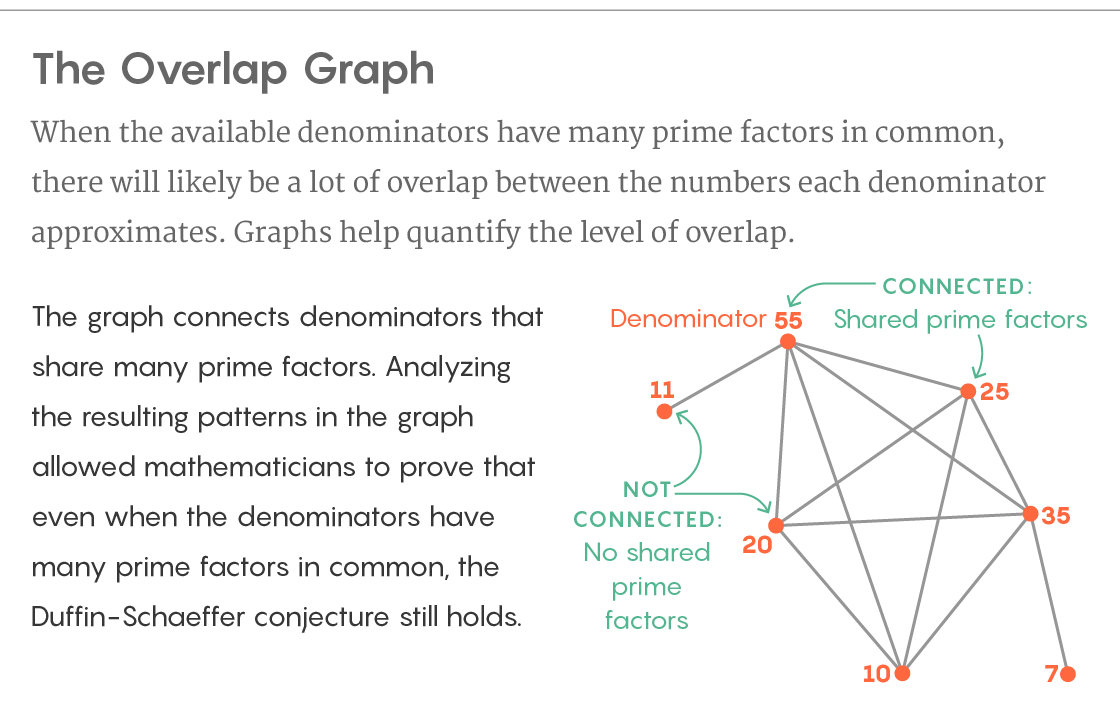
تنعكس الدرجة التي تأخذ بها القواسم المختلفة مجموعات متقاطعة من الأرقام غير المنطقية في عدد المقسومات البسيطة المشتركة بين جميع القواسم. النظر في الأرقام 12 و 35. المقسومات الأولية من 12 هي 2 و 3. المقسومات الأولية من 35 هي 5 و 7. وبعبارة أخرى ، فإن العوامل الأولية المشتركة من 12 و 35 لا - نتيجة لذلك ، هناك العديد من الأرقام غير المنطقية التي يمكن تقريبها بواسطة الكسور من القواسم 12 و 35 لا تتقاطع بشكل خاص.

ماذا عن القواسم 12 و 20؟ في 20 ، المقسومات البسيطة تتقاطع مع 2 و 5 مقسومة على المقسومات 12. وبنفس الطريقة ، فإن الأرقام غير المنطقية التي يمكن تقريبها بالكسور مع قاسم من 20 تتقاطع مع تلك التي يمكن تقريبها بواسطة الكسور مع قاسم 12. فرضية Duffin-Shaffer هي الأصعب إثبات في مثل هذه الحالات - عندما يكون للأرقام في تسلسل التقريب العديد من المقسومات الأولية الصغيرة الشائعة ، ويحدث تقاطع العديد من المجموعات الفرعية من الأرقام التي يقترب كل مقام من القواسم.

وقال سام شاو من جامعة أكسفورد: "عندما يكون لدى العديد من القواسم التي تختارها العديد من المقسومات البسيطة الصغيرة ، فإنها تبدأ في التدخل مع بعضها البعض".

كان مفتاح حل الفرضية هو إيجاد طريقة لحساب التداخل الدقيق للمجموعات الفرعية من الأرقام غير المنطقية التي يتم تقريبها بواسطة القواسم التي لها مقسومات أولية مشتركة. لمدة 80 عامًا ، لم يتمكن أحد من القيام بذلك. نجح كوكولوبولس وماينارد في إيجاد وجهة نظر جديدة تمامًا حول المشكلة.


المتبادل تراكب العد

في دليلهم الجديد ، يبنون رسمًا بيانيًا من قواسمهم. يبنونها كرؤوس للرسم البياني وتربط القمم بحافة إذا كان لديهم العديد من المقسومات الأولية المشتركة. تصف بنية الرسم البياني تراكب المجموعات الفرعية من الأرقام غير المنطقية التي يقاربها كل من القواسم. وعلى الرغم من صعوبة التحقق من هذا التراكب بشكل مباشر ، فقد اكتشف Kukulopoulos و Maynard طريقة لتحليل بنية الرسم البياني باستخدام أدوات من نظرية الرسوم البيانية - وتم العثور على المعلومات التي يحتاجون إليها بهذه الطريقة.

وقال كوكولوبولوس "الرسم البياني يساعد على فهم المهمة بصريًا ، إنها لغة جميلة يمكنك من خلالها التفكير في المشكلة".

أثبت Cuculopoulos و Maynard أن فرضية Duffin-Schaffer حقيقية بالفعل: إذا أعطيت لك قائمة من القواسم مع وجود أخطاء صحيحة ، يمكنك تحديد ما إذا كان من الممكن تقريبًا جميع الأرقام غير المنطقية تقريبًا ، أو أنه من المستحيل القيام بذلك ببساطة عن طريق التحقق مما إذا كان مجموع المقاييس المتباينة يتباعد إلى ما لا نهاية أو يتقارب إلى قيمة محدودة.

هذا اختبار أنيق ، يأخذ السؤال الواسع حول طبيعة التقريب بالأرقام المنطقية ويخفضه إلى قيمة واحدة محسوبة. بعد أن أثبتوا عالمية الاختبار ، قام كوكولوبولس وماينارد بأحد أعظم الأمور في الرياضيات: لقد أعطوا الإجابة النهائية على سؤال أساسي في مجالهم.

وقال غرين: "لقد أصبح دليلهم نتيجة ضرورية وكافية". "أفترض أنه يمثل نهاية الفصل التالي في الرياضيات."