
التجميع هو جزء مهم من خط أنابيب التعلم الآلي لحل المشكلات العلمية والتجارية. يساعد في تحديد مجموعات من النقاط ذات الصلة الوثيقة (مقياس معين للمسافة) في سحابة البيانات التي قد يصعب تحديدها بوسائل أخرى.
ومع ذلك ، فإن عملية التجميع في معظمها تتعلق بمجال
التعلم الآلي دون وجود معلم ، والذي يتميز بعدد من الصعوبات. لا توجد إجابات أو نصائح حول كيفية تحسين العملية أو تقييم نجاح التدريب. هذه أرض مجهولة.
لذلك ، ليس من المستغرب أن الطريقة الشائعة
للتجميع باستخدام طريقة k-average لا تجيب بالكامل على سؤالنا:
"كيف يمكننا أولاً معرفة عدد المجموعات؟" هذا السؤال مهم للغاية ، لأن التكتلات غالباً ما تسبق المعالجة الإضافية للمجموعات الفردية ، وقد يعتمد مقدار موارد الحوسبة على تقييم عددها.
قد تنشأ عواقب أسوأ في مجال تحليل الأعمال. هنا ، يتم استخدام التجميع لتجزئة السوق ، ومن الممكن تخصيص موظفي التسويق وفقًا لعدد المجموعات. لذلك ، يمكن أن يؤدي التقدير الخاطئ لهذا المبلغ إلى تخصيص غير مثالي للموارد القيمة.
طريقة الكوع
عند التجميع باستخدام طريقة k-الوسائل ، يتم تقدير عدد الكتل في أغلب الأحيان باستخدام
"طريقة الكوع" . وهو ينطوي على تنفيذ دوري للخوارزمية مع زيادة في عدد المجموعات المختارة ، بالإضافة إلى تأجيل لاحق لنقاط المجموعات على الرسم البياني ، وتحسب كدالة لعدد المجموعات.
ما هي هذه النتيجة ، أو المتري ، والتي يتم تأخيرها على الرسم البياني؟ لماذا يطلق عليه طريقة
الكوع ؟
رسم بياني نموذجي يشبه هذا:
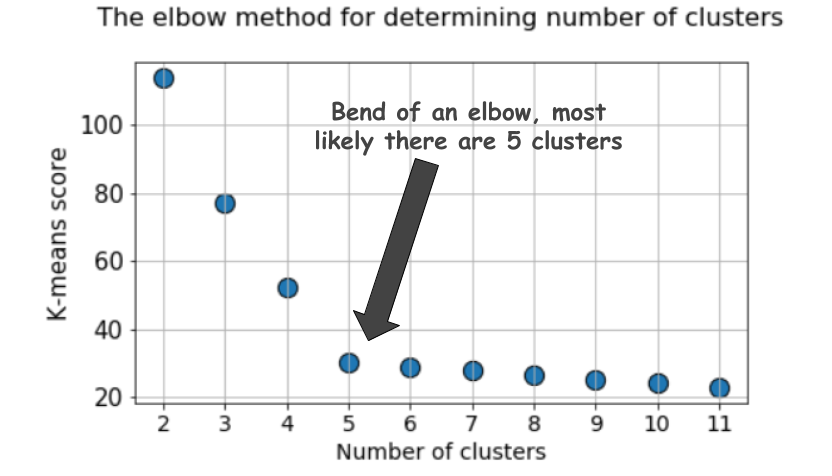
النتيجة ، كقاعدة عامة ، هي مقياس لبيانات الإدخال للدالة الموضوعية للوسائل k ، أي شكل من أشكال نسبة المسافة intracluster إلى مسافة intercluster.
على سبيل المثال ، تتوفر طريقة التسجيل هذه فورًا في
أداة تسجيل النقاط k-الوسائل في Scikit-Learn.
لكن إلقاء نظرة أخرى على هذا الرسم البياني. إنه شعور بشيء غريب. ما هو العدد الأمثل للمجموعات التي لدينا ، 4 ، 5 أو 6؟
هذا غير واضح ، أليس كذلك؟
صورة ظلية هو متري أفضل
يتم حساب معامل صورة ظلية باستخدام متوسط المسافة intracluster (أ) ومتوسط المسافة إلى أقرب مجموعة (ب) لكل عينة. يتم حساب الصورة الظلية على أنها
(b - a) / max(a, b) . اسمحوا لي أن أشرح:
b هي المسافة بين وأقرب مجموعة لا تنتمي إليها. يمكنك حساب متوسط قيمة صورة ظلية لجميع العينات واستخدامها كمقياس لتقدير عدد الكتل.
إليك مقطع فيديو يشرح هذه الفكرة:
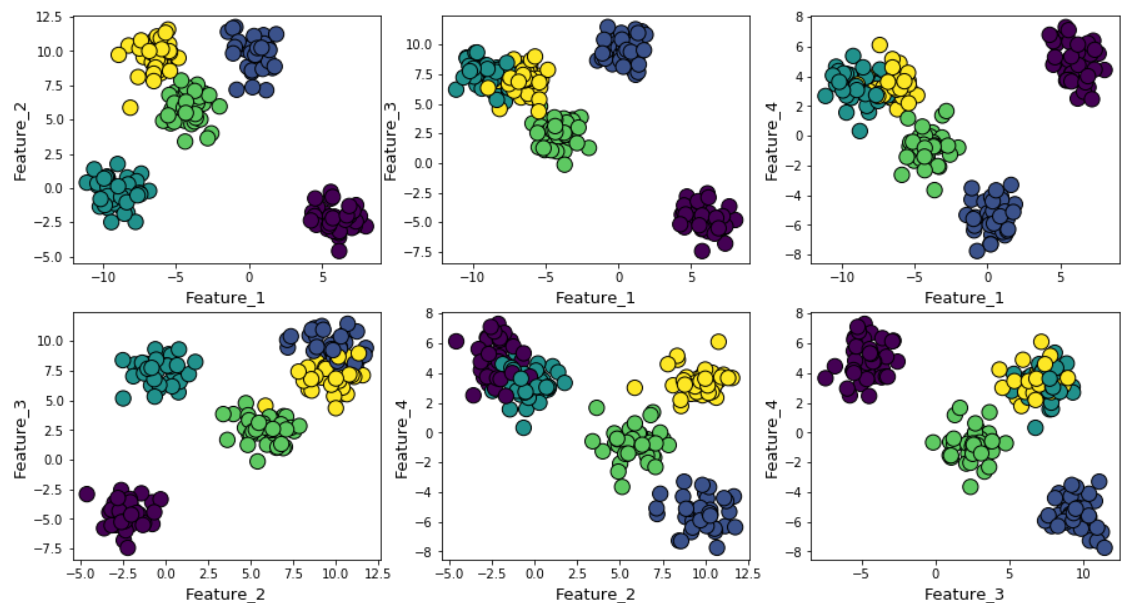
افترض أننا أنشأنا بيانات عشوائية باستخدام الدالة make_blob من Scikit-Learn. توجد البيانات في أربعة أبعاد وحوالي خمسة مراكز عنقودية. جوهر المشكلة هو أن يتم إنشاء البيانات حول خمسة مراكز الكتلة. ومع ذلك ، فإن خوارزمية k- يعني لا يعرف عن هذا.
يمكن عرض المجموعات على المخطط كما يلي (علامات الزوجية):
بعد ذلك ، نقوم بتشغيل خوارزمية k-mean مع القيم من
k = 2 إلى
k = 12 ، ثم نقوم بحساب المقياس الافتراضي إلى k-mean ومتوسط قيمة الصورة الظلية لكل تشغيل ، مع عرض النتائج في رسومات بيانية متجاورة.
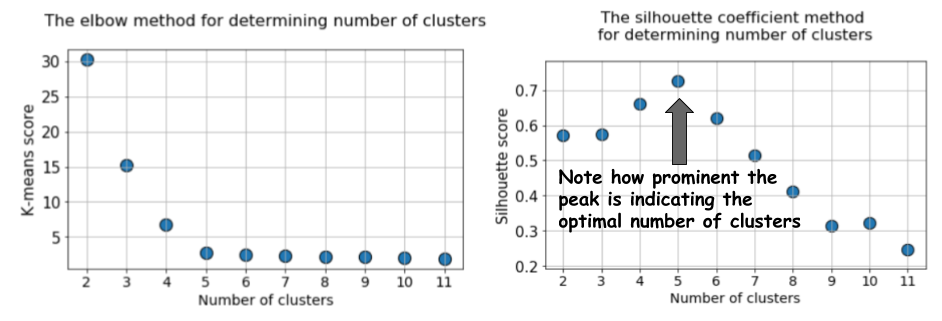
الفرق واضح. يزيد متوسط قيمة الصورة الظلية إلى
k = 5 ، ثم ينخفض بشكل حاد للقيم الأعلى من
k . بمعنى ، حصلنا على ذروة واضحة عند
k = 5 ، وهذا هو عدد المجموعات التي تم إنشاؤها في مجموعة البيانات الأصلية.
يحتوي الرسم البياني للصورة الظلية على أعلى درجة ، على عكس الرسم البياني المنحني برفق عند استخدام طريقة الكوع. فمن الأسهل تصور وتبرير.
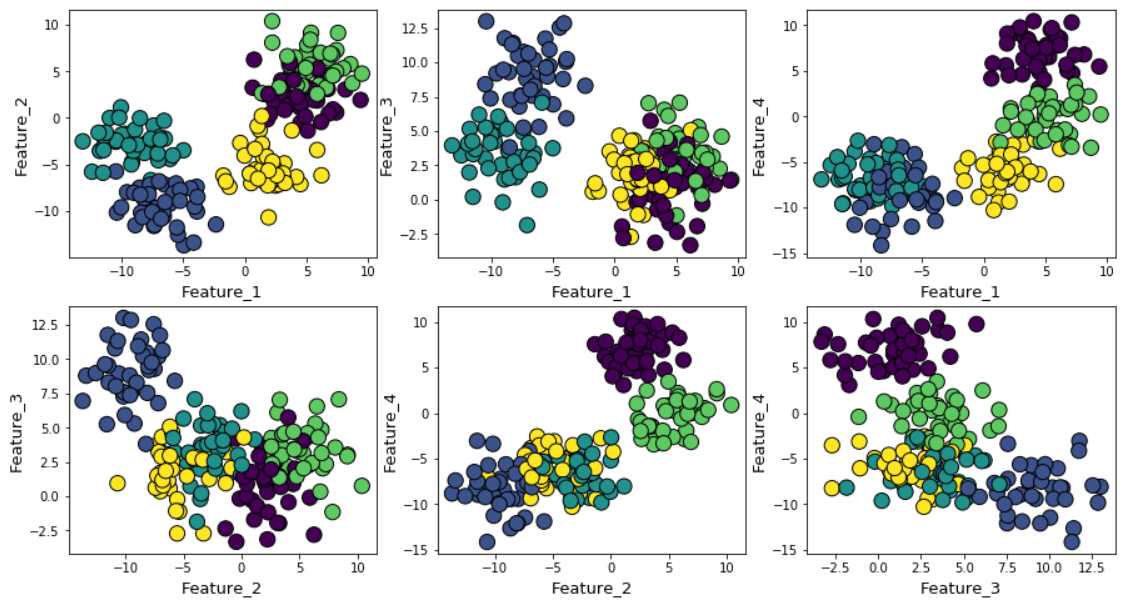
إذا قمت بزيادة الضوضاء الغوسية أثناء توليد البيانات ، فستتداخل المجموعات بقوة أكبر.
في هذه الحالة ، يعطي حساب الوسائل الافتراضية باستخدام طريقة الكوع نتيجة غير مؤكدة. يوجد أدناه رسم بياني لطريقة الكوع ، يصعب عندها اختيار نقطة مناسبة ينحني فيها الخط فعليًا. هل هو 4 ، 5 ، 6 أو 7؟
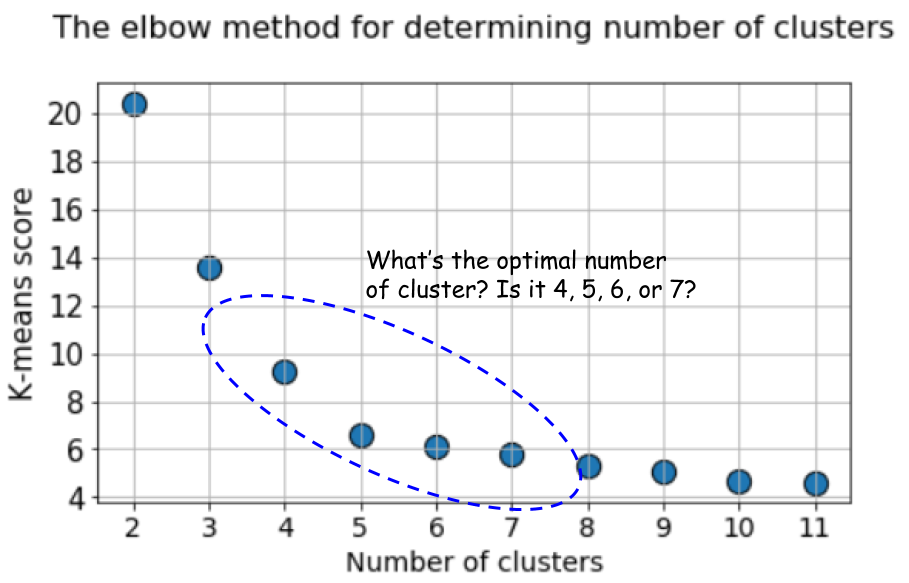
في الوقت نفسه ، لا يزال الرسم البياني للصور الظلية يظهر ذروة في المنطقة من 4 أو 5 مراكز عنقودية ، مما يسهل حياتنا إلى حد كبير.
إذا نظرت إلى مجموعات تتداخل مع بعضها البعض ، فسترى أنه على الرغم من حقيقة أننا قمنا بإنشاء بيانات حول 5 مراكز ، نظرًا للتشتت الشديد ، يمكن تمييز 4 مجموعات فقط من الناحية الهيكلية. صورة ظلية يكشف بسهولة هذا السلوك ويظهر العدد الأمثل من الكتل بين 4 و 5.

النتيجة BIC مع نموذج مزيج التوزيع الطبيعي
هناك مقاييس أخرى رائعة لتحديد العدد الحقيقي للمجموعات ، مثل
معيار المعلومات البايزي (BIC). ولكن لا يمكن استخدامها إلا إذا كنا بحاجة إلى الانتقال من طريقة k-الوسائل إلى إصدار أكثر عمومية - خليط من التوزيعات الطبيعية (Gaussian Mixture Model (GMM)).
ترى GMM سحابة البيانات كتراكب للعديد من مجموعات البيانات ذات التوزيع العادي ، مع وجود قيم وتغيرات منفصلة في المتوسط. ثم يستخدم GMM خوارزمية
لزيادة التوقعات لتحديد هذه المتوسطات والفروق.

BIC للتنظيم
ربما تكون قد واجهت بالفعل BIC في التحليل الإحصائي أو عند استخدام الانحدار الخطي. يتم استخدام BIC و AIC (معيار معلومات Akaike ، معيار معلومات Akaike) في الانحدار الخطي كتقنيات تنظيم لعملية اختيار المتغيرات.
تنطبق فكرة مماثلة على BIC. من الناحية النظرية ، يمكن تصميم المجموعات المعقدة للغاية على هيئة تراكبات لعدد كبير من مجموعات البيانات ذات التوزيع الطبيعي. لحل هذه المشكلة ، يمكنك تطبيق عدد غير محدود من هذه التوزيعات.
لكن هذا يشبه زيادة تعقيد النموذج في الانحدار الخطي ، عندما يمكن استخدام عدد كبير من الخصائص لمطابقة البيانات بأي تعقيد ، فقط لفقدان إمكانية التعميم ، لأن نموذج معقد للغاية يتوافق مع الضوضاء ، وليس مع نمط حقيقي.
أسلوب BIC يفرض العديد من التوزيعات الطبيعية ويحاول الحفاظ على النموذج بسيطًا بدرجة كافية لوصف نمط معين.
لذلك ، يمكنك تشغيل خوارزمية GMM لعدد كبير من مراكز نظام المجموعة ، وستزداد قيمة BIC إلى حد ما ، ثم تبدأ في الانخفاض كلما ازدادت الغرامة.
يؤدي
هنا هو
دفتر Jupyter لهذا المقال. لا تتردد في شوكة والتجربة.
ناقشنا في Jet Infosystems اثنين من البدائل لطريقة الكوع الشائعة من حيث اختيار العدد المناسب من المجموعات عند التعلم دون استخدام المعلم خوارزمية الوسائل k.
لقد تأكدنا أنه بدلاً من طريقة الكوع ، من الأفضل استخدام معامل "صورة ظلية" وقيمة BIC (من امتداد GMM للوسائل k) لتحديد العدد الأمثل من المجموعات بصريًا.