تحية!
نحن هنا نصف عمل حقل معين ، ثم نصنع بعض الميزات الجميلة (كل شيء بسيط جدًا هنا).
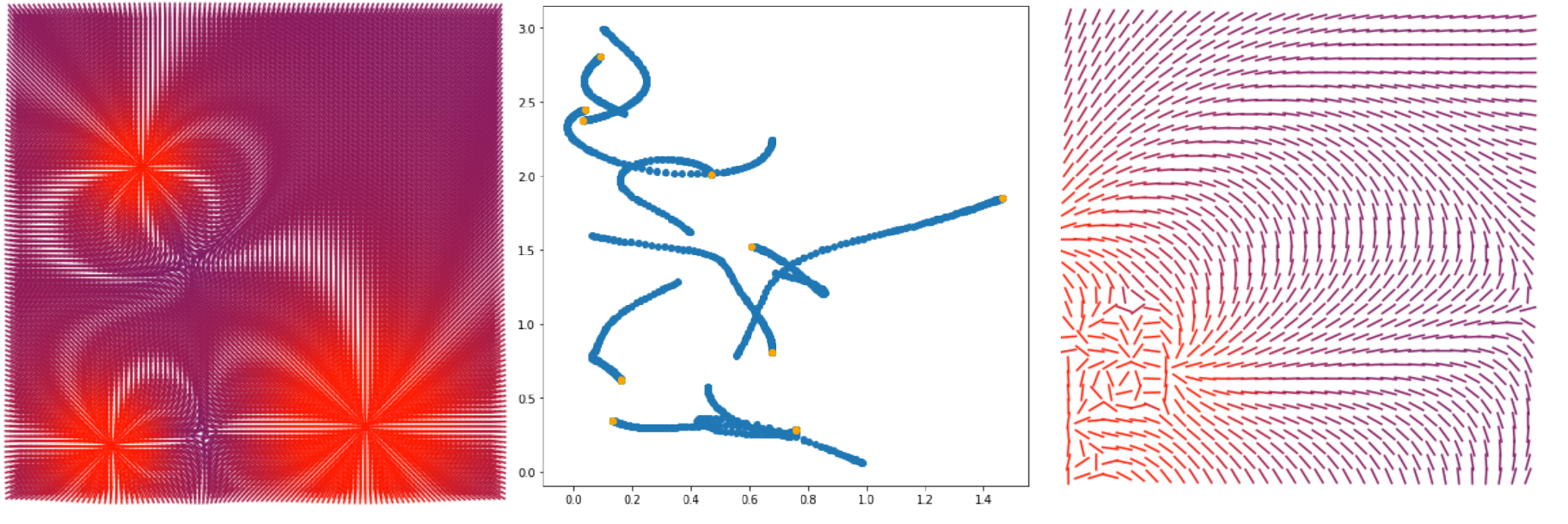
ماذا سيحدث في هذا المقال.
الحالة العامة:
- وصفنا القاعدة ، وهي العمل مع المتجهات (دراجة هوائية لأولئك الذين ليس لديهم شرير في متناول اليد)
- وصفنا النقطة المادية ومجال التفاعل
حالة خاصة (على أساس عام):
- لنقم بتصور لحقل المتجه لشدة المجال الكهرومغناطيسي (الصورتان الأولى والثالثة)
- سوف نتصور حركة الجزيئات في المجال الكهرومغناطيسي
مقابلتي تحت خفض!
برمجة الخلفية النظرية
سهم التوجيه
أساس كل الأسس هو ناقل (وخاصة في حالتنا). لذلك ، مع وصف المتجه سنبدأ. ماذا نحتاج؟ العمليات الحسابية على ناقل ، المسافة ، وحدة ، واثنين من الأشياء التقنية. ناقل سوف نرث من القائمة. هكذا يبدو التهيئة:
class Vector(list): def __init__(self, *el): for e in el: self.append(e)
وهذا هو ، الآن يمكننا إنشاء ناقل مع
v = Vector(1, 2, 3)
لنقم بإضافة عملية حسابية:
class Vector(list): ... def __add__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] + other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self + other
ممتاز:
v1 = Vector(1, 2, 3) v2 = Vector(2, 57, 23.2) v1 + v2 >>> [3, 59, 26.2]
نحدد بالمثل جميع العمليات الحسابية (الكود الكامل للمتجه سيكون أقل). أنت الآن بحاجة إلى وظيفة المسافة. يمكن أن أقوم بتقسيم ريفي (الإصدار 1 ، الإصدار 2) - لكن هذا ليس جميلًا ، لذا أعد تحديد عامل التشغيل٪:
class Vector(list): ... def __mod__(self, other): return sum((self - other) ** 2) ** 0.5
ممتاز:
v1 = Vector(1, 2, 3) v2 = Vector(2, 57, 23.2) v1 % v2 >>> 58.60068258988115
نحتاج أيضًا إلى طريقتين لتوليد ناقلات أسرع وإخراج جميل. لا يوجد شيء صعب هنا ، لذلك يوجد رمز فئة Vector بأكمله:
جميع المتجهات رمز الفئة class Vector(list): def __init__(self, *el): for e in el: self.append(e) def __add__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] + other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self + other def __sub__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] - other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self - other def __mul__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] * other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self * other def __truediv__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] / other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self / other def __pow__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] ** other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self ** other def __mod__(self, other): return sum((self - other) ** 2) ** 0.5 def mod(self): return self % Vector.emptyvec(len(self)) def dim(self): return len(self) def __str__(self): if len(self) == 0: return "Empty" r = [str(i) for i in self] return "< " + " ".join(r) + " >" def _ipython_display_(self): print(str(self)) @staticmethod def emptyvec(lens=2, n=0): return Vector(*[n for i in range(lens)]) @staticmethod def randvec(dim): return Vector(*[random.random() for i in range(dim)])
نقطة المواد
هنا ، من الناحية النظرية ، كل شيء بسيط - النقطة تحتوي على الإحداثيات والسرعة والتسارع (للبساطة). بالإضافة إلى ذلك ، لديها كتلة ومجموعة من المعلمات المخصصة (على سبيل المثال ، بالنسبة للحقل الكهرومغناطيسي ، فإن الشحنة لا تؤذينا ، لكن لا أحد يزعجك لتعيين حتى تدور).
التهيئة ستكون كما يلي:
class Point: def __init__(self, coords, mass=1.0, q=1.0 speed=None, **properties): self.coords = coords if speed is None: self.speed = Vector(*[0 for i in range(len(coords))]) else: self.speed = speed self.acc = Vector(*[0 for i in range(len(coords))]) self.mass = mass self.__params__ = ["coords", "speed", "acc", "q"] + list(properties.keys()) self.q = q for prop in properties: setattr(self, prop, properties[prop])
ومن أجل تحريك وجهة نظرنا وتسريعها وتسريعها ، سنكتب الطرق التالية:
class Point: ... def move(self, dt): self.coords = self.coords + self.speed * dt def accelerate(self, dt): self.speed = self.speed + self.acc * dt def accinc(self, force):
أحسنت ، النقطة نفسها هي القيام به.
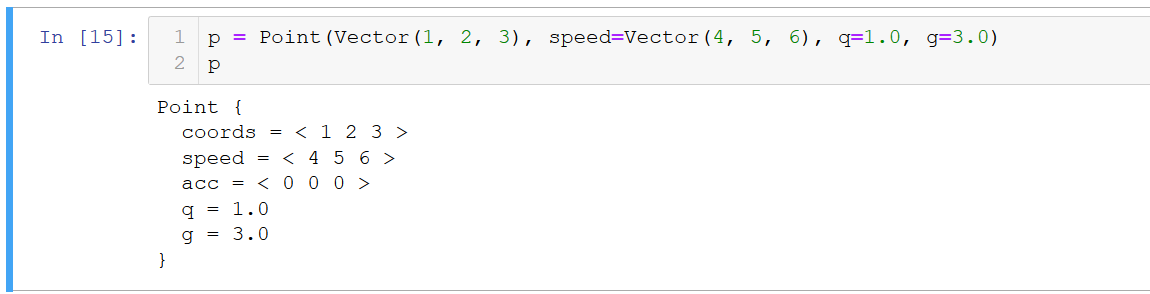
كود النقطة (مع الإخراج لطيفة) class Point: def __init__(self, coords, mass=1.0, q=1.0 speed=None, **properties): self.coords = coords if speed is None: self.speed = Vector(*[0 for i in range(len(coords))]) else: self.speed = speed self.acc = Vector(*[0 for i in range(len(coords))]) self.mass = mass self.__params__ = ["coords", "speed", "acc", "q"] + list(properties.keys()) self.q = q for prop in properties: setattr(self, prop, properties[prop]) def move(self, dt): self.coords = self.coords + self.speed * dt def accelerate(self, dt): self.speed = self.speed + self.acc * dt def accinc(self, force): self.acc = self.acc + force / self.mass def clean_acc(self): self.acc = self.acc * 0 def __str__(self): r = ["Point {"] for p in self.__params__: r.append(" " + p + " = " + str(getattr(self, p))) r += ["}"] return "\n".join(r) def _ipython_display_(self): print(str(self))
النتيجة:
مجال التفاعل
نحن نسمي مجال التفاعل كائناً يتضمن مجموعة من جميع النقاط المادية ويمارس القوة عليها. سننظر في حالة خاصة لكوننا الرائع ، لذلك سيكون لدينا تفاعل مخصص واحد (بالطبع ، هذا سهل التوسيع). أعلن المنشئ وأضف نقطة:
class InteractionField: def __init__(self, F):
الآن الجزء الممتع هو الإعلان عن وظيفة تعيد "التوتر" في تلك المرحلة. على الرغم من أن هذا المفهوم يشير إلى التفاعل الكهرومغناطيسي ، فإنه في حالتنا هو بعض المتجهات المجردة التي سنعمل على تحريكها. في هذه الحالة ، سيكون لدينا خاصية النقطة q ، في الحالة المعينة - تكلفة النقطة (بشكل عام - كل ما نريد ، حتى الموجه). إذن ما هو التوتر عند النقطة C؟ شيء مثل هذا:
وهذا هو ، والتوتر في هذه المرحلة
يساوي مجموع قوى جميع النقاط المادية التي تعمل على نقطة وحدة معينة.
class InteractionField: ... def intensity(self, coord): proj = Vector(*[0 for i in range(coord.dim())]) single_point = Point(Vector(), mass=1.0, q=1.0)
في هذه المرحلة ، يمكنك بالفعل رسم حقل متجه ، لكننا سنفعله في النهاية. الآن لنأخذ خطوة في تفاعلنا
class InteractionField: ... def step(self, dt): self.clean_acc() for p in self.points: p.accinc(self.intensity(p.coords) * pq) p.accelerate(dt) p.move(dt)
كل شيء بسيط هنا. لكل نقطة ، نحدد التوتر في هذه الإحداثيات ومن ثم تحديد القوة النهائية على نقطة المواد ETU:
تحديد الوظائف المفقودة.
كل رمز InteractionField class InteractionField: def __init__(self, F): self.points = [] self.F = F def move_all(self, dt): for p in self.points: p.move(dt) def intensity(self, coord): proj = Vector(*[0 for i in range(coord.dim())]) single_point = Point(Vector(), mass=1.0, q=1.0) for p in self.points: if coord % p.coords < 10 ** (-10): continue d = p.coords % coord fmod = self.F(single_point, p, d) * (-1) proj = proj + (coord - p.coords) / d * fmod return proj def step(self, dt): self.clean_acc() for p in self.points: p.accinc(self.intensity(p.coords) * pq) p.accelerate(dt) p.move(dt) def clean_acc(self): for p in self.points: p.clean_acc() def append(self, *args, **kwargs): self.points.append(Point(*args, **kwargs)) def gather_coords(self): return [p.coords for p in self.points]
حالة خاصة. حركة الجسيمات والتصور مجال ناقلات
لذلك وصلنا إلى الأكثر إثارة للاهتمام. لنبدأ بـ ...
نمذجة حركة الجزيئات في المجال الكهرومغناطيسي
u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 2 + 0.1)) for i in range(3): u.append(Vector.randvec(2) * 10, q=random.random() - 0.5)
في الواقع ، يجب أن يكون المعامل k مساويا لنوع المليارات (9 * 10 ^ (- 9)) ، لكن بما أنه سيتم إخماده بحلول الوقت t -> 0 ، فقد قررت على الفور جعل كل منهما أعدادًا كافية. لذلك ، في الفيزياء لدينا ك = 300'000. ومع كل شيء آخر ، أعتقد أنه واضح.
ص ** 2 + 0.1
- هذا هو تجنب القسمة على 0. بالطبع ، يمكننا الخلط ، ونحل نظامًا كبيرًا من الاختلافات ، لكن أولاً لا توجد معادلة للحركة لأكثر من جثتين ، وثانياً لا يتم تضمين ذلك بوضوح في مفهوم "مقالة للمبتدئين"
بعد ذلك ، نضيف عشر نقاط (مساحة ثنائية الأبعاد) مع إحداثيات من 0 إلى 10 على طول كل محور. أيضًا ، نحن نمنح كل نقطة تكلفة من -0.25 إلى 0.25. الآن قم بعمل حلقة وارسم النقاط وفقًا للإحداثيات (والتتبعات):
X, Y = [], [] for i in range(130): u.step(0.0006) xd, yd = zip(*u.gather_coords()) X.extend(xd) Y.extend(yd) plt.figure(figsize=[8, 8]) plt.scatter(X, Y) plt.scatter(*zip(*u.gather_coords()), color="orange") plt.show()
ما كان يجب أن يحدث:
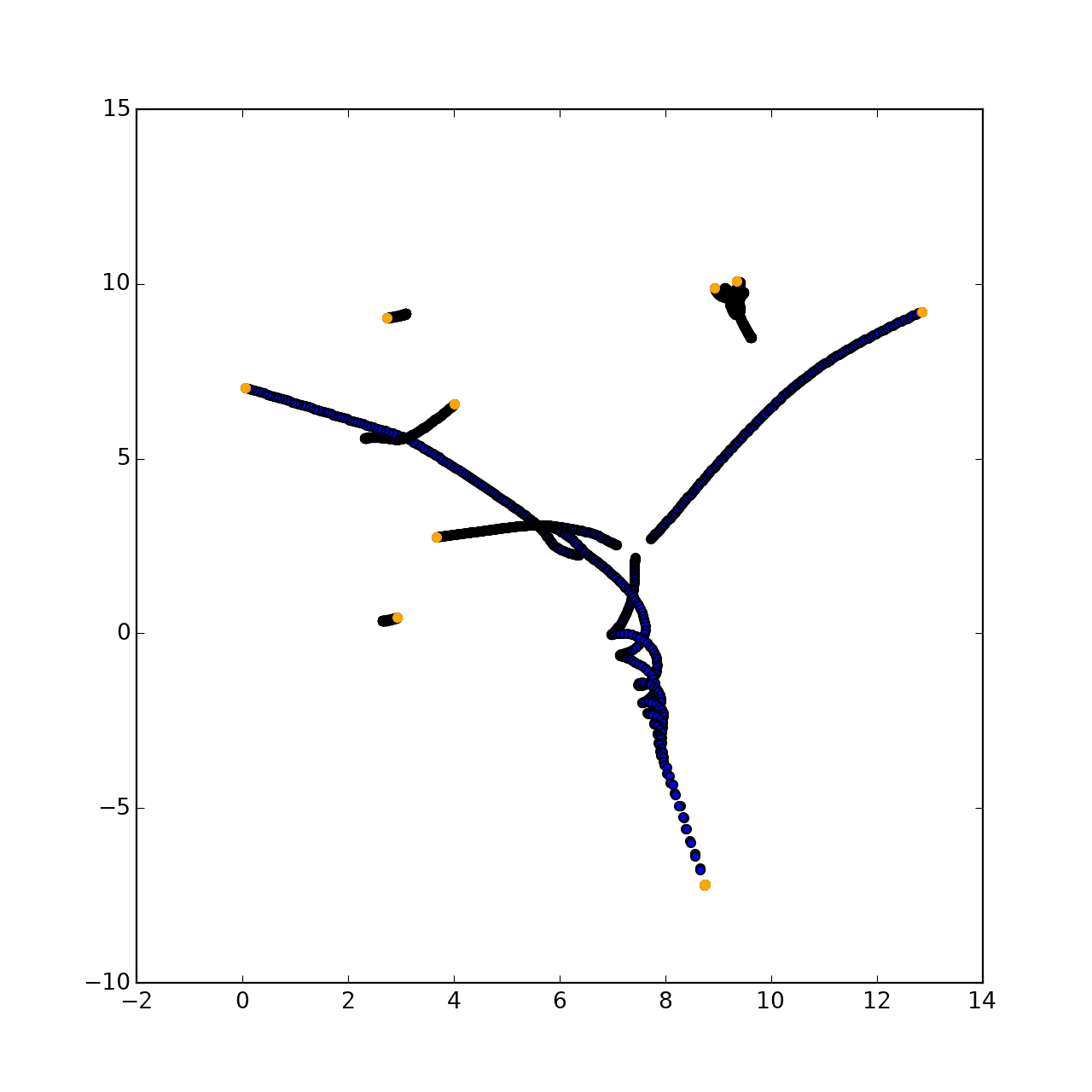
في الواقع ، سيكون هناك رسم عشوائي تمامًا ، لأن مسار كل نقطة لا يمكن التنبؤ به في لحظة تطور الميكانيكا.
ناقل مجال التصور
كل شيء بسيط هنا. نحن بحاجة إلى الذهاب من خلال الإحداثيات مع بعض الخطوة ورسم متجه في كل منهم في الاتجاه الصحيح.
fig = plt.figure(figsize=[5, 5]) res = [] STEP = 0.3 for x in np.arange(0, 10, STEP): for y in np.arange(0, 10, STEP): inten = u.intensity(Vector(x, y)) F = inten.mod() inten /= inten.mod() * 4
تقريبا هذا الاستنتاج كان ينبغي الحصول عليها.
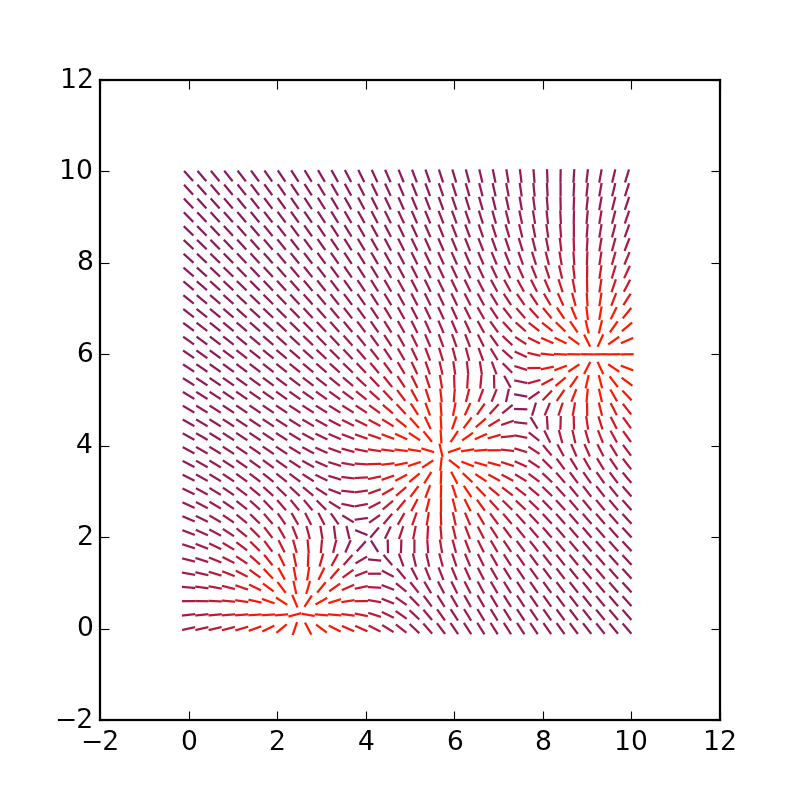
يمكنك إطالة المتجهات نفسها ، استبدل * 4 بـ * 1.5:
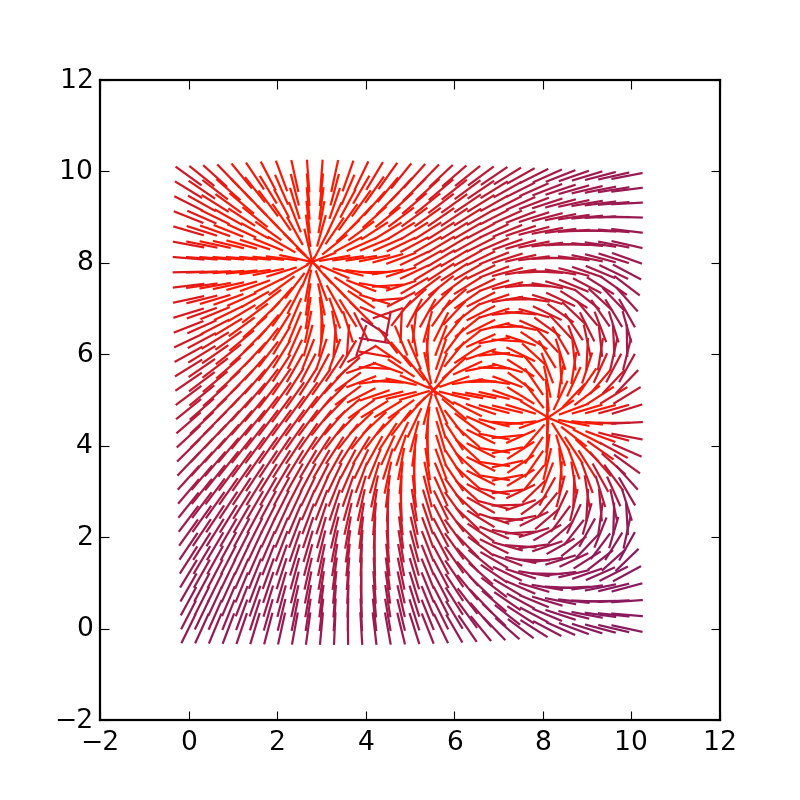
نحن نلعب مع البعد والنمذجة
إنشاء مساحة ثلاثية الأبعاد مع 200 نقطة وتفاعل لا يعتمد على مربع المسافة ، ولكن على الدرجة الرابعة.
u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 4 + 0.1)) for i in range(200): u.append(Vector.randvec(5) * 10, q=random.random() - 0.5)
الآن يتم تحديد جميع الإحداثيات والسرعات ، وما إلى ذلك في خمسة أبعاد. الآن دعونا نمثل شيئًا:
velmod = 0 velocities = [] for i in range(100): u.step(0.0005) velmod = sum([p.speed.mod() for p in u.points])
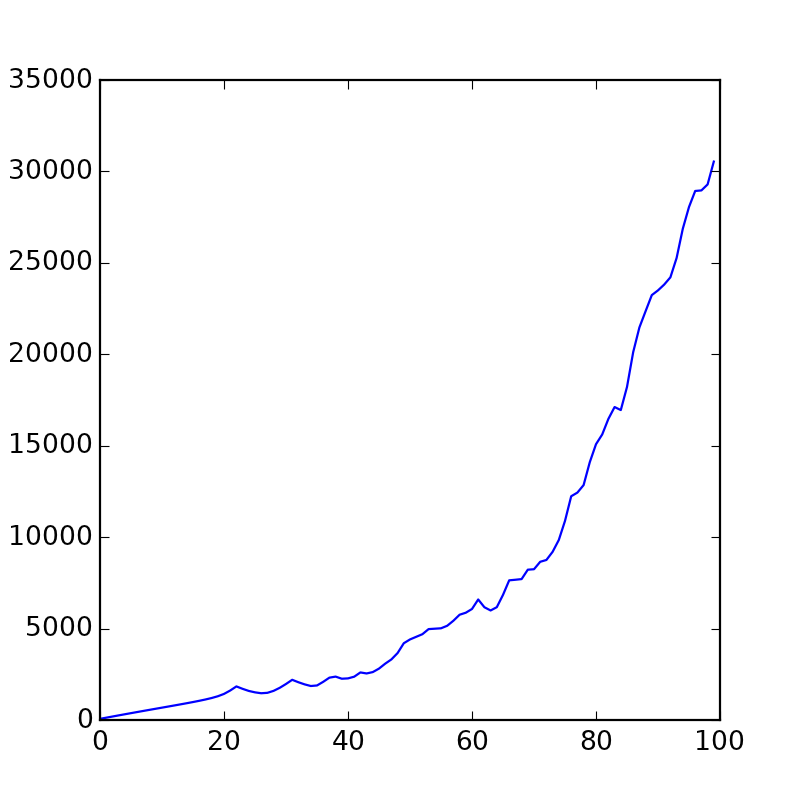
هذا رسم بياني لمجموع جميع السرعات في أي وقت. كما ترون ، مع مرور الوقت تتسارع ببطء.
حسنًا ، لقد كانت هذه تعليمات قصيرة حول كيفية صنع شيء بسيط. ولكن ماذا يحدث إذا كنت تلعب مع الزهور:
كل رمز مع التجريبي import random class Vector(list): def __init__(self, *el): for e in el: self.append(e) def __add__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] + other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self + other def __sub__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] - other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self - other def __mul__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] * other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self * other def __truediv__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] / other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self / other def __pow__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] ** other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self ** other def __mod__(self, other): return sum((self - other) ** 2) ** 0.5 def mod(self): return self % Vector.emptyvec(len(self)) def dim(self): return len(self) def __str__(self): if len(self) == 0: return "Empty" r = [str(i) for i in self] return "< " + " ".join(r) + " >" def _ipython_display_(self): print(str(self)) @staticmethod def emptyvec(lens=2, n=0): return Vector(*[n for i in range(lens)]) @staticmethod def randvec(dim): return Vector(*[random.random() for i in range(dim)]) class Point: def __init__(self, coords, mass=1.0, q=1.0, speed=None, **properties): self.coords = coords if speed is None: self.speed = Vector(*[0 for i in range(len(coords))]) else: self.speed = speed self.acc = Vector(*[0 for i in range(len(coords))]) self.mass = mass self.__params__ = ["coords", "speed", "acc", "q"] + list(properties.keys()) self.q = q for prop in properties: setattr(self, prop, properties[prop]) def move(self, dt): self.coords = self.coords + self.speed * dt def accelerate(self, dt): self.speed = self.speed + self.acc * dt def accinc(self, force): self.acc = self.acc + force / self.mass def clean_acc(self): self.acc = self.acc * 0 def __str__(self): r = ["Point {"] for p in self.__params__: r.append(" " + p + " = " + str(getattr(self, p))) r += ["}"] return "\n".join(r) def _ipython_display_(self): print(str(self)) class InteractionField: def __init__(self, F): self.points = [] self.F = F def move_all(self, dt): for p in self.points: p.move(dt) def intensity(self, coord): proj = Vector(*[0 for i in range(coord.dim())]) single_point = Point(Vector(), mass=1.0, q=1.0) for p in self.points: if coord % p.coords < 10 ** (-10): continue d = p.coords % coord fmod = self.F(single_point, p, d) * (-1) proj = proj + (coord - p.coords) / d * fmod return proj def step(self, dt): self.clean_acc() for p in self.points: p.accinc(self.intensity(p.coords) * pq) p.accelerate(dt) p.move(dt) def clean_acc(self): for p in self.points: p.clean_acc() def append(self, *args, **kwargs): self.points.append(Point(*args, **kwargs)) def gather_coords(self): return [p.coords for p in self.points]
من المحتمل أن يكون المقال التالي حول النمذجة الأكثر تعقيدًا ، وربما معادلات السوائل و Navier-Stokes.
محدث: مقال كتبه زميلي
هنابفضل
MomoDev للمساعدة في تقديم الفيديو.