🧕🏿 🧑🏿‍🤝‍🧑🏽 ❕ ومع ذلك ، لماذا تعتبر Posit بديلاً يستحق IEEE 754 🤐 🙋🏾 👩‍👩‍👦‍👦

تم إعلان شهر Posit على Habré مفتوحًا ، مما يعني أنه لا يمكنني المرور وتجاهل الانتقادات التي تعرضت لها. في السلسلة السابقة:

يمكن أن يساعدنا نهج جديد في التخلص من حسابات الفاصلة العائمة
الوضع الحسابي: هزيمة نقطة عائمة في مجالها الخاص. الجزء 1
الوضع الحسابي: هزيمة نقطة عائمة في مجالها الخاص. الجزء 2
تحديات موقف الكبار

أعتقد أن العديد منكم يمكن أن يتذكر على الفور حالة واحدة على الأقل من التاريخ عندما تعرضت الأفكار الثورية وقت تشكيلها إلى الرفض من قبل مجتمع من الخبراء. كقاعدة عامة ، فإن خطأ مثل هذا السلوك هو الأمتعة الواسعة للمعرفة المتراكمة بالفعل والتي لا تسمح بالنظر إلى المشكلة القديمة في ضوء جديد. وبالتالي ، فإن الفكرة الجديدة تفقد من حيث الخصائص للنهج الثابتة ، لأنه يتم تقييمها فقط من خلال تلك المقاييس التي كانت تعتبر مهمة في المرحلة السابقة من التطوير.

هذا هو بالضبط نوع النفور الذي يواجهه تنسيق Posit اليوم: غالبًا ما ينظر النقاد ببساطة إلى "الاتجاه الخاطئ" ويستخدمون Posit في تجاربهم بطريقة خاطئة. في هذه المقالة سأحاول شرح السبب.

لقد تم ذكر مزايا Posit بالفعل كثيرًا: الأناقة الرياضية ، والدقة العالية في القيم ذات الأس المنخفض ، ومجموعة واسعة من القيم ، وتمثيل ثنائي واحد فقط لل NaN والصفر ، وغياب القيم دون الطبيعية ، ومكافحة الفائض / التدفق الزائد. لقد تم التعبير عن النقاد قليلاً: دقة عديمة الفائدة لقيم كبيرة جدًا أو صغيرة جدًا ، وتنسيق تمثيل ثنائي معقد ، وبطبيعة الحال ، نقص دعم الأجهزة.

لا أريد تكرار الحجج التي سبق أن قلتها ؛ وبدلاً من ذلك ، سأحاول التركيز على الجانب الذي يتم تجاهله كقاعدة عامة.

لقد تغيرت قواعد اللعبة

يصف معيار IEEE 754 أرقام الفاصلة العائمة التي تم تنفيذها في Intel 8087 منذ ما يقرب من 40 عامًا. حسب معايير صناعتنا ، هذا وقت لا يصدق ؛ لقد تغير كل شيء منذ ذلك الحين: أداء المعالج ، تكلفة الذاكرة ، أحجام البيانات وحجم العمليات الحسابية. تم تطوير تنسيق Posit ليس فقط كأفضل إصدار من IEEE 754 ، ولكن كنهج للعمل مع الأرقام التي تلبي المتطلبات الجديدة للوقت.

ظلت المهمة رفيعة المستوى كما هي - نحتاج جميعًا إلى حسابات فعالة على مجال الأرقام المنطقية بأقل قدر من فقدان الدقة. لكن الظروف التي يتم فيها حل المهمة تتغير بشكل جذري.

أولاً ، تغيرت أولويات التحسين. قبل 40 عامًا ، كان أداء الكمبيوتر يعتمد بالكامل تقريبًا على أداء المعالج. اليوم ، فإن أداء معظم الحوسبة يقع في الذاكرة. للتحقق من ذلك ، ما عليك سوى إلقاء نظرة على المجالات الرئيسية لتطوير معالجات العقود الأخيرة: التخزين المؤقت على ثلاثة مستويات ، تنفيذ المضاربة ، خطوط الأنابيب للحسابات ، التنبؤ بالفرع. تهدف جميع هذه الأساليب إلى تحقيق أداء عالٍ في ظروف الحوسبة السريعة والوصول البطيء إلى الذاكرة.

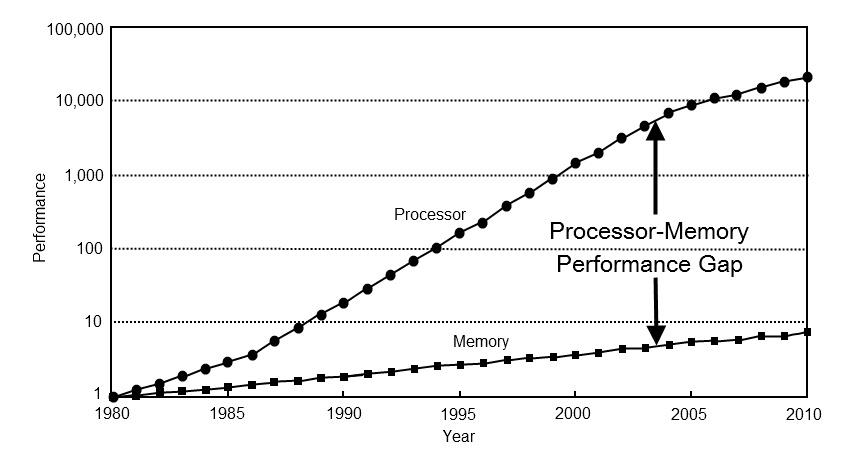
ثانياً ، احتل شرط جديد مكان الصدارة وهو الاستهلاك الفعال للطاقة. على مدى العقود الماضية ، تطورت تكنولوجيا القياس الأفقي للحوسبة كثيرًا لدرجة أننا بدأنا لا نهتم كثيرًا بسرعة هذه الحسابات ، بل بفاتورة الكهرباء. هنا يجب أن أؤكد على جزء مهم لفهم. من وجهة نظر كفاءة استخدام الطاقة ، تكون الحسابات رخيصة ، لأن سجلات المعالج قريبة جدًا من أجهزة الكمبيوتر الخاصة به. سيكون دفع تكلفة نقل البيانات أكثر تكلفة بكثير ، سواء بين المعالج والذاكرة (× 100) ، وعلى مسافات طويلة (× 1000 ...).

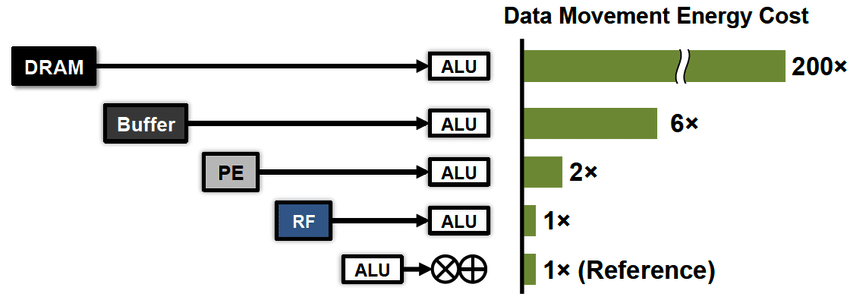
فيما يلي مثال واحد فقط لمشروع علمي تخطط Posit لاستخدامه:

تولد شبكة التلسكوبات هذه 200 بتة من البيانات في الثانية ، حيث تستهلك معالجتها طاقة محطة طاقة صغيرة - 10 ميجاوات . من الواضح ، بالنسبة لمثل هذه المشاريع ، فإن تقليل استهلاك البيانات والطاقة أمر بالغ الأهمية.

إلى البداية

إذن ما الذي يوفره معيار Posit؟ لفهم هذا ، تحتاج إلى العودة إلى بداية المناقشة وفهم المقصود من دقة أرقام الفاصلة العائمة.

هناك بالفعل جانبان مختلفان يتعلقان بالدقة. الجانب الأول هو دقة الحسابات - كم تنحرف نتائج العمليات الحسابية خلال العمليات المختلفة. الجانب الثاني هو دقة العرض - مقدار القيمة الأصلية المشوهة في وقت التحويل من حقل الأرقام المنطقية إلى حقل أرقام الفاصلة العائمة بتنسيق معين.

الآن ستكون هناك لحظة مهمة للتوعية. Posit هو في المقام الأول تنسيق لتمثيل الأرقام المنطقية ، وليس وسيلة لأداء العمليات عليها. وبعبارة أخرى ، Posit هو تنسيق ضغط عقلاني ضياع. ربما تكون قد سمعت الادعاء بأن Posit 32 بت هو بديل جيد لـ 64 بت Float. لذلك ، نحن نتحدث عن خفض كمية البيانات المطلوبة لتخزين ونقل نفس مجموعة الأرقام إلى النصف. ذاكرة أقل مرتين - استهلاك طاقة أقل مرتين تقريبًا وأداء عال للمعالج بسبب انخفاض توقعات الوصول إلى الذاكرة.

الطرف الثاني من العصا

يجب أن يكون لديك هنا سؤال منطقي: ما الهدف من تمثيل الأرقام المنطقية بكفاءة إذا لم تسمح بإجراء العمليات الحسابية بدقة عالية.

في الواقع ، هناك طريقة لإجراء حسابات دقيقة ، ويسمى Quire. هذا تنسيق آخر لتمثيل الأرقام المنطقية ، المرتبطة ارتباطًا وثيقًا مع Posit. بخلاف Posit ، تم تصميم تنسيق Quire خصيصًا لإجراء العمليات الحسابية ولتخزين القيم الوسيطة في السجلات ، وليس في الذاكرة الرئيسية.

باختصار ، Quire ليس أكثر من بطارية عدد صحيح واسع (حساب النقطة الثابتة). الوحدة ، باعتبارها تمثيل ثنائي لـ Quire ، تتوافق مع الحد الأدنى للقيمة الإيجابية لـ Posit. تتطابق قيمة Quire القصوى مع قيمة Posit القصوى. كل قيمة Posit لها تمثيل فريد في Quire دون فقدان الدقة ، ولكن لا يمكن تمثيل كل قيمة Quire في Posit دون فقدان الدقة.

فوائد Quire واضحة. إنها تسمح لك بإجراء العمليات بدقة أعلى بشكل لا يضاهى من Float ، ولن يكون هناك أي فقدان للدقة على الإطلاق لعمليات الضرب والضرب. السعر الذي يتعين عليك دفعه مقابل ذلك هو سجلات المعالج الواسعة (Posit 32 بت مع es = 2 تتوافق مع 512 بت Quire) ، لكن هذه ليست مشكلة خطيرة للمعالجات الحديثة. وإذا كانت الحوسبة قبل أكثر من 40 عامًا تبدو صحيحة غير مقبولة ، فقد أصبحت اليوم بديلاً مناسبًا للوصول الواسع إلى الذاكرة.

وضع اللغز معا

وبالتالي ، لا تقدم Posit معيارًا جديدًا فقط في شكل بديل لـ Float / Double ، بل يقدم أيضًا طريقة جديدة للتعامل مع الأرقام. على عكس Float - وهو تمثيل فردي يحاول إيجاد حل وسط بين الدقة وكفاءة التخزين والكفاءة الحسابية ، يوفر Posit تنسيقين مختلفين للعرض ، أحدهما لتخزين ونقل الأرقام - وضع نفسه والآخر لإجراء العمليات الحسابية والوسيطة القيم - Quire.

عندما نحل المشكلات العملية باستخدام أرقام الفاصلة العائمة ، من وجهة نظر المعالج ، يمكن تمثيل العمل معهم كمجموعة من الإجراءات التالية:

قراءة قيم الأرقام من الذاكرة.
أداء بعض تسلسل العمليات. في بعض الأحيان يكون عدد العمليات كبيرًا جدًا. في هذه الحالة ، يتم تخزين جميع القيم المتوسطة للحسابات في السجلات.
اكتب نتيجة العمليات على الذاكرة.

مع Float / Double ، يتم فقد الدقة في كل عملية. مع Posit + Quire ، فإن فقدان الدقة أثناء الحساب لا يكاد يذكر. يتم فقدها فقط في المرحلة الأخيرة ، في وقت تحويل قيمة Quire إلى Posit. هذا هو السبب في أن معظم مشاكل "تراكم الأخطاء" في Posit + Quire ليست ببساطة ذات صلة.

على عكس Float / Double ، عند استخدام Posit + Quire ، يمكننا عادةً تقديم تمثيل أكثر إحكاما للأرقام. نتيجة لذلك - وصول أسرع إلى البيانات من الذاكرة (أداء أفضل) وتخزين ونقل معلومات أكثر كفاءة.

نسبة مولر

كإظهار مرئي ، سأقدم مثالًا واحدًا فقط - علاقة تكرار Muller الكلاسيكية ، التي تم اختراعها خصيصًا لإظهار كيف أن تراكم الأخطاء في حسابات الفاصلة العائمة يشوه بشكل جذري نتيجة الحسابات.

في حالة استخدام الحساب بدقة تعسفية ، يجب تقليل تسلسل التكرار إلى قيمة 5. في حالة حساب النقطة العائمة ، يكون السؤال هو فقط حول التكرار الذي ستبدأ به نتائج الحساب بانحراف كبير بدرجة غير كافية.

لقد أجريت تجربة لـ IEEE 754 بدقة مفردة ومزدوجة ، وكذلك مع Posit + Quire 32 بت. تم إجراء العمليات الحسابية في حساب Quire ، ولكن تم تحويل كل قيمة في الجدول إلى Posit.

نتائج التجربة

 
  # تعويم (32) مزدوج (64) موقف (32)
 ------------------------------------------------
  0 4.000000 4.000000 4
  1 4.250000 4.250000 4.25
  2 4.470589 4.470588 4.470588237047195
  3 4.644745 4.644737 4.644736856222153
  4 4.770706 4.770538 4.770538240671158
  5 4.859215 4.855701 4.855700701475143
  6 4.983124 4.910847 4.91084748506546
  7 6.395432 4.945537 4.94553741812706
  8 27.632629 4.966962 4.966962575912476
  9 86.993759 4.980042 4.980045706033707
 10 99.255508 4.987909 4.98797944188118
 11 99.962585 4.991363 4.992770284414291
 12 99.998131 4.967455 4.99565589427948
 13 99.999908 4.429690 4.997391253709793
 14 100.000000 -7.817237 4.998433947563171
 15 100.000000 168.939168 4.9990600645542145
 16 100.000000 102.039963 4.999435931444168
 17 100.000000 100.099948 4.999661535024643
 18 100.000000 100.004992 4.999796897172928
 19 100.000000 100.000250 4.999878138303757
 20 100.000000 100.000012 4.999926865100861
 21 100.000000 100.000001 4.999956130981445
 22 100.000000 100.000000 4.999973684549332
 23 100.000000 100.000000 4.9999842047691345
 24 100.000000 100.000000 4.999990522861481
 25 100.000000 100.000000 4.999994307756424
 26 100.000000 100.000000 4.999996602535248
 27 100.000000 100.000000 4.999997943639755
 28 100.000000 100.000000 4.999998778104782
 29 100.000000 100.000000 4.99999925494194
 30 100.000000 100.000000 4.999999552965164
 31 100.000000 100.000000 4.9999997317790985
 32 100.000000 100.000000 4.999999850988388
 33 100.000000 100.000000 4.999999910593033
 34 100.000000 100.000000 4.999999940395355
 35 100.000000 100.000000 4.999999970197678
 36 100.000000 100.000000 4.999999970197678
 37 100.000000 100.000000 5
 38 100.000000 100.000000 5
 39 100.000000 100.000000 5
 40 100.000000 100.000000 5
 41 100.000000 100.000000 5
 42 100.000000 100.000000 5
 43 100.000000 100.000000 5
 44 100.000000 100.000000 5
 45 100.000000 100.000000 5
 46 100.000000 100.000000 5
 47 100.000000 100.000000 5
 48 100.000000 100.000000 5
 49 100.000000 100.000000 5
 50 100.000000 100.000000 5
 51 100.000000 100.000000 5
 52 100.000000 100.000000 5.000000059604645
 53 100.000000 100.000000 5.000000983476639
 54 100.000000 100.000000 5.000019758939743
 55 100.000000 100.000000 5.000394910573959
 56 100.000000 100.000000 5.007897764444351
 57 100.000000 100.000000 5.157705932855606
 58 100.000000 100.000000 8.057676136493683
 59 100.000000 100.000000 42.94736957550049
 60 100.000000 100.000000 93.35784339904785
 61 100.000000 100.000000 99.64426326751709
 62 100.000000 100.000000 99.98215007781982
 63 100.000000 100.000000 99.99910736083984
 64 100.000000 100.000000 99.99995517730713
 65 100.000000 100.000000 99.99999809265137
 66 100.000000 100.000000 100
 67 100.000000 100.000000 100
 68 100.000000 100.000000 100
 69 100.000000 100.000000 100
 70 100.000000 100.000000 100

كما ترون من الجدول ، فإن Float 32 بت يستسلم بالفعل بالقيمة السابعة ، و Float 64 بت يستمر حتى التكرار الرابع عشر. في الوقت نفسه ، ترجع حسابات Posit باستخدام Quire إلى نتيجة ثابتة تصل إلى 58 تكرارًا!

أخلاقية

بالنسبة للعديد من الحالات العملية ، وعند استخدامها بشكل صحيح ، سيتيح لك تنسيق Posit حقًا حفظ الذاكرة من ناحية ، وضغط الأرقام بشكل أفضل من Float ، ومن ناحية أخرى يوفر دقة حسابية أفضل بفضل Quire.

ولكن هذه ليست سوى نظرية! عندما يتعلق الأمر بالدقة أو الأداء ، قم دائمًا بإجراء الاختبارات قبل الوثوق العمياء بأسلوب أو بآخر. في الواقع ، في الواقع العملي ، سوف تتحول حالتك الخاصة إلى حالة استثنائية أكثر بكثير من الناحية النظرية.

حسنًا ، لا تنسَ قانون كلارك الأول (التفسير المجاني): عندما يزعم خبير محترم وذوي خبرة أن فكرة جديدة ستنجح ، فمن المؤكد أنه على حق. عندما يدعي أن الفكرة الجديدة لن تنجح ، فمن المرجح أن يكون مخطئًا. لا أعتبر نفسي خبيراً ذا خبرة يسمح لك بالاعتماد على رأيي ، لكنني أطلب منك أن تكون حذراً من انتقاد حتى الأشخاص ذوي الخبرة والاحترام. بعد كل شيء ، الشيطان هو في التفاصيل ، وحتى الأشخاص ذوي الخبرة يمكن أن تفوت عليهم.