مشكلة المشكلة

في المهمة الشهيرة مع العملات المعدنية ، والتي تحتاج إلى حساب التغيير ، كما تعلمون ، هناك مشكلتان .
- الأول هو عدد فئات العملات ،
- والثاني هو عدد الأرقام التي تمثل التغيير.
ولكل من هاتين الكميتين تأثيرًا كبيرًا على حمل آلة Turing ، والتي تشارك فعليًا في الحساب.
إن إدراك أن الشخص لديه إثنين من التبعيات في وقت واحد غير مقبول حتى في مجتمع مدمني الكحول. لذلك ، قررت أن ألعبها بشكل آمن وأن أتخلص من إحدى هذه المشكلات مسبقًا. الطريقة التي سيكون بها هذا هو عدد فئات العملات.

باختصار ، يوصف جوهر المشكلة على النحو التالي: الاعتماد الأسي. أي أن إصدار نوع جديد من العملات المعدنية من فئة غير موجودة يستلزم زيادة مضاعفة في عدد مجموعات العملات. طائفة أخرى - ضعف ذلك ، وهكذا إلى اللانهاية الشرطية. مع التضخم الهائل ، عندما يتم إصدار عملات معدنية / فواتير جديدة في كثير من الأحيان بما فيه الكفاية ، سيكون عليك شراء جهاز كمبيوتر أكثر قوة لحل المشكلة. وأين يمكن الحصول على المال من أجل ذلك في تضخم متسارع؟

لذلك ، الحل الذي هو في الواقع بسيط جدا.
إذا كنت تتخيل شريحة من صفر إلى C (تغيير) مع وجود نقاط عليها تقابل فئات العملات ، فإن أي شخص ذكي سيرى الصورة التالية تقريبًا:

حسنا ، ربما بألوان مختلفة.
فماذا يمكن أن نقول عن النقاط الحمراء؟ بالطبع ، حقيقة أن الرقم المقابل لأي من هذه النقطة هو المبلغ الذي يمكن أن نعطيه في شكل التغيير. ومع عملة واحدة. ربما رأى شخص ما شيئًا آخر ، لكنني كفنان ، استثمر هذا المعنى بالضبط. وكفنان ، سأرسم نقطة أخرى في هذه الصورة تقابل مجموع النقطة الأولى (من اليسار إلى اليمين) بنقطة واحدة (كل شيء صحيح: سيضاعف القيمة الاسمية). أرسم بنفس اللون ، لأن نقطة جديدة تعني نفس الشيء - يمكن أن يكون هذا المبلغ أيضًا تغييرًا.

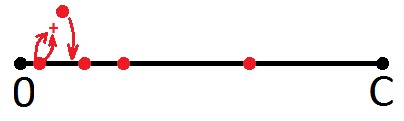
بعد ذلك ، آخذ النقطة الأولى وألخص النقطة الثانية ، حتى لو كانت النقطة الثانية هي المبلغ السابق (هذا لا يهم ، لأن جميع النقاط متساوية هنا). سوف أضع نقطة جديدة على الجزء مرة أخرى.

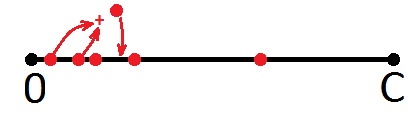
إذا تجاوزت النقطة الجديدة حدود الشريحة ، فلن نرسم أي شيء ، لكننا نرجع إلى بداية المقطع ونأخذ النقطة التالية ، وهي النقطة الثانية. كذلك نفس الشيء (من اليسار إلى اليمين).
في الواقع ، عندما تتحول النقطة C (أذكرك ، هذا تغيير) إلى اللون الأحمر ، يمكننا أن نفترض أنه تم العثور على حل. ويمكنك متابعة الدورة الكاملة والعثور على الحل الأمثل بحيث يكون عدد العملات المعدنية ضئيلًا.

من وجهة نظر البرمجة ، هناك دورتان. الأول هو من 0 إلى C / 2 (ليست هناك حاجة لأخذ النقطة الأولى من C / 2 أكبر ، لأن النقطة الثانية دائمًا أكبر من الأولى وفي المجموع ستتجاوز حدود المقطع). تم بناء الدورة الثانية في الأول ، وتبدأ من نفس النقطة التي تشير إليها الدورة الخارجية إلى أن يترك المجموع حدود القطاع.
في الواقع ، هذا تمثال نصفي: نحن لا نفقد خيارًا واحدًا ، ونحن نضمن إيجاد الحل الأمثل ، أو سنخلص إلى أنه لا يوجد حل.

دعنا نحسب كمية التكرار داخل حلقاتنا. في الدورة الخارجية يكون C / 2 ، في الدورة الداخلية هو نفسه تقريبا. اضرب C / 2 * C / 2 = (C ^ 2) / 4. الدائرية إلى C مربعة. هذا هو الخيار الأسوأ عندما يتكون قطاعنا بالكامل من نقاط حمراء. إذا كانت هناك مسافات بين النقاط ، فإن عدد التكرارات سينخفض ​​بشكل كبير.
كما ترون ، عند تحديد صعوبة حل المشكلة ، لا نستخدم عدد فئات العملة. هذه القيمة لا تؤثر بشكل مباشر على تعقيد الحل. تؤثر قيم هذه الطوائف ، قل عملة واحدة سنت ، وجعل هذا الجزء أحمر بالكامل. لذلك ، من الأفضل عدم أخذ هذه العملة في الاعتبار ، وفي نهاية القرار ، خذ النقطة الحمراء الأقرب إلى C ورسم أعلى سنت واحد. ولكن هذه هي بالفعل لحظة تحسين الخوارزمية ، وهي خارج نطاق هذه المقالة.

هذا في الواقع كل ما أود قوله. يمكن العثور على نسخة عاملة من البرنامج هنا: رابط github

1. في ملف init.h ، عيّن COINS_NUMBER - عدد فئات العملات ، و AMOUNT - مقدار التغيير.
2. في الملف coinc.c حدد فئات العملات في مجموعة العملات.
3. ضمن نظام Linux ، قم بتشغيل make_sh.
4. قم بتشغيل برنامج التطبيق للتنفيذ


دعني أعطيك بعض الأمثلة المضحكة. تخيل أنه في بعض البلاد وصل علماء الرياضيات إلى السلطة ووضعوا في تداول 32 طائفة من العملات المعدنية: 2 ، 3 ، 5 ، 7 ، 11 ، 13 ، 17 ، 19 ... 131. من أجل راحة العد ، تم اختيار الأعداد الأولية فقط (حسنًا ، ليس مضحكا ؟). وللتأكد من نجاح الإصلاح النقدي ، أرسلوا رسلاً في متجر المراسلة لتبادل فاتورة رقم 5333 (أيضًا رقم أولي). قام أمين الصندوق في حل قديم وحيد النواة بحل المشكلة: 39 قطعة نقدية بقيمة اسمية تبلغ 131 فيثاغورس ، عملة واحدة 127 و 97. استغرق الحساب 3 ثوانٍ وأكثر بقليل من الذاكرة. وأبلغت الحكومة أن الناس راضون عن الإصلاح ، ويعتقد بسرعة.


ومثال يصعب التحقق منه. عملات معدنية ، مائة فئة في هذا التسلسل الغريب: 0101 ، 0202 ، 0303 ... 9898 ، 9999 ، 100100. مقدار التغيير: 101010. استغرق البحث عن حل 1 ثانية وأكثر بقليل من ميغابايت من الذاكرة. لكن القرار ، في الواقع ، ليس كذلك ، فمن المستحيل جمع هذا المبلغ بهذه القطع النقدية. باستخدام العملات المعدنية نفسها ، يستغرق التحقق من المليون 1 26 ميغا بايت ومئات الثواني ، مما يدل على الاعتماد الأسي على المبلغ ، ولكن ليس على عدد فئات العملة.